导数处理极值点偏移问题

第二讲 导数应用-------极值点偏移问题的处理策略及探究

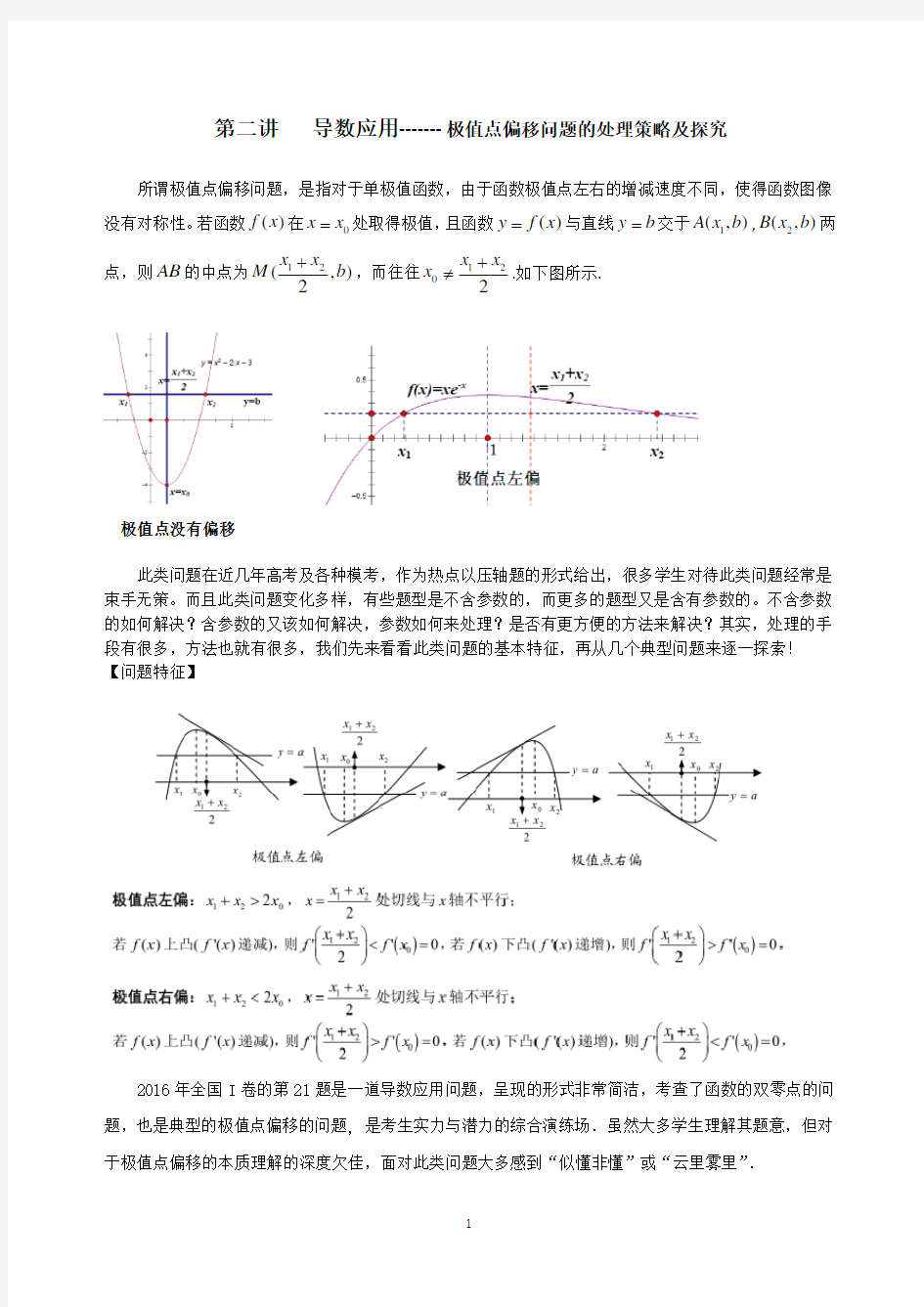
所谓极值点偏移问题，是指对于单极值函数，由于函数极值点左右的增减速度不同，使得函数图像

没有对称性。若函数()f x 在0x x =处取得极值，且函数()y f x =与直线y b =交于1(,)A x b ,2(,)B x b 两点，则AB 的中点为12(

,)2x x M b +，而往往1202

x x

x +≠.如下图所示.

极值点没有偏移

此类问题在近几年高考及各种模考，作为热点以压轴题的形式给出，很多学生对待此类问题经常是束手无策。而且此类问题变化多样，有些题型是不含参数的，而更多的题型又是含有参数的。不含参数的如何解决？含参数的又该如何解决，参数如何来处理？是否有更方便的方法来解决？其实，处理的手段有很多，方法也就有很多，我们先来看看此类问题的基本特征，再从几个典型问题来逐一探索！ 【问题特征】

2016年全国I 卷的第21题是一道导数应用问题，呈现的形式非常简洁，考查了函数的双零点的问题，也是典型的极值点偏移的问题, 是考生实力与潜力的综合演练场．虽然大多学生理解其题意，但对于极值点偏移的本质理解的深度欠佳，面对此类问题大多感到“似懂非懂”或“云里雾里”．

一、试题再现及解析 （一）题目

（2016年全国I 卷）已知函数()()()2

21x

f x x e a x =-+-有两个零点．

(1)求a 的取值范围；

(2)设12,x x 是()f x 的两个零点，证明：122x x +<．

本题第（1）小题含有参数的函数()f x 有两个零点，自然想到研究其单调性，结合零点存在性定理求得a 的取值范围是()0,+∞．第（2）小题是典型的极值点偏移的问题，如何证明呢？

（二）官方解析

(2)不妨设12x x <，由（1）知，()()()122,1,1,,2,1x x x ∈-∞∈+∞-∈-∞，()f x 在(),1-∞上单调递减，所以122x x +<等价于()()122f x f x >-，即()()222f x f x >-．

由于()()2

2222221x f x x e

a x --=-+-，而()()()22

22221x f x x e a x =-+-，

所以()()()2

22222222x x f x f x x e x e ---=---．令()()22x x g x xe x e -=---，

则()()()

21x x g x x e e -'=--，所以当1x >时，()0g x '<，而()10g =， 故当1x >时，()()10g x g <=．从而()()2220g x f x =-<，故122x x +<． 二、对解析的分析

本问待证是两个变量的不等式，官方解析的变形是122x x <-，借助于函数的特性及其单调性，构造以2x 为主元的函数．由于两个变量的地位相同，当然也可调整主元变形为212x x <-，同理构造以1x 为主元的函数来处理．此法与官方解析正是极值点偏移问题的处理的通法．

不妨设12x x <，由（1）知，()()()121,1,1,,21,x x x ∈-∞∈+∞-∈+∞，()f x 在()1,+∞上单调递增，所以122x x +<等价于()()212f x f x <-，即()()1120f x f x --<．

令()()()()()2221x

x u x f x f x xe

x e x -=--=--<，则()()()210x x u x x e e -'=-->，

所以()()10u x u <=，即()()()21f x f x x <-<，

所以()()()1212f x f x f x =<-；所以212x x <-，即122x x +<.

极值点偏移问题的处理策略： 【处理策略一】主元法

所谓主元法就是在一个多元数学问题中以其中一个为“主元”，将问题化归为该主元的函数、方程或不等式等问题，其本质是函数与方程思想的应用．作为一线的教育教学工作者，笔者尝试用主元法破解函数的极值点偏移问题，理性的对此类进行剖析、探究，旨在为今后的高考命题和高考复习教学提供一点参考.

一般地，主元法破解极值点偏移问题思路是：

第一步：根据()()()1212f x f x x x =≠建立等量关系，并结合()f x 的单调性，确定12,x x 的取值范围； 第二步：不妨设12x x <，将待证不等式进行变形，进而结合原函数或导函数的单调性等价转化． 第三步：构造关于1x （或2x ）的一元函数()()()()21,2i i T x f x f a x i =--=，应用导数研究其单调性，并借助于单调性，达到待证不等式的证明．

题型一：不含参数的问题.

例1.（2010天津理）已知函数()()x

f x xe x R -=∈ ，如果12x x ≠，且12()()f x f x = ，

证明：12 2.

x x +>

【解析】法一：()(1)x

f x x e -'=-，易得()f x 在(,1)-∞上单调递增，在(1,)+∞上单调递减，x →-∞时，()f x →-∞，

(0)0f =，x →+∞时，()0f x →， 函

数()f x 在1x =处取得极大值(1)f ，且1

(1)f e

=

,如图所示. 由1212()(),f x f x x x =≠，不妨设12x x <，则必有1201x x <<<，

欲证122x x +>，即证212x x >-，故122,(1,)x x -∈+∞，又因为()f x 在(1,)+∞上单调递减，故只需证21()(2)f x f x <-，又因为12()()f x f x =，故也即证11()(2)f x f x <-，构造函数

()()(2),(0,1)H x f x f x x =--∈，则等价于证明()0H x <对(0,1)x ∈恒成立.

由221()()(2)(1)0x x x

H x f x f x e e

--'''=+-=

->，则()H x 在(0,1)x ∈上单调递增，所以()(1)0H x H <=，即已证明()0H x <对(0,1)x ∈恒成立，故原不等式122x x +>亦成立.

法二：由12()()f x f x =，得1

212x x x e

x e --=，化简得212

1

x x x e x -=

…①， 不妨设21x x >，由法一知，121o x x <<<.令21t x x =-，则210,t x t x >=+，代入①式，得1

1

t

t x e x +=，反解出11t t x e =

-，则121

221t t x x x t t e +=+=+-，故要证：122x x +>，即证：221

t t

t e +>-，又因为10t

e ->，等价于证明：2(2)(1)0t

t t e +-->…②，

构造函数()2(2)(1),(0)t G t t t e t =+-->，则()(1)1,()0t t

G t t e G t te '''=-+=>，

故()G t '在(0,)t ∈+∞上单调递增，()(0)0G t G ''>=，从而()G t 也在(0,)t ∈+∞上单调递增，

()(0)0G t G >=，即证②式成立，也即原不等式122x x +>成立.

法三：由法二中①式，两边同时取以e 为底的对数，得221211ln

ln ln x x x x x x -==-，也即21

21

ln ln 1x x x x -=-，从而2

212121212122212111

1

1

ln ln ()

ln ln 1x x x x x x x x

x x x x x x x x x x x x +-++=+==---， 令21(1)x t t x =

>，则欲证：122x x +>，等价于证明：1ln 21

t t t +>-…③， 构造(1)ln 2()(1)ln ,(1)11

t t M t t t t t +==+>--，则22

12ln ()(1)t t t M t t t --'=-， 又令2

()12ln ,(1)t t t t t ?=-->，则()22(ln 1)2(1ln )t t t t t ?'=-+=--，由于1ln t t ->对(1,)t ?∈+∞恒成立，故()0t ?'>，()t ?在(1,)t ∈+∞上单调递增，所以()(1)0t ??>=，从而()0M t '>，故

()

M t 在

(1,)

t ∈+∞上单调递增，由洛比塔法则知：

1

111(1)ln ((1)ln )1

lim ()lim

lim lim(ln )21(1)x x x x t t t t t M t t t t t

→→→→'+++===+='--，即证()2M t >，即证③式成立，也

即原不等式122x x +>成立.

【点评】以上三种方法均是为了实现将双变元的不等式转化为单变元不等式，方法一利用构造新的函数

来达到消元的目的，方法二、三则是利用构造新的变元，将两个旧的变元都换成新变元来表示，从而达到消元的目的.

例2.已知()ln f x x x =的图像上有,A B 两点，其横坐标为1201x x <<<，且12()()f x f x =.

（1）证明：

122

1x x e <+<；

（2）证明：1<<. 【解析】（1）证明：由()ln ,()ln 1f x x x f x x '==+，令()0f x '=，得1

x e

=， 故12101x x e <<

<<，构造函数21()()(),(0),F x f x f x x e e

=--<< 则2221()ln ln()2ln ()2ln 20F x x x x x e e e '=+-+=-+<+=，故()F x 在1

(0,)e

上单调递减，即

1()()0F x F e >=，∴2()()f x f x e >-，令1x x =，则2112

()()()f x f x f x e =>-，再由

2121,(,1)x x e e -∈，且()f x 在1(,1)e 上单调递增，故212x x e >-，即证：122x x e

+>. 又构造函数：1

()()(1),(0)2

g x f x f x x =--<<，

则1112()ln ln(1)2,()01(1)x g x x x g x x x x x -'''=+-+=

-=>--，故()g x '在1(0,)2

上单调递增，由于0x →时，()g x '→-∞，且1()ln(1)0g e e '=->，故必存在01

(0,)x e ∈，使得0()0g x '=，故()g x 在

0(0,)x 上单调递减，在01(,)2x 上单调递增，又0x →时，()0g x →，且1

()02

g =，故()0g x <在

1(0,)2x ∈上恒成立，也即()(1)f x f x <-在1

(0,)2

x ∈上恒成立，令1x x =，有

121()()(1)f x f x f x =<-，再由211,1(,1)x x e -∈，且()f x 在1

(,1)e 上单调递增，故211x x <-，即证：

121x x +<成立.

综上：即证122

1x x e

<+<成立.

（2）令12t t =则22112212,,,(0,1)x t x t t t ==∈，且

2

12()2ln ,()(),()2(2ln 1)h t t t h t h t h t t t '===+，令()0h t '=，得t =

， 故

1201t t <<

<<.构造函数()()),(0H t h t h t t =-<<，则 ()()),()())H t h t h t H t h t h t

'''''''''=+-=-，由于4

()0h t t '''=>，则()h t ''在上单调

递增，

因为t t <

-，故()0H t ''<，()H t '

在上单调递减，

故()0H t H ''>=，即()H t

在

上单调递增，即()0H t H <=

，即())h t h t <-

，同理得出：12t t +<； 再构造1

()()(1),(0)2G x h t h t t =--<<，同样求导利用单调性可得出1()()02

G t G >=，从而

()(1)h t h t >-对1

(0,)2

t ∈恒成立，同理得出：121t t +>.

综上：即证121t t <+<

成立，也即原不等式1<<成立.

练习1：已知函数2

()ln f x x x x =++，正实数12,x x 满足1212()()0f x f x x x ++=，

证明：12x x +≥

. 【解析】由1212()()0f x f x x x ++=，得22

11122212ln ln 0x x x x x x x x ++++++= 从而2

12121212()()ln()x x x x x x x x +++=-，令12t x x =，构造函数()ln t t t ?=-，

得11

()1t t t t

?-'=-=

，可知()t ?在(0,1)上单调递减，在(1,)+∞上单调递增，所以()(1)1t ??≥=，也即2

1212()()1x x x x +++≥

，解得：12x x +≥

.

练习2（2013年湖南文科第21题）已知函数()2

11x

x f x e x

-=+. (1)求()f x 的单调区间；

(2)证明:当()()()1212f x f x x x =≠时，120x x +<.

解： (1) ()f x 在(),0-∞上单调递增，在()0,+∞上单调递减；

(2)由(1)知当1x <时，()0f x >． 不妨设12x x <，因为()()12f x f x =，即

12

1222

12

1111x x x x e e x x --=++，则1201x x <<<， 要证明120x x +<，即120x x <-<，只需证明()()12f x f x <-，即()()22f x f x <-．

而22()()f x f x <-等价于2

222(1)10x x e x ---<，

令()2()(1)10x

g x x e

x x =--->，则2'()(12)1x g x x e =--，

令2()(12)1x

h x x e

=--，则2()40x h x xe '=-<，

所以()h x 单调递减，()()00h x h <=，即()0g x '<，所以()g x 单调递减， 所以()()00g x g <=，得证．

题型二：含参数的问题

例3.已知函数x ae x x f -=)(有两个不同的零点12,x x ，求证：221>+x x . 【解析】思路1：函数()f x 的两个零点，等价于方程x

xe

a -=的两个实根，从而这一问题与例1完全等

价，例1的四种方法全都可以用；

思路2：也可以利用参数a 这个媒介去构造出新的函数.解答如下：

因为函数()f x 有两个零点12,x x ， 所以???==)

2()1(2

1

2

1x x ae x ae x ，由)2()1(+得：)(2121x

x e e a x x +=+，

要证明122x x +>，只要证明12()2x x a e e +>，

由)2()1(-得：1212()x

x

x x a e e -=-，即12

12

x x x x a e e -=

-，

即证：12

1

212()2x x x

x e e x x e e

+->-211)(212121>-+-?--x x x x e e x x ， 不妨设12x x >，记12t x x =-， 则0,1t

t e >>， 因此只要证明：121

t t

e t e +?>-01)1(2>+--?t t e e t ， 再次换元令x t x e t ln ,1=>=，即证2(1)

ln 0(1,)1

x x x x --

>?∈+∞+ 构造新函数2(1)

()ln 1

x F x x x -=-+，0)1(=F

求导2'

22

14(1)()0(1)(1)x F x x x x x -=-

=>++，得)(x F 在),1(+∞递增， 所以0)(>x F ，因此原不等式122x x +>获证.

【点评】含参数的极值点偏移问题，在原有的两个变元12,x x 的基础上，又多了一个参数，故思路很自然的就会想到：想尽一切办法消去参数，从而转化成不含参数的问题去解决；或者以参数为媒介，构造出一个变元的新的函数。

变式：.已知21,x x 是函数ax e x f x

-=)(的两个零点，且21x x <，（1）求证：221>+x x ； （2）求证：121

【解析】(1)问题可以转化为：x e x y =

与a

y 1=有两个交点，由图知，2110x x <<< 且?????==2

121ax e ax e x x ，即???

????==a e x a e x x x 2

1

21，∴)(121

2x x a e e x x -=-，1212x x e e a x x --=

故要证：221>+x x ，即证：221>+a e e x x ，也即证：1

22

12

21x x e e e e x x x x ->-+， 也即1

22

11212x x e e x x x x ->

-+--，令,12x x t -=则),0(+∞∈t 设)1(2)1()(--+=t

t

e e t t g ，则0)(,1)(>=''+-='t

t

t

te t g e te t g ， ∴)(t g '在),0(+∞单调递增，即0)0()(='>'g t g .

∴)(t g 在),0(+∞单调递增，即0)0()(=>g t g ，故原不等式得证.

(2)要证：121

21

2)(122

1x x e e e e x x x x --

21x x e e e e x x x x -<-?，等价于2122)

(1

)1(1212x x e e x x x x -<---，令012>-=x x t 等价于)0(1)1(22><-t t e e t t

，也等价于)0(112

><-t t

e e t

t

，等价于即证：012

<+-?t t

e e t 令)0(1)(2>+-?=t e e t t h t

t

，则)2

1(21)(2

222

t

t t t t e t e e e t e t h -+=-?+='，

又令)0(21)(2>-+=t e t t t ?，得02

21)(2

e t

t ?，∴)(t ?在),0(+∞单调递减，

0)0()(=

【点评】从消元的角度，消掉参数a ，得到一个关于21,x x 的多元不等式证明，利用换元思想，将多元不等式变成了一元不等式，并通过构造函数证明相应不等式.

例4.已知函数()ln f x x ax =-，a 为常数，若函数()f x 有两个零点12,x x ，试证明：2

12.

x x e ?>

【解析】法一：消参转化成无参数问题：

ln ()0ln ln x f x x ax x ae =?=?=，12,x x 是方程()0f x =的两根，也是方

程ln ln x

x ae

=的两根，则12ln ,ln x x 是x

x ae =，设1122ln ,ln u x u x ==，()x g x xe -=，则12()()g u g u =，

从而2

121212ln ln 22x x e x x u u >?+>?+>，此问题等价转化成为例1，下略.

法二：利用参数a 作为媒介，换元后构造新函数：

不妨设12x x >，∵1122ln 0,ln 0x ax x ax -=-=，∴12121212ln ln (),ln ln ()x x a x x x x a x x +=+-=-， ∴

12

12

ln ln x x a x x -=-，欲证明212x x e >，即证12ln ln 2x x +>.

∵1212ln ln ()x x a x x +=+，∴即证12

2

a x x >

+，

∴原命题等价于证明

121212ln ln 2

x x x x x x ->-+，即证：1122122()ln x x x x x x ->+，令12

,(1)x t t x =>，构造

2(1)

ln ,1

)1(t t g t t t -=-

>+，此问题等价转化成为例2中思路二的解答，下略. 法三：直接换元构造新函数：12221211ln ln ln ,ln x x x x a x x x x =

=?=设2121

,,(1)x

x x t t x <=>， 则11

2111

ln ln ln ,

ln ln tx t x x tx t t x x +==?=， 反解出：1211ln ln ln ln ,ln ln ln ln ln 111

t t t t

x x tx t x t t t t =

==+=+=

---， 故2

12121ln ln 2ln 21

t x x e x x t t +>?+>?>-，转化成法二，下同，略.

例 5.设函数()()x

f x e ax a a R =-+∈的图像与x 轴交于1212(,0),(,0)()A x B x x x <两点，求证：

1212x x x x <+.

【解析】证明：由12

12(1)

(1)

x x e a x e a x ?=-??=-??，易知211x x >>且a e >，

从而1122

1211

x x x

x x e e e x --==-，令121,1x x αβ=-=-，则ln ln 1e αβααββαβ--=?=-， 由于12121x x x x αβ<+?<，下面只要证明：1

1,(01)αββαβα

<<<，结合对数函数

ln y x =的图像可知，只需证：11

(,ln ),(,ln )αααα

两点连线的斜率要比(,ln ),(,ln )ααββ两点连线的

斜率小即可，又因为ln ln 1k αβ

αβ

-=

=-，即证：

1

ln ln

112ln 0(01)1αααααααα

-<<-， 令1

()2ln 0,(01)g ααααα

=

-+><<，则2

2

2

1

2

(1)()10g ααα

α

α

-'=-

-+

=-

<，

∴()g α在(0,1)上单调递减，∴()(1)0g g α>=， ∴原不等式1212x x x x <+成立.

例 6.设函数()()x

f x e ax a a R =-+∈，其图像与x 轴交于)0,(,)0,(21x B x A 两点，且21x x <.

证明：

0f '<.

【解析】由(),()x x f x e ax a f x e a '=-+=-，易知：a 的取值范围为2

(,)e +∞，()f x 在(,ln )a -∞上单调递减，在(ln ,)a +∞上单调递增. 法一：利用通法构造新函数，略； 法二：将旧变元转换成新变元：

∵12

120,0,

x x e ax a e ax a ?-+=??-+=??两式相减得：2121x x e e a x x -=-，

记21,(0)2x x t t -=

>，则12

12

21

2

122

21()(2())2

2x x x x x x t t x x

e e e

f e t e e x x t

++-+-'=-

=---，

设()2(),(0)t

t

g t t e e t -=-->，则()2()0t

t

g t e e -'=-+<，所以()g t 在(0,)t ∈+∞上单调递减，故

()(0)0g t g <=,而

12

2

02x x e

t +>，所以12

(

)02

x x f +'<，

又∵()x

f x e a '=-是R

122

x x +<，∴0)(21

容易想到，但却是错解的过程：

欲证：0)(21

()02x x f +'<，亦要证12

20x x e a +-<，也即证：122x x e a +<，很自然会想到：对112211220,(1),0,(1),x x x x e ax a e a x e ax a e a x ??-+==-?????-+==-????

两式相乘得：122

12(1)(1)x x e a x x +=--，即证：

12(1)(1)1x x --<.考虑用基本不等式2

12122(1)(1)(

)2

x x x x +---<，也即只要证：124x x +<.由于

121,ln x x a >>.当取3a e =将得到23x >，从而124x x +>.而二元一次不等式124x x +<对任意2(,)a e ∈+∞不恒成立，故此法错误.

【迷惑】此题为什么两式相减能奏效，而变式相乘却失败？两式相减的思想基础是什么？其他题是否也可以效仿这两式相减的思路?

【解决】此题及很多类似的问题，都有着深刻的高等数学背景. 拉格朗日中值定理：若函数()f x 满足如下条件： （1）函数在闭区间[,]a b 上连续；

（2）函数在开区间(,)a b 内可导，则在(,)a b 内至少存在一点ξ，使得()()

()f b f a f b a

ξ-=-.

当()()f b f a =时，即得到罗尔中值定理. 上述问题即对应于罗尔中值定理，

设函数图像与x 轴交于12(,0),(,0),A x B x 两点，因此

21211221()()(e )()0002x x AB

f x f x e a x x k x x ----=?=?=-，∴21

21

x x e e a x x -=

-，…… 由于12()()0f x f x ==，显然11()()0f x f x +=与11()()0f x f x ?=，与已知

12()()0f x f x ==不是充要关系，转化的过程中范围发生了改变.

例7.已知函数2

()(2)ln f x x a x a x =---，若方程()f x c =有两个不相等的实数根12,x x ，求证：

12

(

)02

x x f +'>. 【解析】证明：法一：由2

()(2)ln f x x a x a x =---，

得22(2)(2)(1)

()2(2)2

a x a x a x a x f x x a x x ----+'=---==，故只有0a >时，方程()f x c =才

有两个不相等的实数根12,x x ，不妨设12x x <，则1202

a

x x <<

<， 满足2

1112222(2)ln ,(2)ln ,

x a x a x c x a x a x c ?---=??---=??，

两式相减得：22

111222(2)ln (2)ln 0x a x a x x a x a x ----+-+=……

化简得：221122

1122

22ln ln x x x x a x x x x +--=+--.

欲证：12(

)0()22x x a f f +''>=，结合()f x '的单调性，即证：1222

x x a

+> 等价于证明：221122

121122

22ln ln x x x x x x x x x x +--+>+--1

112212122

2

2

22ln 1x x x x x x x x x x --?<=++

令12,(01)x t t x =

<<，构造函数22()ln ,(01)1

t g t t t t -=-<<+，求导由单调性易得原不等式成立，略. 法二：接①后续解:

由①得：11212122()()(2)()ln 0x x x x x a x x a x +-----=，

即：1

2

1212ln

()(2)0x a x x x a x x +---=-……②

而1

122

1212

ln

()()(2)2x a x x x f x x a x x +'=+---

-……③ 由②③得：1

1221212

ln

2()2x a x x x a

f x x x x +'=-

-+ 1

11212112212122

2

2(

1)

2()(ln )(ln )1x x x x x x a a x x x x x x x x x x --=

-=--+-+……④ 要证：12

()02x x f +'>1

1211222

2(

1)

(ln )01x x x a x x x x x -?

->-+，令12,(01)x t t x =<< 构造函数2(1)

()ln ,(01)1t m t t t t -=-

<<+，求导由单调性易得()0m t <在(0,1)t ∈恒成立，又因为120,0a x x >-<，故12()02

x x

f +'>成立.

法三：接④后续解：

视1x 为主元，设2222222

2222()4()1

()ln ln ,()0()()x x x x x g x x x g x x x x x x x x --'=--=-=>+++

则()g x 在2(0,)x x ∈上单调递增，故2()()0g x g x <=，再结合120,0a x x >-<，故12

()02

x x f +'>成立.

法四：构造函数()()(),(0)222

a a a h x f x f x x =--+<<

， 则24()()()022()()22

a a x h x f x f x a a x x '''=---+=

>+-，从而()h x 在(0,)2a

上单调递增，故()(0)0h x h >=，即()()22a a f x f x ->+对(0,)2

a

x ∈恒成立，

从而()(),(0)2a f x f a x x >-<<，则211()()()f x f x f a x =>-，由21,(,)2

a

x a x -∈+∞，且()f x 在

(,)2a +∞单调递增，故21x a x >-，即1222x x a

+>，从而12()02

x x f +'>成立.

练习1：已知函数1

()ln ()f x a x a R x

=--∈有两个零点1212,()x x x x <，求证：112231a x x e -<+<-. 【解析】21()x

f x x

-'=

，知()f x 在(0,1)上单调递增，在(1,)+∞上单调递减， 且1201x x <<<，故要证：122x x +>，即证：2121x x >->，只要证：21()(2)f x f x >-，又因为

12()()f x f x =，即证：11(2)()0f x f x --<.

构造函数()(2)(),(0,1)F x f x f x x =--∈.即证()0F x <对(0,1)x ∈恒成立，前面有类似证明，此处略；

下证：1

1231a x x e -+<-.

因为()0f x =，本质上是1ln 0ax x x --=，令()1ln h x ax x x =--，则12,x x 也是()h x 的两个零点.由()1ln 0h x a x '=--=，得1

a x e -=，故要证1

1231a x x e -+<-，结合122x x +>，

只要证：1

121232

a x x x x e

-++<-

即证：1122a x x e -+<，即证：1

212a x e x -<-，由()h x 的单调性知，只需证：1

121()()(2e )a h x h x h x -=>-，

同理构造函数1

()()(2),(0,1)a H x h x h e x x -=--∈，利用单调性证明，下略.

练习2：设函数2

()ln f x a x bx =-，其图像在点(2,(2))P f 处切线的斜率为3-.当2a =时，令

()()g x f x kx =-，设1212,()x x x x <是方程()0g x =的两个根，0x 是12,x x 的等差中项，求证：0()0g x '<(()g x '为函数()g x 的导函数）.

【解析】由2

()2ln g x x x kx =--的两个零点12,x x ，则2

1112

2222ln 0,

2ln 0,

x x kx x x kx ?--=??--=??

相减得：22

1212122(ln ln )()()0x x x x k x x -----=，∵12x x ≠，

∴1212122(ln ln )()x x k x x x x -=

-+-，故120001212

2(ln ln )24

()2x x g x x k x x x x x -'=--=-+-

1

12211211212122

2

2(

1)

2()22[(ln ln )][ln ]1x x x x x x x x x x x x x x x x --=

--=--+-+ 令12,(0,1)x t t x =

∈，2(1)4()ln 2ln 11

t t t t t t ?-=-=--++， 则222

41(1)()0(1)(1)t t t t t t ?-'=-=-<++，()t ?在(0,1)上单调递减，故()(1)0t ??>=，又12

2

0x x <-，所以0()0g x '<，证毕.

（备用）例6.已知函数()(0)ax

f x x e a =->，若存在1212,()x x x x <，使12()()0f x f x ==，求证：

1

2

x ae x <. 【解析】函数()f x 的零点等价于方程ln x a x =

的实根，令ln (),(0)x

g x x x

=>，求导可知，()g x 在(0,)e 上单调递增，在(,)e +∞上单调递减，1

()().Max g x g e e

==

（i ）下证：当10a e <<时，方程ln x a x =ln x

a x

=

有两个实根. ①当(0,)x e ∈时，()g x 是减函数，∵1

(1)0,(e),(1)(e)g g g a g e

==<<

∴当(0,),x e ∈()g x 为增函数，1

(1)0,(),(1)(),g g e g a g e e

=<<

∴当(0,)x e ∈时，ln x

a x

=有一解，记为1x .

②当(,)x e ∈+∞时，()g x 为减函数，2

21()2ln ,g a a a

=-

先证：21()g a a <，即证：1

ln 2a a >-，令()ln ,(0)h a a a a =>，求导由()h a 的单调性可得:

min 111()()2h a h e e ==->-,故不等式1ln 2a a >-即证，也即原不等式21

()g a a

<成立.

∴当(,)x e ∈+∞时，ln x

a x

=有一解，记为2x .

（2）再证：12x ae x <.∵111222ln x ax ax x ax x ==，而120x e x <<<，2ln 1x >，∴1122

ln 1x ax ae ae x x =<=.证

毕.

【处理策略二】根据对称性构造一元差函数求解

若()f x 的极值点为0x ，则根据对称性构造一元差函数()()()00F x f x x f x x =+--，巧借

()F x 的单调性以及()00F =，借助于()()()12002f x f x f x x x ==--????与()002f x x x +-????()022f x x =-，比较2x 与012x x -的大小，即比较0x 与

21

2

x x +的大小．

例1.（2010天津理）已知函数()()x

f x xe x R -=∈ ，如果12x x ≠，且12()()f x f x = ，

证明：12 2.x x +>

【解析】

法一：()(1)x

f x x e -'=-，易得()f x 在(,1)-∞上单调递增，在

(1,)+∞上单调递减，x →-∞时，()f x →-∞，(0)0f =，

x →+∞时，()0f x →， 函

数()f x 在1x =处取得极大值(1)f ，且1

(1)f e

=

,如图所示. 由1212()(),f x f x x x =≠，不妨设12x x <，则必有1201x x <<<， 构造函数()(1)(1),(0,1]F x f x f x x =+--∈， 则21

()(1)(1)(1)0x x x F x f x f x e e

+'''=++-=

->，所以()F x 在(0,1]x ∈上单调递增，

()(0)0F x F >=，也即(1)(1)f x f x +>-对(0,1]x ∈恒成立.由1201x x <<<，则11(0,1]x -∈，

所以11112(1(1))(2)(1(1))()()f x f x f x f x f x +-=->--==，即12(2)()f x f x ->，又因为

122,(1,)x x -∈+∞，且()f x 在(1,)+∞上单调递减，所以122x x -<，即证12 2.

x x +>

例8.已知函数()()()2

21x

f x x e a x =-+-有两个零点.设12,x x 是()f x 的两个零点，证明：

122x x +<. 解:不妨设12x x <由题意知()()120f x f x ==.要证不等式成立，只需证当121x x <<时，原不等式成

立即可.令()()()11F x f x f x =--+，则()(

)'

11x

x F x x e

e -+=-，当0x >时，()'0F x <.

()()00F x F ∴<=.即()()11f x f x -<+.令11x x =-，

则

()()()()()()()2111111112f x f x f x f x f x ==--<+-=-,即

()()212f x f x <-.而

()21,21,x x -∈+∞，且()f x 在()1+∞，上递增，故212x x <-，即122x x +<.

练习：已知函数2

()ln f x x x

=

+， 若1x ≠2x ，且f(1x )=f(2x ),证明：1x +2x >4. 证

明

：

【处理策略三】对数平均不等式

我们熟知平均值不等式：,a b R +∈

有

2

112a b a b

+≤≤≤+ 即“调和平均数”小于等于“几何平均数”小于等于“算术平均值”小于等于“平方平均值” 等号成立的条件是a b =.

我们还可以引入另一个平均值：对数平均值：

两个正数a 和b 的对数平均定义：(),(,)ln ln ().

a b

a b L a b a b a a b -?≠?

=-??=?对数平均与算术平均、几何平均的大小

(,)2

a b

L a b +≤≤

（此式记为对数平均不等式），取等条件：当且仅当a b =时，等号成立. 只证：当a b ≠

(,)2

a b

L a b +<<.不失一般性，可设a b >.证明如下：

（I

(,)L a b <……

不等式

①1ln ln ln 2ln (1)a a b x x x b x ?-<

?其中

构造函数1()2ln (),(1)f x x x x x

=-->，则22211

()1(1)f x x x x

'=

--=--.因为1x >时，()0f x '<，所以函数()f x 在(1,)+∞上单调递减，故()(1)0f x f <=，从而不等式①成立； （II ）再证：(,)2

a b

L a b +<

……② 不等式

②2(1)

2()2(1)ln ln ln ln (1)(1)(1)a a b a x b a b x x a a b b x b

---?->?>?>=>+++其中

构造函数2(1)

()ln ,(1)(1)

x g x x x x -=->+，则222

14(1)()(1)(1)x g x x x x x -'=-=++.因为1x >时，()0g x '>，所以函数()g x 在(1,)+∞上单调递增，故()(1)0g x g <=，从而不等式②成立； 综合（I ）（II ）知，对,a b R +

?∈，

(,)2

a b

L a b +≤≤成立，当且仅当a b =时，等号成立.

前面例题用对数平均不等式解决

根据()()12f x f x =建立等式，通过消参、恒等变形转化为对数平均，捆绑构造函数，利用对数平均不等式链求解．

例1.（2010天津理）已知函数()()x

f x xe x R -=∈ ，如果12x x ≠，且12()()f x f x = ，

证明：12 2.

x x +>

【解析】法五：由前述方法四，可得12121ln ln x x x x -=

-，利用对数平均不等式得：

1212121ln ln 2

x x x x

x x -+=<-，即证：122x x +>，秒证.

说明：由于例2，例3最终可等价转化成例1的形式，故此处对数平均不等式的方法省略.

例 6.设函数)()(R a a ax e x f x

∈+-=，其图像与x 轴交于)0,(,)0,(21x B x A 两点，且21x x <.证明：

0)(21

【解析】法三：由前述方法可得：12

1212(1ln )11

x x e e a x a x x x ==<<<--，等式两边取以e 为底的对数，

得1122ln ln(1)ln(1)a x x x x =--=--，化简得：1212(1)(1)

1ln(1)ln(1)

x x x x ---=

---

，由对数平均不等式知：

1212(1)(1)

1ln(1)ln(1)

x x x x ---=

>---，即

1212()0

x x x x -+<，

故

要

证

1122ln(1)ln(01)ln f a x x x x --+-'

1212121212ln(1)ln(1)ln(()1)x x x x x x x x x x ??-+-<+--++<+-证证∵

1212()0x x x x -+< ∴1212ln(()1)ln10x x x x -++<=，

而2

120x x +-=>

∴121212ln(()1)x x x x x x -++<+-.

例9.（11年，辽宁理）

已知函数2

()ln (2).f x x ax a x =-+- （I ）讨论()f x 的单调性； （II ）设0a >，证明：当10x a <<

时，11

()()f x f x a a

+>-； （III ）若函数()y f x =的图像与x 轴交于,A B 两点，线段AB 中点的横坐标为0x ，证明：0()0f x '<. 【解析】（I ）（II ）略，

（III ）由12()()0f x f x ==22

111222ln (2)ln (2)0x ax a x x ax a x ?-+-=-+-=

2212121212ln ln 2()()x x x x a x x x x ?-+-=-+-1212221212

ln ln 2()

x x x x a x x x x -+-?=

-+-

故要证12001

()02x x f x x a

+'

> 221212121212

121212

1

ln ln 2ln ln 2()2

x x x x x x x x x x x x x x x x +-+-++?>=

--+-+- 121212

ln ln 2

x x x x x x -?

<+-.根据对数平均不等，此不等式显然成立，故原不等式得证.

练习1：（2014江苏南通市二模）设函数()x

f x e ax a =-+ ()a R ∈，其图象与x 轴交于

()()12,0,0A x B x 两点，且12x x <.

证明：0f '

<（()f x '为函数()f x 的导函数）.

【解析】根据题意：110x e ax a -+=，220x e ax a -+=移项取对数得：

11ln(1)ln x x a =-+① 22ln(1)ln x x a =-+②

①-②得：1212ln(1)ln(1)x x x x -=---，即： 1212(1)(1)

1ln(1)ln(1)

x x x x ---=---

根据对数平均值不等式：

1212(1)(1)

1ln(1)ln(1)

x x x x ---=---

1212(1)(1)1ln(1)(1)0x x x x ∴--

12122ln ln(1)(1)2ln x x a x x a +=+--<

12

ln 2x x a +<

<，

∵函数()f x 在(,ln )a -∞单调递减

∴0f <

练习2：已知函数()ln f x x x =与直线y m =交于1122(,),(,)A x y B x y 两点.求证：122

1

0x x e <<

【解析】由11ln =x x m ，22ln =x x m ，可得：11ln m x x =

①，22

ln m x x =② ①-②得： 211212121212

ln ln (

)ln ln ln ln ln ln ----=?=-x x x x m

x x m x x x x x x ③

①+②得：211212(ln ln )ln ln m x x x x x x ++=

④，根据对数平均值不等式121212()2ln ln +->

≠-x x m

x x x x 利用③④式可得：

121212

(ln ln )2ln ln ln ln m x x m

x x x x +->

，

由题于y m =与ln y x x =交于不同两点， 易得出则0m <，∴上式简化为:212ln()2ln x x e -?<-=，∴1221

0<<

x x e

【再看2016全国高考压轴题】

（2016年新课标I 卷理数压轴21题）已知函数2

)1()2()(-+-=x a e x x f x

有两个零点21,x x .证明：

122x x +<.

【解析】由2()(2)(1)x f x x e a x =-+-，得()(1)(2)x

f x x e a '=-+，可知()f x 在(,1)-∞上单调递减，在(1,)+∞上单调递增.要使函数()y f x =有两个零点12,x x ，则必须0a >. 法一：构造部分对称函数

不妨设12x x <，由单调性知12(,1),(1,)x x ∈-∞∈+∞，所以22(,1)x -∈-∞，又∵()f x 在(,1)-∞单调递减，故要证：122x x +<，等价于证明：21(2)()0f x f x -<=， 又∵2

22222(2)(1)x f x x e a x --=-+-，且22222()(2)(1)0x f x x e a x =-+-=

∴2

22222(2)(2)x x f x x e x e --=---，构造函数2g()(2),((1,))x x

x xe x e x -=---∈+∞，由单调性可证，

此处略.

法二：参变分离再构造差量函数

由已知得：()()120f x f x ==，不难发现11x ≠，21x ≠，故可整理得：()()

()()

1

2

122

2

122211x x x e x e a x x ---==--

设()()()

221x x e g x x -=-，则()()12g x g x =，那么()()()2

321'1x x g x e x -+=-，当1x <时，()'0g x <，()g x 单调递减；当1x >时，()'0g x >，()g x 单调递增． 设0m >，构造代数式：()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-??+--=

-=+ ?+??

设()2111m m h m e m -=++，0m >，则()()

2

22

2'01m m h m e m =>+，故()h m 单调递增，有()()00h m h >=． 因此，对于任意的0m >，()()11g m g m +>-．

由()()12g x g x =可知1x 、2x 不可能在()g x 的同一个单调区间上，不妨设12x x <，则必有121x x << 令110m x =->，则有()()()()()1111211112g x g x g x g x g x +->--?->=???????? 而121x ->，21x >，()g x 在()1,+∞上单调递增，因此：()()121222g x g x x x ->?-> 整理得：122x x +<．