(完整版)BP神经网络原理
第三讲-BPnn

学习规则
1.隐含层与输出层之间的权值修正量
( 2) wij
E ( 2) wij
E E ( 2) ( 2) wij I i
( 2) I i ( 2) wij
I i( 2) ( 2 ) (1) ( 2) ( w O b l i ) ( 2) ( 2 ) il wij wij l
BP 算法的基本原理是梯度最速下降法,它的中 心思想是调整权值使网络总误差最小。运行 BP 学习 算法时,包含正向和反向传播两个阶段。 正向传播 输入信息从输入层经隐含层逐层处理,并传向输出 层,每层神经元的状态只影响下一层神经元的状态。 反向传播 将误差信号沿原来的连接通道返回,通过修改各层 神经元的权值,使误差信号最小。
net pi 计算一个样本各单元净输入
a pi 和输出
e Ti a pi 计算目标值与实际输出误差
pi 计算输出单元的一般化误差
Wij 计算各个权重变化
(k ) ( k 1) ( k 1) wij i( k )O(j k 1) i( k ) f ( I i( k ) ) p wpi
bi( k )
(k ) i
p
误差反向传播
BP算法总结
权值和偏置值修正量为
w
(k ) ij
(k ) i
O
( k 1) j
(1) ( 2) ( 2) f1 ( I i ) k wki k
误差反向传播
误差反向传播示意图
w
x1 x2 x3 xm
( 2) i
(1) ij
(1) i
( 2) wij
( 2) 1 ( 2) 2
bp人工神经网络的原理及其应用

廷塑签凰.B P人工神经网络的原理及其应用焦志钦(华南理工大学,广东广州510000)f}商鞫人工神经网络是计算智能和机器学习研究中最活跃的分交之一。
本文对神经网络中的BP算法的原理做了详尽的阐述,并用M a da b 程序对其进行了应用。
表明它具有强大的拟合功能。
房;建闭B P算法;M adab1人工神经网络的发展人工神经网络是一个由多个简单神经元相互关联构成的能够实现某种特定功能的并行分布式处理器。
单个神经元由杈值、偏置值、净输^和传输函数组成。
多输入单神经元模型如图1—1所示。
岛见:●仇图1—1多输入单神经元模型其中P为输入值,w.为连接权值,b为偏置值,f似o√为传输函数。
神经元值n=w p+b,输出值为a=f M。
人工神经网络的第一个应用是感知机网络和联想学习规则。
不幸的是,后来研究表明基本的感知机网络只能解决有限的几类问题。
单层感知机只能解决线性分类问题。
不能解决异或问题,也不能解决非线性问题,因此就有单层感知机发展为多层感知机。
多层神经网络中—个重要的方法是B P算法。
BP网络属于多层前向网络,如图1—2所示:卫咒鼍旬k图卜2卵网络模型2B P算法B P网络计算方法如式(2—1)所示,为简化,将神经元的阈值8视为连接权值来处理,并令xo=go=ho=一1,故式(5-1)可以改写为式(2—2)。
92‘i互%蕾一8少j=I,2,…,,17也=,f∑峭一日.J j卢7,22,…,n2(2,1)^=,f2郴一日。
Jj卢7,,…,(2—1)心y,--f凭峭叫i j=1,2,…,n29=7i互w刚∥j=1,2,..’,几7^-f嚷郴一日小』=7,2,…,n2(2—2)M=f f三峭一日,Jj j=l,2,…,n2,=,B P算法是一种有导师的学习算法,这种算法通常是应用最速下降法。
图2—1描述了B P网络的一部分,其中包括工作信号(实线)和误差信号(虚线)两部分。
2002。
10。
1。
0。
’。
年。
BP神经网络及深度学习研究-综述(最新整理)

BP神经网络及深度学习研究摘要:人工神经网络是一门交叉性学科,已广泛于医学、生物学、生理学、哲学、信息学、计算机科学、认知学等多学科交叉技术领域,并取得了重要成果。
BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
本文将主要介绍神经网络结构,重点研究BP神经网络原理、BP神经网络算法分析及改进和深度学习的研究。
关键词:BP神经网络、算法分析、应用1 引言人工神经网络(Artificial Neural Network,即ANN ),作为对人脑最简单的一种抽象和模拟,是人们模仿人的大脑神经系统信息处理功能的一个智能化系统,是20世纪80 年代以来人工智能领域兴起的研究热点。
人工神经网络以数学和物理方法以及信息处理的角度对人脑神经网络进行抽象,并建立某种简化模型,旨在模仿人脑结构及其功能的信息处理系统。
人工神经网络最有吸引力的特点就是它的学习能力。
因此从20世纪40年代人工神经网络萌芽开始,历经两个高潮期及一个反思期至1991年后进入再认识与应用研究期,涌现出无数的相关研究理论及成果,包括理论研究及应用研究。
最富有成果的研究工作是多层网络BP算法,Hopfield网络模型,自适应共振理论,自组织特征映射理论等。
因为其应用价值,该研究呈愈演愈烈的趋势,学者们在多领域中应用[1]人工神经网络模型对问题进行研究优化解决。
人工神经网络是由多个神经元连接构成,因此欲建立人工神经网络模型必先建立人工神经元模型,再根据神经元的连接方式及控制方式不同建立不同类型的人工神经网络模型。
现在分别介绍人工神经元模型及人工神经网络模型。
1.1 人工神经元模型仿生学在科技发展中起着重要作用,人工神经元模型的建立来源于生物神经元结构的仿生模拟,用来模拟人工神经网络[2]。
人们提出的神经元模型有很多,其中最早提出并且影响较大的是1943年心理学家McCulloch和数学家W. Pitts在分析总结神经元基本特性的基础上首先提出的MP模型。
BP神经网络基本原理

BP神经网络基本原理2.1 BP神经网络基本原理BP网络模型处理信息的基本原理是:输入信号Xi通过中间节点(隐层点)作用于输出节点,经过非线形变换,产生输出信号Yk,网络训练的每个样本包括输入向量X和期望输出量t,网络输出值Y与期望输出值t之间的偏差,通过调整输入节点与隐层节点的联接强度取值Wij和隐层节点与输出节点之间的联接强度Tjk以及阈值,使误差沿梯度方向下降,经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练即告停止。
此时经过训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线形转换的信息。
2.2 BP神经网络模型BP网络模型包括其输入输出模型、作用函数模型、误差计算模型和自学习模型。
(1)节点输出模型隐节点输出模型:Oj =f(∑Wij×Xi-qj) (1)输出节点输出模型:Yk =f(∑Tjk×Oj-qk) (2)f-非线形作用函数;q -神经单元阈值。
图1典型BP网络结构模型(2)作用函数模型作用函数是反映下层输入对上层节点刺激脉冲强度的函数又称刺激函数,一般取为(0,1)内连续取值Sigmoid函数: f(x)=1/(1+e-x)(3)(3)误差计算模型误差计算模型是反映神经网络期望输出与计算输出之间误差大小的函数: E p =1/2×∑(t pi -O pi )2 (4)t pi - i 节点的期望输出值;O pi -i 节点计算输出值。
(4)自学习模型神经网络的学习过程,即连接下层节点和上层节点之间的权重拒阵W ij 的设定和误差修正过程。
BP 网络有师学习方式-需要设定期望值和无师学习方式-只需输入模式之分。
自学习模型为△W ij (n+1)= h ×Фi ×O j +a ×△W ij (n) (5)h -学习因子;Фi -输出节点i 的计算误差;O j -输出节点j 的计算输出;a-动量因子。
BP(BackPropagation)反向传播神经网络介绍及公式推导
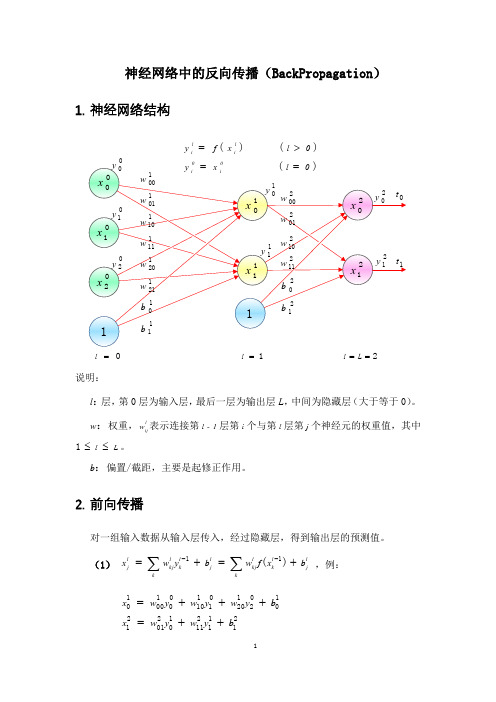
5. 链式法则
如果函数 u (t )及 v (t )都在 t 点可导,复合函数 z f(u,v)在对应点(u,v)具 有连续偏导数,z 在对应 t 点可导,则其导数可用下列公式计算:
dz z du z dv dt u dt v dt
6. 神经元误差
定义 l 层的第 i 个神经元上的误差为 il 即: (7)
5
附:激活函数
非线性: 当激活函数是线性的时候,一个两层的神经网络就可以逼近基 本上所有的函数了。但是,如果激活函数是恒等激活函数的时候(即 f(x)=x) ,就不满足这个性质了,而且如果 MLP 使用的是恒等激活函数, 那么其实整个网络跟单层神经网络是等价的。 可微性: 当优化方法是基于梯度的时候,这个性质是必须的。 单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数。 f(x)≈x: 当激活函数满足这个性质的时候, 如果参数的初始化是 random 的很小的值, 那么神经网络的训练将会很高效; 如果不满足这个性质, 那 么就需要很用心的去设置初始值。 输出值的范围: 当激活函数输出值是 有限 的时候,基于梯度的优化方 法会更加 稳定,因为特征的表示受有限权值的影响更显著;当激活函数 的输出是 无限 的时候, 模型的训练会更加高效, 不过在这种情况小, 一 般需要更小的 learning rate.
l i
j
l 1 E x j x lj 1 xil
j
x lj 1 x
l i
jl 1 ,其中 l L
将公式(1) x j
l 1
w
k
l 1 l kj k
y blj 1
w
k
l 1 kj
f( xkl ) blj 1 ,对 x i 的求导
基于BP神经网络PID整定原理和算法步骤

基于BP神经网络PID整定原理和算法步骤PID(比例、积分、微分)控制是一种常用的控制算法,用于调节系统的输出使其接近期望值。
BP(Back Propagation)神经网络是一种具有强大机器学习能力的神经网络模型。
基于BP神经网络的PID整定方法结合了PID控制算法和神经网络的优点,通过神经网络的学习能力优化PID 参数的选择,提高了控制系统的鲁棒性和适应性。
以下是基于BP神经网络的PID整定原理和算法步骤:一、原理:1.神经网络模型:建立一个具有输入层、隐藏层和输出层的BP神经网络模型,其中输入层接收系统的输入信号,输出层输出控制信号的PID 参数,隐藏层的神经元通过学习调整连接权重以优化参数选择。
2.参数训练:基于反向传播算法,通过输入输出样本对神经网络进行训练,使其学习输入输出之间的映射关系。
训练过程是一个迭代过程,通过不断调整连接权重和偏置,使神经网络的输出结果逼近期望值。
3.PID原理:PID控制算法根据系统当前误差,通过比例、积分和微分项生成控制信号。
调节PID参数可以改变控制信号的响应特性,使其更好地适应控制对象的动态特性。
二、算法步骤:1.数据采集:收集系统的输入输出数据,用于训练神经网络模型。
2.数据预处理:对采集到的数据进行预处理,包括去除噪声、归一化等处理,以提高神经网络的训练效果。
3.网络构建:根据需要构建BP神经网络模型,包括输入层、隐藏层和输出层。
隐藏层的神经元数量和层数可以根据实际情况进行选择。
4.神经网络训练:将预处理后的数据输入到神经网络中,利用反向传播算法对神经网络进行训练。
根据实际需求设置训练的轮数和学习率等参数。
5.训练结果评估:通过评估神经网络的训练结果,包括误差曲线、训练时间等指标,来判断训练是否达到预期效果。
6.PID参数优化:根据神经网络的输出结果调整PID的比例、积分和微分参数。
可以通过试错法或者自适应控制方法对参数进行调整。
7.控制性能评估:利用调整后的PID参数进行控制,通过评估系统的性能指标,例如超调量、调整时间等,来判断PID参数的选择是否合理。
BP反向传播算法原理及公式推导
BP反向传播算法原理及公式推导反向传播算法(Backpropagation,BP)是神经网络中常用的一种训练算法,通过基于梯度下降的方式来调整神经网络的权重和偏差,以最小化网络的损失函数。
本文将对BP算法的原理及公式推导进行详细介绍。
1.BP算法原理BP算法的原理是基于反向误差传播,即通过将误差从输出层逐层向前传播,更新每一层的权重和偏差。
它的基本思想是先将输入样本通过前向传播得到输出值,然后计算输出值与真实值之间的误差,最后通过反向传播调整网络参数。
2.BP算法过程BP算法的过程可以分为三部分:前向传播、计算误差、反向传播。
(1)前向传播:从输入层开始,将输入样本通过网络的每一层逐层计算得到输出值。
具体步骤如下:-将输入样本赋值给输入层。
- 对于每一层,计算该层的输出值:$o_j = f(\sumw_{ij}x_i+b_j)$,其中$o_j$为第j个神经元的输出值,$w_{ij}$为第i 个输入与第j个神经元的连接权重,$x_i$为第i个输入值,$b_j$为第j 个神经元的偏差,$f$为激活函数。
-将每一层的输出作为下一层的输入,逐层进行计算,直至得到输出层的输出值。
(2)计算误差:计算输出值与真实值之间的误差,用于评估网络的性能。
- 根据网络的输出值和真实值,计算输出层的误差项:$E_j=\frac{1}{2}(y_j-o_j)^2$,其中$E_j$为第j个输出神经元的误差项,$y_j$为真实值,$o_j$为网络的输出值。
-对于其他层,计算误差项:$E_j=f'(net_j)\sum E_kw_{kj}$其中$E_j$为第j个神经元的误差项,$f'(net_j)$为激活函数的导数,$net_j$为输入值,E为下一层的误差项,$w_{kj}$为第j个神经元与下一层的第k个神经元的连接权重。
(3)反向传播:根据误差项通过梯度下降法更新权重和偏差。
- 根据参数的更新率和误差项计算权重的更新量:$\Delta w_{ij}=-\eta\frac{\partial E}{\partial w_{ij}}$,其中$\eta$为学习率,$\frac{\partial E}{\partial w_{ij}}$为损失函数对权重$w_{ij}$的偏导数。
BP神经网络及深度学习研究 - 综述
BP网络的基本结构如图21所示,其模型拓扑结构包括输入层(input)、隐层(hidden layer)和输出层(output layer)三层结构。
输入层各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,负责信息变换,根据信息变化能力的需求。中间层可以设计为单隐层或者多隐层结构;最后一个隐层传递到输出层各神经元的信息,经进一步处理后,完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。隐层节点一般采用Sigmoid型函数,输入和输出节点可以采用Sigmoid型函数或者线性函数。
(3)网络的结构设计,即隐节点数的选择,尚无理论指导,具有很大的盲目性。
(4)新加入的样本对已经学好的样本影响较大,且每个输入样本的特征数目要求相同,泛化能力较差。
针对BP算法存在的缺陷,目前国内外已有不少人对BP网络进行了大量的研究,提出了各种不同的改进方案,如优化训练输入参数,加入动量参数,以及学习步长的适应调整,采用带动量的自学习率BP算法,动态全参数自调整学习算法,记忆式初值权值和阀值方法,快速自适应学习算法等,这些方案均提高BP神经网络收敛速度。
作用函数是反映下层输入对上层节点刺激脉冲强度的函数又称刺激函数,一般取为(0,1)内连续取值Sigmoid函数:
它反映了神经元的饱和特性。上式中,Q为表示神经元非线性的参数,称增益值(Gain),也称调节参数。Q值越大,S形曲线越陡峭;反之,Q值越小,S形曲线越平坦;一般取Q=1。
(3)误差计算模型
关键词:BP神经网络、算法分析、应用
1
人工神经网络(Artificial Neural Network,即ANN),作为对人脑最简单的一种抽象和模拟,是人们模仿人的大脑神经系统信息处理功能的一个智能化系统,是20世纪80年代以来人工智能领域兴起的研究热点。人工神经网络以数学和物理方法以及信息处理的角度对人脑神经网络进行抽象,并建立某种简化模型,旨在模仿人脑结构及其功能的信息处理系统。
BP神经网络的简介
BP神经网络的发展在人工神经网络发展历史中,很长一段时间里没有找到隐层的连接权值调整问题的有效算法。
直到误差反向传播算法(BP算法)的提出,成功地解决了求解非线性连续函数的多层前馈神经网络权重调整问题。
BP (Back Propagation)神经网络,即误差反传误差反向传播算法的学习过程,由信息的正向传播和误差的反向传播两个过程组成。
输入层各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,负责信息变换,根据信息变化能力的需求,中间层可以设计为单隐层或者多隐层结构;最后一个隐层传递到输出层各神经元的信息,经进一步处理后,完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。
当实际输出与期望输出不符时,进入误差的反向传播阶段。
误差通过输出层,按误差梯度下降的方式修正各层权值,向隐层、输入层逐层反传。
周而复始的信息正向传播和误差反向传播过程,是各层权值不断调整的过程,也是神经网络学习训练的过程,此过程一直进行到网络输出的误差减少到可以接受的程度,或者预先设定的学习次数为止。
BP神经网络模型BP网络模型包括其输入输出模型、作用函数模型、误差计算模型和自学习模型。
(1)节点输出模型隐节点输出模型:Oj=f(∑Wij×Xi-qj) (1)输出节点输出模型:Yk=f(∑Tjk×Oj-qk) (2)f-非线形作用函数;q -神经单元阈值。
图1 典型BP网络结构模型(2)作用函数模型作用函数是反映下层输入对上层节点刺激脉冲强度的函数又称刺激函数,一般取为(0,1)内连续取值Sigmoid函数: f(x)=1/(1 e) (3)(3)误差计算模型误差计算模型是反映神经网络期望输出与计算输出之间误差大小的函数:(4)tpi- i节点的期望输出值;Opi-i节点计算输出值。
(4)自学习模型神经网络的学习过程,即连接下层节点和上层节点之间的权重矩阵Wij的设定和误差修正过程。
BP算法的基本原理
BP算法的基本原理BP算法(反向传播算法)是一种神经网络训练算法,用于更新神经网络的权重和偏置,以使之能够适应所需任务的输入输出关系。
BP算法基于梯度下降优化方法,通过求解损失函数关于权重和偏置的偏导数来进行参数更新。
其基本原理涉及到神经网络的前向传播和反向传播两个过程。
以下将详细介绍BP算法的基本原理。
1.前向传播:在神经网络的前向传播过程中,输入数据通过网络的各个层,通过各个神经元的激活函数,最终得到网络的输出。
在前向传播过程中,每个神经元接收到上一层的信号,并通过权重和偏置进行加权求和,然后经过激活函数处理后输出。
具体而言,假设神经网络有L层,第l层的神经元为h(l),输入为x,激活函数为f(l),权重为w(l),偏置为b(l)。
其中,输入层为第1层,隐藏层和输出层分别为第2层到第L层。
对于第l层的神经元h(l),其输入信号为:z(l)=w(l)*h(l-1)+b(l)其中,h(l-1)表示第(l-1)层的神经元的输出。
然后,通过激活函数f(l)处理输入信号z(l)得到第l层的输出信号:h(l)=f(l)(z(l))。
依次类推,通过前向传播过程,神经网络可以将输入信号转化为输出信号。
2.反向传播:在神经网络的反向传播过程中,根据网络的输出和真实值之间的差异,通过链式法则来计算损失函数对于各层权重和偏置的偏导数,然后根据梯度下降法则对权重和偏置进行更新。
具体而言,假设网络的输出为y,损失函数为L,权重和偏置为w和b,求解L对w和b的偏导数的过程为反向传播。
首先,计算L对于网络输出y的偏导数:δ(L)/δy = dL(y)/dy。
然后,根据链式法则,计算L对于第L层的输入信号z(L)的偏导数:δ(L)/δz(L)=δ(L)/δy*δy/δz(L)。
接着,计算L对于第(L-1)层的输入信号z(L-1)的偏导数:δ(L)/δz(L-1) = δ(L)/δz(L) * dz(L)/dz(L-1)。
依次类推,通过链式法则得到L对于各层输入信号z(l)的偏导数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BP 神经网络原理2。
1 基本BP 算法公式推导基本BP 算法包括两个方面:信号的前向传播和误差的反向传播.即计算实际输出时按从输入到输出的方向进行,而权值和阈值的修正从输出到输入的方向进行.图2—1 BP 网络结构Fig.2-1 Structure of BP network图中:jx 表示输入层第j 个节点的输入,j =1,…,M ;ijw 表示隐含层第i 个节点到输入层第j 个节点之间的权值;iθ表示隐含层第i 个节点的阈值;()x φ表示隐含层的激励函数;ki w 表示输出层第k 个节点到隐含层第i 个节点之间的权值,i =1,…,q ;ka 表示输出层第k 个节点的阈值,k =1,…,L ; ()x ψ表示输出层的激励函数;ko 表示输出层第k 个节点的输出.(1)信号的前向传播过程 隐含层第i 个节点的输入net i :1Mi ij j ij net w x θ==+∑ (3—1)隐含层第i 个节点的输出y i :1()()Mi i ij j i j y net w x φφθ===+∑ (3-2)输出层第k 个节点的输入net k :111()qqMk ki i k ki ij j i ki i j net w y a w w x a φθ====+=++∑∑∑ (3—3)输出层第k 个节点的输出o k :111()()()qq M k k ki i k ki ij j i k i i j o net w y a w w x a ψψψφθ===⎛⎫==+=++ ⎪⎝⎭∑∑∑ (3—4)(2)误差的反向传播过程误差的反向传播,即首先由输出层开始逐层计算各层神经元的输出误差,然后根据误差梯度下降法来调节各层的权值和阈值,使修改后的网络的最终输出能接近期望值。
对于每一个样本p 的二次型误差准则函数为E p :211()2Lp k k k E T o ==-∑ (3—5)系统对P 个训练样本的总误差准则函数为:2111()2P Lp p k k p k E T o ===-∑∑ (3—6)根据误差梯度下降法依次修正输出层权值的修正量Δw ki ,输出层阈值的修正量Δa k ,隐含层权值的修正量Δw ij ,隐含层阈值的修正量i θ∆。
kiki w Ew ∂∂-=∆η;k k E a a η∂∆=-∂;ij ij E w w η∂∆=-∂;i i Eθηθ∂∆=-∂ (3-7) 输出层权值调整公式:kikk k k ki k k ki ki w net net o o E w net net E w E w ∂∂∂∂∂∂-=∂∂∂∂-=∂∂-=∆ηηη(3—8)输出层阈值调整公式:k k kk k k k k k k net o net E E E a a net a o net a ηηη∂∂∂∂∂∂∆=-=-=-∂∂∂∂∂∂ (3—9)隐含层权值调整公式:i i iij ij i ij i i ijnet y net E E E w w net w y net w ηηη∂∂∂∂∂∂∆=-=-=-∂∂∂∂∂∂ (3—10)隐含层阈值调整公式:i i ii i i i i i i net y net E E E net y net θηηηθθθ∂∂∂∂∂∂∆=-=-=-∂∂∂∂∂∂ (3-11)又因为:11()P Lp p k k p k k ET o o ==∂=--∂∑∑ (3-12)ikiky w net =∂∂,1k k net a ∂=∂,i j ij net x w ∂=∂,1ii net θ∂=∂ (3-13)11()'()P Lp p k k k ki p k i ET o net w y ψ==∂=--⋅⋅∂∑∑ (3—14))(i iinet net y φ'=∂∂ (3-15)'()kk ko net net ψ∂=∂ (3-16)所以最后得到以下公式:()11()'PLp p ki k k k ip k w T o net y ηψ==∆=-⋅⋅∑∑ (3—17)()11()'P Lp p k k k k p k a T o net ηψ==∆=-⋅∑∑ (3-18)()11()'()PLp p ij k k k ki i jp k w T o net w net x ηψφ=='∆=-⋅⋅⋅⋅∑∑ (3-19)()11()'()PLp p i k k k ki i p k T o net w net θηψφ=='∆=-⋅⋅⋅∑∑ (3-20)图2-2 BP算法程序流程图Fig。
2—2 The flowchart of the BP algorithm program2。
2 基本BP算法的缺陷BP算法因其简单、易行、计算量小、并行性强等优点,目前是神经网络训练采用最多也是最成熟的训练算法之一。
其算法的实质是求解误差函数的最小值问题,由于它采用非线性规划中的最速下降方法,按误差函数的负梯度方向修改权值,因而通常存在以下问题:(1)学习效率低,收敛速度慢(2)易陷入局部极小状态2.3 BP 算法的改进2.3.1附加动量法附加动量法使网络在修正其权值时,不仅考虑误差在梯度上的作用,而且考虑在误差曲面上变化趋势的影响。
在没有附加动量的作用下,网络可能陷入浅的局部极小值,利用附加动量的作用有可能滑过这些极小值。
该方法是在反向传播法的基础上在每一个权值(或阈值)的变化上加上一项正比于前次权值(或阈值)变化量的值,并根据反向传播法来产生新的权值(或阈值)变化。
带有附加动量因子的权值和阈值调节公式为:)()1()1(k w mc p mc k w ij j i ij ∆+-=+∆ηδ)()1()1(k b mc mc k b i i i ∆+-=+∆ηδ其中k 为训练次数,mc 为动量因子,一般取0。
95左右。
附加动量法的实质是将最后一次权值(或阈值)变化的影响,通过一个动量因子来传递.当动量因子取值为零时,权值(或阈值)的变化仅是根据梯度下降法产生;当动量因子取值为1时,新的权值(或阈值)变化则是设置为最后一次权值(或阈值)的变化,而依梯度法产生的变化部分则被忽略掉了.以此方式,当增加了动量项后,促使权值的调节向着误差曲面底部的平均方向变化,当网络权值进入误差曲面底部的平坦区时, i将变得很小,于是)()1(k w k w ij ij ∆=+∆,从而防止了0=∆ij w 的出现,有助于使网络从误差曲面的局部极小值中跳出.根据附加动量法的设计原则,当修正的权值在误差中导致太大的增长结果时,新的权值应被取消而不被采用,并使动量作用停止下来,以使网络不进入较大误差曲面;当新的误差变化率对其旧值超过一个事先设定的最大误差变化率时,也得取消所计算的权值变化。
其最大误差变化率可以是任何大于或等于1的值。
典型的取值取1。
04。
所以,在进行附加动量法的训练程序设计时,必须加进条件判断以正确使用其权值修正公式。
训练程序设计中采用动量法的判断条件为:⎪⎩⎪⎨⎧=mc mc 95.00其它)1()(04.1*)1()(-<->k E k E k E k E , E (k )为第k 步误差平方和。
2。
3.2自适应学习速率对于一个特定的问题,要选择适当的学习速率不是一件容易的事情。
通常是凭经验或实验获取,但即使这样,对训练开始初期功效较好的学习速率,不见得对后来的训练合适。
为了解决这个问题,人们自然想到在训练过程中,自动调节学习速率。
通常调节学习速率的准则是:检查权值是否真正降低了误差函数,如果确实如此,则说明所选学习速率小了,可以适当增加一个量;若不是这样,而产生了过调,那幺就应该减少学习速率的值。
下式给出了一个自适应学习速率的调整公式:⎪⎩⎪⎨⎧=+)()(7.0)(05.1)1(k k k k ηηηη 其它)(04.1)1()()1(k E k E k E k E >+<+ , E(k )为第k 步误差平方和。
初始学习速率(0)的选取范围可以有很大的随意性。
2。
3.3动量—自适应学习速率调整算法当采用前述的动量法时,BP 算法可以找到全局最优解,而当采用自适应学习速率时,BP 算法可以缩短训练时间, 采用这两种方法也可以用来训练神经网络,该方法称为动量-自适应学习速率调整算法.2。
4 网络的设计2。
4。
1网络的层数理论上已证明:具有偏差和至少一个S 型隐含层加上一个线性输出层的网络,能够逼近任何有理数.增加层数可以更进一步的降低误差,提高精度,但同时也使网络复杂化,从而增加了网络权值的训练时间.而误差精度的提高实际上也可以通过增加神经元数目来获得,其训练效果也比增加层数更容易观察和调整.所以一般情况下,应优先考虑增加隐含层中的神经元数. 2.4.2隐含层的神经元数网络训练精度的提高,可以通过采用一个隐含层,而增加神经元数了的方法来获得.这在结构实现上,要比增加隐含层数要简单得多。
那么究竟选取多少隐含层节点才合适?这在理论上并没有一个明确的规定。
在具体设计时,比较实际的做法是通过对不同神经元数进行训练对比,然后适当地加上一点余量。
2。
4.3初始权值的选取由于系统是非线性的,初始值对于学习是否达到局部最小、是否能够收敛及训练时间的长短关系很大。
如果初始值太大,使得加权后的输入和n 落在了S 型激活函数的饱和区,从而导致其导数f’(n )非常小,而在计算权值修正公式中,因为)('n f ∝δ,当f’(n )0→时,则有0→δ。
这使得0→∆ij w ,从而使得调节过程几乎停顿下来.所以一般总是希望经过初始加权后的每个神经元的输出值都接近于零,这样可以保证每个神经元的权值都能够在它们的S 型激活函数变化最大之处进行调节.所以,一般取初始权值在(-1,1)之间的随机数。
2.4。
4学习速率学习速率决定每一次循环训练中所产生的权值变化量。
大的学习速率可能导致系统的不稳定;但小的学习速率导致较长的训练时间,可能收敛很慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差值.所以在一般情况下,倾向于选取较小的学习速率以保证系统的稳定性。
学习速率的选取范围在0。
01—0。
8之间.3 BP神经网络的应用现给出一药品商店一年当中12个月的药品销售量(单位:箱)如下:2056 2395 2600 2298 1634 1600 1873 1487 1900 1500 2046 1556训练一个BP网络,用当前的所有数据预测下一个月的药品销售量。
有两种方法实现,一种是编写matlab程序,一种是使用nntool工具箱。
3。
1 matlab程序实现我们用前三个月的销售量预测下一个月的销售量,也就是用1-3月的销售量预测第4个月的销售量,用2-4个月的销售量预测第5个月的销售量,如此循环下去,直到用9-11月预测12月份的销售量。
