(衡水金卷)2018年普通高等学校招生全国统一考试模拟数学试题四文(含答案)

合集下载

衡水金卷2018年普通高等学校招生全国统一考试模拟试题理数(二)(附答案)

衡水金卷2018年普通高等学校招生全国统一考试模拟试题理数(二)（附答案）第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知i 为虚数单位，复数12aii +- (a R ∈)为纯虚数，则a 的值为 A ．-2 B ．12-C ．2D ．122. 已知集合{}2log 3A x x =<，{}2450B x x x =-->，则()R A C B =（）A ．[)1,8- B ． (]05, C ．[)1,5- D ．()0,8 3. 已知n S 是各项均为正数的等比数列{}n a 的前n 项和，764a =，15320a a a +=，则5S =（）A ．31B ．63C ． 16D ． 1274.设向量a =，(,3)b x =-，(1,c =，若//b c ，则a b -与b 的夹角为（） A ．30︒ B ．60︒ C. 120︒ D ．150︒5.大约2000多年前，古希腊数学家最先开始研究圆锥曲线，并获得了大量的成果，古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究这几种曲线，用垂直于锥轴的平面去截圆锥，得到的是圆；把平面再渐渐倾斜得到椭圆.若用周长为24的矩形ABCD 截某圆锥得到椭圆Γ，且Γ与矩形ABCD 的四边相切.设椭圆Γ在平面直角坐标系中的方程为22221(0)x y a b a b +=>>，测得Γ的离心率为，则椭圆Γ的方程为（）A ．221164x y +=B ．2214x y += C. 2216416x y += D ．22154x y +=6.已知某服装厂生产某种品牌的衣服，销售量()q x (单位：百件)关于每件衣服的利润x(单位：元)的函数解析式为1260,020,1()9020180,xxq xx⎧<≤⎪+=⎨⎪-<≤⎩, 则当该服装厂所获效益最大时，x=A．20 B．60 C. 80 D．407. 已知,x y满足不等式组240,20,30,x yx yy+-≥⎧⎪--≤⎨⎪-≤⎩则1z x y=+-的最小值为（）A．2 B．．18. 已知函数21()10sin10sin2f x x x=---，,2x mπ⎡⎤∈-⎢⎥⎣⎦的值域为1,22⎡⎤-⎢⎥⎣⎦，则实数m的取值范围是（）A．,03π⎡⎤-⎢⎥⎣⎦ B．,06π⎡⎤-⎢⎥⎣⎦ C.,36ππ⎡⎤-⎢⎥⎣⎦ D．,63ππ⎡⎤-⎢⎥⎣⎦9.已知21(1+2)nx xx⎛⎫-⎪⎝⎭的展开式中常数项为-42，则n=（）A． 10 B． 8 C. 12 D．1110. 某几何体的三视图如图所示，则该几何体的表面积为（）A．30π．803π923π．763π11.已知22221x y a b Γ-=：（0,0a b >>1）的左、右焦点分别为1F ，2F ，点P 是双曲线Γ右支上一点，且212PF F F ⊥，过点P 作1F P 的垂线交x 轴于点A ，且22P M M F =，若PA 的中点E 在1F M 的延长线上，则双曲线Γ的离心率是（）A．．D．12. 已知函数22()(2)()f x x x x mx n =+++，且对任意实数x ,均有(3)(3)f x f x -+=--，若方程()f x a =有且只有4个实根，则实数a 的取值范围（）A ．(16,9)-B ．(]16,9- C. (]16,0- D ．(]16,5--第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知圆心角为120︒的扇形的圆心为O ，在其弧AB 上任取一点P ，则使AOP ∠和BOP ∠同时大于50︒的概率为．14.已知直线m ，n 和平面α，β，且m α⊂，n β⊂，则“//m β，//n α”是“//αβ”的条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要” 15.执行如图所示的程序框图，若输出的2017s =，则正整数T = ．16. 已知数列{}n a 满足11a =，22a =，212n na +是(2)n n a +，2(2)a n λ+的等差中项，若{}n a 为单调递增数列，则实数λ的取值范围为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在ABC ∆中，,,a b c 分别为内角,,A B C的对边，向量,)m A a =，(,cos )n b B =，2m n a ⋅=（1）求B ；（2）若ABC ∆外接圆的直径为sin sin()2sin2B C AA +-=，求ABC ∆的面积. 18.在如图所示的多面体中，平面11ABB A ⊥平面ABCD ，四边形11ABB A 为边长为2的菱形，ABCD 为直角梯形，四边形11BCC B 为平行四边形，且//AB CD ，AB BC ⊥，1CD =. （1）若E ，F 分别为11AC ，1BC 的中点，求证：EF ⊥平面11AB C ；（2）若160A AB ∠=︒，1AC 与平面ABCD所成角的正弦值为，求二面角11A AC D --的余弦值.19.某企业从某种型号的产品中抽取了N 件对该产品的某项指标E 的数值进行检测，将其整理成如图所示的频率分布直方图，已知数值在100~110的产品有2l 件.（1）求N 和a 的值；（2）规定产品的级别如下表：已知一件,,C B A 级产品的利润分别为10，20，40元,以频率估计概率，现质检部门从该批产品中随机抽取两件，两件产品的利润之和为X ，求X 的分布列和数学期望；（3）为了了解该型号产品的销售状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图，由折线图可以看出，可用线性回归模型拟合月度市场卢有率y （%）与月份代码x 之间的关系.求y 关于x 的线性回归方程，并预测2017年4月份(即7x =时)的市场占有率.(参考公式：回归直线方程为ˆˆˆybx a =+，其中121()()ˆ()niii nii x x y y bx x ==--=-∑∑，ˆˆ)a y bx =-20.已知抛物线2:2x py Γ=（0p >），直线2y =与抛物线Γ交于,A B (点B 在点A 的左侧)两点，且AB =.（1）求抛物线Γ在,A B 两点处的切线方程；（2）若直线l 与抛物线Γ交于,M N 两点，且,M N 的中点在线段AB 上，MN 的垂直平分线交y 轴于点Q ，求QMN ∆面积的最大值.21.已知函数()x f x e mx =-，()()2x g x xf x e =-+，e 为自然对数的底数. （1）若函数()f x 在点(1,(1))f 处的切线为(1)y e x n =-+，求,m n 的值；（2）当2m >时，若()g x 在区间[)0,+∞上有两个零点1x ,212()x x x <，试判断14lnx e +，2x ，m 的大小关系.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的长度单位.已知直线l的参数方程为,222xy⎧=⎪⎪⎨⎪=-+⎪⎩(t为参数)，曲线1C的参数方程为,2sinx ay a⎧=⎪⎨=⎪⎩(a为参数)，曲线2C的极坐标方程为[)0,2)ρθπ=∈.（1）求曲线1C和2C的公共点的极坐标；（2）若P为曲线1C上的一个动点，求P到直线l的距离的最大值.23.选修4-5：不等式选讲已知函数()224f x x x=-++.（1）解不等式：()34f x x≥-+；（2）若函数()f x的最小值为a，且(0,0)m n a m n+=>>，试求2018201810071007m n+++的最小值.理数（二）一、选择题1-5: CBADA 6-10: CDBBC 11、12：CA二、填空题13.16 14. 必要不充分 15. 2016 16.[)0,+∞三、解答题17.解:（1）因为2m n a⋅=，sin cos2A aB a+=.sin sin cos 2sin B A A B A +=，又sin 0A ≠，cos 2sin()26B B B π+=⇒+=.因为0B π<<，所以7666B πππ<+<，所以62B ππ+=，即3B π=.（2）由（1）和正弦定理，得32b B ===.因为sin sin()2sin 2B C A A +-=，所以sin()sin()2sin 2C A C A A ++-=，sin cos cos sin sin cos cos sin 4sin cos C A C A C A C A A A ++-=，即 sin cos 2sin cos C A A A =.当cos 0A =时，2A π=，由正弦定理，得a =c =所以12ABC S bc ∆==. 当cos 0A ≠时，有sin 2sin C A =，即2c a =，由余弦定理，得222a cb ac +-=，所以239a a =⇒=c =所以1sin 22ABC S ac B ∆==综上，ABC ∆的面积为.18.解:（1）连接1A B ,因为四边形11ABB A 为菱形，所以11A B AB ⊥.因为平面11ABB A ⊥平面A B C D ，平面11ABB BA 平面A B C D A B =，BC ⊂平面A B C D ，AB BC ⊥，所以BC ⊥平面11ABB A . 又1A B ⊂平面11ABB A ，所以1A B BC ⊥. 因为11//BC B C ，所以111A B B C ⊥. 因为1111B C AB B =，所以1A B ⊥平面11AB C .因为,E F 分别为11AC ，1BC 的中点，所以1//EF A B ，所以EF ⊥平面11AB C（2）设11B C a =，由（1）得11B C ⊥平面11ABB A .由160A AB ∠=︒，2BA =，得1AB =1AC =过点1C 作1C M DC ⊥，与DC 的延长线交于点M ，取AB 的中点H ，连接1A H ，AM ，如图所示，又160A AB ∠=︒，所以1ABA ∆为等边三角形，所以1A H AB ⊥，又平面11ABB A ⊥平面ABCD ，平面11ABB A 平面ABCD AB =，1A H ⊂平面11ABB A ，故1A H ⊥平面ABCD .因为11BCC B 为平行四边形，所以11//CC BB ，所以1//CC 平面11AA BB .又因为//CD AB ，所以//CD 平面11AA BB .因为1CC CD C =，所以平面11//AA BB 平面1DC M .由（1），得BC ⊥平面11AA BB ，所以BC ⊥平面1DC M ，所以1BC C M ⊥.因为BC DC C =，所以1C M ⊥平面ABCD ，所以1C AM ∠是1AC 与平面ABCD 所成角. 因为11//A B AB ，11//C B CB ，所以11//A B 平面ABCD ，11//B C 平面ABCD ，因为11111A B C B B =，所以平面//ABCD 平面111A B C .所以11A H C M ==111sin MC C AM AC ∠===，解得a =在梯形ABCD 中，易证DE AB ⊥，分别以HA ，HD ，1HA 的正方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系.则(1,0,0)A，D，1A，1(B -，(1,0,0)B -，(1C -，由1(1BB =-，及11BB CC =，得1(C -，所以(1AC =-，(1AD =-，1(1AA =-.设平面1ADC 的一个法向量为111(,,)m x y z =，由10,0,m AC m AD ⎧⋅=⎪⎨⋅=⎪⎩得1111130,0,x x ⎧-+=⎪⎨-=⎪⎩令11y =，得m=(3,1,2) 设平面AA1C1的一个法向量为n=(x2,y2,z2),2)m =.设平面11AAC 的一个法向量为222(,,)n x y z =，由110,0,n AC n AA ⎧⋅=⎪⎨⋅=⎪⎩得2222230,0,x x ⎧-=⎪⎨-+=⎪⎩令21z =，得n =.所以7cos ,8m n m n m n ⋅====又因为二面角11A AC D --是钝角，所以二面角11A AC D --的余弦值是78-.19.解：（1）数值在100~110内的频率为(0.04+0.03)5=0.35⨯，所以21600.35N ==.又因为521(0.020.030.0420.05)5a ⨯=-++⨯+⨯，所以0.01a =.（2）由频率分布直方图，可知抽取的一件产品为C ，B ，A 等级的概率分别为14，35，320，且X 的取值为20，30，40，50，60，80，则111(20)4416P X ==⨯=，133(30)24510P X ==⨯⨯=，339(40)5525P X ==⨯=，133(50)242040P X ==⨯⨯=，339(60)252050P X ==⨯⨯=，339(80)2020400P X ==⨯=，所以X 的分布列为所以139399()203040506080411610254050400E X =⨯+⨯+⨯+⨯+⨯+⨯=.（3）由折线图中所给的数据计算，可得1234563.56x +++++=，111316152021166y +++++==，所以121()()35ˆ217.5()niii nii x x y y bx x ==--===-∑∑，所以ˆ162 3.59a=-⨯=，故月度市场占有率(%)y 与月份序号x 之间的线性回归方程为ˆ29y x =+.当7x =时，ˆ27923y =⨯+=.所以2017年4月份的市场占有率预计为23%.20.解：（1）由22x p y =，令2y =，得x =±所以=解得3p =，26x y =，由26x y =，得3xy '=，故x x y y -=''，所以在A 点的切线方程为2y x -=-，即20x -=，同理可得在B 点的切线方程为20x +=. （2）由题意得直线l 的斜率存在且不为0，故设:l y kx m =+，11(,)M x y ，22(,)N x y ，由26x y =与y kx m =+联立，得2660x kx m --=，236240k m =+>，所以126x x k +=，126x x m =-，故MN ==又21212()2624y y k x x m k m +=++=+=，所以223m k =-，所以MN =，由236240k m ∆=+>，得k <<且0k ≠. 因为,M N 的中点为(3,2)k ，所以,M N 的垂直平分线方程为12(3)y x k k -=--，令0x =，得5y =，即(0,5)Q ，所以点Q 到直线2230kx y k -+-=的距离d ==，所以12QMN S ∆=⋅=令21k u+=，则21k u=-，则713u<<，故QMNS∆=设2()(73)f u u u=-，则2()149f u u u'=-，结合713u<<，令()0f u'>，得1419u<<；令()0f u'<，得14793u<<，所以当149u=，即3k=±时，m a x1147()Q M NS∆=.21.解：（1）由题意，知(1)1f e'=-，(1)1f e n=-+.因为()xf x e m'=-，所以(1)1f e m e'=-=-，即1m=.又因为(1)1f e=-，所以0n=.（2）由题意，知2()2x xg x xe mx e=--+.因为2x>，0x≥，由()(2)0xg x x e m'=-=，得0x=或ln(2)x m=.当ln(2)x m>时，()0g x'>，所以()g x在区间(ln(2),)m+∞上单调递增；当0ln(2)x m<<时，()0g x'<，所以()g x在区间(0,ln(2))m上单调递减；所以()g x的极小值为(ln(2))g m.因为l n(2)l nm>>，且()g x在区间(0,l n(2m上单调递减，所以(ln(2))(1)20g m g m<=-<.又因为(0)10g=>，(1)20g m=-<，所以存在1(0,1)x∈，使得1()0g x=，所以存在2(ln(2),)x m∈+∞，使得2()0g x=，且2ln(2)ln4x m>>，所以214ln41lnx xe->-=，即214lnx xe>+.当x m =时，3()(1)2m g m m e m =--+，2m >. 令3()(1)2x u x x e x =--+，2x >，则22()3(3)xu x xe x x e x '=-=-，设()3xG x e x =-，则()30xG x e '=->在区间(2,)+∞上恒成立，所以()G x 在区间(2,)+∞上单调递增，所以2()(2)60G x G e >=->，所以()0u x '>在区间(2,)+∞上恒成立，即()u x 在区间(2,)+∞上单调递增，故2()(2)60u m u e >=->，所以当2m >时，()0g m >. 又因为2()0g x =，()g x 在区间(ln(2),)m +∞上单调递增，所以2m x >所以124lnx x m e +<<.22.解：（1）因为曲线1C的参数方程为,2sin x a y a ⎧=⎪⎨=⎪⎩,(a 为参数)所以曲线1C 的直角坐标方程为221124x y +=.因为222x y ρ=+，所以曲线2C 的直角坐标方程为226x y +=.两方程联立得x y ⎧=⎪⎨=⎪⎩或x y ⎧=⎪⎨=⎪⎩或x y ⎧=⎪⎨=⎪⎩或x y ⎧=⎪⎨=⎪⎩所以其极坐标分别为)4π，3)4π，，5)4π，，7)4π，. （2）直线l 的普通方程为20x y --=. 设点(3co s ,2s i n )P a a ，则点P到l l的距离d ==当26a k πππ+=+，即526a k ππ=+，k Z ∈时，maxd =23.解：（1）()224f x x x =-++32,2,6,22,32,2,x x x x x x --<-⎧⎪=+-≤≤⎨⎪+>⎩可得当2x <-时，3234x x --≥-+，即24-≥，可知无解；当22x -≤≤时，634x x +≥-+，得12x ≥-，可得122x -≤≤；当2x >时，3234x +≥-+，得13x ≥，可得2x >.∴不等式的解集为12x x ⎧⎫≥-⎨⎬⎩⎭. （2）根据函数32,2,()6,22,32,2,x x f x x x x x --<-⎧⎪=+-≤≤⎨⎪+>⎩,可知当2x =-时，函数取得最小值(2)4f -=，可知4a =，4m n +=，∴100710072018m n +++=. ∴2018201810071007m n +++100710071007100710071007m n m n m n ++++++=+++ 10071007210071007n m m n ++=++++4≥=，当且仅当2m n ==时，取得最小值为4.。

2018年衡水金卷普通高等学校招生全国统一考试模拟试卷分科综合卷理科数学(三)(解析版)

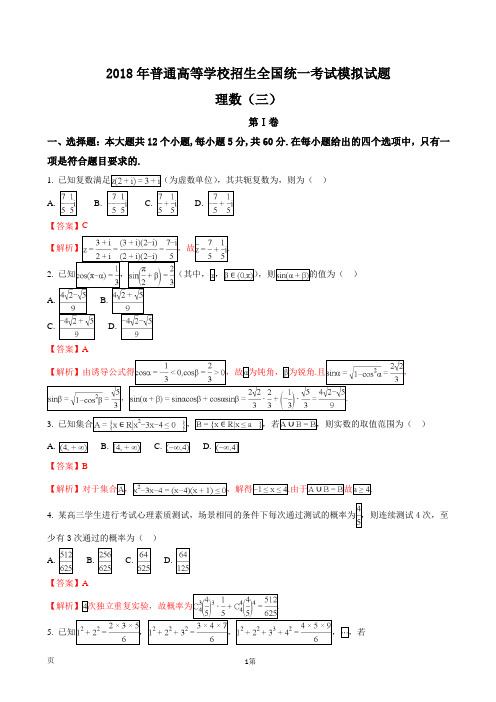
2018年普通高等学校招生全国统一考试模拟试题理数（三）第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 为虚数单位），其共轭复数为，则为（）B. D.【答案】C2. ，（其中，，）B.D.【答案】A为钝角，.3. 已知集合，，若，则实数的取值范围为（）B. C.【答案】B故4. 4次，至少有3次通过的概率为（）【答案】A5. ，）A. 8B. 9C. 10D. 11【答案】C【解析】通过归纳得，故解得.学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...6. 的左顶点为为（）【答案】D7. 图像上的所有点向右平移调递增，则的最大值为（）【答案】D递增，故的最大值为8. 若输出的则判断框中应填入的条件是（）【答案】B9. 朱世杰是历史上有名的数学家之一，他所著的《四元玉鉴》卷中“如像招数一五间”，有如下问题：“今有官司差夫一千八百六十四人筑堤，只云初日差六十四人，次日转多七人，每人日支米三升，共支米四百三石九斗二升，问筑堤几日？”其大意为：“官府陆续派遣1864人前往修筑堤坝，第一天派出64人，从第二天开始，每天派出的人数比前一天多7人，修筑堤坝的每人每天发大米3升，共发出大米40392升，问修筑堤坝多少天”，在这个问题中，第8天应发大米（）A. 350升B. 339升C. 2024升D. 2124升【答案】D.10. 已知三棱锥的三视图如图所示，则该三棱锥内切球的半径为（）【答案】B，故11. 如图所示，中，）B. 2 D. 4【答案】A【解析】故四边形所成角的正切值为【点睛】本题主要考查直线与平面的位置关系，考查两条异面直线所成的角.要求两条异面直线所成的角，思路是将它们平移到同一个平面、同一个三角形内，然后利用解三角形来求得它们所成角的大小或某个三角函数值.本题中通过平行四边形构造了线线平行，解这个直角三角形即可得到所求.12. 为函数生点对”，则实数的值为（）A. 0B. 2C. 4D. 6【答案】A.处取得极小值.根据孪生点对的性质可知，要恰好有两个孪生点对，则需当【点睛】本题主要考查利用导数研究函数的图像与性质，考查新定义问题的处理方法，考查函数图像关于原点对称点的处理策略.要分段函数两段图像有关于原点的对称点，一般可以将较简单的一段，关于原点对，关于原点对称即为第Ⅱ卷二、填空题（每题5分，满分20分，将答案填在答题纸上）13. __________．【答案】18【解析】含项为，故系数为.14. 如图所示，的三等分点，则向量__________．【解析】设正方形的边长为【点睛】本题主要考查平面向量的线性运算.由于题目所给图形为正方形，故考虑建立平面直角坐标系，利用坐标来计算会使得运算简单明了.作为正方形的边长，再根据.15.）分别有一个交点，则该双曲线的离心率的取值范围是__________．设双曲线方程为，解得【点睛】本题主要考查平面解析几何的思想方法，将几何问题代数化.由于题目涉及到双曲线，故首先建立点应该在双曲线图像的上方，由此可列不等式，求得的范围，进而求得离心率的范围.16. ，则数列．【解析】当时，2为底的对数可得1为首项，2为公比的等比数列，即，因此.点睛：本题主要考查了通过数列递推式求数列的通项公式，根据通项公式的特征求数列的前1为首项，2.三、解答题（解答应写出文字说明、证明过程或演算步骤.）17. ，（1（2的大小.【答案】(1)2;(2) 的大小为【解析】【试题分析】（1）利用三角形内角和定理和两角和的正弦、余弦公式，将题目所给等式化简为只含.（2又由已知【试题解析】（1因为在中，，所以（2）在中，由余弦定理，所以，所以，所以.的大小为18. 如图所示，在三棱锥中，平面（1（2的平面角的大小为.【答案】(1)见解析；（2所成角的正弦值为【解析】【试题分析】（1为直角三角形，即2），连接.【试题解析】（1所以.故，即有（2由（1）.又由（1的平面角，即，所成角的正弦值为.19. 某葡萄基地的种植专家发现，葡萄每株的收获量）和与它“相近”葡萄的株数，并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时，该葡萄每株收获量的相关数据如下：（1关于它“相近”葡萄的株数（2）某葡萄专业种植户种植了1000株葡萄，每株“相近”的葡萄株数按2株计算，当年的葡萄价格按10元（精确到0.01）（3）该葡萄基地在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株葡萄，其中.（注：每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据）【答案】（17；（2（3）见解析.【解析】【试题分析】（1）利用回归直线方程的公式，计算.利用样本方差的公式计算得方差.（2代入回归直线方程，求得对应预报变量的值，进而求得总收入.（3出期望值.【试题解析】.，故该葡萄每株收获量关于它“相近”葡萄的株数（2）由，可知当时，因此总收入为（万元）.（3）由题知，.由（1）（2），时，与之相对应的的值分别为13,12,11，，所以在所种葡萄中随机选取一株，它的收获量20. 的焦点为.（1，且与圆定值；（2）设抛物线.【答案】（1）见解析；（2，使得四边形【解析】试题分析：(1) 1.(2)由题意可得当直线的斜率为0试题解析：，，联立1，(为定值，定值为1．（Ⅱ）当直线的斜率为0在处的切线为……①同理抛物线在，代入①式解得，所以，的中点为．方法二：，则，处的切线为方法三：，，点睛：1.圆锥曲线有关综合问题,常需分析图形的静与动,抓住变化的关键因素.2.“目标先行”是一个永远的话题3.数、形两方面恰当地表示图形的位置关系和数量关系.几何关系如何用代数形式转化,是解圆锥曲线问题的关键.21.（1（2时，令函数在区间范围.【答案】（1；（2【解析】【试题分析】（1时，求出切点和斜率，利用直线方程点斜式可求得切线方程.（2）先化利用导数求得其最小值为上有两个零点的条件是，解这个不等式求得.【试题解析】（1因此所求切线方程为（2因为，所以当时，在则，所以在区间上的最小值为在区间上有两个零点的条件是所以实数的取值范围是.【点睛】本题主要考查函数导数与切线，考查函数导数与零点问题，考查化归与转化的数学思想方法.第一问要求函数在某一点的切线方程，只需求出切点和斜率，利用点斜式即可求得对应的切线方程.第二问利用图像得到其最小值后列不等式组来求.22. .为极点，（1的方程及直线的直角坐标方程；（2.【答案】（1（2【解析】【试题分析】（1消去参数，可得曲线后直接转化为直角坐标方程.（2. 【试题解析】（1，，点的轨迹所以直线的直角坐标方程为（2）由（1）点的轨迹1的圆，到直线的距离为上的点到直线的距离的最大值为【点睛】本题主要考查参数方程和直角坐标方程互化，考查极坐标方程和直角坐标方程互化，考查圆上的点到直线距离的最大值与最小值问题.涉及三角函数的消参方法往往是利用23.（1的图像；（2的最大值为若不存在，说明理由.【答案】（1）见解析；（2【解析】【试题分析】（1）利用零点分段法，去绝对值，将函数用分段函数表示出来来，并作出图像.（2）由（1,值.【试题解析】（1作图如下：（2）由图像可知，的最小值为4，与故不存在正数，，且.。

【衡水金卷】2018年普通高等学校招生全国统一考试模拟试题(二,压轴卷)数学(理)试题

2018年普通高等学校招生全国统一考试模拟试题理科数学(二)本试卷共4页，23题(含选考题)。

全卷满分1 50分。

考试用时120分钟。

第I 卷一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中。

只有一项是符合题目要求的。

1．已知集合{}{}1,1,2,3,5,6,210xA B x Z =-=∈<，则AB=A ．{1}B ．{l ，2}C ．{1，2，3}D ．{一1，1，2，3}2．设i 为虚数单位，复数z 满足2(13)(3)i z i +=-+，则共轭复数z 的虚部为 A ．3i B ．3i - C ．3 D ．3- 3．学生李明上学要经过4个路口，前三个路口遇到红灯的概率均为12，第四个路口遇到红灯的概率为13，设在各个路口是否遇到红灯互不影响，则李明从家到学校恰好遇到一次红灯的概率为 A ．724 B ．14 C ． 124 D ． 184．已知双曲线方程为22221(0,0)x y a b a b-=>>，F 1，F 2为双曲线的左、右焦点，P 为渐近线上一点且在第一象限，且满足120PF PF ⋅=，若1230PF F ︒∠=，则双曲线的离心率为 A ．2 B ．2 C ．22 D ．3 5．已知θ为锐角，1cos 211cos 22θθ-=+，则sin()3πθ+的值为A ．264+ B ．624- C ．366+ D ．3236+ 6．执行如图所示的程序框图，则输出的s 的值为A ．一1B ．一2C ．1D ．27．2101211011112(1)(2)(1)(1)(1)x x a x a x a x a +-=-+-++-+，则01211a a a a ++++的值为A ．2B ．0C ．一 2D ．一48．某几何体三视图如图所示，则该几何体的表面积为 A ．2052π-B ．203π-C ．24π-D ．12π+9．已知34a b ==12，则a ，b 不可能满足的关系是 A ．a +b >4 B ．ab >4C ．(a 一1)2+(b —1)2>2D ．a 2+b 2<8 10．若函数()sin()(0)6f x x πωω=+>在区间(π，2π)内没有最值，则ω的取值范围是 A ．112(0,][,]1243 B ．(0，16][13，23] C ．[12,43] D ．[12,33] 11．过抛物线x 2=2p y (p>0)上两点A ，B 分别作抛物线的切线，若两切线垂直且交于点 P(1，一2)，则直线AB 的方程为 A ．122y x =+ B ．124y x =+ C ．132y x =+ D ．134y x =+ l 2．在正三棱锥(底面是正三角形，顶点在底面的射影是底面三角形的中心的三棱锥)O 一ABC 中，OA ，OB ，OC 三条侧棱两两垂直，正三棱锥O —ABC 的内切球与三个侧面切点分别为D ，E ，F ，与底面ABC 切于点G ，则三棱锥G —DEF 与O —ABC 的体积之比为 A ．23318+ B ．23318- C ．6239+ D ．6239- 第Ⅱ卷本卷包括必考题和选考题两部分。

衡水金卷(一)理科数学试题(卷)含答案

2018年普通高等学校招生全国统一考试模拟试题理数（一）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，，则（）A. B. C. D.2. 设是虚数单位，若，，，则复数的共轭复数是（）A. B. C. D.3. 已知等差数列的前项和是，且，则下列命题正确的是（）A. 是常数B. 是常数C. 是常数D. 是常数4. 七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形）、一块正方形和一块平行四边形组成的．如图是一个用七巧板拼成的正方形中任取一点，则此点取自黑色部分的概率是（）学*科*网...A. B. C. D.5. 已知点为双曲线：（，）的右焦点，直线与双曲线的渐近线在第一象限的交点为，若的中点在双曲线上，则双曲线的离心率为（）A. B. C. D.6. 已知函数则（）A. B. C. D.7. 执行如图所示的程序框图，则输出的的值为（）A. B. C. D.8. 已知函数（）的相邻两个零点差的绝对值为，则函数的图象（）A. 可由函数的图象向左平移个单位而得B. 可由函数的图象向右平移个单位而得C. 可由函数的图象向右平移个单位而得D. 可由函数的图象向右平移个单位而得9. 的展开式中剔除常数项后的各项系数和为（）A. B. C. D.10. 某几何体的三视图如图所示，其中俯视图中六边形是边长为1的正六边形，点为的中点，则该几何体的外接球的表面积是（）A. B. C. D.11. 已知抛物线：的焦点为，过点分别作两条直线，，直线与抛物线交于、两点，直线与抛物线交于、两点，若与的斜率的平方和为1，则的最小值为（）A. 16B. 20C. 24D. 3212. 若函数，，对于给定的非零实数，总存在非零常数，使得定义域内的任意实数，都有恒成立，此时为的类周期，函数是上的级类周期函数．若函数是定义在区间内的2级类周期函数，且，当时，函数．若，，使成立，则实数的取值范围是（）A. B. C. D.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知向量，，且，则__________．14. 已知，满足约束条件则目标函数的最小值为__________．15. 在等比数列中，，且与的等差中项为17，设，，则数列的前项和为__________．16. 如图，在直角梯形中，，，，点是线段上异于点，的动点，于点，将沿折起到的位置，并使，则五棱锥的体积的取值范围为__________．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知的内角，，的对边，，分别满足，，又点满足．（1）求及角的大小；（2）求的值．18. 在四棱柱中，底面是正方形，且，．（1）求证：；（2）若动点在棱上，试确定点的位置，使得直线与平面所成角的正弦值为．19. “过大年，吃水饺”是我国不少地方过春节的一大习俗．2018年春节前夕，市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标，（1）求所抽取的100包速冻水饺该项质量指标值的样本平均数（同一组中的数据用该组区间的中点值作代表）；（2）①由直方图可以认为，速冻水饺的该项质量指标值服从正态分布，利用该正态分布，求落在内的概率；②将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这4包速冻水饺中这种质量指标值位于内的包数为，求的分布列和数学期望．附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为；②若，则，．20. 已知椭圆：的离心率为，且以两焦点为直径的圆的内接正方形面积为2．（1）求椭圆的标准方程；（2）若直线：与椭圆相交于，两点，在轴上是否存在点，使直线与的斜率之和为定值？若存在，求出点坐标及该定值，若不存在，试说明理由．21. 已知函数，其中为自然对数的底数.（1）若函数在区间上是单调函数，试求实数的取值范围；（2）已知函数，且，若函数在区间上恰有3个零点，求实数的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程在平面直角坐标系中，圆的参数方程为（为参数，是大于0的常数）．以坐标原点为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方程为．（1）求圆的极坐标方程和圆的直角坐标方程；（2）分别记直线：，与圆、圆的异于原点的焦点为，，若圆与圆外切，试求实数的值及线段的长．23. 选修4-5：不等式选讲已知函数．（1）求不等式的解集；（2）若正数，满足，求证：．一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，，则（）A. B. C. D.【答案】C【解析】集合，故，集合表示非负的偶数，故，故选C.2. 设是虚数单位，若，，，则复数的共轭复数是（）A. B. C. D.【答案】A【解析】，根据两复数相等的充要条件得，即，其共轭复数为，故选A.3. 已知等差数列的前项和是，且，则下列命题正确的是（）A. 是常数B. 是常数C. 是常数D. 是常数【答案】D【解析】，为常数，故选D.4. 七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形）、一块正方形和一块平行四边形组成的．如图是一个用七巧板拼成的正方形中任取一点，则此点取自黑色部分的概率是（）A. B. C. D.【答案】A【解析】由七巧板的构造可知，，故黑色部分的面积与梯形的面积相等，则所求的概率为，故选A.5. 已知点为双曲线：（，）的右焦点，直线与双曲线的渐近线在第一象限的交点为，若的中点在双曲线上，则双曲线的离心率为（）A. B. C. D.【答案】D【解析】由，解得点，又，则的中点坐标为，于是，，则，解得或（舍去），故选D.【方法点睛】本题主要考查双曲线的定义及离心率，属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出，从而求出;②构造的齐次式，求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解．本题中，根据的中点坐标为在双曲线上找出之间的关系，从而求出离心率．6. 已知函数则（）A. B. C. D.【答案】D【解析】，，的几何意义是以原点为圆心，半径为的圆的面积的，故，故选D.7. 执行如图所示的程序框图，则输出的的值为（）A. B. C. D.【答案】C【解析】图中程序数列的和，因为，故此框图实质计算，故选C.8. 已知函数（）的相邻两个零点差的绝对值为，则函数的图象（）A. 可由函数的图象向左平移个单位而得B. 可由函数的图象向右平移个单位而得C. 可由函数的图象向右平移个单位而得D. 可由函数的图象向右平移个单位而得【答案】B【解析】，因为函数（）的相邻两个零点差的绝对值为，所以函数的最小正周期为，而，，故的图象可看作是的图象向右平移个单位而得，故选B.9. 的展开式中剔除常数项后的各项系数和为（）A. B. C. D.【答案】A【解析】令，得，而常数项为，所以展开式中剔除常数项的各项系数和为，故选A.10. 某几何体的三视图如图所示，其中俯视图中六边形是边长为1的正六边形，点为的中点，则该几何体的外接球的表面积是（）A. B. C. D.【答案】C【解析】由三视图可知，该几何体是一个六棱锥，其底面是边长为的正六边形，有一个侧面是底边上的离为的等腰三角形，且有侧面底面，设球心为，半径为到底面的距离为，底面正六边形外接球圆半径为，解得此六棱锥的外接球表面枳为，故选C.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力以及外接球的表面积，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.11. 已知抛物线：的焦点为，过点分别作两条直线，，直线与抛物线交于、两点，直线与抛物线交于、两点，若与的斜率的平方和为1，则的最小值为（）A. 16B. 20C. 24D. 32【答案】C【解析】易知直线，的斜率存在，且不为零，设，直线的方程为，联立方程，得，，同理直线与抛物线的交点满足，由抛物线定义可知，又（当且仅当时取等号），的最小值为，故选C.12. 若函数，，对于给定的非零实数，总存在非零常数，使得定义域内的任意实数，都有恒成立，此时为的类周期，函数是上的级类周期函数．若函数是定义在区间内的2级类周期函数，且，当时，函数．若，，使成立，则实数的取值范围是（）A. B. C. D.【答案】B【解析】是定义在区间内的级类周期函数，且，，当时，，故时，时，，而当时，，，当时，在区间上单调递减，当时，在区间上单调递增，故，依题意得，即实数的取值范围是，故选B.【方法点睛】本题主要考查分段函数函数的最值、全称量词与存在量词的应用以及新定义问题. 属于难题.解决这类问题的关键是理解题意、正确把问题转化为最值和解不等式问题，全称量词与存在量词的应用共分四种情况：（1）只需；（2），只需；（3），只需；（4），，.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知向量，，且，则__________．【答案】【解析】,,故答案为.14. 已知，满足约束条件则目标函数的最小值为__________．【答案】【解析】，作出约束条件表示的可行域，如图，平移直线，由图可知直线经过点时，取得最小值，且，，故答案为.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.15. 在等比数列中，，且与的等差中项为17，设，，则数列的前项和为__________．【答案】【解析】设的公比为，则由等比数列的性质，知，则，由与的等差中项为，知，得，即，则，，故答案为.16. 如图，在直角梯形中，，，，点是线段上异于点，的动点，于点，将沿折起到的位置，并使，则五棱锥的体积的取值范围为__________．【答案】【解析】，平面，设，则五棱锥的体积，，得或（舍去），当时，单调递增，故，即的取值范围是，故答案为.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知的内角，，的对边，，分别满足，，又点满足．（1）求及角的大小；（2）求的值．【答案】(1) (2)【解析】试题分析：（1）由及正弦定理化简可得即，从而得．又，所以，由余弦定理得；（2）由，得，所以．试题解析：（1）由及正弦定理得，即，在中，，所以．又，所以．在中，由余弦定理得，所以．（2）由，得，所以．18. 在四棱柱中，底面是正方形，且，．（1）求证：；（2）若动点在棱上，试确定点的位置，使得直线与平面所成角的正弦值为．【答案】(1)见解析(2)【解析】试题分析：（1）连接，，，与的交点为，连接，则，由正方形的性质可得，从而得平面，，又，所以；（2）由勾股定理可得，由（1）得所以底面，所以、、两两垂直．以点为坐标原点，的方向为轴的正方向，建立空间直角坐标系，设（），求得，利用向量垂直数量积为零可得平面的一个法向量为，利用空间向量夹角余弦公式列方程可解得，从而可得结果.试题解析：（1）连接，，，因为，，所以和均为正三角形，于是．设与的交点为，连接，则，又四边形是正方形，所以，而，所以平面．又平面，所以，又，所以．（2）由，及，知，于是，从而，结合，，得底面，所以、、两两垂直．如图，以点为坐标原点，的方向为轴的正方向，建立空间直角坐标系，则，，，，，，，，由，易求得．设（），则，即，所以．设平面的一个法向量为，由得令，得，设直线与平面所成角为，则，解得或（舍去），所以当为的中点时，直线与平面所成角的正弦值为．【方法点晴】本题主要考查利用线面垂直证明线线垂直以及利用空间向量求二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.19. “过大年，吃水饺”是我国不少地方过春节的一大习俗．2018年春节前夕，市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标，（1）求所抽取的100包速冻水饺该项质量指标值的样本平均数（同一组中的数据用该组区间的中点值作代表）；（2）①由直方图可以认为，速冻水饺的该项质量指标值服从正态分布，利用该正态分布，求落在内的概率；②将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这4包速冻水饺中这种质量指标值位于内的包数为，求的分布列和数学期望．附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为；②若，则，．【答案】(1) (2) （3）的分布列为0 1 2 3 4∴．【解析】试题分析：（1）直方图各矩形中点值的横坐标与纵坐标的积的和就是所抽取的100包速冻水饺该项质量指标值的样本平均数；（2）①∵服从正态分布，且，，由可得落在内的概率是，②的可能取值为，根据独立重复试验概率公式求出各随机变量对应的概率，从而可得分布列，进而利用二项分布的期望公式可得的数学期望.试题解析：（1）所抽取的100包速冻水饺该项质量指标值的样本平均数为．（2）①∵服从正态分布，且，，∴，∴落在内的概率是．②根据题意得，；；；；．∴的分布列为0 1 2 3 4∴．20. 已知椭圆：的离心率为，且以两焦点为直径的圆的内接正方形面积为2．（1）求椭圆的标准方程；（2）若直线：与椭圆相交于，两点，在轴上是否存在点，使直线与的斜率之和为定值？若存在，求出点坐标及该定值，若不存在，试说明理由．【答案】(1) (2) 存在点，使得为定值，且定值为0．【解析】试题分析：（1）由椭圆的离心率为，且以两焦点为直径的圆的内接正方形面积为可得，解方程组即可的结果；（2）由得，根据韦达定理以及过两点的直线的斜率公式可得，只需令，即可得结果.试题解析：（1）由已知可得解得，，所求椭圆方程为．（2）由得，则，解得或．设，，则，，设存在点，则，，所以．要使为定值，只需与参数无关，故，解得，当时，．综上所述，存在点，使得为定值，且定值为0．21. 已知函数，其中为自然对数的底数.（1）若函数在区间上是单调函数，试求实数的取值范围；（2）已知函数，且，若函数在区间上恰有3个零点，求实数的取值范围．【答案】(1) (2)【解析】试题分析：（1）函数在区间上单调递增等价于在区间上恒成立，可得，函数在区间单调递减等价于在区间上恒成立，可得，综合两种情况可得结果；（2），由，知在区间内恰有一个零点，设该零点为，则在区间内不单调，所以在区间内存在零点，同理，在区间内存在零点，所以只需在区间内恰有两个零点即可，利用导数研究函数的单调性，结合函数单调性讨论的零点，从而可得结果．试题解析：（1），当函数在区间上单调递增时，在区间上恒成立，∴（其中），解得；当函数在区间单调递减时，在区间上恒成立，∴（其中），解得．综上所述，实数的取值范围是．（2）．由，知在区间内恰有一个零点，设该零点为，则在区间内不单调，所以在区间内存在零点，同理，在区间内存在零点，所以在区间内恰有两个零点．由（1）知，当时，在区间上单调递增，故在区间内至多有一个零点，不合题意．当时，在区间上单调递减，故在内至多有一个零点，不合题意；所以．令，得，所以函数在区间上单调递减，在区间上单调递增．记的两个零点为，（），因此，，必有，．由，得，所以，又，，所以．综上所述，实数的取值范围为．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22. 选修4-4：坐标系与参数方程在平面直角坐标系中，圆的参数方程为（为参数，是大于0的常数）．以坐标原点为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方程为．（1）求圆的极坐标方程和圆的直角坐标方程；（2）分别记直线：，与圆、圆的异于原点的焦点为，，若圆与圆外切，试求实数的值及线段的长．【答案】(1) ， (2) ，【解析】试题分析：（1）先将圆的参数方程化为直角坐标方程，再利用可得圆的极坐标方程，两边同乘以利用互化公式即可得圆的直角坐标方程；（2）由（1）知圆的圆心，半径；圆的圆心，半径，圆与圆外切的性质列方程解得，分别将代入、的极坐标方程，利用极径的几何意义可得线段的长.试题解析：（1）圆：（是参数）消去参数，得其普通方程为，将，代入上式并化简，得圆的极坐标方程，由圆的极坐标方程，得．将，，代入上式，得圆的直角坐标方程为．（2）由（1）知圆的圆心，半径；圆的圆心，半径，，∵圆与圆外切，∴，解得，即圆的极坐标方程为．将代入，得，得；将代入，得，得；故．【名师点睛】本题考查圆的参数方程和普通方程的转化、圆的极坐标方程和直角坐标方程的转化以及极径的几何意义，消去参数方程中的参数，就可把参数方程化为普通方程，消去参数的常用方法有：①代入消元法；②加减消元法；③乘除消元法；④三角恒等式消元法；极坐标方程化为直角坐标方程，只需利用转化即可.23. 选修4-5：不等式选讲已知函数．（1）求不等式的解集；（2）若正数，满足，求证：．【答案】(1) (2)见解析【解析】试题分析：（1）对分三种情况讨论，分别求解不等式组，然后求并集，即可得不等式的解集；（2）先利用基本不等式成立的条件可得，所以.学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...试题解析：（1）此不等式等价于或或解得或或．即不等式的解集为．（2）∵，，，，即，当且仅当即时取等号．∴，当且仅当，即时，取等号．∴．。

2018年普通高校招生全国卷一(A) 衡水金卷高三信息卷 (二)理科数学试题(解析版)

2018年普通高等学校招生全国统一考试模拟试题理数(二)第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知为虚数单位，复数 ()为纯虚数，则的值为A. -2B.C. 2D.【答案】C【解析】因为为纯虚数,所以所以a=2.故选C.2. 已知集合，，则（）A. B. C. D.【答案】B【解析】由得0＜x＜8，所以A={x|0<x<8},由得x＞5或x＜-1,所以B={x| x＞5或x＜-1}，所以={x|-1≤x≤5}，所以=.故选B.3. 已知是各项均为正数的等比数列的前项和，，，则（）A. 31B. 63C. 16D. 127【答案】A【解析】设公比为q(q＞0)，因为，所以即所以故选A.4. 设向量，，，若，则与的夹角为（）A. B. C. D.【答案】D【解析】因为b||c,所以所以与的夹角的余弦值为所以夹角为.故选D.5. 大约2000多年前，古希腊数学家最先开始研究圆锥曲线，并获得了大量的成果，古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究这几种曲线，用垂直于锥轴的平面去截圆锥，得到的是圆；把平面再渐渐倾斜得到椭圆.若用周长为24的矩形截某圆锥得到椭圆，且与矩形的四边相切.设椭圆在平面直角坐标系中的方程为，测得的离心率为，则椭圆的方程为（）A. B. C. D.【答案】A【解析】由题得4a+4b=24，即a+b=6 (1),由得a=2b（2），由（1）（2）解得a=4，b=2.所以椭圆T的方程为，故选A.6. 已知某服装厂生产某种品牌的衣服，销售量 (单位：百件)关于每件衣服的利润 (单位：元)的函数解析式为, 则当该服装厂所获效益最大时，A. 20B. 60C. 80D. 40【答案】C【解析】设该服装厂所获效益为f(x)（单位：元），则当0＜x≤20时，在区间（0,20]上单调递增，所以当x=20时，f(x)有最大值120000.当20＜x≤180时，则令当20＜x＜80时，单调递增，当80≤x≤180时，单调递减，所以当x=80时，f(x)有最大值240000.故选C.7. 已知满足不等式组则的最小值为（）A. 2B.C.D. 1【答案】D【解析】不等式组对应的可行域如图所示，因为所以z表示可行域内一点到直线x+y-1=0距离的倍，由可行域可知点A（2,0）到直线x+y-1=0的距离最短，故故选D.点睛：本题的关键是找到的几何意义，要找到的几何意义，必须变形，所以z表示可行域内一点到直线x+y-1=0距离的倍.突破了这一点，后面的解答就迎刃而解了.8. 已知函数，的值域为，则实数的取值范围是（）A. B. C. D.【答案】B【解析】由题得由g(t)的图像，可知当时，f(x)的值域为，所以故选B.9. 已知的展开式中常数项为-42，则（）A. 10B. 8C. 12D. 11【答案】B【解析】设的展开式中的第r+1项为项为当n为偶数时，令n-2r=0,得令n-2r=-2，得故原式展开式中常数项为代入下面的选项检验得n=8，显然当n为奇数时，不存在常数项，故可得n=8. 故选B.10. 某几何体的三视图如图所示，则该几何体的表面积为（）A. B. C. D.【答案】C【解析】由三视图可知该几何体是一个圆柱切去两个弓形柱和半个球所得的几何体，圆柱的底面半径为2，高为6，弓形弦到圆心的距离为2-1=1，故弓形弦所对的圆心角为，弓形柱的高为2，所以几何体的表面积为故选C.11. 已知（1）的左、右焦点分别为，，点是双曲线右支上一点，且，过点作的垂线交轴于点，且，若的中点在的延长线上，则双曲线的离心率是（）A. B. C. D.【答案】C【解析】因为点E为PA的中点，且,所以M为的重心，所以为的中点，又可得故故选C.点睛：本题主要是分析，本题的条件比较多，能够对已知条件综合分析得到简洁的结论是解题的关键. 本题通过点E为PA的中点且,推理出M为的重心，这是关键，后面找关于离心率e的方程难度就不大了.12. 已知函数，且对任意实数,均有，若方程有且只有4个实根，则实数的取值范围（）A. B. C. D.【答案】A【解析】依题意，函数f(x)的图像关于直线x=-3对称，所以f(-6)=f(0)=0,f(-4)=f(-2)=0,于是此时，因为方程f(x)=a有四个根，且f(x)的图像关于直线x=-3对称，即函数y=f(x)-a的图像在区间有两个零点，所以g(t)-a的图像在区间上有两个零点，所以由g(t)的图像，可知-16＜a＜9.故选A.点睛：本题解题用到了数学转化的思想，首先把方程f(x)=a有四个根，且f(x)的图像关于直线x=-3对称，转化成函数y=f(x)-a的图像在区间有两个零点，再转化成函数g(t)-a的图像在区间上有两个零点.转化的思想是高中数学里最普遍的数学思想，在高中数学里最常见，特别是遇到较复杂的问题，更应想到转化，把复杂的问题转化得简单，把不熟悉的数学问题转化成熟悉的数学问题，大家在今后的学习中要理解掌握和灵活运用.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知圆心角为的扇形的圆心为，在其弧上任取一点，则使和同时大于的概率为__________．【答案】【解析】由几何概型的定义和几何概型的公式可知使和能同时大于50°的概率为故填.14. 已知直线，和平面，，且，，则“，”是“”的__________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”【答案】必要不充分【解析】由不一定推出由得由得所以“，”是“”的必要不充分条件.故填必要不充分.15. 执行如图所示的程序框图，若输出的，则正整数__________．【答案】2016【解析】第一次循环：s=1,1>T?,否，s=1,k=3,i=2;第二次循环，s=2,2>T?,否，s=4,k=5,i=3;第三次循环，s=3,3>T?,否，s=9,k=7,i=4;最后一次循环，是，输出2017.故T=2016，故填2016.16. 已知数列满足，，是，的等差中项，若为单调递增数列，则实数的取值范围为__________．【答案】【解析】由题可知=+，即-=，所以设则所以当n为奇数时，当n为偶数时，所以，由数列为单调递增数列，得.当n为奇数时，；所以当n＞1时，易知当n为偶数时，，即综上，实数的取值范围为.故填点睛：本题的关键是得到后，能设换元得到这主要是对数列的性质的认识，从这里看出数列的奇数项成等差数列，偶数项成等差数列.突破这一点，后面就迎刃而解了.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在中，分别为内角的对边，向量，，（1）求；（2）若外接圆的直径为，且，求的面积.【答案】(1) (2)【解析】试题分析：（1）第（1）问，利用正弦定理和向量的数量积化简得到，再解这个三角方程即可得到B的值.(2)第（2）问，利用三角恒等变换化简得到，再分类讨论求出a,c的值，最后求三角形的面积.试题解析：（1）因为，所以.由正弦定理，得，又，即.因为，所以，所以，即.（2）由（1）和正弦定理，得.因为，所以，，即.当时，，由正弦定理，得，，所以.当时，有，即，由余弦定理，得，所以，，所以综上，的面积为.18. 在如图所示的多面体中，平面平面，四边形为边长为2的菱形，为直角梯形，四边形为平行四边形，且，，.（1）若，分别为，的中点，求证：平面；（2）若，与平面所成角的正弦值为，求二面角的余弦值.【答案】(1)见解析(2)【解析】试题分析：（1）第（1）问，转化成证明平面 ,再转化成证明和.(2)第（2）问，先利用几何法找到与平面所成角，再根据与平面所成角的正弦值为求出再建立空间直角坐标系，求出二面角的余弦值.试题解析：（1）连接,因为四边形为菱形，所以.因为平面平面，平面平面，平面，，所以平面.又平面，所以.因为，所以.因为，所以平面.因为分别为，的中点，所以，所以平面（2）设，由（1）得平面.由，，得，.过点作，与的延长线交于点，取的中点，连接，，如图所示，又，所以为等边三角形，所以，又平面平面，平面平面，平面，故平面.因为为平行四边形，所以，所以平面.又因为，所以平面.因为，所以平面平面.由（1），得平面，所以平面，所以.因为，所以平面，所以是与平面所成角.因为，，所以平面，平面，因为，所以平面平面.所以，，解得.在梯形中，易证，分别以，，的正方向为轴，轴，轴的正方向建立空间直角坐标系.则，，，，，，由，及，得，所以，，. 设平面的一个法向量为，由得令，得m=(3,1,2) 设平面的一个法向量为，由得令，得. 所以又因为二面角是钝角，所以二面角的余弦值是.19. 某企业从某种型号的产品中抽取了件对该产品的某项指标的数值进行检测，将其整理成如图所示的频率分布直方图，已知数值在100~110的产品有2l件.（1）求和的值；（2）规定产品的级别如下表：已知一件级产品的利润分别为10，20，40元,以频率估计概率，现质检部门从该批产品中随机抽取两件，两件产品的利润之和为，求的分布列和数学期望；（3）为了了解该型号产品的销售状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图，由折线图可以看出，可用线性回归模型拟合月度市场卢有率（%）与月份代码之间的关系.求关于的线性回归方程，并预测2017年4月份(即时)的市场占有率.(参考公式：回归直线方程为，其中，【答案】(1) (2)见解析（3）2017年4月份的市场占有率预计为【解析】试题分析：（1）第（1）问，根据频率公式求N,利用频率分布直方图的矩形的面积和为1求a. (2)第（2）问，先写出X的值，再列出分布列和求X的数学期望. (3)第（3）问，先利用最小二乘法求关于的线性回归方程，再预测2017年4月份(即时)的市场占有率.试题解析：（1）数值在100~110内的频率为，所以.又因为，所以.（2）由频率分布直方图，可知抽取的一件产品为，，等级的概率分别为，，，且的取值为20，30，40，50，60，80，则，，，，，，所以的分布列为所以.（3）由折线图中所给的数据计算，可得，，所以，所以，故月度市场占有率与月份序号之间的线性回归方程为.当时，.所以2017年4月份的市场占有率预计为.20. 已知抛物线（），直线与抛物线交于 (点在点的左侧)两点，且. （1）求抛物线在两点处的切线方程；（2）若直线与抛物线交于两点，且的中点在线段上，的垂直平分线交轴于点，求面积的最大值.【答案】(1) (2)【解析】试题分析：（1）第（1）问，先求出抛物线的方程得到，再求导求出切线斜率，最后求出抛物线在两点处的切线方程.(2)第（2）问，先利用弦长公式求出，再利用点到直线的距离求三角形的高，最后写出面积的表达式，再换元利用导数求它的最大值.试题解析：（1）由，令，得，所以，解得，，由，得，故所以在点的切线方程为，即，同理可得在点的切线方程为.（2）由题意得直线的斜率存在且不为0，故设，，，由与联立，得，，所以，，故.又，所以，所以，由，得且.因为的中点为，所以的垂直平分线方程为，令，得，即，所以点到直线的距离，所以.令，则，则，故.设，则，结合，令，得；令，得，所以当，即时，.点睛：本题有两个特点.一是计算量大，字母参数多，计算比较复杂，所以计算要认真仔细，需要有耐心. 二是综合性比较强，求切线的方程用到了导数的几何意义，后面求出后，换元得到一个新的函数，又利用了导数来研究函数的单调性.所以要求导数的知识熟练.21. 已知函数，，为自然对数的底数.（1）若函数在点处的切线为，求的值；（2）当时，若在区间上有两个零点,，试判断，，的大小关系.【答案】(1) (2)【解析】试题分析：（1）第（1）问，直接利用导数的几何意义求出的值. (2)第（2）问，先研究函数g(x)在的单调性得到它的两个零点的范围，，，再作差比较和的大小，最后利用函数的图像和性质比较和的大小.学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...试题解析：（1）由题意，知，.因为，所以，即.又因为，所以.（2）由题意，知.因为，，由，得或.当时，，所以在区间上单调递增；当时，，所以在区间上单调递减；所以的极小值为.因为，且在区间上单调递减，所以.又因为，，所以存在，使得，所以存在，使得，且，所以，即.当时，，.令，，则，设，则在区间上恒成立，所以在区间上单调递增，所以，所以在区间上恒成立，即在区间上单调递增，故，所以当时，.又因为，在区间上单调递增，所以所以.点睛：本题的难点在比较和的大小. 本题利用了函数的图像和性质进行分析，分析出，得到时，.而，在区间上单调递增，所以，这个地方要结合图像理解清楚.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程以平面直角坐标系的原点为极点，轴的正半轴为极轴，且两个坐标系取相等的长度单位.已知直线的参数方程为 (为参数)，曲线的参数方程为(为参数)，曲线的极坐标方程为.（1）求曲线和的公共点的极坐标；（2）若为曲线上的一个动点，求到直线的距离的最大值.【答案】(1) ，，， (2)【解析】试题分析：（1）第（1）问，先把曲线化成直角坐标方程，再解方程组得到两曲线交点的坐标，再把交点直角坐标化成极坐标. (2)第（2）问，利用参数方程设点，再求出到直线的距离，最后利用三角函数求它的最大值.试题解析：（1）因为曲线的参数方程为,(为参数)所以曲线的直角坐标方程为.因为，所以曲线的直角坐标方程为.两方程联立得或或或所以其极坐标分别为，，，.（2）直线的普通方程为.设点，则点到l的距离，当，即，时，.23. 选修4-5：不等式选讲已知函数.（1）解不等式：；（2）若函数的最小值为，且，试求的最小值.【答案】(1) (2)4【解析】试题分析：（1）第（1）问，直接利用零点分段讨论法解不等式. (2)第（2）问，先由题得到，再利用基本不等式求的最小值.试题解析：（1）可得当时，，即，所以无解；当时，，得，可得；当时，，得，可得.∴不等式的解集为.（2）根据函数,可知当时，函数取得最小值，可知，，∴.∴，当且仅当时，取得最小值为4.。

【数学】【衡水金卷压轴卷】2018年普通高等学校招生全国统一考试模拟试题数学(理)(二)

2018年普通高等学校招生全国统一考试模拟试题理科数学(二) 第Ⅰ卷一、选择题：本大题共12个小题,每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{1,1,2,3,5,6}A =-,{|210}xB x Z =∈<,则AB =（）A ．{1}B ．{1,2}C ．{1,2,3}D ．{1,1,2,3}-2. 设i 为虚数单位,复数z 满足(1z +=2(i)，则共轭复数z 的虚部为（）A B ． C D ． 3. 学生李明上学要经过4个路口,前三个路口遇到红灯的概率均为12,第四个路口遇到红灯的概率为13,设在各个路口是否遇到红灯互不影响,则李明从家到学校恰好遇到次红灯的概率为（） A ．724 B ．14 C ．124 D ．184. 已知双曲线方程为22221(0,0)x y a b a b -=>>,1F F ，为双曲线的左、右焦点, P 为渐近线上一点且在第一象限,且满足120PF PF ⋅=,若1230PF F ∠=,则双曲线的离心率为（）A B ．2 C. D ．35. 已知θ为锐角,1cos 211cos 22θθ-=+,则sin()3πθ+的值为（）A ．4 B ．4 C. 36+．6+ 6.执行如图所示的程序框图,则输出的s 的值为（）A ．1-B ．2- C. 1 D ．27. 210(1)(2)x x +-=121101(1)(1)a x a x -+-11112(1)a x a ++-+，则0111a a a +++的值为（）A ．2B ．0 C. 2- D ．4- 8. 某几何体三视图如图所示,则该几何体的表面积为（）A ．5202π-B ．203π- C. 24π-D ．12π+9. 已知3412ab==,则,a b 不可能满足的关系是（） A ．4a b +>B ．4ab > C. 22(1)(1)2a b -+-> D ．223a b +<10. 若函数()sin()6f x x πω=+(0)ω>在区间(,2)ππ内没有最值,则ω的取值范围是（）A ．112(0,][,]1243 B ．112(0,][,]633C. 12[,]43D ．12[,]3311. 过抛物线22(0)x py p =>上两点,A B 分别作抛物线的切线,若两切线垂直且交于点(1,2)P -,则直线AB 的方程为（）A ．122y x =+ B ．124y x =+ C. 132y x =+ D ．134y x =+ 12. 在正三棱锥(底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥)O ABC -中，,,OA OB OC 三条侧棱两两垂直，正三菱锥O ABC -的内切球与三个侧面切点分别为,,D E F ,与底面ABC 切于点G ,则三棱锥G DEF -与O ABC -的体积之比为（）A BD第Ⅱ卷二、填空题:本题共4小题,每小题5分.13. 在ABC ∆中, 2,4BC AB ==,1,2DB AD CE EA ==,则BE 与CD 的夹角为．14. 由不等式组212436y x y x y x ≤+⎧⎪≥-+⎨⎪≥-⎩,组成的区域为Ω,作Ω关于直线1y x =--的对称区域'Ω,点P 和点Q 分别为区域Ω和'Ω内的任一点,则||PQ 的最小值为．15. 函数()f x 满足()()f x f x =-,()(2)f x f x =-,当[0,1]x ∈时, 2()f x x =,过点9(0,)4P 且斜率为k 的直线与()f x 在区间[0,4]上的图象恰好有3个交点,则k 的取值范围为．16. 在ABC ∆中, D 是边BC 上的一点,2,2AD BD DC ==,1tan 2BAD ∠=1tan 3DAC ∠=,则AB = ．三、解答题：解答应写出文字说明、证明过程或演算步骤. 17. 在数列{}n a 中,已知121,4a a ==,216n n n a a a ++=+. (1)若1{}n n a a λ++是等比数列,求λ的值； (2)求数列{}n a 的通项公式.18. 如图所示, 1CC ⊥平面ABC ,平面11ABB A ⊥平面ABC ,四边形11ABB A ⊥为正方形，60ABC ∠=, 1BC CC ==122AB =,点E 在棱1BB 上.(1)若F 为11A B 的中点E 为1BB 的中点,证明:平面1EC F ∥平面1A CB ；(2)设1BE BB λ=,是否存在λ,使得平面11A EC ⊥平面1A EC ?若存在,求出λ的值;若不存在,说明理由.19. 中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备，某高中每年招收学生1000人,开设大学先修课程已有两年,共有300人参与学习先修课程，两年全校共有优等生200人,学习先修课程的优等生有50人，这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分)，结果如下表所示:(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系，根据列联表的独立性体验，能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?（2）已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率; ②某班有4名学生参加了大学先修课程的学习,设获得某高校自主招生通过的人数为ξ,求ξ的分布列,并求今年全校参加大学先修课程的学生获得大学自主招生通过的人数. 参考数据:参考公式: 2K = 2()()()()()n ad bc a b c d a c b d -++++，期中n a b c d =+++，20. 已知椭圆的方程为22221(0)x y a b a b+=>>,其离心率e =且短轴的个端点与两焦点过椭圆上的点P 作y 轴的垂线,垂足为Q ,点E 满足12QE QP =,设点E 的轨迹为曲线Γ. (1)求曲线Γ的方程;（2）若直线l 与曲线Γ相切,且交椭圆于A B 、两点, (1,0),(1,0)C D -,记ABC ∆的面积为1S ,ABC ∆的面积为2S ,求12S S 的最大值 .21. 知函数1n ()xf x x=,()1n g x x x ax b =-+,()f x 与()g x 在交点(1,0)处的切线相互垂直.(1)求()g x 的解析式；(2)已知0k >,若函数()()()F x kf x g x =+有两个零点,求k 的取值范围 . 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程在平面直角坐标系xOy 中,圆221:2C x y +=经过伸缩变换2,x x y '=⎧⎪⎨'=⎪⎩后得到曲线2C ,相互垂直的直线12l l 、过定点1(1,0),P l 与曲线2C 相交于A B 、两点, 2l 与曲线2C 相交于C D 、两点.(1)求曲线2C 的直角坐标方程； (2)求||||||||PA PB PC PD 的最小值. 23.选修4-5：不等式选讲已知函数()f x =|1||||1|x x x -+++. (1)求关于x 的不等式()6f x <的解集； (2) 0,0x R x ∀∈∃>,使得200()(0)af x x a x ≥+>成立,求实数a 的取值范围.理科数学（二）一、选择题1.D 【解析】易知集合{|210}xB x Z =∈<=2{|1og 10}x Z x ∈<,所以{1,1,2,3}A B =-.故选D .2.C 【解析】2(1=(i)z +22i (1=+,所以1z =--,共轭复数为1z =-+,虚部为故选C .3.A 【解析】前三个路口恰好遇到一个红灯且第四个路口是绿灯的概率为13312C ()23,前三个路口都是绿灯且第四个路口是红灯的概率为311()23，故李明从家到学校恰好遇到一次红灯的概率为133312117C ()()232324+=，故选A . 4,B 【解析】设O 为坐标原点,因为120PF PF ⋅=,故12PF F ∆为直角三角形,又因为O 为12F F 中点,故2||||OF OP =,因为1230PF F ∠=,所以1260PF F ∠=,故2POF ∆为正三角形,所以直线OP的倾斜角为60,即ba=2e =.故选B .5.D 【解析】1cos 21cos 2θθ-=+2222sin 1tan 2sin 2θθθ==，又θ为锐角, tan 2θ∴=，sin θ∴=，cos θ=，sin()3πθ+=1cos sin 2θθ+=故选D . 6.B 【解析】第一次执行循环体, 1,1,1,1s a b i =-==-=；第二次执行循环体2,1s a =-=-，2,2b i =-=；第三次执行循环体, 1,2s a =-=-，1,3b i =-=；第四次执行循环体, 1,1,1,4s a b i ==-==；第五次执行循环体, 2,1,2,5s a b i ====；第六次执行循环体, 1,2,1,6s a b i ====；第七次执行循环体, 1,1,1,7s a b i =-==-=，所以s 的值周期出现，周期为6,故2018i =时, 2s =-.故选B . 7.C 【解析】令2x =,得010a a =++1112a a ++,令1x =,得122a =,所以01112a a a +++=-.故选C .8.C 【解析】几何体是正方体被切去了18个球,如下图所示,则几何体表面积为223(22)π⨯⨯+⨯-213428π⨯+⨯⨯24π=-，故选C .9.D 【解析】3412ab==,得34112,112a og b og ==，121113og a b+=12141og +=,即()a b ab a b +=≠,对于2,()2a b A a b ab ++=<,解之得4a b +>,成立;对于,2B ab a b =+>4ab ⇒>,成立;对于22,(1)(1)C a b -+-222()2a b a b =+-++2222a b ab =+-+=2()22a b -+>，成立;对于,4D a b <+<228a b +>,故D 错.故选D .10.B 【解析】函数sin y x =的单调区间为3(,)22k k ππππ++()k Z ∈，令26k x πππω+≤+32k ππ≤+，k Z ∈,解得433k k ππππωω++≤，k Z ∈.若函数()sin()6f x πωπ=+(0)ω>在区间(,2)ππ内没有最值,则3,432,k k πππωπππω⎧+⎪≤⎪⎪⎨⎪+⎪≤⎪⎩解得12323k k ω+≤≤+， k Z ∈由12323k k +<+,得23k <,当1k =-时,2136ω-≤≤,又因为0ω>,所以106ω<≤；当0k =时, 1233ω≤≤,符合题意.故选B .11.B 【解析】设1122(,),(,)A x y B x y ,由22x y p =,求导得1,|x x xy y p =''=212,|x x x x y p p='==,在A点的切线方程为2112x x y x p p =-，在B 点的切线方程为2222x x y x p p =-，联立解得122x x x +=，122x x y p =，所以1212x x +=，1222x x p =-，即122x x +=，124(*)x x p =-，又因为两切线垂直,则211x x p p⋅=-, 212x x p =-,所以4p =,抛物线方程为28x y =,由题易知直线AB 的斜率存在,设直线AB 方程为y kx b =+,代人抛物线方程得2880x kx b --=,由韦达定理得128x x k +=,128x x b =-,和(*)联立可得82k =且2b =,即14k =,2b =.所以直线AB 的方程为124y x =+.故选B . 12.B 【解析】法一:设正三棱锥侧棱长为a ,内切球半径为r ,内切球的球心为1O ,则316O ABCV a -=,11O ABC O OAB V V --++1113O OBC O OAC V V --+=223()2a r +，31163a ∴=2a r ⋅，解得32r a =.如下图，把面ODGC 单独拿出来分析: G 为ABC ∆的中心，11O G O D r ==，,HG OG ==， tan HOG ∴∠=HG OG =，sin HOG ∠=，过D 作DM OG ⊥于M ，则1DOM O DM ∠=∠,111sin O M O D MDO =∠1sin O D HOG =∠=r =，11cos DM O D O DM =⋅∠==，11MG O M O G ++=1366a -+13a a =，显然DEF ∆为等边三角形，DE ==6a .31316DEF G DEFO ABCS MGVV a--⋅=231134316DE a a ⨯=3310816a=3108=.故选B .法二:设正三棱锥侧棱长为a ,内切球半径为r ,内切球的球心为1O ,则131,6O ABCO ABC V a V --=+11O OAB O OBC V V --++1213(32O OAC a V -=+2)r31163a ∴=2a r ⋅，解得r =.如下图，由OC OA ⊥,OC OB ⊥,OAOB A =,得OC ⊥平面OAB ，又由1O D ⊥平面OAB 得1O D OC ∥,同理1O E OA ∥，1O F OB ∥，因为,,OA OB OC 两两垂直,所以111,,O D O E O F 两两垂直,故EF =，3DEF S r ∆=.点1O 到平面DEF 的距离. d==.故G 到平面DEF的距离为r+r =，所以213G DEFV -===G DEF O ABCV V --∴=331081186a =.故选B .二、填空题13.2π【解析】设,BA a BC b ==, 则CD BD BC =-1,2a b BE BC =-=11()33CA b a b +=+-1233a b =+.所以1()2CD BE a b ⋅=-12()33a b ⋅+=2212063a b -=，所以BE 与CD 的夹角为2π.14. 作出区域Ω,如图所示，三个交点分别为35(,),(20)42B C ，, (7,15)A ,当区域Ω的点到直线1y x =--的距离取最小值时，区域Ω的点到直线1y x =--的距离取最小值时,||PQ 取得最小值,由图可知,区域Ω内的点(20)C ，到直线1y x =--的距离最小，最小值为2，则min ||PQ =15. 13(1,)12【解析】因为()()f x f x =-,()(2)f x f x =-,所以()(2)f x f x -=-,即()(2)f x f x =+，即()f x 是2T =的周期函数,由[0,1]x ∈时, 2()f x x =,知[1,0]x ∈-时, [0,1]x -∈,2()()f x f x x =-=,则当[1,1]x ∈-时, 2()f x x =,又()f x 是周期为2的周期函数,画出()([0,4])f x x ∈的图象如下图所示，由图象得,当[0,1]x ∈时, 2()f x x =同94y kx =-,联立得2904x kx -+=，由0∆=得3k =或3k =- (舍),此时3=[0,1]22k x =∉切,故不可能有三个交点,当[2,3]x ∈时, 9(0,)4-与(3,1)连线的斜率为1312,此时直线与()y f x =有两个交点,又2()(2)f x x =-,若同94y kx =-相切,两式联立得2(4)x k x -+ 2504+=，由0∆=,得1k =或9k =-(舍),此时45=22k x +=切(2,3)x ∈.所以当13112k <<时有三个交点,综上: 13112k <<.【解析)】在ABC ∆中,由1tan 2BAD ∠=,1tan 3DAC ∠=，得tan tan BAC ∠=()1BAD DAC ∠+∠=,4BAC π∴∠=,过点B 作BE AC ∥,交AD 的延长线于点E ,如下图,则ABE π∠=-34BAC π∠=，2BD DE DC AD==，24DE AD ==，BEA DAC ∠=∠，在ABE ∆中,用正弦定理得sin sin AE AB ABE BEA=∠∠，则sin sin AE BEA AB ABE ⋅∠=∠65==. 三、解答题17.解:(1)设1{}n n a a λ++的公比为q ，则21n n a a λ+++=1()n n q a a λ++2()n a q λ+⇒=-1n n a qa λ++，1,36q q λλ-=⎧∴⇒-⎨=⎩或2.(2) 3λ=-时, 2q =-,此时1{3}n n a a +-为等比数列，可得13n n a a +-=121(3)(2)n a a ---1(2)n -=-，①2λ=时, 3q =，1{2}n n a a ++为等比数列，可得12n n a a ++=121(2)323n n a a --⋅=⋅②①-②得15(2)n n a --=-23n n a -⋅⇒=123(2)55n n -⨯--. 18.解:(1) 平面11ABB A ⊥平面1,ABC BB BA ⊥，平面11ABB A 平面ABC AB =, 1BB ∴⊥平面ABC .又1CC ⊥平面ABC ,11BB CC ∴⊥∥，又112CC AB =112BB BE ==，∴四边形1CC EB 为平行四边形,1C E BC ∴∥.又BC ⊂平面1A BC ,1C E ∴∥平面1A BC .111,BE EB A F FB ==1EF A B ∴∥.又1A B ⊂平面1A BC ,EF ∴∥平面1A BC .又11,C E EF E C E =⊂平面1EFC FE ⊂平面1EFC ，∴平面1EFC ∥平面1A BC .（2）在底面ABC ∆中,由余弦定理，得222AC AB BC =+-2cos6012AB BC ⋅=， 222AB AC BC ∴=+，AC BC ∴⊥，1CC ⊥平面ABC ,11,CC AC CC BC ∴⊥⊥，1,CA CB CC ∴，两两垂直.以C 点为坐标原点, 1,,CA CB CC 依次为,,x y z 轴正方向,建立空间直角坐标系,如下图，则1(0,0,0),(0,0,2)C C ,1(0,2,4)A E λ，设面11A EC 的一个法向量为1111(,,)n x y z =，则111110,0,n C A n C E ⎧⋅=⎪⎨⋅=⎪⎩即111120,2(42)0,z y z λ⎧+=⎪⎨+-=⎪⎩令11z =,解得1x =,112y λ=-，1(,12,1)3n λ∴=--. 设平面1A EC 的一个法向量为2222(,,)n x y z =，则2120,0,n CA n CE ⎧⋅=⎪⎨⋅=⎪⎩即222240,240,z y z λ⎧+=⎪⎨+=⎪⎩令22x =,得22z y ==.2,n ∴=当平面11A EC ⊥平面1A EC 时,则12n n ⋅=+(12)λ-0=，化简得212650λλ-+=,方程无解，∴不存在λ,使得平面11A EC ⊥平面1A EC .19.解:(1)列联表如下：通过图形可判断学习先修课程与优等生有关系.又2K 的观測值k =22000(501550150250)30017002001800⨯-⨯⨯⨯⨯17.429 6.635≈>，因此,在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系.(2)①20550.9300300p =⨯+1050.80.6300⨯+⨯+70500.50.40.6300300⨯+⨯=. ②设获得某高校自主招生通过的人数为ξ,则: 3(4,)5B ξ, ()443()5k k P kC ξ-== 42(),0,1,2,3,45kk -=, ξ的分布列为:今年全校参加大学生先修课程的学生获得大学自主招生通过的人数为1500.690⨯=.20.解:(1)依题意可得12ca =⨯2cb ⨯=, 由222a bc =+，解得2,1a b ==，椭圆方程为2214x y +=. 设000(,),(,),(0,)E x y P x y Q y ，由12QE QP =,得002,x x y y ==，代人椭圆方程得曲线Γ的方程为221x y +=. (2)由题知直线l 的斜率存在，设直线l 的方程为y kx m =+，由l1=,即221m k =+.由22,1,4y kx m x y =+⎧⎪⎨+=⎪⎩消y ，得22(14)8k x kmx ++2440,0m +-=∆>得0k ≠.设1122(,),(,)A x y B x y ，则122841km x x k -+=+，21224441m x x k -=+， 12|||AB x x =-==则11||2S AB =21S ||2AB =2121||4S S AB =222||114m k k -=+221||1AB k + 242218(4(41)k k k +=⨯⨯+）22221121(41)k k k =++ 222121681k k k ==++222121168k k k ++123164≤= 当且仅当12k =±时,上式取等号. 综上所述, 12S S 的最大值为3421.解:(1) 211()nx f x x -'=，(1)1f '∴=，又()11g x nx a '=+-，(1)1g a '=-，()f x 与()g x 在交点(1,0)处的切线相互垂直，11a ∴-=-,2a ∴=.又(1,0)在()g x 上, 2b ∴=，故()122g x x nx x =-+.(2)由题知2(11)()k nx F x x -'=112nx ++- 2(11)11k nx nx x-=+- 22(11)()k x nx x -=-()2211()x k nx x-=-.①01<<,即01k <<时,令()0F x '<,x e <<;令()0F x '>,得0x <<x e >，()F x ∴在区间上单调递增,在区间)e 上单调递减,在区间(,)e +∞上单调递增,000001n ()k1n x F x x x x ∴=+0001n 22x x k x -+<021n 20k x +<+=. 又222(e )20ek F =+>， ()F x ∴在区间上有一个零点,在区间)e 上有一个零点,在区间(,)e +∞上有一个零点,共3个零点,不符合题意,舍去.②1k =时,令()0F x '<,得1x e <<，令()0F x '>,得01x <<或x e >，()F x ∴在区间(0,1)上单调递增,在区间(1,)e 上单调递减,在区间(,)e +∞上单调递增，又(1)0,()0F F e =<,222(e )20e F =+>, ()F x ∴有两个零点,符合题意.③1e <<,即21k e <<时,令()0F x '<,x e <<,令()0F x '>,得0x <<x e >， ()F x ∴在区间上单调递增,在区间)e 上单调递减,在区间∴上单调递增，(1)0F =，()F x ∴在区间上存在一个零点,若要()F x 有两个零点,必有()0F e =,解得222(1,)k e e e =-∈.e ≥,即2k e ≥时,令()0F x '<,得e x <<令()0F x '>,得0x e <<或x >()F x∴在区间(0,)e上单调递增,在区间(e上单调递减,在区间)+∞上单调递增，(1)0F =,()F x∴在区间(0,)e上存在一个零点，又F=2=21)+=20+>，∴在区间∴上不存在零点,即()F x只有一个零点,不符合题意. 综上所述, 1k=或2e2ek=-.22.解:(1)圆221:2C x y+=经过伸缩变换2,x xy'=⎧⎪⎨'=⎪⎩后得到曲线2C的方程为22186x y+=.(2)设直线1l的参数方程为1cos,sinx ty tαα=+⎧⎨=⎩(t为参数),代入22186x y+=，得22(3cos4sin)αα+26cos210t tα+-=，设12||||||PA PB t t==22213cos4sinαα+2213sinα=+.同理，221||||3sinPC PDα=+.||||||||PA PB PC PD=22221(3cos)(3sin)αα++2244112sin cosαα=+⋅2441112sin4α=+.当sin21α=±时,上式取得最小值为36.23.解:(1) ()|1|f x x=-+|||1|x x++3,1,2,10,2,01,3,1,x x x x x x x x -≤-⎧⎪-+-<<⎪=⎨+≤<⎪⎪≥⎩由()6f x <,得1,36,x x ≤-⎧⎨-<⎩或10,26,x x -<<⎧⎨-+<⎩或01,26,x x ≤<⎧⎨+<⎩ 或1,36,x x ≥⎧⎨<⎩解得22x -<<，所以不等式()6f x <的解集为(2,2)-.(2) 0R,0x x ∀∈∃>,使得200()(0)a f x x a x ≥+>成立, 等价于2min 0min 0()()a f x x x ≥+. 由(1)知min ()2f x =,当00x >时, 2200002a a x x x x +=+032a x +≥3=当0x =,取等号)，从而23≥故实数a的取值范围为(0,9.2018年高考考前猜题卷理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数z 满足ii i z 2|2|++=，则=||z （） A ．3 B ．10 C ．9 D ．102．已知全集R U =，集合}012|{2≥--=x x x M ，}1|{x y x N -==，则=N M C U )(（）A ．}1|{≤x xB ．}121|{≤<-x x C ．}121|{<<-x x D ．}211|{<<-x x3．已知蚂蚁在边长为4的正三角形区域内随机爬行，则它在离三个顶点的距离都大于2的区域内的概率P 为（）A ．631π-B ．43C ．63πD ．414．已知双曲线)0,0(12222>>=-b a by a x ，过双曲线左焦点1F 且斜率为1的直线与其右支交于点M ，且以1MF 为直径的圆过右焦点2F ，则双曲线的离心率是（） A ．12+ B ．2 C ．3 D ．13+5．一个算法的程序框图如图所示，如果输出y 的值是1，那么输入x 的值是（）A ．2-或2B ．2-或2C ．2-或2D ．2-或26．已知函数)2||,0)(3sin()(πϕωπω<>+=x x f 的图象中相邻两条对称轴之间的距离为2π，将函数)(x f y =的图象向左平移3π个单位后，得到的图象关于y 轴对称，那么)(x f y =的图象（） A ．关于点)0,12(π对称 B ．关于点)0,12(π-对称C ．关于直线12π=x 对称 D ．关于直线12π-=x 对称7．如下图，网格纸上小正方形的边长为1，图中实线画的是某几何体的三视图，则该几何体最长的棱的长度为（）A.32 B.43C. 2D. 411 8．已知等差数列}{n a 的第6项是6)2(xx -展开式中的常数项，则=+102a a （）A ．160B ．160-C ．350D ．320- 9．已知函数)0(212)(<-=x x f x与)(log )(2a x x g +=的图象上存在关于y 轴对称的点，则a 的取值范围是（）A ．)2,(--∞B ．)2,(-∞C ．)22,(--∞D ．)22,22(- 10．已知正四棱台1111D C B A ABCD -的上、下底面边长分别为22,2，高为2，则其外接球的表面积为（）A ．π16B ．π20C ．π65D ．π465 11．平行四边形ABCD 中，2,3==AD AB ，0120=∠BAD ，P 是平行四边形ABCD 内一点，且1=AP ，若y x +=，则y x 23+的最大值为（） A ．1 B ．2 C ．3 D ．412．设n n n C B A ∆的三边长分别为n n n c b a ,,，n n n C B A ∆的面积为,3,2,1,=n S n …，若n n a a a c b ==++1111,2，2,211nn n n n n a b c a c b +=+=++，则（） A ．}{n S 为递减数列 B ．}{n S 为递增数列C ．}{12-n S 为递增数列，}{2n S 为递减数列D ．}{12-n S 为递减数列，}{2n S 为递增数列二、填空题（每题4分，满分20分，将答案填在答题纸上）13．函数x a x a x x f )3()1()(24-+--=的导函数)('x f 是奇函数，则实数=a .14．已知y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤-≥+-002043y x x y x （R y x ∈,），则22y x +的最大值为 .15．已知F 为抛物线x y C 4:2=的焦点，过点F 作两条互相垂直的直线21,l l ，直线1l 与C 交于B A ,两点，直线2l 与C 交于E D ,两点，则||||DE AB +的最小值为 . 16．在锐角三角形ABC 中，角C B A ,,的对边分别为c b a ,,，且满足ac a b =-22，则BA tan 1tan 1-的取值范围为 . 三、解答题（本大题共6题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．已知等比数列}{n a 的前n 项和为n S ，且满足)(221R m m S n n ∈+=+.（1）求数列}{n a 的通项公式；（2）若数列}{n b 满足)(log )12(112+⋅+=n n n a a n b ，求数列}{n b 的前n 项和n T .18．小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时，顾客从装有1个黑球，3个红球和6个白球（除颜色外其他都相同）的不透明的袋子中依次不放回地摸出3个球，根据摸出的球的颜色情况进行兑奖.顾客中一等奖，二等奖，三等奖，四等奖时分别可领取的奖金为a 元，10元，5元，1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况：1:A 个黑球2个红球；3:B 个红球；:c 恰有1个白球；:D 恰有2个白球；3:E 个白球，且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖，中二等奖，中三等奖，中四等奖，不中奖.（1）通过计算写出中一至四等奖分别对应的情况（写出字母即可）；（2）已知顾客摸出的第一个球是红球，求他获得二等奖的概率；（3）设顾客抽一次奖小张获利X 元，求变量X 的分布列；若小张不打算在活动中亏本，求a 的最大值.19．如图，三棱柱111C B A ABC -中，侧面C C BB 11为菱形，0160=∠CBB ，1AC AB =.（1）证明：平面⊥C AB 1平面C C BB 11；（2）若C B AB 1⊥，直线AB 与平面C C BB 11所成的角为030，求直线1AB 与平面C B A 11所成角的正弦值.20．如图，圆),(),0,2(),0,2(,4:0022y x D B A y x O -=+为圆O 上任意一点，过D 作圆O 的切线，分别交直线2=x 和2-=x 于F E ,两点，连接BE AF ,，相交于点G ，若点G 的轨迹为曲线C .（1）记直线)0(:≠+=m m x y l 与曲线C 有两个不同的交点Q P ,，与直线2=x 交于点S ，与直线1-=y 交于点T ，求OPQ ∆的面积与OST ∆的面积的比值λ的最大值及取得最大值时m 的值.（注：222r y x =+在点),(00y x D 处的切线方程为200r yy xx =+）21．已知函数x a x g x x f ln )(,21)(2==. （1）若曲线)()(x g x f y -=在2=x 处的切线与直线073=-+y x 垂直，求实数a 的值；（2）设)()()(x g x f x h +=，若对任意两个不等的正数21,x x ，2)()(2121>--x x x h x h 恒成立，求实数a 的取值范围；（3）若在],1[e 上存在一点0x ，使得)(')()('1)('0000x g x g x f x f -<+成立，求实数a 的取值范围.请考生在22、23二题中任选一题作答，如果都做，则按所做的第一题记分. 22．选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为⎪⎩⎪⎨⎧==21t a y t x （其中t 为参数，0>a ），以坐标原点O 为极点，x 轴的正半轴为极轴建立的极坐标系中，直线l ：0sin cos =+-b θρθρ与2C ：θρcos 4-=相交于B A ,两点，且090=∠AOB . （1）求b 的值；（2）直线l 与曲线1C 相交于N M ,两点，证明：||||22N C M C ⋅（2C 为圆心）为定值. 23．选修4-5：不等式选讲已知函数|1||42|)(++-=x x x f . （1）解不等式9)(≤x f ；（2）若不等式a x x f +<2)(的解集为A ，}03|{2<-=x x x B ，且满足A B ⊆，求实数a 的取值范围.参考答案一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的．二、填空题：本大题共4小题，每小题5分，共20分． 13．3 14．8 15．16 16．)332,1( 三、解答题：本大题共6小题，满分70分．解答须写出文字说明、证明过程和演算步骤．17．解：（1）由)(221R m m S n n ∈+=+得⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=282422321m S m S m S ，)(R m ∈，从而有4,2233122=-==-=S S a S S a ，所以等比数列}{n a 的公比223==a a q ，首项11=a ，因此数列}{n a 的通项公式为)(2*1N n a n n ∈=-.（2）由（1）可得12)22(log )(log 1212-=⋅=⋅-+n a a nn n n ，∴)121121(21)12)(12(1+--⨯=-+=n n n n b n∴)1211215131311(2121+--++-+-⨯=+++=n n b b b T n n 12+=n n. 18．解：（1）4011203)(31023===C C A P ；12011)(310==C B P ，10312036)(3102416===C C C C P ，2112060)(3101426===C C C D P ，6112020)(31036===C C E P∵)()()()()(D P C P E P A P B P <<<<， ∴中一至四等奖分别对应的情况是C E A B ,,,.（2）记事件F 为顾客摸出的第一个球是红球，事件G 为顾客获得二等奖，则181)|(2912==C C F G P .（3）X 的取值为3,2,2,7,3---a ，则分布列为由题意得，若要不亏本，则03212103)2(61)7(401)3(1201≥⨯+⨯+-⨯+-⨯+-⨯a ，解得194≤a ，即a 的最大值为194.19．解：（1）证明：连接1BC ，交C B 1于O ，连接AO ， ∵侧面C C BB 11为菱形，∴11BC C B ⊥ ∵为1BC 的中点，∴1BC AO ⊥ 又O AO C B = 1，∴⊥1BC 平面C AB 1又⊂1BC 平面C C BB 11，∴平面⊥C AB 1平面C C BB 11.（2）由B BO AB C B BO C B AB =⊥⊥ ,,11，得⊥C B 1平面ABO 又⊂AO 平面ABO ，∴C B AO 1⊥，从而1,,OB OB OA 两两互相垂直，以O 为坐标原点，OB 的方向为x 轴正方向，建立如图所示的空间直角坐标系xyz O -∵直线AB 与平面C C BB 11所成角为030，∴030=∠ABO设1=AO ，则3=BO ，∵0160=∠CBB ，∴1CBB ∆是边长为2的等边三角形∴)0,1,0(),0,1,0(),0,0,3(),1,0,0(1-C B B A ，则)1,0,3(),0,2,0(),1,1,0(1111-==-=-=AB B A C B AB 设),,(z y x =是平面C B A 11的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00111C B n B A n 即⎩⎨⎧=-=-0203y z x ，令1=x ，则)3,0,1(=n 设直线1AB 与平面C B A 11所成的角为θ，则46|||||||,cos |sin ==><=n AB θ. 20．解：（1）易知过点),(00y x D 的切线方程为400=+y y x x ，其中42020=+y x ，则)24,2(),2,2(000y x F y x E +--， ∴4116416416424424220020000021-=-=--=-⋅-+=y y y x y x y x k k 设),(y x G ，则144122412221=+⇒-=+⋅-⇒-=y x x y x y k k （0≠y ）故曲线C 的方程为1422=+y x （0≠y ）（2）联立⎩⎨⎧=++=4422y x mx y 消去y ，得0448522=-++m mx x ，设),(),,(2211y x Q y x P ，则544,5822121-=-=+m x x m x x ，由0)44(206422>--=∆m m 得55<<-m 且2,0±≠≠m m∴22221221255245444)58(24)(11||m m m x x x x PQ -=-⨯--⨯=-++=，易得)1,1(),2,2(---+m T m S ， ∴)3(2)3()3(||22m m m ST +=+++=，∴22)3(554||||m m ST PQ S S OSTOPQ +-===∆∆λ，令)53,53(,3+-∈=+t t m 且5,3,1≠t ，则45)431(4544654222+--⨯=-+-=t t t t λ，当431=t ，即43=t 时，λ取得最大值552，此时35-=m .21．解：（1）xa x y x a x x g x f y -=-=-=',ln 21)()(2 由题意得322=-a，解得2-=a （2）)()()(x g x f x h +=x a x ln 212+=对任意两个不等的正数21,x x ，2)()(2121>--x x x h x h 恒成立，令21x x >，则)(2)()(2121x x x h x h ->-，即2211)(2)(x x h x x h ->-恒成立则问题等价于x x a x x F 2ln 21)(2-+=在),0(+∞上为增函数 2)('-+=xax x F ，则问题转化为0)('≥x F 在),0(+∞上恒成立，即22x x a -≥在),0(+∞上恒成立，所以1)2(max 2=-≥x x a ，即实数a 的取值范围是),1[+∞.（3）不等式)(')()('1)('0000x g x g x f x f -<+等价于0000ln 1x ax a x x -<+，整理得01ln 000<++-x a x a x ，构造函数xax a x x m ++-=1ln )(，由题意知，在],1[e 上存在一点0x ，使得0)(0<x m2222)1)(1()1(11)('x x a x x a ax x x a x a x m +--=+--=+--= 因为0>x ，所以01>+x ，令0)('=x m ，得a x +=1①当11≤+a ，即0≤a 时，)(x m 在],1[e 上单调递增，只需02)1(<+=a m ，解得2-<a ； ②当e a ≤+<11，即10-≤<e a 时，)(x m 在a x +=1处取得最小值.令01)1ln(1)1(<++-+=+a a a a m ，即)1l n (11+<++a a a ，可得)1ln(11+<++a aa （*）令1+=a t ，则e t ≤<1，不等式（*）可化为t t t ln 11<-+ 因为e t ≤<1，所以不等式左端大于1，右端小于或等于1，所以不等式不能成立. ③当e a >+1，即1->e a 时，)(x m 在],1[e 上单调递减，只需01)(<++-=eaa e e m 解得112-+>e e a .综上所述，实数a 的取值范围是),11()2,(2+∞-+--∞e e . 22．解：（1）由题意可得直线l 和圆2C 的直角坐标方程分别为0=+-b y x ，4)2(22=++y x∵090=∠AOB ，∴直线l 过圆2C 的圆心)0,2(2-C ，∴2=b . （2）证明：曲线1C 的普通方程为)0(2>=a ay x ，直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+-=ty t x 22222（t 为参数），代入曲线1C 的方程得04)2222(212=++-t a t ， 04212>+=∆a a 恒成立，设N M ,两点对应的参数分别为21,t t ，则821=t t ， ∴8||||22=N C M C ， ∴||||22N C M C 为定值8.23．解：（1）由9)(≤x f 可得9|1||42|≤++-x x ，即⎩⎨⎧≤->9332x x 或⎩⎨⎧≤-≤≤-9521x x 或⎩⎨⎧≤+--<9331x x解得42≤<x 或21≤≤-x 或12-<≤-x ，故不等式9)(≤x f 的解集为]4,2[-.（2）易知)3,0(=B ，由题意可得a x x x +<++-2|1||42|在)3,0(上恒成立⇒1|42|-+<-a x x 在)3,0(上恒成立1421-+<-<+-⇒a x x a x 在)3,0(上恒成立 3->⇒x a 且53+->x a 在)3,0(上恒成立⎩⎨⎧≥≥⇒50a a 5≥⇒a .。

衡水金卷2018年普通高等学校招生全国统一考试分科综合卷理科数学模拟试题2

2018 年普通高等学校招生全国统一考试模拟试题理数(二)第Ⅰ卷（共 60 分）一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，则（）A.B.C.D.【答案】B【解析】∵,∴故选：B2. 已知，且是虚数单位，，则（）A. 4 B.C.D.【答案】C【解析】，由题意知：，解得：故选：C3. 已知为直线的倾斜角，若，则直线的斜率为( )A. 3 B. -4 C.D.【答案】D第1页/共22页【解析】由题意知：，故选：D4. 双曲线的渐近线与抛物线（）A.B.【答案】DC.D.【解析】由题意，知双曲线的一条渐近线为. 相切，则双曲线的离心率为联立，得到：，由相切，得,解得：，∴ .故选：D 点睛：解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于 a， b，c 的方程或不等式，再根据 a，b，c 的关系消掉 b 得到 a，c 的关系式，建立关于 a，b，c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等. 5. 袋中装有 4 个红球、3 个白球，甲、乙按先后次序无放回地各摸取一球，在甲摸到了白球的条件下，乙摸到白球的概率是（）A.B.C.D.【答案】B【解析】用 A 表示甲摸到白球，B 表示乙摸到白球，则∴.故选：B，，第2页/共22页6. 《算法统宗》是中国古代数学名著，由程大位所著，其中记载这样一首诗：九百九十九文钱，甜果苦果买一千，四文钱买苦果七，十一文钱九个甜，甜苦两果各几个？请君布算莫迟疑！其含义为：用九百九十九文钱共买了一千个甜果和苦果，其中四文钱可以买苦果七个，十一文钱可以买甜果九个，请问究竟甜、苦果各有几个？现有如图所示的程序框图，输入分别代表钱数和果子个数，则符合输出值的为（）A. 为甜果数 343 B. 为苦果数 343C. 为甜果数 657 D. 为苦果数 657【答案】B【解析】由题意知，，，即若按全是甜果来算钱超出文，一个苦果和一个甜果差价位，则 p 为苦果数，.故选：B7.在区间内的所有零点之和为（）A.B.C.D.【答案】C第3页/共22页【解析】函数零点即与图象交点的横坐标，在区间象有两个交点，由得：，取于对称，故两个零点的和为,.故选：C内，与图，可知两个交点关8. 已知恒成立，若为真命题，则实数的最小值为（）A. 2 B. 3 C. 4 D. 5 【答案】A【解析】化为，即有，又时，的最小值为 2，故由存在性的意义知 .故实数的最小值为 2. 故选：A 9. 已知某几何体的三视图如图所示，则该几何体的体积为（）A.B.C.D.【答案】B【解析】由三视图，可知该几何体为一个半圆柱与一个三棱锥结合而成的（如图第4页/共22页所示）.半圆柱的底面半径为 1，侧棱长为 2，三棱锥的底面为半圆柱的底面的内接直角三角形，直角边长为，两个侧面是全等的等腰三角形，腰长为 2，底边为，另一个侧面是边长为 2 的等边三角形，因此.故选：B点睛：三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．10. 如图为正方体，动点从点出发，在正方体表面上沿逆时针方向运动一周后，再回到，运动过程种，点与平面的距离保持不变，运动的路程与之间满足函数关系，则此函数图象大致是（）A.B.C.D.第5页/共22页【答案】C【解析】取线段中点为 N，计算得：.同理，当 N 为线段 AC 或 C 的中点时，计算得.符合 C 项的图象特征.故选：C11. 抛物线的准线交轴于点，过点的直线交抛物线于两点，为抛物线的焦点，若，则直线的斜率为（）A. 2 B.C.D.【答案】D【解析】易知直线的斜率存在，且不为零.设得，即，带入，由得：，设，，由韦达定理得，由题知，得，,把，带入整理，得故选：D12. 已知函数，其中为自然对数的底数，若有两个零点，则实数的取值范围是（）A.B.C.D.【答案】C 【解析】画出与的大致图象，如图，第6页/共22页①先求时，与相切时的 a 值：设切点为，则,解得：，，把，得 ;②再求时，与有唯一公共点，且在此点有公切线时的 a 值：，解得：，而显然是增函数，故是唯一的解，此时，把，得，函数的图象是由的图象向左平移 1 个单位，再向上平移 a 个单位（或向下平移-a 个单位），由图象可知：时，仅在上与有两个公共点；③把代入得，可知时，与在区间和内各有一个交点综上，实数的取值范围是故选：C点睛：已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．第Ⅱ卷（共 90 分）二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上）第7页/共22页13. 若向量, 是椭圆上的动点，则的最小值为_________．【答案】【解析】设，则，当时，取最小值为 .故答案为：14. 已知满足，则的取值范围是__________．【答案】【解析】如图，阴影部分即为不等式表示的区域，的几何意义是：可行域中的点与点连线的斜率，且点在直线上，由图形可得最小值为 1，最大值为过点且与抛物线相切的直线的斜率.设切点为，则，把代入，解得或 5，由图可知不合题意，舍去，故切线斜率为，∴ 的取值范围为故答案为：点睛：线性规划问题，首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围.第8页/共22页15. 中，角的对边分别为，当最大时，__________．【答案】【解析】,当且仅当，取等号，∴∠C 的最大值为 75°，此时 sinC= ,，∴.故答案为： 16. 3 位逻辑学家分配 10 枚金币，因为都对自己的逻辑能力很自信，决定按以下方案分配： (1)抽签确定各人序号：1，2，3； (2)1 号提出分配方案，然后其余各人进行表决，如果方案得到不少于半数的人同意（提出方案的人默认同意自己方案），就按照他的方案进行分配，否则 1 好只得到 2 枚金币，然后退出分配与表决； (3)再由 2 号提出方案，剩余各人进行表决，当且仅当不少于半数的人同意时(提出方案的人默认同意自己方案），才会按照他的提案进行分配，否则也将得到 2 枚金币，然后退出分配与表决； (4)最后剩的金币都给 3 号. 每一位逻辑学家都能够进行严密的逻辑推理，并能很理智的判断自身的得失，1 号为得到最多的金币，提出的分配方案中 1 号、2 号、3 号所得金币的数量分别为__________．第9页/共22页【答案】9,0,1【解析】先看一下个人的利益最大化：①3 号：如果 1 号的方案被否定，此时剩余金币有 8 枚，那么 2 号的方案必然是 2 号 8 枚，3 号 0 枚，然后 2 号方案不低于半数通过，②由①的分析可知，只要 1 号的分配方案分配给 3 号的金币数量多于 0，3 号就会同意，方案就会通过，所以 1 号的利益最大化的分配方案是 1 号，2 号，3 号所得金币数量分别是 9，0，1.故答案为：9，0，1三、解答题（本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.）17. 已知数列满足，且 .(1)求数列的通项公式；(2)求的值.【答案】(1);(2).【解析】试题分析：（1）由，作差易得：差数列，即可得到数列的通项公式；（2）利用错位相减法求出的值.试题解析：(1)当时，由，得，，为等第10页/共22页两式相减得.由，得，故为等差数列，公差为 2.当时，由，所以.(2)易知，，两式相减得，，所以.点睛：用错位相减法求和应注意的问题(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn－qSn”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于 1 和不等于 1 两种情况求解.18. 某校高三年级有 1000 人，某次考试不同成绩段的人数,且所有得分都是整数.(1)求全班平均成绩；(2)计算得分超过 141 的人数；（精确到整数）(3)甲同学每次考试进入年级前 100 名的概率是，若本学期有 4 次考试，表示进第11页/共22页入前 100 名的次数，写出的分布列，并求期望与方差.参考数据：.【答案】(1);(2)23 人；（3）见解析.【解析】试题分析：（1）由易知全班平均成绩；（2）由正太分布曲线的对称性易得，从而计算出得分超过 141 的人数；(3) 的取值为 0，1，2，3，4，计算出相应的概率值，利用公式即可算得期望与方差.试题解析：(1)由不同成绩段的人数服从正态分布，可知平均成绩 .(2),故 141 分以上的人数为人.(3) 的取值为 0，1，2，3，4，,,,,, 故的分布列为01234第12页/共22页期望，方差.19. 已知在直角梯形中，，，使二面角为直角.，将沿折起至(1)求证：平面平面；(2)若点满足,，当二面角为 45°时，求的值.【答案】（1）见解析；（2） .【解析】试题分析：（1）要证平面平面，转证平面即可；（2）建立空间直角坐标系计算平面的法向量，利用二面角为 45°建立等量关系求出的值............................试题解析：(1)梯形中，∵∴.又∵,∴,∴.∴.折起后，∵二面角为直角，∴平面平面 .又平面平面,第13页/共22页∴ 平面 .又平面，∴.又∵,∴ 平面 .又∵ 平面，∴平面平面 .(2)由(1)知，平面，∴以为原点，轴正方向，建立如图所示的空间直角坐标系 .方向分别为轴、轴、则,设，由,得，得.取线段的中点，连结，则,∵,∴.又∵,∴ 平面 .∴平面的一个法向量为.第14页/共22页设平面的一个法向量为，则取，则.∴，即或.∵ ，∴ .20. 如图，矩形中，且点.,交于(1)若点的轨迹是曲线的一部分，曲线关于轴、轴、原点都对称，求曲线的轨迹方程； (2)过点作曲线的两条互相垂直的弦，四边形的面积为，探究是否为定值？若是，求出此定值，若不是，请说明理由.【答案】（1）曲线的轨迹方程为；（2）为定值 .【解析】试题分析：（1）可得 M（﹣2，2λ），N（﹣2+4λ，2），，设 Q（x，y），整理得：，即可得曲线 P 的轨迹方程为；（2）设直线的斜率为，把代入椭圆方程，化简整理得.利用韦达定理易得四边形 GFHE 的面积为第15页/共22页，试题解析：(1)设，由,求得,∵,∴,∴，整理得.，所以，可知点的轨迹为第二象限的椭圆，由对称性可知曲线的轨迹方程为.（2）设，当直线斜率存在且不为零时，设直线的斜率为，把代入椭圆方程，化简整理得.，. ∴.∵,∴把换成，即得.第16页/共22页∴，，，∴.当直线斜率不存在或为零时，.∴为定值 .点睛：求定值问题常见的方法①从特殊入手，求出定值，再证明这个值与变量无关． ②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．21. 已知函数，其中为自然对数的底数.(1)若有极值点，求证：必有一个极值点在区间内；(2)求证：对任意，有.【答案】（1）见解析；（2）见解析.【解析】试题分析：（1）易知，设，若有极值点，则有两个不相等的实根；（2）对任意，有等价于，记可得：，即证.试题解析：第17页/共22页(1)易知，设，若有极值点，则有两个不相等的实根，∴，∴或，此时，，∴ 有两个零点，且有一个在区间内.即有一个极值点在区间内.(2)由，得，得，.∴只需证.令，则.∴当时，为增函数，∴，即 .∴只需证，即证，令第18页/共22页则，∴当时，为增函数，∴，即.∴原不等式成立.22. 在平面直角坐标系中，以坐标原点为极点，轴正半轴为极轴，取相同的长度单位建立极坐标系，曲线的极坐标方程为.(1)求曲线的直角坐标方程；(2)在平面直角坐标系中，将曲线的纵坐标不变，横坐标变为原来的 2 倍，得到曲线，过点作直线，交曲线于两点，若，求直线的斜率.【答案】（1）；（2）线的斜率为 .【解析】试题分析：（1）利用把极坐标方程化为直角坐标方程；（2）设直线的参数方程为（为参数，），代入曲线的方程，整理得，利用韦达定理可得，得同向共线. 由可得直线的斜率.试题解析：(1)由，得，将，代入整理得.(2)把中的换成，即得曲线的直角坐标方程.设直线的参数方程为（为参数，），代入曲线的方程，整理得，,第19页/共22页. 设两点所对应的参数分别为，则为上述方程的两个根.由，得同向共线. 故由.由，得，即直线的斜率为 .23. 已知，且.（1)的最小值；(2)证明：.【答案】（1）最小值为 9；（2）见解析.【解析】试题分析：（1）利用柯西不等式求出的最小值；（2）由，得.同理得累加即可得结果. 试题解析：(1)由柯西不等式，得当且仅当时，取等号.，.，第20页/共22页所以的最小值为9.(2)由，得.同理得，.三式相加得，∴，当且仅当时，取等号.。

【衡水金卷压轴卷】2018年普通高等学校招生全国统一考试模拟试题(压轴卷)文科数学(一)(含答案)

sin cos _______ 。 sin 2 cos
15．若不等式组
, f( ) )处的切线的倾斜角为，则 4 4
1 x 3 x 2y 1 表示的点集记为 A，不等式组表示的点集记为 B， 2 y 2 x 3y 1
2018 年普通高等学校招生全国统一考试模拟试题文科数学（一）
本试卷共 4 页，23 题（含选考题）。全卷满分 150 分。考试用时 120 分钟。第Ⅰ卷一、选择题：本题共 12 小題，毎小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的。 1．已知集合 A ( x, y ) y x , B ( x, y ) y 2 ，则 A B A.
4 7 3 1 i或 i 5 5 5 5
B.
4 7 i 5 5
C.
3 1 i 5 5
D.
3 1 i 5 5
x2 y2 1( a 0, b 0) 的渐近线与动曲线 a 2 b2
y ( x 2) 3( R ) 在第一象限内相交于一定点 A，则双曲线 C 的离心率为

2
B.
2, 2
2
C.
(2, 2)
D,
(2, 2), (2, 2)
1 ai 的共轭 2i
2．已知 i 为虚数单位，若复数 z (a 2a 3) (a 3)i 是纯虚数，则复数复数为 A．
3．在某次月考中，一名生物老师从他所任教的某班中抽取了甲、乙两组学生的生物成绩（每组恰好各 10 人），并将获取的成绩制作成如图所示的茎叶图．观察茎叶图，下面说法错误的是 A．甲组学生的生物成绩高分人数少于乙组 B．甲组学生的生物成绩比乙组学生的生物成绩更稳定 C．甲组学生与乙组学生的生物平均成绩相同 D．甲组学生与乙组学生生物成绩的中位数相同 4．已知双曲线 C：

【全国百强校】【衡水金卷】2018年普通高等学校招生全国统一考试模拟试题(一)理科数学(解析版)

2018年普通高等学校招生全国统一考试模拟试题（一）理数第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，，则（）A. B. C. D.【答案】B【解析】∵集合∴∵集合∴∴∵集合∴故选B.2. 设是虚数单位，若，，，则复数的共轭复数是（）A. B. C. D.【答案】A【解析】，根据两复数相等的充要条件得，即，其共轭复数为，故选A.........................3. 已知等差数列的前项和是，且，则下列命题正确的是（）A. 是常数B. 是常数C. 是常数D. 是常数【答案】D【解析】，为常数，故选D.4. 七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形）、一块正方形和一块平行四边形组成的．如图是一个用七巧板拼成的正方形，现从该正方形中任取一点，则此点取自黑色部分的概率是（）A. B. C. D.【答案】A【解析】设，则.∴，∴所求的概率为故选A.5. 已知点为双曲线：（，）的右焦点，点到渐近线的距离是点到左顶点的距离的一半，则双曲线的离心率为（）A. 或B.C.D.【答案】B【解析】由题意可得，双曲线的渐近线方程为，即.∵点到渐近线的距离是点到左顶点的距离的一半∴，即.∴，即.∴∴双曲线的离心率为.故选B.点睛：本题主要考查双曲线的标准方程与几何性质．求解双曲线的离心率问题的关键是利用图形中的几何条件构造的关系,处理方法与椭圆相同,但需要注意双曲线中与椭圆中的关系不同．求双曲线离心率的值或离心率取值范围的两种方法：（1）直接求出的值,可得；（2）建立的齐次关系式,将用表示,令两边同除以或化为的关系式,解方程或者不等式求值或取值范围．6. 已知函数则（）A. B. C. D.【答案】D【解析】，，的几何意义是以原点为圆心，半径为的圆的面积的，故，故选D.7. 执行如图程序框图，则输出的的值为（）A. B. C. D.【答案】C【解析】第1次循环后，，不满足退出循环的条件，；第2次循环后，，不满足退出循环的条件，；第3次循环后，，不满足退出循环的条件，；…第次循环后，，不满足退出循环的条件，；…第次循环后，，不满足退出循环的条件，；第次循环后，，满足退出循环的条件，故输出的的值为.故选C.8. 已知函数的相邻两个零点差的绝对值为，则函数的图象（）A. 可由函数的图象向左平移个单位而得B. 可由函数的图象向右平移个单位而得C. 可由函数的图象向右平移个单位而得D. 可由函数的图象向右平移个单位而得【答案】B【解析】，因为函数（）的相邻两个零点差的绝对值为，所以函数的最小正周期为，而，，故的图象可看作是的图象向右平移个单位而得，故选B.9. 的展开式中剔除常数项后的各项系数和为（）A. B. C. D.【答案】A【解析】令，得，而常数项为，所以展开式中剔除常数项的各项系数和为，故选A.10. 某几何体的三视图如图所示，其中俯视图为一个正六边形及其三条对角线，则该几何体的外接球的表面积是（）A. B. C. D.【答案】B【解析】由三视图可得该几何体是六棱锥，底面是边长为1的正六边形，有一条侧棱垂直底面，且长为2，可以将该几何体补成正六棱柱，其外接球与该正六棱柱外接球是同一个球．故该几何体的外接球的半径，则该几何体的外接球的表面积是.点睛：空间几何体与球接、切问题的求解方法：(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解；(2)若球面上四点构成的三条线段两两互相垂直，且，一般把有关元素“补形”成为一个球内接长方体，利用求解．11. 设为坐标原点，点为抛物线：上异于原点的任意一点，过点作斜率为的直线交轴于点，点是线段的中点，连接并延长交抛物线于点，则的值为（）A. B. C. D.【答案】C【解析】设点，点，则，.∵过点作斜率为的直线交轴于点，点是线段的中点∴∴直线的方程为.∴联立，解得，即.∴故选C.12. 若函数，，对于给定的非零实数，总存在非零常数，使得定义域内的任意实数，都有恒成立，此时为的类周期，函数是上的级类周期函数，若函数是定义在区间内的2级类周期函数，且，当时，函数，若，，使成立，则实数的取值范围是（）A. B. C. D.【解析】是定义在区间内的级类周期函数，且，，当时，，故时，时，，而当时，，，当时，在区间上单调递减，当时，在区间上单调递增，故，依题意得，即实数的取值范围是，故选B.【方法点睛】本题主要考查分段函数函数的最值、全称量词与存在量词的应用以及新定义问题. 属于难题.解决这类问题的关键是理解题意、正确把问题转化为最值和解不等式问题，全称量词与存在量词的应用共分四种情况：（1）只需；（2），只需；（3），只需；（4），，.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知向量，，且，则__________．【答案】【解析】∵向量，，且∴，即.∵∴故答案为.14. 已知，满足约束条件则目标函数的最小值为__________．【解析】由约束条件作出可行域如图所示：联立，解得.由目标函数化为，由图可知过时，直线在轴上的截距最大，此时最小，的最小值为.故答案为.点睛：本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.15. 在等比数列中，，且与的等差中项为，设，，则数列的前项和为__________．【答案】【解析】设等比数列的首项为，公比为.∵∴，即.∵与的等差中项为∴，即.∴，.∴∵∴数列的前项和为.故答案为.16. 有一个容器，下部是高为的圆柱体，上部是与圆柱共底面且母线长为的圆锥，现不考虑该容器内壁的厚度，则该容器的最大容积为__________．【答案】【解析】设圆柱的底面半径为，圆锥的高为，则，故.∴该容器的体积.∴当时，，即在上为增函数；当时，，即在上为减函数.∴当时，取得最大值，此时，.故答案为点睛：求实际问题中的最大值或最小值时，一般是先设自变量、因变量，建立函数关系式，并确定其定义域，利用求函数最值的方法求解，注意结果要与实际情况相结合，用导数求解实际问题中的最大（小）值时，如果函数在开区间内只有一个极值点，那么依据实际意义，该极值点也就是最值点.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知的内角，，的对边，，分别满足，，又点满足．（1）求及角的大小；（2）求的值．【答案】（1）,；（2）.【解析】试题分析：（1）由及正弦定理化简可得即，从而得．又，所以，由余弦定理得；（2）由，得，所以．试题解析：（1）由及正弦定理得，即，在中，，所以．又，所以．在中，由余弦定理得，所以．（2）由，得，所以．18. 在四棱柱中，底面是正方形，且，．（1）求证：；（2）若动点在棱上，试确定点的位置，使得直线与平面所成角的正弦值为．【答案】（1）证明见解析；（2）为的中点.【解析】试题分析：（1）连接，，，与的交点为，连接，则，由正方形的性质可得，从而得平面，，又，所以；（2）由勾股定理可得，由（1）得所以底面，所以、、两两垂直．以点为坐标原点，的方向为轴的正方向，建立空间直角坐标系，设（），求得，利用向量垂直数量积为零可得平面的一个法向量为，利用空间向量夹角余弦公式列方程可解得，从而可得结果.试题解析：（1）连接，，，因为，，所以和均为正三角形，于是．设与的交点为，连接，则，又四边形是正方形，所以，而，所以平面．又平面，所以，又，所以．（2）由，及，知，于是，从而，结合，，得底面，所以、、两两垂直．如图，以点为坐标原点，的方向为轴的正方向，建立空间直角坐标系，则，，，，，，，，由，易求得．设（），则，即，所以．设平面的一个法向量为，由得令，得，设直线与平面所成角为，则，解得或（舍去），所以当为的中点时，直线与平面所成角的正弦值为．【方法点晴】本题主要考查利用线面垂直证明线线垂直以及利用空间向量求二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.19. “过大年，吃水饺”是我国不少地方过春节的一大习俗．2018年春节前夕，市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标，检测结果如频率分布直方图所示．（1）求所抽取的100包速冻水饺该项质量指标值的样本平均数（同一组中数据用该组区间的中点值作代表）；（2）①由直方图可以认为，速冻水饺的该项质量指标值服从正态分布，利用该正态分布，求落在内的概率；②将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这4包速冻水饺中这种质量指标值位于内的包数为，求的分布列和数学期望．附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为；②若，则，．【答案】（1）；（2）①，②分布列见解析，.【解析】试题分析：（1）根据频率分布直方图，直方图各矩形中点值的横坐标与纵坐标的积的和就是所抽取的100包速冻水饺该项质量指标值的样本平均数；（2）①根据服从正态分布，从而求出；②根据题意得，的可能取值为，根据独立重复试验概率公式求出各随机变量对应的概率，从而可得分布列，进而利用二项分布的期望公式可得的数学期望.试题解析：（1）所抽取的100包速冻水饺该项质量指标值的样本平均数为：．（2）①∵服从正态分布，且，，∴，∴落在内的概率是．②根据题意得，；；；；. ∴的分布列为∴．20. 已知椭圆：的离心率为，且以两焦点为直径的圆的内接正方形面积为2．（1）求椭圆的标准方程；（2）若直线：与椭圆相交于，两点，点的坐标为，问直线与的斜率之和是否为定值？若是，求出该定值，若不是，试说明理由．【答案】（1）；（2）定值为.【解析】试题分析：（1）由椭圆的几何性质可得，即可求得，的值，从而可得椭圆的标准方程；（2）联立直线与椭圆的方程得，根据判别式可得的取值范围，设，，结合韦达定理，对化简，从而可得出定值.试题解析：（1）由已知可得解得，.故所求的椭圆方程为．（2）由得，则，解得或．设，，则，，则，，∴，∴为定值，且定值为0．点睛：（1）解题时注意圆锥曲线定义的两种应用，一是利用定义求曲线方程，二是根据曲线的定义求曲线上的点满足的条件，并进一步解题．（2）求定值问题常见的方法：①从特殊入手，求出定值，再证明这个值与变量无关；②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．21. 已知函数，其中为自然对数的底数．（1）若函数在区间上是单调函数，试求实数的取值范围；（2）已知函数，且，若函数在区间上恰有3个零点，求实数的取值范围．【答案】（1）；（2）.【解析】试题分析：（1）根据题意，由函数的解析式计算可得，由函数的导数与函数单调性的关系，分函数在区间上是为单调增函数和单调减函数两种情况讨论，分别求出的取值范围，综合即可得答案；（2）根据题意，对求导分析可得，由，知在区间内恰有一个零点，设该零点为，则在区间内不单调，在区间内存在零点，同理，在区间内存在零点，由（1）的结论，只需在区间内两个零点即可，利用导数研究函数的单调性，从而可得实数的取值范围.试题解析：（1）由题意得，当函数在区间上单调递增时，在区间上恒成立.∴（其中），解得；当函数在区间上单调递减时，在区间上恒成立，∴（其中），解得．综上所述，实数的取值范围是．（2）．由，知在区间内恰有一个零点，设该零点为，则在区间内不单调.∴在区间内存在零点，同理，在区间内存在零点.∴在区间内恰有两个零点．由（1）知，当时，在区间上单调递增，故在区间内至多有一个零点，不合题意．当时，在区间上单调递减，故在区间内至多有一个零点，不合题意，∴．令，得，∴函数在区间上单调递减，在区间内单调递增．记的两个零点为，,∴，，必有，．由，得.∴，又∵，，∴．综上所述，实数的取值范围为．点睛：已知函数有零点求参数取值范围常用的方法和思路：(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.选修4-4：坐标系与参数方程22. 在平面直角坐标系中，圆的参数方程为（是参数，是大于0的常数）．以坐标原点为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方程为．（1）求圆的极坐标方程和圆的直角坐标方程；（2）分别记直线：，与圆、圆的异于原点的交点为，，若圆与圆外切，试求实数的值及线段的长．【答案】（1），；（2），.【解析】试题分析：（1）先将圆的参数方程化为直角坐标方程，再利用可得圆的极坐标方程，两边同乘以利用互化公式即可得圆的直角坐标方程；（2）由（1）知圆的圆心，半径；圆的圆心，半径，圆与圆外切的性质列方程解得，分别将代入、的极坐标方程，利用极径的几何意义可得线段的长.试题解析：（1）圆：（是参数）消去参数，得其普通方程为，将，代入上式并化简，得圆的极坐标方程，由圆的极坐标方程，得．将，，代入上式，得圆的直角坐标方程为．（2）由（1）知圆的圆心，半径；圆的圆心，半径，，∵圆与圆外切，∴，解得，即圆的极坐标方程为．将代入，得，得；将代入，得，得；故．【名师点睛】本题考查圆的参数方程和普通方程的转化、圆的极坐标方程和直角坐标方程的转化以及极径的几何意义，消去参数方程中的参数，就可把参数方程化为普通方程，消去参数的常用方法有：①代入消元法；②加减消元法；③乘除消元法；④三角恒等式消元法；极坐标方程化为直角坐标方程，只需利用转化即可.选修4-5：不等式选讲23. 已知函数．（1）求不等式；（2）若正数，满足，求证：．【答案】（1）；（2）证明见解析.【解析】试题分析：（1）对分三种情况讨论，分别求解不等式组，然后求并集，即可得不等式的解集；（2）先利用基本不等式成立的条件可得，所以.试题解析：（1）此不等式等价于或或解得或或．即不等式的解集为．（2）∵，，，，即，当且仅当即时取等号．∴，当且仅当，即时，取等号．∴．。

衡水金卷2018年普通高等学校招生全国统一考试模拟试卷理科数学(一)试题Word版含答案

衡水金卷2018年普通高等学校招生全国统一考试模拟试卷理科数学(一)试题Word版含答案2018年普通高等学校招生全国统一考试模拟试题理数（一）第Ⅰ卷（共60分）一、选择题：1.已知集合A={x|2-x>1}，B={x| x<1}，则（）A．A∩B={x| x≤2}B．A∩B={x| x<0}C．A∪B={x| x<2}D．A∪B= R解析：由A的定义可得x<1，结合B的定义得到A∩B={x| x<1}，故选B。

2.已知i为虚数单位，a为实数，复数z满足z+3i=a+ai，若复数z是纯虚数，则（）A．a=3B．a=0C．a≠3D．a<3.解析：由z+3i=a+ai，得到z=(a-3)i，因为z是纯虚数，所以a-3=0，即a=3，故选A。

3.我国数学家XXX利用下图证明了勾股定理，该图中用勾a和股b分别表示直角三角形的两条直角边，用弦c来表示斜边，现已知该图中勾为3，股为4，若从图中随机取一点，则此点不落在中间小正方形中的概率是（）A．25/244B．1/2XXXD．1/4解析：由题意可知，中间小正方形的对角线长为4，设其为AB，则由勾股定理可得AC=3，BC=1，所以此点不落在中间小正方形中的概率为（4^2-2^2πr^2）/4^2=12/16=3/4，即选D。

4.已知等差数列(an)的前n项和为Sn，且S9=6π，则tana5=（）A．3B．3C.−3D．−3解析：由等差数列的通项公式可得，an=a1+(n-1)d，其中d为公差，将其代入Sn的通项公式可得S9=(a1+a9)×9/2=9a1+36d，又因为a5=a1+4d，所以tana5=(a5/a1)=(2a5/(a5+a1))=(2(S5-S4)/(S5+S4))=2(2π-5π/6)/(2π+5π/6)=3，故选A。

5.已知函数f(x)=x+a(a∈R)，则下列结论正确的是（）A．对于任意a∈R，f(x)在区间（x，+∞）内单调递增B．存在a∈R，使得f(x)在区间（x，+∞）内单调递减C．存在a∈R，使得f(x)是偶函数D．存在a∈R，使得f(x)是奇函数，且f(x)在区间（x，+∞）内单调递增解析：由题意可知，f(x)的导数为f'(x)=1，即f(x)在任意区间内单调递增，故选A。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 （衡水金卷）2018年普通高等学校招生全国统一考试模拟试题数学文四第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合0,1,3A，120Bxxx，则ABI（） A．0 B．0,1,3 C．0,1 D．0,1,2 2．若复数3i12iz（i是虚数单位），则4iz（） A．26 B．10 C．2 D．4 3．若,,abcR，且ab，则下列不等式一定成立的是（）

A．ccab B．20cab C．22ab D．2211abcc 4．下列结论中正确的个数是（） ①“3x”是“1sin22x”的充分不必要条件； ②命题“,sin1xxR”的否定是“,sin1xxR”； ③函数cosfxxx在区间0,内有且仅有两个零点. A．1 B．2 C．3 D．0 5．已知关于x的不等式2680kxkxk对任意的xR恒成立，若k的取值范围为区间D，在区间1,3上随机取一个数k，则kD的概率是（） A．12 B．13 C．14 D．15 6．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，目取其半，万事不竭”，其意思是：一尺长木棍，每天截取一半，永远截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度（单位：尺），则空白处可填入的是（） A．SSi B．1SSi C．2SSi D．12SSi 2

7．如图所示是一个几何体的三视图，则该几何体的体积为（） A．163 B．643 C．16643 D．1664 8．已知某函数在,上的图象如图所示，则该函数的解析式可能是（）

A．sin2xy B．cosyxx C．lncosyx D．sinyxx 9．《九章算术》卷第五《商功》中有记载：“刍甍者，下有袤有广，而上有袤无广.刍，草也.甍，屋盖也.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍，如图，四边形ABCD为正方形，四边形ABFE、CDEF为两个全等的等腰梯形，4AB，12EFAB∥，若这个刍甍的体积为403，则CF的长为（）

A．1 B．2 C．3 D．4 3

10．在ABC中，角,,ABC的对边分别为,,abc，coscos2cosaBbAcC，7c，且ABC的面积为332，则ABC的周长为（） A．17 B．27 C．47 D．57 11．设12,FF分别是椭圆2222:10xyEabab的左，右焦点，过点1F的直线交椭圆E于,AB两点，若12AFF的面积是12BFF的三倍，23cos5AFB，则椭圆E的离心率为（）

A．12 B．23 C．32 D．22

12．已知定义在区间0,2上的函数fx，fx为其导函数，且sincos0fxxfxx恒成立，则（）

A．226ff B．3243ff

C．363ff D．12sin16ff

第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13．某乡镇中学有初级职称教师160人，中级职称教师30人，高级职称教师10人，要从其中抽取20人进行体检，如果采用分层抽样的方法，则高级职称教师应该抽取的人数为． 14．已知平面向量,abrr，7,4abrr，且6abrr，则ar在br方向上的投影是．

15．若双曲线222210,0xyabab的渐近线与圆2232xy相交，则此双曲4

线的离心率的取值范围是． 16．已知三棱锥PABC的各顶点都在同一球面上，且PA平面ABC，若2AB，1AC，60BAC，4PA，则球的体积为．

三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．已知数列na满足11a，1nnnnanaan*N. （1）求数列na的通项公式；（2）若数列nb的前n项和为nS，23nnSb，求数列nnba的前n项和nT. 18．在直三棱柱111ABCABC中，AD平面1ABC，其垂足D落在直线1AB上. （1）求证：BC平面1AAB；（2）若3AD，2ABBC，P为AC的中点，求三棱锥1PABC的体积.

19．某市甲、乙两地为了争创“市级文明城市”，现市文明委对甲、乙两地各派10名专家进行打分评优，所得分数情况如下茎叶图所示.

（1）分别计算甲、乙两地所得分数的平均值，并计算乙地得分的中位数；（2）从乙地所得分数在60,80间的成绩中随机抽取2份做进一步分析，求所抽取的成绩中，至少有一份分数在75,80间的概率；（3）在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性，求这2份成绩都是来自甲地的概率. 20．已知点00,Mxy在圆22:4Oxy上运动，且存在一定点6,0N，点,Pxy为线段MN的中点. （1）求点P的轨迹C的方程； 5

（2）过0,1A且斜率为k的直线l与点P的轨迹C交于不同的两点,EF，是否存在实数k使得12OEOFuuuruuur，并说明理由. 21．已知函数lnfxxaxaR. （1）求函数fx的单调区间；（2）当1a时，方程2fxmm有两个相异实根12,xx，且12xx，证明：2122xx.

请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．选修4-4：坐标系与参数方程

在平面直角坐标系xOy中，曲线C的参数方程为3cos,sinxy（是参数），以原点O为

极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为sin24. （1）将直线l的极坐标方程化为普通方程，并求出直线l的倾斜角；（2）求曲线C上的点到直线l的最大距离. 23．选修4-5：不等式选讲已知函数22fxxxaa，若7fx的解集是3xx或4x. （1）求实数a的值；（2）若xR，不等式31fxfm恒成立，求实数m的取值范围. 6

文数（四）答案一、选择题 1-5:CBDAC 6-10:BCACD 11、12：DC 二、填空题

13．1 14．138 15．1,3 16．2053 三、解答题 17．解：（1）∵1nnnnanaa，

∴11nnanan.

∴121121nnnnnaaaaaaaaL121121nnnnnL， ∴数列na的通项公式为nan. （2）由23nnSb，得13b，又11232nnSbn， ∴1122nnnnnbSSbb，即122,nnbbnn*N， ∴数列nb是以3为首项，2为公比的等比数列， ∴132nnbn*N， ∴132nnnban， ∴012131222322nnTnL， 123231222322n

nTnL

，

两式相减，得0121322222nnnTnL3121nn， ∴3123nnTn. 7

18．解：（1）∵三棱柱111ABCABC为直三棱柱， ∴1AA平面ABC. 又BC平面ABC，∴1AABC. ∵AD平面1ABC，且BC平面1ABC， ∴ADBC. 又1AA平面1AAB，AD平面1AAB，1AAADAI， ∴BC平面1AAB. （2）在直三棱柱111ABCABC中，1AAAB. ∵AD平面1ABC，其垂足D落在直线1AB上， ∴1ADAB. 在RtABD中，3AD，2ABBC， ∴3sin2ADABDAB，即60ABD，在1RtABA中，1tan6023AAAB. 由（1）知，BC平面1AAB，AB平面1AAB，从而BCAB， ∴1122222ABCSABBC. ∵F为AC的中点， ∴112BCFABCSS.

∴11113PABCAPBCBCFVVSAA12312333. 19．解：（1）由题得，甲地得分的平均数为17778838580898892979986.810， 8

乙地得分的平均数为1657275798280848696918110，乙地得分的中位数为8280812. （2）由茎叶图可知，乙地得分中分数在60,80间的有65,72,75,79四份成绩，随机抽取2份的情况有：65,72，65,75，65,79，72,75，72,79，75,79，共6种，其中至少有一份分数在70,80间的情况有：65,75，65,79，72,75，72,79，75,79，共5种.

故所求概率56P. （3）甲、乙两地所得分数中超过90分的一共有5份，记甲地中的三份分别为,,ABC，乙地中的两份分别为,ab. 随机抽取其中2份，所有情况如下：,AB，,AC，,BC，,ab，,Aa，,Ab，,Ba，,Bb，,Ca，,Cb，一共10种.

其中两份成绩都来自甲地的有3种情况：,AB，,AC，,BC，. 故所求概率310p.

20．解：（1）由中点坐标公式，得00622xxyy 即fx，fx. ∵点00,Mxy在圆224xy上运动， ∴22004xy，即222624xy，整理，得2231xy. ∴点P的轨迹C的方程为2231xy. （2）设11,Exy，22,Fxy，直线l的方程是1ykx，代入圆2231xy.