伊嘉儿数学五年级春第13讲鸟头模型

合集下载

奥数三角形等高模型与鸟头模型一学生版精编版

三角形等高模型与鸟头模型4-3-1.例题精讲三角形等高模型板块一高底我们已经知道三角形面积的计算公式：三角形面积??2?从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．；)，三角形面积也就越大(小)如果三角形的底不变，高越大(小；，三角形面积也就越大(小)如果三角形的高不变，底越大(小)当三角形的底和高但是，这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．1，则三角同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的3而不仅仅一个三角形的面积变化与否取决于它的高和底的乘积，形面积与原来的一样．这就是说：可以有无数多个不同一个三角形在面积不改变的情况下，取决于高或底的变化．同时也告诉我们：的形状．在实际问题的研究中，我们还会常常用到以下结论：等底等高的两个三角形面积相等；①两个三角形高相等，面积比等于它们的底之比；②两个三角形底相等，面积比等于它们的高之比；如左图ba:SS:?21BASS21baDC③夹在一组平行线之间的等积变形，如右上图；SS?BCD△△ACD CDAB．反之，如果，则可知直线平行于SS?BCD△△ACD④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．【例1】你有多少种方法将任意一个三角形分成：⑴3个面积相等的三角形；⑵4个面积相等的三角形；⑶6个面积相等的三角形．在同一条直线上．和D厘米，B、C如图，】BD长12厘米，DC长4【例2 ABD面积的多少倍？求三角形ABC的面积是三角形⑴ADC面积的多少倍？求三角形ABD的面积是三角形⑵ABCD厘米，那么图中阴的长是都是矩形，的长是厘米，和【例3】如右图，3CDEFBC4ABABFE平方厘米．影部分的面积是AB FEDC平方厘米，则阴影部如图所示，平行四边形的面积是50【巩固】(2009年四中小升初入学测试题) 平方厘米．分的面积是，的长是20拼成了长方形【巩固】如下图，长方形和长方形，长方形ABCDABCDFDCEAFEB．，则它内部阴影部分的面积是宽是12ABFEDC【例4】如图，长方形的面积是平方厘米，点、、分别是长方形边上的ABCDABCDG56FE中点，为边上的任意一点，求阴影部分的面积．ADHHHDDAAEEGGCCBBFF、、，那三条边的三等分点，如果正方形的边长是分别是正方形【巩固】图中的ABCDG12EF．么阴影部分的面积是HAADD6GG512EE43BBCCFF【例5】长方形的面积为36，、、为各边中点，为边上任意一点，问阴影GABCDADHEF部分面积是多少？HDAEGBCF)(HDA DHAGE EG CBF BCF，将正方形的一组对边二等分，另一组对内任取一点6厘米的正方形【巩固】在边长为ABCDP ,求阴影部分面积．边三等分，分别与点连接PDDD(P)AAAPPCCCBBB的面积垂直E在AD上，ADBC，厘米，ABC厘米．求三角形】【例6如右图，3?DE12AD? EBC 面积的几倍？是三角形AECBD等BECBFAE、、CF、那么与BEACEFABCD7【例】如图，在平行四边形中，平行，连结△积的三角形一共有哪几个三角形？FADEBC等积的、CE，那么与ABED是BC中点，E是AD中点，连结BE中，【巩固】如图，在ABC△△三角形一共有哪几个三角形？AECBD【巩固】如图，在梯形ABCD中，共有八个三角形，其中面积相等的三角形共有哪几对？DAOCB的面积是多，三角形如图，三角形】的面积为1，其中，【例8BC2ABCBD?ABAE?3BDE少？BBEAEACCDD的面积平方厘米，，已知阴影部分面积为如右图，，5】【例9ABC?AEEF?FC?DBAD?平方厘米．是BBDDAACCFEFE倍，长的3的面积是180平方厘米，是的中点，的长是【巩固】图中三角形BCABCEFDADAE3的长是长的倍．那么三角形的面积是多少平方厘米？AEFBF AEFBCD厘米，如果是的中点，【巩固】如图，在长方形中，是的中点，8ABCDBC?24ZABDYYBD?厘米，求三角形的面积．ZCYCDZYBADEF的中点．求三角形分别是BC、AC和ADD【巩固】如图，三角形ABC的面积是24，、E和F 的面积．AEFCBD的中点，那和ACF分别为AB、中，【巩固】如图，在三角形ABC厘米，高是6厘米，E8?BC的面积是多少平方厘米？EBF么三角形AFECB△平方厘米。

小升初几何常考五大模型（等积变换、鸟头、蝴蝶、相似、燕尾）

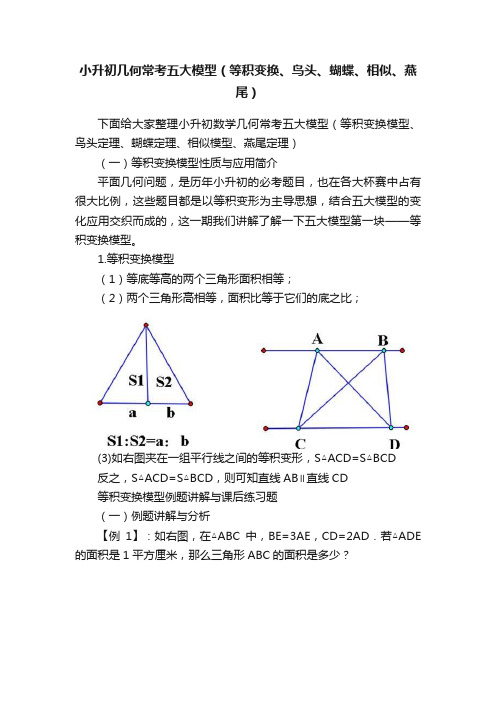
小升初几何常考五大模型（等积变换、鸟头、蝴蝶、相似、燕尾）下面给大家整理小升初数学几何常考五大模型（等积变换模型、鸟头定理、蝴蝶定理、相似模型、燕尾定理）（一）等积变换模型性质与应用简介平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，这一期我们讲解了解一下五大模型第一块——等积变换模型。

1.等积变换模型（1）等底等高的两个三角形面积相等；（2）两个三角形高相等，面积比等于它们的底之比；(3)如右图夹在一组平行线之间的等积变形，S△ACD=S△BCD反之，S△ACD=S△BCD，则可知直线AB∥直线CD等积变换模型例题讲解与课后练习题（一）例题讲解与分析【例1】：如右图，在△ABC中，BE=3AE，CD=2AD．若△ADE 的面积是1平方厘米，那么三角形ABC的面积是多少？【解答】连接BD,S△ABD和S△ AED同高，面积比等于底边比，所以三角形ABD的面积是4，S△ABD和S△ABC同高面积比等于底边比，三角形ABC的面积是ABD的3倍，是12.【总结】要找准那两个三角形的高相同。

【例2】：如图，四边形ABCD中，AC和BD相交于O点，三角形ADO的面积=5，三角形DOC的面积=4，三角形AOB的面积=15，求三角形BOC的面积是多少？【解答】S△ADO=5,S△DOC=4根据结论2，△ADO与△DOC同高所以面积比等于底的比,即AO/OC=5:4同理S△AOB/S△BOC=AO/OC=5:4,因为S△AOB=15所以S△BOC=12。

【总结】从这个题目我们可以发现，题目的条件和结论都是三角形的面积比，我们在解题过程中借助结论2，先把面积比转化成线段比，再把线段比用结论2转化成面积比，解决了问题。

事实上，这2次转化的过程就相当于在条件和结论中搭了一座'桥梁'，请同学们体会一下。

（二）鸟头定理（共角定理）模型平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，第二期我们讲解了解一下五大模型第二块——鸟头定理（共角定理）模型。

小学奥数几何五大模型鸟头模型.

三角形等高模型与鸟头模型模型二鸟头模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角 )两夹边的乘积之比．如图在△ABC中，D,E分别是AB,AC上的点如图⑴(或D在BA的延伸线上，E在AC上如图2)，则S△ABC:S△ADE(AB AC):(AD AE)ADADEEB C B C图⑴图⑵【例1】如图在△ABC中，D,E分别是AB,AC上的点，且AD:AB2:5，AE:AC4:7，S△ADE16平方厘米，求△ABC的面积．AAD DE EB C B C【分析】连结BE，S△ADE:S△ABE AD:AB2:5(24):(54)，S△ABE:S△ABC AE:AC4:7(45):(75)，所以S△ADE:S△ABC(24):(75)，设S△ADE8份，则△35份，△16平方厘米，所以1份是2平方厘米，35份就是70平方厘米，△ABC的SABC SADE面积是平方厘米．由此我们获得一个重要的共角定理：共角三角形的面积比等于(相70定理，对应角等角或互补角)两夹边的乘积之比．page1of7【坚固】如图，三角形ABC中，AB是AD的5倍，AC是AE的3倍，假如三角形ADE的面积等于1，那么三角形ABC的面积是多少？A ADE D EB CB C【分析】连结BE．∵EC3AE∴S ABC3S ABE又∵AB5AD∴S ADE S ABE5 S ABC 15，∴S ABC15S ADE15．【坚固】如图，三角形ABC被分红了甲(暗影部分)、乙两部分，BD DC 4，BE 3，AE6，乙部分面积是甲部分面积的几倍？A AEB甲【分析】连结AD．∵BE3，AE6∴AB3BE，SABD乙E乙甲C B CD D3S BDE又∵BD DC4，∴S ABC2S ABD，∴S ABC6S BDE，S乙5S甲．【例2】如图在△ABC中，D在BA的延伸线上，E在AC上，且AB:AD5:2，AE:EC3:2，S△ADE12平方厘米，求△ABC的面积．D DA AEEB C B C【分析】连结BE，S△ADE:S△ABE AD:AB2:5(23):(53)S△ABE:S△ABC AE:AC3:(32)(35):(32)5，所以S△ADE:S△ABC(32):5(32)6:25，设S△ADE6份，则S△ABC25份，S△ADE12平方厘米，所以1份是2平方厘米，25份就是50平方厘米，△ABC的面积是50平方厘米．由此我们获得一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】以以下图，在平行四边形ABCD中，E为AB的中点，AF2CF，三角形AFE(图中暗影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？page2of7D CFAEB【分析】连结FB ．三角形AFB 面积是三角形CFB 面积的 2倍，而三角形 AFB 面积是三角形 AEF 面积的2倍，所以三角形ABC 面积是三角形 AEF 面积的3倍；又因为平行四边形的面积是三角形 ABC 面积的2倍，所以平行四边形的面积是三角形AFE面积的（32） 6倍．所以，平行四边形的面积为648(平方厘米)．【例 4】已知△DEF 的面积为7平方厘米，BE CE,AD2BD,CF 3AF ，求△ABC 的面积．AFDBCE【分析】S △BDE :S △ABC(BD BE):(BABC)(1 1):(2 3) 1:6，S△CEF:S△ABC(CE CF):(CBCA)(1 3):(2 4) 3:8S △ADF :S △ABC(AD AF):(AB AC)(21):(3 4)1:6设△ ABC 24份，则 △BDE 4份，△ 4份，△ CEF 9份，△24 4 497份，恰巧是7S S S ADFSS DEF平方厘米，所以S △ABC 24平方厘米【例 5】如图，三角形ABC 的面积为 3平方厘米，此中 AB:BE2:5，BC:CD3:2 ，三角形BDE 的面积是多少？ABEABEC CDD【分析】因为ABC DBE 180，所以能够用共角定理，设 AB2份，BC3份，则BE5份，BD 3 25份，由共角定理 S △ABC :S △BDE (AB BC):(BE BD)(23):(55)6:25，设S△ABC6份，恰巧是 3平方厘米，所以1份是0.5平方厘米，25份就是250.5 12.5平方厘米，三角形BDE 的面积是12.5 平方厘米【例 6】(2007年”走美”五年级初赛试题)以以下图，正方形ABCD 边长为6厘米，AE1AC ，CF1BC ．三角形DEF 的面积为_______平方厘米．3 3ADEBF Cpage3of7【分析】由题意知AES △CEF :S △ABC11 2AC ．依据”共角定理”可得，AC 、CFBC ，可得CE333(CFCE):(CB AC)12:(3 3)2:9；而△ABC662 18；所以△CEF4；SS同理得，S △CDE :S △ACD 2:3;，S △CDE 18 3212，S △CDF 6故△ △ △ △4 126 10(平方厘米)．S DEF S CEF S DEC S DFC【例 7】如图，已知三角形 ABC 面积为1 ，延伸AB 至D ，使BDAB ；延伸BC 至E ，使CE2BC ；延伸CA 至F ，使AF 3AC ，求三角形DEF 的面积．FFA EAEBCBCDD【分析】(法1)此题是性质的频频使用．连结AE 、CD ．S ABC 11 ，∵，S ABCS DBC 1∴S DBC1．同理可得其他，最后三角形 DEF 的面积18．(法2)用共角定理∵在 ABC 和CFE 中，ACB 与FCE 互补，S ABC AC BC 1 11∴FC CE 4 2．SFCE8又S ABC1，所以S FCE 8 ．同理可得S ADF 6，S BDE3．所以S DEF S ABCSFCESADFSBDE 186318．【例 8】如图，平行四边形ABCD ，BE AB ，CF 2CB ，GD 3DC ，HA 4AD ，平行四边形ABCD 的面积是2，求平行四边形 ABCD 与四边形 EFGH 的面积比．HHA B EABEGDCGDCFF【分析】连结AC 、BD ．依据共角定理∵在△ABC 和△BFE 中， ABC 与 FBE 互补，S△ABC AB BC 1 1 1．∴BE BF 1 3 3S△FBE又S △ABC 1，所以S △FBE 3．同理可得S△GCF8，S △DHG 15，S △AEH 8．page4of7所以S EFGH S△AEH S△CFG S△DHG S△BEF S ABCD8815+3+236．SABCD21所以36．SEFGH18【例9】如图，四边形EFGH的面积是66平方米，EAAB，CB BF，DC CG，HD DA，求四边形ABCD 的面积．H HD C GDC GA BF A BFE E【分析】连结BD．由共角定理得S△BCD:S△CGF(CDCB):(CG CF)1:2，即S△CGF2S△CDB同理S△ABD:S△AHE1:2，即S△AHE2S△ABD所以S△AHE S△CGF2(S△CBDS△ADB)2S四边形ABCD连结AC，同理能够获得S△DHG S△BEF2S四边形ABCDS四边形EFGH S△AHES△CGFS△HDGS△BEFS四边形ABCD5S四边形ABCD所以S四边形ABCD66513.2平方米【例10】如图，将四边形ABCD的四条边AB、CB、CD、AD分别延伸两倍至点E、F、G、H，若四边形ABCD的面积为5，则四边形EFGH的面积是．F FE B A E B AG C GCD DH H【分析】连结AC、BD．因为BE2AB，BF2BC，于是S BEF4S ABC，同理S HDG4S ADC．于是S BEF S HDG4S ABC4S ADC4S ABCD．再因为AE3AB，AH3AD，于是S AEH9S ABD，同理S CFG9S CBD．于是S AEH S CFG9S ABD9S CBD9S ABCD．那么S EFGH S BEF S HDG S AEH S CFG S ABCD4S ABCD9S ABCD S ABCD12S ABCD60．【例11】如图，在△ABC中，延伸AB至D，使BD AB，延伸BC至E，使CE 1，F是AC的BC中点，若△ABC的面积是2，则△DEF的面积是多少？2AFB C ED【分析】∵在△ABC和△CFE中，ACB与FCE互补，page5of7∴S△ABC AC BC224．S△FCE FC CE111又S ABC2，所以S FCE0.5．同理可得S△ADF2，S△BDE3．所以S△DEF S△ABC S△CEF S△DEB S△ADF20.5323.5【例12】如图，S△ABC1，BC5BD，AC4EC，DG GS SE，AF FG．求S FGS．AFG SEB CD【分析】此题题目自己很简单，但它把本讲的两个重要知识点交融到一同，既能够看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的频频运用，也能够看作是找点，最妙的是此中包括了找点的3种状况．最后求得S△432111．FGS的面积为△S FGS4322105【例13】以以下图，正方形ABCD边长为8厘米，E是AD的中点，F是CE的中点，G是BF的中点，三角形ABG的面积是多少平方厘米？A ED AEDF FB GC BGC【分析】连结AF、EG．因为S△BCF1216，依据”当两个三角形有一个角相等或互补时，这两个三角形的面积S△CDE84比等于夹这个角的两边长度的乘积比”SAEF8，S EFG8，再依据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，获得S BFC16，S ABFE32，SABF24，所以S ABG12平方厘米．【例14】四个面积为1的正六边形如图摆放，求暗影三角形的面积．F HA EBG CD【分析】如图，将原图扩展成一个大正三角形DEF，则AGF与CEH都是正三角形．假定正六边形的边长为为a，则AGF与CEH的边长都是4a，所以大正三角形DEF的边长为4 2 1 7，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角page6of7形构成的，所以一个单位小正三角形的面积为1，三角形DEF 的面积为49．66因为FA 4a ，FB3a ，所以AFB 与三角形DEF 的面积之比为4 3 12．77 49同理可知BDC 、AEC 与三角形DEF 的面积之比都为12，所以ABC 的面积占三角形DEF 面积49的112 313，所以ABC 的面积的面积为 49 13 13．49 49649 6【坚固】已知图中每个正六边形的面积都是 1，则图中虚线围成的五边形 ABCDE 的面积是．EA DB C【分析】从图中能够看出，虚线AB 和虚线CD 外的图形都等于两个正六边形的一半，也就是都等于一个正六边形的面积；虚线BC 和虚线DE 外的图形都等于一个正六边形的一半，那么它们合起来等于一个正六边形的面积；虚线AE 外的图形是两个三角形，从右图中能够看出，每个三角形都是一个正六边形面积的 1，所以虚线外图形的面积等于 1 3 1 2 31，所以五边形的面积是10 3162．6 6 333精选文档page7of7。

小升初数学专题详解鸟头模型与等积变形超常版

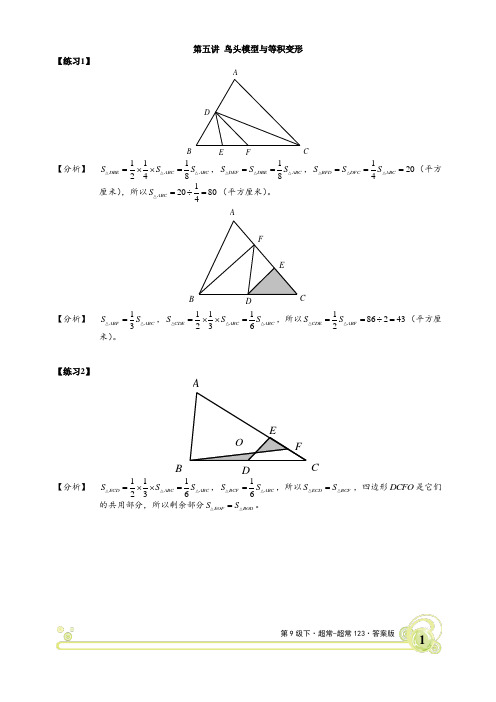
1第9级下·超常-超常123·答案版第五讲鸟头模型与等积变形【练习1】【分析】 111248DBEABCABC SS S =⨯⨯=，18DEF DBE ABCS S S ==，1204BFDDFCABCS SS ===（平方厘米），所以120804ABCS=÷=（平方厘米）。

【分析】 13ABFABC S S =，111236CDEABCABC SS S =⨯⨯=，所以1862432CDEABFSS ==÷=（平方厘米）。

【练习2】【分析】 111236ECDABC ABC S S S =⨯⨯=，16BCF ABC S S =，所以ECDBCFS S=，四边形DCFO 是它们的共用部分，所以剩余部分EOF BOD S S =。

FAB CDE CABDABCD2第五讲学理科到学而思【练习3】【分析】梯形总面积为2(25)4214cm +⨯÷=，21124422BCF ABCES Scm ∆==⨯⨯=， 212442ABD S cm ∆=⨯⨯=，所以阴影部分面积为214446S cm =--=。

【练习4】【分析】连结AH ，设FGH S a ∆=。

因为AF FG =，所以AFH S a ∆=，2AGH S a ∆=。

而DG GH HE ==，所以36ADE AGH S S a ∆∆==。

5AC EC =，45AE AC =，因此47.55ADC ADE S S a ∆∆=÷=。

6BC BD =,所以596ABC ADC S S a ∆∆=÷=。

::91:9FGH ABC S S a a ∆∆==【练习5】【分析】如右图，将小正方形折叠过去，160302CDGF DHGC S S ==⨯=（平方厘米）。

【练习6】EDBA ABDA【分析】连结AG 、CG ，如右图所示，AF EC =，有AGFCGESS=，又因为ED BG =，有AEDABGSS=，且CDEBCGSS=由此可见：EFG ∆的三个部分中ABGS补到了EADS，AFGS补到了BCD S ∆，而AEB S ∆的位置不变，由此一来相当于将EFG ∆等积变形到了四边形ABCD ，两者面积相同，即：1EFGS =。

小学的奥数-几何五大模型(鸟头模型)

模型二鸟头模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．如图在ABC △中，,D E 分别是,AB AC 上的点如图⑴(或D 在BA 的延长线上，E 在AC 上如图 2)，则:():()ABC ADES S AB AC AD AE △△EDCBAEDCBA图⑴图⑵【例1】如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB，:4:7AE AC，16ADES △平方厘米，求ABC △的面积．EDCBAEDCB A【解析】连接BE ，::2:5(24):(54)ADE ABES S AD AB △△，::4:7(45):(75)ABE ABC S S AE AC△△，所以:(24):(75)ADE ABCS S △△，设8ADES △份，则35ABCS △份，16ADE S △平方厘米，所以1份是2平方厘米，35份就是70平方厘米，ABC △的面积是70平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．三角形等高模型与鸟头模型【巩固】如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？E D CBA A BCD E【解析】连接BE ．∵3EC AE ∴3ABCABESS又∵5AB AD ∴515ADEABEABCSSS，∴1515ABCADESS．【巩固】如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ，3BE，6AE，乙部分面积是甲部分面积的几倍？乙甲E D CBAABCDE甲乙【解析】连接AD ．∵3BE ，6AE ∴3AB BE ，3ABDBDES S又∵4BD DC ，∴2ABCABDSS，∴6ABCBDE SS ，5S S 乙甲．【例2】如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD，:3:2AE EC ，12ADE S △平方厘米，求ABC △的面积．EDC B A EDCB A【解析】连接BE ，::2:5(23):(53)ADE ABES S AD AB △△::3:(32)(35):(32)5ABE ABCS S AE AC△△，所以:(32):5(32)6:25ADE ABC S S △△，设6ADES △份，则25ABCS △份，12ADES △平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AFCF ，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？EFDCBA【解析】连接FB ．三角形AFB 面积是三角形CFB 面积的2倍，而三角形AFB 面积是三角形AEF 面积的2倍，所以三角形ABC 面积是三角形AEF 面积的3倍；又因为平行四边形的面积是三角形ABC 面积的2倍，所以平行四边形的面积是三角形AFE 面积的326（）倍．因此，平行四边形的面积为8648(平方厘米)．【例4】已知DEF △的面积为7平方厘米，,2,3BECE AD BD CF AF ，求ABC △的面积．FED CBA【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC △△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA △△:():()(21):(34)1:6ADF ABC S S ADAF ABAC △△设24ABCS △份，则4BDES △份，4ADF S △份，9CEFS △份，244497DEFS △份，恰好是7平方厘米，所以24ABCS △平方厘米【例5】如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE，:3:2BC CD，三角形BDE 的面积是多少？AB EC DDC EB A【解析】由于180ABC DBE，所以可以用共角定理，设2AB 份，3BC份，则5BE 份，325BD 份，由共角定理:():()(23):(55)6:25ABC BDES S ABBC BE BD △△，设6ABCS △份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5平方厘米，三角形BDE 的面积是12.5平方厘米【例6】(2007年”走美”五年级初赛试题)如图所示，正方形ABCD 边长为6厘米，13AEAC ，13CF BC ．三角形DEF 的面积为_______平方厘米．FED C BA【解析】由题意知13AEAC 、13CFBC ，可得23CEAC ．根据”共角定理”可得，:():()12:(33)2:9CEF ABC S S CF CE CB AC △△；而66218ABCS △；所以4CEF S △；同理得，:2:3CDE ACD S S △△;，183212CDE S △，6CDF S △故412610DEFCEFDECDFCS S S S △△△△(平方厘米)．【例7】如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB ；延长BC 至E ，使2CEBC ；延长CA 至F ，使3AF AC ，求三角形DEF 的面积．F EDCB A AB CDEF【解析】(法1)本题是性质的反复使用．连接AE 、CD ．∵11ABC DBC S S ，1ABCS ，∴S1DBC．同理可得其它，最后三角形DEF 的面积18．(法2)用共角定理∵在ABC 和CFE 中，ACB 与FCE 互补，∴111428ABC FCES AC BC SFC CE ．又1ABCS，所以8FCES．同理可得6ADFS ，3BDES．所以186318DEFABCFCEADFBDESS SSS．【例8】如图，平行四边形ABCD ，BE AB ，2CF CB ，3GD DC ，4HA AD ，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．HGAB CD EFHGA B CDEF【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC 与FBE 互补，∴111133ABC FBES AB BC S BE BF△△．又1ABC S △，所以3FBES △．同理可得8GCF S △，15DHGS △，8AEH S △．所以8815+3+236EFGH AEH CFG DHGBEFABCDS S S S S S △△△△．所以213618ABCD EFGHS S ．【例9】如图，四边形EFGH 的面积是66平方米，EAAB ，CBBF ，DCCG ，HD DA ，求四边形ABCD 的面积．H GFED CB A A BCDEFG H 【解析】连接BD ．由共角定理得:():()1:2BCD CGFS S CD CB CGCF △△，即2CGFCDBS S △△同理:1:2ABD AHE S S △△，即2AHE ABDS S △△所以2()2AHECGFCBDADB ABCDS S S S S △△△△四边形连接AC ，同理可以得到2DHGBEFABCDS S S △△四边形5AHECGFHDGBEFEFGHABCDABCDS S S S S S S △△△△四边形四边形四边形所以66513.2ABCDS 四边形平方米【例10】如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是．A B CD EF GHA B CD EFGH【解析】连接AC 、BD ．由于2BE AB ，2BFBC ，于是4BEFABCS S，同理4HDGADCSS．于是444BEFHDGABC ADCABCD SS S SS ．再由于3AE AB ，3AH AD ，于是9AEHABDSS，同理9CFGCBDSS．于是999AEHCFG ABDCBDABCD SS S S S ．那么491260EFGHBEFHDG AEHCFGABCDABCD ABCDABCDABCDS SSSSS S S S S ．【例11】如图，在ABC △中，延长AB 至D ，使BD AB ，延长BC 至E ，使12CEBC ，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？A BCDEF【解析】∵在ABC △和CFE △中，ACB 与FCE 互补，∴224111ABC FCES AC BC S FC CE △△．又2ABCS，所以0.5FCES．同理可得2ADF S △，3BDES △．所以20.532 3.5DEFABC CEF DEB ADF S S S S S △△△△△【例12】如图，1ABCS △，5BCBD ，4AC EC ，DGGSSE ，AFFG ．求FGSS．SGF E DCBA 【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为4321115432210FGSS △．【例13】如图所示，正方形ABCD 边长为8厘米，E 是AD 的中点，F 是CE 的中点，G 是BF 的中点，三角形ABG 的面积是多少平方厘米？ABCDEF GABCDEF G【解析】连接AF 、EG ．因为218164BCFCDES S △△，根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEFS，8EFGS，再根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，得到16BFCS，32ABFE S ，24ABFS，所以12ABGS平方厘米．【例14】四个面积为1的正六边形如图摆放，求阴影三角形的面积．HGFEDCB A【解析】如图，将原图扩展成一个大正三角形DEF ，则AGF 与CEH 都是正三角形．假设正六边形的边长为为a ，则AGF 与CEH 的边长都是4a ，所以大正三角形DEF 的边长为4217，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角形组成的，所以一个单位小正三角形的面积为16，三角形DEF 的面积为496．由于4FAa ，3FBa ，所以AFB 与三角形DEF 的面积之比为43127749．同理可知BDC、AEC与三角形DEF的面积之比都为1249，所以ABC的面积占三角形DEF面积的1213134949，所以ABC的面积的面积为4913136496．【巩固】已知图中每个正六边形的面积都是1，则图中虚线围成的五边形ABCDE的面积是．BDCEA【解析】从图中可以看出，虚线AB和虚线CD外的图形都等于两个正六边形的一半，也就是都等于一个正六边形的面积；虚线BC和虚线DE外的图形都等于一个正六边形的一半，那么它们合起来等于一个正六边形的面积；虚线AE外的图形是两个三角形，从右图中可以看出，每个三角形都是一个正六边形面积的16，所以虚线外图形的面积等于11132363，所以五边形的面积是12103633．。

小学奥数平面几何五种面积模型等积鸟头蝶形相似共边

4
以三角形 AOE 和 DOG 的面积之和为120 3 70 20 ；
4
又三角形
AOE
、
DOG
和四边形
EFGO
的面积之和为120

1 2

1 4

30
，所以四边形
EFGO 的面积为 30 20 10 ．
另解：从整体上来看，四边形 EFGO 的面积三角形 AFC 面积三角形 BFD 面积
所以阴影部分的面积是： S阴影 18 SEBF 18 4.5 13.5
解法二：特殊点法．找 H 的特殊点，把 H 点与 D 点重合，
那么图形就可变成右图：
，而，
A
D (H)
E
G
B
F
C
这样阴影部分的面积就是 DEF 的面积，根据鸟头定理，则有：
S阴影

S ABCD

SAED
边部分面积是 38，右边部分面积是 65，那么三角形 ADG 的面积是
．
A
A
CD E B
FG
CD E
F
G
B
【解析】连接 AF ， BD ．根据题意可知， CF 5 7 15 27 ； DG 7 15 6 28 ；
所以， SBEF

15 27 SCBF
， SBEC

存在于任何一个三角形之中，为三角形中的三角形面积对应底边之
O
间提供互相联系的途径.
B
D
C
典型例题
【例 1】如图，正方形 ABCD 的边长为 6，AE 1.5，CF 2．长方形 EFGH 的面积为
．
_H

(完整版)小升初几何鸟头、蝴蝶、燕尾模型

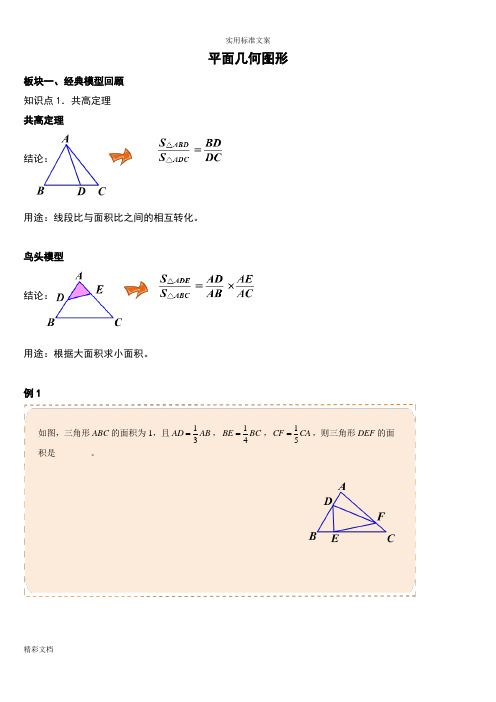
平面几何图形板块一、经典模型回顾知识点1．共高定理共高定理结论：用途：线段比与面积比之间的相互转化。

鸟头模型结论：用途：根据大面积求小面积。

例1如图，三角形ABC的面积为1，且13 ADAB=，14BE BC=，15CF CA=，则三角形DEF的面积是________。

例2知识点2：蝴蝶模型结论：1．2．S1×S3＝S2×S4用途：借助面积比来反求线段比。

例3如图，将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H，若四边形ABCD的面积为5，则四边形EFGH的面积是。

如图，正方形ABCD的面积是64平方厘米，正方形CEFG的面积是36平方厘米，DF与BG相交于O。

则DBO的面积等于多少平米厘米？知识点3：梯形蝴蝶结论：1．S 2＝S 32．S 1×S 4＝S 22＝S 32 3．4．S 1＝a 2份，S 4＝b 2份，S 2＝S 3＝ab 份；S ＝(a ＋b )2份用途：梯形中的面积比例关系。

例4知识点4：燕尾定理结论：用途：推面积间的比例关系。

如图所示，在梯形ABCD 中，AB ∥CD ，对角线AC ，BD 相交于点O ，已知AB ＝5，CD ＝3，且梯形ABCD 的面积为4，求三角形OAB 的面积。

例5【阶段总结1】1．五大模型分别是什么？各有什么妙用？ 2．每个模型中都应注意的小技巧有哪些？板块二、综合运用（一）例6如图，ABC△中BD DA =2，CE EB =2，AF FC =2，那么ABC △的面积是阴影三角形面积的__________倍。

三条边长分别为5、12、13的直角三角形如图所示，将它的短直角边对折到斜边上去，与斜边相重合，问图中阴影部分的面积是多少？例7如图，在△ABC中，△AEO的面积是1，△ABO的面积是2，△BOD的面积是3，则四边形DCEO的面积是多少？例8如图所示，长方形ABCD内部的阴影部分的面积之和为70，AB＝8，AD＝15，四边形EFGO 的面积为______。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

伊嘉儿数学五年级春第13讲鸟头模型
伊嘉儿数学五年级春第13讲鸟头模型
在数学教学中，许多教师会运用各种具体的模型来帮助学生更好地理解抽象的概念和解决问题。

其中，鸟头模型是一种常见且有趣的模型之一。

伊嘉儿数学五年级春第13讲中，老师使用了鸟头模型来教授
一些有关几何和数学的知识。

鸟头模型是由一个圆形和两个弧线组成的，看起来形状像一只鸟的头部。

学生们可以通过观察和操作这个模型来学习和探索各种几何和数学概念。

首先，在几何方面，鸟头模型可以帮助学生学习圆形和弧线的属性。

他们可以观察到圆形有一个中心点，半径相等的所有点到中心点的距离也相等。

通过旋转鸟头模型，学生可以看到弧线的角度和半径的关系，以及不同角度的弧线所代表的扇形的大小。

其次，在数学方面，鸟头模型可以用来教授角度的概念和测量。

学生们可以使用鸟头模型来测量不同角度的大小，并学习如何以度数或弧度表示角度。

他们还可以通过将鸟头模型与其他角度的模型进行比较，来进一步理解角度的概念。

此外，鸟头模型还可以用来解决一些几何和数学问题。

例如，学生可以使用这个模型来解决关于扇形的面积和周长的问题，或者通过旋转和放置鸟头模型来比较不同角度的大小。

总之，伊嘉儿数学五年级春第13讲的鸟头模型为学生们提供了一个
直观且趣味的学习工具。

通过观察和操作这个模型，学生们可以更好地理解几何和数学的概念，并应用它们解决问题。

这种形式的教学不仅能够激发学生的学习兴趣，还能够帮助他们建立深刻且持久的知识。