求函数解析式习题 (含答案)
高中三角函数解析式求法练习题

三角函数解析式求法练习题一、单选题(本大题共9小题,共45.0分)1.为了得到函数y=sin(2x−π3)的图象,只需把函数y=sin(2x+π6)的图象()A. 向左平移π4个单位长度 B. 向右平移π4个单位长度C. 向左平移π2个单位长度 D. 向右平移π2个单位长度2.若函数f(x)=2sin(2x−π3+φ)是偶函数,则φ的值可以是()A. 5π6B. π2C. π3D. −π23.已知函数的图象(部分)如图所示,则f(x)的解析式是()A. f(x)=2sin(x+π6)(x∈R) B. f(x)=2sin(2x+π6)(x∈R)C. f(x)=2sin(x+π3)(x∈R) D. f(x)=2sin(2x+π3)(x∈R)4.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π2)的部分图像如图所示,则f(x)的解析式是()A. f(x)=2sin(2x+π3)B. f(x)=2sin(x+π3)C. f(x)=2sin(2x+π6)D. f(x)=2sin(x+π6)5.已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图像如下图,则函数f(x)的解析式为()A. f(x)=2sin(12x+π4) B. f(x)=2sin(12x+3π4)C. f(x)=2sin(14x+3π4) D. f(x)=2sin(2x+π4)6.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,若将其纵坐标不变,横坐标变为原来的两倍,得到的新函数g(x)的解析式为()A. y=2sin(2x+π3)B. y=2sin(2x+π)C. y=2sin(12x+π3)D. y=2sin(12x+π2)7.函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π2)的部分图象如图所示,则f(x)的解析式是()A. f(x)=2sin(2x+π3)B. f(x)=2sin(2x+π6)C. f(x)=2sin(x+π3)D. f(x)=2sin(x+π6)8.函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的图象如图所示,则ω,φ的值为()A. ω=3,φ=π4 B. ω=3,φ=−π4 C. ω=6,φ=−π2D. ω=6,φ=π29. 若函数f(x)=sin(ωx +φ)(ω>0,−π<φ<π)的图象(部分)如图所示,则ω和φ的取值分别是( )A. ω=1,φ=π3. B. ω=1,φ=−π3. C. ω=12,φ=π6. D. ω=12,φ=−π6.二、多选题(本大题共3小题,共15.0分) 10. 已知函数的部分图象如图所示,下列说法正确的是( )A. 函数y =f (x )的图象关于点对称B. 函数y =f (x )的图象关于直线对称C. 函数y =f (x )在单调递减D. 该图象向右平移个单位可得y =2sin2x 的图象11.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图所示,则()A. 该函数的解析式为B. 该函数的对称中心为C. 该函数的单调递增区间是D. 把函数的图象上所有点的横坐标变为原来的3,纵坐标不变,2可得到该函数图象)的部分图像如图所示,则下12.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π2列关于函数f(x)的说法中正确的是()A. 函数f(x)最靠近原点的零点为−π3B. 函数f(x)的图象与y轴交点的纵坐标为√3)是偶函数C. 函数f(x−5π6)上单调递增D. 函数f(x)在(2π,7π3第II卷(非选择题)三、单空题(本大题共4小题,共20.0分)13.已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,则ω=________.14.函数y=Asin(ωx+ϕ)在一个周期内的图象如图,此函数的解析式为_______________________.15.若函数y=sin(ωx+φ)(ω>0)的部分图象如图所示,则ω的值为_____.16.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象如图所示,则函数f(x)的解析式为____________.四、解答题(本大题共2小题,共24.0分)17.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象如图所示.(1)求f(x)的解析式;(2)当x∈[−π4,π4]时,求f(x)的值域.,x∈18.如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2 R)的部分图象.(1)求函数解析式;(2)求函数f(x)的对称轴的方程.答案和解析1.【答案】B【解析】【分析】本题考查三角函数图象的平移,根据题意利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,即可得出结论.【解答】解:y=sin(2x+π6)=sin2(x+π12),y=sin(2x−π3)=sin2(x−π6),所以将y=sin(2x+π6)的图象向右平移π4个单位长度得到y=sin(2x−π3)的图象.故选B.2.【答案】A【解析】【分析】本题主要考查了函数y=Asin(ωx+φ)的图象与性质,属于基础题.利用偶函数关于y轴对称得出f(0)=±2,则sin(φ−π3)=±1,依次判断即可.【解答】解:令x=0,得f(0)=2sin(−π3+φ)=±2,∴sin(φ−π3)=±1,把φ=5π6代入,符合.故选A.3.【答案】C【解析】【分析】本题考查了的函数图象和性质,属于基础题.由函数图象得到最值和周期,从而得,结合图象上点坐标,得到函数解析式.【解答】解:∵由图象可知:,∴由得ω=1,因此.∵点在图象上,,,因此,即.∵|φ|<π2,,因此.故选C.4.【答案】B【解析】【分析】本题主要考查了三角函数的图象和性质.由函数y= Asin(ωx+φ)的图象确定A,ω,φ的题型,常常以“五点法”中的五个点作为突破口,要从图象的升降情况找准第一个“零点”和第二个“零点”的位置.要善于抓住特殊量和特殊点.【解答】解:由图像可知T4=7π6−2π3=π2,所以T=2π,ω=2πT=1.又因为sin(2π3+φ)=0,且0<φ<π2,所以φ=π3.由图像可知A=2,所以f(x)=2sin(x+π3).故选B.5.【答案】B【解析】【分析】本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查识图能力与运算能力,属于中档题.由图知,A=2,T2=3π2−(−π2)=2π,于是可求得φ,又y=f(x)的图象经过(−π2,2),由12×(−π2)+φ=2kπ+π2(k∈Z),0<φ<π可求得φ,于是可得其解析式.【解答】解:由图知,A=2,T2=3π2−(−π2)=2π,又ω>0,∴T=2πω=4π,∴ω=12;又y=f(x)的图象经过(−π2,2),∴12×(−π2)+φ=2kπ+π2(k∈Z),∴φ=2kπ+3π4(k∈Z),又0<φ<π,∴φ=3π4.∴f(x)=2sin(12x+3π4).故选:B.6.【答案】C【解析】解:由图象的最高点和最低点可知,A=2,周期T=4(π6−(−π3))=2π,∴ω=1;由图象过点(π6,2),可得:2=2sin(1×π6+φ)即sin(π6+φ)=1.∵0<φ<π,∴φ=π3.故函数f(x)=2sin(x+π3)将其纵坐标不变,横坐标变为原来的两倍,可得:2sin(12x+π3)=g(x),故选:C.根据图象求出A,ω和φ,即可求函数f(x)的解析式;根据图象的平移变换,可得g(x)的解析式.本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.7.【答案】C【解析】【分析】本题考查函数y=Asin(ωx+φ)的图象与性质,由周期得ω,由特殊点的坐标求出φ即可.【解答】解:由图象可知,振幅为2,即A=2,又14T=76π−23π,解得T=2π,又因为T=2πω,故ω=1,此时函数f(x)=2sin(x+ϕ),将点(76π,−2)代入,得2sin(7π6+ϕ)=−2,所以7π6+ϕ=2kπ+3π2,k∈Z,因为0<ϕ<π2,所以ϕ=π3,因此函数f(x)=2sin(x+π3),故选C.8.【答案】A【解析】解:根据函数f(x)=Asin(ωx+φ)(其中A> 0,ω>0,|φ|<π)的图象,可得A=1,14⋅2πω=5π12−π4,求得ω=3.再根据五点法作图可得3⋅π4+φ=π,求得φ=π4,故选:A.由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,求出函数的解析式.本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.9.【答案】C【解析】【分析】本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查识图用图的能力,属于中档题.由T4=π可求得ω,再由2π3×12+φ=π2+2kπ(k∈Z)可求得φ,从而可得答案.【解答】解:由f(x)=sin(ωx+φ)的部分图象可知,14T=π,∴T=4π,又T=2πω,∴ω=12;又2π3×12+φ=π2+2kπ(k∈Z),∴φ=π6+2kπ(k∈Z),由−π<φ<π,即φ=π6.故选C.10.【答案】BD【解析】【分析】本题考查函数y=Asin(ωx+φ)的图象与性质,属于中档题.由函数的图象可得A=2,由14·2πω=π3−π12,解得ω=2.再根据最值得2×π12+φ=2kπ+π2,k∈Z,结合所给范围可得φ=π3,得函数f(x)=2sin(2x+π3),然后逐项判断即可求解.【解答】解:由函数的图象可得A=2,由14·2πω=π3−π12,解得ω=2.再根据最值得2×π12+φ=2kπ+π2,k∈Z;又|φ|<π2,得φ=π3,得函数f(x)=2sin(2x+π3),当x=−π3时,f(x)≠0,所以函数y=f(x)的图象不关于点对称(−π3,0),所以A不正确;当x=−5π12时,f(x)=−2,函数y=f(x)的图象关于直线x=−5π12对称,所以B正确;由π2+2kπ≤2x+π3≤3π2+2kπ,k∈Z;解得π12+kπ≤x≤7π12+kπ,k∈Z,所以C错误;将函数f(x)=2sin(2x+π3)向右平移π6个单位可得到的图象,故D正确.故选BD.11.【答案】ACD【解析】【分析】本题主要考查了根据三角函数图像求解解析式,属于中档题.根据三角函数图像得出振幅,再求解函数的周期,再代入最高点求解函数解析式.【解答】解:由图可知,函数的周期为,故.即,代入最高点有.因为,可得,又因为,所以当k=0,,故,故A正确.对B,的对称中心:k∈Z .故该函数的对称中心为,故B错误.对C,单调递增区间为,k∈Z 解得,故C正确.对D,把函数的图象上所有点的横坐标变为原来的,纵坐标不变,可得到.故D正确.故选:ACD.12.【答案】ABC【解析】【分析】本题考查了函数y=Asin(ωx+φ)的图象与性质,是一般题.对各个选项逐一验证可以得出答案.【解答】解:根据函数f(x)=Acos(ωx+φ)的部分图像知,A=2,设f(x)的最小正周期为T,则T4=2π3−π6=π2,∴T=2π,ω=2πT=1.∵f(π6)=2cos(π6+φ)=2,且|φ|<π2,∴φ=−π6,故f(x)=2cos(x−π6).令f(x)=2cos(x−π6)=0,得x−π6=π2+kπ,k∈Z,即x=2π3+kπ,k∈Z,因此函数f(x)最靠近原点的零点为−π3,故A正确;由f(0)=2cos(−π6)=√3,因此函数f(x)的图像在y轴上的截距为√3,故B正确;由f(x−5π6)=2cos(x−π)=−2cosx,因此函数f(x−5π6)是偶函数,故C正确;令2kπ−π≤x−π6≤2kπ,k∈Z,得2kπ−5π6≤x≤2kπ+π6,k∈Z,此时函数f(x)单调递增,于是函数f(x)在(2π,13π6)上单调递增,在(13π6,7π3)上单调递减,故D不正确.故选:ABC.13.【答案】32【解析】【分析】本题考查函数y=Asin(ωx+φ)的图象与性质,属于基础题.直接根据图,知T4=2π3−π3=π3,则T=4π3,又T=2πω=4π3,可得ω.【解答】解:由题图,知T4=2π3−π3=π3,∴T=4π3,又T=2πω=4π3,∴ω=32.14.【答案】y=2sin(2x+2π)【解析】【分析】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.【解答】解:根据函数y=Asin(x+φ)(A>0,>0,0<φ<π)在一个周期内的图象,可得A=2,1⋅ 2π = ω5π−(−π),∴=2.再根据当x=−π时,y=2sin(−π+φ)=2,可得sin(−π+φ)=1,故有−π+φ=2kπ+π,求得φ=2kπ+2π,结合0<φ<π,求得φ=3,故函数y=2sin(2x+2π3).故答案为y=2sin(2x+2π3).15.【答案】4【解析】【分析】本题考查了函数y=Asin(ωx+φ)的图象与性质,属于基础题.利用函数y=Asin(ωx+φ)的图象可先求出函数的周期,再求ω.【解答】解:由图知函数的周期为(11π24−5π24)×2=π2,所以ω=2ππ2=4.故答案为4.16.【答案】f(x)=√2sin(π8x+π4)【解析】【分析】本题考查的知识点正弦型函数解析式的求法,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值.根据已知中函数y=A sin(ωx+ϕ)(ω>0,的图象,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将(2,√2)代入解析式,结合,可求出ϕ值,进而求出函数的解析式.【解答】解:由题图知f(x)的最大值为√2,周期为16,且过点(2,√2),所以A=√2,T=2πω=16,即ω=π8,将点(2,√2)代入,得√2=√2sin(π8×2+φ),解得φ=π4+2kπ,k∈Z,因为|φ|<π2,所以φ=π4.所以f(x)=√2sin(π8x+π4).17.【答案】解:(1)因为T=2×(5π6−π3)=π,所以ω=2ππ=2;因为f(x)的图象经过点(π3,0),所以Asin(2×π3+φ)=0,即φ=−2π3+kπ,k∈Z;又|φ|<π2,所以φ=π3;因为f(x)的图象经过点(0,2√3),所以A=sin(2×0+π3)=2√3,即A=4;故f(x)的解析式为f(x)=4sin(2x−π6);(2)因为x∈[−π4,π4 ],所以2x+π3∈[−π6,5π6],从而sin(2x+π3)∈[−12,1],故当x∈[−π4,π4]时,f(x)的值域为[−2,4].【解析】(1)根据函数的图象求出T、ω和φ的值,即可写出f(x)的解析式;(2)根据x的取值范围,利用正弦型函数的性质求得f(x)的值域.本题考查了正弦函数的图象与性质的应用问题,是基础题.18.【答案】解:(1)由题中的图象知,A=2,T4=π3−π12=π4=14⋅2πω,即ω=2πT =2,根据五点作图法,2×π12+φ=π2,∴φ=π3,故函数的解析式为f(x)=2sin(2x+π3).(2)对于f(x),令2x+π3=kπ+π2,求得x=kπ2+π12,可得它的对称轴的方程x=k2π+π12,k∈Z.【解析】(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.(2)由题意利用正弦函数的图象的对称性,得出结论.本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,正弦函数的图象的对称性,属于基础题.。
必修一 数学 定义域,值域,解析式 求法,例题,习题(含答案)

函数的定义域(1)函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合 (2)求函数定义域的注意事项☉分式分母不为零; ☉偶次根式的被开方数大于等于零; ☉零次幂的底数不为零; ☉实际问题对自变量的限制若函数由几个式子构成,求其定义域时要满足每个式子都要有意义(取“交集”)。
(3)抽象复合函数定义域的求法☉已知y=f (x )的定义域是A ,求y=f (g (x ))的定义域,可通过解关于g (x )∈A 的不等式,求出x 的范围☉已知y=f (g (x ))的定义域是A ,求y=f (x )的定义域,可由x ∈A ,求g (x )的取值范围(即y=g (x )的值域)。
例1.函数()f x =的定义域为 ( ) A. (-∞,4) B. [4,+∞) C. (-∞,4] D. (-∞,1)∪(1,4] 【答案】D 【解析】要使解析式有意义需满足:40{10x x -≥-≠,即x 4≤且1x ≠所以函数()1f x x =- 的定义域为(-∞,1)∪(1,4] 故选:D例2( )A. {|11}x x x ≥≤-或B. {|11}x x -≤≤C. {1}D. {-1,1}【答案】D : 2210{ 10x x -≥-≥,解得: 1x =±.{-1,1}.故选D.例3.已知函数()21y f x =-的定义域为()2,2-,函数()f x 定义域为__________.【答案】[]1,3-【解析】由函数()21y f x =-的的定义域为(−2,2),得: 2113x -≤-≤,故函数f (x )的定义域是[]1,3-.例4.若函数()y f x =的定义域为[]0,2, )A. [)0,1B. []0,1C. [)(]0,11,4⋃ D. ()0,1 【答案】A 函数()y f x =的定义域是[]0,2, 022{ 10x x ≤≤∴-≠,解不等式组:01x ≤<,故选A.例5.已知函数()1y f x =+的定义域是[]2,3-,则()2y f x =的定义域是( )A. []1,4-B. []0,16C. []2,2-D. []1,4【答案】C 【解析】解:由条件知: ()1f x +的定义域是[]2,3-,则1x 14-≤+≤,所以214x -≤≤,得[]x 2,2∈-例6.已知函数y f x =+()1定义域是[]-23,,则y f x =-()21的定义域是( )A B. []-14, C. []-55, D. []-37,【答案】A例7___________.【答案】[]3,4-【解析】要使函数有意义,则2120x x +-≥,即2120x x --≤,即34x -≤≤,故函数的定义域为[]3,4-,故答案为[]3,4-.函数值域定义:对于函数y=f (x ),x ∈A 的值相对应的y 值叫函数值,函数值得集合{f (x )|x ∈A }叫做函数的值域。
八年级一次函数解析式典型例题及答案

一次函数解析式典型题型一. 定义型(一次函数即X 和Y 的次数为1) 例1. 已知函数y m xm =-+-()3328是一次函数,求其解析式。
解:由一次函数定义知m m 28130-=-≠⎧⎨⎩∴=±≠⎧⎨⎩m m 33∴=-m 3,故一次函数的解析式为y x =-+33注意:利用定义求一次函数y kx b =+解析式时,要保证k ≠0。
如本例中应保证m -≠30 二. 点斜型(已知斜率和经过的一点)例2. 已知一次函数y kx =-3的图像过点(2,-1),求这个函数的解析式。
解: 一次函数y kx =-3的图像过点(2,-1) ∴-=-123k ,即k =1故这个一次函数的解析式为y x =-3变式问法:已知一次函数y kx =-3,当x =2时,y =-1,求这个函数的解析式。
三. 两点型(已知图像经过的两点)已知某个一次函数的图像与x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),则这个函数的解析式为 解:设一次函数解析式为y kx b =+由题意得024=-+=⎧⎨⎩k b b ∴==⎧⎨⎩k b 24故这个一次函数的解析式为y x =+24 四. 图像型例4. 已知某个一次函数的图像如图所示,则该函数的解析式为y=-2x+2。
y2O 1 x解:设一次函数解析式为y kx b =+由图可知一次函数y kx b =+的图像过点(1,0)、(0,2)∴有020=+=+⎧⎨⎩k b b ∴=-=⎧⎨⎩k b 22故这个一次函数的解析式为y x =-+22 五. 斜截型(已知斜率k 和截距b )两直线平行,则k1=k2;两直线垂直,则k1=-1/k2例5. 已知直线y kx b =+与直线y x =-2平行,且在y 轴上的截距为2,则直线的解析式为 解析:两条直线l 1:y k x b =+11;l 2:y k x b =+22。
当k k 12=,b b 12≠时,l l 12// 直线y kx b =+与直线y x =-2平行,∴=-k 2 又 直线y kx b =+在y 轴上的截距为2,∴=b 2 故直线的解析式为y x =-+22六. 平移型(向上/右平移则截距增加;向左平移则截距减小)例6. 把直线y x =+21向下平移2个单位得到的图像解析式为 y=2x-1。
求一次函数的解析式练习题

∵y=kx+b的图象过点(3,5)与(-4,-9).
∴ 3k+b=5 -4k+b=-9 解得 k=2 b=-1
∴这个一次函数的解析式为y=2x-1
Page 2
变式1:已知一次函数y=kx+b,当x=1时, y=1,当x=2时,y=3.求这个一次函数的解 析式.
解:
∵当x=1时,y=1,当x=2时,y=3. ∴ k+b=1 2k+b=3
在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱 月数x(月)之间的关系如图所示,根据下图回答下列问题: (1)求出y关于x的函数解析式。 (2)根据关系式计算,小明经过几个月才能存够200元?
Page 8
解:设这个一次函数的解析式为 y=kx+b
因为y=kx+b的图象过点(3,5)与(-4,-9), 所以
设
3k+b=5 -4k+b=-9 k=2 解得 b=-1
列 解 答
一次函数的解析式为
y=2x-1
练习2.如下图,两摞相同规格的碗整齐地放在桌面上,请根 据图中的数据信息,解答下列问题:
(1)求整齐摆放在桌面上的碗的高度y(cm)与碗的个数x(个) 之间的函数关系式;(y与x成一次函数关系)
(2)把这两摞碗整齐地摆成一摞时,碗的高度是多少?
11cm
14cm
• 已知y+a与x-b成正比例 (1)试说明:y是x的一次函数 (2)若x=2时,y=3;x=1,y=-5时,求函数解 析式
变式6:如图,一次函数y=kx+b 的图象过 点A(3,0).与y轴交于点B,若△AOB的面积 为6,求这个一次函数的解析式 解:∵y=kx+b的图象过点A(3,0). y 1 1 ∴OA=3,S= OA×OB= ×3×OB=6 B 2 2
二次函数解析式的求法练习题
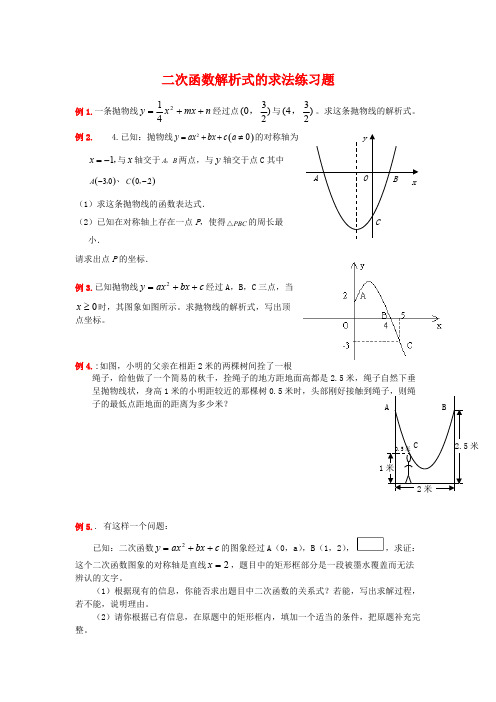
二次函数解析式的求法练习题例1.一条抛物线经过点与。
求这条抛物线的解析式。
y x mx n =++142()032,(432,例2. 4.已知:抛物线的对称轴为()20y ax bx c a =++≠与轴交于两点,与轴交于点C 其中1x =-,x A B ,y 、()30A -,()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得的周长最PBC △小.请求出点P 的坐标.例3.已知抛物线经过A ,B ,C 三点,当y ax bx c =++2时,其图象如图所示。
求抛物线的解析式,写出顶x ≥0点坐标。
例4.:如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5子的最低点距地面的距离为多少米?例5.. 有这样一个问题:已知:二次函数的图象经过A (0,a ),B(1,2),,求证:y ax bx c =++2这个二次函数图象的对称轴是直线,题目中的矩形框部分是一段被墨水覆盖而无法x =2辨认的文字。
(1)根据现有的信息,你能否求出题目中二次函数的关系式?若能,写出求解过程,若不能,说明理由。
(2)请你根据已有信息,在原题中的矩形框内,填加一个适当的条件,把原题补充完整。
米根据下列条件,求二次函数的解析式1、图象经过点(-1,3),(1,3),(2,6)2、抛物线顶点坐标为(-1,9),并且与y 轴交于(0,-8)3、抛物线的对称轴是直线,与x 轴的一个交点为(-2,0),与y 轴交于点x =1(0,12)4、图象顶点坐标是(2,-5),且过原点5、图象与x 轴的交点坐标是(-1,0),(-3,0)且函数有最小值-5。
6、当x =2时,函数的最大值是1,且图象与x 轴两个交点之间的距离为2。
7、已知:抛物线在x 轴上所截线段为4,顶点坐标为(2,4),求这个函数的关系式8、已知抛物线经过点(-1,0),(2,3),并与y 轴交于点(0,3) ,请求出此抛物线解析式。
求一次函数的解析式练习题

五、融会贯通——分类与分层
(三)与求函数解析式有关的实际应用题 4、小明将父母给的零用钱按每月相等的数额存放
1.已知正比例函数的图象经过点 (-2,4). 求这个正比例函数的解析式.
Page 1
例1:已知一次函数的图象经过点(3,5)与 (-4,-9).求这个一次函数的解析式. 解:设这个一次函数的解析式为y=kx+b.
∵y=kx+b的图象过点(3,5)与(-4,-9).
∴ 3k+b=5 -4k+b=-9 解得 k=2 b=-1
2 0 b,
b 2.
∴过A,B两点的直线的表达式为y=x-2. ∵当x=4时,y=4-2=2. ∴点C(4,2)在直线y=x-2上. ∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
融会贯通——分类与分层
(一)求函数解析式的综合应用
1. (2011 浙江湖州) 已知:一次函数 y=kx+b的图象经过M(0, 2),(1,3)两点. (l) 求k、b的值; (2) 若一次函数的图象与x轴的交点为A(a,0),求a的值.
Page 6
变式5: 已知弹簧长度y(厘米)在一定限度内 所挂重物质量x(千克)的一次函数,现已测得 不挂重物时弹簧的长度是6厘米,挂4千克质量 的重物时,弹簧的长度是7.2厘米,求这个一次 函数的解析式。
解:设这个一次函数的解析式为:y=kx+b 根据题意,把x=0,y=6和x=4,y=7.2代入,得: b=6 k=0.3 4k+b=7.2 解得 b=6
求函数解析式的数学练习题初二
求函数解析式的数学练习题初二数学练习题:求函数解析式一、填空题1. 已知函数 y = 2x + 3,求函数解析式 h(x) =_________。
2. 函数 f(x) 的图像为一条直线,(1, 4) 是该图像上的一个点,斜率为 3,求函数解析式 f(x) =_________。
3. 若函数 g(x) 的解析式为 g(x) = kx + 2,且 g(4) = 10,求 k 的值。
4. 已知函数 p(x) 的图像关于 x 轴对称,且 p(2) = -5,求函数解析式p(x) =_________。
5. 函数 q(x) 的图像恒在 x 轴上方,且 q(-2) = 7,求函数解析式 q(x) =_________。
二、计算题1. 已知函数 y = 3x - 1 和 h(x) = 5x + 2,求函数 g(x) = y + h(x) 的解析式。
2. 若函数 f(x) 和 g(x) 的解析式分别为 f(x) = x^2 + 2x - 3 和 g(x) = 2x^2 - x + 4,求函数 p(x) = 3f(x) - g(x) 的解析式。
3. 函数 f(x) 的图像经过点 (1, 5),且斜率为 2,求函数解析式 f(x) =_________。
4. 若函数 g(x) 的图像经过点 (2, 4),且斜率为 -3/4,且 g(1) = 1,求函数解析式 g(x) =_________。
5. 函数 h(x) 的图像经过点 (3, 7),且经过点 (-2, 2),求函数解析式h(x) =_________。
三、应用题1. 设函数 f(x) 的解析式为 f(x) = kx + a,且图像经过点 (2, 4),(3, 6),求函数 f(x) 的解析式。
2. 已知函数 y = ax + b 和 h(x) = cx + d,且 h(x) = 2y + 1,求系数 a、b、c、d 的值。
3. 若函数 f(x) 和 g(x) 的解析式分别为 f(x) = 2x + 3 和 g(x) = 3x - 4,求函数解析式 h(x),使得 h(x) = f(x) + g(x) - 7。
二次函数练习题及答案(解析版)
二次函数练习题及答案(解析版)一、选择题:1 下列关系式中,属于二次函数的是(x为自变量)( )2 函数y=x2-2x+3的图象的顶点坐标是( )A (1,-4) B(-1,2) C (1,2) D(0,3)23 抛物线y=2(x-3)的顶点在( )A 第一象限B 第二象限C x轴上D y轴上4 抛物线的对称轴是( )A x=-2 Bx=2 C x=-4 D x=45 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中,正确的是( )A ab>0,c>0B ab>0,c<0C ab<0,c>0D ab<0,c<06 二次函数y=ax2+bx+c的图象如图所示,则点在第___象限( )A 一B 二C 三D 四7 如图所示,已知二次函数y=ax2+bx+c(a≠0) 的图象的顶点P 的横坐标是4,图象交 x 轴于点A(m,0) 和点B ,且m>4,那么AB 的长是( )A 4+mB mC 2m-8D 8-2m8 若一次函数y=ax+b的图象经过第二、三、四象限,则二次函数y=ax2+bx的图象只可能是( )9 已知抛物线和直线在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P 1(x1,y 1) ,P 2(x2,y 2) 是抛物线上的点,P3(x3,y 3) 是直线上的点,且-1A y110 把抛物线物线的函数关系式是( ) AC 的图象向左平移2个单位,再向上平移3个单位,所得的抛B D二、填空题:11 二次函数y=x2-2x+1的对称轴方程是______________12 若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式,则y=________13 若抛物线y=x2-2x-3与x 轴分别交于A 、B 两点,则AB 的长为_________14 抛物线y=x2+bx+c,经过A(-1,0) ,B(3,0) 两点,则这条抛物线的解析式为_____________15 已知二次函数y=ax2+bx+c的图象交x 轴于A 、B 两点,交y 轴于C 点,且△ABC 是直角三角形,请写出一个符合要求的二次函数解析式________________16 在距离地面2m 高的某处把一物体以初速度v 0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:(其中g 是常数,通常取10m/s2) 若v 0=10m/s,则该物体在运动过程中最高点距地面_________m17 试写出一个开口方向向上,对称轴为直线x=2,且与y 轴的交点坐标为(0,3) 的抛物线的解析式为______________18 已知抛物线y=x2+x+b2经过点,则y 1的值是_________三、解答题:19 若二次函数的图象的对称轴方程是,并且图象过A(0,-4) 和B(4,0) ,(1)求此二次函数图象上点A 关于对称轴对称的点A ′的坐标; (2)求此二次函数的解析式;20 在直角坐标平面内,点 O 为坐标原点,二次函数y=x2+(k-5)x-(k+4) 的图象交 x 轴于点A(x1,0) 、B(x2,0) ,且(x1+1)(x2+1)=-8 (1)求二次函数解析式;(2)将上述二次函数图象沿x 轴向右平移2个单位,设平移后的图象与y 轴的交点为C ,顶点为P ,求△POC 的面积21 已知:如图,二次函数y=ax2+bx+c的图象与x 轴交于A 、B 两点,其中A 点坐标为(-1,0) ,点C(0,5) ,另抛物线经过点(1,8) ,M 为它的顶点(1)求抛物线的解析式; (2)求△MCB 的面积S △MCB22 某商店销售一种商品,每件的进价为250元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是1350元时,销售量为500件,而单价每降低1元,就可以多售出200件请你分析,销售单价多少时,可以获利最大二次函数练习题参考答案与解析一、选择题1 考点:二次函数概念选A2 考点:求二次函数的顶点坐标解析:法一,直接用二次函数顶点坐标公式求法二,将二次函数解析式由一般形式转换为顶点式,即y=a(x-h)2+k的形式,顶点坐标即为(h,k) ,y=x2-2x+3=(x-1)2+2,所以顶点坐标为(1,2) ,答案选C3 考点:二次函数的图象特点,顶点坐标解析:可以直接由顶点式形式求出顶点坐标进行判断,函数y=2(x-3)2的顶点为(3,0) ,所以顶点在x 轴上,答案选C4 考点:数形结合,二次函数y=ax2+bx+c的图象为抛物线,其对称轴为解析:抛物线,直接利用公式,其对称轴所在直线为答案选B5 考点:二次函数的`图象特征解析:由图象,抛物线开口方向向下,抛物线对称轴在y 轴右侧,抛物线与y 轴交点坐标为(0,c) 点,由图知,该点在x 轴上方,答案选C6 考点:数形结合,由抛物线的图象特征,确定二次函数解析式各项系数的符号特征解析:由图象,抛物线开口方向向下,抛物线对称轴在y 轴右侧,抛物线与y 轴交点坐标为(0,c) 点,由图知,该点在x 轴上方,在第四象限,答案选D7 考点:二次函数的图象特征解析:因为二次函数y=ax2+bx+c(a≠0) 的图象的顶点P 的横坐标是4,所以抛物线对称轴所在直线为x=4,交x 轴于点D ,所以A 、B 两点关于对称轴对称,因为点A(m,0) ,且m>4,所以AB=2AD=2(m-4)=2m-8,答案选C8 考点:数形结合,由函数图象确定函数解析式各项系数的性质符号,由函数解析式各项系数的性质符号画出函数图象的大致形状解析:因为一次函数y=ax+b的图象经过第二、三、四象限,所以二次函数y=ax2+bx的图象开口方向向下,对称轴在y 轴左侧,交坐标轴于(0,0) 点答案选C9 考点:一次函数、二次函数概念图象及性质解析:因为抛物线的对称轴为直线x=-1,且-1-1时,由图象知,y 随x 的增大而减小,所以y 210 考点:二次函数图象的变化抛物线平移2个单位得到,再向上平移3个单位得到的图象向左答案选C二、填空题11 考点:二次函数性质解析:二次函数y=x2-2x+1,所以对称轴所在直线方程答案x=112 考点:利用配方法变形二次函数解析式解析:y=x2-2x+3=(x2-2x+1)+2=(x-1)2+2答案y=(x-1)2+213 考点:二次函数与一元二次方程关系解析:二次函数y=x2-2x-3与x 轴交点A 、B 的横坐标为一元二次方程x 2-2x-3=0的两个根,求得x 1=-1,x 2=3,则AB=|x2-x 1|=4答案为414 考点:求二次函数解析式解析:因为抛物线经过A(-1,0) ,B(3,0) 两点,解得b=-2,c=-3,答案为y=x2-2x-315 考点:此题是一道开放题,求解满足条件的二次函数解析式,答案不唯一解析:需满足抛物线与x 轴交于两点,与y 轴有交点,及△ABC 是直角三角形,但没有确定哪个角为直角,答案不唯一,如:y=x2-116 考点:二次函数的性质,求最大值解析:直接代入公式,答案:717 考点:此题是一道开放题,求解满足条件的二次函数解析式,答案不唯一解析:如:y=x2-4x+318 考点:二次函数的概念性质,求值三、解答题19 考点:二次函数的概念、性质、图象,求解析式解析:(1)A′(3,-4)(2)由题设知:∴y=x2-3x-4为所求(3)20 考点:二次函数的概念、性质、图象,求解析式解析:(1)由已知x 1,x 2是x 2+(k-5)x-(k+4)=0的两根又∵(x1+1)(x2+1)=-8 ∴x 1x 2+(x1+x2)+9=0 ∴-(k+4)-(k-5)+9=0 ∴k=5 ∴y=x2-9为所求 (2)由已知平移后的函数解析式为: y=(x-2)2-9 且x=0时y=-5 ∴C(0,-5) ,P(2,-9)21 解: (1)依题意:(2)令y=0,得(x-5)(x+1)=0,x 1=5,x 2=-1 ∴B(5,0)由,得M(2,9)作ME ⊥y 轴于点E ,则可得S △MCB =1522 思路点拨:通过阅读,我们可以知道,商品的利润和售价、销售量有关系,它们之间呈现如下关系式:总利润=单个商品的利润×销售量要想获得最大利润,并不是单独提高单个商品的利润或仅大幅提高销售量就可以的,这两个量之间应达到某种平衡,才能保证利润最大因为已知中给出了商品降价与商品销售量之间的关系,所以,我们完全可以找出总利润与商品的价格之间的关系,利用这个等式寻找出所求的问题,这里我们不妨设每件商品降价x 元,商品的售价就是(135-x)元了单个的商品的利润是(135-x-25)这时商品的销售量是(500+200x)总利润可设为y 元利用上面的等量关式,可得到y 与x 的关系式了,若是二次函数,即可利用二次函数的知识,找到最大利润解:设销售单价为降价x 元顶点坐标为(425,91125)即当每件商品降价425元,即售价为135-425=925时,可取得最大利润91125元数学速算的技巧1、“凑整”先算1.计算:(1)24+44+56 (2)53+36+47解:(1)24+44+56=24+(44+56)=24+100=124因为44+56=100是个整百的数,所以先把它们的和算出来。
高中数学函数经典复习题含答案
高中数学函数经典复习题含答案1、求函数的定义域1)y=(x-1)/(x^2-2x-15)先求分母为0的解:x^2-2x-15=0x-5)(x+3)=0得到:x=5或x=-3但是x=-3不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,-3)∪(-3,5)∪(5,+∞)2)y=1-((x+1)/(x+3))-3先求分母为0的解:x+3=0得到:x=-3但是x=-3不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,-3)∪(-3,-1)∪(-1,+∞)2、设函数1/(x-1)+(2x-1)+4-x^2的定义域为[1,∞),则函数f(x^2)的定义域为[1,∞);函数f(x-2)的定义域为[3,∞)。
3、若函数f(x+1)的定义域为[-2,3],则函数f(2x-1)的定义域为[-1,2],函数f(2x-1)的值域为[-2,3]。
4、已知函数f(x)的定义域为[-1,1],且函数F(x)=f(x+m)-f(x-m)的定义域存在,求实数m的取值范围。
因为F(x)的定义域存在,所以f(x+m)和f(x-m)的定义域必须都存在,即:1≤x+m≤11≤x-m≤1将两个不等式联立,得到:1≤x≤1m≤x≤m所以m的取值范围为[-1,1]。
二、求函数的值域5、求下列函数的值域:1)y=x+2/x-3 (x∈R)先求分母为0的解:x-3=0得到:x=3但是x=3不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,3)∪(3,+∞)当x→±∞时,y→±∞,所以值域为(-∞,-2]∪[2,+∞)2)y=x+2/x-3 (x∈[1,2])先求分母为0的解:x-3=0得到:x=3但是x=3不在定义域内,因为分母为0时分式无意义,所以定义域为[1,3)∪(3,2]∪(2,+∞)当x→1+时,y→-∞,当x→2-时,y→+∞,所以值域为(-∞,-2]∪[2,+∞)3)y=22/(3x-13x-1)先求分母为0的解:3x-13x-1=0得到:x=4但是x=4不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,4)∪(4,+∞)当x→±∞时,y→0,所以值域为(0,+∞)4)y=(5x^2+9x+4)/(2x-6) (x≥5)当x→+∞时,y→+∞,当x→5+时,y→+∞,所以值域为[5,+∞)5)y=(x-3)/(x+1)+x+1先求分母为0的解:x+1=0得到:x=-1但是x=-1不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,-1)∪(-1,+∞)化简得到y=x-2,所以值域为(-∞,-2]∪[-2,+∞)6)y=(x-3+x+1)/(2x-1x+2)先求分母为0的解:2x-1=0或x+2=0得到:x=1/2或x=-2但是x=1/2不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,1/2)∪(1/2,-2)∪(-2,+∞)化简得到y=1/2,所以值域为{1/2}7)y=x^2-x/(x+2)先求分母为0的解:x+2=0得到:x=-2但是x=-2不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,-2)∪(-2,+∞)化简得到y=x-2-5/(x+2),所以值域为(-∞,-13/4]∪[1/4,+∞)8)y=(2-x^2-x)/(3x+6)先求分母为0的解:3x+6=0得到:x=-2但是x=-2不在定义域内,因为分母为0时分式无意义,所以定义域为(-∞,-2)∪(-2,+∞)化简得到y=-1/3,所以值域为{-1/3}三、求函数的解析式1、已知函数f(x-1)=x-4x,求函数f(x),f(2x+1)的解析式。
八上数学每日一练:待定系数法求一次函数解析式练习题及答案_2020年综合题版
八上数学每日一练:待定系数法求一次函数解析式练习题及答案_2020年综合题版答案解析2020年八上数学:函数_一次函数_待定系数法求一次函数解析式练习题1.(2020苍南.八上期末) 如图,直角坐标系中,直线y=kx+b 分别与x 轴、y 轴交于点A(3,0),点B(0,-4),过D(0,8)作平行x 轴的直线CD ,交AB 于点C ,点E(0,m)在线段OD 上,延长CE 交x 轴于点F ,点G 在x 轴正半轴上,且AG=AF 。
(1) 求直线AB 的函数表达式。
(2) 当点E 恰好是OD 中点时,求△ACG 的面积。
(3) 是否存在m ,使得△FCG 是直角三角形?若存在,直接写出m 的值;若不存在,请说明理由。
考点: 坐标与图形性质;待定系数法求一次函数解析式;直角三角形的性质;2.(2020连云港.八上期末)(1)【模型建立】如图1,等腰直角三角形中,,,直线经过点,过作于点 ,过作于点 .求证:;(2) 【模型应用】①已知直线:与轴交于点,与轴交于点,将直线绕着点 逆时针旋转 至直线 ,如图2,求直线 的函数表达式;答案解析答案解析答案解析②如图3,在平面直角坐标系中,点,作轴于点,作 轴于点,是线段 上的一个动点,点是直线上的动点且在第一象限内.问点、 、能否构成以点为直角顶点的等腰直角三角形,若能,请直接写出此时点的坐标,若不能,请说明理由.考点: 待定系数法求一次函数解析式;与一次函数有关的动态几何问题;等腰直角三角形;3.(2020深圳.八上期中) 如图,两直线l :y =kx ﹣2b +1和l :y =(1﹣k )x +b ﹣1交于x 轴上一点A , 与y 轴分别交于点B 、C , 若A 的横坐标为2.(1) 求这两条直线的解析式;(2) 求△ABC 的面积.考点: 一次函数图象与坐标轴交点问题;待定系数法求一次函数解析式;4.(2020金山.八上期末) 如图,已知直角坐标平面内的两点A(3,2),点B(6,0)过点B 作Y 轴的平行线交直线OA 于点C(1) 求直线OA 所对应的函数解析式(2) 若某一个反比例函数的图像经过点A,且交BC 于点D,联结AD,求△ACD 的面积.考点: 待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;5.(2020苏州.八上期末) 如图,在平面直角坐标系中,一次函数y=kx+3的图像与x 轴y 轴分别交于点A 、B ,点A 的坐标为(2,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1、已知f (x x +-11)=2211x x +-,则f (x )的解析式可取为( )
A. 21x x +
B. -212x x +
C. 212x x
+
D. -21x x + 2、若f (sin x )=2-cos2x ,则f (cos x )等于( )
A. 2-sin2x
B. 2+sin2x
C. 2-cos2x
D. 2+cos2x 3、已知(10)x f x =,则(5)f =( )
A. 510
B. 10
5 C. lg10 D. lg 5
*4、北京市为成功举办2008年奥运会,决定从2003年到2007年五年间更新市内现有的全部出租车,若每年更新的车辆数比前一年递增10%,则2003年底将更新现有总车辆数的(参考数据:1. 14=1. 46,1. 15=1. 61) ( ) A. 10% B. 16.4% C. 16.8% D. 20%
**5、函数y =22
11x x +-的值域是( )
A. [-1,1]
B. ]1,1(-
C. [-1,1)
D. (-1,1)
6、已知函数f (x )=2x ,则f (1-x )的图像为 ( )
7、已知2211()1f x x x x -=++,则()f x =
8、已知
2(3)21f x x =-,则()f x = 9、(1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=.
(2)指数函数()x f x a =,()()(),(1)0f x y f x f y f a +==≠.
(3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠.
(4)幂函数()f x x α=,'()()(),(1)f xy f x f y f α==.
(5)余弦函数()cos f x x =,正弦函数()sin g x x =,()()()()()f x y f x f y g x g y -=+, 0()(0)1,lim 1x g x f x
→==. 10、从盛满20升纯酒精的容器里倒出1升,然后用水填满,摇匀后再倒出1升,再用水填满,这样持续进行,如果倒k 次(k ≥1)后共倒出纯酒精x 升,倒第k +1次后共倒出纯酒精f (x )升,则函数f (x )的表达式为 。
三、解答题
11、已知f (x )是一次函数, 且f [f (x )]=4x -1, 求f (x )的解析式。
12、用长为l 的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x ,求此框架围成的面积y 与x 的函数关系式,并写出其定义域。
13、函数y=f(x)与y=g(x)的图像如图所示,设F(x)=f(x)g(x),求F(x)取得最大值时相应的x的值.
【试题答案】
一、选择题:
1、解析:令x x +-11=t ,则x =t t +-11,
∴f (t )=122+t t 。
∴f (x )=122+x x。
答案:C 2、解析:∵f (sin x )=2-(1-2sin 2x )=1+2sin 2x ,
∴f (cos x )=f [sin (2π-x )]=1+2sin 2(2π
-x )=1+2cos 2x =2+cos2x 。
答案:D
3、D
4、B
5、B 解法一:y =2211x x +-=212
x +-1。
∵1+x 2≥1,
∴0<212
x +≤2∴-1<y ≤1。
解法二:由y =22
11x x +-,得x 2=y y +-11。
∵x 2≥0,∴y y
+-11≥0,解得-1<y ≤1。
6、C
二
7、
2()3f x x =+ 8、22()19f x x =-
10、f (x )=19x/20+1(倒k 次后剩余酒精为20-x 升)
三、解答题
11、解:设f (x )=kx +b 则 k (kx +b )+b =4x -1
则
⎪⎩⎪⎨⎧-==⇒⎩⎨⎧-=+=3121)1(42b k b k k 或 ⎩⎨⎧=-=12b k ∴312)(-=x x f 或12)(+-=x x f
12、解:∵AB =2x ,则=πx ,AD =2π2x x l --。
∴y =2x ·2π2x x l --+22πx =-(2π
+2)x 2+lx 。
由⎪⎩⎪⎨⎧-->2π2,02x x l x >0,解得0<x <2π+l 。
13、解:2,[0,16)()1344,[16,24]8 x x f x x x +∈⎧⎪=⎨-+∈⎪⎩,1()10,[0,24]3g x x x =-+∈
1(2)10,[0,16)3()1314410,[16,24]83 x x x F x x x x ⎧+-+∈⎪⎪=⎨⎪-+-+∈⎪⎩()()() =2212820,[0,16)3313371440,[16,24]2412 x x x x x x ⎧-++∈⎪⎪⎨⎪-+∈⎪⎩
当x ∈)16,0[时,F (x )= -21282033x x ++=-13(x -14)2+3256,当x =14
时,F (x )max =256
3
当[16,24]x ∈时,F (x )=2133714402412x x -+,因为其对称轴-2b a =12371>24,故
当x =16时,F (x )max =84,又因为84<256
3,所以x =14时,F (x )取得最大值。
