反演原理及公式介绍
地震反演方法概述

地震反演方法概述地震反演:由地震信息得到地质信息的过程;地震反射波法勘探的基础在于:地下不同地层存在波阻抗差异,当地震波传播有波阻抗差异的地层分界面时,会发生反射从而形成地震反射波。
地震反射波等于反射系数与地震子波的褶积,而某界面的法向入射反射系数就等于该界面上下介质的波阻抗差与波阻抗和之比。
也就是说,如果已知地下地层的波阻抗分布,我们可以得到地震反射波的分布,即地震反射剖面。
即由地层波阻抗剖面得到地震反射波剖面的过程称为地震波阻抗正演,反之,由地震反射剖面得到地层波阻抗剖面的过程称为地震波阻抗反演。
叠前反演主要是指AVO反演,通过AVO反演,可以获得全部的岩石参数,如:岩石密度、纵横波速度、纵横波阻抗、泊松比等。
叠前反演与叠后反演的根本区别在于叠前反演使用了未经叠加的地震资料。
多道叠加虽然能够改善资料的品质,提高信噪比,但是另一方面,叠加技术是以动校正后的地震反射振幅、波形等特征不随炮检距变化的假设为基础的。
实际上,来自同一反射点的地震反射振幅在不同炮检距上是不同的,并且反射波形也随炮检距的变化而发生变化。
这种地震反射振幅、波形特征随炮检距的变化关系很复杂,主要原因就在于不同炮检距的地震波经过的地层结构、弹性性质、岩性组合等许多方面都是不同的。
叠加破坏了真实的振幅关系,同时损失了横波信息。
叠前反演通过叠前地震信息随炮检距的变化特征,来揭示岩性和油气的关系。
叠前反演的理论基础是地震波的反射和透射理论。
理论上讲,利用反射振幅随入射角的变化规律可以实现全部岩性参数的反演,提取纵波速度、横波速度、纵横波速度比、岩石密度、泊松比、体积模量、剪切模量等参数。
叠后地震剖面相当于零炮检距的自激自收记录。
与叠前反演不同,叠后反演只能得到纵波阻抗。
虽然叠后反演与叠前反演相比有很多不足之处,但由于其技术方法成熟完备,到目前为止,叠后反演仍然是主流的反演类型,是储层预测的核心技术。
介绍几种叠后反演方法:1)道积分:利用叠后地震资料计算地层相对波阻抗(速度)的直接反演方法。
mobius反演公式运用复值函数

Mobius反演公式是复分析中的重要定理,它在复值函数的研究中发挥着至关重要的作用。
在本文中,我们将深入探讨mobius反演公式在复值函数中的运用,以及其对复分析的重要性。
1. Mobius反演公式的定义和基本概念Mobius反演公式是指对于一个复值函数f(z),如果我们知道了它的莫比乌斯变换g(z),那么可以通过反演公式重新得出原函数f(z)。
具体来说,如果有一个函数F(s)和其Laplace变换f(t),那么在s平面上,F(s)与f(t)是一一对应的。
而mobius反演公式则表明了,在s平面上的某点s0的邻域内,可以通过F(s)的逆变换得出f(t)在t0的邻域内的性质。
2. Mobius反演公式的应用举例在复分析的研究中,mobius反演公式有着广泛的应用。
在数论中,mobius反演公式被用来解决莫比乌斯函数的性质和一些相关问题。
在傅里叶分析中,mobius反演公式也被广泛应用,可以用于解决一些与复值函数相关的积分和级数问题。
在控制理论和信号处理领域,mobius反演公式也有着重要的应用,可以应用于解决一些复值函数的反问题和逆问题。
3. 我对Mobius反演公式的个人观点和理解在我看来,mobius反演公式是复分析中的一个非常重要的定理,它可以帮助我们更深入地理解复值函数的性质和行为。
通过mobius反演公式,我们可以在s平面和t平面之间建立起一种对偶关系,从而可以轻松地将复值函数在不同平面上进行来回的转换和分析。
mobius反演公式也为我们解决复值函数相关问题提供了一种非常便利和高效的方法,有助于我们更加全面和深入地理解复分析领域中的一些重要问题。
mobius反演公式在复值函数的研究中具有重要的地位和作用。
通过对mobius反演公式的深入探讨,我们可以更全面、深刻和灵活地理解复值函数的性质和相关问题。
希望本文对您理解mobius反演公式在复值函数中的运用有所帮助。
4. 深入探讨Mobius反演公式的数学原理和推导Mobius反演公式的数学原理可以通过复函数论和积分变换理论来进行深入探讨和推导。
地球物理学反演第三章广义反演法

x y
4 7
cond(A) 17.9443
x y
2 1
1 2
2 3
x y
4.001 7.001
x 1.999
y
1.001
1.001 2.001
2.001 3.001
x y
4 7
cond(A) 17.9603
x y
2.003 0.997
2. 特征值对观测数据的影响(正演)
2. G是M阶非对称、非奇异矩阵
G = UΛVT
U、V分别是GGT和GTG 对应的特 征向量组成的特征向量矩阵, 正交矩阵
Λ是GGT或GTG的特征值正根组成 的对角线矩阵
UTU = UUT = EM VTV = VVT = EN VTU UTV E
第二节 奇异值分解和自然逆
奇异值分解:SVD(singular value decomposition)
• 纯欠定 单位矩阵
非单位矩阵
• 超定 非单位矩阵
单位矩阵
• 混定 非单位矩阵
非单位矩阵
层析成像原理
CT (Computerized tomography) 技术
与地震层析成像技术
s(x)dl ti
Pi
地震CT
数据
天然地震 层析成像
混定情况
1 0 1 0
G=
0 0
1
0
1
2
2
0
2 0 0 2
•条件数事实上表示了矩阵计算对于误差的敏感性。
•对于线性方程组Ax=b, 如果A的条件数小,b有微小的改变,x的改变也很微小,数值稳定性好。 它也可以表示b不变,而A有微小改变时,x的变化情况。
cond ( A) A • A1 max
汉克尔变换的反演公式

汉克尔变换的反演公式汉克尔变换是一种在电磁学和地球物理学中广泛应用的积分变换方法,它的反演公式如下:如果F(x)是一个在区间[0,∞)上的函数,那么其汉克尔变换F^(h)(ω) 的反演公式为:F(x)=1/π∫_0^∞F^(h)(ω)* e^(-jωx) dω汉克尔变换的反演公式具有以下特点:1.线性性质:汉克尔变换具有线性性质,即对任意两个函数F(x) 和g(x),它们的汉克尔变换满足F^(h)(ω)=F^(h)(ω) + g^(h)(ω)。
2.卷积性质:汉克尔变换具有卷积性质,即如果F(x) 和g(x)都是汉克尔变换的输入函数,那么它们的卷积F(x)* g(x) 的汉克尔变换等于F^(h)(ω)* g^(h)(ω)。
3.频率域分析:汉克尔变换将时域信号转换到频率域,可以帮助我们分析信号的频率成分和周期性。
4.适用场景:汉克尔变换广泛应用于电磁学、地球物理学、信号处理、通信等领域,例如在地震勘探、重力勘探、电法勘探等地球物理勘探中,汉克尔变换可以用于分析地下结构的性质和位置。
5.研究价值:汉克尔变换在理论研究和实际应用中具有重要意义,对于揭示复杂系统的内在规律、提高信号处理和通信技术的性能具有重要作用。
汉克尔变换在地球物理学中具有广泛的应用,以下是一些典型案例:1.地震勘探:地震勘探是地球物理学中的一种重要方法,通过分析地震波的传播特性,可以揭示地下结构的性质和位置。
汉克尔变换可以用于地震数据的处理和解释,例如在频率域分析中,通过汉克尔变换可以将地震信号转换为频率域,帮助分析地下结构的周期性和频率成分。
2.重力勘探:重力勘探是利用地球重力场观测数据来推断地下结构的一种方法。
汉克尔变换可以用于重力数据的处理和反演,例如在重力异常数据处理中,通过汉克尔变换可以提取地下结构的信息,从而推断地壳厚度、地下岩层位置等。
3.电法勘探:电法勘探是利用地下电性差异来推断地下结构的一种方法。
汉克尔变换可以用于电法数据的处理和反演,例如在电法数据处理中,通过汉克尔变换可以分析地下结构的电性分布,从而推断地下岩层的位置和性质。
ndvi在温度反演(lst)公式

ndvi在温度反演(lst)公式
温度反演(LST)是一种用于确定地表温度的技术,它可以通过一种被称为归一化差异植被指数(NDVI)的指标来实现。
NDVI是一种衡量植被生长和健康状况的指标,它基于植被对红外和可见光的反射率差异。
在温度反演中,NDVI被用作一个关键参数,以帮助推断地表温度。
NDVI的计算方法是通过测量地表的红外和可见光反射率来获得的。
这个指标可以用来反映植被的状况,因为植被通常具有较高的可见光反射率和较低的红外反射率。
因此,当植被生长得更好时,NDVI 值会增加。
NDVI与地表温度之间存在一种相反的关系。
当地表温度升高时,植被的生长和健康状况可能会受到影响,导致NDVI值下降。
相反,当地表温度下降时,植被的生长和健康状况可能会改善,导致NDVI 值增加。
基于NDVI和地表温度之间的这种关系,可以通过建立一个数学模型来进行温度反演。
该模型可以使用已知的NDVI值来推断地表温度。
这种方法可以在遥感技术中广泛应用,特别是在农业、环境和气候研究中。
通过NDVI在温度反演中的应用,我们可以更好地了解地表温度的变化趋势,并对植被生长和健康状况进行评估。
这对于农业管理、
环境监测和气候研究都具有重要意义。
NDVI在温度反演中起着重要的作用。
通过测量地表的红外和可见光反射率差异,NDVI可以帮助我们推断地表温度。
这种方法在农业、环境和气候研究中具有广泛的应用前景,为我们提供了更好地了解地表温度和植被状况的机会。
反演原理——精选推荐
第二章地震反演技术地震反射波法的基础是由于地下不同的地层存在着波阻抗的差异,从而形成了反射波法。
所以从本质上来讲,地震反演的目标就是根据已经获得的地震反射波形,以已知地质规律和钻井、测井资料为约束,对地下岩层空间结构和物理性质所进行的成像(求解),广义的地震反演包含了地震资料处理解释的整个内容。
波阻抗反演是利用地震资料反演地层波阻抗(或)速度的地震特殊处理解释技术。
与地震模式识别预测油气、神经网络预测地层参数、振幅拟合预测储层厚度等统计性方法相比,波阻抗反演具有明确的物理意义,是储层岩性预测、油藏特征描述的确定性方法,在实际应用中取得了明显的地质效果,因此地震反演通常特指波阻抗反演。
李庆忠院士指出:“波阻抗反演是高分辨率地震资料处理的最终表达方式”,说明了波阻抗反演在地震技术中的特殊地位。
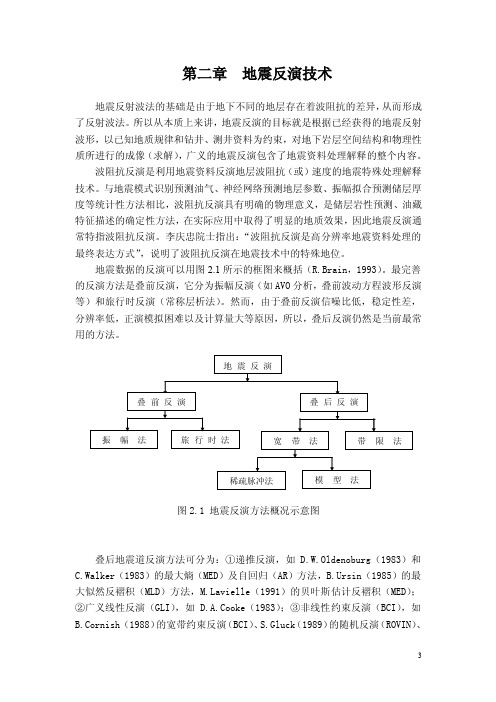
地震数据的反演可以用图2.1所示的框图来概括(R.Brain,1993)。
最完善的反演方法是叠前反演,它分为振幅反演(如AVO分析,叠前波动方程波形反演等)和旅行时反演(常称层析法)。
然而,由于叠前反演信噪比低,稳定性差,分辨率低,正演模拟困难以及计算量大等原因,所以,叠后反演仍然是当前最常用的方法。
图2.1 地震反演方法概况示意图叠后地震道反演方法可分为:①递推反演,如D.W.Oldenoburg(1983)和C.Walker(1983)的最大熵(MED)及自回归(AR)方法,B.Ursin(1985)的最大似然反褶积(MLD)方法,vielle(1991)的贝叶斯估计反褶积(MED);②广义线性反演(GLI),如 D.A.Cooke(1983);③非线性约束反演(BCI),如B.Cornish (1988)的宽带约束反演(BCI)、S.Gluck(1989)的随机反演(ROVIN)、R.D.Martinez(1988)的多参数约束反演(包括BCI、WLI和LCI)。
根据反演结果的频带特性又可分为:①带限法(如GLI、合成声波测井);②稀疏脉冲法(如MED、AR、MLD、BED方法等);③模型法(如BCI、ROVIN、LCI、Strata和Jason 方法等)。
拉普拉斯变换的反演公式
拉普拉斯变换的反演公式
拉普拉斯变换是一种重要的数学工具,它可以将一个函数从时间域转换到频率域。
在工程学、物理学、数学和其他领域中,拉普拉斯变换被广泛应用。
在这篇文章中,我们将探讨拉普拉斯变换的反演公式。
拉普拉斯变换的反演公式是指,如果我们知道一个函数的拉普拉斯变换,那么我们可以通过反演公式将其转换回时间域。
具体来说,如果我们有一个函数f(t),它的拉普拉斯变换为F(s),那么反演公式可以表示为:
f(t) = (1/2πi) ∫γ [F(s) e^(st) ds]
其中,γ是一个逆时针围绕所有极点的曲线,i是虚数单位,e是自然对数的底数,s是复变量。
这个公式的意义是,我们可以通过对F(s)进行逆拉普拉斯变换,得到原始函数f(t)。
这个过程可以看作是将一个函数从频率域转换回时间域的过程。
需要注意的是,拉普拉斯变换的反演公式并不总是适用。
如果函数F(s)有无穷多个极点,或者它的极点不在γ内部,那么反演公式就不成立。
此外,如果F(s)的极点在γ上,那么反演公式也需要进行修正。
在实际应用中,我们通常会使用一些数值方法来计算拉普拉斯变换的反演。
这些方法包括数值逆拉普拉斯变换、快速逆拉普拉斯变换等。
这些方法可以帮助我们更快、更准确地计算反演公式。
拉普拉斯变换的反演公式是一个非常重要的数学工具,它可以帮助我们将一个函数从频率域转换回时间域。
在实际应用中,我们需要注意反演公式的适用条件,并使用适当的数值方法来计算反演。
拉格朗日反演公式
拉格朗日反演公式拉格朗日反演公式是一种用于计算组合数的重要工具,它在数学分析和组合数学的研究中起着至关重要的作用。
拉格朗日反演公式通过将组合数转化为幂级数的方式,使我们能够通过求解幂级数的系数来计算组合数。
本文将介绍拉格朗日反演公式的由来、基本形式和应用,并给出详细的证明过程。
首先,我们来介绍拉格朗日反演公式的基本形式。
对于两个函数$f(n)$和$g(n)$,我们定义它们的乘积形式$F(n)=f*g(n)$为:$$F(n)=\sum_{d,n} f(d)g\left(\frac{n}{d}\right)$$其中$d,n$表示$d$是$n$的因子。
如果我们已知$g(n)$,我们希望通过计算$F(n)$来求解$f(n)$。
拉格朗日反演公式的基本形式可以表示为:$$f(n)=\sum_{d,n} \mu(d)F\left(\frac{n}{d}\right)$$其中$\mu(n)$是莫比乌斯函数,它在数论中具有重要的应用,定义如下:$$\mu(n)=\begin{cases} 1 & \text{如果$n$是一个平方数且含有奇数个质因子}\\ -1 &\text{如果$n$是一个平方数且含有偶数个质因子}\\ 0 &\text{如果$n$有一个大于1的平方因子}\end{cases}$$换句话说,拉格朗日反演公式给出了通过计算$F(n)$来求解$f(n)$的方法,只需要将$F(n)$展开成为幂级数的形式,并将相应的系数与$\mu(n)$相乘即可。
假设我们希望计算经过$k$个点的$n$次多项式函数的系数,那么我们可以定义函数$g(n)$为:$$g(n)=[n=k]$$其中$[n=k]$是指示函数,当$n=k$时为1,否则为0。
我们知道,经过$k$个点的$n$次多项式函数的系数为$\binom{n}{k}$。
我们可以通过计算$g(n)$来求解$f(n)$。
根据拉格朗日反演公式,我们有:$$f(n)=\sum_{d,n} \mu(d)g\left(\frac{n}{d}\right)$$我们希望将$g(n)$展开成幂级数的形式,将系数与$\mu(n)$相乘,即可求解$f(n)$。
地球物理反演理论课件-1
i-1
i
↓
Hi
i i+1
i+1
2 2 x 2 x2 e x1 erf x 3 (t ) ? (正演公式, 略。 ) 3 PE sn sin (t ) 2r 4
N N+1
(t ) ( PE , sn, , r , t ; 1 , i , N , H1 , , H i , H N 1 )
2.0
2.0
1.8
1.0
1.6
1.4 -6 -5 -4 -3 -2 -1 0
0.0 0.0 -0.2 -0.4 -0.6 Depth (Km) -0.8 -1.0 -1.2
Log10 ( t ) (s)
Black square: theoretical response Red cross: initial model response Blue dot: fit response 60 delay time data points;radius=250m rms =2.05%; Number of iteration =98
反演的 ( x, z )二维电阻率 深度剖面 红色: 高电阻率层; 兰色: 低电阻率层。
Yangtze University
• 电法勘探
B Y
瞬变电磁测深法
16
LowTEM法-均匀各向同性水平层状介质电磁场的特性
Transmitter
φ
A
r
X
hz
Receiver s
ρ2
h1
2
┋
i-1
对水平层状介质, 接收线圈中的感应电动势
(地面地质调查和地下地质研究) 主要是在地面和井
地球物理反演的数学原理
地球物理反演的数学原理地球物理反演是一种通过收集地球物理数据,并基于数学原理进行处理和分析,以推断地球内部结构和性质的方法。
数学原理在地球物理领域发挥着至关重要的作用,下面我们来详细介绍地球物理反演的数学原理。
首先,地球物理反演的数学原理主要包括反问题的建立和求解两个方面。
在地球物理实践中,我们通常会遇到一种反问题,即通过观测数据来推断造成这些数据的地下结构或性质。
这种反问题要通过数学方法来建立模型,并求解该模型以获得地下结构的信息。
其次,地球物理反演的数学原理涉及各种数学方法和技术的应用,比如线性代数、偏微分方程、最优化理论等。
其中,线性代数在地球物理反演中起着重要作用,因为地球物理问题通常可以用线性代数描述和求解。
偏微分方程则用于描述地下介质的物理特性,以及模拟地球物理过程。
而最优化理论则用于寻找最优解,即通过优化方法求解地球物理反演问题,以获得更准确的地下结构信息。
另外,地球物理反演的数学原理还包括观测数据的处理和分析方法。
在地球物理实践中,我们通常会通过地震、重力、磁场等各种物理方法来获取地下结构的信息。
这些观测数据需要经过预处理、分析和解释,以提取有用的信息。
数学方法在观测数据处理中发挥着至关重要的作用,包括信号处理、数据挖掘、统计分析等各种技术。
最后,地球物理反演的数学原理还涉及反演结果的验证和解释。
通过数学方法求解地球物理反演问题所得到的地下结构信息需要进行验证和解释,以确保反演结果的准确性和可靠性。
这需要借助地球物理知识、地质知识以及统计学等学科的知识,对反演结果进行分析和解释,以获得对地下结构的深入理解。
综上所述,地球物理反演的数学原理是一种重要的地球科学方法,在研究地球内部结构和性质方面发挥着重要作用。
通过数学原理的应用,我们可以更准确地推断地下结构信息,为地球科学研究和资源勘探提供重要支持。
希望通过对地球物理反演的数学原理的介绍,读者能够更深入了解这一领域,并加深对地球科学的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反演原理及公式介绍
反演原理是一种数学方法,用来将一个复杂问题转化为更简单的问题,通过解决简单问题来得到原问题的解。
它在数学、物理、工程等领域中广
泛应用,并具有重要的理论和实际意义。
反演原理的基本思想是通过利用变换的逆变换来解决问题。
它是一种
从目标空间到解空间的映射方法,通过反演这种映射关系,可以从解空间
推导出目标空间的信息。
反演原理的关键在于建立目标空间和解空间之间
的映射关系,以及确定逆变换的具体形式。
反演原理可以分为两类:线性反演和非线性反演。
线性反演是指目标
空间和解空间之间的映射关系是线性的,可以用线性变换来表示。
非线性
反演是指映射关系是非线性的,需要用非线性变换来表示。
在数学中,反演原理有许多具体的公式和方法。
其中一个著名的例子
是拉普拉斯变换与反演变换之间的关系。
拉普拉斯变换是一种重要的积分
变换,它将函数从时域变换到复频域。
而反演变换则将函数从复频域反演
回时域。
拉普拉斯变换与反演变换之间的关系可以用以下公式表示:F(s) = ∫f(t)e^(-st)dt
f(t) = 1/(2πi) * ∫F(s)e^(st)ds
其中,f(t)是时域函数,F(s)是复频域函数,s是复变量。
这个公式表达了拉普拉斯变换与反演变换之间的一一对应关系,可以
通过拉普拉斯变换得到函数的复频域表示,然后通过反演变换将其恢复到
时域表示。
这个公式在信号处理、控制系统、电路分析等领域中有广泛的
应用。
除了拉普拉斯变换,反演原理还有其他一些重要的公式和方法。
例如,傅里叶变换与反演变换之间的关系、哈尔变换与反演变换之间的关系等。
这些公式和方法可以用来解决各种数学问题,并在实际应用中发挥重要作用。
总之,反演原理是一种重要的数学方法,通过建立目标空间和解空间
之间的映射关系,可以将复杂问题转化为简单问题,并通过解决简单问题
来得到原问题的解。
通过具体的公式和方法,可以实现目标空间与解空间
之间的映射和反演。
反演原理在数学、物理、工程等领域中有广泛应用,
并对解决实际问题具有重要的理论意义和实际价值。
