理论力学第四章摩擦问题
合集下载
【工程力学】第四章 摩擦

Fmin Ptg( f )
Fmin
m P FR1
f P FR1
当物体处于向上滑动的临界
Fmin
平衡状态时,受力如图,可得力三 角形如图。由力三角形可得:
Fmax Ptg( f )
Fmax
P
f
FR2
故力 F 应满足的条件为:
Ptg( f ) F Ptg( f )
将上式展开亦可得同上结果。
X 0 : FN B FsA 0 ———(1) Y 0 : FN A FsB P 0 ——(2)
mA(F) 0 :
FsB
x
P min A
FsA
FNA
Pa cosmin FsB 2a cosmin FN B 2a sin min 0——(3)
由摩擦定律: FsA fs FN A ————(4) FsB fs FN B ————(5)
2
f
2 f
FRA
故
应满足的条件是:
2
2
2 f
P
物块重5KN,与水平面间的摩擦角为 φm=35°,今用与铅垂线成60°角的力P
推动物块,若P= 5KN,则物块将( )
A.不动;
B.滑动;
C.处于临界状态;
D.滑动与否无法确定
P
P
R
例4
α
A
P
R
T
P
套筒A与物块B重量均为 P=5KN,套筒A与铅垂立柱间 的摩擦角为φm=35°,问:套 筒A在α=45°的位置上能否自 锁?
将式(4)、(5)代入(1)、(2)得:
FN B fs FN A
FN A P fsFN B
即可解出:
FN A
P 1 fs2
FN B
Fmin
m P FR1
f P FR1
当物体处于向上滑动的临界
Fmin
平衡状态时,受力如图,可得力三 角形如图。由力三角形可得:
Fmax Ptg( f )
Fmax
P
f
FR2
故力 F 应满足的条件为:
Ptg( f ) F Ptg( f )
将上式展开亦可得同上结果。
X 0 : FN B FsA 0 ———(1) Y 0 : FN A FsB P 0 ——(2)
mA(F) 0 :
FsB
x
P min A
FsA
FNA
Pa cosmin FsB 2a cosmin FN B 2a sin min 0——(3)
由摩擦定律: FsA fs FN A ————(4) FsB fs FN B ————(5)
2
f
2 f
FRA
故
应满足的条件是:
2
2
2 f
P
物块重5KN,与水平面间的摩擦角为 φm=35°,今用与铅垂线成60°角的力P
推动物块,若P= 5KN,则物块将( )
A.不动;
B.滑动;
C.处于临界状态;
D.滑动与否无法确定
P
P
R
例4
α
A
P
R
T
P
套筒A与物块B重量均为 P=5KN,套筒A与铅垂立柱间 的摩擦角为φm=35°,问:套 筒A在α=45°的位置上能否自 锁?
将式(4)、(5)代入(1)、(2)得:
FN B fs FN A
FN A P fsFN B
即可解出:
FN A
P 1 fs2
FN B
理论力学第四章例题资料
先设 处摩擦力达最大值,取杆与轮。
对杆 得 又 得 对轮 得
得
得
当
时,
处无滑动
先设 处摩擦力达最大值,取杆与轮,受力图不变
对杆 得 但 对轮
不变
得
(1)
(2)
(3)
此时
(4)
共有
四个未知数
在
时,解得
即在 当
时, 处不会先滑动 时,解得
处无滑动
例4-7 用几何法求解例5-2。 解: 物块有向上滑动趋势时,
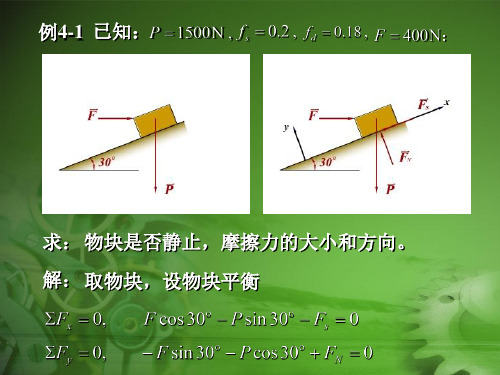
例4-1 已知:
求: 物块是否静止,摩擦力的大小和方向。 解: 取物块,设物块平衡
解得:
(向上)
而
物块处于非静止状态。 向上。
例4-2 已知: 求: 使物块静止,水平推力 的大小。 解:使物块有上滑趋势时,推力为 ,
画物块受力图
(1) (2)
(3)
解得: 设物块有下滑趋势时,推力为 , 画物块受力图:
(1) (2)
(3)
为使物块静止
若 对此题,是否有
? ?
例4-3
已知:
不计凸轮与挺杆处摩擦,不计挺杆质
求:挺杆不被卡量住;之 值。
解:取挺杆,设挺杆处于刚好卡住位置。
解得: 则:挺杆不被卡住时, 。
例4-4 已知:物块重 P, 鼓轮重心位于
各尺寸如图所示:
求: 制动鼓轮所需铅直力F。
处,闸杆重量不 计,
求: 抽拉抽屉不被卡住之e值。
解: 取抽屉,设抽屉刚好被卡住
又 联立解得 则抽屉不被卡住, 。
例4-13 已知:
各构件自重不计,
尺寸如图;
求:保持系统平衡的力偶矩 。
解:设
时,系统即将逆时针方向转动,
第四章 摩擦原理

尽管上述能量平衡理论至今尚未建立可供定量分析的数学模型,但它可 以较全面地描述摩擦学系统的摩擦过程,并可更合理地分析影响该摩擦过程 的各种因素。
输入能量
摩擦学系统 能量损失 (摩擦能量)
输出能量
弹性及塑性 变形能
储存 热能
断裂能量
第二次过程 能量
吸热、散热、摩擦化学反应、结 构转变、摩擦辐射、机械振动、 摩擦升华、噪音、摩擦发光等
库仑摩擦定律可近似地应用于工程实际,但存在以下问题:
1、摩擦系数的大小不仅取决于该材料本身固有的特性,而且与它所在的 摩擦学系统的特性密切相关。
即
f ( x, s)
式中 x--工况条件或工况参数,包括载荷、相对运动的速 度和形式以及时间等; s--摩擦学系统的结构, s={A,P,R}
A--组成摩擦学系统的各元素(包括环境); P--组成摩擦学系统的各元素的性质; R--组成摩擦学系统的各元素之间的相互关系。
4、混合摩擦 又可分为半干摩擦和半流体摩擦两种。前者是指同时存在干摩擦和边 界摩擦的一种混合状态的摩擦。而后者则是指同时存在边界摩擦和流体摩 擦的一种混合状态的摩擦。
按照摩擦副的运动形式,可以将摩擦分为以下两大类:
1.滑动摩擦
如在各种滑动轴承和机床导轨以及钻机中的刹车与气动离合器中相 对滑动表面上产生的摩擦。
按照摩擦副的各种特性,又可将摩擦分为如下两大类:
1、减摩摩擦 这类摩擦的作用是通过减小摩擦以减小摩擦损失,从而提高机 器的效率和能量利用率。 2、增摩摩擦 这类摩擦的作用是通过增加摩擦以实现特定的功能,或达到特 定的工作要求(如刹车副增加摩擦以更好地吸收动能)。
特殊工况下的摩擦
1、高速摩擦 这类摩擦的作用面相对速度在50m/s—600m/s的摩擦问题。 2、高温摩擦 这类摩擦的作用面间温度较高,影响摩擦系数的变化 3、低温摩擦 一般在0~-273度条件下的摩擦,低温下摩擦系数较小 4、真空摩擦 真空条件下,摩擦表面失去氧化膜或吸附膜的保护,摩擦系数较空气 空气中高,真空度高摩擦系数大
理论力学第四章

所以在切线上必然平衡!
jf
FRA
jf
jf
A
2、如果作用于物块的全部主动力的合力FR的作 用线在摩擦角jf之外,则无论这个力怎样小,物 块必滑动。
因为 >jf,而 j ≤ jf ,因此主动力的合力FR和 全约束力FRA不能满足二力平衡条件。
理论力学 中南大学土木工程学院
FR
FRA 滑动
jf
j
10
3、自锁应用举例
( f s只与材料和表面情况有关,与接触面积大小无关)
理论力学
中南大学土木工程学院
4
二、动滑动摩擦力(与静滑动摩擦力不同之处是已经产生了滑动) 大小:摩擦力是一常数;(无平衡范围) 动摩擦力特征: 方向:与物体运动方向相反; 定律: Fd f FN
(f 只与材料和表面情况有关,与接触面积大小无关)
G tan jf F1 G tan jf
理论力学
中南大学土木工程学院
19
[例] 梯子长AB=l,重为P,若梯子与墙和地面的静摩擦因数均为 f s=0.5, FNB 求 多大时,梯子能处于平衡? B
解:考虑取最小时梯子处于下滑趋势的临界 平衡状态,作受力图。 列平衡方程 FSB
自锁应 用实列
理论力学
中南大学土木工程学院
11
<jf
理论力学
中南大学土木工程学院
12
[例] 水平梯子放在直角V形槽内,略去梯重,梯子与两个斜面间的静摩擦 因数为 fs(摩擦角均为j f ),如人在梯子上走动,试分析不使梯子滑动, E 人的活动应限制在什么范围内?P130,4-10
H
解:①作法线AH和BH ②作A,B点的摩擦角jf 交E,G两点 ③E,G两点间的水平距离CD为人的 jf jf 活 动范围 证明:由几何关系 AEB AGB 90 0
jf
FRA
jf
jf
A
2、如果作用于物块的全部主动力的合力FR的作 用线在摩擦角jf之外,则无论这个力怎样小,物 块必滑动。
因为 >jf,而 j ≤ jf ,因此主动力的合力FR和 全约束力FRA不能满足二力平衡条件。
理论力学 中南大学土木工程学院
FR
FRA 滑动
jf
j
10
3、自锁应用举例
( f s只与材料和表面情况有关,与接触面积大小无关)
理论力学
中南大学土木工程学院
4
二、动滑动摩擦力(与静滑动摩擦力不同之处是已经产生了滑动) 大小:摩擦力是一常数;(无平衡范围) 动摩擦力特征: 方向:与物体运动方向相反; 定律: Fd f FN
(f 只与材料和表面情况有关,与接触面积大小无关)
G tan jf F1 G tan jf
理论力学
中南大学土木工程学院
19
[例] 梯子长AB=l,重为P,若梯子与墙和地面的静摩擦因数均为 f s=0.5, FNB 求 多大时,梯子能处于平衡? B
解:考虑取最小时梯子处于下滑趋势的临界 平衡状态,作受力图。 列平衡方程 FSB
自锁应 用实列
理论力学
中南大学土木工程学院
11
<jf
理论力学
中南大学土木工程学院
12
[例] 水平梯子放在直角V形槽内,略去梯重,梯子与两个斜面间的静摩擦 因数为 fs(摩擦角均为j f ),如人在梯子上走动,试分析不使梯子滑动, E 人的活动应限制在什么范围内?P130,4-10
H
解:①作法线AH和BH ②作A,B点的摩擦角jf 交E,G两点 ③E,G两点间的水平距离CD为人的 jf jf 活 动范围 证明:由几何关系 AEB AGB 90 0
E第4章 摩擦
人所能到达的最高点C到点的距离S应为多少?
B C
解:取梯子为研究对象
D
画受力图
A
WP
问题:有几个未知量
FBs
FBN
B C D s l
解:
研究梯子,考虑A、B两处同时 处于即将滑动的临界平衡状态。
FAS FAN f s FBS FBN f s
W
P
FAs
A
X 0 , FBN FAs 0 Y 0 , FAN FBs W P 0 M (F ) 0,
可见: Fs Fmax
Fd f FN 269.8 N
(2)确定平衡范围
此类问题为考虑摩擦的平衡问题的重点, 同时也是静力学的难点问题。分析方法很重要, 即所谓的“临界平衡分析”。
确定平衡的范围,关键是确定最大值和最小 值,而这些极值是与临界的平衡状态相对应的,需 由相应的临界状态求出。只要求得了极值,并明确 它是最大值还是最小值,那么平衡的范围就可以以 不等式的形式写出。需要说明,有的问题同时包括 最大值和最小值,有些问题只包括其中之一。
FCx
' FCN
C
M
O
(F ) 0 ,
F
' C
r O P
Fmax
X 0, Y 0,
FD
D
FDN
解得:
F 26.6 N
FDN 184.6 N
当 fD=0.3 时,处的最大静摩擦力为
FDmax f D FDN 55.39 N
由于FD=40 N<Fdmax ,D处无滑动,故前面假设成立。而上 述所的 F 26.6 N ,确为维持系统平衡的最小水平推力。 (2)当fD=0.15时, FDmax=fDFDN=27.7 N 。前面所求得的FD> Fdmax ,不合理,说明此时 D处应先达到临界状态,应假设D处 的静摩擦力达到最大值,轮将沿地面滑动。
B C
解:取梯子为研究对象
D
画受力图
A
WP
问题:有几个未知量
FBs
FBN
B C D s l
解:
研究梯子,考虑A、B两处同时 处于即将滑动的临界平衡状态。
FAS FAN f s FBS FBN f s
W
P
FAs
A
X 0 , FBN FAs 0 Y 0 , FAN FBs W P 0 M (F ) 0,
可见: Fs Fmax
Fd f FN 269.8 N
(2)确定平衡范围
此类问题为考虑摩擦的平衡问题的重点, 同时也是静力学的难点问题。分析方法很重要, 即所谓的“临界平衡分析”。
确定平衡的范围,关键是确定最大值和最小 值,而这些极值是与临界的平衡状态相对应的,需 由相应的临界状态求出。只要求得了极值,并明确 它是最大值还是最小值,那么平衡的范围就可以以 不等式的形式写出。需要说明,有的问题同时包括 最大值和最小值,有些问题只包括其中之一。
FCx
' FCN
C
M
O
(F ) 0 ,
F
' C
r O P
Fmax
X 0, Y 0,
FD
D
FDN
解得:
F 26.6 N
FDN 184.6 N
当 fD=0.3 时,处的最大静摩擦力为
FDmax f D FDN 55.39 N
由于FD=40 N<Fdmax ,D处无滑动,故前面假设成立。而上 述所的 F 26.6 N ,确为维持系统平衡的最小水平推力。 (2)当fD=0.15时, FDmax=fDFDN=27.7 N 。前面所求得的FD> Fdmax ,不合理,说明此时 D处应先达到临界状态,应假设D处 的静摩擦力达到最大值,轮将沿地面滑动。
理论力学教程(第四章)

静滑动摩擦力的特点
1 方向:沿接触处的公切线,
与相对滑动趋势反向;
2 大小:
3
(库仑摩擦定律)
④静摩擦系数的测定方法(倾斜法)
两种材料做成物体
和可动平面测沿下面滑
动时的 。
p
F=mgsin =fmgcos
2)、动滑动摩擦
tg f
两物体接触表面有相对运动时,沿接触面产生的切向 阻力称为动滑动摩擦力。
1)、静滑动摩擦
① 定义 两相接触物体虽有相对运动趋势,但仍保持相对静止F时,
给接触面产生的切向阻力,称为静滑动摩擦力或简称静摩 擦力。
满足
0 F Fmax (最大静摩擦力)
当 F Fmax时,则物体处于临界平衡状态
F
P Fmax f N (库仑静摩擦定律)
若物体静止,则 F P
摩擦的现象和概念
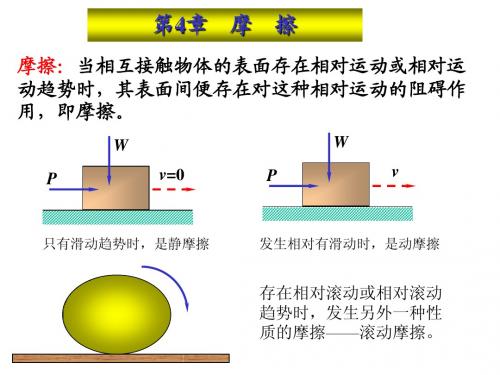
在大学物理已经讲到什么是摩擦:当物体与另一物体 沿接触面的切线方向运动或有相对运动的趋势时,在两物 体的接触面之间有阻碍它们相对运动的作用力,这种力叫 摩擦力。接触面之间的这种现象或特性叫“摩擦”。这里 来作更深入的研究,首先来看它的分类:滑动摩擦和滚动 摩擦。
滑动摩擦:相对运动为滑动或具有滑动趋势时的摩擦。
第四章 摩擦
欢迎加入湖 工大考试资
料群:
引言
前几章我们把接触表面都看成是绝对光滑的,忽略了物体 之间的摩擦,事实上完全光滑的表面是不存在的,一般情况下 都存在有摩擦。 [例]
平衡必计摩擦 3
摩擦
☆§4–1 滑动摩擦 ☆§4–2 摩擦角和自锁现象 ☆§4–3 考虑摩擦时物体的平衡问题 ☆§4–4 滚动摩阻的概念
性质:当物体静止在支承面时,支承面的总反力的偏角
(精品)第四章摩擦
P
R
M
m
O
ax
F FN' d
Fs A
FN
滚动摩阻系数
M max d FN
滚动摩阻系数δ可看成在即将滚动时,法向约束力距
F1maxPscions ffsscso ins
§4-3 考虑摩擦时物体的平衡问题
例4-1 重为P 的滑块放在倾角为θ的斜面上,它与斜面间的摩擦 因数为fs 。当物体处于平衡时,试求水平力的大小。
下滑
Fx 0, F 1co s P sin F m ' a x 0 Fy 0, F N ' F 1sin P co s0
FB
Fy 0, F N D P F N ' c C 6 o o 0 F s s ' s C6 io n 0 0A MO(F)0, Fs'CrFsDr0
O P
D
F
FsDFs' C4N 0;F26.6N;FND18.64N fsD 0.3 F D m afx sF D N D 5.3 5 N 9 FsD
a极限
b 2 fs
挺杆不被卡住 a b 2 fs
FsA FNA A
FsB
b B FNB
a FN
O O FN
ee a
§4-3 考虑摩擦时物体的平衡问题
例4-3 制动器的构造和主要尺寸如图所示,制动块与鼓轮表面间
的摩擦因数为fs ,物块重 P,闸杆重量不计,求制止鼓轮转动所需 的铅直力F。
补充方程 Fm' axfs FN'
y
F1 O
Fmax
P
x
F'
max
FF NN'
F1minPscion sffsscsoins
第四章摩擦
m
FPmax
FP max FQ tan( )
FP min FQ tan( )
FQ tan( ) FP FQ tan( )
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
例4-1
【解法三】 解不等式 FP
FQ
由 X i = 0, FPcos-FS-FQsin= 0 由 Y i = 0, FN -FP sin-FQcos= 0 得
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-2 滑动摩擦
二、摩擦角 全约束反力(全反力) FR = FN + FS 物体处于临界平衡状态时, 静摩擦力达到最大值F max,全反 力FR与接触面法线的夹角,称为 摩擦角。 FW
FP
FS
FN FR
m
Fmax
Fmax f S FN tan m fS FN FN
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-1
摩擦现象和概念
重
力
坝
FW Fq
工程中的摩擦现象
水土学院理论力学课程组
FS FN
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-1
摩擦现象和概念
摩
擦
FP
桩
基 础 摩擦桩 地 基
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-2 滑动摩擦
一、滑动摩擦
两个物体接触面作相对滑动或 具有相对滑动趋势时的摩擦。 静滑动摩擦—具有相对滑动趋势 动滑动摩擦─具有相对滑动
FPmax
FP max FQ tan( )
FP min FQ tan( )
FQ tan( ) FP FQ tan( )
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
例4-1
【解法三】 解不等式 FP
FQ
由 X i = 0, FPcos-FS-FQsin= 0 由 Y i = 0, FN -FP sin-FQcos= 0 得
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-2 滑动摩擦
二、摩擦角 全约束反力(全反力) FR = FN + FS 物体处于临界平衡状态时, 静摩擦力达到最大值F max,全反 力FR与接触面法线的夹角,称为 摩擦角。 FW
FP
FS
FN FR
m
Fmax
Fmax f S FN tan m fS FN FN
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-1
摩擦现象和概念
重
力
坝
FW Fq
工程中的摩擦现象
水土学院理论力学课程组
FS FN
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-1
摩擦现象和概念
摩
擦
FP
桩
基 础 摩擦桩 地 基
水土学院理论力学课程组
理论力学电子教程
第五章 第四章 摩擦 摩擦
§4-2 滑动摩擦
一、滑动摩擦
两个物体接触面作相对滑动或 具有相对滑动趋势时的摩擦。 静滑动摩擦—具有相对滑动趋势 动滑动摩擦─具有相对滑动
理论力学—摩擦
角jf之内,则无论这个力怎样大,
物块必保持静止。这种现象称为 自锁现象。因为在这种情况下, 主 动 力 的 合 力 FR 与 法 线 间 的 夹
角q < jf,因此, FR和全约束反
力FRA必能满足二力平衡条件,
且q j < jf 。
jf
jf
FR
q
A
j
FRA
jf
4.2.2 自锁现象
(2) 如果全部主动力的合力
线的方位也随之改变;在临界状态下,FR的作用线将 画出一个以接触点A为顶点的锥面,称为摩擦锥。设物 块与支承面间沿任何方向的摩擦系数都相同,即摩擦
角都相等,则摩擦锥将是一个顶角为2jf的圆锥。
4.2.2 自锁现象
物块平衡时,静摩擦力不一定达到最大值,可在
零与最大值Fmax之间变化,所以全约束反力与法线间
同而引起的切向力。
滑动摩擦——由于物体间相对滑动或有相 ② 对滑动趋势引起的摩擦。
滚动摩擦——由于物体间相对滚动或有相 对滚动趋势引起的摩擦。
三、摩擦有害的一面和有利的一面
⑴ 有害的一面:它是机械的多余阻力,使机械发热,引起 零部件的磨损,从而消耗能量,降低效率和使用寿命。
⑵ 有利的一面:可利用其进行传动、制动、调速、联接、 夹卡物体等。另外,人类的生活也时时离不开摩擦。
解2:(几何法)
jm B C
当梯子处于向下滑动的临界平衡 RB
状态时,受力如图,显然 RARB ,
E
于是
P
A amin
aj j j j m RA m i2 n m C A 2 m E A C 2 2 E m
故 a应满足的条件是:
2
a22jm
物块必保持静止。这种现象称为 自锁现象。因为在这种情况下, 主 动 力 的 合 力 FR 与 法 线 间 的 夹
角q < jf,因此, FR和全约束反
力FRA必能满足二力平衡条件,
且q j < jf 。
jf
jf
FR
q
A
j
FRA
jf
4.2.2 自锁现象
(2) 如果全部主动力的合力
线的方位也随之改变;在临界状态下,FR的作用线将 画出一个以接触点A为顶点的锥面,称为摩擦锥。设物 块与支承面间沿任何方向的摩擦系数都相同,即摩擦
角都相等,则摩擦锥将是一个顶角为2jf的圆锥。
4.2.2 自锁现象
物块平衡时,静摩擦力不一定达到最大值,可在
零与最大值Fmax之间变化,所以全约束反力与法线间
同而引起的切向力。
滑动摩擦——由于物体间相对滑动或有相 ② 对滑动趋势引起的摩擦。
滚动摩擦——由于物体间相对滚动或有相 对滚动趋势引起的摩擦。
三、摩擦有害的一面和有利的一面
⑴ 有害的一面:它是机械的多余阻力,使机械发热,引起 零部件的磨损,从而消耗能量,降低效率和使用寿命。
⑵ 有利的一面:可利用其进行传动、制动、调速、联接、 夹卡物体等。另外,人类的生活也时时离不开摩擦。
解2:(几何法)
jm B C
当梯子处于向下滑动的临界平衡 RB
状态时,受力如图,显然 RARB ,
E
于是
P
A amin
aj j j j m RA m i2 n m C A 2 m E A C 2 2 E m
故 a应满足的条件是:
2
a22jm
理论力学课件 摩擦
5
如果改变水平力QK的作用 线方向, 则Fm及FRm的方向 也将随之作相应的改变; 若 QK在水平面转过一圈, 则全 约束力FRm的作用线将在空 间画出一个锥面,称为摩擦 锥.
O
f
全约束力与接触面法线所形成的夹角不会大 于f ,即FR作用线不可能超出摩擦锥.即: 静止时, ‹ f
6
如果物体所受的 主动力合力 S (G,Q S 的合力)的作用线 在摩擦锥之外,即 > f时,则全约束力FR 就不可能与S共线. 此时两力不符合二 力平衡条件,物体将 发生滑动.
f
FR
7
如果物体所受的主动力合 力 S 的作用线在摩擦锥之内, 即 < f时,则无论主动力多 大,它总是与FR相平衡,因而 物体将保持不动.
主动力合力的作用线在 摩擦锥的范围内,物体依靠 摩擦总能静止而与主动力 大小无关的现象,称为自锁.
S
f
FR
8
S
如果物体所受的主
动力合力 S 的作用线
N
2sin
W f
cos
17
取OA板为研究对象画受力图.此时的 水平力有极小值Pmin
mO(Fi) = 0
A
F1 P1 N1
C
N1 r ctg Pmind ctg
Pm in
2dsin
Wr f
cos
Fx O
Fy
(2)求P的极大值
当P达到极大值时,圆柱处于上滑临界状态.只要改变
W P
a
b
25
假定方块处于滑动临界平衡状 态画受力图.
Fy = 0 N - W = 0
Fx = 0 P - Fm = 0 Fm=f N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自锁条件:α≤ φf
liluchang
FA
G
α
F
x
f
FN
Fm ax R
此时FA在水平方向的投影永远小于最大静滑动摩擦力。
6
当主动力的合力FA的作用线在摩擦角以内, 则无论合力FA有多大,物体必定保持平衡。
当主动力的合力FA的作用线在摩擦角以外, 则无论合力FA有多小,物体一定会滑动。
螺纹螺旋角: 4 543
螺纹自锁条件: f 543
(休止角)沙堆滑塌、山体滑坡现象。
liluchang
7
liluchang
§4-3 考虑滑动摩擦时物体的平衡问题
仍为平衡问题,平衡方程可用,求解步骤与前面基本相同。
几个新特点 1 、画受力图时,必须考虑摩擦力; 2 、严格区分物体处于临界、非临界状态;
3 、因 0 Fs Fmax,问题的解有时在一个范围内。
故⑴处假设是正确的。
liluchang
22
第六版 . P125:5—2、14、19. 第七版 . P127:4—2、21、27.
liluchang
23
liluchang
例5—6*图示一折叠梯放在地面上,与地面的夹角θ=60°。
脚端A与B和地面的摩擦因数分别为 fsA 0.2, fsB 0.6 。 在折叠梯的AC侧的中点处有一重为G=500N 的重物。不计折
4、静滑动摩擦定律:F max = f s N 的应用要慎重。 5、物体相对滑动趋势与运动方向之间的区别。
分析自行车前、后轮胎受到的摩擦力。
8
liluchang 例4-1 在一个可调整倾角上放一物体重为W, 接触面间的摩擦 系数为 f , 试求物体刚开始下滑时的斜面倾角θ 。
解:(1)、取物体为研究对象.画受力图
F
线与接触面法线间的夹角φf 称为摩擦角。
tg f
Fm a x FN
fS FN FN
fS
摩擦角只与 fS有关,它是全约束力与法线所成角度的最大值。
G
f
FN
x
Fm ax
R
5
3、自锁现象:
主动力的合力FA 的作用线与接 触面法线的夹角为α,当主动力的合 力FA的作用线在摩擦角以内,则无 论合力FA有多大,全约束力R总能与 之平衡,物体必定保持平衡,这种 现象称为自锁现象。
(b) .分析向前滑动情况: F=F max= f N, P=f W=0.62000=1200N。
(3)分析讨论:此题说明滚动要比滑动省力得多,所以通常以滚 动代替滑动。
19
liluchang 例4-7、 重为P1=980N,半径为r =10cm 的滚子A与重P2=490N 的板块B,通过绳索相连,板块B与斜面间的静滑动摩擦系数 f=0.1,A与B间的滚阻系数δ= 0.05,斜面倾角α=30°,绳索与 斜面平行。试求作用在板块B上、平行于斜面并能拉动B的拉 力的最小值。
动摩擦系数 f =0.6 ,滚动摩擦系数δ =0.24cm ,试求推动此轮 胎前进的力P。
解: (1)选轮子为研究对象, 画受力图。
(2)轮子有两种前进可能:
(a).分析向前滚动情况: m= mmax = δ N ∑mA=0 m-Pr=0 P=δW/r=0.242000/40=12N
所以只要12N 的力就可以使轮子向前滚动.
liluchang
G
O
A
Ff
圆柱体放在水平面上,受力如图,F与Ff 形成一个 力偶,即使F 很小,也将使圆柱体发生滚动。
但实际情况并非如此:力F 太小、接触面越软,滚 动越困难,而滑动更难。
当力F不太大时,圆柱体保持平衡,说明必有一个 阻力矩m f 作用在物体上,与力偶(F,Ff )平衡。
m f 从何而来?分析滚动摩擦,必须考虑变 形的影响。物体接触面上受力情况较复杂。
Ff F Fmax N G m f Fr mmax
(r 为圆柱体半径 )
liluchang
G
F
O
A
Ff
Mf
N
FR
(2)、当滚子处于将滚未滚的临界状态时,滚动摩阻力偶矩达到最 大值, m f =m max ,称为最大滚动摩阻力偶矩m max 。
⑶、当F·r > m max 时,滚子处于滚动状态。此时,仍有 m f =m max 。
叠梯的重量,问它是否平衡?如果平衡,计算两脚与地面的
摩擦力。
处理此类问题时首先假定系统为平衡。 由于系统不一定处于静摩擦的临界情况,可
x y
NA
FSmax m N
12
例4-4 * 已知: b , d , fs ,
不计凸轮与挺杆处摩擦,不计挺杆质量;
求:挺杆不被卡住之a 值。
解:取挺杆为研究对象,设挺杆处于卡 住临界状态。
Fx 0
FAN FBN 0
Fy 0
M A 0
FA FB F 0
F
(a
b) 2
FBd
FBN b
补充方程 F2 f N2
解得:Qmin 381N
21
⑴ 设滚子A在板块B上作纯滚动时:
mf mmax N1 (F1 f N1 ,是未知量)
⑷、如果假设滚子在板块上先发生滑 动,则有:
F1 f N1 (mf N1,是未知量)
解得:Qm in 542N
而 Qm in > Qmin 381N
cos f sin
cos f sin
11
liluchang
例4-3 杆AB的A端置于光滑水平面上,AB与水平面夹角
为20°,杆重为P=50 KN。B处有摩擦。当杆在此处临界平衡 时,试求B处摩擦角。
解: 以AB为研究对象,画受 力图,N为B处的正压力。
Fx 0
N tgΦm. cosθ=N sinθ tgΦm = tgθ ∴ Φm =θ=20°
F G
F
x
F
F
F
分析运 动状态
FN
G
4
第二节 摩擦角与自锁现象
liluchang
1、全约束力 R:法向反力FN与摩擦力Fs 的合
力称为支承面对物体的全约束力 R。
FG
其大小为:R FN 2 FS2
x
其方向为:tg FS
FN
2、摩擦角φf :
Fs FN φ R
随着摩擦力的增大,φ角逐渐增大,
当摩擦力达到最大值F max 时,全约束力R作用
1
第一节 滑动摩擦
liluchang
1、定义:两个相互接触的物体,发生沿着接触面的相对滑 动或滑动趋势时,在公切线上彼此间产生阻碍运动或运动 趋势的力,称为滑动摩擦力。
2、滑动摩擦力的方向:与被研究对象相对滑动或滑动趋势的 方向相反。
3、滑动摩擦力大小的三种情况(三种滑动运动状态):
如⑴何、确有定相摩对擦滑力动的趋具势体时值-和--方--向静?滑动
m max=δN
δ 称为滚动摩擦系数,其量纲为长度 单位,其物理意义是将摩擦力简化为纯 主矢时,合力作用点B到简化中心A点的 距离,与接触物体的性质有关。
liluchang
G
F O B Ff N R
G
ቤተ መጻሕፍቲ ባይዱ
F
O
A
Ff
Mf
N
FR
18
liluchang
例4-6 轮胎半径为r =40cm,载重W=2000N,推力为P,设滑
0
liluchang
13
FA fs FAN
FB fs FBN
解得: a b 2 fs
则:挺杆不被卡住时,a b 2 fs
liluchang
14
liluchang
例4-5* 已知:物块重 P, 鼓轮重心位于O1处,闸杆重量
不计,各尺寸如图所示。求:制动鼓轮所需铅直力F。
解: (1)设鼓轮被制动处于平衡状态, 取鼓轮为研究对象。
20
liluchang
补充方程 mf mmax N1 (F1 f N1 ,是未知量)
解得:N1=P1 cos ;
T=P(1 sin
r
cos );F1
P1
r
cos
⑶ 取板块B为研究对象,画受力图,建立坐标系,列平衡方程:
Fx 0
T
F1
F2
P2si n
Qmin
Fy 0 N2 N1 P2 cos 0
Fs=∑F x 且0≤ Fs ≤Fmax
FF G
F
G
x
⑵、临界平衡状态时-----最大静滑动
摩擦力Fmax :
F
x Fs
FFmsax
当外力增加到某个值时,物体处于 将动未动的临界平衡状态,这时静摩 擦力达到最大值称为最大静摩擦力, 以Fmax表示。
FN 摩F擦N 力大小
如何计算?
静滑动摩擦定律:最大静摩擦力的大小与法向反力成正比。
F max = f s N
其中:f s 称为静滑动摩擦因数
3
liluchang
⑶、有相对滑动时-----动滑动摩擦力F′: 当物体接触面间有相对滑动时,出现的滑动摩擦力,
称为动滑动摩擦力,它的方向与两物体间相对滑动的方向 相反。
F = f N
其中: f 称为动滑动摩擦因数。
一般情况, f < f s ,要求不高时,f = f s 。
α o
X 0 Y 0
Pmax cos F2 max Q sin 0 Pmax sin N2 Q cos 0
liluchang
x
F2max N1
F2max f N2
Pmax
sin cos
f cos f sin
Q
3、综上得出:要维持物体平衡时,力P的值应满足的条件是:
sin f cos Q P sin f cos Q
liluchang
FA
G
α
F
x
f
FN
Fm ax R
此时FA在水平方向的投影永远小于最大静滑动摩擦力。
6
当主动力的合力FA的作用线在摩擦角以内, 则无论合力FA有多大,物体必定保持平衡。
当主动力的合力FA的作用线在摩擦角以外, 则无论合力FA有多小,物体一定会滑动。
螺纹螺旋角: 4 543
螺纹自锁条件: f 543
(休止角)沙堆滑塌、山体滑坡现象。
liluchang
7
liluchang
§4-3 考虑滑动摩擦时物体的平衡问题
仍为平衡问题,平衡方程可用,求解步骤与前面基本相同。
几个新特点 1 、画受力图时,必须考虑摩擦力; 2 、严格区分物体处于临界、非临界状态;
3 、因 0 Fs Fmax,问题的解有时在一个范围内。
故⑴处假设是正确的。
liluchang
22
第六版 . P125:5—2、14、19. 第七版 . P127:4—2、21、27.
liluchang
23
liluchang
例5—6*图示一折叠梯放在地面上,与地面的夹角θ=60°。
脚端A与B和地面的摩擦因数分别为 fsA 0.2, fsB 0.6 。 在折叠梯的AC侧的中点处有一重为G=500N 的重物。不计折
4、静滑动摩擦定律:F max = f s N 的应用要慎重。 5、物体相对滑动趋势与运动方向之间的区别。
分析自行车前、后轮胎受到的摩擦力。
8
liluchang 例4-1 在一个可调整倾角上放一物体重为W, 接触面间的摩擦 系数为 f , 试求物体刚开始下滑时的斜面倾角θ 。
解:(1)、取物体为研究对象.画受力图
F
线与接触面法线间的夹角φf 称为摩擦角。
tg f
Fm a x FN
fS FN FN
fS
摩擦角只与 fS有关,它是全约束力与法线所成角度的最大值。
G
f
FN
x
Fm ax
R
5
3、自锁现象:
主动力的合力FA 的作用线与接 触面法线的夹角为α,当主动力的合 力FA的作用线在摩擦角以内,则无 论合力FA有多大,全约束力R总能与 之平衡,物体必定保持平衡,这种 现象称为自锁现象。
(b) .分析向前滑动情况: F=F max= f N, P=f W=0.62000=1200N。
(3)分析讨论:此题说明滚动要比滑动省力得多,所以通常以滚 动代替滑动。
19
liluchang 例4-7、 重为P1=980N,半径为r =10cm 的滚子A与重P2=490N 的板块B,通过绳索相连,板块B与斜面间的静滑动摩擦系数 f=0.1,A与B间的滚阻系数δ= 0.05,斜面倾角α=30°,绳索与 斜面平行。试求作用在板块B上、平行于斜面并能拉动B的拉 力的最小值。
动摩擦系数 f =0.6 ,滚动摩擦系数δ =0.24cm ,试求推动此轮 胎前进的力P。
解: (1)选轮子为研究对象, 画受力图。
(2)轮子有两种前进可能:
(a).分析向前滚动情况: m= mmax = δ N ∑mA=0 m-Pr=0 P=δW/r=0.242000/40=12N
所以只要12N 的力就可以使轮子向前滚动.
liluchang
G
O
A
Ff
圆柱体放在水平面上,受力如图,F与Ff 形成一个 力偶,即使F 很小,也将使圆柱体发生滚动。
但实际情况并非如此:力F 太小、接触面越软,滚 动越困难,而滑动更难。
当力F不太大时,圆柱体保持平衡,说明必有一个 阻力矩m f 作用在物体上,与力偶(F,Ff )平衡。
m f 从何而来?分析滚动摩擦,必须考虑变 形的影响。物体接触面上受力情况较复杂。
Ff F Fmax N G m f Fr mmax
(r 为圆柱体半径 )
liluchang
G
F
O
A
Ff
Mf
N
FR
(2)、当滚子处于将滚未滚的临界状态时,滚动摩阻力偶矩达到最 大值, m f =m max ,称为最大滚动摩阻力偶矩m max 。
⑶、当F·r > m max 时,滚子处于滚动状态。此时,仍有 m f =m max 。
叠梯的重量,问它是否平衡?如果平衡,计算两脚与地面的
摩擦力。
处理此类问题时首先假定系统为平衡。 由于系统不一定处于静摩擦的临界情况,可
x y
NA
FSmax m N
12
例4-4 * 已知: b , d , fs ,
不计凸轮与挺杆处摩擦,不计挺杆质量;
求:挺杆不被卡住之a 值。
解:取挺杆为研究对象,设挺杆处于卡 住临界状态。
Fx 0
FAN FBN 0
Fy 0
M A 0
FA FB F 0
F
(a
b) 2
FBd
FBN b
补充方程 F2 f N2
解得:Qmin 381N
21
⑴ 设滚子A在板块B上作纯滚动时:
mf mmax N1 (F1 f N1 ,是未知量)
⑷、如果假设滚子在板块上先发生滑 动,则有:
F1 f N1 (mf N1,是未知量)
解得:Qm in 542N
而 Qm in > Qmin 381N
cos f sin
cos f sin
11
liluchang
例4-3 杆AB的A端置于光滑水平面上,AB与水平面夹角
为20°,杆重为P=50 KN。B处有摩擦。当杆在此处临界平衡 时,试求B处摩擦角。
解: 以AB为研究对象,画受 力图,N为B处的正压力。
Fx 0
N tgΦm. cosθ=N sinθ tgΦm = tgθ ∴ Φm =θ=20°
F G
F
x
F
F
F
分析运 动状态
FN
G
4
第二节 摩擦角与自锁现象
liluchang
1、全约束力 R:法向反力FN与摩擦力Fs 的合
力称为支承面对物体的全约束力 R。
FG
其大小为:R FN 2 FS2
x
其方向为:tg FS
FN
2、摩擦角φf :
Fs FN φ R
随着摩擦力的增大,φ角逐渐增大,
当摩擦力达到最大值F max 时,全约束力R作用
1
第一节 滑动摩擦
liluchang
1、定义:两个相互接触的物体,发生沿着接触面的相对滑 动或滑动趋势时,在公切线上彼此间产生阻碍运动或运动 趋势的力,称为滑动摩擦力。
2、滑动摩擦力的方向:与被研究对象相对滑动或滑动趋势的 方向相反。
3、滑动摩擦力大小的三种情况(三种滑动运动状态):
如⑴何、确有定相摩对擦滑力动的趋具势体时值-和--方--向静?滑动
m max=δN
δ 称为滚动摩擦系数,其量纲为长度 单位,其物理意义是将摩擦力简化为纯 主矢时,合力作用点B到简化中心A点的 距离,与接触物体的性质有关。
liluchang
G
F O B Ff N R
G
ቤተ መጻሕፍቲ ባይዱ
F
O
A
Ff
Mf
N
FR
18
liluchang
例4-6 轮胎半径为r =40cm,载重W=2000N,推力为P,设滑
0
liluchang
13
FA fs FAN
FB fs FBN
解得: a b 2 fs
则:挺杆不被卡住时,a b 2 fs
liluchang
14
liluchang
例4-5* 已知:物块重 P, 鼓轮重心位于O1处,闸杆重量
不计,各尺寸如图所示。求:制动鼓轮所需铅直力F。
解: (1)设鼓轮被制动处于平衡状态, 取鼓轮为研究对象。
20
liluchang
补充方程 mf mmax N1 (F1 f N1 ,是未知量)
解得:N1=P1 cos ;
T=P(1 sin
r
cos );F1
P1
r
cos
⑶ 取板块B为研究对象,画受力图,建立坐标系,列平衡方程:
Fx 0
T
F1
F2
P2si n
Qmin
Fy 0 N2 N1 P2 cos 0
Fs=∑F x 且0≤ Fs ≤Fmax
FF G
F
G
x
⑵、临界平衡状态时-----最大静滑动
摩擦力Fmax :
F
x Fs
FFmsax
当外力增加到某个值时,物体处于 将动未动的临界平衡状态,这时静摩 擦力达到最大值称为最大静摩擦力, 以Fmax表示。
FN 摩F擦N 力大小
如何计算?
静滑动摩擦定律:最大静摩擦力的大小与法向反力成正比。
F max = f s N
其中:f s 称为静滑动摩擦因数
3
liluchang
⑶、有相对滑动时-----动滑动摩擦力F′: 当物体接触面间有相对滑动时,出现的滑动摩擦力,
称为动滑动摩擦力,它的方向与两物体间相对滑动的方向 相反。
F = f N
其中: f 称为动滑动摩擦因数。
一般情况, f < f s ,要求不高时,f = f s 。
α o
X 0 Y 0
Pmax cos F2 max Q sin 0 Pmax sin N2 Q cos 0
liluchang
x
F2max N1
F2max f N2
Pmax
sin cos
f cos f sin
Q
3、综上得出:要维持物体平衡时,力P的值应满足的条件是:
sin f cos Q P sin f cos Q
