【2014年秋备课】七年级数学上册 1.2.4 绝对值课件 (新版)新人教版
合集下载
新人教版七年级上册数学1.2.4绝对值——绝对值的定义及性质优质课件

| b-1 | 0,又 | a-2 |+| b-1 |=0 ,所以a -2 =0 ,
b-1=0.
解:根据题意可知:a-2=0,b-1=0 ,
所以:a=2 ,b=1.
第二十一页,共二十五页。
总结
若几个非负数的和为0,则这几个数都为0.
知3-讲
第二十二页,共二十五页。
1 绝对值最小的数是______0__;绝对值最小的负整数
第七页,共二十五页。
1 (中考·连云港)数轴上表示-2的点与原点的距离是
____2____.
知1-练
第八页,共二十五页。
知识点 2 绝对值的求法
1.几何定义:一般地,数轴上表示数a的点与原点的距
离叫做数a的绝对值,记作 a .
2.代数定义:一个正数的绝对值是它本身;一个负数
的绝对值是它的相反数;0的绝对值是0;任意一个
所以x 的相反数为-4,y 的相反数为2.
第十九页,共二十五页。
总结
知3-讲
本题运用了巧用非负性技巧,考查了非负数的性质,
该性质可巧记为“0+0=0”,可以推广为:如果几个非 负数的和为0,那么这几个非负数均为0.
第二十页,共二十五页。
知3-练
例 5
已知
a-2 + b-,1 求=0a、b的值.
导引:因为 | a-2 | 和 | b-1 | 都是非负数,所以 | a-2 | 0 ,
=
__2._5__,-
2
=
2 (中考·东营)
-
1 3的相反数是(
A. 1 B.- 1 C.3
3
3
)B
D.-3
第十六页,共二十五页。
知2-练
知识点 3 绝对值的性质
人教版七年级上册数学绝对值ppt课堂课件

人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
2.若|a|+ |b-3| =0.则a =__0___,
b= __3___. 3.如果一个数的绝对值等于4.53 ,
则这个数是__4_._5_3或__-__4_.5_3____. 4.如果|x-1|=2,则x=___3或__-__1___. 5.如果a 的相反数是-0.86,那么|a|
东、西方向行驶10km,到达A、B两处(图
1.2-5)。
方向不同, (正负性)
(1)它们的行驶路线的方向相同吗?距(不离。管相方同向,)
(2)它们行驶路程的距离(线段OA、OB的长 度)相同吗?
A
10
-10
O
10
B
0
10
人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
1.2.4
人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
学习目标
1. 初步理解绝对值的概念,能求一个
数的绝对值. 2.通过应用绝对值解决相关问题,体 会绝对值的意义和作用.
人教版七年级上册数学课件:1.2.4绝 对值
❖
6本课的突出特点是拟人手法的运用, 把植物 和种子 分别当 作“妈 妈”和 “孩子 ”来写 。“妈 妈孩子 ”这样 的关联 ,易触 动儿童 的情感 世界, 易激发 想象、 引发思 考,读 起来亲 切、有 趣,易 于调动 小读者 的阅读 兴趣。
❖
7学习这篇课文,应该重点引导学生运 用探究 式的学 习方式 ,注意 激发学 生了解 植物知 识、探 究大自 然奥秘 的兴趣 ,把向 书本学 习和向 大自然 学习结 合起来 ,引导 学生养 成留心 身边的 事物、 认真观 察的好 习惯。
人教版七年级数学上册 1.2.4.1 绝对值的定义及性质 教学课件(共28张PPT)

练习1:判断并改错: (1)一个数的绝对值等于本身,则这个数一定是正数; (2)一个数的绝对值等于它的相反数,则这个数一定是负数; (3)如果两个数的绝对值相等,那么这两个数一定相等; (4)如果两个数不相等,那么这两个数的绝对值一定不相等; (5)有理数的绝对值一定是非负数;
课堂精练
练习2:写出下列各数的绝对值:
人教版七年级数学上册
第一章 有理数 1.2.4.1 绝对值的定义及性质
新课导入
1. 什么是数轴?数轴定义包含哪几层含义? 2. 数轴上的点与有理数间的关系是怎样的? 3. 什么是相反数? 4. 相反数的代数意义和几何意义分别是什么?
合作探究
问题1 看图回答问题: 两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处, 它们的行驶路线相同吗?它们的行驶路程相同吗?
6,8,3.9, 5 , 2 ,100,0 2 11
3.口答:
6 = 0=
2 = 7
-3 =
8.2 =
-1 = 3
合作探究
问题1 结合上面口答题结果,一个数的绝对值与这个数有什么 关系?你能从中发现什么规律?
(1)一个正数的绝对值是它本身; (1)若a 0,则 a a;
(2)一个负数的绝对值是它的相反数;(2)若a 0,则 a -a;
(3)0的绝对值是0.
例如:上面的问题中在数轴上表示-3的点和表示3的点到原 点的距离都是3,所以3和-3的绝对值都是3,即|-3|=|3|=3. 你能说说-2和2吗?
合作探究
-3 -2 -1 0 1 2 3 4
大象离原点4个单位长度:|4|=4. 那么两只小狗呢?
合作探究
1.-2的绝对值是____,说明数轴上表示-2的点到____的距离是 ____个长度单位. 2.-0.8的绝对值是____ .
课堂精练
练习2:写出下列各数的绝对值:
人教版七年级数学上册
第一章 有理数 1.2.4.1 绝对值的定义及性质
新课导入
1. 什么是数轴?数轴定义包含哪几层含义? 2. 数轴上的点与有理数间的关系是怎样的? 3. 什么是相反数? 4. 相反数的代数意义和几何意义分别是什么?
合作探究
问题1 看图回答问题: 两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处, 它们的行驶路线相同吗?它们的行驶路程相同吗?
6,8,3.9, 5 , 2 ,100,0 2 11
3.口答:
6 = 0=
2 = 7
-3 =
8.2 =
-1 = 3
合作探究
问题1 结合上面口答题结果,一个数的绝对值与这个数有什么 关系?你能从中发现什么规律?
(1)一个正数的绝对值是它本身; (1)若a 0,则 a a;
(2)一个负数的绝对值是它的相反数;(2)若a 0,则 a -a;
(3)0的绝对值是0.
例如:上面的问题中在数轴上表示-3的点和表示3的点到原 点的距离都是3,所以3和-3的绝对值都是3,即|-3|=|3|=3. 你能说说-2和2吗?
合作探究
-3 -2 -1 0 1 2 3 4
大象离原点4个单位长度:|4|=4. 那么两只小狗呢?
合作探究
1.-2的绝对值是____,说明数轴上表示-2的点到____的距离是 ____个长度单位. 2.-0.8的绝对值是____ .
1.2.4绝对值(课时2)课件(新人教版七年级上数学)

求两个负数的大小的步骤:(1)先求出 两个负数的绝对值;(2)比较两个绝 (1) -1和 – 5; (2)- 5 和 2.7 6 对值的大小;(3)写出正确的判断. 解法一(利用绝对值比较两个负数的大小) 解: (1)因为| -1| = 1,| -5 | = 5 ,1﹤5
例1. 比较下列每组数的大小
任意两个有理数的大小如何比较?
1.利用数轴比较: 2.由数轴上数的特点可知:
数轴上表示的两个数,右边的总比左边的大。
正数大于0, 0大于负数,正数大于负数.
特别地,两个负数,绝对值大的反而小.
例题
1.利用数轴比较有理数的大小. 2.利用绝对值比较有理数的大小.
达标题
1.异号两数比较大小,要考虑它们的 要考虑它们的 . 2.用“>、=、<”号填空: -3 -5; -2.25
所以 - 1> - 5
(2)因为| 5 6
5 | 6
=
5 6
,|- 2.7| =2.7,
﹤2.7,所以 -
5 ﹥-2.7 6
解法二 (利用数轴比较两个负数的大小) 解:(1) 因为- 5在 –1左边,所以 - 5﹤ - 1
(2) 因为- 2.7在 - 5 的左边,所以 2.7 ﹤- 5 6 6
总结归纳
1. 在数轴上表示下列各数,并比较 它们的大小: - 1.5 , - 3 , - 1 , - 5
2. 求出(1)中各数的绝对值,并比 较它们的大小
解:(1)
1.5
3. 你发现了什么?
-5
-3 -2 -1 0 1 2
- 5 < - 3 <- 1.5 < - 1 (2)| -1.5 | = 1.5 ; | - 3 | = 3; | -1 | = 1 ; | - 5 | = 5. 1 < 1.5 <3 <5 (3)由以上知:两个负数比较大小, )由以上知:两个负数比较大小, 绝对值大的反而小
初中数学教学课件:1.2.4 绝对值 第1课时(人教版七年级上)_1-8
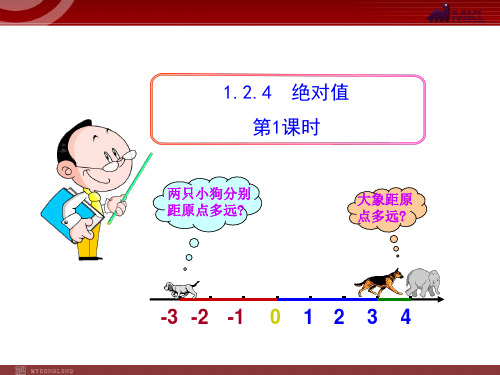
1.2.4 绝对值 第1课时
两只小狗分别 距原点多远?
大象距原 点多远?
-3 -2 -1 0 1 2 3 4
1.理解绝对值的概念及其几何意义. 2.会求一个数(不涉及字母)的绝对值. 3.会求绝对值已知的数. 4.了解绝对值的非负性,并能用其非负性解决相关问题.
1.什么叫做相反数? 2.你能找出互为相反数的两个数在数轴上表示的点的共 同特点吗?
+ 2 的绝对值是 2,即| + 2|= 2;
3
3
33
0的绝对值是0,即|0|=0;
-2.3的绝对值是2.3,即|-2.3|=2.3;
+0.56的绝对值是0.56,即|+0.56|=0.56;
-6的绝对值是6,即|-6|=6;
+6的绝对值是6 ,即|+6|=6;
− 21 的绝对值是 21 ,即| − 21|=
2
2ห้องสมุดไป่ตู้
2
21.
2
绝对值的表示 数a的绝对值,记作:|a|.
在数轴上表示-5的点与原点的距离是5, 即-5的绝对值是5,记作:|-5|=5.
11 的绝对值是 1 1 , 记作: 11 = 11 .
3
3
3
3
例1 求下列各数的绝对值.
-19, + 2 ,0,-2.3,+0.56,-6,+6,− 21 .
3
2
【解析】-19的绝对值是19,即|-19|=19;
两只小狗分别距原点 多远?
大象距原点多 远?
-3 -2 -1 0 1 2 3 4
一般地,数轴上表示数a的点与原点的距离叫做数a 的绝对值. 想一想 这里的数a可以表示什么样的数?
这里的数a可以是正数,负数和0.
两只小狗分别 距原点多远?
大象距原 点多远?
-3 -2 -1 0 1 2 3 4
1.理解绝对值的概念及其几何意义. 2.会求一个数(不涉及字母)的绝对值. 3.会求绝对值已知的数. 4.了解绝对值的非负性,并能用其非负性解决相关问题.
1.什么叫做相反数? 2.你能找出互为相反数的两个数在数轴上表示的点的共 同特点吗?
+ 2 的绝对值是 2,即| + 2|= 2;
3
3
33
0的绝对值是0,即|0|=0;
-2.3的绝对值是2.3,即|-2.3|=2.3;
+0.56的绝对值是0.56,即|+0.56|=0.56;
-6的绝对值是6,即|-6|=6;
+6的绝对值是6 ,即|+6|=6;
− 21 的绝对值是 21 ,即| − 21|=
2
2ห้องสมุดไป่ตู้
2
21.
2
绝对值的表示 数a的绝对值,记作:|a|.
在数轴上表示-5的点与原点的距离是5, 即-5的绝对值是5,记作:|-5|=5.
11 的绝对值是 1 1 , 记作: 11 = 11 .
3
3
3
3
例1 求下列各数的绝对值.
-19, + 2 ,0,-2.3,+0.56,-6,+6,− 21 .
3
2
【解析】-19的绝对值是19,即|-19|=19;
两只小狗分别距原点 多远?
大象距原点多 远?
-3 -2 -1 0 1 2 3 4
一般地,数轴上表示数a的点与原点的距离叫做数a 的绝对值. 想一想 这里的数a可以表示什么样的数?
这里的数a可以是正数,负数和0.
数学人教版七年级上册1.2.4绝对值 PPT课件

解:
|-19|=19;
| 2|= 2 ;
3
3
|0|=0;
|-2.3|=2.3;
练习: 课本第11页第1、2、3题
4
练习
1.-2的绝对值是_2___, 说明数轴上表示-2 的点到原___点_的距离是__2__个长度单位.
2.-0.8的绝对值是_0_._8_ .
3.口答:
6 = 6 8.2 = 8.2 0= 0
示出来, 它们有什么相同之处和不同之处?
8
8
-8
0
8
-8与8在数轴上所表示的点到原点的距离是8
个单位长度, 它们的符号不同。我们把这个距离
8叫做+8和-8的绝对值。
一般地, 数轴上表示数a的点与原点的距离叫做 数a的绝对值(absoute value), 记作: |a|
绝对值的定义
2
|10|=10
3
(2) | 3 |=___1_0_0___;
100
(3) |y|=__-y__(y<0); (4) | 3 . 1 4 |=_____ _3_. 1_4___.
8
做一做:
(5) 若 |a|= |3| 则a =_____3__;
(6)若 |a|= | -3 | 则a =_____3___;
(7)若
数学中规定: 在数轴上表示有理数, 它们从 左到右的顺序, 就是从小到大的顺序, 即左边的 数小于右边的数.
有规定可知, 对于正数、0和负数这三类数, 它 们之间有大小关系是:
1.正数大于0, 0大于负数, 正数大于负数; 2.两个负数, 绝对值大的反而小.
例如, 1 > 0, 0 > -1,
1 > -1, -1 > -2
|-19|=19;
| 2|= 2 ;
3
3
|0|=0;
|-2.3|=2.3;
练习: 课本第11页第1、2、3题
4
练习
1.-2的绝对值是_2___, 说明数轴上表示-2 的点到原___点_的距离是__2__个长度单位.
2.-0.8的绝对值是_0_._8_ .
3.口答:
6 = 6 8.2 = 8.2 0= 0
示出来, 它们有什么相同之处和不同之处?
8
8
-8
0
8
-8与8在数轴上所表示的点到原点的距离是8
个单位长度, 它们的符号不同。我们把这个距离
8叫做+8和-8的绝对值。
一般地, 数轴上表示数a的点与原点的距离叫做 数a的绝对值(absoute value), 记作: |a|
绝对值的定义
2
|10|=10
3
(2) | 3 |=___1_0_0___;
100
(3) |y|=__-y__(y<0); (4) | 3 . 1 4 |=_____ _3_. 1_4___.
8
做一做:
(5) 若 |a|= |3| 则a =_____3__;
(6)若 |a|= | -3 | 则a =_____3___;
(7)若
数学中规定: 在数轴上表示有理数, 它们从 左到右的顺序, 就是从小到大的顺序, 即左边的 数小于右边的数.
有规定可知, 对于正数、0和负数这三类数, 它 们之间有大小关系是:
1.正数大于0, 0大于负数, 正数大于负数; 2.两个负数, 绝对值大的反而小.
例如, 1 > 0, 0 > -1,
1 > -1, -1 > -2
数学人教版七年级上册1.2.4绝对值 PPT课件
(4) |-6|=_____;(5) |y|=____(y<0); (6)| 3.14|=_____.
想一想:(1)绝对值是3的数有几个? 各是什么? (2)绝对值是0的数有几个? 各是什么? (3)绝对值是-2的数是否存在? 若存在, 请说出来?
练一练 判断
(1)+7的绝对值与-7的绝对值互为相反数。( ) (2)既不是正数也不是负数的有理数的绝对值是零。( ) (3)数a的绝对值就是数轴上表示数a的点与原点的距离。( ) (4)绝对值最小的数是0。( ) (5)如果数a的绝对值等于a, 那么a一定为正数。( ) (6)符号相反且绝对值相等的数互为相反数。( ) (7)一个数的绝对值越大, 表示它的点在数轴上越靠右。( ) (8)一个数的绝对值越大, 表示它的点在数轴上离原点越远。( )
活动4 求下列各数的绝对值。
0的 绝对 值是
0
︱ 9 ︱= 9 ︱ 2.5︱= 2.5
︱- 9 ︱= 9 ︱ -2.5 ︱= 2.5
︱ 0︱= 0
负数的绝对值是 它的相反数
议一议: 上述各数的绝对值与这些数本身有什么关系?
正数的绝对值是它本身; 负数的绝对值是它的相反数; 0的绝对值是0。
绝对值的代 数意义
绝对值
创设情景 巩固练习 课后作业
讲授新课 回顾小结 学有所思
结束
创设问题情境,引入新课
活动1: 想一想, 你会想些什么?
问题: 两辆汽车从同一处O出发, 分别向东、西方向行驶
10km, 到达A、B两处(图1.2-5)。
方向不同,
距离相同(绝对值 相等, 不管方向)
它们的行驶路线相同吗?
正负性
它们行驶路程的远近(线段OA、OB的长度)相同吗?
想一想:(1)绝对值是3的数有几个? 各是什么? (2)绝对值是0的数有几个? 各是什么? (3)绝对值是-2的数是否存在? 若存在, 请说出来?
练一练 判断
(1)+7的绝对值与-7的绝对值互为相反数。( ) (2)既不是正数也不是负数的有理数的绝对值是零。( ) (3)数a的绝对值就是数轴上表示数a的点与原点的距离。( ) (4)绝对值最小的数是0。( ) (5)如果数a的绝对值等于a, 那么a一定为正数。( ) (6)符号相反且绝对值相等的数互为相反数。( ) (7)一个数的绝对值越大, 表示它的点在数轴上越靠右。( ) (8)一个数的绝对值越大, 表示它的点在数轴上离原点越远。( )
活动4 求下列各数的绝对值。
0的 绝对 值是
0
︱ 9 ︱= 9 ︱ 2.5︱= 2.5
︱- 9 ︱= 9 ︱ -2.5 ︱= 2.5
︱ 0︱= 0
负数的绝对值是 它的相反数
议一议: 上述各数的绝对值与这些数本身有什么关系?
正数的绝对值是它本身; 负数的绝对值是它的相反数; 0的绝对值是0。
绝对值的代 数意义
绝对值
创设情景 巩固练习 课后作业
讲授新课 回顾小结 学有所思
结束
创设问题情境,引入新课
活动1: 想一想, 你会想些什么?
问题: 两辆汽车从同一处O出发, 分别向东、西方向行驶
10km, 到达A、B两处(图1.2-5)。
方向不同,
距离相同(绝对值 相等, 不管方向)
它们的行驶路线相同吗?
正负性
它们行驶路程的远近(线段OA、OB的长度)相同吗?
2024年秋季新人教版七年级上册数学教学课件 1.2.4 绝对值
(1) 根据调查结果,指出哪些产品是合乎要求的 (即在误 差范围内的); (2) 指出合乎要求的产品中哪一个质量好一些,并用绝对 值的知识说明.
同学们,通过这节课的学习, 你有什么收获呢?
谢谢 大家
爱心.诚心.细心.耐心,让家长放心.孩子安心。
1. 判断对错:
(1) 一个数的绝对值等于本身,则该数一定是正数; ( )
(2) 一个数的绝对值等于它的相反数,这个数一定是
负数;
()
(3) 如果两个数的绝对值相等,那么这两个数一定
相等;
()
(4) 如果两个数不相等,那么这两个数的绝对值
一定不等;
()
(5) 有理数的绝对值一定是非负数.
()
2. 化简:
B -10
分析:行驶路线 行驶路程
O
A
0
10
方向 + 距离 方向不同 距离 距离相同
绝对值的定义: 一般地,数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值,记作|a|.
B
O
A
-10
0
10
例:因为点 A 表示10,与原点的距离是 10 个单位长度,
所以|10| = 10.
1.利用数轴,口答下列问题:
|5|=5
–5 –4 –3 –2 –1 0 1 2 3 4 5
| 3.5 | = 3.5 –5 –4 –3 –2 –1 0 1 2 3 4 5
| -3 | = 3
–5 –4 –3 –2 –1 0 1 2 3 4 5
| -3.5 | =3.5 –5 –4 –3 –2 –1 0 1 2 3 4 5
|0|= 0
有理数
新知一览
正数和负数
有理数
数轴
同学们,通过这节课的学习, 你有什么收获呢?
谢谢 大家
爱心.诚心.细心.耐心,让家长放心.孩子安心。
1. 判断对错:
(1) 一个数的绝对值等于本身,则该数一定是正数; ( )
(2) 一个数的绝对值等于它的相反数,这个数一定是
负数;
()
(3) 如果两个数的绝对值相等,那么这两个数一定
相等;
()
(4) 如果两个数不相等,那么这两个数的绝对值
一定不等;
()
(5) 有理数的绝对值一定是非负数.
()
2. 化简:
B -10
分析:行驶路线 行驶路程
O
A
0
10
方向 + 距离 方向不同 距离 距离相同
绝对值的定义: 一般地,数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值,记作|a|.
B
O
A
-10
0
10
例:因为点 A 表示10,与原点的距离是 10 个单位长度,
所以|10| = 10.
1.利用数轴,口答下列问题:
|5|=5
–5 –4 –3 –2 –1 0 1 2 3 4 5
| 3.5 | = 3.5 –5 –4 –3 –2 –1 0 1 2 3 4 5
| -3 | = 3
–5 –4 –3 –2 –1 0 1 2 3 4 5
| -3.5 | =3.5 –5 –4 –3 –2 –1 0 1 2 3 4 5
|0|= 0
有理数
新知一览
正数和负数
有理数
数轴
新人教版七年级上1.2.4绝对值(2)课件
5.已知:|x-2|+|y+3|=0,则x= 2 ,y= 3 .
6.任何有理数的绝对值都是( D ) A.正数 B.负数 C.非正数 D.非负数
7.已知|a-1|与|b-4|互为相反数,且c为绝对值最小的有理数, d为有理数中最大的负整数,求a+d+c+b的值. 解:由题意得,|a-1|+|b-4|=0,
1.在数轴上,-3.1在-2.1的 左 边,则它们之间的大小关系 为-3.1 < -2.1 . 2.下列式子不正确的是( B )
5 1 5 2 A.7.1>-9.5 B. < C.3.1>-1.3 D.- >- 12 13 2 5
3.下列说法中不正确的是( B ) A.数轴上两个有理数,绝对值大的离原点远 B.数轴上两个有理数,大的在左边 C.数轴上两个负有理数,大的离原点近 D.数轴上两个正有理数,大的离原点远 2 1 3 4.用“<”把下列各数- ,0, ,- ,0.01连接起来. 3 10000 4 3 2 1 解: < < 0 < 0.01 < 4 3 10000
∴a-1=0,且b-4=0, ∴a=1,b=4, 又c=0,d=-1,
∴原式=1+(-1)+0+4=4
绝对值的拓展应用
例题3
有理数a、b、c在数轴上的位置如图所示,化简 |c-b|+|a-c|+|b-c|.
解析: 由图可知a<0,b>0,c<0且c-b<0,a-c<0,b-c>0. 所以|c-b|+|a-c|+|b-c| =-(c-b)+(c-a)+(b-c) =-c+b+c-a+b-c =-a+2b-c. 点评: 数轴上右边的数比左边的大,大数减小数结果是正数, 绝对值是本身;小数减大数结果是负数,绝对值是它的相反数.
