希望杯数学竞赛五年级培训100题
五年级数学希望杯试题

五年级数学希望杯试题第五届“希望杯”全国数学邀请赛(五年级第1试)1.2007÷=______。
2.对不为零的⾃然数a,b,c ,规定新运算“☆”:☆(a,b ,c)= ,则☆(1,2,3)=______。
3.判断:“⼩明同学把⼀张电影票夹在数学书的51页⾄52页之间”这句话是______的。
(填“正确”或“错误”)4.已知a,b,c是三个连续⾃然数,其中a是偶数。
则a+1,b+2,c+3的积是奇数还是偶数5.某个⾃然数除以2余1,除以3余2,除以4余1,除以5也余1,则这个数最⼩是______。
6.当p和p3+5都是质数时,+5=______.7.下列四个图形是由四个简单图形A、B、C、D(线段和正⽅形)组合(记为*)⽽成。
则图中①~④中表⽰A*D的是______。
(填序号)8.下⾯四幅图形中不是轴对称图形的是______。
(填序号)9.⼩华⽤相同的若⼲个⼩正⽅形摆成⼀个⽴体(如图)。
从上⾯看这个⽴体,看到的图形是图①~③中的______。
(填序号)10.图中内部有阴影的正⽅形共有______个。
11.下图中的阴影部分BCGF是正⽅形,线段FH长18厘⽶,线段AC长24厘⽶,则长⽅形ADHE的周长是______厘⽶。
12.图中的熊猫图案的阴影部分的⾯积是______平⽅厘⽶。
(注:阴影部分均由半圆和正⽅形组成,图中⼀个⼩正⽅形的⾯积是1平⽅厘⽶,π取3.14) 13.⼩红看⼀本故事书,第⼀天看了这本书的⼀半⼜10页,第⼆天看了余下的⼀半⼜10页,第三天看了10页正好看完。
这本故事书共有______页。
14.有⼀副扑克牌中(去掉⼤、⼩王),最少取______张牌就可以保证其中3张牌的点数相同。
15.如图,摩托车⾥程表显⽰的数字表⽰摩托车已经⾏驶了24944千⽶,经过两⼩时后,⾥程表上显⽰的数字从左到右与从右到左的读数相同,若摩托车的时速不超过90千⽶,则摩托车在这两⼩时内的平均速度是______千⽶/时。
05 年级“希望杯”培训题

五年级“希望杯”培训试题1、将20082007 ,20072008 ,20092008 ,20082009 这四个数从小到大排列是:____________________________。
2、计算:1.01•+2.12•+3.23•+4.34•+5.45•+…+9.89•3、计算:1×2+2×4+3×6+…+1005×20104、计算:2009×0.23+34×20.09+4.3×200.95、计算:1×(2×3)÷(3×4)×(4×5)÷(5×6)×……×(2008×2009)÷(2009×2010)6、计算:(12345+23451+34512+45123+51234)÷(1+2+3+4+5)7、计算:1-2-3+4+5-6-7+8+9-……+2004+2005-2006-2007+40178、计算:29292929×88888888÷10101010÷111111119、计算:2008×200920092009-2009×20082008200810、计算:2÷3÷7+4÷6÷14+14÷21÷494÷7÷9+8÷14÷18+28÷49÷6311、以m表示个位及十位数字均为偶数的两位数的个数,以n表示个位十位数字均为奇数的两位数的个数,则m与n之间的大小关系是__________。
12、在两位数中,个位数字与十位数字奇偶性不同的数共有__________个。
13、在三位数中,百位数字是十位数字的2倍,十位数字是个位数字的2倍的数有__________个。
希望杯第1-8届五年级数学试题及答案(WORD版)

第一届小学“希望杯”全国数学邀请赛五年级第1试一、填空题1.计算=_______ .2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点.4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E 赛了场.14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9。
希望杯数学竞赛五年级培训题 2

希望杯数学竞赛五年级培训题231.已知ABCDEF×B=EFABCD,相同的字母表示相同的数字,不同的字母表示不同的数字。
那么ABCDEF的可能情况有_____种。
32.下表中,15位于第4行第2列,2021位于第a行第b列,则a+b= ____ 。
33.四个连续自然数 a,b,c,d依次是3,4,5,6的倍数(倍数大于1), 则 a+b+c+d 最小值是_____。
34.5个连续奇数的乘积是135135,则这5个数中最大的是_____。
35.一个三位自然数abc减去它各个数位上的数字,得到的差是三位数□44,那么a=_____。
36.棱长为4 c m 的密封正方体盒子中,有一个半径为1 c m 的小球,小球可以在盒子里随意移动,盒子也可以任意翻转.小球可以接触到的正方体盒子的内表面面积是_____cm²。
37.被9除所得余数是5的四位数有_____个。
38.用两个8,三个7,一个0可以组成_____个不同的六位数。
39.如图,△ABC被分成四部分,各部分的面积已在图上标出,则△BEF 的面积为_____。
40.电视台打算5天播完10集电视剧(按顺序播完),其中可以有若干天不播,共有______种播出的方法。
41.图中包含*的正方形有____个。
42.如图,长方形ACDF 中,AC=3BC, FD=3FE, 阴影部分的面积为30,△AFG 的面积为_____。
43.如图, AD//EFI/BC,AB//GH//DC. 若平行四边形 BEPH 的面积为4,△PAC的面积为3,则平行四边形 PFDG 的面积为_____。
44.下图是一个正方体的平面展开图,若该正方体相对的两个面上的数相等,则c-a+b=_____。
45.从1到100这100个自然数中至少选出____个数,才能保证其中一定有两个数的和是10的倍数。
46.如图,2根绳子系在一起,现在绳子的某处点火,如果每分钟火燃烧的长度是1,那么烧光这些绳子至少需要_______分钟。
希望杯五年级考前培训 题 含答案 几何模块
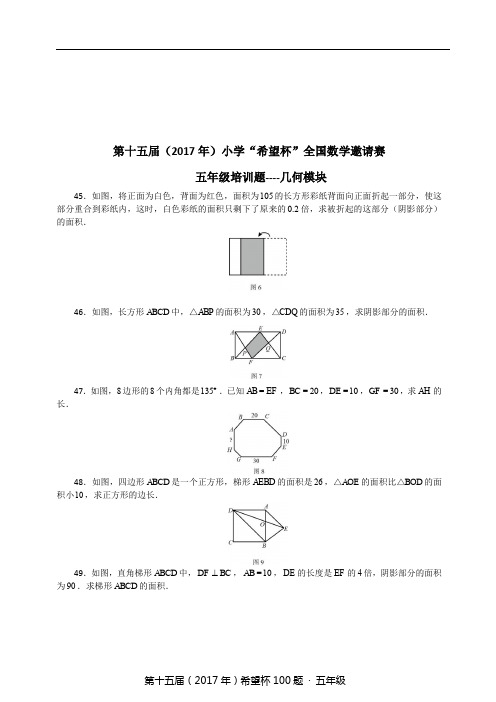
第十五届(2017年)小学“希望杯”全国数学邀请赛五年级培训题----几何模块45.如图,将正面为白色,背面为红色,面积为105的长方形彩纸背面向正面折起一部分,使这部分重合到彩纸内,这时,白色彩纸的面积只剩下了原来的0.2倍,求被折起的这部分(阴影部分)的面积.46.如图,长方形ABCD 中,ABP △的面积为30,CDQ △的面积为35,求阴影部分的面积.47.如图,8边形的8个内角都是135︒.已知AB EF =,20BC =,10DE =,30GF =,求AH 的长.48.如图,四边形ABCD 是一个正方形,梯形AEBD 的面积是26,AOE △的面积比BOD △的面积小10,求正方形的边长.49.如图,直角梯形ABCD 中,DF BC ⊥,10AB =,DE 的长度是EF 的4倍,阴影部分的面积为90.求梯形ABCD 的面积.50.如图,在梯形ABCD中,15△的面积.AB=,5CD=,梯形的面积为80,求AOB51.如图,过平行四边形ABCD内的一点P作边的平行线EF,GH,若平行四边形BEPH的面积为4,平行四边形PFDG的面积为7,求PAC△的面积.52.如图,ABC△,△中,试在AB上取点E,在AC上取点F,D,连接EF,ED,BD,使得AEF △,BCD△,BDEEDF△的面积都相等(说出一种方法即可,但要证明其正确性).53.如图(a),边长分别为13,5的两个正方形叠故在一起.两个正方形内部的明影部分的面积差为M.如图(b)边长分别为15,9的两个正方形叠放在一起,两个正方形内部的阴影部分的面积差为N.试比较M与N的大小,55.(程新林)张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD EF),如图所示.若DE的长为10m,则梯形场地CDEF的最大面积是多少?56.如图,ABCD是正方形,AEGD,EFHG,FBCH都是长方形,若图中所有长方形(含正方形)的周长之和为190,5EF=,求正方形ABCD的面积.57.用2017个等腰直角三角形能不能拼成一个正方形?请说明理由.(注:等腰直來三角形不要求一样大).58.一只乌鸦从其鸟巢飞出,飞向其巢北10千米东7千米的A地,在A地它发现有一个稻草人,所以就转向巢北4千米东5千米的B地飞去,在B地吃了一些谷物后立即返巢,其所飞的途径构成了一个三角形,这个三角形的面积为多少平方千米?59.如图是一个正方体纸盒的展开图,当折叠成纸盒时,与点1重合的点的编号有哪些?60.一组积木组成的图形,从正面看是,从侧面看是,则(1)这组积木最少是用多少块正方体积木摆出来的?(2)这组积木最多是用多少块正方体积木摆出来的?五年级培训题----几何模块 答案解析45.()10510.2242⨯-÷=.46.解法1 如图,连接EF ,根据三角形等底等高面积相等,得ABF BEF S S ∆∆=,所以ABP PEF S S ∆∆=,同理FED ECD S S ∆∆=,所以EFQ CDQ S S ∆∆=,故四边形PEQF 的面积等于PEF EFQ ABP CDQ S S S S ∆∆∆∆++=,即阴影部分面积是303565+=.解法2 如图,连接EF ,在四边形ABFE 中,由蝴蝶模型,得30PEF ABP S S ∆∆==,同理,在四边形EFCD 中,由蝴蝶模型,得35CDQ EFQ S S ∆∆==,故四边形PEQF 的面积等于303565PEF EFQ S S ∆∆++==,即阴影部分面积是65.47.如图,把8边形补成一个矩形,那么四个角上的三角形都是等腰直角三角形,即AI BI =,CJ DJ =,EK FK =,GL HL =,又因为AB EF =,所以AIB △和EKF △完全一样,因此AI BI EK FK===,从而,矩形长与宽的差是K L L I I J J K --++-==201B C D E --===,即10LG GF FK IA AH HL ++---=,所以10GF AH -=,故301020AH -==.48.因为AOE △的面积比BOD △的面积小10,所以ABE △的面积比ABD △的面积小10.因此,ABD △的面积为()2610218+÷=,则正方形的面积为18236⨯=,又3666⨯=,故正方形的边长为6.49.EF 的长为()10412÷+=,DE 的长为248⨯=,所以,BF 的长为()90210215⨯÷+=,因此,ACD △的面积为1510275⨯÷=,ADE △的面积为158260⨯÷=,CDE △的面积为756015-=,从面,CF 的长为1528 3.75⨯÷=,故梯形ABCD 的面积为()1515 3.75102168.75++⨯÷=.50.由1553÷=,得AB 的长是CD 的3倍,所以AO 的长是OC 的3倍,因此AOD △的面积是COD △面积的3倍,同理AOB △的面积是AOD △面积的3倍,又AOD △与BOC △的面积相等.所以,COD △的面积为()80133335÷+++⨯=,故AOB △的面积为53345⨯⨯=.51.设四边形AEPG 的面积为1S ,四边形PHCF 的面积为2S .则PAC △的面积比ABD △的面积为()12121211147474 1.5222S S S S S S +++----⨯+++=.52.(1)在AC上取D点,使得14DC AC=,连接BD;(2)在AB上取E点,使得13BE AB=,连接DE;(3)取AD中点F,连接EF,AEF△,EDF△,BDE△,BCD△的面积相等.说明因为14DC AC=,所以BCD△的面积14ABC△=的面积,又因为13BE AB=,所以BDE△的面积13ABD△=的面积11134ABC⎛⎫⨯-⎪⎝⎭△=的面积14ABC△=的面积.这样,AED△的面积ABC△=的面积的一半.又F为AD的中点,所以AEF△和EDF△的面积都等于ABC△面积的14,故AEF△,EDF△,BDE△和BCD△的面积都相等,上述方法正确.53.在图(a)中,如果两个正方形的重叠部分的面积为0,则M即为两个正方形的面积之差;如果重叠部分面积不为0,则相当于被减数和减数都减少了同样的量,其差不变.故13135516925144M⨯-⨯-===.同理15159922581144N⨯-⨯-===,所以M N=.。
2018年-第16届希望杯考前训练100题-五年级

2018年-第16届希望杯考前训练100题-五年级第16届希望杯考前训练100题学前知识点梳理“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1、整数的四则运算,运算定律,简便运算,等差数列求和。
2、基本图形,图形的拼组合(分、合、移、补),图形的变换,折叠与展开。
3、角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4、整除概念,数的整除特征,带余数除法,平均数。
5、小数意义和性质,分数的初步认识(不要求运算)。
6、应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
7、几何计数(数图形),找规律,归纳,统计,可能性。
8、数谜,分析与推理,数位,十进制表示法。
9、生活数学(钟表、时间、人民币、位置与方向、长度、质量的单位)。
考前100题选讲1.计算:1.1+1.91+1.991+……+20189 1.99个991。
2.计算:1+2+3+…+2016+2017+2016+…+3+2+1。
3.计算:2015.2015+2016.2016+20172017+2018.2018+1934.1934。
4.已知a=20130.125个00000,b=20170.8个00000。
求a ×b+a ÷b 。
5.定义:a ⊕b=a ×b 一(a+b),求(3⊕4)⊕5。
6.定义:a ⊕b=a ×b.c ◎d=d ×d ×d ×…×d (c 个d 相乘),求(5⊕8)⊕(3◎7)。
7.定义a △b=a ×b 1个00000+b ,a 口b=a ×10+b (其中,a ,b 都是自然数),求2018口(123△4)8.观察下列数表的规律,求2018是第几行的第几个数?9.观察下列数的规律,求第2018个数。
1,2018,2017,1,2016,2015,1,…10.根据下列算式的规律,求第2018个算式的和。
第十届小学“希望杯”全国数学邀请赛五年级试题及答案
第十届小学“希望杯”全国数学邀请赛五年级第1试2012年03月11日星期日1. 计算:1.2×67+6.7×88=2. 计算:21.49+52.37-0.4+5.51-11.37-6.6=3. 用1,2,3,4,5和+,-,×,÷组合成一个算式(不使用括号),计算结果最大是()。
4. 一件商品,对原价打八折和打六折的售价相差4.8元,那么这件商品的原价是()元。
5. 将252块巧克力,294盒饼干,336袋牛奶分成相同的份数,并且都没有余数,那么最多可以分成()份。
6. 若8只羊一星期要吃168千克饲料,一头牛的食量是一只羊的食量的2.8倍,那么,200只羊和180头牛一个月(按30天计)要吃()千克饲料。
7. 图1中,阴影面积最大的图形是(),阴影面积最小的图形是()。
(填序号)、8.一个两位数,将它的十位数字和个位数字对调,得到的数比原来的数大18,这样的两位数有()个。
9.如图2,如果小数的愿望能够实现,那么它的身高平均每年要增长到上一年的()倍。
10.两个不同的三位数被13除,若得到相同的余数,那么,这两个三位数的和最大是(),他们的差最大是()。
11.如图3,从左到右,在每列各选出一个框,组成算式(如:5×2+3),则有()种不同的结果。
12.A、B两地间有一条公路。
甲车从A驶到B,需60分钟;乙车从B驶到A,需120分钟。
若甲、乙两车分别从A、B两地同时出发,则在出发后()分钟相遇。
13.学校购买了数量相同的课桌和椅子,用小货车装运,每车装17张课桌和13把椅子。
装了若干车后,课桌剩9张,椅子剩77把。
那么,此时已经装了()车;按1桌1椅为1套,那么学校购买了()套课桌和椅子。
14.如图4,甲、乙、丙三个大小相同的杯子在桌面上一次排列,其中甲杯中盛满水,乙和丙是空杯。
现把水全部倒入相邻(左或右)的空杯中,那么,经过55次倒水后,有水的是()杯。
2017年希望杯五年级考前培训100题(含答案) - 行程模块
80.有 A , B , C 三辆车同时从同一地点出发,沿同一条公路追赶前面的一个骑车人,这三辆车 分别用 6 分钟、10 分钟、12 分钟追上骑车人.现在知道 A 车每小时行 24 千米, B 车每小时行 20 千米, 那么, C 车每小时行多少千米?
81.某人沿着电车道旁的便道以 4.5 千米每小时的速度步行,每 14.4 分钟有一辆电车迎面开过, 每 24 分钟有一辆电车从后面追过来,如果电车按相等的时间间隔以同一速度不停的往返运行,问:电 车发生间隔是多少分?
60 26 24 = 120 2 = 16 (秒),若相背跑,则 400 80 3 2 = 64 (秒),若同向 跑 , 熊 二 在 前 , 熊 大 在 后 , 则 80 3 2 = 80 ( 秒 ) , 若 同 向 跑 , 熊 大 在 前 , 熊 二 在 后 , 则
400 80 3 2 = 320 (秒).
86.设甲的时速为 x 千米,则乙的时速为 2 x 10 千米.出发时甲在前,乙在后,则有两种情况:
第十五届(2017 年)希望杯 100 题 · 五年级
(1)甲、乙的距离由 20 千米缩短到了 15 千米; (2)乙追上甲以后,超过加 15 千米. 对于情况(1),有 20 x 2 x 10 = 15 ,解得 x = 15 .则 2x 10 = 20 ,符合题意; 对于情况(2),有 2 x 10 20 x = 15 ,解得 x = 45 .则 出发时若乙在前,甲在后.则也有两种情况; (3)甲、乙的距离由 20 千米缩短到了 15 千米; (4)甲追上乙以后,超过加 15 千米. 对于情况(3)有 20 2 x 10 x = 15 ,解得 x = 5 .则 2 x 10 = 0 ,符合题意; 对于情况(4) x 20 2 x 10 方程无正数解. 综上,甲,乙二人的时速分别为: 15 千米, 20 千米(甲在前,乙在后);或 5 千米, 0 千米(乙 在前,甲在后).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
希望杯数学竞赛五年级培训100题1.对于任意的两个自然数 a 和 b, 规定新运算*:a*b=a(a+1)(a+2)…(a+b-1)。
如果(x*3)*2=3660, 那么 x= ()。
2.3+33+333+..+33..3的末三位数字是()。
2007个33.我们知道,2013,2014,2015的因数个数相同,那么具有这样性质(因数个数相同)的三个连续自然数 n,n+1,n+2 中,n 最小是()。
4.把2~11这10个数填到下图的10个方格中,每格填一个数,要求3个2×2的正方形中的4个数之和相等.那么,这个和最小是()。
5.3333×5555+6×4444×2222=()。
6.同学们参加收集废电池的公益活动,甲组同学平均每人收集17个,乙组同学平均每人收集20个,丙组同学平均每人收集21个。
若这三个小组共收集了233个废旧电池,则这三个小组共有学()人。
7.甲、乙、丙、丁四种商品的单价分别为2,3,5,7元,现从中选购6件,共花费36元,其中至少包含3种商品,则购买了________件丁商品。
8.旅游团的游客乘坐汽车出游,要求每辆汽车坐的人数相等。
如果每辆汽车乘坐30人,那么有一人未能上车;如果少一辆汽车,那么所有游客正好能平均分到各辆汽车上。
已知每辆汽车最多容纳40人,那么游客共有()人。
9.在12,22,32,…,952这95个数中,十位数字是奇数的数共有()个。
10.甲乙两车从同一地点同时出发,沿着同一条公路追赶前面的一个骑车人。
甲车追上骑车人用6分钟,乙车追上骑车人用10分钟。
已知甲车速度是24千米/时,乙车速度是20千米/时。
那么,两车出发时距离骑车人()千米。
11.两列火车分别从两座城市同时出发,相向而行,3.3小时后在途中相遇。
如果甲车提前24分钟出发,那么乙车出发3小时后两车还需行14千米才能相遇;如果乙车提前36分钟出发,那么甲车出发3小时后两车还需行9千米才能相遇。
两座城市相距()千米。
12.对于自然数n, 如果能找到非零自然数 a 和 b, 使得 n=a+b+a×b, 那么n 就称为"好数"。
例如3=1+1+1×1,所以3是“好数”。
在1~100 这100个自然数中,有()个“好数”。
13.边长是10厘米的正方形纸片,正中间挖了一个正方形的洞,成为一个宽1厘米的方框。
把五个这样的方框放在桌面上,如图。
桌面上被这些方框盖住的面积是()平方厘米。
14.有个六位数11□□11,它能被17和19整除,“□□”里的两位数是()。
15.两个互质的合数,它们的最小公倍数是126,则它们的和是()。
16.有些三位数,各位数字之积为质数,这样的三位数最小是(),最大是()。
17.三个合数A,B,C两两互质,且A×BxC=11011×28, 那么 A+B+C 的最大值为()。
18.七位数2013□□□能同时被2,3,4,5,6,7,8,9整除,那么它的最后三位数是()。
19.在小于5000的自然数中,能被11整除,并且数字和为13的数,共有()个。
20.有一串数,第一个数是1,第二个数是3,从第三个数起,每个数恰好是前两个数之和的2倍:1,3,8,22,60,164,448,………在这串数中,第2000个数除以9的余数是()。
21.一条直线上有2021个点,把所有线段的中点标出,至少有()个互不重合的中点。
22.如图,给 A,B,C,D,E 这五部分涂色,要求相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色,有四种不同的颜色供选择。
那么,这幅图一共有()种不同的涂色方法。
23.从1~1999的1999个自然数中,最多可以取出()个数,使其中任意两个数的差不等于4。
24.300只猴子围成一圈,准备选出一只猴子为猴王。
规则如下:先把这些猴子按顺时针编号,从1到300号,从300号开始逆时针操作:留下300号,淘汰299号,留下298号,淘汰297号,……一直进行下去,直到剩余一只猴子为止,剩下的这只猴子成为猴王。
猴王的编号是()。
25.在一次巴西和英格兰的足球比赛中,巴西始终领先,最多领先5个球,而且曾经出现过领先5球的情况,最后以7:5结束比赛。
那么这次比赛中共有()种不同的进球情况。
26.如图,有9张同样大小的圆形纸片,其中标有数字“1”的有1张,标有数字"2”的有2张,标有数字“3"的有3张,标有数字“4”的也有3张.把这9张圆形纸片放置在一起,但标有相同数字的纸片不许靠在一起.(1)如果 M 位置上放置标有数字“3”的纸片,一共有______种不同的放置方法;(2)如果 M 位置上放置标有数字“2”的纸片,一共有_____种不同的放置方法27.在平面上有7个点,其中任意3个点都不在同一条直线上.如果在这7个点之间连结18条线段,那么这些线段最多能构成_____个三角形.计算:128×0.125-0.625×20+1.25×5.2 =___.28.填上适当的数,使算式成立. [75+50÷(_ _-3.3)]×1.9=199.5 30.对于数 a 和 b, 规定“☆”运算: a☆b=2÷a+3÷b.请比较:6☆7____7☆6. (填“>”、“<”或“=”)31.已知ABCDEF×B=EFABCD,相同的字母表示相同的数字,不同的字母表示不同的数字。
那么ABCDEF的可能情况有_____种。
32.下表中,15位于第4行第2列,2021位于第a行第b列,则a+b= ____ 。
33.四个连续自然数 a,b,c,d依次是3,4,5,6的倍数(倍数大于1), 则 a+b+c+d 最小值是_____。
34.5个连续奇数的乘积是135135,则这5个数中最大的是_____。
35.一个三位自然数abc减去它各个数位上的数字,得到的差是三位数□44,那么a=_____。
36.棱长为4 c m 的密封正方体盒子中,有一个半径为1 c m 的小球,小球可以在盒子里随意移动,盒子也可以任意翻转.小球可以接触到的正方体盒子的内表面面积是_____cm²。
37.被9除所得余数是5的四位数有_____个。
38.用两个8,三个7,一个0可以组成_____个不同的六位数。
39.如图,△ABC被分成四部分,各部分的面积已在图上标出,则△BEF 的面积为_____。
40.电视台打算5天播完10集电视剧(按顺序播完),其中可以有若干天不播,共有______种播出的方法。
41.图中包含*的正方形有____个。
42.如图,长方形ACDF 中,AC=3BC, FD=3FE, 阴影部分的面积为30,△AFG 的面积为_____。
43.如图, AD//EFI/BC,AB//GH//DC. 若平行四边形 BEPH 的面积为4,△PAC的面积为3,则平行四边形 PFDG 的面积为_____。
44.下图是一个正方体的平面展开图,若该正方体相对的两个面上的数相等,则c-a+b=_____。
45.从1到100这100个自然数中至少选出____个数,才能保证其中一定有两个数的和是10的倍数。
46.如图,2根绳子系在一起,现在绳子的某处点火,如果每分钟火燃烧的长度是1,那么烧光这些绳子至少需要_______分钟。
47.某快递公司已囤积部分快件,但仍有快件不断运来,公司决定用快递专车送货.若用9辆车送货,12小时可以送完;若用8辆车送货,15小时可以送完.如果先用8辆车送货,3小时后再增加_____辆车,再过4小时可以送完。
48.李叔叔加工一批产品,他每加工出一件正品,得报酬2.5元;每加工出一件次品,扣款20元。
一天,他加工的正品数量是次品的49倍,共得到205元的报酬。
那么他这天加工出_____件次品。
49.一种商品20元,甲店:“买五赠一”,乙店:“满100减15",丙店:"打八八折”。
如果只从经济方面考虑,买8件这种商品,应选择_______店。
灰太狼的体重比喜羊羊的体重的3倍少2kg。
那么喜羊羊的体重的9倍比灰太狼的体重的3倍还多 ______kg。
51.东东从家到学校上课,先以每分钟70米的速度走了2分钟,发现这样走下去将迟到3分钟,于是她提高速度,以每分钟140米的速度前进,结果提前2分钟到校。
东东家离学校_______米。
52.将1~9这9个数字分别填入下面的各个方框内,每个数字只能用一次,则计算结果最大是____。
53.一个三位数各位数字的乘积是18,满足条件的所有三位数的总和是________。
54.有四个不同的自然数,它们的和是1991.如果要求这四个数的最大公因数尽可能大,那么这四个数中最大的数是_____。
55.甲乙两人分别从 A、B 两地同时出发,相向而行,在距 A 地8千米处相遇.相遇后他们继续前行,甲到达B 地,乙到达 A 地后都立即返回,第二次相遇点距A 地4千米. A、B 两地相距____千米.56.东东有9张卡片,其中4张卡片上写有数字2,2张卡片上写有数字3,3张卡片上写有数字5.从这些卡片中任意取出若干张,并计算卡片上数字的乘积(可以只取1张,也可以9张都取),一共可以得到___个不同的乘积.57.如图,圆圈内分别填有1~7这7个数字.计算每个三角形顶点上的三个数字之和,再把得到的6个和相加,最后得64,那么中间圆圈内填入的数字是_______.58.下图是两个相同的直角梯形重叠在一起,阴影部分的面积是 __.59.10名工人给1250个魔法球涂色,每人每6分钟可以给5个魔法球涂色,那么他们涂完所有魔法球最少用_______分钟.60.如图,沿着图中的线段从A 点走到B 点,每个点最多只能经过一次,那么一共有______条不同的路线.61.自然数M 乘13的积的末三位数是123, M 最小是____。
62.的乘积由9个不同数字组成,这9个数字中不包含数字______。
63.一个正方体被切成24个完全相同的小长方体(如图所示),这些小长方体的表面积之和为162平方厘米.原正方体的体积是_____立方厘米.64.64.两个不同两位数的乘积是完全平方数,它们的和最大是_____.65.和为1998的两个自然数的最大公因数是6.这样的两个自然数共有 _ 种情况.66.一个七位数,从左到右,相邻的两个数字依次相加,得到的和分别是9、7、9、2、8、11.这个七位数是__ __.67.一个长方体药盒的展开图如图所示,药盒的长比宽多4厘米,则这个药盒的体积是_______立方厘米.68.一条河流有 A、B 两港, B 港在A 港下游100千米处.甲船从A 港、乙船从B 港同时出发,相向而行.甲船到达 B 港、乙船到达A 港后,都立即按原来路线返航.如果水速为2米/秒,且两船在静水中的速度相同,两船两次相遇的地点相距20千米,那么两船在静水中的速度是____米/秒.69.如图,正六边形ABCDEF的面积是54, AP=2PF,CQ=2BQ, 则阴影四边形 CEPQ 的面积是_______.70.如图,四边形ABCD 是矩形, E,F 分别是AB,BC 上的点,且AE= 31AB,CF=41BC ,AF 与 C E 相交于 G . 若矩形ABCD 的面积为120,则△AEG 与△CGF 的面积之和为 ___。
