北京初中数学习题书
垂径定理-初中数学习题集含答案
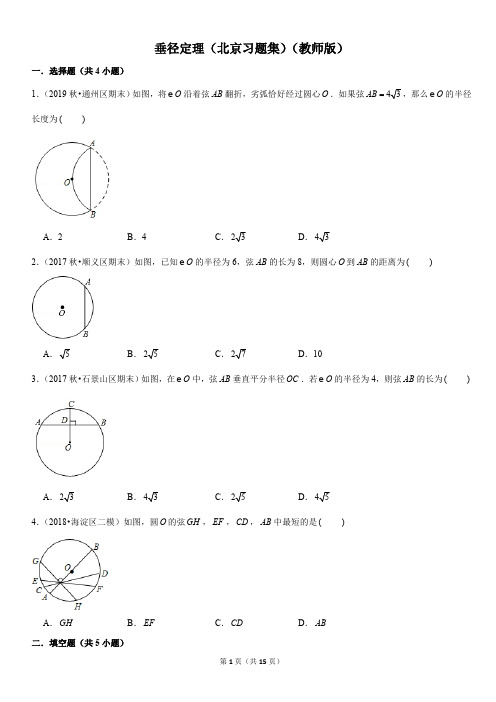
一.选择题(共 4 小题) 1.(2019 秋•通州区期末)如图,将 e O 沿着弦 AB 翻折,劣弧恰好经过圆心 O .如果弦 AB 4 3 ,那么 e O 的半径 长度为 ( )
A.2
B.4
C. 2 3
D. 4 3
2.(2017 秋•顺义区期末)如图,已知 e O 的半径为 6,弦 AB 的长为 8,则圆心 O 到 AB 的距离为 ( )
15.(2019 秋•西城区校级期中)已知: e O 的半径为 25cm ,弦 AB 40cm ,弦 CD 48cm , AB / /CD .求这两条平 行弦 AB , CD 之间的距离.
第 3 页(共 15 页)
垂径定理(北京习题集)(教师版)
一.选择题(共 4 小题)
参考答案与试题解析
1.(2019 秋•通州区期末)如图,将 e O 沿着弦 AB 翻折,劣弧恰好经过圆心 O .如果弦 AB 4 3 ,那么 e O 的半径
键.
第 4 页(共 15 页)
2.(2017 秋•顺义区期末)如图,已知 e O 的半径为 6,弦 AB 的长为 8,则圆心 O 到 AB 的距离为 ( )
A. 5
B. 2 5
C. 2 7
D.10
【分析】连接 OA ,作 OE AB 于 E .根据垂径定理可得 AE 4 ,利用勾股定理可以求出 OE 的长度. 【解答】解:如图,连接 OA ,作 OE AB 于 E . Q OE AB , AB 8 AE EB 1 AB 4 ,
13.(2019 秋•东城区校级期中)如图,点 P 是 e O 内一点, (1)过点 P 画弦 AB ,使点 P 是 AB 的中点,并简述作图过程. (2)连接 OP 并延长交 e O 于点 C ,若 AB 8 , PC 2 ,求 e O 的半径.
算术平均数-初中数学习题集含答案

算术平均数(北京习题集)(教师版)一.选择题(共6小题)1.(2017秋•昌平区校级月考)某班有48人,在一次数学测验中,全班平均分为81分,已知不及格人数为6人,他们的平均分为46分,则及格学生的平均分是 A .78分B .86分C .80分D .82分2.(2016秋•昌平区校级月考)8名学生在一次数学测试中的成绩分别为80,81,80,69,74,78,,81.这组学生成绩的平均分为77分,则的值为 A .73B .74C .75D .763.(2014•丰台区二模)某班第一小组6名女生在测仰卧起坐时,记录下她们的成绩(单位:个分),48,46,50,50,49.这组数据的平均数是 A .49B .48C .47D .464.(2014春•海淀区期末)某汽车从甲地以速度匀速行驶至乙地后,又从乙地以速度匀速返回甲地,则汽车在整个行驶过程中的平均速度为 A . B . C .D .5.(2012•密云县二模)一组数据1,,2,5,6,5的平均数和极差分别是 A .7和3B .3和7C .5和7D .3和56.(2011•门头沟区模拟)如果一组数据2,4,,6的平均数是5,那么等于 A .3B .4C .5D .8二.填空题(共3小题)7.(2017春•西城区校级期中)若一个三角形的三条边满足:一边等于其他两边的平均数,我们称这个三角形为“平均数三角形”.(1)下列各组数分别是三角形的三条边长: ①5,7,5; ②3,3,3;③6,8,4; ④12.其中能构成“平均数三角形”的是 ;(填写序号)(2)已知的三条边长分别为,,,且.若既是“平均数三角形”,又是直角三角形,则的值为 .8.(2015春•丰台区期末)如果数据2,5,,8的平均数是4,那么 .()x x ()/:45()1v 2v ()1212v v v v +1212v v v v +122v v +12122v v v v +1-()x x ()ABC ∆a b c a b c <<ABC ∆abx x =9.(2014春•门头沟区期末)我市六月份连续五天的日最高气温(单位:分别为35,33,37,34,39,则我市这五天的日最高气温的平均值为 .三.解答题(共2小题)10.(2007春•北京期中)已知10个数据的平均数是15,若对各个数据分别加上以下各数: 1,0,,3,5,,2,8,5,. 求所得新数据的平均数.11.(2003•西城区模拟)宏欣机械厂生产某种型号鼓风机,一月份至六月份的产量如下:月份 一 二 三 四 五 六 产量(单位:台)505148505249(1)求上半年鼓风机月产量的平均数、中位数;(2)由于改进了生产技术,计划八月份生产鼓风机72台,与上半年月产量平均数相比,七月,八月鼓风机生产量平均每月的增长率是多少?C)︒C ︒2-3-4-算术平均数(北京习题集)(教师版)参考答案与试题解析一.选择题(共6小题)1.(2017秋•昌平区校级月考)某班有48人,在一次数学测验中,全班平均分为81分,已知不及格人数为6人,他们的平均分为46分,则及格学生的平均分是 A .78分B .86分C .80分D .82分【分析】利用平均数的定义先求出全班学生的总分和不及格人数的总分,进而求出及格人数的总分,再除以及格的人数即可.【解答】解:全班学生的总分为:(分, 不及格人数的总分为:(分, 及格人数的总分为:(分, 则及格学生的平均分为(分; 故选:.【点评】此题考查了平均数,正确理解平均数的概念是解题的关键.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数.2.(2016秋•昌平区校级月考)8名学生在一次数学测试中的成绩分别为80,81,80,69,74,78,,81.这组学生成绩的平均分为77分,则的值为 A .73B .74C .75D .76【分析】根据算术平均数的计算公式列出算式,求出的值即可. 【解答】解:名学生的平均成绩是77, ,解得:. 则的值为74. 故选:.【点评】此题考查了算术平均数,掌握算术平均数的计算公式是本题的关键,是一道基础题.3.(2014•丰台区二模)某班第一小组6名女生在测仰卧起坐时,记录下她们的成绩(单位:个分),48,46,50,50,49.这组数据的平均数是 ()81483888⨯=)466276⨯=)38882763612-=)361286486=-)B x x ()x 8Q (80818069747881)877x ∴+++++++÷=74x =x B /:45()A .49B .48C .47D .46【分析】求得数据的和,然后除以数据的个数即可求得其平均数. 【解答】解:平均数为.故选:.【点评】本题考查的是样本平均数的求法.熟记公式是解决本题的关键.4.(2014春•海淀区期末)某汽车从甲地以速度匀速行驶至乙地后,又从乙地以速度匀速返回甲地,则汽车在整个行驶过程中的平均速度为 A . B . C .D .【分析】由题意知,设两地距离为,从甲地行驶至乙地的时间为,从乙地返回甲地的时间为,则关键时间的计算公式求得及,再关键平均速度的计算公式即可求得平均速度.【解答】解:设两地距离为,从甲地行驶至乙地的时间为,从乙地返回甲地的时间为, 则有,; 平均速度; 故选:.【点评】本题考查了平均数实际中的运用.平均速度总路程总时间.5.(2012•密云县二模)一组数据1,,2,5,6,5的平均数和极差分别是 A .7和3B .3和7C .5和7D .3和5【分析】根据平均数和极差的概念直接求解即可. 【解答】解:平均数; 极差. 故选:.【点评】考查了平均数和极差的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据的最大值和最小值的差即是极差.6.(2011•门头沟区模拟)如果一组数据2,4,,6的平均数是5,那么等于 A .3B .4C .5D .81(454846505049)486=+++++=B 1v 2v ()1212v v v v +1212v v v v +122v v +12122v v v v +S 1T 2T 1T 2T S 1T 2T 11S T v =22S T v =∴12121212222v v S SS S T T v v v v ===+++D =÷1-()(112565)63=-++++÷=6(1)7=--=B x x ()【分析】利用平均数的定义,列出方程即可求解.【解答】解:由题意知2,4,,6的平均数是5,则 , .故选:.【点评】本题考查了平均数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数. 二.填空题(共3小题)7.(2017春•西城区校级期中)若一个三角形的三条边满足:一边等于其他两边的平均数,我们称这个三角形为“平均数三角形”.(1)下列各组数分别是三角形的三条边长: ①5,7,5; ②3,3,3;③6,8,4; ④12.其中能构成“平均数三角形”的是 ②③ ;(填写序号)(2)已知的三条边长分别为,,,且.若既是“平均数三角形”,又是直角三角形,则的值为 .【分析】(1)根据平均数三角形的定义验证即可得问题答案; (2)由是“平均数三角形”,可得,又是直角三角形由勾股定理可得:,进而可求出的值.【解答】解:(1)由“平均数三角形”的概念可知②中满足条件;③中满足条件;其他不符合题意,故答案为:②③(2)是“平均数三角形”,且, ①, 是直角三角形,②,由①②可知:, 故答案为:. 【点评】本题考查了勾股定理的运用以及对新定义题目的解答,是中考常见题型,此类题目难度不大,解题的关键是正确理解题目给出的:“新定义”.8.(2015春•丰台区期末)如果数据2,5,,8的平均数是4,那么 1 .1(246)54x +++=x 1(246)54x +++=8x ∴=D ABC ∆a b c a b c <<ABC ∆abABC ∆2a c b +=222a b c +=ab3332+=8462+=ABC ∆Q a b c <<2a cb +∴=ABC ∆Q 222a b c ∴+=34a b =34x x =【分析】根据平均数的公式列出方程求出的值. 【解答】解:由题意得 ,解得:. 故答案为:1.【点评】本题考查了平均数的知识,掌握公式是解答本题的关键.9.(2014春•门头沟区期末)我市六月份连续五天的日最高气温(单位:分别为35,33,37,34,39,则我市这五天的日最高气温的平均值为 35.6 .【分析】平均数是指在一组数据中所有数据之和再除以数据的个数.本题可把所有的气温加起来再除以5即可.【解答】解:依题意得:平均气温. 故答案为:35.6.【点评】本题考查的是平均数的求法.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数.三.解答题(共2小题)10.(2007春•北京期中)已知10个数据的平均数是15,若对各个数据分别加上以下各数: 1,0,,3,5,,2,8,5,. 求所得新数据的平均数.【分析】计算出所有数据的和后,除以10即为新数据的平均数.【解答】解:所有数据的和为, 所以新数据的平均数.【点评】本题利用了平均数的概念求解.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数.11.(2003•西城区模拟)宏欣机械厂生产某种型号鼓风机,一月份至六月份的产量如下:月份 一 二 三 四 五 六 产量(单位:台)505148505249(1)求上半年鼓风机月产量的平均数、中位数;(2)由于改进了生产技术,计划八月份生产鼓风机72台,与上半年月产量平均数相比,七月,八月鼓风机生产量x 25844x +++=⨯1x =C)︒C ︒(3533373439)535.6C ︒=++++÷=2-3-4-1510[10(2)35(3)285(4)]165⨯+++-+++-++++-=1651016.5=÷=平均每月的增长率是多少?【分析】(1)只要运用求平均数公式:,即可求出上半年的月产量的平均数;求中位数时,可将所有数据从小到大进行排列,然后求出第三和第四位的平均数即可得出本组数据的中位数; (2)本题为平均增长率问题.一般形式为,为起始时间的有关数量,为终止时间的有关数量.据此可列出方程进行求解.【解答】解:(1)上半年鼓风机月产量的平均数为50(台,中位数为50(台(2)设七月、八月鼓风机生产量平均每月的增长率为 依题意,得: 整理,得: 解得:,(舍答:七月、八月鼓风机生产量平均每月的增长率是.【点评】本题考查了样本平均数和中位数的求法以及平均增长率问题的应用.12nx x x x n++⋯+=2(1)a x b +=a b ))x 250(1)72x +=2(1) 1.44x +=10.2x =2 2.2x =-)20%。
根与系数的关系-初中数学习题集含答案

(2)若方程有一个根是 0,求此时方程的另一个根. 12.(2019•怀柔区模拟)已知关于 x 的一元二次方程 x2 (2k 1)x k 2 2k 0 有两个实数根 x1 , x2 . (1)求实数 k 的取值范围. (2)是否存在实数 k ,使得 x1x2 x12 x22 16 成立?若存在,请求出 k 的值;若不存在,请说明理由.
C. x1 1 , x2 4 D. x1 2 , x2 3
二.填空题(共 6 小题)
4.(2018 秋•海淀区校级期中)对于方程 x2 px 4 0 ①与方程 x2 5x q 0 ②,已知方程②的一个根比方程①的
较大根大 2,方程②的另一个根比方程①的较小根小 2,则 q .
第 2 页(共 8 页)
根与系数的关系(北京习题集)(教师版)
参考答案与试题解析
一.选择题(共 3 小题)
1.(2018 秋•海淀区校级期中)已知 xy 1 ,且有 3x2 2018x 9 0 及 9 y2 2018y 3 0 ,则 xy 的值为 ( ) x2 y2
A. 1 2018
则 c 1 (4) 4 ,
则原方程为 x2 3x 4 0 , 整理,得
难点.
2.(2017•西城区校级自主招生) x1 , x2 是方程 x2 x k 0 的两个实根,若恰 x12 x1x2 x22 2k 2 成立, k 的值为 (
)
A. 1
B. 1 或 1 2
C. 1 2
D. 1 或 1 2
【分析】根据一元二次方程的根与系数的关系得到,两根之和与两根之积,再根据 x12 x1x2 x22 (x1 x2 )2 x1x2 代
根与系数的关系(北京习题集)(教师版)
配方法的应用-初中数学习题集含答案

14.(2017 秋•西城区校级期中)若 a2 b2 2a 6b 10 0 ,则 a b . 15.(2016 秋•海淀区校级期中)代数式 (2 x)(6 x) 有最 值是 .
第 2 页(共 7 页)
配方法的应用(北京习题集)(教师版)
参考答案与试题解析
解得: x 3 , y 2 ,
则 yx (2)3 8 . 故选: B . 【点评】考查了配方法的应用和非负数的性质.配方法的理论依据是公式 a2 2ab b2 (a b)2 .
3.(2018 春•房山区期中)已知 a 、 b 满足等式 x a2 b2 6 , y 2(a 3b 2) ,则 x 、 y 的大小关系是 ( )
A. (x 2)2 5
B. (x 2)2 3
C. (x 2)2 5
D. (x 2)2 3
A.8
B. 8
C.9
D. 1 9
3.(2018 春•房山区期中)已知 a 、 b 满足等式 x a2 b2 6 , y 2(a 3b 2) ,则 x 、 y 的大小关系是 ( )
A. x y
B. x„ y
C. x y
D. x… y
4.(2017 春•昌平区校级期中)无论 x 、 y 取何值, x2 y2 2x 12 y 37 的值都是 ( )
A. 2(a 1)2 3
B. (a 1)2 3 2
C. 2(a 1)2 1
D. 2(a 1)2 3
7.(2015•延庆县一模)若把代数式 x2 2x 3 化为 (x m)2 k 形式,其中 m , k 为常数,结果为 ( )
A. (x 1)2 4
B. (x 1)2 2
C. (x 1)2 4
配方法的应用(北京习题集)(教师版)
图形的剪拼-初中数学习题集含答案

的线段 AB , CD 分割为四部分,将这四部分图形分别标号,以 CD 为一边画大正方形,把这四部分图形分别移入 正方形内,就解决问题. 请你参考小明的画法,完成下列问题: (1)如图 3,边长分别为 a , b 的两个正方形被两条互相垂直的线段 AB , CD 分割为四部分图形,现将这四部分图 形拼接成一个大正方形,请画出拼接示意图 (2)如图 4,一个八角形纸板有个个角都是直角,所有的边都相等,将这个纸板沿虚线分割为八部分,再拼接成一 个正方形,如图 5 所示,画出拼接示意图;若拼接后的正方形的面积为 8 4 2 ,则八角形纸板的边长为 .
CF BC 2 6,
CF 3 CF 6 , 把 ABE 平移到 CDM ,把 CBF 平移到 MEN ,可得正方形 CFNM . 如图③中,同法可得 CG 6 ,把 CDG 平移到 BAM ,把 CBE 平移到 GMN ,可得正方形 BENM .
第 5 页(共 14 页)
故选: B . 【点评】本题考查考查图形的拼剪,矩形的性质,正方形的性质等知识,解题的关键是正确寻找相似三角形解决问 题,属于中考常考题型. 2.(2019•房山区模拟)如图,五个全等的小正方形无缝隙、不重合地拼成了一个“十字”形,连接 A 、 B 两个顶点, 过顶点 C 作 CD AB ,垂足为 D .“十字”形被分割为了①、②、③三个部分,这三个部分恰好可以无缝隙、不重 合地拼成一个矩形,这个矩形的长与宽的比为 ( )
A. 2 :1
B. 10 :1
C. 3 :1D. 2 3源自:13.(2016 秋•西城区校级期中)将两块全等的直角三角形(有一锐角为 30) 拼成一个四边形,其中轴对称图形的四
解直角三角形的应用-方向角问题-初中数学习题集含答案

一.填空题(共 5 小题) 1.(2018 秋•顺义区期末)轮船从 B 处以每小时 50 海里的速度沿南偏东 30 方向匀速航行,在 B 处观测灯塔 A 位于
南偏东 75 方向上,轮船航行半小时到达 C 处,在观测灯塔 A 北偏东 60 方向上,则 C 处与灯塔 A 的距离是 海里.
2.(2019 秋•东城区校级期中)如图,某货船以 24 海里 / 时的速度从 A 处向正东方向的 D 处航行,在点 A 处测得某 岛 C 在北偏东 60 的方向.该货船航行 30 分钟后到达 B 处,此时测得该岛在北偏东 30 的方向上.则货船在航行中 离小岛 C 的最短距离是 .
3.(2017 春•西城区校级期中)如图,在点 A 测得某岛 C 在北偏东 60 方向上,且距 A 点18 3 海里,某船以每小时 36 海里的速度从点 A 向正东方向航行,航行半小时后到达 B 点,此时测得岛 C 在北偏东 30 方向上,已知该岛周围 16 海里内有暗礁. B 点与 C 岛的距离是 B 点暗礁区域 (填内或外)
7.(2016•延庆县一模)如图,甲船在港口 P 的南偏西 60 方向,距港口 86 海里的 A 处,沿 AP 方向以每小时 15 海 里的速度匀速驶向港口 P .乙船从港口 P 出发,沿南偏东 45 方向匀速驶离港口 PC 2x ,现两船同时出发,2 小 时后乙船在甲船的正东方向.求乙船的航行速度.(结果精确到个位,参考数据: 2 1.414 , 3 1.732 , 5 2.236)
【分析】根据题中所给信息,求出 BCA 90 ,再求出 CBA 45 ,从而得到 ABC 为等腰直角三角形,然后根据 解直角三角形的知识解答.
【解答】解:根据题意,得 1 2 30 , Q ACD 60 , ACB 30 60 90 , CBA 75 30 45 , ABC 为等腰直角三角形, Q BC 50 0.5 25 , AC BC 25 (海里). 故答案为:25.
负整数指数幂-初中数学习题集含答案
负整数指数幂(北京习题集)(教师版)一.选择题(共2小题)1.(2019秋•西城区期末)下列运算正确的是 A .B .C .D . 2.(2016秋•西城区期末)下列各式正确的是A .B .C .D . 二.填空题(共3小题)3.(2019秋•西城区校级期中)计算的结果是 .4.(2019秋•西城区校级期中)若有意义,则满足的条件是 .5.(2018春•门头沟区期末) , . 三.解答题(共5小题)6.(2018秋•门头沟区期末)我们规定:,即的负次幂等于的次幂的倒数.例: (1)计算: ; ;(2)如果,那么 ;如果,那么 ; (3)如果,且、为整数,求满足条件的、的取值. 7.(2019春•顺义区期末)计算:; 8.(2018春•延庆区期末)计算: 9.(2018春•怀柔区期末)计算:. 10.(2016秋•西城区校级期中)化简:.()328-=-326-=-3128-=3126-=()6212121x x x x --==g 62331x x x x --÷==323322()x xy x y y--==32123()y x x y -=33-3(25)x -+x 0(3)π-=11()2-=1(0)p p a a a -=≠a P a p 22144-=25-=2(2)--=128p -=p =2116a -=a =19p a -=a p a p 20182022(1)()(4)33π---+---201601(1)(3)2π----+2018021(1)( 3.14)(2π----+32232()(2)m n m n ----g负整数指数幂(北京习题集)(教师版)参考答案与试题解析一.选择题(共2小题)1.(2019秋•西城区期末)下列运算正确的是 A .B .C .D . 【分析】直接利用负指数幂的性质化简得出答案.【解答】解:, 故选:.【点评】此题主要考查了负整数指数幂的性质,正确掌握定义是解题关键.2.(2016秋•西城区期末)下列各式正确的是 A .B .C .D . 【分析】根据同底数幂的乘法,同底数幂的除法,积的乘方,负整数指数幂,可得答案.【解答】解:、,故不符合题意;、,故不符合题意;、,故不符合题意; 、负整数指数幂与正整数指数幂互为倒数,故符合题意;故选:.【点评】本题考查了负整数指数幂,利用同底数幂的乘法,同底数幂的除法,积的乘方,负整数指数幂是解题关键.二.填空题(共3小题)3.(2019秋•西城区校级期中)计算的结果是 . 【分析】直接利用负指数幂的性质化简得出答案.【解答】解:. 故答案为:. 【点评】此题主要考查了负指数幂的性质,正确掌握定义是解题关键.()328-=-326-=-3128-=3126-=3128-=C ()6212121x x x x --==g 62331x x x x --÷==323322()x xy x y y--==32123()y x x y -=A 624x x x -=g A B 628x x x -÷=B C 323366()x xy x y y--==C D D D 33-12733113327-==1274.(2019秋•西城区校级期中)若有意义,则满足的条件是 . 【分析】根据负整数指数幂的底数不等于0列式计算即可得解.【解答】解:有意义,,满足的条件是. 故答案为:. 【点评】本题考查了负整数指数幂与零次幂成立的条件,需熟记. 5.(2018春•门头沟区期末) 1 , . 【分析】直接利用零指数幂的性质以及负指数幂的性质分别化简得出答案.【解答】解:,. 故答案为:1,2.【点评】此题主要考查了零指数幂的性质以及负指数幂的性质,正确把握相关定义是解题关键.三.解答题(共5小题) 6.(2018秋•门头沟区期末)我们规定:,即的负次幂等于的次幂的倒数.例: (1)计算: ; ; (2)如果,那么 ;如果,那么 ; (3)如果,且、为整数,求满足条件的、的取值. 【分析】(1)根据负整数指数幂的计算法则计算即可求解;(2)根据负整数指数幂的计算法则找到指数即可求解;(3)根据负整数指数幂的计算法则找到底数和指数即可求解. 【解答】解:(1);; (2)如果,那么;如果,那么; (3)由于、为整数,所以当时,;当时,;当时,.3(25)x -+x 52x ≠-3(25)x -+Q 250x ∴-≠x ∴52x ≠-52x ≠-0(3)π-=11()2-=0(3)1π-=11()22-=1(0)p p a a a -=≠a P a p 22144-=25-=1252(2)--=128p -=p =2116a -=a =19p a -=a p a p 21525-=21(2)4--=128p -=3p =2116a -=4a =±a p 9a =1p =3a =2p =3a =-2p =故答案为:(1);;(2)3;. 【点评】考查了负整数指数幂,负整数指数幂:,为正整数),注意:①;②计算负整数指数幂时,一定要根据负整数指数幂的意义计算,避免出现的错误;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数;④在混合运算中,始终要注意运算的顺序.7.(2019春•顺义区期末)计算:; 【分析】直接利用负指数幂的性质和零指数幂的性质分别化简进而得出答案.【解答】解:原式 . 【点评】此题主要考查了实数运算,正确化简各数是解题关键.8.(2018春•延庆区期末)计算:【分析】直接利用负整数指数幂的性质以及零指数幂的性质化简进而得出答案.【解答】解:原式 . 【点评】此题主要考查了负整数指数幂的性质以及零指数幂的性质,正确化简各数是解题关键.9.(2018春•怀柔区期末)计算:. 【分析】直接利用零指数幂的性质以及负指数幂的性质化简各数得出答案.【解答】解:原式,.【点评】此题主要考查了负指数幂的性质和零指数幂的性质,正确掌握相关定义是解题关键.10.(2016秋•西城区校级期中)化简:. 【分析】利用负整数指数幂的法则求解即可.【解答】解: , , . 【点评】本题主要考查了负整数指数幂,解题的关键是熟记负整数指数幂的法则.125144±1(0p p a a a -=≠p 0a ≠2(3)(3)(2)--=-⨯-20182022(1)()(4)33π---+---411199=+--13=201601(1)(3)2π----+1112=-+12=2018021(1)( 3.14)(2π----+114=-+4=32232()(2)m n m n ----g32232()(2)m n m n ----g624614m n m n --=⨯g 2414m n -=424n m =。
二次函数的三种形式-初中数学习题集含答案
二次函数的三种形式(北京习题集)(教师版)一.选择题(共3小题)1.(2018秋•丰台区期末)将二次函数241y x x =-+化成2()y a x h k =-+的形式为( ) A .2(4)1y x =-+B .2(4)3y x =--C .2(2)3y x =--D .2(2)3y x =+-2.(2017秋•房山区期中)将二次函数241y x x =--化为2()y x h k =-+的形式,结果为( ) A .2(2)5y x =++B .2(2)5y x =--C .2(2)5y x =-+D .2(2)5y x =+-3.(2016秋•昌平区期末)将二次函数表达式223y x x =-+用配方法配成顶点式正确的是( ) A .2(1)2y x =-+B .2(1)4y x =++C .2(1)2y x =--D .2(2)2y x =+-二.填空题(共7小题)4.(2019秋•朝阳区校级月考)将二次函数解析式2285y x x =-+配方成2()y a x h k =-+的形式为 . 5.(2017秋•怀柔区期末)将245y x x =-+化成2()y a x h k =-+的形式 .6.(2017秋•平谷区期末)将二次函数223y x x =-+化为2()y x h k =-+的形式,则h = ,k = . 7.(2018秋•朝阳区期中)将抛物线265y x x =-+化成2()y a x h k =--的形式,则hk = . 8.(2017秋•顺义区校级期中)若将二次函数223x x --配方为2()y x h k =-+的形式,则 . 9.(2016秋•通州区期末)把二次函数223y x x =-+化成2()y a x h k =-+的形式为 .10.(2016秋•房山区期中)若把函数265y x x =++化为2()y x m k =-+的形式,其中m 、k 为常数,则k m -= . 三.解答题(共5小题)11.(2019秋•通州区期末)把二次函数表达式24y x x c =-+化为2()y x h k =-+的形式. 12.(2018秋•门头沟区期末)已知二次函数243y x x =-+. (1)用配方法将其化为2()y a x h k =-+的形式; (2)在所给的平面直角坐标系xOy 中,画出它的图象.13.(2019秋•西城区校级期中)将下列各二次函数解析式化为2()y a x h k =-+的形式,并写出顶点坐标. (1)261y x x =-- (2)2246y x x =--- (3)213102y x x =++. 14.(2018秋•房山区期中)已知二次函数223y x x =--. (1)将223y x x =--化成2()y a x h k =-+的形式;(2)与y 轴的交点坐标是 ,与x 轴的交点坐标是 ; (3)在坐标系中利用描点法画出此抛物线.x ⋯⋯ y ⋯⋯(4)不等式2230x x -->的解集是 .15.(2018秋•西城区校级期中)已知二次函数21322y x x =-++(1)将21322y x x =-++成2()y a x h k =-+的形式:(2)在坐标系中利用描点法画出此抛物线x⋯⋯y⋯⋯(3)当33-<<时,观察图象直接写出函数值y的取值的范围.x(4)将该抛物线在x上方的部分(不包含与x的交点)记为G,若直线y x b=+与G只有一个公共点,则b的取值范围是.二次函数的三种形式(北京习题集)(教师版)参考答案与试题解析一.选择题(共3小题)1.(2018秋•丰台区期末)将二次函数241y x x =-+化成2()y a x h k =-+的形式为( ) A .2(4)1y x =-+B .2(4)3y x =--C .2(2)3y x =--D .2(2)3y x =+-【分析】先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式. 【解答】解:241y x x =-+2(44)14x x =-++- 2(2)3x =--.所以把二次函数241y x x =-+化成2()y a x h k =-+的形式为:2(2)3y x =--. 故选:C .【点评】本题考查了二次函数的三种形式.二次函数的解析式有三种形式: (1)一般式:2(0y ax bx c a =++≠,a 、b 、c 为常数); (2)顶点式:2()y a x h k =-+;(3)交点式(与x 轴)12:()()y a x x x x =--.2.(2017秋•房山区期中)将二次函数241y x x =--化为2()y x h k =-+的形式,结果为( ) A .2(2)5y x =++B .2(2)5y x =--C .2(2)5y x =-+D .2(2)5y x =+-【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式. 【解答】解:222414441(2)5y x x x x x =--=-+--=--. 故选:B .【点评】本题主要考查二次函数的三种形式的知识点,二次函数的解析式有三种形式:(1)一般式:2(0y ax bx c a =++≠,a 、b 、c 为常数);(2)顶点式:2()y a x h k =-+;(3)交点式(与x 轴)12:()()y a x x x x =--. 3.(2016秋•昌平区期末)将二次函数表达式223y x x =-+用配方法配成顶点式正确的是( ) A .2(1)2y x =-+B .2(1)4y x =++C .2(1)2y x =--D .2(2)2y x =+-【分析】利用配方法把一般式化为顶点式即可.【解答】解:2223(1)2y x x x =-+=-+. 故选:A .【点评】本题考查了二次函数的三种形式:一般式:2(y ax bx c a =++,b ,c 是常数,0)a ≠,该形式的优势是能直接根据解析式知道抛物线与y 轴的交点坐标是(0,)c ;顶点式:2()(y a x h k a =-+,h ,k 是常数,0)a ≠,其中(,)h k 为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(,)h k ;交点式:12()()(y a x x x x a =--,b ,c 是常数,0)a ≠,该形式的优势是能直接根据解析式得到抛物线与x 轴的两个交点坐标1(x ,0),2(x ,0). 二.填空题(共7小题)4.(2019秋•朝阳区校级月考)将二次函数解析式2285y x x =-+配方成2()y a x h k =-+的形式为22(2)3y x =-- .【分析】先提出二次项系数,再加上一次项系数一半的平方,即得出顶点式的形式. 【解答】解:提出二次项系数得,22(4)5y x x =-+, 配方得,22(44)58y x x =-++-, 即22(2)3y x =--. 故答案为:22(2)3y x =--.【点评】本题考查了二次函数的三种形式,一般式:2y ax bx c =++,顶点式:2()y a x h k =-+;两根式:12()()y a x x x x =--.5.(2017秋•怀柔区期末)将245y x x =-+化成2()y a x h k =-+的形式 2(2)1y x =-+ .【分析】化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式. 【解答】解:245y x x =-+,2441y x x ∴=-++, 2(2)1y x ∴=-+. 故答案为2(2)1y x =-+.【点评】本题考查了二次函数的三种形式,二次函数的解析式有三种形式:(1)一般式:2(0y ax bx c a =++≠,a 、b 、c 为常数); (2)顶点式:2()y a x h k =-+;(3)交点式(与x 轴)12:()()y a x x x x =--.6.(2017秋•平谷区期末)将二次函数223y x x =-+化为2()y x h k =-+的形式,则h = 1 ,k = . 【分析】利用配方法把函数解析式写成2(1)2y x =-+,进而可得答案. 【解答】解:22223212(1)2y x x x x x =-+=-++=-+, 则1h =,2k =, 故答案为:1;2;【点评】此题主要考查了二次函数的顶点式,关键是掌握顶点式:2()(y a x h k a =-+,h ,k 是常数,0)a ≠,其中(,)h k 为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(,)h k .7.(2018秋•朝阳区期中)将抛物线265y x x =-+化成2()y a x h k =--的形式,则hk = 12 . 【分析】利用配方法把一般式化为顶点式,得到h 、k 的值,代入求值即可. 【解答】解:265y x x =-+2694x x =-+-2(3)4x =--, 3h ∴=,4k =, 3412hk ∴=⨯=.故答案是:12.【点评】本题考查的是二次函数的三种形式,灵活运用配方法把一般式化为顶点式是解题的关键.8.(2017秋•顺义区校级期中)若将二次函数223x x --配方为2()y x h k =-+的形式,则 2(1)4y x =-- . 【分析】根据配方法整理即可得解. 【解答】解:223y x x =--,2(21)31x x =-+--, 2(1)4x =--, 所以,2(1)4y x =--. 故答案为:2(1)4y x =--.【点评】本题考查了二次函数的三种形式,熟练掌握配方法是解题的关键.9.(2016秋•通州区期末)把二次函数223y x x =-+化成2()y a x h k =-+的形式为 2(1)2y x =-+ . 【分析】根据配方法的操作整理即可得解. 【解答】解:223y x x =-+, 2212x x =-++,2(1)2x =-+, 所以,2(1)2y x =-+. 故答案为:2(1)2y x =-+.【点评】本题考查了二次函数的三种形式,主要利用了配方法.10.(2016秋•房山区期中)若把函数265y x x =++化为2()y x m k =-+的形式,其中m 、k 为常数,则k m -= 1- . 【分析】用配方法将抛物线的一般式转化为顶点式,比较系数,可知m 、k 的值,再代入k m -,计算即可求解. 【解答】解:265y x x =++2(69)95x x =++-+ 2(3)4x =+-,所以,3m =-,4k =-, 所以,4(3)1k m -=---=-. 故答案为:1-.【点评】本题考查了二次函数的三种形式,熟练掌握配方法的步骤是解题的关键. 三.解答题(共5小题)11.(2019秋•通州区期末)把二次函数表达式24y x x c =-+化为2()y x h k =-+的形式.【分析】本题是将一般式化为顶点式,由于二次项系数是1,只需加上一次项系数的一半的平方来凑成完全平方式. 【解答】解:2224444(2)4y x x c x x c x c =-+=-++-=-+-,即2(2)4y x c =-+-. 【点评】本题考查了二次函数解析式的三种形式: (1)一般式:2(0y ax bx c a =++≠,a 、b 、c 为常数); (2)顶点式:2()y a x h k =-+;(3)交点式(与x 轴)12:()()y a x x x x =--.12.(2018秋•门头沟区期末)已知二次函数243y x x =-+.(1)用配方法将其化为2()y a x h k =-+的形式; (2)在所给的平面直角坐标系xOy 中,画出它的图象.【分析】(1)利用配方法把二次函数解析式化成顶点式即可; (2)利用描点法画出二次函数图象即可. 【解答】解:(1)243y x x =-+22224223(2)1x x x =-+-+=--; (2)2)(2)1y x =--,∴顶点坐标为(2,1)-,对称轴方程为2x =.函数二次函数243y x x =-+的开口向上,顶点坐标为(2,1)-,与x 轴的交点为(3,0),(1,0),∴其图象为:【点评】本题考查了二次函数的配方法,用描点法画二次函数的图象,掌握配方法是解答此题的关键. 13.(2019秋•西城区校级期中)将下列各二次函数解析式化为2()y a x h k =-+的形式,并写出顶点坐标. (1)261y x x =-- (2)2246y x x =---(3)213102y x x =++. 【分析】(1)加上一次项系数6的一半的平方是9,再减去9; (2)提取二次项2-后,再加一次项系数2的一半的平方1,再减去1; (3)提取二次项系数12后,再加上一次项系数6的一半的平方9,再减去9. 【解答】解:(1)222616991(3)10y x x x x x =--=-+--=--,∴顶点( 3,10- );(2)2222462(211)62(1)4y x x x x x =---=-++--=-+-, 顶点(1-,4- ); (3)22211111310(699)10(3)2222y x x x x x =++=++-+=++, 顶点(3-,112). 【点评】本题考查了把二次函数的一般式化为顶点式,解题思路为:化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式. 14.(2018秋•房山区期中)已知二次函数223y x x =--. (1)将223y x x =--化成2()y a x h k =-+的形式;(2)与y 轴的交点坐标是 (0,3)- ,与x 轴的交点坐标是 ; (3)在坐标系中利用描点法画出此抛物线.x ⋯⋯ y ⋯⋯(4)不等式2230x x -->的解集是 .【分析】(1)利用配方法将一次项和二次项组合,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.(2)将已知方程转化为两点式方程即可得到该抛物线与x 轴的交点坐标;令0x =即可得到该抛物线与y 轴交点的纵坐标;(3)将抛物线223y x x =--上的点的坐标列出,然后在平面直角坐标系中找出这些点,连接起来即可; (4)结合图象可以直接得到答案.【解答】解:(1)222232131(1)4y x x x x x =--=-+--=--,即2(1)4y x =--;(2)令0x =,则3y =-,即该抛物线与y 轴的交点坐标是(0,3)-, 又223(3)(1)y x x x x =--=-+,所以该抛物线与x 轴的交点坐标是(3,0)(1-,0). 故答案是:(0,3)-;(3,0)(1-,0);(3)列表:x⋯ 1-0 1 2 3 ⋯ y⋯3-4-3-⋯图象如图所示:;(4)如图所示,不等式2230x x -->的解集是1x <-或3x >. 故答案是:1x <-或3x >.【点评】本题考查了二次函数的三种形式、二次函数的对称性和由函数图象确定坐标、直线与图象的交点问题,综合体现了数形结合的思想.15.(2018秋•西城区校级期中)已知二次函数21322y x x =-++(1)将21322y x x =-++成2()y a x h k =-+的形式: (2)在坐标系中利用描点法画出此抛物线x ⋯⋯ y⋯ ⋯ (3)当33x -<<时,观察图象直接写出函数值y 的取值的范围 52y -< .(4)将该抛物线在x 上方的部分(不包含与x 的交点)记为G ,若直线y x b =+与G 只有一个公共点,则b 的取值范围是 .【分析】(1)用配方法把二次函数一般式写成顶点式.(2)由顶点式得对称轴为直线1x =,列表描点画图象.(3)观察图象,在31x -<<时,y 随x 的增大而增大,随后y 减小,结合计算可得3x =-时y 的值,即求出y 的范围.(4)利用抛物线方程和直线方程联立求出两函数图象只有一个交点时b 的值.由于抛物线只取x 轴上方的部分,故需求直线经过抛物线与x 轴的交点时b 的值,再根据直线的平移得到相应b 的范围.【解答】解:(1)222221313131131(2)(211)(1)(1)22222222222y x x x x x x x x =-++=--+=--+-+=--++=--+(2)列表得:用描点画图象得:(3)3x =-时,6y =-,3x =时,0y =当31x -<<时,y 随x 的增大而增大,且1x =时,2y =故答案为:52y -<(4)21322y x b y x x =+⎧⎪⎨=-++⎪⎩ 整理得:232x b =- 当方程只有一个解时,即对应的两函数图象只有一个交点320b ∴-=,解得:32b = 把1x =-,0y =代入y x b =+,得1b =把3x =,0y =代入y x b =+,得3b =-3b ∴-时,直线y x b =+与G 没有交点;31b -<时,直线y x b =+与G 有一个交点;312b <<时,直线y x b =+与G 有两个交点;32b =时,直线y x b =+与G 有一个交点,32b >,直线y x b =+与G 无交点. 故答案为:31b -<或32b =【点评】本题考查了二次函数的图象与性质,一次函数与二次函数的交点问题,根据图象利用数形结合是解决此类问题的关键.。
众数-初中数学习题集含答案
学校
平均分
中位数
众数
甲
74.2
n
85
乙
73.5
76
84
根据以上信息,回答下列问题: (1)写出表中 n 的值;
第 2 页(共 19 页)
(2)在此次测试中,某学生的成绩是 74 分,在他所属学校排在前 20 名,由表中数据可知该学生是 校的学生
(填“甲”或“乙” ) ,理由是 ;
(3)假设乙校 800 名学生都参加此次测试,估计成绩优秀的学生人数.
众数(北京习题集)(教师版)
一.选择题(共 2 小题) 1.(2020•朝阳区校级二模)某商场一名业务员 12 个月的销售额(单位:万元)如下表:则这组数据的众数和中位 数分别是 ( )
月份(月 )
1 2 3 45 6 7 8
9 10 11 12
销售额(万元) 6.2 9.8 9.8 7.8 7.2 6.4 9.8 8 7 9.8 10 7.5
10.(2020 春•海淀区校级月考)某工厂甲、乙两个部门各有员工 400 人,为了解这两个部门员工的生产技能情况,
进行了抽样调查,过程如下,请补充完整.
从甲、乙两个部门各随机抽取 20 名员工,进行了生产技能测试,测试成绩(百分制)如下
甲
78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
100
第 3 页(共 19 页)
60
81
【整理数据】
课外阅读时间 x(min)
120 140
70
81
10
20
100
81
0„ x 40
40„ x 80
80„ x 120
钟面角-初中数学习题集含答案
钟面角(北京习题集)(教师版)一.选择题(共5小题)1.(2014秋•西城区校级期末)9点30分这一时刻,分针与时针的夹角是 A .B .C .D .2.(2011秋•通州区期末)下午2点整(如图所示),时钟的分针与时针所成角的度数为 A .B .C .D .3.(2010秋•怀柔区期末)在时刻,时钟上时针和分针之间的夹角(小于平角的角)为 A .B .C .D .4.(2009秋•顺义区期末)钟表在8点30分时,时钟上的时针与分针之间的夹角为 A .B .C .D .5.(2009秋•门头沟区期末)上午这一时刻,时钟上分针与时针所夹的角是 A .B .C .D .二.填空题(共8小题)6.(2019秋•大兴区期末)11时整,钟表的时针与分钟所构成锐角的度数是 .7.(2012秋•怀柔区期末)钟表的指针恰好是10点整,此时,钟表上时针与分针所夹的锐角的度数为 .8.(2009秋•延庆县期末)下午这一时刻,时钟上分针与时针所夹的角等于 度.9.(2009秋•怀柔区期末)由8点10分到8点30分,时钟的分针转过的角度是 .10.(2009秋•海淀区校级期末)时钟4时30分时,分针与时针的夹角是 .11.(2009秋•西城区期末)从下午到当天下午,时钟的分针转过的角度为 度.12.(2008秋•海淀区期末)在钟表的表盘上四点整时,时针与分针之间的夹角约为 度.13.(2008秋•丰台区校级期末)学生每天下午分上第六节课,此时时针与分针成 度的角.三.解答题(共1小题)14.(2012秋•海淀区校级月考)在点之间,有两个时刻时针与分针的夹角是,求这两个时刻的间隔时间.()75︒105︒90︒125︒()90︒80︒70︒60︒9:30()95︒105︒110︒115︒()60︒70︒75︒85︒10:00()72︒60︒30︒24︒3:3013:0013:501:306~7120︒钟面角(北京习题集)(教师版)参考答案与试题解析一.选择题(共5小题)1.(2014秋•西城区校级期末)9点30分这一时刻,分针与时针的夹角是 A .B .C .D .【分析】根据时针旋转的角度减去分针旋转的角度,可得答案.【解答】解:, 故选:.【点评】本题考查了钟面角,利用了时针旋转的角度减去分针旋转的角度等于分针与时针的夹角.2.(2011秋•通州区期末)下午2点整(如图所示),时钟的分针与时针所成角的度数为 A .B .C .D .【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是,借助图形,找出时针和分针之间相差的大格数,用大格数乘即可.【解答】解:下午2点整,时针和分针中间相差两大格.钟表12个数字,每相邻两个数字之间的夹角为,下午2点整分针与时针的夹角是.故选:.【点评】此题考查的知识点是钟面角的计算,用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为.3.(2010秋•怀柔区期末)在时刻,时钟上时针和分针之间的夹角(小于平角的角)为 A .B .C .D .【分析】根据时针与分针相距的份数乘以每份的度数,可得答案.【解答】解:时针与分针相距3.5份,每份的度数是,在时刻,时钟上时针和分针之间的夹角(小于平角的角)为.故选:.【点评】本题考查了钟面角,利用时针与分针相距的份数乘以每份的度数是解题关键.()75︒105︒90︒125︒1309306301052︒⨯+⨯-︒⨯=︒B ()90︒80︒70︒60︒30︒30︒Q 30︒∴23060⨯︒=︒D 30︒9:30()95︒105︒110︒115︒9:3030︒9:30 3.530105⨯︒=︒B4.(2009秋•顺义区期末)钟表在8点30分时,时钟上的时针与分针之间的夹角为 A .B .C .D .【分析】画出草图,利用钟表表盘的特征解答.【解答】解:8点30分,时针和分针中间相差2.5个大格.钟表12个数字,每相邻两个数字之间的夹角为,点30分分针与时针的夹角是.故选:.【点评】本题考查了钟面角,用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为.5.(2009秋•门头沟区期末)上午这一时刻,时钟上分针与时针所夹的角是 A .B .C .D .【分析】午这一时刻,时针指到10上,分针指到12上,根据钟表表盘的特征解答.【解答】解:上午这一时刻,时针指到10上,分针指到12上,所夹两个大格,每格是,因而夹角是.故选:.【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动时针转动,并且利用起点时间时针和分针的位置关系建立角的图形. 二.填空题(共8小题)6.(2019秋•大兴区期末)11时整,钟表的时针与分钟所构成锐角的度数是 .【分析】由于钟表的指针恰好是11点整,时针指向11,分针指向12,根据钟面被分成12大格,每大格为30度得到此时钟表上时针与分针所夹的锐角的度数是.【解答】解:钟表的指针恰好是11点整,时针指向11,分针指向12,所以此时钟表上时针与分针所夹的锐角的度数是.故答案为:.【点评】本题考查了钟面角.解题的关键是明确钟面角:钟面被分成12大格,每大格为30度;分针每分钟转6度,时针每分钟转0.5度.7.(2012秋•怀柔区期末)钟表的指针恰好是10点整,此时,钟表上时针与分针所夹的锐角的度数为 .【分析】由于钟表的指针恰好是10点整,时针指向10,分针指向12,根据钟面被分成12大格,每大格为30度得到此时钟表上时针与分针所夹的锐角的度数.【解答】解:钟表的指针恰好是10点整,时针指向10,分针指向12,所以此时钟表上时针与分针所夹的锐角的度数.()60︒70︒75︒85︒Q 30︒8∴ 2.53075⨯︒=︒C 30︒10:00()72︒60︒30︒24︒10:0010:0030︒23060⨯=︒B 1︒1()12︒30︒30︒30︒30︒60︒230=⨯︒23060=⨯︒=︒【点评】本题考查了钟面角:钟面被分成12大格,每大格为30度;分针每分钟转6度,时针每分钟转0.5度.8.(2009秋•延庆县期末)下午这一时刻,时钟上分针与时针所夹的角等于 75 度.【分析】画出草图,利用钟表表盘的特征解答.【解答】解:,时针和分针中间相差2.5个大格.钟表12个数字,每相邻两个数字之间的夹角为,下午分针与时针的夹角是.【点评】用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为.9.(2009秋•怀柔区期末)由8点10分到8点30分,时钟的分针转过的角度是 120 .【分析】时针和分针的运动可以看做一种匀速的旋转运动,8时10分到8时30分,分针用了20分钟时间.由此再进一步分别计算它们旋转的角度.【解答】解:钟表12个数字,每相邻两个数字之间的夹角为,从8点10分到8点30有20分钟时间,分针旋转了,故从8点10分到8点30,时钟的分针转过的角度是.【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每分钟转动,时针每小时转动,并且利用起点时间时针和分针的位置关系建立角的图形.10.(2009秋•海淀区校级期末)时钟4时30分时,分针与时针的夹角是 .【分析】根据时钟4时30分时,时针在4与5中间位置,分针在6上,可以得出分针与时针的夹角是一个半格,每一格之间的夹角为,可得出结果.【解答】解:钟表上从1到12一共有12格,每个大格,时钟4时30分时,时针在4与5中间位置,分针在6上,可以得出分针与时针的夹角是一个半格,分针与时针的夹角是.故答案为:.【点评】此题主要考查了钟面角的有关知识,得出钟表上从1到12一共有12格,每个大格,是解决问题的关键.11.(2009秋•西城区期末)从下午到当天下午,时钟的分针转过的角度为 300 度.【分析】时针和分针的运动可以看做一种匀速的旋转运动,到当天下午,分针用,50分钟时间.由此再进一步分别计算它们旋转的角度.【解答】解:钟表12个数字,每相邻两个数字之间的夹角为,到当天下午,分针用50分钟时间.分针旋转了,3:303:30Q 30︒∴3:30 2.53075⨯︒=︒30︒30︒Q ∴304120︒⨯=︒120︒6︒30︒45︒30︒Q 30︒∴∴45︒45︒30︒13:0013:5013:0013:5030︒13:00Q 13:50∴3010300︒⨯=︒【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每分钟转动,时针每小时转动,并且利用起点时间时针和分针的位置关系建立角的图形.12.(2008秋•海淀区期末)在钟表的表盘上四点整时,时针与分针之间的夹角约为 120 度.【分析】4点钟时,钟表的时针指向数字4,分针指向12,再根据钟面上每一大格的度数为即可求出答案.【解答】解:4点整,时针指向4,分针指向12,钟表12个数字,每相邻两个数字之间的夹角为,因此4点整分针与时针的夹角正好是.故答案为:120.【点评】本题考查了钟面角,钟面一周平均分60格,相邻两格刻度之间的时间间隔是1分钟,时针1分钟走格,分针1分钟走1格.钟面上每一格的度数为.13.(2008秋•丰台区校级期末)学生每天下午分上第六节课,此时时针与分针成 135 度的角.【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是,借助图形,找出时针和分针之间相差的大格数,用大格数乘即可.【解答】解:下午分,时针和分针之间相差4.5个大格. 钟表12个数字,每相邻两个数字之间的夹角为,下午分针与时针的夹角是.故答案为135.【点评】本题是一个钟表问题,解题时经常用到每两个数字之间的度数是30度.借助图形,更容易解决.三.解答题(共1小题)14.(2012秋•海淀区校级月考)在点之间,有两个时刻时针与分针的夹角是,求这两个时刻的间隔时间.【分析】根据时针旋转的速度乘以时针旋转的时间,可得时针旋转的角度,分针旋转的速度乘以分针旋转的时间,可得分针旋转的角度,根据角的和差,可得答案.【解答】解:6时30分之前,设分钟时针与分针的夹角是,得. 解得, 即6时时时针与分针的夹角是; 6时30分之后,.解得 时间间隔为6︒30︒30︒30︒430120⨯︒=︒1123601230︒÷=︒1:3030︒30︒1:30Q 30︒∴1:30 4.530135⨯︒=︒6~7120︒x 120︒0.51806120x x ︒+︒-︒=︒12011x =12011120︒61800.5120x x ︒-︒-︒=︒60011x =600120480-=【点评】本题考查了钟面角,利用了时针旋转的速度乘以时针旋转的时间得时针旋转的角度,分针旋转的速度乘以分针旋转的时间得出分针旋转的角度.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京初中数学习题书
北京初中数学习题书涵盖了初中数学的各个领域,包括代数、几何、
概率与统计等等。下面按照列表的形式来介绍这些内容。
一、代数
1. 基本代数运算——加减乘除
2. 一元一次方程
3. 二元一次方程组
4. 二次方程
5. 不等式
二、几何
1. 基本图形的认识——点、线、面
2. 直线和角
3. 三角形
4. 平行四边形和梯形
5. 圆的基本性质
三、概率与统计
1. 随机实验和样本空间
2. 频率与概率
3. 事件的概率——加法与乘法原理
4. 抽样与估计
5. 统计图表的制作和分析
四、函数
1. 函数的定义与性质
2. 初等函数(包括常函数、一次函数、二次函数、指数函数、对数函
数等)
3. 函数的图象及其性质
4. 函数的应用
五、立体几何
1. 空间图形的认识——点、线、面、体
2. 空间直线和平面的位置关系
3. 空间角和面的性质
4. 空间直线和平面的交角和交线
5. 空间图形的投影与截面
六、三角函数
1. 三角函数及其定义
2. 三角函数的基本性质
3. 三角函数的图象及其性质
4. 三角函数的应用
以上就是北京初中数学习题书的内容列表。在学习过程中,我们需要
不断巩固基础知识,注重习题练习,同时要把握好思维方法和技巧,
才能在数学学习中有所突破。
