2011年北京中考数学选择填空训练(3)
北京四中2011中考数学全真模拟试题

北京四中2011中考数学全真模拟试题作者:来源:《数学金刊·初中版》2012年第02期(说明:时间120分钟满分150分)一、选择题(本大题共10小题,每小题4分,共40分)1.芜湖地处长江中下游,水资源丰富,素有“江南水乡”之美称.据测量,仅浅层地下水蕴藏量就达56000万m3,用科学记数法记作()A. 5.6×109 m3 B. 56×108 m3C. 5.6×108 m3?摇D. 56000×104 m32.图1是由纸板拼成的立体图形,有两面是黑色纸板,将该图形展开后是()■3.在“手拉手,献爱心”捐款活动中,九年级七个班级的捐款数分别为:260、300、240、220、240、280、290(单位:元),则捐款数的中位数为()A. 280 B. 260 C. 250 D. 2704.已知⊙O■和⊙O■的半径分别是5和4,O■O■=3,则⊙O■和⊙O■的位置关系是()A.外离B.外切C.相交D.内切5.在平面直角坐标系中,点(4,-3)所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限6.如图2,已知一坡面的坡度i=1:■,则坡角α为()A. 15°B. 20°C. 30°D. 45°■7. 下列图形中,是轴对称而不是中心对称图形的是()A. 平行四边形B.菱形C.等腰梯形D.直角梯形8. 若使分式■的值为0,则x的取值为()A. 1或-1 B.-3或1C.-3 D.-3或-19. 若一个多边形的内角和为外角和的3倍,则这个多边形为()A. 八边形B.九边形C.十边形D.十二边形10. 估算■的值()A. 在4和5之间B.在5和6之间C.在6和7之间D.在7和8之间二、填空题(本大题共6小题,每小题4分,共24分)11. 函数y=■中,自变量x的取值范围是________.12. 已知等腰三角形两边长为7和3,则它的周长为______.13. 若反比例函数y=-■的图象经过点(-3,-2),则m=________.14. 计算:2a3·(3a)3=________.15. 在珠穆朗玛峰周围2 km的范围内,还有较著名的洛子峰(海拔8516 m)、卓穷峰(海拔7589 m)、马卡鲁峰(海拔8463 m)、章子峰(海拔7543 m)、努子峰(海拔7855 m)、和普莫里峰(海拔7145 m)六座山峰,则这六座山峰海拔高度的极差为________m.16. 已知三个边长分别为2、3、5的正方形如图3排列,则图中阴影部分面积为________.■三、解答题(大题共8小题,共86分)17. (12分)(1)解不等式组:2x-3(2)因式分解:y3-4x2y.18. (10分)如图4,已知在半圆AOB中,AD=DC,∠CAB=30°,AC=2■,求AD的长度.19. (10分)?摇图5是由权威机构发布的在1993年4月~2005年4月期间由中国经济状况指标之一中国经济预警指数绘制的图表.(1)请你仔细阅读图表,可从图表中得出:我国经济发展过热的最高点出现在________?摇年;我国经济发展过冷的最低点出现在________年.(2)根据该图表提供的信息,请你简单描述我国从1993年4月到2005年4月经济发展状况,并预测2005年度中国经济发展的总体趋势将会怎样.20. (10分)图6为⊙O的切线,A为切点,PO交⊙O于点B,OA=3,OP=6,求∠BAP 的度数.21. (10分)图7一上面无盖的正方体纸盒,现将其剪开展成平面图,如图8所示.已知展开图中每个正方形的边长为1.(1)求在该展开图中可画出最长线段的长度,这样的线段可画几条?(2)试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系.22. (10分)已知二次函数图象经过(2,-3),对称轴x=1,抛物线与x轴两交点距离为4,求这个二次函数的解析式.23. (12分)小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心,小胖对小瘦说:“真可惜!我只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我就能翘到1.25 m,甚至更高!”(1)你认为小胖的话对吗?请你作图分析说明.(2)你能否找出将小瘦翘到1.25 m高的方法?试说明.24. (12分)在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图10,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.(1)试问小球通过第二层A位置的概率是多少?(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层B位置和第四层C位置处的概率各是多少?。
2011年北京市中考数学模拟试卷

2011年北京市中考数学模拟试卷2011年北京市中考数学模拟试卷一、选择题(共8小题,每小题4分,满分32分)D±2.(4分)(2010•西藏)已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()3.(4分)(2010•东城区一模)布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸.C D.4.(4分)(2010•海淀区二模)某班的9名同学的体重分别是(单位:千克):61,59,70,59,65,67,59,63,5.(4分)(2010•朝阳区二模)全球可被人类利用的淡水总量仅占总水量的0.00003,因此珍惜水,保护水是我们每6.(4分)(2010•东城区二模)如图,模块①﹣⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①﹣⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为()7.(4分)(1999•南京)如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,则两圆组成的圆环的面积是()8.(4分)(2009•临沂)矩形ABCD 中,AD=8cm ,AB=6cm .动点E 从点C 开始沿边CB 向点B 以2cm/s 的速度运动,动点F 从点C 同时出发沿边CD 向点D 以1cm/s 的速度运动至点D 停止.如图可得到矩形CFHE ,设运动时间为x (单位:s ),此时矩形ABCD 去掉矩形CFHE 后剩余部分的面积为y (单位:cm 2),则y 与x 之间的函数关系用图象表示大致是下图中的( ).CD .二、填空题(共4小题,每小题4分,满分16分) 9.(4分)(2013•昌平区二模)若分式的值为0,则x 的值为 _________ .10.(4分)(2012•开平区二模)如图,点A 、B 、C 是半径为6的⊙O 上的点,∠B=30°,则的长为 _________ .11.(4分)(2010•西城区一模)如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,若AD=3,DB=5,DE=1.2,则BC= _________ .12.(4分)(2009•桂林)如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1得∠A1,∠A1BC 的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2008BC的平分线与∠A2008CD的平分线交于点A2009,得∠A2009,则∠A2009=_________.三、解答题(共13小题,满分72分)13.(5分)(2008•石景山区一模)14.(5分)(2011•广东模拟)解不等式组,并把它的解集表示在数轴上.15.(5分)(2009•长沙)如图,E、F是平行四边形ABCD对角线AC上两点,BE∥DF,求证:AF=CE.16.(5分)(2010•海淀区二模)已知x2﹣6xy+9y2=0,求代数式的值.17.(5分)(2012•中山二模)列方程(组)解应用题:小明乘坐火车从某地到上海去参观世博园,已知此次行程为2160千米,城际直达动车组的平均时速是特快列车的1.6倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时,求小明乘坐动车组到上海需要的时间.18.(5分)(2012•潮阳区模拟)如图,点P的坐标为,过点P作x轴的平行线交y轴于点A,作PB⊥AP 交双曲线(x>0)于点B,连接AB.已知.求k的值和直线AB的解析式.19.(5分)(2010•东城区一模)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E为DC中点,tanC=.求AE的长度.20.(5分)(2009•德州)如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.求证:四边形OBEC是菱形.21.(5分)(2011•兴国县模拟)根据北京市统计局的2006﹣2009年空气质量的相关数据,绘制统计图如下:(1)由统计图中的信息可知,北京全年市区空气质量达到二级和好于二级的天数与上一年相比,增加最多的是_________年,增加了_________天;(2)表上是根据《中国环境发展报告(2010)》公布的数据会置的2009年十个城市供气质量达到二级和好于二级的天数占全年天数百分比的统计表,请将表1中的空缺部分补充完整(精确到1%)A组,不低于85%且低于95%的为B组,低于85%的为C组.按此标准,C组城市数量在这十个城市中所占的百分比为_________%;请你补全右边的扇形统计图.22.(5分)(2010•朝阳区二模)阅读下列材料并解答后面的问题:利用完全平方公式(a±b)2=a2±2ab+b2,通过配方可对a2+b2进行适当的变形,如a2+b2=(a+b)2﹣2ab或a2+b2=(a﹣b)2+2ab.从而使某些问题得到解决.例:已知a+b=5,ab=3,求a2+b2的值.解:a2+b2=(a+b)2﹣2ab=52﹣2×3=19.问题:(1)已知a+=6,则a2+=_________;(2)已知a﹣b=2,ab=3,求a4+b4的值.23.(7分)(2011•广东模拟)一开口向上的抛物线与x轴交于A,B两点,C(m,﹣2)为抛物线顶点,且AC⊥BC.(1)若m是常数,求抛物线的解析式;(2)设抛物线交y轴正半轴于D点,抛物线的对称轴交x轴于E点.问是否存在实数m,使得△EOD为等腰三角形?若存在,求出m的值;若不存在,请说明理由.24.(8分)(2006•常德)把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=_________;(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)25.(7分)(2006•长沙)如图1,已知直线y=﹣x与抛物线y=﹣x2+6交于A,B两点.(1)求A,B两点的坐标;(2)求线段AB的垂直平分线的解析式;(3)如图2,取与线段AB等长的一根橡皮筋,端点分别固定在A,B两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A,B构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.2011年北京市中考数学模拟试卷参考答案与试题解析一、选择题(共8小题,每小题4分,满分32分)D±2.(4分)(2010•西藏)已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()3.(4分)(2010•东城区一模)布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸.C D.=;4.(4分)(2010•海淀区二模)某班的9名同学的体重分别是(单位:千克):61,59,70,59,65,67,59,63,5.(4分)(2010•朝阳区二模)全球可被人类利用的淡水总量仅占总水量的0.00003,因此珍惜水,保护水是我们每6.(4分)(2010•东城区二模)如图,模块①﹣⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①﹣⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为()7.(4分)(1999•南京)如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,则两圆组成的圆环的面积是()=AB8.(4分)(2009•临沂)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的().C D.二、填空题(共4小题,每小题4分,满分16分)9.(4分)(2013•昌平区二模)若分式的值为0,则x的值为﹣2.解:若分式10.(4分)(2012•开平区二模)如图,点A、B、C是半径为6的⊙O上的点,∠B=30°,则的长为2π.∴l=.11.(4分)(2010•西城区一模)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,若AD=3,DB=5,DE=1.2,则BC= 3.2.∴12.(4分)(2009•桂林)如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1得∠A1,∠A1BC 的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2008BC的平分线与∠A2008CD的平分线交于点A2009,得∠A2009,则∠A2009=.(∠BD=∠A=α∠.=三、解答题(共13小题,满分72分)13.(5分)(2008•石景山区一模)×﹣,﹣,.14.(5分)(2011•广东模拟)解不等式组,并把它的解集表示在数轴上.,对不等式;不等式的解集为:15.(5分)(2009•长沙)如图,E、F是平行四边形ABCD对角线AC上两点,BE∥DF,求证:AF=CE.16.(5分)(2010•海淀区二模)已知x2﹣6xy+9y2=0,求代数式的值.(故答案为17.(5分)(2012•中山二模)列方程(组)解应用题:小明乘坐火车从某地到上海去参观世博园,已知此次行程为2160千米,城际直达动车组的平均时速是特快列车的1.6倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时,求小明乘坐动车组到上海需要的时间.依题意,得18.(5分)(2012•潮阳区模拟)如图,点P的坐标为,过点P作x轴的平行线交y轴于点A,作PB⊥AP 交双曲线(x>0)于点B,连接AB.已知.求k的值和直线AB的解析式.的坐标为)中,由)在双曲线上,可得的图象上,可得的解析式为的坐标为)中,,∴∴的解析式为19.(5分)(2010•东城区一模)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E为DC中点,tanC=.求AE的长度.DM=CF=tanC==20.(5分)(2009•德州)如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.求证:四边形OBEC是菱形.21.(5分)(2011•兴国县模拟)根据北京市统计局的2006﹣2009年空气质量的相关数据,绘制统计图如下:(1)由统计图中的信息可知,北京全年市区空气质量达到二级和好于二级的天数与上一年相比,增加最多的是2008年,增加了28天;(2)表上是根据《中国环境发展报告(2010)》公布的数据会置的2009年十个城市供气质量达到二级和好于二级的天数占全年天数百分比的统计表,请将表1中的空缺部分补充完整(精确到1%)A组,不低于85%且低于95%的为B组,低于85%的为C组.按此标准,C组城市数量在这十个城市中所占的百分比为30%;请你补全右边的扇形统计图.×个城市,所占的百分比为:22.(5分)(2010•朝阳区二模)阅读下列材料并解答后面的问题:利用完全平方公式(a±b)2=a2±2ab+b2,通过配方可对a2+b2进行适当的变形,如a2+b2=(a+b)2﹣2ab或a2+b2=(a﹣b)2+2ab.从而使某些问题得到解决.例:已知a+b=5,ab=3,求a2+b2的值.解:a2+b2=(a+b)2﹣2ab=52﹣2×3=19.问题:(1)已知a+=6,则a2+=34;(2)已知a﹣b=2,ab=3,求a4+b4的值.)∵23.(7分)(2011•广东模拟)一开口向上的抛物线与x轴交于A,B两点,C(m,﹣2)为抛物线顶点,且AC⊥BC.(1)若m是常数,求抛物线的解析式;(2)设抛物线交y轴正半轴于D点,抛物线的对称轴交x轴于E点.问是否存在实数m,使得△EOD为等腰三角形?若存在,求出m的值;若不存在,请说明理由..解析式为:,时,∴m时,∴m24.(8分)(2006•常德)把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=8;(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)∴ACAP=AB﹣(AP=,PB=﹣∴解得.MQ(﹣(或y=25.(7分)(2006•长沙)如图1,已知直线y=﹣x与抛物线y=﹣x2+6交于A,B两点.(1)求A,B两点的坐标;(2)求线段AB的垂直平分线的解析式;(3)如图2,取与线段AB等长的一根橡皮筋,端点分别固定在A,B两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A,B构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.)依题意得OA=3OB=2AB=5,得:∴OD=,)∴∴﹣x+m∴∴﹣)×,x++得:y=)x+中,()GH=∵OG∵×d=××d=AB×参与本试卷答题和审题的老师有:自由人;HJJ;星期八;hbxglhl;lf2-9;Linaliu;wenming;733599;MMCH;110397;CJX;开心;ln_86;nhx600;zhjh;疯跑的蜗牛;xiu;117173;心若在;lanchong;王岑;zcx;gsls;lbz;jingjing;Liuzhx(排名不分先后)菁优网2014年3月16日。
2011年中考数学试题及答案(Word版)
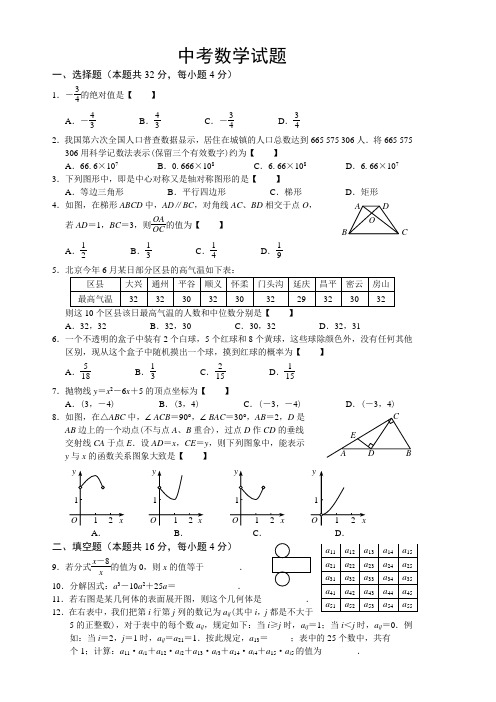
A OBCD A B C ED 中考数学试题一、选择题(本题共32分,每小题4分)1.- 34的绝对值是【 】A .- 4 3B . 4 3C .- 3 4D . 342.我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665 575 306人.将665 575 306用科学记数法表示(保留三个有效数字)约为【 】A .66.6×107B .0.666×108C .6.66×108D .6.66×107 3.下列图形中,即是中心对称又是轴对称图形的是【 】A .等边三角形B .平行四边形C .梯形D .矩形 4.如图,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O , 若AD =1,BC =3,则OAOC的值为【 】 A . 1 2 B . 1 3 C . 1 4 D . 195则这10个区县该日最高气温的人数和中位数分别是【 】A .32,32B .32,30C .30,32D .32,316.一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为【 】 A .5 18 B . 1 3 C . 2 15 D . 1157.抛物线y =x 2-6x +5的顶点坐标为【 】A .(3,-4)B .(3,4)C .(-3,-4)D .(-3,4)8.如图,在△ABC 中,∠ACB =90°,∠BAC =30°,AB =2,D 是AB 边上的一个动点(不与点A 、B 重合),过点D 作CD 的垂线交射线CA 于点E .设AD =x ,CE =y ,则下列图象中,能表示y 与x 的函数关系图象大致是【 】二、填空题(本题共16分,每小题4分)9.若分式x ―8x的值为0,则x 的值等于________. 10.分解因式:a 3―10a 2+25a =______________.11.若右图是某几何体的表面展开图,则这个几何体是__________.12.在右表中,我们把第i 行第j 列的数记为a ij (其中i ,j 都是不大于5的正整数),对于表中的每个数a ij ,规定如下:当i ≥j 时,a ij =1;当i <j 时,a ij =0.例如:当i =2,j =1时,a =a =1.按此规定,a =_____;表中的25个数中,共有_____A .B .C .D .FE x13.计算:01)2(2730cos 221π-++-⎪⎭⎫⎝⎛- .14.解不等式:4(x -1)>5x -6.15.已知a 2+2ab +b 2=0,求代数式a (a +4b )-(a +2b )(a -2b )的值.16.如图,点A 、B 、C 、D 在同一条直线上,BE ∥DF ,∠A =∠F ,AB =FD .求证:AE =FC .17.如图,在平面直角坐标系xOy 中,一次函数y =-2x 的图象与反比例函数y = kx 的图象的一个交点为A (-1,n ).(1)求反比例函数y = kx的解析式;(2)若P 是坐标轴上一点,且满足P A =OA ,直接写出点P 的坐标.18.列方程或方程组解应用题:京通公交快速通道开通后,为响应市政府“绿色出行”的号召,家住通州新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米.他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的 37.小王用自驾车方式上班平均每小时行驶多少千米?A B C D19.如图,在△ABC 中,∠ACB =90°,D 是BC 的中点,DE ⊥BC ,CE ∥AD .若AC =2,CE =4,求四边形ACEB 的周长.21.以下是根据北京市国民经济和社会发展统计公报中的相关数据,绘制统计图的一部分.请根据以上信息解答下列问题:(1)2008年北京市私人轿车拥有是多少万辆(结果保留三个有效数字)? (2)补全条形统计图;(3)汽车数量增多除造成交通拥堵外,还增加了碳排放量,为了了解汽车碳排放量的情况,小明同学通过网络了解到汽车的碳排放量与汽车排量有关.如:一辆排量为1.6L 的轿车,如果一年行驶1万千米,这一年,它碳排放量约为2.7吨.于是他调查了他所居住小区的150辆私人轿车,不同排量的轿车数量如下表所示.如果按照小明的统计数据,请你通过计算估计,2010年北京市仅排量为1.6L 的这类私人轿车(假设每辆车平均一行行驶1万千米)的碳排放总量约为多少万吨? 北京市2001~2010年私人轿车拥有量的年增长率统计图 北京市2001~2010年 私人轿车拥有量统计图A E F 图3 22.阅读下面材料:小伟遇到这样一个问题:如图1,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O .若梯形ABCD 的面积为1,试求以AC 、BD 、AD +BC 的长度为三边长的三角形的面积.小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D 作AC 的平行线交BC 的延长线于点E ,得到的△BDE 即是以AC 、BD 、AD +BC 的长度为三边长的三角形(如图2).参考小伟同学的思考问题的方法,解决下列问题:如图3,△ABC 的三条中线分别为AD 、BE 、CF .(1)在图3中利用图形变换画出并指明以AD 、BE 、CF的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以AD 、BE 、CF 的长度为三边长的三角形的面积等于_______.24.(7分)在□ABCD 中,∠BAD 的平分线交直线BC 于点E ,交直线DC 于点F .(1)在图1中,证明:CE =CF ; (2)若∠ABC =90°,G 是EF 的中点(如图2),直接写出∠BDG 的度数; (3)若∠ABC =120°,FG ∥CE ,FG =CE ,分别连结DB 、DG (如图3),求∠BDG 的度数.B BADADC C EE G FABC DE GF 图1图2图3BBCADOADCEO图2图1数学试卷答案及评分参考13、解:()0122730221π-++-⎪⎭⎫⎝⎛- cos=1332322++⨯- =13332++- =332+.14、解:去括号,得6544->-x x移项, 得6454->-x x合并, 得2->-x 解得 2<x所以原不等式的解集是2<x . 15、解:()()()b a b a b a a 224-+-+ =()22244b a ab a --+ =244b ab +∵0222=++b ab a ∴0=+b a∴原式=()b a b +4=0. 16、证明:∵BE ∥DF , ∴∠ABE=∠D .在△ABE 和△FDC 中,∴△ABE ≌△FDC . ∴AE =FC .17、解(1)∵A (-1,n )在一次函数x y 2-=∴n =2-×(1-)=2.∴点A 的坐标为(-1,2).∵点A 在反比例函数xky =的图象上,∴2-=k .∴反比例函数的解析式为xy 2-=. ∠ABE=∠D AB=FD∠A=∠F18、解:设小王用自驾车方式上班平均每小时行使x 千米. 依题意,得xx 18739218⨯=+ 解得 27=x .经检验,27=x 是原方程的解,且符合题意. 答;小王用自驾车方式上班平均每小时行使27千米. 四、解答题19、解:∵∠ACB=90°,DE ⊥BC , ∴AC ∥DE .又∵CE ∥AD ,∴四边形ACED 的是平行四边形. ∴DE=AC=2.在Rt △CDE 中,由勾股定理得3222=-=DE CE CD . ∵D 是BC 的中点, ∴BC=2CD=34.在Rt △ABC 中,由勾股定理得13222=+=BC AC AB . ∵D 是BC 的中点,DE ⊥BC , ∴EB=EC=4.∴四边形ACEB 的周长= AC+CE+EB+BA=10+132. 21、解(1)146×(1+19%) =173.74≈174(万辆).∴2008年北京市私人轿车拥有量约是174万辆.(2)如右图. (3)276×15075×2.7=372.6(万吨) 估计2010年北京市仅排量为1.6L的这类私人轿车的碳排放总量约为372.6万吨.22、解:△BDE 的面积等于1 . (1)如图.以AD 、BE 、CF 的长度为三边长的一个三角形是 △CFP . (2)以AD 、BE 、CF 的长度为三边长的三角形的面积等于43. . 24、(1)证明:如图1. ∵AF 平分∠BAD , ∴∠BAF=∠DAF .∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AB ∥CD .∴∠DAF=∠CEF ,∠BAF=∠F .E∴CE =CF .(2)∠BDG =45°.(3)分别连结GB 、GE 、GC (如图2) ∵AB ∥DC ,∠ABC =120°, ∴∠ECF=∠ABC=120°.∵FG ∥CE 且FG =CE ,∴四边形CEGF 是平行四边形. 由(1)得CE =CF , ∴□CEGF 是菱形.∴EG =EC ,∠GCF=∠GCE=21∠ECF= 60°.∴△ECG 是等边三角形.∴EG =CG , ① ∠GEC=∠EGC=60°. ∴∠GEC=∠GCF .∴∠BEG=∠DCG . ②由AD ∥BC 及AF 平分∠BAD 可得∠BAE =∠AEB . ∴AB=BE .在□ABCD 中,AB=DC . ∴BE=DC . ③ 由①②③得△BEG ≌△DCG . ∴BG=DG ,∠1=∠2.∴∠BGD=∠1+∠3=∠2+∠3=∠EGC=60°. ∴∠BDG=2180BGD∠- =60°.图2。
2011-2023北京中考真题数学汇编:反比例函数

2011-2023北京中考真题数学汇编反比例函数7.(2014北京中考真题)如图,在平面直角坐标系(0)ky k x=≠,使它的图象与正方形9.(2011北京中考真题)如图,在平面直角坐标系图象的一个交点为A(﹣(1)求反比例函数y=(2)若P是坐标轴上一点,且满足10.(2018北京中考真题)在平面直角坐标系线14l y x b=+∶与图象G(1)求k的值;∴由上述结果可知,分母不能为,故【点睛】本题考查反比例函数与一次函数的交点问题,曲线上点的坐标与方程的关系.9.(1)y=﹣2x;(2)(【详解】解:(1)∵点∴n=﹣2×(﹣1)=2∴点A的坐标为(﹣1∵点A在反比例函数的图象上.∴k=﹣210.(1)4;(2)①3个.【详解】分析:(1)根据点(2)①当1b =-时,根据整点的概念,直接写出区域②分a .当直线过(4,0时四种情况进行讨论即可详解:(1)解:∵点A (∴14k=,∴4k =.(2)①3个.(1,0),(②a .当直线过(4,0)时:b .当直线过(5,0)时:c .当直线过(1,2)时:1124b ⨯+=,解得74b =d .当直线过(1,3)时:1134b ⨯+=,解得114b =∴综上所述:514b -≤<-或71144b <≤.点睛:属于反比例函数和一次函数的综合题,考查待定系数法求反比例函数解析式,一次函数的图象与性质,掌握整点的概念是解题的关键,注意分类讨论思想在解题中的应用.11.(1)1(0)y x x =>不是有界函数,y=x+1(-4<x ≤2)是有界函数,边界值是3;(2)-1<b≤3;(3)0≤m≤14或34≤m≤1.【分析】(1)分析题意,结合已知中有界函数的定义可进行判断;(2)根据一次函数的性质可得1y x =-+的增加性,再结合自变量的取值范围和题意可得此不等式组可得b 的取值范围;(3)要分情况讨论,易判断1m >不符合题意,故1m;结合已知函数解析式可得函数过点以此求得其平移后的点坐标,进而可得34≤1-m≤1或-1≤-m≤34,由此即可求得m 【详解】解:(1)结合已知根据有界函数的定义可知1(0)y x x=>不是有界函数,数,边界值是3;(2)1y x =-+Q 中10-<,y 随x 的增大而减小,∴当x a =时,12=-+=y a ,故1a =-.当x b =时,1=-+y b ,根据题意可得:212b b a--+<⎧⎨>⎩ ,31b ∴>- ;(3)若1m >,函数向下平移m 个单位后,0x =时,函数值小于1-,此时函数的边界值不符,故1m.当=1x -时,1y =,即过(1,1)-,当0x =时,0min y =,即过(0,0),将(1,1)-,(0,0)都向下平移m 个单位,得到(1,1)m --,(0,)m -,根据题意可得:1m t -=或m t -=,∴34≤1-m≤1或-1≤-m≤34,0≤m≤14或34≤m≤1.【点睛】本题考查了二次函数综合题,解题的关键是结合新定义,弄清函数边界值的定义,同时要熟悉平移变换的性质.。
2011年北京延庆县中考一模《数学》试题及答案

全善学校2011—2012学年下期初三数学试题卷(总分150分,120分钟完卷)参考公式:抛物线2(0)y ax bx c a =++≠的顶点坐标为24(,)24b ac b a a--,对称轴公式为2b x a=-。
一、选择题(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.在17,0,3π-,sin30°四个实数中,无理数是 ( )A .17 B.0 C.3π- D.sin30°2.下列运算中,正确的是( )A.-4(x-1)=-4x-1B.-4(x-1)=-4x-4C.-4(x-1)=-4x+1D.-4(x-1)=-4x+43. 下列长度的三条线段能组成三角形的是 ( ) A .2cm, 2cm, 5cm B. 4cm, 4cm, 8cm C. 6cm, 8cm, 15cm D. 6cm, 8cm, 10cm4.下列图形中,是轴对称图形的是 ()5. 下列调查方式合适的是 ( )A.为了了解市民对重庆市创建全国环保模范城市的关注程度,王华在学校随机采访了8名初三学生;B.为了了解学校学生参加课外活动的情况,张民同学在初三年级向3位好友做了调查;C.为了了解“天宫一号”飞船零部件的状况,检测人员采用了普查的方式;D.为了了解中央电视台2012年春节联欢晚会的收视率,统计人员采用了普查的方式。
6. 如图,点O 是⊙O 的圆心,点A 、B 、C 在⊙O 上,AO ∥BC ,∠AOB = 40°,则∠OAC 的度数等于 ( ). A .40° B.60° C. 50° D. 20°7.二次函数2(0)y ax bx c a =++≠的图象如下图,以下结论正确的是( ) A.0abc > B.方程ax 2+bx+c=0有两个实数根分别为-2和6 C.0a b c -+< D.当4y =时,x 的取值只能为08.初三年级将要进行中招体育考试,为了提高成绩,同学们训练都很认真,黄量同学在进行1分钟跳绳训练时,制定了适合自己的训练方案,前20秒匀加速BC O CBA(第6题图)AD进行,20秒至40秒保持跳绳速度不变,后20秒继续匀加速进行,下列能反映黄量同学1分钟内跳绳速度y 个/秒与时间x 秒关系的函数图象为 ( )9. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第8个图形需要黑色棋子的个数是( )A .48B .80C .90D .8610.如图,△ABC 和△CDE 均为等腰直角三角形,点B,C,D 在一条直线上,点M 是AE 的中点,下列结论:①tan ∠AEC=CDBC; ②四边形CGMH 是矩形 ③△EGM ≌△MHA;④S △ABC +S △CDE ≥S △ACE ; ⑤图中的相似三角形有10对。
2011年北京四中分班考试数学真题答案

32 42
25
24、 解:设工作总量为“1” , 则甲做一天后余下的工作总量为: 1 所以共需要用 2+1=3 天。 25、 解:令大块阴影部分面积为 S1 ,小块阴影部分面积为 S 2 ,其余空白不过分面积为: S空白 。 则得: S1 S 2 S1 S空白 S 2 S空白 = 42 2 4+ 22 =3 -8 。 4 4 26、 (1)解:根据题意得: 1 2 11 66 ,可以分为两组和均为 66,每组和为 33.则得到:
五 C 答案
一、计算题: 1~5: 3;1
1 7 11 1 ;6~8: 2; ; ; ; 4;1; 12 108 16 12
二、选择题: 9~13:BCDBC; 14~16:CBA 部分题说明: 第 12 题:由于为直角三角形,所以共有 6 个。 第 16 题:根据题意,和为 2011,最早的为 4+2007.所以为第 1004 项。 三、填空题:
15 x 40 32 y ,根据观察,x 必为 8 的倍数, 而由于原来的新生人数在 500 到 1000 之间, 所以 x 可取 40、
48、56、64,经验证
x 40 ,所以该年级入学时该校有男生 320 名,女生 280 名。 y 20
1 3 3 1 1 , 1 ,甲、乙还需要用: 2 (天) 4 4 4 4 8
1
1
10 1 9 2 8 3 1 4 5 6 7 11
(2)解: 1 2 498 499 249 不为 2 的倍数,所以不能分成两堆数字之和相等的部分。 27、解:令快车速度为 x, 慢车速度为 y ,所以有:
北京市2011年数学中考模拟试卷及答案
ABCDE 122010~2011学年九年级综合水平质量调研数学试卷 2011.3学校___________________班级_______________姓名________________学号_____________ 考 生 须 知1. 本试卷共8页,共五道大题,25道小题,满分120分,考试时间120分钟. 2. 在试卷和答题卡上准确填写学校.班级.姓名.学号.3. 试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4. 考试结束,请将本试卷和答题卡一并交回.注意事项 1. 考生要按规定的要求在机读答题卡上作答,题号要对应,填涂要规范. 2. 考试结束后,试卷和机读答题卡由监考人一并收回.第一卷(机读卷32分)一 选 择 题 本 题32分 ,每 小 题 4 分1. 4的算术平方根是A .2B .±2C .16D .±16 2.如图,已知△ABC 为直角三角形,∠C =90°,若沿图中虚线剪去∠C , 则∠1+∠2等于 A . 90° B . 135° C . 150°D . 270°第2题图3.布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任 意摸出一个球,摸出的球是白球..的概率是 A .13B .16C .12D .564. 某班的9名同学的体重分别是(单位:千克): 61,59, 70,59,65,67,59, 63,57,这组数据的众数和中位数分别是A .59,61B .59,63C .59,65D . 57,615.全球可被人类利用的淡水总量仅占地球上总水量的0.00003,因此珍惜水、保护 水,是我们每一位公民义不容辞的责任.其中数字0.00003用科学记数法表示为 A .4103-⨯ B .5103-⨯ C .4103.0-⨯ D .5103.0-⨯6.如图,模块①-⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成. 现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体. 则下列选择方案中,能够完成任务的为A.模块②,④,⑤B.模块①,③,⑤C.模块①,②,⑤D.模块③,④,⑤一选择题本题32 分,每小题4分7. 如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是A.16π B.36π C.52π D.81π8. 矩形ABCD中,8cm6cmA D A B==,.动点E从点C开始沿边CB向点B以2cm/s的速度运动至点B停止,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:2cm),则y与x之间的函数关系用图象表示大致是下图中的第8题图第7题图注意事项1.第Ⅱ卷包括4道填空题和13道解答题,共8页.答题前要认真审题,看清题目要求,按要求认真作答.2.答题时字迹要工整,画图要清晰,卷面要整洁.3.考生除画图可以用铅笔外,答题必须用蓝色或黑色钢笔、圆珠笔.第二卷(非机读卷88分)二填空题本题共16分,每小题4分9.若分式2x4x2--的值为0,则x的值为.10. 如图,点A、B、C是半径为6的⊙O上的点,30B∠=︒,则的长为_____________.第10题图11. 如图,在△ABC中,D、E分别AB、AC边上的点,DE∥BC.若AD=3,DB=5,DE=1.2,则BC=.第11题图12. 如图,在ABC∆中,α=∠A,ABC∠的平分线与ACD∠的平分线交于点1A,得1A∠,则1A∠= .BCA1∠的平分线与CDA1∠的平分线交于点2A,得2A∠,……,BCA2009∠的平分线与CDA2009∠的平分线交于点2010A,得2010A∠,则2010A∠= .第12题图三解答题本13. (本小题5分)(31)4sin6027-+-ACOABCCAEDB题共30分,每小题5 分14. (本小题5分)解不等式组31422xx x->-⎧⎨<+⎩,并把它的解集表示在数轴上.15. (本小题5分)如图,E F、是平行四边形A B C D对角线A C上两点,BE D F∥,求证:A F C E=。
2011年北京丰台区中考一模数学试卷.pdf
纯收入分项项目 金额(元)
康
B
22.认真阅读下列问题,并加以解决: 问题 1:如图 1,△ABC 是直角三角形,∠C =90º.现将△ABC 补成一个矩形.要求:使△ABC 的两 个顶点成为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上.请将符合条件的所有矩形在图 1 中画出来;
1对
B
请根据以上信息解答下列问题: (1) “十一五”期间,农村居民人均纯收入年增长最快的是 年,计算这五年农村居民 (精确到 1%) .根据此平均增长率预测 2011 年农村居 人均纯收入的平均增长率是 民纯收入人均约为__________元(精确到个位) ; ; (2)请将图 2 中的空缺部分补充完整(补图所用数据精确到个位) (3)填写表 1 中的空缺部分.
A.
1 9
B.
1 3
C.
1 2
D.
2 3
中考交流 1 群:179048080 国际班政策群:313814793
中考交流 2 群:336717298 北京中考资料库:365384296
8. 一电工沿着如图所示的梯子 NL 往上爬,当他爬到中点 M 处时,由于地面太滑,梯子沿墙面与地面滑 下,设点 M 的坐标为(x,y) (x>0),则 y 与 x 之间的函数关系用图象表示大致是
L M N
L M N
y y y
y
O
A.
x
O
B.
x
O
C.
x
O
D.
x
9.分解因式: x y 4 xy 4 y
2
10.在函数 y
1 中,自变量 x 的取值范围是 x 2
1对
. .
二、填空题 (本题共 16 分,每小题 4 分)
2011北京中考数学模拟题
要做两个形状为三角形的框架,其中一个三角形框架的三边长分别为 角形框架的一边长为 2,欲使这两个三角形相似,三角形框架的两边长可以是 6•三角形纸片ABC 中,• A =55,■ B=75,将纸片的一角折叠,使点C 落在 MBC 内(如图),则N 1+Z 2的度数为 ___________________; 7•下面的扑克牌中,牌面是中心对称图形的是 ___________________ ;(填序号)&对于-2x y 1 = 0,当 y _____________ 时,x 0 ;9•有两个完全相同的抽屉和 3个完全相同的白色球,要求抽屉不能空着,那么第一个抽屉中 有2个球的概率是12 •点1,m ,2,n 在函数y 二-X ,1的图象上,贝U m 、n 的关系是( )1. 2. 3. 4. 2011北京中考数学模拟题•填空题(每题3分,共30分) 某公司员,月工资由 m 元增长了 10%后达到 3分解因式x -9x = 元;ACOB在函数八二2中,自变量X的取值范围是 如图,在O O 中,若半径OC 与弦AB 互相平分,且 AB =6cm ,则OC cm ; )5. 5, 6,另一个三14.如图,四边形 ABCD 内接于O O , AB 为O O 的直径, C M 切O O 于点C , . BCM =60,则.B 的正切值是A 、1B 、23C 、 2D 、 23315.如图,在方格纸中有四个图形(1)、( 2)、( 3)、(4),其中面积相等的图形是 (成x =2040,但他的计算结果仍然是正确的,你说是怎么回事?A 、 m _ nB 、 m = n 13. —个形式如圆锥的冰淇淋纸筒,其底面直径为纸筒所需纸片的面积是2 2A 、66二cmB 、30二cmc 、 m ::D 、 m n 6cm ,母线长为 5cm ,围成这样的冰淇淋( )2C 、 28二 cmD 、15: cm 2(2)和(4) D .( 1)和(4)三•解答题: 17.(本题满分 8 分)先化简,再求2X 2-2x 1 x -1 2H "2 ,X -1 X X-X 的值: ,其中x =2004,但是, 甲抄错 X = 2004 ,抄A . (1 )和(2)B . (2)和(3)C .16下面的4幅图中,经过折叠 不能围成一个立体图的一幅是D 、(在本学期某次考试中,某校初二⑴、初二⑵两班学生数学成绩统计如下表:分数5060708090100二⑴班351631112人数二⑵班251112137请根据表格提供的信息回答下列问题:⑴ 二⑴班平均成绩为__________ 分,二⑵班平均成绩为 _________ 分,从平均成绩看两个班成绩谁优谁次?⑵ 二⑴班众数为_________ 分,二⑵班众数为_________ 分。
2011年中考数学复习选择题填空题专题训练精选(精)
170.如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是() A.2 个或 3 个 B.3 个或 4 个 C.4 个或 5 个 D.5 个或 6 个主视图俯视图(第 170 题) 171.如图所示,半径为 2 的圆和边长为 5 的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过的时间为 t ,圆与正方形重叠部分(阴影部分)的面积为 S ,则 S 与 t 的函数关系式的大致图象为(). s t (A s t (B 图 s t (C s t (D ) O O O O 172. 如右图,□ABCD 中, E 为 AD 的中点。
已知△DEF 的面积为 1,则□ABCD 的面积为( A.9 B.12 C.15 D.18 A E F D B C 173.如图,在等边△ ABC 中, AC ,点 O 在 AC 上,且,点 P 是 AB 上一动点,连结 OP ,将线段 OP 绕点 O 逆时针旋转 60 得到线段 OD .要使点 D 恰好落在 BC 上,则 AP 的长是 C D O A P B 174.(2006 重庆)如图,是有几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是。
36175.用相同的小正方体搭一个几何体,使得它的主视图和俯视图如图所示,则搭这样的几何体至少需要小正方体的个数是()。
A、16 个 B、12 个 C、10 个D、8 个俯视图主视图 ( 第 175 题图 176.如图 4,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是() A.7 个B .8 个C .9 个 D.10 个 177.展览厅内要用相同的正方体木块搭成一个三视图如右图的展台,则此展台共需这样的正方体______块. 178.一个几何体由一些大小相同的小正方体组成,如图是它的主视图和俯视图,那么组成该几何体所需小正方体的个数最少为() A.3 B .4 C .5 D.6 主视图俯视图(第 178 题) 179.在一仓库里堆放着若干个相同的正方体小货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体小货箱共有( A.11 箱 B.10 箱 C .9 箱 D.8 箱 180.右图哪一个是左边正方体的展开图() 37181.(贵阳市)如图 6-1 所示,将长为 20cm,宽为 2cm 的长方形白纸条,折成图 6-2 所示的图形并在其一面着色,则着色部分的面积为( B ) A.34cm 2 B.36cm 2 C.38cm 2 D.40cm 2 182.如图,在直角梯形 ABCD 中, AD // BC ,,,,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年北京中考数学选择填空三十练(三)
一、选择题(每题只有一个正确答案,共8个小题,每小题4分,共32分) 1.-6的倒数是( ) A .6
B .
1
6
C .-
1
6
D .-6
2.下列计算中,正确的是( ) A .325a b ab =+
B .33a a a ⋅=
C .623÷a a a =
D .3262()a b a b =
3.把222a ab b -+分解因式,分解结果正确的是( ) A .2()a b -
B .2()a b +
C .222()a b -
D .22a b -
4.上海世博会主办机构预计吸引世界各地7000万人次参观者前往,总投资达450亿人民币,超过北京奥运会,是世界博览会史上最大规模的一届博览会.将“7000....万.”用科学记数法表示,并保留两个有效数字.下列表示正确的是( ) A .3710⨯
B .77.010⨯
C .87.00010⨯
D .47.010⨯
5.从小明、小凡、小丽、小红四人中用抽签的方式,选取两人为上海世博会的志愿者,那么能选中小明、小丽两人同时为上海世博会志愿者的概率为( ) A .
1
4
B .
112
C .
12
D .
16
6.下列图案中,是中心对称图形但不是轴对称图形的是( )
A .
B .
C .
D .
7.已知⊙O 1与⊙O 2相切,⊙O 1的直径为9cm ,⊙O 2的直径为4cm ,则O 1O 2的长是( ) A .5cm 或13cm B .2.5cm
C .6.5cm
D .2.5cm 或6.5cm
8.如图,如果从半径为9cm 的圆形纸片剪去1
3
圆周
的一个扇形,将留下的扇形围成一个圆锥(接缝
处不重叠),那么这个圆锥的高为( ) A .6cm B .35cm
C .8cm
D .53cm (第8题图)
二、填空题:(共4道小题,每题4分,共16分)
9.不等式组
10
x x -><,
的解集是 .
10.如图,AB 是⊙O 的弦,OD ⊥AB 于点D ,C 是AB 优弧
上任意一点,则图中所有相等的线段有 ;所
有相等的角有 . (第10题图)
11.已知甲、乙两组数据的平均数分别是80x =甲,90x =乙,方差分别是210S =甲,2
5S =乙,
比较这两组数据,说一说你从中可以得出怎样的结论: . 12.某些植物发芽有这样一种规律:当年所发新芽第二年不发芽,老芽在以后每年都发芽.
发芽规律见下表(设第一年前的新芽数为a ) 第n 年 1 2 3 4 5 … 老芽率 a a 2 a 3 a 5 a … 新芽率 0 a a 2 a 3 a … 总芽率
a
2 a
3 a
5 a
8 a
…
照这样下去,第8年老芽数与总芽数的比值为 .
一、选择题:(每题4分,共32分)
1.C.
2.D.
3. A.
4. B.
5. D.
6. C.
7. D.
8. B. 二、填空题:(每题4分,共16分)
9.0<x
10.OA=OB,AD=DB;C BOD AOD BDO ADO OBD OAD ∠=∠=∠∠=∠∠=∠,,
11.说明乙组数据平均值高且比较稳定,偏离平均值的幅度小. 12.3421。
