超前进位的原理以及应用
加法器设计介绍
加法器设计介绍算术逻辑部件主要处理算术运算指令和逻辑运算指令,它的核心单元是加法器。
这个加法器是影响算术逻辑部件整体性能的关键部分,因为几乎所有的算术运算和逻辑运算,都要通过它来完成。
加法器结构包括串行进位加法器(Carry Ripple Adder,CRA)、进位跳跃加法器(cany skip Adder,CKA),以及较高速度的进位选择加法器(carry select Adder,CSA)、超前进位加法器(Can 了Look—a}lead Adder,CLA)和并行前缀加法器(Parallel Prcfix Adder)等。
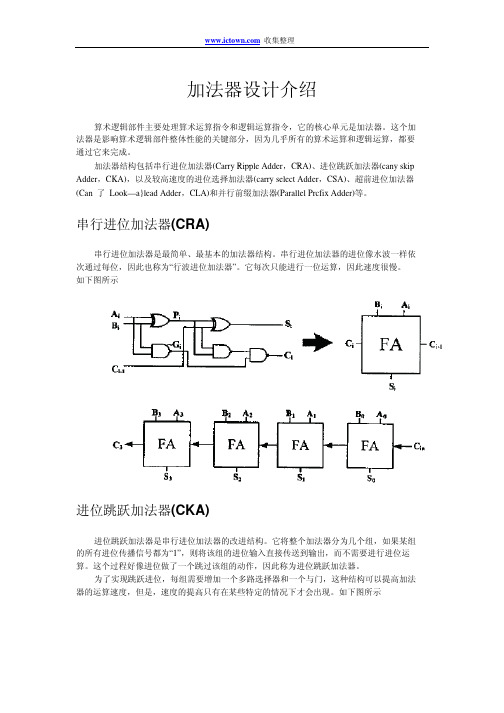
串行进位加法器(CRA)串行进位加法器是最简单、最基本的加法器结构。
串行进位加法器的进位像水波一样依次通过每位,因此也称为“行波进位加法器”。
它每次只能进行一位运算,因此速度很慢。
如下图所示进位跳跃加法器(CKA)进位跳跃加法器是串行进位加法器的改进结构。
它将整个加法器分为几个组,如果某组的所有进位传播信号都为“1”,则将该组的进位输入直接传送到输出,而不需要进行进位运算。
这个过程好像进位做了一个跳过该组的动作,因此称为进位跳跃加法器。
为了实现跳跃进位,每组需要增加一个多路选择器和一个与门,这种结构可以提高加法器的运算速度,但是,速度的提高只有在某些特定的情况下才会出现。
如下图所示进位选择加法器(CSA)进位选择加法器采用资源复制的基本思想,用硬件来换取速度。
它将整个加法器分为几个组,每组有两条路径,进位输入为“O”和“1”的两种情况通过两条路径同时计算。
一旦该组进位输入信号到来,通过多路选择器选择正确的进位输出与和值。
如下图所示由于采用了前瞻的思想,因此进位选择加法器的速度有很大提高。
如果整个加法器分为M 组,则运算延时可由第一组进位延时、M 个多路选择器的延时及一个和产生延时相加得到。
进位选择加法器虽然具有较快的速度,但由于它采用了资源复制的方法,因此实现代价也成倍增加。
超前进位加法器的verilog写法

超前进位加法器(Carry Look-Ahead Adder)是一种快速加法器,它能够在一次时钟周期内完成所有的进位计算。
与传统的串行进位加法器相比,超前进位加法器具有更高的性能。
下面是一个简单的超前进位加法器的Verilog实现:verilogmodule CLA_adder(input [3:0] a,input [3:0] b,output reg [3:0] sum,output reg cout);// Generate individual full adderswire [2:0] c_in;wire [2:0] s_in;wire [2:0] c_out;wire [2:0] g, p;FA fa0(.a(a[0]), .b(b[0]), .cin(c_in[0]), .sum(s_in[0]), .cout(c_out[0]));FA fa1(.a(a[1]), .b(b[1]), .cin(c_in[1]), .sum(s_in[1]), .cout(c_out[1]));FA fa2(.a(a[2]), .b(b[2]), .cin(c_in[2]), .sum(s_in[2]), .cout(c_out[2]));FA fa3(.a(a[3]), .b(b[3]), .cin(c_in[2]), .sum(s_in[3]), .cout(cout));// Generate carry generate and propagate signalsassign g[0] = a[0] & b[0];assign p[0] = a[0] ^ b[0];assign g[1] = a[1] & b[1] | (a[1] & p[0]) | (b[1] & p[0]);assign p[1] = a[1] ^ b[1] ^ c_out[0];assign g[2] = a[2] & b[2] | (a[2] & p[1]) | (b[2] & p[1]);assign p[2] = a[2] ^ b[2] ^ c_out[1];assign c_in[2] = g[1] | (p[1] & c_out[0]);assign c_in[1] = g[0] | (p[0] & c_out[0]);assign c_in[0] = 0;// Generate sumassign sum[0] = s_in[0];assign sum[1] = s_in[1] ^ c_out[0];assign sum[2] = s_in[2] ^ c_out[1];assign sum[3] = s_in[3] ^ cout;endmodule// Full adder modulemodule FA(input a,input b,input cin,output sum,output cout);assign {cout, sum} = a + b + cin;endmodule在这个实现中,我们首先定义了一个名为CLA_adder的模块,它接收两个4位输入a和b,并输出它们的和sum以及最高位的进位cout。
先行进位加法器

实验四32位先行进位加法器一、功能概述串行进位加法器延时很大,每级的输出结果都要等上一级的进位到来才可以求和算出结果,这次实验对普通全加器进行改良,改良为先行进位加法器。
先行进位加法器,各级的进位彼此是独立产生,只与输入数据A,B和C_in有关,将各级间的进位级联传播给去掉了,这样就可以减小进位产生的延时。
每个等式与只有三级延迟的电路对应,第一级延迟对应进位产生信号和进位传递信号,后两级延迟对应上面的积之和。
通过这种进位方式实现的加法器称为超前进位加法器。
因为各个进位是并行产生的,所以是一种并行进位加法器。
二、实验原理1、设二进制加法器第i位为A i,B i,输出为S i,进位输入为C i,进位输出为C i+1,则有:S i=A i⊕B i⊕C i(1-1)C i+1 =A i * B i+ A i *C i+ B i*C i =A i * B i+(A i+B i)* C i(1-2)令G i = A i * B i , P i = A i+B i,则C i+1= G i+ P i *C i当A i和B i都为1时,G i = 1,产生进位C i+1 = 1当A i和B i有一个为1时,P i = 1,传递进位C i+1= C i因此G i定义为进位产生信号,P i定义为进位传递信号。
G i的优先级比P i高,也就是说:当G i = 1时(当然此时也有P i = 1),无条件产生进位,而不管C i是多少;当G i=0而P i=1时,进位输出为C i,跟C i之前的逻辑有关。
下面推导4位超前进位加法器。
设4位加数和被加数为A 和B,进位输入为C in,进位输出为C out,对于第i位的进位产生G i = A i·B i ,进位传递P i=A i+B i , i=0,1,2,3。
于是这各级进位输出,递归的展开Ci,有:C0 = C inC1=G0 + P0·C0C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0▪C0C3=G2+ P2·C2= G2+ P2·G1+ P2·P1·G0+P2·P1·P0·C0C4=G3+ P3·C3= G3+ P3·G2+ P3·P2·G1+P3·P2·P1·G0 + P3·P2·P1·P0·C0 (1-3)C out=C4由此可以看出,各级的进位彼此独立产生,只与输入数据Ai、Bi和Cin有关。
东南大学数字电路实验报告(四)

数字逻辑电路实验简易数字钟日期:2013年12月6日地点:104姓名:学号:审阅教师:得分:一、实验目的(1)掌握时序逻辑电路的一般设计过程;(2)掌握时序逻辑电路的时延分析方法,了解时序电路对时钟信号相关参数的基本要求;(3)掌握QuartusⅡ5.0的使用二、实验原理特点外引线排列图•用于快速计数的内部超前进位•用于n 位级联的进位输出•同步可编程序•有置数控制线•二极管箝位输入•直接清零•同步计数典型参数:f 工作频率=32MHzPd=93mW说明:这种同步可预置十进计数器是由四个D 型触发器和若干个门电路构成,内部有超前进位,具有计数、置数、禁止、直接(异步)清零等功能。
对所有触发器同时加上时钟,使得当计数使能输入和内部门发出指令时输出变化彼此协调一致而实现同步工作。
这种工作方式消除了非同步(脉冲时钟)计数器中常有的输出计数尖峰。
缓冲时钟输入将在时钟输入上升沿触发四个触发器。
这种计数器是可全编程的,即输出可预置到任何电平。
当预置是同步时,在置数输入上将建立一低电平,禁止计数,并在下一个时钟之后不管使能输入是何电平,输出都与建立数据一致。
清除是异步的(直接清零),不管时钟输入、置数输入、使能输入为何电平,清除输入端的低电平把所有四个触发器的输出直接置为低电平。
超前进位电路无须另加门,即可级联出n 位同步应用的计数器。
它是借助于两个计数使能输入和一个动态进位输出来实现的。
两个计数使能输入(ENP 和ENT)计数时必须是高电平,且输入ENT 必须正反馈,以便使能动态进位输出。
因而被使能的动态进位输出将产生一个高电平输出脉冲,其宽度近似等于QA 输出高电平。
此高电平溢出进位脉冲可用来使能其后的各个串联级。
使能ENP 和ENT 输入的跳变不受时钟输入的影响。
电路有全独立的时钟电路。
改变工作模式的控制输入(使能ENP、ENT 或清零)纵使发生变化,直到时钟发生为止,都没有什么影响。
计数器的功能(不管使能、不使能、置数或计数)完全由稳态建立时间和保持时间所要求的条件来决定。
74LS283

S i Ai B i C i 1 C i Ai B i AiC i 1 B i C i 1
定义两个中间变量Gi和Pi : Gi= AiBi
……产生变量
Pi= Ai+Bi ……传输变量 Ki= GiPi = Ai ⊕Bi ……中间变量 Si= Ki ⊕ Ci-1
Ci= Gi+Pi Ci-1
因为进位信号只与变量Gi、Pi和 C-1有关,而C-1是向最低 位的进位信号,其值为0,即各位的进位信号都只与两个加 数A和B有关,所以它们是可以并行产生的。
74LS283逻辑图
1
& &
≥1
CO
&
Si= Ki ⊕Ci-1 Ci= Gi+Pi Ci-1 Gi= AiBi Pi= Ai+Bi Ki= GiPi = Ai ⊕Bi
Ci
0 0
0 0 1 1 1 1
0 0
1 1 0 0 1 1
0 1
0 1 0 1 0 1
0 1
1 0 1 0 0 1
0 0
0 1 0 1 1 1
如A=1101,
A3=1,A2=1,A1=0, A0=1 Ci-1表示进位输入 例:11+10=101 若看高位则A1=1 , B1=1,而低位进位输入C0=0,所以相 Ci表示进位输出 加之后C1=1,S1=0。输出的结果就是 C1S1S0=101 S表示本位和
CI CI
A3
B3
A2
B2
A1
B1
A0
B0
C 0 -1
所求结果为:C3S3S2S1S0
超前进位全加器-----74LS283
•超前进位加法原理
A0 B0 C -1 A 0 B 0 A1 B1 C -1 A 0 A 1 B 0 B 1 A 2 B 2 C -1 A 0 … A2 B0 … B2 A3 B3 C -1 A 0 … A3 B0 … B3
全加器

Ai
∑
Si
Bi
Ci-1 CI CO Ci
44
3. 加法器 实现多位加法运算的电路
两个4 位二进数制相加的过程
1101 + 1001
1 0 01
101 1 0
两个二进制数相加时,也分为不考虑低 位来的进位和考虑低位进位两种情况。 同时必须考虑各个位的进位
55
3. 加法器 4位加法器逻辑框图
加数 被加数 低位进位
组合逻辑电路
1.加法器概念 2.加法器应用
11
加法器概念: 两个1 位二进制数相加
分为不考虑低位来的进位和考虑低位进位两种情况
1.半加器:只考虑本位两个二进制数相加,而不考虑来自低位进 位的运算电路。
2.全加器:除考虑本位两个二进制数相加外,还考虑来自低位进 位的运算电路。
A
S
∑
B
C
Ai
Si
Bi
∑
C2 FA3
C3 进位逻辑 C3
S0
S1
S2
S3
• 进位输入是由专门的“进位逻辑门”来提供 • 该门综合所有低位的加数、被加数及最低位进位输入
超前进位加法器使每位的进位直接由加数和被加数 产生,而无需等待低位的进位信号
99
74LS283逻辑图
B3
&
≥1
A3
B2
&
≥1
A2
B1
&
≥1
A1
B0
&
≥1
A0
进位 和
66
3. 加法器 实现多位加法运算的电路
串行进位加法器
其低位进位输出端依次连至相邻高位的进
位输入端,最低位进位输入端接地。因此,高位 数的相加必须等到低位运算完成后才能进行,这 种进位方式称为串行进位。运算速度较慢。
加法器的门级结构
两个二进制数之间的运算无论是加减乘除,目前在计算机中都是化作若干步加法运算进行的。
因此加法器是构成算数运算器的基本单元。
1 半加器如果不考虑来自低位的进位,将两个一位二进制数相加,称为半加。
半加器真值表输入输出A B S CO 0 0 0 0 0 1 1 0 1 0 1 0 111半加器逻辑表达式以及其逻辑图和符号S=A BCO=AB加法器一位加法器半加器全加器多位加法器串行进位加法器超前进位加法器=1B A S &BA CO∑ BA S CO COCO2 全加器将两个对应位的加数和来自低位的进位3个数相加,这种运算称为全加,对应电路称为全加器。
全加器真值表全加器的逻辑表达式由真值表观察:S= A B CI + A B CI + A B CI + A B CICO= A B CI + A B CI + A B CI + A B CICO的卡诺图由卡诺图化简CO的逻辑表达:CO= B CI + A CI + A B反演定理:对于任意一个逻辑式Y ,若将其中所有的的”.”换成”+”,”+”换成”.”,0换成1,1换成0,原变量换成反变量,反变量换成原变量。
则得到的结果就是Y 。
这个规律叫做反演定理。
根据反演定理,CO =(A+B )(A+CI)(B+CI) = AB+A CI+B CI最终得到结果CO = AB+A CI+B CI ①至于为什么要化成带有非门的形式,我也正在收集资料。
以后再研究吧利用卡诺图合并0再求反的方法可以直接得到表达式①CO 的卡诺图S 的卡诺图不能合并,直接写出0项再求反: S=A B CI+ A B CI+ A B CI+A B CI ②全加器的逻辑图和符号3串行进位加法器4位串行进位加法器每一位的相加结果都必须等到低一位的进位产生以后才能建立起来。
因此把这种结构的加法器叫做串行进位加法器。
它的缺点是运算速度慢,优点是结构简单。
在对运算速度要求不高的设备中,这种加法器也是一种可取的选择。
加法器、比较器
74LS85逻辑表达式
Y( A B ) A3 B3 ( A3 B3 ) A2 B2 ( A3 B3 ) ( A2 B2 ) A1 B1 ( A3 B3 ) ( A2 B2 ) ( A1 B1 ) A0 B0 (A3 B 3 ) (A 2 B 2 ) (A1 B1 ) A 0 B 0 ) I ( A B )
1位数值比较器
设A>B时L1=1;A<B时L2=1;A=B时L3=1。 得1位数值比较器的真值表。
A 0 0 1 1
B 0 1 0 1
L1 (A>B) 0 0 1 0
L2 (A<B) 0 1 0 0
L3 (A=B) 1 0 0 1
逻 辑 表 达 式
L1 AB L2 A B L3 A B AB A B AB
VCC B2 A2 S2 B3 A3 S3 C3 16 15 14 13 12 11 10 9 74LS283 1 2 3 4 5 6 7 8 S1 B1 A1 S0 B0 A0 C0-1 GND TTL 加法器 74LS283 引脚图
V DD B3 C3 S3 S2 S1 S0 C0-1 16 15 14 13 12 11 10 9 4008 1 2 3 4 5 6 7 8 A3 B2 A2 B1 A1 B0 A0 VSS CMOS 加法器 5、4.26、2.27
《数字电子技术基础》(第五版) 清华大学自动化系 阎石 王红
第四章 组合逻辑电路
4.3.5 数值比较器
一 1位数值比较器
二 4位数值比较器
三 数值比较器的位数扩展
本节小结
比较器:用来完成两个二进制数的大小比较的逻辑 电路称为数值比较器,简称比较器。
※ 加法器工作原理※
第十六讲 若干常用中规模组合逻辑电路-加法器※ 加法器工作原理 ※Lecture《数字电子技术基础》第十六讲 若干常用中规模组合逻辑电路-加法器█ 加法器概述两个二进制数之间的算术运算无论是加、减、乘、除, 目前在数字计算机中都是化为若干步加法运算和移位进行 的。
因此,加法器是构成算术运算器的基本单元。
目前,常用加法器分类如下:加 法 器1位加法器半加器 全加器多位加法器串行进位加法器 超前进位加法器《数字电子技术基础》第十六讲 若干常用中规模组合逻辑电路-加法器█ 1位全加器 ◆ 半加器(Half-adder)若不考虑有来自低位的进位将两个1位二进制数相加, 称为半加。
实现半加运算的电路叫做半加器。
半加器的逻辑表达式:表1 半加器的真值表 输入 A B 0 0 1 1 0 1 0 1 输出 S CO 0 1 1 0 0 0 0 1⎧ S = AB + AB = A ⊕ B ⎨ ⎩CO = AB 半加器的逻辑电路及符号:Σ《数字电子技术基础》第十六讲 若干常用中规模组合逻辑电路-加法器◆ 全加器(Full-adder)将两个多位二进制数相加时,除了最低位以外,每一位 都应考虑来自低位的进位,即将两个对应的加数和来自低位 的进位3个数相加。
这种运算称为全加,所用电路称为全加器。
表2 全加器的真值表输 入 CI A B 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1输 出 S CO 0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1⎧ ⎪S = A⋅ B⋅ CI + AB⋅ CI + AB⋅ CI + AB⋅ CI ⎨ ⎪ ⎩CO = A⋅ B + B⋅ CI + A⋅ CI⎧S = A⊕ B ⊕ CI 或⎨ ⎩CO = AB+ CI( A + B)《数字电子技术基础》第十六讲 若干常用中规模组合逻辑电路-加法器图11位全加器74LS183的逻辑图和惯用图形符号 《数字电子技术基础》第十六讲 若干常用中规模组合逻辑电路-加法器█ 1位全加器的Verilog-HDL设计⎧ S = A ⊕ B ⊕ CI 或⎨ ⎩CO = AB + CI ( A + B )and (m1,a,b), (m2,b,cin), (m3,a,cin); xor (s1,a,b), (sum,s1,cin); or (cout,m1,m2,m3); endmodule//1位全加器设计module full_add1 (a,b,cin,sum,cout); input a,b,cin; output sum,cout; wire s1,m1,m2,m3;《数字电子技术基础》第十六讲 若干常用中规模组合逻辑电路-加法器█ 多位全加器 ◆ 串行进位加法器设计思想:依次将低位全加器的进位输出端CO接到高 位全加器的进位输入端CI即可构成多位串行加法器。
第2章+组合逻辑电路-解玉凤
输出逻辑函数表达式:
Y=
∑ EN ⋅ m ⋅ I
i i =0
MUX En S0 S1 S2 EN 0 2 0 1 2 3 4 5 6 7
7
i
}
G
0 7
Y Y
I0 I1 I2 I3 I4 I5 I6 I7
Y Y
2011-3-14
数字逻辑基础
23
复旦大学信息科学与工程学院
2.2 组合逻辑电路的设计
基于门电路的设计 基本的设计方法。 基于组合逻辑模块的设计 利用组合电路模块实现主要功能,辅以门电 路,结构比较简单。 运算电路设计 需要熟悉二进制运算的特点,采用迭代设计。
2011-3-14
数字逻辑基础
24
复旦大学信息科学与工程学院
一、基于门电路的设计方法
逻辑抽象 确定输入 输出关系 定义输入 输出变量
真 值 表
逻辑函数 表达式
化简 与 变换
逻辑图 (电路图)
2011-3-14
数字逻辑基础
25
复旦大学信息科学与工程学院
例1: 完成以下设计
带控制端的 3 位输入代码检测电路 当控制端 P 为 0 时,输入 >3 并且 <6 时输出为 1 当控制端 P 为 1 时,输入 <6 时输出为 1 要求完成最简设计
数字逻辑基础
Y 1 1 1 1 1 1 0 0
27
复旦大学信息科学与工程学院
步骤2、卡诺图以及化简
PA BC
00 01 11 10
0 1 1 1 0 1 1 1 0 0 0 1 0 0 0 1
00 01 11 10
Y = AB + P A
2011-3-14
数字逻辑基础
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超前进位的原理以及应用
1. 什么是超前进位
超前进位是计算机领域中的一种进位方式。
在二进制计算中,进位是当两个二
进制数相加时,某一位的和大于等于2时,需要进位到高位的过程。
而超前进位
是指当某一位的和超过了一个固定的阈值时,就会提前进位。
2. 超前进位的原理
超前进位的原理是基于二进制计算的进位规则进行的优化。
在传统的二进制进
位规则中,只有当两个二进制数相加后的和大于等于2时,才会发生进位。
然而,如果事先知道某一位要进位的概率很大,就可以提前进位,从而提高计算的效率。
3. 超前进位的应用
超前进位主要应用于数字信号处理、高性能计算和加密算法等领域。
下面列举
了一些超前进位的应用:
•高性能计算中的并行计算:在并行计算中,超前进位可以减少处理器之间的通信和同步开销,从而提高整体计算速度。
•数字信号处理中的滤波器设计:超前进位可以优化滤波器的结构,减少计算复杂度,提高滤波器的性能。
•加密算法中的数据加密和解密:超前进位可以在加密和解密过程中提高计算效率,从而加快数据的加密和解密速度。
4. 超前进位的优势
超前进位相比传统的进位方式有以下优势:
•提高计算速度:超前进位利用提前进位的方式,减少了多次进位的次数,从而提高了计算的速度。
•减少资源消耗:超前进位减少了多次进位的次数,减少了处理器和存储器之间的数据传输次数,从而降低了资源的消耗。
•降低功耗:超前进位减少了计算中的多次进位操作,降低了功耗,有助于节能和延长设备的使用寿命。
•提高系统的稳定性:超前进位减少了多次进位操作的次数,减少了出现进位错误的可能性,从而提高了系统的稳定性和可靠性。
5. 超前进位的实现方式
超前进位的实现方式主要包括以下几种:
•基于硬件的超前进位:通过硬件电路实现超前进位,例如使用逻辑门、加法器等电路实现超前进位。
•基于软件的超前进位:通过编程实现超前进位,例如使用编程语言的位运算符号来实现超前进位。
•基于算法的超前进位:通过优化算法实现超前进位,例如通过矩阵运算、排序算法等来实现超前进位。
6. 总结
超前进位是一种优化的进位方式,通过提前进位来提高计算效率,减少资源消耗,并提高系统的稳定性。
超前进位在数字信号处理、高性能计算和加密算法等领域有广泛的应用。
通过硬件、软件和算法等方式可以实现超前进位的功能。
采用超前进位技术可以提高计算效率,从而进一步推动计算机技术的发展和应用。
