模型的分割和拼接(精)
三年级秋季班第17讲-图形的拼割-教师版

图形的拼割【教学目标】1.学生参与剪割、拼摆、粘贴等活动、初步掌握形的分解与组合方法,提高动手能力。
2.培养和发展学生的形象思维能力、创造能力和审美能力3.感受学习几何数学所带来的乐趣【教学重点】1.了解认识两个图形的组合能拼出不同的图形2.掌握形的分解组合方法,发展学生的形象思维和创造能力【教学难点】感受学习几何数学所带来的乐趣【教学工具】三角板、若干三角形纸片、正方形纸片、长方形纸片、圆形纸片等【教学过程】※知识精讲图形的分割与拼接的概念把一个几何图形按某种要求分成几个图形,就叫做图形的分割.反过来,按一定的要求也可以把几个图形拼成一个完美的图形,就叫做图形的拼合.将一个或者多个图形先分割开,再拼成一种指定的图形,则叫做图形的剪拼.我们在图形的分割、拼合和剪拼的过程中,都要结合所提供的图形特点来思考.如果把一个图形分割成若干个大小、形状相等的部分,那么就要想办法找图形的对称点,把图形先分少,再分多.图形中,如果有数量方面的要求,可以先从数量入手,找出平分后每块上所含数量的多少,再结合数量来分割图形.如果是要把几个图形拼合成一个大图形,要特别注意每条边的长度,把相等的边长拼合在一起,先拼少的,再拼多的.如果是剪拼图形,要抓住“剪、拼前后图形的面积相等”这个关键,根据已知条件和图形的特点,通过分析推理和必要的计算,确定剪拼的方法.※习题精讲例1.右图是一个3×4的方格纸,请用四种不同的方法将它分割成完全相同的两部分,但要保持每个小方格的完整.【分析与解】因为要分割成完全相同的两块,即大小、形状完全相同.方格纸一共有3×4=12(个)小格,所以分成的两块每块有12÷2=6(个)小格,并且这两块要关于中心点对称,大小和形状完全一样,我们从对称线入手,介绍一种分割技巧——染色法,先选中一个小格,找它关于中心点或中心线的对称位置,标上相应的符号,当找它关于中心线的对称位置时是一种情况,关于中心点的对称位置是另一种情况,具体如下图所示.例2.将右图分割成五个大小相等的图形分析与解:因为图中共有15个小正方形,所以分割成的图形的面积应该等于15÷5=3(个)小正方形的面积。
积木中的数学知识

积木中的数学知识积木作为一种深受儿童喜爱的玩具,不仅具有娱乐性,还蕴含了丰富的数学知识。
本文将探讨积木中涉及的数学知识,主要包含以下几个方面:1.几何形状:积木通常由各种几何形状组成,如矩形、正方形、三角形、圆形等。
通过组合这些形状,可以构建出各种不同的结构。
在搭积木的过程中,孩子们可以学习到不同几何形状的性质和特点。
2.空间关系:在搭积木时,需要考虑到各部分之间的空间关系,如大小、位置、方向等。
这有助于培养孩子们的空间感知能力和对空间关系的理解。
3.比例与尺度:在构建较大的模型时,需要使用不同大小和比例的积木。
通过调整比例和尺度,可以训练孩子们对比例和尺度的感知和运用能力。
4.组合与排列:搭积木的过程涉及到组合和排列的问题。
不同的组合和排列方式可以产生不同的效果,有助于培养孩子们的逻辑思维和创造性思维。
5.空间想象力:通过观察和想象积木的组合方式,可以培养孩子们的空间想象力和创造力。
他们可以尝试在脑海中构建出不同的形状和结构,并将其表现出来。
6.体积与表面积:在计算使用多少积木来构建某个形状时,会涉及到体积和表面积的概念。
这有助于孩子们理解物体的三维属性和二维属性。
7.对称性与旋转:许多积木形状具有对称性,通过旋转或翻转某些部分,可以形成对称的结构。
这有助于培养孩子们对对称性和旋转的理解。
8.分割与拼接:将一个整体分割成多个部分,或者将多个部分拼接成一个整体,是搭积木中常见的操作。
这有助于培养孩子们的分割思维和整体思维。
9.逻辑推理:在解决搭积木过程中遇到的问题时,需要进行逻辑推理。
例如,确定某个形状需要多少块积木、如何组合这些积木以达到预期效果等。
这有助于培养孩子们的逻辑推理能力。
总之,搭积木是一种充满数学知识的活动。
通过搭积木,孩子们可以在玩乐中学习到各种数学概念和方法,提高自己的数学素养和思维能力。
图形的剪拼
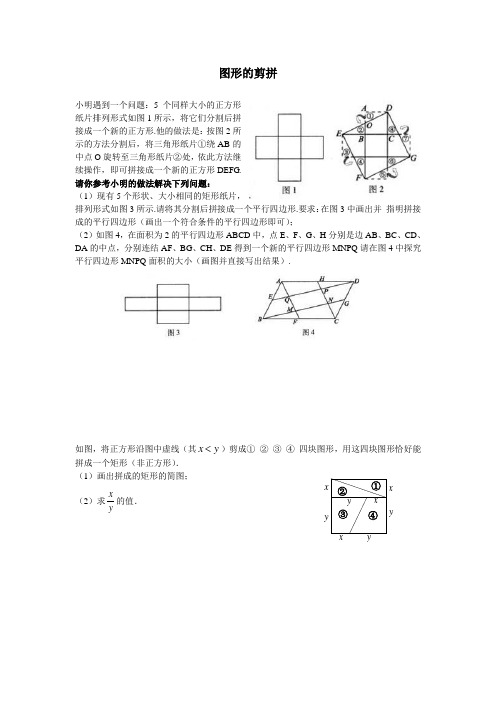
图形的剪拼小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB 的中点O 旋转至三角形纸片②处,依此方法继续操作,即可拼接成一个新的正方形DEFG . 请你参考小明的做法解决下列问题:(1)现有5个形状、大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形.要求:在图3中画出并 指明拼接成的平行四边形(画出一个符合条件的平行四边形即可);(2)如图4,在面积为2的平行四边形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,分别连结AF 、BG 、CH 、DE 得到一个新的平行四边形MNPQ 请在图4中探究平行四边形MNPQ 面积的大小(画图并直接写出结果).如图,将正方形沿图中虚线(其x y )剪成① ② ③ ④ 四块图形,用这四块图形恰好能拼成一个矩形(非正方形). (1)画出拼成的矩形的简图;(2)求xy的值.yy xy x y x x④③②①小明想把一个三角形拼接成面积与它相等的矩形.他先进行了如下部分操作,如图1所示:①取△ABC 的边AB 、AC 的中点D 、E ,联结DE ;②过点A 作AF ⊥DE 于点F ;(1)请你帮小明完成图1的操作,把△ABC 拼接成面积与它相等的矩形.(2)若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形,那么原三角形的一边与这边上的高之间的数量关系是________________.(3)在下面所给的网格中画出符合(2)中条件的三角形,并将其拼接成面积与它相等的正方形.已知等边三角形纸片ABC 的边长为8,D 为AB 边上的点,过点D 作DG BC ∥交AC 于点G .DE BC ⊥于点E ,过点G 作GF BC ⊥于点F ,把三角形纸片ABC 分别沿DG DE GF ,,按图1所示方式折叠,点A B C ,,分别落在点A ',B ',C '处.若点A ',B ',C '在矩形DEFG 内或其边上,且互不重合,此时我们称A B C '''△(即图中阴影部分)为“重叠三角形”.(1)若把三角形纸片ABC 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A B C D ,,,恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A B C '''的面积;(2)实验探究:设AD 的长为m ,若重叠三角形A B C '''存在.试用含m 的代数式表示重叠三角形A B C '''的面积,并写出m 的取值范围(直接写出结果,备用图供实验,探究使用).ABCDEF(图1)A GC F B ' C ' E BD A '图1 AG C F B ' C ' E B D A ' 图2 A A解:(1)重叠三角形A B C '''的面积为 ;(2)用含m 的代数式表示重叠三角形A B C '''的面积为 ;m 的取值范围为 .问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为(0)x x >.依题意,割补前后图形的面积相等,有25x =,解得5x =.由此可知新正方形的边长等于两个正方形组 成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.请你参考小东同学的做法,解决如下问题:现有10个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形.要求:在图4中画出分割线,并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形. 说明:直接画出图形,不要求写分析过程. 解:图1 图2 图3 图4 图5图4F E DC BA如图1是一个三棱柱包装盒,它的底面是边长为10cm 的正三角形,三个侧面都是矩形.现将宽为15cm 的彩色矩形纸带AMCN 裁剪成一个平行四边形ABCD (如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A 的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究. (1)请在图4中画出拼接后符合条件的平行四边形; (2)请在图2中,计算裁剪的角度(即∠ABM 的度数).已知菱形纸片ABCD 的边长为8,∠A=60°,E 为AB 边上的点,过点E 作E F ∥BD 交AD 于点F .将菱形先沿EF 按图1所示方式折叠,点A 落在点A '处,过点A '作GH ∥BD 分别交线段BC 、DC 于点G 、H,再将菱形沿GH 按图1所示方式折叠,点C 落在点C '处, C G '与C 'H 分别交A E '与A F '于点M 、N .若点C '在△CN DBMA 图2图1C'A 'N M HG FE DCBAAB CDE F GHM N A 'C'DCBAA 'EF 的内部或边上,此时我们称四边形A MC N ''(即图中阴影部分)为“重叠四边形”.图1 图2 备用图(1)若把菱形纸片ABCD 放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A 、B 、C 、D 、E 恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形A MC N ''的面积;(2)实验探究:设AE 的长为m ,若重叠四边形A MC N ''存在.试用含m 的代数式表示重叠四边形A MC N ''的面积,并写出m 的取值范围(直接写出结果,备用图供实验,探究使用). 解:(1)重叠四边形A MC N ''的面积为 ;(2)用含m 的代数式表示重叠四边形A MC N ''的面积为______________;m 的取值范围为_____________.1)观察与发现小明将三角形纸片()ABC AB AC >沿过点A 的直线折叠,使得AC 落在AB 边上,折痕为AD ,展开纸片(如图①);再次折叠该三角形纸片,使点A 和点D 重合,折痕为EF ,展平纸片后得到AEF △(如图②).你认为AEF △是什么形状的三角形?A A图⑤图④图③GF FC'GD'FABCDEABC D EABCD E(2)实践与运用将矩形纸片ABCD (AB <CD )沿过点B 的直线折叠,使点A 落在BC 边上的点F 处,折痕为BE (如图③);再沿过点E 的直线折叠,使点D 落在BE 上的点D '处,折痕为EG (如图④);再展平纸片(如图⑤).猜想△EBG 的形状,证明你的猜想,并求图⑤中∠FEG 的大小.(1)如图22(1),△ABC 中,DE ∥BC 分别交AB ,AC 于D ,E 两点,过点E 作EF ∥AB 交BC 于点F .请按图示数据填空:四边形DBFE 的面积S = ,△EFC 的面积1S = , △ADE 的面积2S = . 22(1)探究发现(2)在(1)中,若BF a =,FC b =,DE 与BC 间的距离为h .请证明2124S S S =. 拓展迁移(3)如图22(2),□DEFG 的四个顶点在△ABC 的三边上,若△ADG 、△DBE 、△GFC 的面积分别为2、5、3,试利用..(2.)中的结论....求△ABC 的面积. 22(2)问题背景:在△ABC 中,AB 、BC 、AC 三边的长分别为2、13、17,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网BCDG FE AB CD FEAS1S 2 S 3 6 2格中画出格点△ABC (即△ABC 三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC 的高,而借用网格就能计算出它的面积.AB C图3图2图1(1)请你将△ABC 的面积直接填写在横线上.________ 思维拓展:(2)我们把上述求△ABC 面积的方法叫做构图法.若△ABC 三边的长分别为2a 、25a 、26a (0)a >,请利用图2的正方形网格(每个小正方形的边长为a )画出相应的△ABC ,并求出它的面积是: . 探索创新:(3)若△ABC 三边的长分别为224m n +、2216m n +、222m n +(0,,)m n o m n >>≠ ,请运用构图法在图3指定区域内画出示意图,并求出△ABC 的面积为: .小伟遇到这样一个问题:如图1,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O .若梯形ABCD 的面积为1,试求以AC 、BD 、AD +BC 的长度为三边长的三角形的面积.A B D CE F 图3小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D 作AC 的平行线交BC 的延长线于点E ,得到的△BDE 即是以AC 、BD 、AD +BC 的长度为三边长的三角形(如图2).参考小伟同学的思考问题的方法,解决下列问题:如图3,△ABC 的三条中线分别为AD 、BE 、CF .(1)在图3中利用图形变换画出并指明以AD 、BE 、CF的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以AD 、BE 、CF 的长度为三边长的三角形的面积等于_______. 如图1,在△ABC 中,已知∠BAC =45°,AD ⊥BC 于D ,BD =2,DC =3,求AD 的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB 、AC 为对称轴,画出△ABD 、△ACD 的轴对称图形,D 点的对称点为E 、F ,延长EB 、FC 相交于G 点,得到四边形AEGF 是正方形.设AD =x ,利用勾股定理,建立关于x 的方程模型,求出x 的值. (1)请你帮小萍求出x 的值.(2) 参考小萍的思路,探究并解答新问题: 如图2,在△ABC 中,∠BAC =30°,AD ⊥BC 于D ,AD =4.请你按照小萍的方法画图,得到四边形AEGF ,求△BGC 的周长.(画图所用字母与图1中的字母对应)图1 图222.阅读下列材料:小明遇到一个问题:如图1,正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点,连结AF 、BG 、CH 、DE ,形成四边形MNPQ .求四边形MNPQ 与正方形ABCD 的面积比(用含n 的代数式表示).小明的做法是:先取n=2,如图2,将△ABN 绕点B 顺时针旋转90゜至△CBN ′,再将△ADM 绕点D 逆时针旋转90゜至△CDM ′,得到5个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是15; BBCAD OADC EO图2图1然后取n=3,如图3,将△ABN 绕点B 顺时针旋转90゜至△CBN ′,再将△ADM 绕点D 逆时针旋转90゜至△CDM ′,得到10个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是410,即25; ……请你参考小明的做法,解决下列问题:(1)在图4中探究n=4时四边形MNPQ 与正方形ABCD 的面积比(在图4上画图并直接写出结果);(2)图5是矩形纸片剪去一个小矩形后的示意图,请你将它剪成三块后再拼成正方形(在图5中画出并指明拼接后的正方形).22. 阅读下列材料:小贝遇到一个有趣的问题:在矩形ABCD 中,AD=8cm ,AB=6cm. 现有一动点P 按下列方式在矩形内运动:它从A 点出发,沿着AB 边夹角为45︒的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45︒的方向作直线运动,并且它一直按照这种方式不停地运动,即当P 点碰到BC 边,沿着BC 边夹角为45︒的方向作直线运动,当P 点碰到CD 边,再沿着与CD 边夹角为45︒的方向作直线运动,…,如图1所示,问P 点第一次与D 点重合前与边相碰几次,P 点第一次与D 点重合时所经过的路线的总长是多少. 小贝的思考是这样开始的:如图2,将矩形ABCD 沿直线CD 折迭,得到矩形A 1B 1CD ,由轴对称的知识,发现P 2P 3=P 2E ,P 1A=P 1E.请你参考小贝的思路解决下列问题:M’N’Q P N G H F E DCB A M Q P NG H F E D C B A M M’N’M A B C D E F H G N P Q C P G D Q H M N F B E A 图图 图1 图3 图4图5 圖1 ABC D P P 1P 2 P 3 A B C D EP A 1 P 1 P 2 P 3 B 1 圖2(1) P 点第一次与D 点重合前与边相碰_____次;P 点从A 点出发到第一次与D 点重合时所经过的路径的总长是_________cm ;(2) 进一步探究:改变矩形ABCD 中AD 、AB 的长,且满足AD>AB ,动点P 从A 点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD 相邻的两边上。
2019年秋七年级数学校本--第四节《分割图形》教案

第4节分割图形授课时间:教学目标:让学生了解图形的分割;会根据要求进行分割图形;利用分割图形来解决计算等问题.教学重难点:根据题目需要找合适的方法进行图形的分割教学过程:分割图形是使我们的头脑灵活,增强观察能力的一种有趣的游戏。
我们先来看一个简单的分割图形的题目──分割正方形。
在正方形内用4条线段作“井”字形分割,可以把正方形分成大小相等的9块,这种图形我们常称为九宫格。
用4条线段还可以把一个正方形分成10块,只是和九宫格不同的是,每块的大小不一定都相等。
那么,怎样才能用4条线段把正方形分成10块呢?请你先动脑筋想想,在动脑的同时还要动手画一画其实,正方形是不难分割成10块的,下面就是其中两种分割方法。
一、图形的分割把一个几何图形按某种要求分成几个图形,就叫做图形的分割.如果把一个图形分割成若干个大小、形状相等的部分,那么就要想办法找图形的对称点,把图形先分少,再分多.在图形中,如果有数量方面的要求,可以先从数量入手,找出平分后每块上所含数量的多少,再结合数量来分割图形.怎样把一个图形按照要求分割成若干部分?怎样把一个图形分割成若干部分后,再按要求拼接成另一个图形?这就是本节的问题。
例1将下图分割成五个大小相等的图形。
分析与解:因为图中共有15个小正方形,所以分割成的图形的面积应该等于15÷5=3(个)小正方形的面积。
3个小正方形有和两种形式,于是可得到很多种分割方法,下图是其中的三种。
例2下图是一个4×4的方格纸,请在保持每个小方格完整的情况下,将它分割成大小、形状完全相同的两部分。
分析与解:因为分割成完全相同的两块,所以每块有8个小方格,并且这两块关于中心点对称。
下面是六种分割方法。
例3下图分割成两块,然后拼成一个正方形。
分析与解:图形的面积等于16个小方格,如果以每个小方格的边长为1,那么拼成的正方形的边长应是4。
因为题图是缺角长方形,长为6宽为3,所以分割成两块后,右边的一块应向上平移1(原来宽为3,向上平移1使宽为4),向左平移2(原来长为6,向左平移2使长为4)。
基于Transformer的脊柱CT图像分割

基于Transformer的脊柱CT图像分割作者:毛孝鑫,宋烨,郝泳涛来源:《电脑知识与技术》2021年第20期摘要:脊柱侧弯是青少年群体常见的一种脊柱疾病,老年群体中因脊柱骨质疏松引起的脊柱骨折也尤为普遍。
CT成像技术作为脊柱外科的主要检查手段之一,广泛用于临床以及研究目的的筛查,诊断和图像引导治疗。
研究以脊柱CT图像为研究对象,将目前在NLP领域表现优异的Transformer模型与经典的U-Net图像分割网络相结合,运用到CT图像的分割处理工作当中;同时在模型训练过程中基于脊柱自身的结构特点,采用由粗到精的训练方法,首先对脊柱的各个椎骨进行定位模型训练,然后在定位結果的基础上再训练分割模型。
最终模型的分割结果与真实值之间的Dice相似系数达到了94.37%以上,实验结果表明了该方法的有效性以及临床应用的可行性。
关键词:CT图像;U-Net;图像分割;Transformer;自注意力中图分类号:TP399 文献标识码:A文章编号:1009-3044(2021)20-0124-03Spine CT Image Segmentation Based on TransformerMAO Xiao-xin1, SONG Ye2, HAO Yong-tao1(1.CAD Research Center of Tongji University, Shanghai 201804, China; 2.Xiaoyi Technology co., LTD., Shanghai 201203, China)Abstract:Scoliosis is a common spinal disease in adolescents, and spinal fractures caused by osteoporosis of the spine are particularly common in the elderly. As one of the main detection methods of spinal surgery, CT imaging technology is widely used in clinical and research purposes for screening, diagnosis, and image-guided treatment. This research takes CT images of the spine as the research object and combines the Transformer model, which is currently excellent in the field of NLP, with the classic U-Net image segmentation network, and applies it to the segmentation of CT images. And based on the structural characteristics of the spine itself, the training method from coarse to fine is adopted in the model training process. First, a model is trained for performing vertebra localization, and then the segmentation model is trained based on the vertebra localization results. Finally, the Dice similarity coefficient between the segmentation result and the true value reached more than 94.37%. The experimental results show the effectiveness of the method and the feasibility of a clinical application.Key words: CT image; U-net; image segmentation; transformer; self-attention脊柱作为人体中最为重要的中轴骨骼,是肌肉骨骼系统的重要组成部分。
单体化模型实训总结报告

一、实训背景随着三维地理信息系统(3D GIS)的广泛应用,单体化模型作为3D GIS中重要的组成部分,其构建质量直接影响着系统的应用效果。
为了提高单体化模型的构建效率和质量,本实训旨在通过实际操作,掌握单体化模型的构建方法和流程,并对实训过程中遇到的问题进行分析和总结。
二、实训目的1. 熟悉单体化模型的构建方法和流程;2. 掌握不同类型单体化模型的构建技巧;3. 提高单体化模型的构建效率和质量;4. 分析实训过程中遇到的问题,并提出解决方案。
三、实训内容1. 单体化模型概述单体化模型是指将复杂的建筑物、道路、桥梁等实体拆分成多个独立的部分,以便进行单独的编辑、处理和分析。
单体化模型在3D GIS中具有以下作用:(1)提高可视化效果,使场景更加真实;(2)方便进行空间分析和查询;(3)提高模型的交互性和可操作性。
2. 单体化模型的构建方法单体化模型的构建方法主要有以下几种:(1)基于倾斜摄影测量数据:利用倾斜摄影测量数据,通过分割、贴图、优化等步骤,构建单体化模型;(2)基于建筑信息模型(BIM):利用BIM数据进行单体化模型的构建,结合遥感影像进行纹理贴图;(3)基于三维激光扫描数据:利用三维激光扫描数据,通过分割、贴图、优化等步骤,构建单体化模型。
3. 单体化模型的构建流程单体化模型的构建流程主要包括以下步骤:(1)数据预处理:对原始数据进行检查、清洗和预处理,确保数据质量;(2)模型分割:将建筑物、道路、桥梁等实体进行分割,得到多个子模型;(3)贴图处理:根据需要,对子模型进行纹理贴图,提高模型的视觉效果;(4)模型优化:对模型进行优化处理,包括网格简化、压缩等,提高模型的加载速度和渲染效果;(5)模型拼接:将多个子模型进行拼接,生成完整的单体化模型。
4. 实训案例本次实训选取了某城市建筑群作为案例,通过倾斜摄影测量数据和建筑信息模型,构建了单体化模型。
具体步骤如下:(1)数据预处理:对倾斜摄影测量数据和建筑信息模型进行预处理,确保数据质量;(2)模型分割:利用倾斜摄影测量数据,对建筑物进行分割,得到多个子模型;(3)贴图处理:根据建筑信息模型,对子模型进行纹理贴图;(4)模型优化:对模型进行优化处理,包括网格简化、压缩等;(5)模型拼接:将多个子模型进行拼接,生成完整的单体化模型。
三维裁剪算法
三维裁剪算法三维裁剪算法是计算机图形学中的一种重要算法,它可以用来对三维模型进行裁剪,从而实现对三维模型的显示和处理。
在计算机图形学中,三维裁剪算法是非常重要的,因为它可以帮助我们实现对三维模型的精确处理和显示,从而提高计算机图形学的应用效果和实用性。
三维裁剪算法的基本原理是将三维模型分割成多个小块,然后对每个小块进行裁剪,最后将所有小块合并起来,得到完整的三维模型。
这个过程需要使用到一些数学知识和计算机图形学的基本算法,比如平面方程、向量运算、矩阵变换等等。
三维裁剪算法的实现过程可以分为以下几个步骤:1. 将三维模型分割成多个小块。
这个过程需要根据三维模型的形状和大小来确定分割的方式和数量。
一般来说,可以将三维模型分割成多个立方体或长方体,然后对每个小块进行裁剪。
2. 对每个小块进行裁剪。
这个过程需要使用到平面方程和向量运算等数学知识。
首先,需要确定裁剪面的位置和方向,然后将裁剪面转换成平面方程的形式。
接着,需要将小块中的每个顶点和面都进行裁剪,得到裁剪后的顶点和面。
这个过程需要使用到向量运算和矩阵变换等计算机图形学的基本算法。
3. 将所有小块合并起来,得到完整的三维模型。
这个过程需要将每个小块的裁剪结果进行合并,得到完整的三维模型。
这个过程需要使用到三维模型的拼接和合并算法,以及一些计算机图形学的基本算法。
三维裁剪算法的应用非常广泛,可以用来实现对三维模型的显示和处理。
比如,在计算机游戏中,三维裁剪算法可以用来实现对游戏场景的裁剪,从而提高游戏的运行效率和流畅度。
在工业设计和建筑设计中,三维裁剪算法可以用来实现对产品和建筑模型的裁剪,从而提高设计的精度和效率。
在医学图像处理中,三维裁剪算法可以用来实现对医学图像的裁剪和分割,从而提高医学诊断的准确性和效率。
三维裁剪算法是计算机图形学中非常重要的一种算法,它可以帮助我们实现对三维模型的精确处理和显示,从而提高计算机图形学的应用效果和实用性。
在未来的发展中,三维裁剪算法将会得到更广泛的应用和发展,成为计算机图形学领域中的重要技术和工具。
ply模型的切片算法_解释说明
ply模型的切片算法解释说明1. 引言1.1 概述在当今的制造业和建筑设计领域中,3D打印技术得到了广泛应用。
针对三维模型进行切片是3D打印中一项重要的算法,它将模型按照一系列水平层次进行切割,以便于后续的打印和制造。
本文将重点讨论ply模型的切片算法。
1.2 文章结构本文分为五个部分:引言、ply模型的切片算法、应用场景和意义、算法评估与改进以及结论。
在引言部分,我们将介绍文章的背景和目的,并概括阐述ply模型切片算法所涉及的内容。
接下来,在ply模型的切片算法部分,我们将详细介绍该算法的基本原理、预处理步骤和实现过程。
然后,在应用场景和意义部分,我们将探讨该算法在制造业领域、建筑设计领域以及计算机图形学研究中的具体应用价值。
随后,在算法评估与改进部分,我们将介绍评估该切片算法精度与效率的方法,并讨论其局限性以及可能的改进思路和措施。
最后,在结论部分,我们将总结文章的主要内容,并提出一些展望。
1.3 目的本文旨在深入探究ply模型的切片算法,全面了解其原理和实现方式。
通过介绍和讨论该算法的应用场景和意义,我们希望读者能够更好地理解该算法在实际领域中的重要性。
同时,通过评估和改进该算法,我们希望能够提高其切片精度和效率,并为今后的研究提供参考。
本文旨在为读者提供一个全面而清晰的ply模型切片算法指南,以促进相关领域的发展和应用。
2. ply模型的切片算法2.1 切片算法介绍切片算法是一种基于三维模型的分层处理技术,它将三维模型转化为一系列二维平面切片,并提取出每个切片所包含的几何信息。
在ply模型的切片算法中,我们使用面元数据结构来表示三角网格模型。
2.2 点云数据预处理在进行切片算法之前,需要对ply模型中的点云数据进行预处理。
首先,我们需要通过采样或者降采样等方法来减少点云数据的数量,从而提高算法效率。
其次,对采样后的点云数据执行滤波操作,以去除可能存在的离群点和噪声。
最后,根据需要进行坐标变换或者旋转操作,使得点云数据符合切片算法的要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拼接示例2
同时成型两个不同原型
Thank You!
模型的分割和拼接
引言
在实际快速原型制作过 程中,若原型尺寸相对于快 速成型系统台面尺寸过大、 过复杂无法去除支撑或过小, 就必须对STL模型进行分割 处理或拼接处理。
快速成型技术数据处理
原型尺寸过大
ห้องสมุดไป่ตู้
原型尺寸过小
无法去除内部支持
快速成型技术数据处理
1. 分 割
原理:将一个STL文件分成两个新STL文件,即用多个面 将一个STL模型分成若干个部分,每个部分重新构成一个 独立的STL模型。
快速成型技术数据处理
由于模型基本无较大的 曲面,且零件为蜂窝状 结构,制作时不易变形,
分割成4个子块
所以分割主要考虑尺寸
的均匀及拼合
2 1 Contents 3
4
各字块成型完成后,需要将其粘结复原再进行后处理。
快速成型技术数据处理
分割示例2
无法去除 支撑,内 表面无法 进行后处 理打磨
2. 拼 接
快速成型技术数据处理
原理:在两个原STL模型不发生干涉的情况下,按一定
的要求对某一个STL模型进行平移或旋转变换,然后把 两个STL模型数据都保存在一个STL文件中,从而两个
STL模型变成了一个新STL模型。
拼接形式:
同一模型拼接
不同模型拼接
快速成型技术数据处理
拼接示例1
同时成型多个相同原型
快速成型技术数据处理
分割时需要考虑的因素: 不要从零件结构上的曲面部分进行分割 分割好的每一个部分尺寸能尽可能均匀收缩 后续拼合方便且不留明显痕迹 Contents Contents
快速成型技术数据处理
分割示例1
上图所示零件外形尺寸为:
854.2×349.8×71.2mm, Contents Contents 受限于成型设备的工作空间尺寸,必须对其进行分割
