奥数精讲与测试
(完整版)八年级奥数精讲与测试中位线及其应用(无答案)
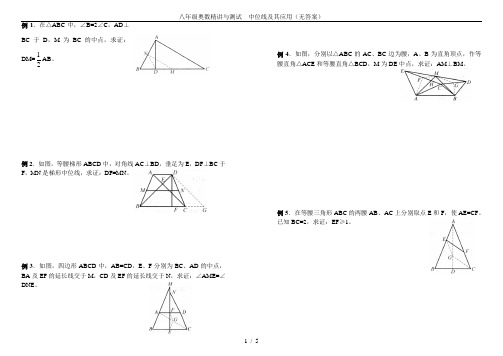
例1.在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证:DM=12 AB。
例2.如图,等腰梯形ABCD中,对角线AC⊥BD,垂足为E,DF⊥BC于F,MN是梯形中位线,求证:DF=MN。
例3.如图,四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA及EF的延长线交于M,CD及EF的延长线交于N,求证:∠AME=∠DNE。
例4.如图,分别以△ABC的AC、BC边为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为DE中点,求证:AM⊥BM。
例5.在等腰三角形ABC的两腰AB、AC上分别取点E和F,使AE=CF。
已知BC=2,求证:EF≥1。
A卷一、填空题01.如果等腰梯形底角是45°,高等于上底的2倍,那么梯形中位线与高之比为_________。
02.已知梯形两对角线中点连线长5cm,梯形下底长20cm,则上底长为_________。
03.如图128,E是AC的中点,D在边BC上,且CD=2BD,AD与BE 相交于F。
已知△BDF的面积是1,那么△ABC的面积是_________。
04.如图129,梯形ABCD的面积是12,则以梯形四边中点为顶点的四边形EFMN的面积是_________。
05.已知梯形ABCD中,AD∥BC,对角线AC把中位线EF(E在AB上)分成1 : 3两部分,则S ADFE:S BCFE=_________。
06.如图130,在梯形ABCD中,AB∥CD,EF是中位线,EF与AC相交于G,且EF=16cm,EG−GF=4cm,则AB的长是_________cm。
07.如图131,已知△ABC中,AB=AC,延长AB至D,使BD=AB,E 是AB的中点,CD=4,则CE=_________。
08.如图132,在△ABC中,E、F分别为AB、AC上的点,且BE=CF,M、N分别为BF、CE的中点,过M、N的直线交AB于P,交AC于Q。
八年级奥数精讲与测试 中位线及其应用
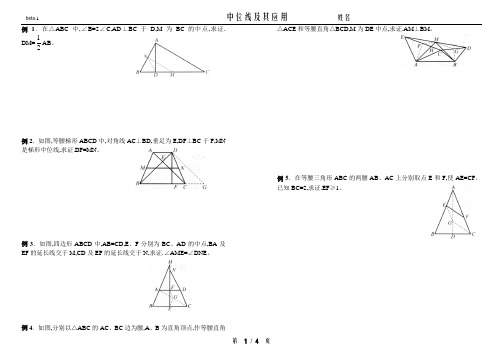
例1.在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证.DM=12 AB。
例2.如图,等腰梯形ABCD中,对角线AC⊥BD,垂足为E,DF⊥BC于F,MN 是梯形中位线,求证.DF=MN。
例3.如图,四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA及EF的延长线交于M,CD及EF的延长线交于N,求证.∠AME=∠DNE。
例4.如图,分别以△ABC的AC、BC边为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为DE中点,求证.AM⊥BM。
例5.在等腰三角形ABC的两腰AB、AC上分别取点E和F,使AE=CF。
已知BC=2,求证.EF≥1。
A卷一、填空题01.如果等腰梯形底角是45°,高等于上底的2倍,那么梯形中位线与高之比为_________。
02.已知梯形两对角线中点连线长5cm,梯形下底长20cm,则上底长为_________。
03.如图128,E是AC的中点,D在边BC上,且CD=2BD,AD与BE相交于F。
已知△BDF的面积是1,那么△ABC的面积是_________。
04.如图129,梯形ABCD的面积是12,则以梯形四边中点为顶点的四边形EFMN的面积是_________。
05.已知梯形ABCD中,AD∥BC,对角线AC把中位线EF(E在AB上)分成1 : 3两部分,则S ADFE:S BCFE=_________。
06.如图130,在梯形ABCD中,AB∥CD,EF是中位线,EF与AC相交于G,且EF=16cm,EG−GF=4cm,则AB的长是_________cm。
07.如图131,已知△ABC中,AB=AC,延长AB至D,使BD=AB,E是AB的中点,CD=4,则CE=_________。
08.如图132,在△ABC中,E、F分别为AB、AC上的点,且BE=CF,M、N分别为BF、CE的中点,过M、N的直线交AB于P,交AC于Q。
因式分解-奥数精讲与测试8年级

例1.分解因式:⑴a6-b6;⑵a2+b2+c2-2bc+2ca-2ab;⑶a7-a5b2+a2b5-b7例2.分解因式:⑴a3+b3+c3-3abc;⑵x3+y3+3xy-1. 例3.分解因式:(x-1)3+(x-2) 3+(3-2x) 3例4.分解因式:x3-5x+4.例5.分解因式:x5n+x n+1.例6.分解因式:(x+1)4+(x2-1)2十(x-1) 4.例7.分解因式:a4+b4+c4-2a2b2-2b2c2-2c2a2A卷一、填空题01.分解因式(a+b)2+(a-b) 2+c(a2+b2)=_________。
02.计算2222002200120032002200220012001的结果等于_________。
03.已知x3+x2+x+1=0,那么x2008十2x2000+5x1996的值是_________。
04.分解因式(x2+3x-3)(x2十3x+4)-8=_________。
05.将多项式x2-4y2-9z2-12yz分解成因式的积,结果是_________。
06.把(1- x2)(1- y2)+4xy因式分解,结果是_________。
07.已知x-1是多项式x3-3x+k的一个因式,那么这个多项式的其它因式有_________。
08.分解因式(x2-1)(x4+x2+1)- (x3+1)2 =_________。
09.分解因式a3b+ab+30b的结果是_________。
10.分解因式(x-2y)x3-(y-2x) y3=_________。
二、解答题11.分解因式a3+b3+c3-3abc.12.已知x y,且x3-x=7,y3-y=7,那么x2+xy+y2的值是多少?B卷一、填空题01.分解因式ab(c2-d2)-cd(a2-b2)=_________。
02. 若x2+y2+54=2x+y,那么x y+y x= _________。
03.分解因式x4+x3+6x2+5x+5=_________。
九年级奥数培训和圆有关的比例线段-奥数精讲与测试

知识点、重点、难点在圆中,有相交弦定理、切割线定理及其推论,这些定理统称圆幂定理。
1.相交弦定理:圆内的两条相交弦被交点分成的两条线段长的积相等。
推论:若弦与直径垂直相交,则弦的一半是它分直径所成的两部分的比例中项。
2.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段的积相等。
3.与圆有关的比例线段问题的一般思考方法:(1)直接应用圆幂定理; (2)找相似三角形,当证明有关线段的比例式、等积式不能直接运用基本定理时,通常是由“三点定形法”证三角形相似,其一般思路为等积式→比例式→中间比→相似三角形。
圆幂定理用乘积的形式反映了圆内的线段的比例关系,它们之间有着密切的联系,我们应当熟悉以下基本图形。
例题精讲例1:如图,已知⊙1O 与⊙2O 相交于A 、B 两点,过点A 作⊙1O 的切线,交⊙2O 于点C ,过点B 作两圆的割线分别交⊙1O 、⊙2O 于点D 、E ,DE 与AC 相交于点P .当AD 与⊙2O 相切,且PA = 6,PC =2,PD =12时,求AD 的长。
解 连结AB .因为CA 切⊙1O ;于点A ,所以∠1 =∠D .又∠1=∠E ,所以∠D =∠E .又∠2=∠3,所以△APD ∽△CPE ,所以PA PDPC PE=, 即PA ·PE = PC ·PD .因为PA =6,PC =2,PD =12,得6×PE =2×12,得PE =4.由相交弦定理得PE ·PB =PA ·PC ,所以4PB =6×2,得PB =3.所以BD = PD -PB =9,DE =DP +PE =12+4=16.因为DA 切⊙2O 于点A ,所以DA 2= DB ·DE ,即AD 2=9×16,得AD =12.例2:如图,已知圆内接四边形ABCD ,延长AB 、DC 交于E ,延长AD 、BC 交于F ,EM 、FN 为圆的切线,分别以E 和F 为圆心、EM 和FN 为半径作弧,两弧交于K ,求证:EK ⊥FK .证明 连结EF ,过B 、C 、E 三点作圆交EF 于H ,连结CH .因为B 、C 、H 、E 共圆,所以∠1=∠2.因为A 、B 、C 、D 共圆,所以∠1=∠3,于是∠2 =∠3,故D 、C 、H 、F 共圆.由切割线定理得EM 2=EC ·ED=EH ·EF ,FN2= FC ·FB=FH ·FE ,所以EM2+FN 2=(EH +FH )·EF =EF 2.又因为EM=EK ,FN=FK ,所以EK 2+FK 2=EF 2.故△EKF 为直角三角形,且∠EKF =90°,即EK ⊥FK .例3:如图,⊙1O 与⊙2O 相交于P 、Q 两点,在公共弦QP 延长线上取一点M ,过M 作两圆割线分别交两圆于A 、B 、C 、D . 求证:.AD BD DMAC CB CM=证明 由切割线定理得MA ·MB = MP ·MQ =MC ·MD ,所以A 、B 、D 、C 四点共圆,可得∠ADB =∠ACB .又11sin ,sin 22ADB ACB S AD BD ADB S AC BC ACB ∆∆=∠=∠,所以.ADB ACB S AD BDS AC BC∆∆=过C 作CG ⊥MB ,垂足为G ,过D 作DH ⊥MB ,垂足为H .所以CG ∥DH ,得△MGC ∽△MHD ,得.ADB ACB S DH DMS CG CM∆∆==所以AD BD AC BC =.DMCM例4:如图,两个同心圆的圆心为O ,大圆的弦AD 交小圆于B 、C ,大 圆的弦AF 切小圆于E ,经过B 、E 的直线交大圆于M 、N ,求证:(1) AE 2= BN ·EN ;(2)若AD 经过圆心O ,且AE = EC ,求 ∠AFC 的度数。
奥数小学三年级精讲与测试 第二讲 平均数

第二讲平均数知识点、重点、难点在日常生产和生活中,我们经常遇见求平均数问题,如求一个年级学生的平均身高、体重等等.将几个不相等的数,在它们的总数一定的情况下,通过”移多补少”的方法,使这几个不相等的数变成相等的数,这个相等的数,叫做这几个数的平均数.解答平均数应用题时,要搞清总数、份数和平均数三者之间的关系:平均数=总数÷份数,必须注意的是”份数应与总数、平均数相对应”.例题精讲例1 在4个同样的杯子中倒有饮料,高度分别是11厘米、12厘米、14厘米和15厘米,这四个杯子中饮料的平均高度是多少?分析:求平均高度,要先将所有饮料的高度加起来,再除以4就可以了.解(11+12+14+15)÷4=13(厘米)答:这四个杯子中饮料的平均高度是13厘米例2 佩明小学有28位女教师,平均年龄35岁,有4位男教师,平均年龄27岁,这些教师平均年龄是多少岁?分析:要求平均年龄,先要求出所有教师的年龄总和:女教师的年龄和+男教师的年龄和,再用年龄总和除以所有教师的人数.解(35×28+27×4)÷(28+4)=34(岁)答:这些教师平均年龄是34岁例3 某电脑大卖场七月份卖出了1924台组装电脑,八月份卖出了2096台组装电脑,九月份卖出了2420台组装电脑,这个大卖场第三季度平均每天卖出电脑多少台?分析:要求出每天的销售量,必须用总的销售量除以第三季度的总天数.解(1924+2096+2420)÷(31×2+30)=70(台)答:这个大卖场第三季度平均每天卖出电脑70台例4 连续5个正整数的和是100,这五个数分别是多少?分析:连续五个和是100,中间的数就是这五个数的平均数.只要将100除以5就可以求出中间数,然后再写出其他的数.解100÷5=20.其他的数分别是18、19、21、22答:这五个数分别是18、19、20、21、22例5 连续8个单数的和是160,这八个单数分别是多少?分析:把8个单数分成每2个数一组,每组的和相等,可以求出中间两个数的和,由于是连续的单数,那么中间两个数的差是2,就能求出中间两个数.解160÷(8÷2)=40.第四个数为(40-2)÷2=19,第五个数为(40+2)÷2=21答:这八个连续单数分别是13、15、17、19、21、23、25、27.例6 把1~999分成20组,已知这20组中每一组的平均数都相等,求这个相等的平均数分析:每组的平均数就等于1~999的平均数.解(1+999)×999÷2÷999=(1+999)÷2=500.答:这个相等的平均数是500.例7 七个数的平均数是62,把其中一个数改为90,平均值为74,这个数原来是几?分析:现在的平均值提高了,总值也比原来的总值提高了,总值之差就是这个数原来与现在的差,用90减去总值的差就可以算出原来的数解90-(74×7-62×7)=6答:这个数原来是6.例8 有四个数,每次取其中三个数相加,结果分别是32、34、35和37,这四个数分别是几?分析:把这四个数看作A、B、C、D,每次三个数相加,就是A+B+C、A+B+D、A+C+D、B+C+D,四个结果相加就是A+B+C+A+B+D+A+C+B+B+C+D=3(A+B+C+D),这样就可以求出四个数之和,然后再分别求出每一个数.解(32+34+35+37)÷3=46.46-32=14,46-34=12,46-35=11,46-37=9.答:这四个数分别是14、12、11和9.例9 小云爬山,从山脚出发,上山路长18千米,每小时行3千米,到山顶后沿原路下山,每小时行6千米,问小云上山,下山的平均速度是多少?分析:注意不可以用(上山速度+下山速度)÷2,正确的平均速度应该等于总路程÷总时间. 解总路程=18×2=36(千米),总时间=18÷3+18÷6=9(小时).平均速度=36÷9=4(千米/小时).答:小云上山、下山的平均速度是4千米/小时.例10 有8个数的平均数是9,前5个平均数是8,后4个平均数是11,第5个数是多少?分析:分别利用平均数先求出几个数的总数,再考虑第5个数即在前5个数中又在后4个数中,这9个数的总数比8个数的总数就是多了第5个数,所以可以通过前5个数的总数与后4个数的总数之和减去8个数的总数求得解(5×8+4×11)-8×9=84-72=12.答:第5个数是12.水平测试2A 卷一、填空题1.一个同学的语文成绩是85分,数学成绩是93分,体育成绩是92分,则他三门学科的平均成绩是_________分2.植树节10个好朋友去植树,种两棵树的有两人,种三棵树的有三人,种四棵树的有两人,种五棵树的有一人,种七棵树的有两人,那么平均每人种__________棵树.3.小明四门成绩的平均分是92.5,若已知语文,音乐,体育的成绩分别为96、95、80,那么他的数学成绩是_______分4.一个同学学写字,他要求自己平均每天练8张纸.从星期一到星期四每天都已练了9张纸,星期五有事没有练,星期六练了10张,那么星期天要练________张才能达到他的要求. 5.两个班的数学平均成绩分别是85分和89分,若两个班的学生人数相同,那么两个班合起来的平均分是_______分.6.上题中若两个班的学生人数对应是30人和38人,那么此时两个班合起来的平均成绩是______分(结果保留小数一位).7.小红爱吃糖,妈妈规定平均每天吃4颗,小红前10天平均每天吃了5颗,那么后5天中平均吃_________颗才能达到妈妈的要求.8.小明、小刚、小亮三人的平均体重是38千克,小明、小刚的平均体重是40千克,小亮体重______千克;又若小明比小刚重4千克,小明体重是_____千克,小刚体重是_____千克.二、解答题9.小文语文、数学、外语的平均分是92分,若他外语是88分,那么语文、数学平均分是多少?10.某学校派出8人参加数学竞赛,结果有2人分别得了72分,有3人分别得了79分,有3人分别得了73分,那么他们的平均成绩是多少?11.三个好朋友争做好事,一个做好事8件,另一个是他的2倍,第三个则是前两人所做好事之和还多3件,问三人平均做了多少件好事?12.三个数的平均数是120,加上一个数,四个数的平均数是115,这个数是多少?B 卷一、填空题1.一班有书54本,二班有书63本,老师又拿来37本书,应分给一班_______本,其余给二班时两个班的数才会一样多.2.小华玩跳绳,前三次平均跳165下,要使跳四次的平均数达到170下,她第四次应跳绳____下3.小明的数学、英语、语文三门平均成绩是92分,其中数学比平均成绩高6分,英语和语文成绩相同,那么英语是_____分4.一只船从A码头顺水以每小时30千米的速度向B码头驶去,然后又以每小时20千米的速度从B码头逆水驶回A码头.已知两个码头相距300千米,这只船在A、B之间往返一次的平均速度是______.5.18个人合影留念,照3张的价格为四元五角,另外加冲洗费每张三角.如果每人各一张照片,那么每人应付_____角.6.30人组成的老年学习班中,老爷爷的平均年龄70岁,老奶奶的平均年龄75岁,若老爷爷与老奶奶的人数相同,则平均______岁;若老爷爷12位,则平均年龄是______岁.7.三个人跳绳,小红与小新的个数之和是237个,小红与小江的个数之和是258个.而小新与小江的个数之和是255个,则三人平均跳了_____个,其中_____跳得最多,是_____个.8.五个学生的平均成绩是91分,若其中小明与小王的平均分为92分,小李和小刚的平均分为87分,而小刚与小明的平均分是88分.已知小刚比小李多6分,那么这个小组中小明_____分,小王______分,小李______分,小刚_____分;小杨_____分.二、解答题9.已知A、B、C、D、E五个数,前三个数的平均数是12,后三个数的平均数是9,而中间三个数的平均数是10,那么首、尾、中间三个数(即A、C、E)的平均数是多少?10.食品店将3千克单价为18元的水果糖、6千克单价为15元的奶糖混合成什锦糖,则每千克什锦糖的单价是多少元?11.七个数的平均数是136,按从小到大排列,前四个数的平均数为115,最大的四个数的平均数为154,那么从小到大排的第四个数是几?12.邮递员从甲地到乙地送信,上坡路30千米,每小时走5千米;平路16千米,每小时走8千米;下坡路14千米,每小时走7千米,问邮递员平均每小时走多少千米?C 卷一、填空题1.一批水果有苹果和橘子两种,装成若干袋,平均每袋185千克.已知苹果有5袋,平均每袋是203千克.而橘子平均每袋重170千克,则橘子有_____袋.2.在一次考试中,6位学生中的5位成绩分别为85、95、76、97、87,第6位学生的成绩比前5位学生的平均成绩多6分,那么6位学生的平均成绩是_____分.3.原来四人小组的平均分为70.加入一人后,平均成绩提高了2分.那么新加入的同学成绩为_____分4.若A、B、C表示1~9中的数字,若A、B9、C26这三个数的平均数为103,那么A+B+C=_____.5.小文买了3支笔和6本本子,一共用了9.6元.若一支笔比一本本子贵1.4元,那么每本本子_____元.6.甲、乙、丙、丁四人称体重,甲乙共重70.5千克,乙丙共重74.5千克,丙丁共重79千克.若已知甲比丁轻3千克,那么甲、乙、丙、丁分别重______千克?7.小王骑车过桥,上桥时20米/秒,下桥时30米/秒,那么小王过桥的平均速度是______米/秒.8.小明做数学题,前4天每天做20题,后来6天,每天又多做了15题,那么他在这10天中平均每天做_____题.二、解答题9.糖果店将甲种糖4千克、乙种糖3千克、丙种糖5千克混合成什锦糖出售,若甲、乙、丙三种糖的单价分别是每千克14元、10元、8元,那么什锦糖每千克的单价是多少元? 10.一辆汽车越过一个土丘,上坡的距离是下坡距离的一半,上坡速度为30千米/小时,下坡速度是40千米/小时,那么平均速度是多少?11.某班有40名学生,数学期中考试,有两名同学因故缺考,这时班级平均分为89分,缺考的同学补考各得99分,这个班级数学期中考试平均分是多少?12.在一次外语测试中,一小组的6位学生中的5位成绩是98分、86分、89分、78分、95分,第6位学生的成绩比这个小组6位学生的平均成绩多4分,求第6位学生的成绩.平均数答案:水平测试2A 卷1.90 (85+93+92)÷3=90(分).2.4 (2×2+3×3+4×2+5+7×2)÷10=4(课).3.99 92.5×4-(96+95+80)=99(分).4.10 8×7-9×4-10=10(张).5.87 (85+89)÷2=87(分).6.87.2 (85×30+89×38)÷(30+38)=5932÷68≈87.2(分).7.2 [4×(10+5)-5×10]÷5=2(颗).8. 34,42,38.38×3-40×2=34(千克);(40×2+4)÷2=42(千克);(40×2-4)÷2=38(千克).9.语文、数学平均分是94分.(92×3-88)÷2=94(分).10.他们的平均成绩是75分(72×2+79×3+73×3)÷(2+3+3)=(144+237+219)÷8=600÷8=7511.三人平均17件好事.(8+8×2+8+8×2+3)÷3=(48+3)÷3=17(件).12.100 115×4-120×3=100.B 卷1.23 (54+63+37)÷2-54=23(本).2.185 170×4-165×3=185(下).3.89 [92×3-(92+6)]÷2=89(分)或92-6÷2=89(分).4.每小时24千米. 300×2÷[300÷30+300÷20]=24(千米/小时).5.5 [45+3×(18-3)]÷18=5(角)6.72.5;73 (70×15+75×15)÷30=72.5(岁);(70×12+75×18)÷30=73(岁).7.125,小江,138.(237+258+255)÷6=125(个);由于258>255>237,且258个是小红与小江的,255个是小新与小江的,所以小江最多;125×3-237=138(个).8.86,98,84,90,97.小刚:(87×2+6)÷2=90(分);小李:90-6=84(分);小明:88×2-90=86(分);小王:92×2-86=98(分);小杨:91×5-92×2-87×2=97(分).9.由A+C+E=(A+B+C)+(C+D+E)-(B+C+D),可知平均数为(12×3+9×3-10×3)÷3=11.10.16元 (18×3+15×6)÷(3+6)=16(元).11.124 (115×4+154×4)-136×7=124.12.6千米/时.先求出邮政员上坡、平路和下坡各用的时间.上坡:30÷5=6(小时),平路:16÷8=2(小时),下坡:14÷7=2(小时).(30+16+14)÷(6+2+2)=6(千米/时).C 卷1.6 (203-185)×5÷(185-170)=6(袋)2.89 (85+95+76+97+87)÷5+(6÷6)=89(分)3.80 70+(4+1)×2=80(分)4.13 由A+B9+C26=103×3=309,可知A=4,B=7,C=2,所以A+B+C=13.5.0.6 (9.6-1.4×3)÷(6+3)=0.6(元)6.36,34.5,40,39 甲=(70.5+79-74.5-3)÷2=36(千克);乙=70.5-36=34.5(千克);丙=74.5-34.5=40(千克);丁=36+3=39(千克).7.24设整个桥长2s,则平均速度为2s÷(s÷20+s÷30)=(2s×60)÷(s×3+s×2)=120s÷5s=24(米/秒).8.29 20+(15×6÷10)=29(题).9.这种什锦糖的单价为每千克10.5元.(14×4+10×3+8×5)÷(4+3+5)=10.5(元).10.过土丘的平均速度为36千米/小时.设上坡距离为s,则下坡距离为2s.(s+2s)÷(s÷30+2s÷40)=3s÷(s÷30+s÷20) =(3s×60)÷(s×2+s×3)=180×s÷(5×s)=180÷5=36(千米/小时).11.89.5分. (89×38+99×2)÷40=3580÷40=89.5(分).12.(98+86+89+78+95+4×6)÷(6-1)=94(分).。
奥数小学三年级精讲与测试_第4讲_植树问题

第4讲植树问题知识点、重点、难点以植树为内容,研究植树的棵树、棵与棵之间的距离(棵距)和需要植树的总长度(总长)等数量间关系的问题,称为植树问题.植树问题在生活中很有实际运用价值,其基本数量关系和解题的要点是:1.植树问题的基本数量关系:每段距离×段数=总距离.2.在直线上植树要根据以下几种情况,弄清棵数与段数之间的关系:(1)在一段距离中,两端都植树,棵数=段数+1;(2)在一段距离中,两端都不植树,棵数=段数-1;(3)在一段距离中,一端不植树,棵数=段数.3.在封闭曲线上植树,棵数=段数.例1 有一条长1000米的公路,在公路的一侧从头到尾每隔25米栽一棵树苗,一共需要准备多少棵树苗?分析:先将全长1000米的公路每25米分成一段,一共分成多少段?种树的总棵树和分成的段数的关系是棵数=段数+1.解1000÷25+1=41(棵).例2 公路的一旁每隔40米有木电杆一根(两端都有).共121根.现改为水泥电杆51根(包括两端),求两根相邻水泥电杆之间的距离.分析:公路全长为40×(121-1)解40×(121-1)÷(51-1)=40×120÷50=96(米).例3 两幢大楼相隔115米,在其间以等距离的要求埋设22根电杆,从第1根到第15根电杆之间相隔多少米?分析:在相距115米的两幢大楼之间埋设电杆,是两端都不埋电杆的情况,115米应该分成22+1=23段,那么每段长是115÷23=5米,而第1根到第15根电杆间有15-1=14段,所以第1根到第15根电杆之间相隔(5×14)米.解115÷(22+1)×(15-1)=115÷23×14=70(米)例4 工程队打算在长96米,宽36米的长方形工地的四周打水泥桩,要求四角各打一根,并且每相邻两根的距离是4米,共要打水泥桩多少根?分析:先求出长方形的周长是(96+36)×2=264米,每4米打一根桩,因为是沿着长方形四周打桩,所以段数和根数相等,可用264÷4来计算.解 (96+36)×2÷4=132×2÷4=66(根).例 5 一个圆形水库,周长是2430米,每隔9米种柳树一棵.又在相邻两棵柳树之间每3米种杨树1棵,要种杨树多少棵?分析:沿着封闭的圆形水库四周植树,段数与棵数相等,沿着2430米的四周,每隔9米种柳树一棵,共可种2430÷9=270棵,也就是把水库四周平分成270段.又在相邻两棵柳树之间,每隔3米种杨树一棵,每段可种9÷3-1=2棵,总共可种杨树2×270=540棵.解 (9÷3-1)×(2430÷9)=2×270=540(棵)例 6 红星小学有125人参加运动会的入场式,他们每5人为一行,前后两行的距离为2米,主席台长32米.他们以每分钟40米的速度通过主席台,需要多少分钟?分析:这是一道与植树问题有关的应用题.利用"有125人,每5人为一行"可求出一共有125÷5=25行,行数相当于植树问题中的棵数,"前后两行距离是2米"相当于每两棵树之间的距离,这样可求出队伍的长度是2×(25-1)米.再加上主席台的长度,就是队伍所要走的距离.用队伍所要走的距离,除以队伍行走的速度,可求出所需行走的时间了.解 [2×(125÷5-1)+32]÷40=[2×24+32]÷40=80÷40=2(分钟).水平测试 4A 卷一、填空题1.学校有一条长80米的走道,计划在走道的一旁栽树,每隔4米栽一棵.(1)如果两端都栽树,那么共需要______棵树.(2)如果两端栽柳树,中间栽杨树,那么共需要______杨树.(3)如果只有一端栽树,那么共需要______棵树.2.一个圆形水池的周长是60米,如果在水池的四周每隔3米放一盆花,那么一共能放______盆花.3.16米的校园大道两边都种上树苗,从路的两头起每隔2米种一棵,共种______棵4.蚂蚁爬树枝,每上一节需要10秒.它从第一节爬到第13节需要_______秒5.一根木料长24分米,现在要将这跟木料锯成长度相等的6段,每锯一次要10秒,共要______秒.二、解答题6.同学们布置教室,要将一根200厘米长的彩带剪成20厘米长的小段.如果彩带不能折叠,需要剪多少次?7.公园的一个湖的周长是1800米,在这个湖的周围每隔20米种一棵柳树.然后在每两棵柳树之间每隔4米种一棵迎春花,需要柳树多少棵、迎春花多少棵?8.在一幢高25层的大楼里,甲、乙两个比赛爬楼梯.甲到9楼时,乙刚上到5楼.照这样的速度,当甲到了顶层时乙到了几楼?9.一个人以均匀的速度在路上散步,从第1根电线杆走到第7根电线杆用了12分钟,这个人走了30分钟,他走到了第几根电线杆?他走到第30根电线杆处,用了几分钟?10.甲村到乙村,原计划栽树175棵,相邻两棵树距离8米,后决定改为栽树117棵,问相邻两树应相距多少米?11.一次检阅,接受检阅的一列彩车车队共30辆,每辆车长4米,前后两车相隔5米,问这列车队共长多少米?一、填空题1.有一条长1000米的公路,在公路两边从头到尾每隔10米栽一棵树,共可栽______棵树.2.两幢楼房相距90米,现在要在两楼之间每隔10米种一棵树,需要种_____树.3.一根木料锯成4段需要18分钟,改成锯8段要_____分钟.4.园林工人放盆花,每7盆花距离12米.照这样计算,36盆花的距离是______米.5.某街心公园新辟一条小道长50米,从头到尾在小道的一旁等距离放6个长5米的花坛,花坛间隔是_____米.6.师专附小举行运动会入场仪式,四年级有246名同学排成6路纵队,前后每行间隔2米,主席台长40米.他们以每分钟40米的速度通过主席台.需要______分钟.二、解答题7.圆形滑冰场,周长400米,每隔40米装一盏灯.再在相邻两盏灯之间放3盆花,问共需装几盏灯?放几盆花?8.有一个正方形池塘,在它四周种树,四个顶点都有一棵,这样每边都有5棵,问池塘四周共种树多少棵?9.人民公园有一个湖泊,周长168米.现在沿边长等距离做8个长9米的花坛,问花坛间隔是多少米?10.一根木料长4米,锯成每段40厘米,需要36分钟.如果把它锯成每段长50厘米,需要多少时间?11.在铁路一旁,每隔50米有电杆一根.一旅客在行进的火车里,从经过第1根电杆起到第89根电杆为止,恰好经过了4分钟,问火车行进的速度是每小时多少千米?12.有一根长180米厘米的绳子,从它的一端开始,每3厘米作一个记号,每4厘米也作一个记号.然后将有记号的地方剪开,问绳子共可剪成多少段?一、填空题1.在相距100米的两楼之间栽树,每隔10米栽一棵,共栽了______棵树.2.一个长方形的池塘长120米、宽28米,在池塘边每隔2米种一棵树,一共需要种_____棵树.3.一个人以均匀的速度在路上散步,从第一根电线杆走到第七根电线杆用了12分钟,这个人走了30分钟,他走到了第______根电线杆.4.国庆节接受检阅的一列车队共52辆,每辆车长4米,前后每辆车相隔6米,车队每分钟行驶105米,这列车队要通过536米长的检阅场地,要______分钟.5.锯一条4米长的圆柱形的钢条,锯5段耗时1小时20分钟.如果把这样的钢条锯成半米长的小段,需要______分钟.6.小王要到大厦的36层去上班,一日因停电他步行上楼,他从一层到六层用了100秒.如果用同样的速度走到36层,还需要_____秒.二、解答题7.马路的一边每隔10米种一棵树,小明乘汽车2分钟共看到201棵树,汽车每小时行多少千米?8.公园里有个湖,湖边周长是3600米,按等距离共种了120棵柳树.现在要在每3棵柳树间等距离地安放一条长椅供游人休息,沿湖边安放一周需要多少条长椅?两条长椅间相距多少?9.公路两旁距离均匀地栽有一批杨树.清晨琳琳以同一速度在公路一侧跑步,从第1棵树跑到第9棵树用了4分钟.她准备往返跑步30分钟,琳琳应该跑到第几棵树时返回?10.一条道路的一边,每隔30米有一根电线杆,共有51根.现在要进行线路改造,每隔50米设一根电线杆,改造过程中有多少根电线杆不需要移动?11.图2是五个大小相同的铁环连在一起的图形,它的长度是多少毫米?十个这样的铁环连在一起有多少毫米长?12.盒子里有许多黑色和白色的围棋子,明明从盒子里取出19枚,排成一排.他先放1枚白色棋子,放几枚黑色棋子;再放1枚白色棋子,放几枚黑色棋子;......每次放的黑色棋子的枚数都相同.巧的是最后一枚也是白色棋子.请你在图中画出棋子的摆法:一、封闭线路植树:棵树=总距离÷棵距二、不封闭线路植树:①路的两端都植树:棵树=总距离÷棵距+1;②路的一端植树,另一端不植树:棵树=总距离÷棵距;③路的两端都不植树:棵数=总距离÷棵距-1三、在方形线路上植树,如果每个顶点都要植树。
八年级奥数精讲与测试中位线及其应用(无答案)(可编辑修改word版)
例1.在△ABC 中,∠B=2∠C,AD⊥BC1于D,M 为BC 的中点,求证:DM=2AB。
例2.如图,等腰梯形ABCD 中,对角线AC⊥BD,垂足为E,DF⊥BC 于F,MN是梯形中位线,求证:DF=MN。
例3.如图,四边形ABCD 中,AB=CD,E、F 分别为BC、AD 的中点,BA及EF 的延长线交于M,CD 及EF 的延长线交于N,求证:∠AME=∠DNE。
例4.如图,分别以△ABC 的AC、BC 边为腰,A、B 为直角顶点,作等腰直角△ACE 和等腰直角△BCD,M 为DE 中点,求证:AM⊥BM。
例5.在等腰三角形ABC 的两腰AB、AC 上分别取点E 和F,使AE=CF。
已知BC=2,求证:EF≥1。
A 卷一、填空题01.如果等腰梯形底角是 45°,高等于上底的 2 倍,那么梯形中位线与高 之比为 。
202. 已知梯形两对角线中点连线长 5cm ,梯形下底长 20cm ,则上底长为。
03. 如图 128,E 是 AC 的中点,D 在边 BC 上,且 CD=2BD ,AD 与 BE 相交于 F 。
已知△BDF 的面积是 1,那么△ABC 的面积是 。
04. 如图 129,梯形 ABCD 的面积是 12,则以梯形四边中点为顶点的四边形 EFMN 的面积是。
05. 已知梯形 ABCD 中,AD ∥BC ,对角线 AC 把中位线 EF(E 在 AB 上)分成 1 : 3 两部分,则 S ADFE : S BCFE = 。
06. 如图 130,在梯形 ABCD 中,AB ∥CD ,EF 是中位线,EF 与 AC 相交于 G ,且 EF=16cm ,EG −GF=4cm ,则 AB 的长是 cm 。
07. 如图 131,已知△ABC 中,AB=AC ,延长 AB 至 D ,使 BD=AB ,E是 AB 的中点,CD=4,则 CE= 。
08. 如图 132,在△ABC 中,E 、F 分别为 AB 、AC 上的点,且 BE=CF ,M 、N分别为 BF 、CE 的中点,过 M 、N 的直线交 AB 于 P ,交 AC 于 Q 。
八年级奥数精讲与测试 面积问题与面积方法 讲义
例1.如图,在△ABC中,AB=AC=1,∠A=90°,E为AC中点,EF⊥BE,点F在BC上,求△CEF的面积。
例2.如图,已知正方形ABCD的面积为35平方厘米,E、F分别为边AB、BC上的点,AF、CE相交于G,并且△ABF的面积为5平方厘米,△BCE的面积为14平方厘米,那么四边形BEGF的面积是多少平方厘米?例3.如图,△ABC被通过它的三个顶点与一个内点的三条直线分为六个小三角形,其中四个小三角形的面积已在图中标出,试求△ABC的面积。
例4.如图,平行四边形ABCD中,点P是△BAD内一点。
若△PAB的面积为2,△PCB的面积为5,求△PBD的面积。
例5.如图224,已知△ABC,AB>AC,分别以AB、AC为边在形外作等边△ABF与等边△ACE,连结BE、CF交于点O,求证:OA平分∠FOE。
A卷一、填空题01.如图225,在△ABC中,EF∥BC,且AE : EB=m,则S△AEF :S四边形BEFC=_________。
02.如图226,在梯形ABCD中,AB∥CD。
若△DCE面积是△DCB的面积的14,则△DCE的面积是△ADC面积的_________。
03.如图227,已知△ABC的面积为1,且BD=12DC,AF=12FD,CE=12EF,则S△DEF=_________。
04.如图228,是由三个等边三角形△ABE、△ADE和△CDE组成图形,它的面积是1,F为AB中点,则S△CEF=_________。
05.如图229,D在BC上,E在AD上,若△ABE、△BDE、△CDE的面积为16、7、5,求△AEC的面积=_________。
06.如图230,平行四边形ABCD中,EF∥AC,分别交CD、AD于E、F,连AE、BE、BF、CF,那么与△BCE面积相等的三角形有_________。
07.如图231,△ABC中D、E分别为AB、BC中点,连DE、DC。
若△ABC 的面积为1,则S△CDE=_________。
面积问题奥数精讲与测试
例1.如图,两个半径为1的14圆扇形¼''A OB与¼AOB叠放在一起,POQO'是正方形,求整个阴影图形的面积。
例2.如图,四边形ABCD被AC与BD分成甲、乙、丙、丁4个三角形。
已知BE=80厘米,AE=30厘米,CE=60厘米,DE=40厘米,问丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?例3.如图,△ABC中,点P在边AB上,AP=13AB;点Q在边BC上,BQ=14BC;点R在边AC上,CR=15AC。
已知阴影△PQR的面积是19平方厘米,求△ABC的面积。
例4.将任意三角形分成面积相等的五个小三角形,你能给出几种不同的分法?例5.如图,平行四边形ABCD的面积为64cm2,E、F分别为AB、AD的中点,求△CEF的面积。
例6.如图,在△ABC中,E是AB的中点,D是AC上一点,且AD:DC=2:3。
BD与CE交于F,S△ABC=40,求S△AEFD。
例7.如图,在△ABC中,P是∠BAC平分线上一点,BE∥CP交AC于点E,CF∥BP交AB于点F。
求证:BF=CE。
例8.如图,P为△ABC内一点,AP、BP、CP分别交对边于D、E、F。
记△PBD、△PDC、△PCE、△PEA、△PAF、△PFB的面积分别为S1、S2、S3、S4、S5、S6,求证:135246111111S S S S S S++=++。
A卷一、填空题01.若长方形的长增加了a%以后,为了使长方形的面积保持不变,则这个长方形的宽应该减少________。
02.已知凸四边形ABC D的面积是a,E、F、G、H分别是AB、BC、CD、DA的中点,且EG,HF交于点O,四边形AEOH与OFCG面积和是________。
03.如图1,一个矩形被分成A、B、C、D四个矩形。
已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,原来矩形的面积是________平方厘米。
八年级奥数精讲与测试 同余
例1.求证:⑴8︱(551999+17);⑵ 8︱(32n +7);⑶ 17︱(191000−1)。
例2.求使2n −1为7的倍数的所有正整数n 。
例3.把1、2、3、…、127、128这128个数任意排列为a l 、a 2、…、a 128,计算出12a a -、34a a -、…、127128a a -,再将这64个数任意排列为b 1、b 2、…、b 64,计算出12b b -、34b b -、…、6364b b -。
如此继续下去,最后得到一个数x,问x 是奇数还是偶数?例4.m 、n 是正整数,证明:3m +3n +1不可能是完全平方数。
例5.任意平方数除以4,余数为0或1(这是平方数的重要特征)。
例6.任意平方数除以8余数为0,1,4(这是平方数的又一重要特征)。
A卷一、填空题01.a除以5余1,b除以5余4。
如果3a>b,那么3a−b除以5的余数是__________。
02. 71427和19的乘积被7除,余数是__________。
03. 1+22+33+44+55+66+77+88+99≡__________ (mod3)。
04. 一个数除以3余2,除以4余1,这个数除以12的余数是__________。
05. 今天是星期一,过21995是星期__________。
06. 10100被7除的余数是__________。
07. 1至5 000之间同时被3、5、7除都余2的数有__________个。
08. 1至1 000之间同时被2、3、7除都余1的数有__________个。
09.用199433333个除以7,余数是__________。
10. 1993年的元旦是星期五,那么1996年五月一日是星期__________。
二、解答题11.甲、乙两数都只含有质因数3和5,它们的最大公约数是75。
已知甲数有12个约数,乙数有10个约数,那么甲、乙两数的最小公倍数是多少?12. 试证不小于5的质数的平方与1的差必能被24整除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式及其运算
1. 计算711571127654———
2. 已知7373,7373yx,求223103yxyx的值。
3. 若aax1 ,求 224242xxxxxx 的值。
4. 设a,b为有理数,且133332ab,求a,b的值..
5. 化简5210452104—
6. 已知A=53, B=53, 求 3a3b的整数部分。
7. 已知251x, 求531xxx的值
8. 如果3324m, 它的小数部分是p, 求 m(1—p)的值
9.
