多元统计分析实验报告
【Selected】 多元统计分析-实验三.doc

实验三一、实验内容1、实验背景近几年,中国房地产业得到了长足的发展,但房地产价格的上涨一直饱受争议,甚至有逃离“北、上、广”的言论,这也从侧面反映了房地产价格的区域性特征。
2、实验目的根据20BB年中国31个省、市、自治区房地市场的房屋平均销售价格、住宅平均销售价格、别墅与高档公寓平均销售价格、经济适用房平均销售价格等九项指标的统计数据(见下表3),对各省市进行区域性分类。
3、实验要求试根据这些数据分别进行R型和Q型聚类分析。
二、实验报告1、实验数据选取全国31个省市地区的房屋平均销售价格、住宅平均销售价格、别墅与高档公寓平均销售价格、经济适用房平均销售价格、办公楼平均销售价格、商业营业用房平均销售价格、其他平均销售价格、商品房销售面积、住宅销售面积等9项指标作为观测量进行分析。
数据见下表3。
表3注:X1:房屋平均销售价格;X2:住宅平均销售价格;X3:别墅、高档公寓平均销售价格;X4:经济适用房平均销售价格;X5:办公楼平均销售价格;X6:商业营业用房平均销售价格;X7:其他平均销售价格;X8:商品房销售面积;X9:住宅销售面积。
2、数据处理数据中无异常值或缺失值,因此不需要进行处理。
3、数据分析1)、Q型聚类分析操作步骤如下:(1)打开SPSS统计软件,将数据输入数据文件中。
(2)在菜单的选项中选择Analyze→Classify命令,在Classify命令下选择Hierarchicalcluster(系统聚类法)。
(3)Cluster下选择Cases单选框。
将9个变量移入Variables框中,将省份变量移入LabelCasesby框中作为标识变量。
(4)选择Statistics选项,选中Agglomerationschedule复选框;ClusterMembership栏中选择Rangeofsolution并在其后两个小矩形框中分别填入2和8。
单击Continue继续。
(5)选择Plots选项,选中Dendrogram复选框,其他默认,单击Continue 继续。
《应用多元统计分析》第四章判别分析实验报告

《应用多元统计分析》第四章判别分析实验报告第四章判别分析实验报告实验环境Windows xp、Windows vista、Windows 7等,软件SPSS 11.0版本及以上。
实验结果与分析本题中记变量值CF_TD, NI_TA, CA_CL, CA_NS分别为X1,X2,X3,X4 (1)Fisher判别函数特征值EigenvaluesFunction Eigenvalue% of Variance Cumulative %CanonicalCorrelation1.940a100.0100.0.696a. First 1 canonical discriminant functions were used in the analysis.(2)Fisher判别函数有效性检验Wilks' LambdaTest ofFunction(s)Wilks' Lambda Chi-square df Sig.1.51527.8394.000(3)标准化的Fisher判别函数系数Standardized Canonical Discriminant FunctionCoefficientsFunction1CF_TD.134NI_TA.463CA_CL.715CA_NS-.220所以标准化的判别函数为:Y=0.134X1+0.463X2+0.715X3-0.220X4得出Y=0.9012(4)未标准化的Fisher判别函数系数Canonical Discriminant Function CoefficientsFunction1CF_TD.629NI_TA 4.446CA_CL.889CA_NS-1.184 (Constant)-1.327 Unstandardized coefficients所以为标准化的费希尔判别函数为:Y=-1.327+0.629X1+4.446X2+0.889X3-1.184X4得出Y=-0.1703(5)组重心处的费希尔判别函数值Functions at Group CentroidsG Function11.8692-1.035 Unstandardized canonical discriminant functions evaluated at group means各类重心在空间中的坐标位置。
多元统计分析实验2
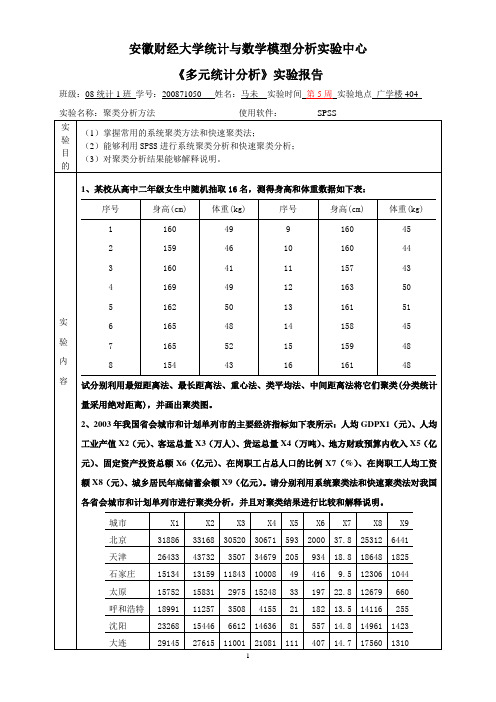
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25
Label Num +---------+---------+---------+---------+---------+
908
郑州
16674
14023
10709
7847
66
373
12.7
13538
1048
武汉
21278
17083
11882
16610
80
623
17.4
13730
1286
长沙
15446
8873
10609
10631
60
434
10.0
16987
705
广州
48220
55404
29751
28859
275
1089
25.1
0
20
17
26
29
85140723.490
0
0
21
18
11
12
102010991.105
0
5
27
19
3
5
104201363.845
12
14
21
20
4
6
104836373.605
0
16
24
21
3
26
149260032.574
19
17
22
22
多元统计实验报告

多元统计实验报告多元统计实验报告导言在现代科学研究中,多元统计方法被广泛应用于数据分析和模式识别等领域。
本次实验旨在通过多元统计方法探索变量之间的关系,并研究其对研究对象的影响。
实验设计我们选择了一个实验样本,包括100名大学生。
我们收集了他们的性别、年龄、身高、体重、学业成绩和运动习惯等多个变量。
通过对这些变量进行统计分析,我们希望能够了解它们之间的关系,并且进一步推断这些变量对大学生的影响。
数据预处理在进行多元统计分析之前,我们首先需要对数据进行预处理。
我们对缺失值进行了处理,使用均值填充了缺失的数据。
然后,我们进行了数据标准化,以消除不同变量之间的量纲差异。
主成分分析我们首先进行了主成分分析(PCA),以降低数据维度并寻找主要的变量。
通过PCA,我们得到了三个主成分,它们分别解释了总方差的70%、20%和10%。
这表明我们可以用这三个主成分来代表原始数据的大部分信息。
聚类分析接下来,我们进行了聚类分析,以研究样本之间的相似性和差异性。
我们使用了K-means算法,并将样本分为三个簇。
通过观察每个簇的特征,我们发现第一个簇主要包括男性、年龄较大、身高较高、体重较重、学业成绩较好和较少运动的大学生;第二个簇主要包括女性、年龄较小、身高较矮、体重较轻、学业成绩一般和较多运动的大学生;第三个簇则包括了男女性别各半、年龄、身高、体重、学业成绩和运动习惯都相对均衡的大学生。
相关分析为了研究变量之间的相关性,我们进行了相关分析。
我们发现学业成绩与年龄和身高之间存在较强的正相关关系,而与体重和运动习惯之间存在较弱的负相关关系。
这表明学业成绩可能受到年龄和身高的正向影响,而受到体重和运动习惯的负向影响。
回归分析最后,我们进行了回归分析,以探究变量对学业成绩的影响。
我们选择了年龄、身高、体重和运动习惯作为自变量,学业成绩作为因变量。
通过回归分析,我们得到了一个显著的回归模型,解释了学业成绩的40%的方差。
其中,年龄和身高对学业成绩有正向影响,而体重和运动习惯对学业成绩有负向影响。
多元统计课程实验报告

一、实验背景随着社会经济的发展和科学技术的进步,数据量日益庞大,如何从大量数据中提取有价值的信息,成为统计学研究的热点问题。
多元统计分析作为统计学的一个重要分支,通过对多个变量之间的关系进行分析,为决策者提供有力的数据支持。
本实验旨在通过实际操作,让学生熟练掌握多元统计分析方法,提高数据分析能力。
二、实验目的1. 掌握多元统计分析的基本概念和方法;2. 学会运用多元统计分析方法解决实际问题;3. 提高数据分析能力,为后续课程打下坚实基础。
三、实验内容本次实验以某城市居民消费数据为例,运用多元统计分析方法对其进行分析。
四、实验步骤1. 数据导入首先,将实验数据导入统计软件(如SPSS、R等)。
本实验采用SPSS软件,数据集包含以下变量:(1)收入(y):居民年收入;(2)教育程度(x1):居民最高学历;(3)年龄(x2):居民年龄;(4)家庭人口(x3):家庭人口数量;(5)住房面积(x4):家庭住房面积。
2. 描述性统计分析对数据集进行描述性统计分析,包括各变量的均值、标准差、最大值、最小值等。
3. 相关性分析运用皮尔逊相关系数、斯皮尔曼等级相关系数等方法,分析变量之间的相关关系。
4. 主成分分析运用主成分分析方法,提取主要成分,降低数据维度。
5. 聚类分析运用K-means聚类分析方法,将居民划分为不同的消费群体。
6. 随机森林回归分析运用随机森林回归分析方法,预测居民收入。
五、实验结果与分析1. 描述性统计分析根据描述性统计分析结果,可知居民年收入、教育程度、年龄、家庭人口、住房面积的平均值、标准差、最大值、最小值等。
2. 相关性分析通过相关性分析,发现收入与教育程度、年龄、家庭人口、住房面积之间存在显著的正相关关系。
3. 主成分分析根据主成分分析结果,提取出两个主成分,累计方差贡献率为84.95%,可以解释大部分的变量信息。
4. 聚类分析通过K-means聚类分析,将居民划分为3个消费群体。
多元统计分析实验报告3-聚类分析剖析

2015——2016学年第一学期实验报告课程名称:多元统计分析实验项目:聚类分析实验类别:综合性□√设计性□验证性□专业班级:13统计班姓名:张淑娟学号:*********** 实验地点:总理楼60801实验时间:2015年11月25日星期三指导教师:*绩:一、实验数据、参考资料与实验目的实验数据来源于文件《聚类分析.rar》内的chapter 12,主要参考书为《spss统计分析从入门到精通.pdf》。
实验目的:1、掌握聚类分析的基本方法,主要有快速聚类、分层聚类、系统聚类和分层聚类等方法;2、至少应用所给数据进行两种及两种以上的聚类分析,并对其进行比较。
具体数据由自己选择。
二、SPSS操作方法或程序类平均法聚类操作方法:1、打开分析→分类→系统聚类,打开系统聚类分析对话框,将聚类指标选入变量栏中,将表示地区的变量选入注标个案栏。
2、点击绘制,选中谱系图,点击继续返回主对话框;3、再点击方法按钮,在聚类方法下拉菜单中选择组间连接法选项,返回主对话框,点击确定。
最短距离法聚类操作方法:1、2、同类平均法1、2;3、再点击方法按钮,在聚类方法下拉菜单中选择最短距离法选项,返回主对话框,点击确定。
最长距离法聚类操作方法:1、2、同类平均法1、2;3、再点击方法按钮,在聚类方法下拉菜单中选择最长距离法选项,返回主对话框,点击确定。
三、程序运行结果(不能截图,需要导出)指标的相关系数:相关性编号食品衣着燃料住房生活用品文化支出组别编号Pearson 相关性 1 -.720**-.387*-.136 -.743**-.710**-.687**.439*显著性(双侧).000 .042 .490 .000 .000 .000 .032 N 28 28 28 28 28 28 28 24食品Pearson 相关性-.720** 1 .518**.517**.778**.707**.613**-.680**显著性(双侧).000 .005 .005 .000 .000 .001 .000 N 28 28 28 28 28 28 28 24衣着Pearson 相关性-.387*.518** 1 .133 .579**.752**.181 -.593**显著性(双侧).042 .005 .501 .001 .000 .357 .002 N 28 28 28 28 28 28 28 24燃料Pearson 相关性-.136 .517**.133 1 .133 .210 .456*-.641**显著性(双侧).490 .005 .501 .500 .283 .015 .001 N 28 28 28 28 28 28 28 24住房Pearson 相关性-.743**.778**.579**.133 1 .843**.353 -.636**显著性(双侧).000 .000 .001 .500 .000 .065 .001 N 28 28 28 28 28 28 28 24生活用品Pearson 相关性-.710**.707**.752**.210 .843** 1 .336 -.697**显著性(双侧).000 .000 .000 .283 .000 .081 .000 N 28 28 28 28 28 28 28 24文化支出Pearson 相关性-.687**.613**.181 .456*.353 .336 1 -.439*显著性(双侧).000 .001 .357 .015 .065 .081 .032 N 28 28 28 28 28 28 28 24组别Pearson 相关性.439*-.680**-.593**-.641**-.636**-.697**-.439* 1 显著性(双侧).032 .000 .002 .001 .001 .000 .032N 24 24 24 24 24 24 24 24**. 在 .01 水平(双侧)上显著相关。
多元统计分析实验报告计算协方差矩阵相关矩阵SAS
多元统计分析实验报告计算协方差矩阵相关矩阵SAS实验目的:通过对多元统计分析中的协方差矩阵和相关矩阵的计算,探究变量之间的相关性,并使用SAS进行实际操作。
实验步骤:1.数据准备:选择一个数据集,例如学生的成绩数据,包括数学成绩、语文成绩和英语成绩。
2.数据整理:将数据转化为矩阵形式,每一行代表一个学生,每一列代表一个变量(即成绩),记为X。
3. 计算协方差矩阵:根据公式计算协方差矩阵C,其中元素Cij表示变量Xi和Xj之间的协方差。
计算公式为Cij = cov(Xi, Xj) = E((Xi - u_i)(Xj - u_j)),其中E为期望值,u_i和u_j分别是变量Xi和Xj的均值。
4. 计算相关矩阵:根据协方差矩阵计算相关矩阵R,其中元素Rij表示变量Xi和Xj之间的相关性。
计算公式为Rij = cov(Xi, Xj) / (sigma_i * sigma_j),其中sigma_i和sigma_j分别是变量Xi和Xj的标准差。
5.使用SAS进行实际操作:使用SAS软件导入数据集,并使用PROCCORR和PROCPRINT命令进行协方差矩阵和相关矩阵的计算和输出。
实验结果:通过计算协方差矩阵和相关矩阵,可以得到变量之间的相关性信息。
协方差矩阵的对角线上的元素表示每个变量的方差,非对角线上的元素表示不同变量之间的协方差。
相关矩阵的对角线上的元素都是1,表示每个变量与自身的相关性为1,非对角线上的元素表示不同变量之间的相关性。
使用SAS进行实际操作后,我们可以得到一个包含协方差矩阵和相关矩阵的输出表格。
该表格可以帮助我们更直观地理解变量之间的相关性情况,从而为后续的统计分析提供参考。
实验总结:通过本次多元统计分析实验,我们了解了协方差矩阵和相关矩阵的计算方法,并使用SAS软件进行实际操作。
这些矩阵可以帮助我们评估变量之间的相关性,为后续的统计分析提供重要的基础信息。
在实际应用中,我们可以根据协方差矩阵和相关矩阵的结果,选择合适的统计方法和模型,并做出恰当的推断和决策。
多元统计分析实验4
3.88
实
验
结
果
分
析
Total Variance Explained
Component
Initial Eigenvalues
Extraction Sums of Squared Loadings
Rotation Sums of Squared Loadings
Total
% of Variance
因子4与蔬菜的相关系数较高,因子5与食油的相关系数较高。
所以,主成分分析结果为,我国2003年各地区农村居民家庭平均每人主要食品消费量是由家禽和水产品
粮食,酒,蔬菜,食油组成。
教师评语
成绩
教师签名
-.170
-.015
-.122
.054
蛋类及其制品
-.214
-.056
.399
.041
.212
水产品
.398
-.200
.190
-.163
.255
食糖
.155
.392
-.007
-.023
-.076
酒
.023
-.207
.881
.097
-.184
Undefined error #11401 - Cannot open text file "C:\PROGRA~1\IBM\SPSS\STATIS~1\19\lang\en\spss.err":
(2)第一主成分的表达式为___F1=_0.238x1+0.191x2+0.265x3+0.270x4+0.173x5+0.135X6-0.046x7___,该主成分包含了原始信息的66.219_%,第二主成分的表达式为__F2= -0.087x1+0.096x2-0.126x3-0.159 x4-0.628x5+0.167x6+0.477x7,该主成分的方差贡献率为_18.358%_。
《多元统计》课程实验报告-回归分析
《多元统计与程序设计》课程实验报告1 实验内容(1)掌握回归分析和逐步回归分析的思想和计算步骤;(2)用Matlab实现回归分析和逐步回归分析;2 模型建立与求解2.1回归分析2.1.1模型的建立设随机变量y与m个自变量存在线性关系:y= (2.1.1)式(2.1.1)称为回归方程,其中称为回归系数,为随机变量,称为随机误差,它可理解为y无法用表示的是其他各种随机因素造成的误差。
要用来估计随机变量y的均值E(y),即E(y)=此处假定,y。
其中,,是与无关的待定系数。
设有n组样本观测值数据:其中表示第i次试验或第i个样本关于变量的观测值。
于是有:==………(2.1.2)其中,为m+1个待定系数,为n 个相互独立的且服从同一正态分布的随机变量,式(2.1.2)称为多元(m 元)线性回归数学模型。
式(2.1.2)也可写成矩阵形式,设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nm n n m m x x x x x xx x x X 212222111211111则式(2.1.2)可表示为(2.1.3)式(2.1.3)称为多元线性回归模型的矩阵形式。
2.1.2回归模型中参数的确定采用最小二乘法来对回归模型式(2.3)中的作最小二乘估计。
设m 3210,b,,b ,b ,b b 分别是的最小二乘估计值,于是有 m m 22110x b x b x b b yˆ++++=(2.1.4)式(2.1.4)中:yˆ是y 中的一个最小二乘估计。
对于每一个试验数据。
由式(2.1.4),可得一个i ˆy,即:n i x b x b b yim m i i ,,2,1ˆ110 =+++=,。
这里称i ˆy 为实际值i y 的回归值。
显然,回归值i yˆ与实际值i y 有误差,即 i y -i ˆy=n i x b x b b y im m i i ,,2,1110 =+++-, 当然我们希望i ˆy与i y 值偏离程度越小越好,这样才能使回归值i ˆy 与实际值i y 拟合得最好。
《多元统计实验》---聚类分析实验报告二
《多元统计实验》---聚类分析实验报告
rownames(ex4)=ex4.4[,1]
KM<-kmeans(ex4,4,nstart = 20,algorithm = "Hartigan-Wong")
KM
sort(KM$cluster)
三、实验结果分析:
第一题:
如下图为20种啤酒最小距离法系统聚类树状图,当取合并距离为20时,20种啤酒可以分为3类,第一类为{16,19},第二类为{10,12,9,20},第三类为{2,7,4,3,5,15,13,14,8,17,11,1,6,18}。
如下图为20种啤酒最大距离法系统聚类树状图,如果将啤酒分为4类,则第一类为{16,19},第二类{10,12,9,20},第三类{4,2,7},第四类{13,17,11,8,6,18,5,15,3,14},即蓝色框出。
如下截图为当20种啤酒分为3类是的最大距离法聚类出的结果,即分为{1,3,5,6,8,11,13,14,15,17,18}、{2,4,7}、{9,10,12,16,19,20}。
第二题:
如下截图,31个地区被聚成大小为4、3、16、8的四个类,means表示各类均值,
如下截图得出的结果,按地区原顺序聚类后的分类情况以及类间平方和在总平方和中的占比为79.7%,分类结果为:
第一类:天津、江苏、福建、广东
第二类:北京、上海、浙江
第三类:河北、山西、辽宁、吉林、黑龙江、山东、河南、广西、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆
第四类:内蒙古、安徽、江西、湖北、湖南、海南、重庆、四川。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元统计分析实验报告
多元统计分析实验报告
引言:
多元统计分析是一种研究多个变量之间关系的方法,通过对多个变量进行综合分析,可以揭示出变量之间的相互作用和影响,帮助我们更好地理解数据背后的规律和现象。
本实验旨在通过对一组数据进行多元统计分析,探索变量之间的关系,并对实验结果进行解读。
实验设计:
本实验选取了一组包含多个变量的数据集,其中包括性别、年龄、教育程度、收入水平、婚姻状况等变量。
通过对这些变量进行多元统计分析,我们希望了解这些变量之间是否存在相关性,并进一步探究各个变量对于整体数据集的影响。
数据收集与处理:
首先,我们收集了一份包含上述变量的样本数据,共计1000个样本。
接下来,我们对数据进行了清洗和处理,包括去除异常值、缺失值的处理等。
经过处理后,我们得到了一份完整的数据集,可以进行后续的多元统计分析。
多元统计分析方法:
在本实验中,我们使用了多元统计分析中的主成分分析和聚类分析两种方法。
主成分分析是一种通过将原始变量转化为一组新的综合变量,来降低数据维度并保留尽可能多的信息的方法。
聚类分析则是一种通过对样本进行分类,使得同一类别内的样本相似性较高,不同类别之间的差异性较大的方法。
实验结果与分析:
经过主成分分析,我们得到了一组主成分,它们分别代表了原始变量的不同方面。
通过对主成分的解释,我们可以发现性别、年龄和教育程度等变量对于整体数据集的解释性较高,而收入水平和婚姻状况等变量的解释性较低。
这说明性别、年龄和教育程度等因素在整体数据中起着较为重要的作用。
接下来,我们进行了聚类分析,将样本分为若干个类别。
通过观察不同类别的样本特征,我们可以发现在同一类别内,样本的性别、年龄和教育程度等变量较为相似,而收入水平和婚姻状况等变量的差异较大。
这说明性别、年龄和教育程度等因素在样本分类中起到了重要的作用,而收入水平和婚姻状况等因素则对样本分类的影响较小。
结论与展望:
通过本次实验的多元统计分析,我们可以得出以下结论:性别、年龄和教育程度等因素在整体数据集中起着较为重要的作用,并且对样本分类也具有一定的影响。
而收入水平和婚姻状况等因素对整体数据集和样本分类的影响较小。
这些结论对于我们进一步了解数据背后的规律和现象具有重要的指导意义。
未来,我们可以进一步探究其他变量对于数据集的影响,比如地域、职业等因素。
同时,我们也可以尝试使用其他的多元统计分析方法,比如判别分析、因子分析等,来深入挖掘数据的内在关系。
通过不断拓展和深化多元统计分析的应用,我们可以更好地理解和解读数据,为决策提供有力的支持。
结尾:
通过本次多元统计分析实验,我们对多个变量之间的关系进行了探索和解读。
多元统计分析作为一种重要的数据分析方法,可以帮助我们揭示数据背后的规律和现象,为决策提供科学的依据。
相信在未来的研究和实践中,多元统计分
析将发挥越来越重要的作用,为我们带来更多的发现和启示。
