062-定积分的性质
定积分性质与应用

定积分性质与应用定积分是微积分学中的一个重要概念,它是对曲线下面的面积进行量化的工具。
在本文中,我将讨论定积分的性质以及其在实际应用中的意义。
1. 定积分的性质定积分具有以下几个性质:(1)可加性:设函数f(x)在区间[a, b]上可积,那么对于任意的c(a<c<b),函数f(x)在区间[a, c]和区间[c, b]上也是可积的。
而且,同一个函数在不同的区间上的定积分值相加等于在整个区间[a, b]上的定积分值。
(2)线性性:设函数f(x)和g(x)在区间[a, b]上可积,以及k是任意常数,那么函数kf(x)和f(x)±g(x)也在区间[a, b]上可积。
此外,函数kf(x)在区间[a, b]上的定积分值为k乘以函数f(x)在相同区间的定积分值。
(3)保号性:如果函数f(x)在区间[a, b]上恒大于等于0(或恒小于等于0),那么f(x)在该区间上的定积分值也大于等于0(或小于等于0)。
即,定积分可以用来判断函数在某个区间上的正负性。
2. 定积分的应用定积分在实际应用中起着重要的作用,下面我将介绍其中的几个应用。
(1)曲线下的面积计算定积分最基本的应用之一是计算曲线下的面积。
通过将曲线下方分为若干个矩形和三角形,然后将它们的面积相加,可以近似地计算出曲线下的总面积。
通过不断增加这些分割形状的数量,可以得到更为准确的结果。
(2)物理学中的位移、速度和加速度定积分在物理学中也有广泛的应用。
例如,我们可以用定积分来计算质点在一段时间内的位移、速度和加速度。
通过对速度和加速度函数进行定积分,我们可以获得质点的位移函数。
(3)统计学中的概率密度函数在统计学中,概率密度函数描述了某个随机变量的概率分布情况。
通过求取概率密度函数曲线下的面积,我们可以计算出变量落在某个指定区间内的概率。
这其中用到了定积分的技巧。
(4)工程学中的工作与功率在工程学领域,定积分可以用来计算工作和功率。
对于某个体力做功的过程,我们可以通过计算力和位移的函数乘积在一段时间内的定积分,来得到所做工作的大小。
定积分性质与运算法则

定积分性质与运算法则引言在微积分中,定积分是一个重要的概念。
定积分可以用来计算曲线所包围的面积、求某一区间上函数的平均值等。
为了更好地理解和应用定积分,我们需要了解定积分的性质和运算法则。
定积分性质定积分的存在性定积分的存在性是指,对于一个定义在区间[a, b]上的函数f(x),如果在[a, b]上连续或者仅有有限个间断点,那么这个函数在[a, b]上就是可积的。
也就是说,函数f(x)在[a, b]上的定积分是存在的。
定积分的线性性质定积分具有线性性质,即对于两个可积函数f(x)和g(x),以及任意实数c,有如下等式成立:∫(c1f(x) + c2g(x)) dx = c1∫f(x) dx + c2∫g(x) dx其中,c1和c2是任意实数。
定积分的加法法则对于一个可积函数f(x),以及给定的区间[a, b]和[c, d],有如下等式成立:∫(a到b) f(x) dx + ∫(b到c) f(x) dx = ∫(a到c) f(x) dx这说明,对于一个函数在不同的区间上的定积分,我们可以通过将这些区间连在一起进行求解,得到整个区间上的定积分。
定积分的比较性质对于两个可积函数f(x)和g(x),如果在[a, b]上满足f(x) ≤ g(x),那么有如下不等式成立:∫(a到b) f(x) dx ≤ ∫(a到b) g(x) dx也就是说,如果在某个区间上一个函数始终小于等于另一个函数,那么这两个函数在该区间上的定积分的大小关系也是相同的。
定积分的运算法则分部积分法分部积分法是一种计算定积分的方法,它可以将一个乘积形式的积分转化为一个易于处理的形式。
分部积分法的公式如下:∫u(x) v’(x) dx = u(x) v(x) - ∫v(x) u’(x) dx其中,u(x)和v(x)是可导的函数。
代换法代换法是另一种常用的计算定积分的方法,它通过引入新的变量来简化积分的计算。
代换法的公式如下:∫f(u(x)) u’(x) dx = ∫f(u) du其中,u是一个可导函数。
定积分的性质

定积分的性质定积分是微积分中的一个重要概念,它的性质在数学的实际应用中起着重要作用。
定积分的性质可以总结为以下几个方面:定积分的基本概念、定积分的性质、定积分的计算方法和定积分的应用。
首先,定积分的基本概念是指将一个定义在闭区间[a,b]上的连续函数f(x)在该区间上的面积求解出来。
定积分可以看作是求和的极限,其中将闭区间[a,b]等分成n个小区间,每个小区间的长度为Δx=(b-a)/n,标记为x_0,x_1,...,x_n。
然后通过计算矩形面积来逼近曲线下的面积,最终得到定积分的值。
定积分的性质包括加法性、恒等性、线性性和区间可加性等。
加法性指如果函数f(x)和g(x)在闭区间[a,b]上连续,则它们的和函数f(x)+g(x)也在[a,b]上连续,并且有∫[a,b] (f(x)+g(x)) dx = ∫[a,b] f(x) dx +∫[a,b] g(x) dx。
恒等性是指如果函数f(x)在闭区间[a,b]上连续,则有∫[a,b] f(x) dx = F(b) - F(a),其中F(x)是f(x)的一个原函数。
线性性是指如果函数f(x)和g(x)在闭区间[a,b]上连续,c是常数,则有∫[a,b] (c*f(x)+g(x)) dx = c*∫[a,b] f(x) dx + ∫[a,b] g(x) dx。
区间可加性指如果函数f(x)在闭区间[a,c]和闭区间[c,b]上连续,则有∫[a,b] f(x) dx = ∫[a,c] f(x) dx + ∫[c,b] f(x) dx。
定积分的计算方法包括基本积分法和换元积分法。
基本积分法是指通过查表或记住一些基本的积分公式来计算定积分。
换元积分法是指通过变量替换的方法来简化积分的计算过程。
另外,还有分部积分法和定积分的数值计算方法。
定积分在物理、经济学、概率论等领域有着广泛的应用。
例如,在物理学中,定积分可以用来求解曲线下的面积、弧长、质心、转动惯量等物理量。
定积分的概念及性质课件

06
定积分的进一步应用
积分变换
积分变换的定义
积分变换是一种将函数在某一区间内的行为转化为另一种函数的方法,常见的积分变换包括傅里叶变换和拉普拉斯变 换等。
积分变换的性质
积分变换具有一些重要的性质,例如线性性质、时间平移性质和微分性质等,这些性质在解决实际问题中具有广泛的 应用。
积分变换的应用
积分变换在信号处理、图像处理和控制系统等领域有着广泛的应用,通过积分变换可以将复杂的信号或 系统转换为易于分析和处理的函数形式。
傅里叶变换
傅里叶变换的定义
傅里叶变换是一种将时间域函数转换为频域函数的方法, 它可以将一个时间函数分解成一系列不同频率的正弦和余 弦函数的线性组合。
傅里叶变换的性质
傅里叶变换具有一些重要的性质,例如线性性质、对称性 质和微分性质等,这些性质在解决实际问题中具有广泛的 应用。
傅里叶变换的应用
傅里叶变换在信号处理、图像处理和控制系统等领域有着 广泛的应用,通过傅里叶变换可以将复杂的信号或系统转 换为易于分析和处理的频域函数形式。
反常积分
反常积分的定义
反常积分是一种在无穷区间上定 义的积分,它通常用于处理一些 在无穷远处收敛的函数。
符号的意义
定积分的符号表示一个函 数在一个区间上的总值, 其中“∫”表示积分号。
计算公式
定积分可以通过一个公式
来计算x,其中a和b
是区间的端点。
02
定积分的性质
连续函数的积分性质
积分区间可加性
对于任意两个不相交的区间[a,b]和[b,c],有$\int_{a}^{c}f(x)dx = \int_{a}^{b}f(x)dx + \int_{b}^{c}f(x)dx$。
课件:定积分的性质

则 f 在I 的任意闭子区间都可积,且
b
a
f
( x)dx
c
a
f
( x)dx
b
c
f
( x)dx.
证明 设I 的任意闭子区间为[a , b] , 由定理1.2有 n f (I ) 0, 0, d() , kxk k 1
将a,b 添加到分割中,记作,则d()<
n
kxk , 记分割在[a ,b ]上的部分为,d()<
22
性质1.7
b
b
a g(x)d x a f (x)d x
若f 在[a,b]上可积, g和f 仅在有限个点处取值不同,
则g在[a,b]上可积,且两积分相同。
n
n1
证明
g(i )xi g(i )xi g(1 )x1 g(n )xn
i 1
i2
n1
f (i )xi f (1 )x1 f (n )xn
an1
,
an ,
n 2 x n 1, n1 xn
n
f ( ) 0 f ( x)d x 1 n
n 0
n i1
i
f (x)d x
i 1
注
a1
a2
an
n
24
内容小结
1.定积分的性质
(注意估值性质、积分中值定理的应用)
2.典型问题
(1)估计积分值; (2)不计算定积分比较积分大小.
注意1 当a b时,推论仍成立.
注意2 积分学中值定理可表示为
ah
a f ( x)d x f (a h)h
ah
或 f (a h) a f ( x)d x h
18
积分学中值定理的几何意义
定积分概念及性质
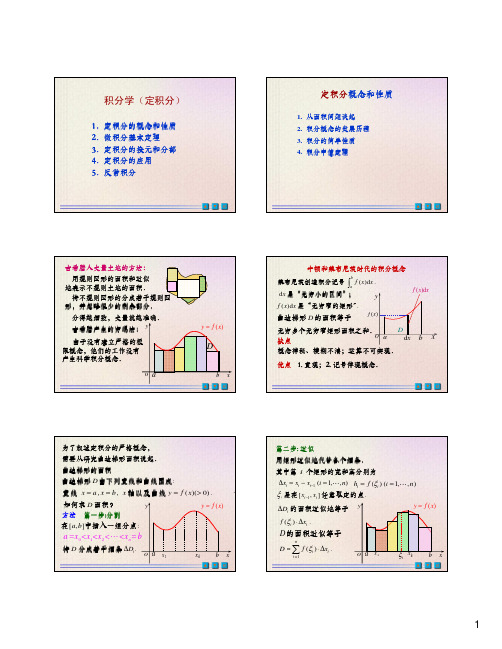
积分学(定积分)1.定积分的概念和性质2.微积分基本定理3.定积分的换元和分部4.定积分的应用5.反常积分)(x f y =i D ∆的面积近似地等于ab yOxD 的面积近似等于()(1,,)i i h f i n ξ==L 第二步第二步: : : 近似近似kx 1x 用矩形近似地代替各个细条用矩形近似地代替各个细条..其中第i 个矩形的宽和高分别为),,1(1n i x x x i i i L =−=∆−.],[1任意取定的点是在i i i x x −ξ().i i f x ξ⋅∆=1().ni i i D f x ξ≈⋅∆∑i ξa bkx k ξ1ξ2ξ定积分的概念a bkx k ξ1ξ2ξ定积分存在的条件定积分存在的充分条件1.()[,]()d .baf x a b f x x ∫若在连续,则存在2.()[,],f x a b 若在有界,且只有有限个间断点()d .baf x x ∫则存在3.()[,]()d .baf x a b f x x ∫若在单调,则存在定积分的性质∫+∫=∫+ba b a b a xx g x x f x x g x f d )(d )(d )]()([βαβα1.()d ()d ,b ba af x xg x x ∫∫假设和都存在则有这个性质称为定积分对于被积函数的线性性质.∫+∫=∫bc c a b a xx f x x f x x f d )(d )(d )(2.()d ,ba f x x ∫假设存在.bc a <<则有这个性质称为定积分对于区间的可加性.3.d ().bak x k b a =−∫(k 为常数).0d 0=∫ba x ()d 0.aaf x x =∫4.()d ()d abbaf x x f x x =−∫∫.5.()d ()d ,bbaaf x xg x x ∫∫假设和都存在()()().f x g x a x b ≤≤≤并且则有∫≤∫ba b a x x g x x f d )(d )(|()d ||()|d bba a f x x f x x≤∫∫)(d )(a b k x x f ba −≤∫()d |()|(),baf x x f x k ≤∫设存在,且常数则有()0()d 0.baf x f x x ≥≥∫若,则积分中值定理)()(d )(a b f x x f ba −=∫ξ.],[)(连续在设b a x f 满足,则存在],[b a ∈ξab)(x f y =证明(1) 设m ≤f (x ) ≤M ,则有Mab x x f m ba≤−≤∫d )(由介值定理立即推出,()d ()()baf x x f b a ξ=⋅−∫∫∫∫≤≤babab axM x x f x m d d )(d [,]a b ξ∈存在,满足()d ().baf x x f b aξ=−∫例31sin lim d 0.n nn xx x+→+∞=∫求证证明根据积分中值定理得到根据积分中值定理得到::.)1(sin d sin1+≤≤=∫+n n x xxn nnn nξξξ于是.1|sin ||d sin |1nx x x n n n n≤=∫+ξξ由此立即得到由此立即得到::.0d sin lim 1=∫++∞→n nn x xx例4证明(0)0,()[0,1]f f x C ′=∈设且..|)(|max 0x f M ax ′=≤≤求证.21|d )(|20Ma x x fa ≤∫()[0,1]f x C ′∈由推出()[0,1]f x 在连续,(0,1).在可导由拉格朗日中值定理推出由拉格朗日中值定理推出::,],0[a x ∈∀,),0(x x ∈∃ξ.)()0()()(x f f x f x f x ⋅′=−=ξ[0,],x a ∀∈于是有.|)(||)(|Mx x f x f x ≤⋅′=ξ因此∫≤∫a a x x f x x f 00d |)(||d )(|∫≤a x Mx 0d ∫≤ax x M 0d .212Ma =Oxy1xy =则有。
第二节定积分的性质
智慧城市的智能公共交通智慧城市的建设已经成为现代城市规划的重要组成部分,其中智能公共交通系统的发展具有关键性的意义。
智慧公共交通通过融合信息技术与交通系统,提供更加高效、便捷、可持续的出行方式,为城市居民带来全新的出行体验。
一、智能公共交通系统智能公共交通系统是指通过网络技术和智能设备,使城市公共交通更加智能化、高效化的系统。
其核心是基于信息技术的数据采集、分析和应用,为公共交通管理实现智能化、精细化的运营管理。
1.1 数据采集与分析智能公共交通系统通过各类传感器、监控设备等手段,实现对城市交通状况、公交车辆运营、乘客需求等数据的实时采集。
这些数据经过处理和分析,可以为公共交通管理者提供决策参考,优化车辆调度,提高运行效率。
1.2 公交信号优化智能公共交通系统还可以通过智能信号控制技术,为公交车辆提供绿波通行的便利。
交通信号可以根据实时交通数据和公交车辆的位置信息,动态调整信号灯的时长,尽量减少红灯等待时间,提高公交出行速度和运行效率。
1.3 公交调度与导航智能公共交通系统通过建立信息平台,将公交车辆的实时位置信息与乘客需求进行匹配,实现公交车辆的实时调度和导航。
乘客可以通过手机或电子显示屏查看公交车辆的实时到站信息和运行状态,提前规划出行路线,减少等待时间。
二、智能公共交通的优势智能公共交通系统的引入,为城市公共交通带来了诸多优势和便利,不仅提升了乘客出行体验,也有助于城市交通管理的提升。
2.1 提高运行效率智能公共交通系统可以实时获取乘客需求和交通状况,通过优化调度和信号控制,提高公交车辆的运行效率。
乘客等待时间减少,公交车辆的行驶速度增加,整体交通流量得以优化,提升了公共交通的吸引力。
2.2 减少碳排放智能公共交通系统的推广使用,可以减少汽车出行需求,降低交通拥堵,从而减少了尾气排放和能源的消耗。
这有助于改善城市的空气质量,减少环境污染,推动可持续交通的发展。
2.3 提升出行体验智能公共交通系统为乘客提供了多种出行信息服务,包括实时车辆到站信息、乘车路线建议、交通状况预测等。
定积分的概念存在条件与性质
• 定积分的概念 • 定积分的存在条件 • 定积分的性质 • 定积分的应用
01
定积分的概念
定义与背景
定义
定积分是积分的一种,是函数在 区间上各点的定积分值相加的总 和。
背景
定积分是为了解决实际问题而产 生的数学工具,如计算曲线下面 积、变速直线运动的路程等。
定积分的几何意义
计算体积
通过微元法,可以将体积转化为定 积分,从而求出给定立体的体积。
微元法在物理学中的应用
计算做功
利用微元法,可以将力在物体上 做的功转化为定积分,从而求出 做功的值。
计算压力
在流体动力学中,利用微元法可 以将压力转化为定积分,从而求 出压力的值。
计算质心
在质点系中,利用微元法可以将 质心位置转化为定积分,从而求 出质心的位置。
详细描述
如果f(x)和g(x)在区间[a, b]上可积,那么对于任意实数k和l,函数k*f(x) + l*g(x)在区间[a, b]上也可积, 且
区间可加性
总结词
定积分的区间可加性是指对于任意分 割的两个子区间,其对应的定积分之 和等于原函数在整体区间上的定积分。
详细描述
如果[a, b]被分成两个子区间[a, c]和[c, b],那么∫(b, a)f(x) dx = ∫(b, c)f(x) dx + ∫(c, a)f(x) dx。
绝对收敛
如果定积分存在且其值小于等于某个正数,则该定积分是绝 对收敛的。
定积分存在的必要条件
区间不可分
如果闭区间不能被分成有限个开子区间,则该函数在该闭区间上不可积。
无界
如果函数在闭区间的任意子区间上都无界,则该函数在该闭区间上不可积。
定积分的性质
f1 ( x ' ) f 2 ( x ' ) f1 ( x" ) f 2 ( x" )
' " 1 1 x ', x ''I k 2
'
"
x ', x ''I k
2
M (k ' k " )
于是, T : , 有:
k 1
n
k
xk M ( k xk k " xk ) 2M
b
定理3Leabharlann 若函数f在[a, b]可积, 则函数kf在[a, b]也可积,且
a kf ( x )dx k a f ( x )dx
证
b
n n
b
b
(k 为常数).
kf ( i )xi a kf ( x )dx lim 0 i 1 lim k f ( i )xi k lim f ( i )xi
5.设函数f ( x)在[a, b]有界, 证明 : (振幅的等价形式 )
sup{ f ( x)} inf { f ( x)} sup { f ( x) f ( y ) }
x[ a ,b ] x[ a ,b ] x , y[ a ,b ]
x , x xk-1,xk ,有
规定当 a= b 时,
规定当 a > b 时,
f ( x)dx 0 f ( x)dx f ( x)dx
a a
b a a b
说明:在下面的性质中,假定定积分都存在,且 不考虑积分上下限的大小.
( x) c(常数),则 定理1:若 x a, b 有 f b
定积分性质
定积分性质1. 定义在微积分中,定积分是一种求解曲线下面的面积的方法。
给定一个函数 f(x),我们可以通过定积分来计算函数 f(x) 在一个区间 [a, b] 上的面积,表示为∫[a, b]f(x)dx。
定积分的定义可以表示为:∫[a, b] f(x)dx = lim(n→∞) Σ(i=1 to n) f(xi)Δx其中,n 是将区间 [a, b] 划分的份数,Δx 是每个子区间的宽度,xi 是每个子区间的中点,f(xi) 是函数在该子区间中点的取值。
2. 定积分的性质2.1 线性性质定积分具有线性性质。
对于任意的函数 f(x) 和 g(x),以及标量 c,有以下线性性质成立:∫[a, b] (cf(x) + g(x))dx = c∫[a, b] f(x)dx + ∫[a, b] g(x)dx这表明如果我们要对一个函数的线性组合进行定积分,可以将其拆分为每个函数的定积分再进行加减操作。
2.2 区间可加性定积分还具有区间可加性。
对于给定的函数 f(x) 和一个区间 [a, b],可以将该区间分为 [a, c] 和 [c, b],则有以下区间可加性成立:∫[a, b] f(x)dx= ∫[a, c] f(x)dx + ∫[c, b] f(x)dx这意味着我们可以对一个区间进行分割,然后对每个子区间进行定积分,最后将结果进行求和,得到整个区间的定积分。
2.3 积分估值定理通过定积分,我们可以得到函数在一个区间上的面积。
而通过积分估值定理,我们还可以用定积分来估计函数在该区间上的平均值。
设函数 f(x) 在区间 [a, b] 上连续,则存在一个介于 a 和 b 之间的数 c,满足以下等式:f(c) = 1/(b-a) ∫[a, b] f(x)dx这意味着通过计算定积分,并除以区间的长度,我们可以得到函数在该区间上的平均值。
2.4 牛顿-莱布尼茨公式牛顿-莱布尼茨公式是定积分的一个重要性质,它建立了定积分与原函数之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使 f()b 1aabf(x)d,x
即 a b f ( x ) d f ( x ) b ( a ) .(ab)
积分中值公式的几何解释:
y
在 区 间 [a,b]上 至 少 存 在 一
个 点 , 使 得 以 区 间 [ a ,b ] 为
f ()
底 边 , 以 曲 线 yf(x )
o a
为 曲 边 的 曲 边 梯 形 的 面 积
补充:不论 a,b,c的相对位置如何, 上式总成立.
例 若 abc,
c
aHale Waihona Puke f(x)dxa bf(x)d xb cf(x)dx
则
b
a
f
c
c
(x)dxaf(x)d xbf(x)dx
c
b
af(x)d xc f(x)d.x
(定积分对于积分区间具有可加性)
第6页
性质4 a b1d x a bd x ba.
性质5 如 果 在 区 间 [ a ,b ] 上 f(x ) 0 ,
第3页
性质1
b
b
b
a [f(x ) g (x )d ] x af(x ) d x a g (x ) d.x
证
b
a[f(x)g(x)d] x
n
l i0m i1[f(i)g(i) ]xi
n
n
lim 0 i1
f(i)xi
lim 0 i1
g(i
)xi
b
a
b
f (x)dxa g(x)dx.
(此性质可以推广到有限多个函数作和的情况)
(此性质可用于估计积分值的大致范围)
第11页
例 2 估 计 积 分 0 3 s 1 3 i x d n 的 值 x .
解 f(x)3s1in3x, x [0,],
0si3n x1,
111 43sin3x3,
0 4 1d x0 3s1i3x n d x0 1 3d,x
40 3s1i3n xd x 3.
使 a b f(x ) d x f()b ( a ).(a b )
积分中值公式
证 m ( b a ) a b f(x ) d M x ( b a ) mb 1aa bf(x)d xM
由闭区间上连续函数的介值定理知
第15页
在 区 间 [ a , b ] 上 至 少 存 在 一 个 点 ,
Mf()2 2, m f()2,
4
2
ba, 24 4
2 4 4 2sx ixn d x22 4,
1
2
4 2sxin xdx
2. 2
第14页
性质7(定积分中值定理)
如 果 函 数 f( x ) 在 闭 区 间 [ a ,b ] 上 连 续 ,
则 在 积 分 区 间 [a ,b ]上 至 少 存 在 一 个 点 ,
第12页
例3 估 计 积 分 4 2sxin xdx的 值 .
解 f(x)sinx, x [, ]
x
42
f(x)xcoxxs 2six ncoxs(xx2taxn) 0, f ( x ) 在 [ , ] 上 单 调 下 降 ,
4 2
故 x 为 极 大 点 , x 为 极 小 点 ,
4
2
第13页
则 a bf(x )d x 0 . (a b )
证 f(x ) 0 ,f(i)0, ( i 1 ,2 , ,n )
n
xi0, f(i)xi 0,
i1 m x 1 , x a 2 , , x x n }{
n
lim
0 i1
f(i
)xi
b
f(x)dx0. a
第7页
例 1比 较 积 分 值 2 e x d 和 x 2 x d的 x 大 小 .
2lim 3f()6.
证 f( x ) g ( x ), g (x ) f(x ) 0 ,
b
a[g(x)f(x)d ] x0,
b
b
ag (x)d x af(x)d x 0 ,
于 是 a b f ( x ) d x a b g ( x ) d . x
第9页
性质5的推论:
(2)
b
b
af(x)d xaf(x)d.x(ab)
0
0
解 令 f(x)exx, x[2,0]
f(x ) 0 , 02(exx)dx 0,
0 exdx
0
xdx,
2
2
于是
2exdx
2
xdx.
0
0
第8页
性质5的推论:
(1)如 果 在 区 间 [ a , b ] 上 f ( x ) g ( x ) ,
则 a b f( x ) d x a b g ( x ) d .x ( a b )
等 于 同 一 底 边 而 高 为 f()
b x 的 一 个 矩 形 的 面 积 。
第16页
例4设f(x)可 导 , 且limf(x)1, x
求limx2tsin 3f(t)d.t
x x
t
解 由积分中值定理知有 [x,x2],
使 xx2tsin3t f(t)dtsi 3 nf()(x2x), xl im xx2tsin 3t f(t)dt 2l imsin3f()
第4页
性质2 a b k (x ) f d k x a b f(x ) dx k (为 常 数 ) .
证
abkf(x)dxlim 0in1kf(i)xi
n
n
limk 0 i1
f(i)xi
klim
0i1
f(i)xi
b
ka f(x)dx.
第5页
性质3 假 设 acb
b
c
b
af(x )d x af(x )d x cf(x )d.x
f ( x ) 在 区 间 [ a , b ] 上 的 最 大 值 及 最 小 值 ,
则 m ( b a ) a b f(x ) d M x ( b a ) .
证 m f ( x ) M ,
b
b
b
am d xaf(x)d xaM,dx
b
m (b a ) af(x ) d x M (b a ).
证 f ( x ) f ( x ) f ( x ) ,
b
b
b
af(x ) d x af(x ) d x af(x ) d ,x
即 a bf(x)d xa bf(x)d.x
说明: |f ( x ) | 在 区 间 [ a , b ] 上 的 可积性是显然的.
第10页
性质6 设 M 及 m 分 别 是 函 数
062-定积分的性质
此处添加副标题内容
6-2 定积分的性质 中值定理
第2页
一、基本内容
对定积分的补充规定:
( 1 ) 当 a b 时 , a bf(x )d x 0 ;
( 2 ) 当 a b 时 , a b f(x ) d x b af(x ) d.x
说明 在下面的性质中,假定定积分都存 在,且不考虑积分上下限的大小.
