第五章古典计算理论简介
北航 计算理论 第五章 分布式计算模型

yx
y(z)
P2?n
P1!n
P1?n
gc的执行规则:
<b, > true
<b, > false
< b P, > <P, >
< b P, >
<b, > true < b;P?x Q, > P?n <Q, [n/x]>
<b, > false < b;P?x Q, >
FORK(i) :: do phil(i) ? pickup( ) phil(i) ? putdown( ) ▯ phil((i-1) mod 5) ? Pickup( ) phil((i-1) mod 5) ? Putdown( ) od
ROOM::
occupancy := 0; do (i: 0..4) occupancy < 4; phil(i) ? enter( ) occupancy := occupancy + 1 ▯ (i: 0..4) phil(i) ? exit( ) occupancy := occupancy -1 od
多进程间的并发通信
显式消息
卫式命令响应消息
主要内容
Dijkstra的卫式命令
Hoare的CSP(顺序通信进程) 理论
CSP应用实例
§1 卫式命令
用于描述程序的不确定性,主要由算术表达式 AExp和布尔表达式BExp组成。
形式:
gc ::=c | b gc | gc▯ gc | gc*
古典概型教案
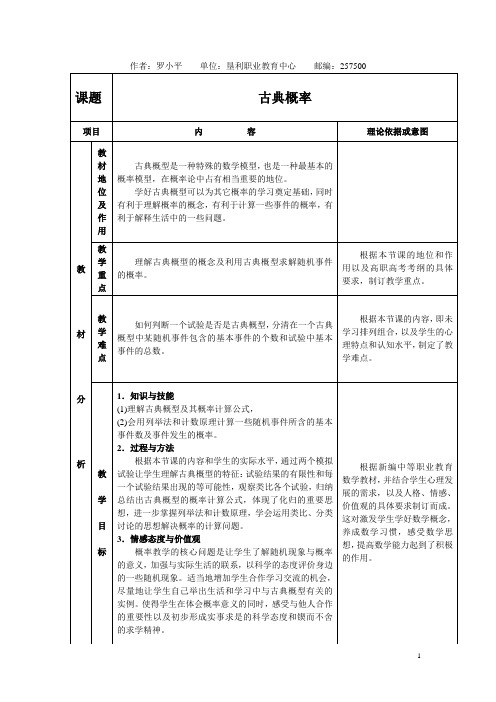
作者:罗小平单位:垦利职业教育中心邮编:257500课题古典概率项目内容理论依据或意图教材分析教材地位及作用古典概型是一种特殊的数学模型,也是一种最基本的概率模型,在概率论中占有相当重要的地位。
学好古典概型可以为其它概率的学习奠定基础,同时有利于理解概率的概念,有利于计算一些事件的概率,有利于解释生活中的一些问题。
教学重点理解古典概型的概念及利用古典概型求解随机事件的概率。
根据本节课的地位和作用以及高职高考考纲的具体要求,制订教学重点。
教学难点如何判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数。
根据本节课的内容,即未学习排列组合,以及学生的心理特点和认知水平,制定了教学难点。
教学目标1.知识与技能(1)理解古典概型及其概率计算公式,(2)会用列举法和计数原理计算一些随机事件所含的基本事件数及事件发生的概率。
2.过程与方法根据本节课的内容和学生的实际水平,通过两个模拟试验让学生理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,观察类比各个试验,归纳总结出古典概型的概率计算公式,体现了化归的重要思想,进一步掌握列举法和计数原理,学会运用类比、分类讨论的思想解决概率的计算问题。
3.情感态度与价值观概率教学的核心问题是让学生了解随机现象与概率的意义,加强与实际生活的联系,以科学的态度评价身边的一些随机现象。
适当地增加学生合作学习交流的机会,尽量地让学生自己举出生活和学习中与古典概型有关的实例。
使得学生在体会概率意义的同时,感受与他人合作的重要性以及初步形成实事求是的科学态度和锲而不舍的求学精神。
根据新编中等职业教育数学教材,并结合学生心理发展的需求,以及人格、情感、价值观的具体要求制订而成。
这对激发学生学好数学概念,养成数学习惯,感受数学思想,提高数学能力起到了积极的作用。
教学过程分析一思考交流形成概念观察对比,发现和总结两个试验共同特点:试验一:连续掷3枚硬币,观察落地后这3枚硬币出现正面还是反面。
计算理论基础课件III

计算理论在其他领域的应用
人工智能与机器学习
计算理论在人工智能和机器学习领域中发挥着重要作用,例如算 法设计、模型优化、数据挖掘等方面。
密码学与网络安全
计算理论在密码学和网络安全领域中用于研究加密算法和破解方法, 保障信息安全。
物理科学计算
计算理论在物理科学计算中用于模拟和预测自然现象,例如气候变 化、材料科学等领域。
04 计算理论中的基本问题
可计算性问题与不可计算性问题
可计算性问题
指那些可以通过有限步骤和算法得到 精确解的问题,如整数分解、旅行商 问题等。
不可计算性问题
指那些无法通过有限步骤和算法得到 精确解的问题,如连续统假设、停机 问题等。
P与NP问题
P问题
指那些可以在多项式时间内求解的问 题,如排序、图着色等。
详细描述
自动机是一个抽象的计算模型,用于模拟计算过程。它具有有限数量的状态,通过一组 转移规则从一个状态转移到另一个状态。根据接受输入的方式,自动机可以分为有限自 动机和无限自动机。有限自动机只能接受有限长度的输入,而无限自动机可以接受无限
长度的输入。
形式语言的定义与分类
总结词
形式语言是由字母表中的字符构成的字符串集合,它 可以描述自然语言中的词汇、句子等结构。根据语法 规则的不同,形式语言可以分为上下文无关语言、上 下文有关语言和图灵可识别语言等。
THANKS FOR WATCHING
感谢您的观看
05 计算理论的前沿研究
量子计算理论
量子计算理论概述
量子计算理论是研究量子力学和 计算科学交叉领域的理论框架, 旨在利用量子力学的特性实现更
高效的计算。
量子算法
量子算法是利用量子力学原理设计 的算法,具有在某些特定问题上超 越经典计算机的能力,例如Shor 算法用于大数因数分解。
古典经济学时期(三)【从西尼尔到约-斯-穆勒】

一、穆勒的生平、著作简介
❖ 约翰·穆勒生于伦敦近郊。父亲詹姆斯·穆勒(James Mill,17731836)是一位颇有影响的历史学家、经济学家,同李嘉图、 边沁是好友。小穆勒在父亲严格到几近残酷的管教和教育下 开始学习,3岁学希腊文、8岁学拉丁文、12岁学逻辑学和哲 学、14岁学经济学。
❖ 由于感觉不到生活的意义,小穆勒20岁时神经失常,企图自 杀。后来此病痊愈,但时有复发。
❖ 1830年是穆勒人生的一个转折点。他偶然遇到挚爱一生的哈 利特·泰勒(Harriet Taylor,1807——1859)。哈利特对穆勒影响 深远,特别是在社会主义、女权主义方面。
❖ 1848年,穆勒发表《政治经济学原理以及对社会哲学的某些 应用》。这是一本统治西方世界半世纪的教科书,前后共修 订出版32次。
❖ 1859年,穆勒夫人去世,这对穆勒打击甚大。 ❖ 在穆勒晚年,仍坚持写作。为降低其作品的销售价格,穆勒
不仅以简装版发行,且常常放弃版税。他曾担当过议会议员, 为妇女的选举权四处奔走,反对美洲的奴隶制。
❖ 1873年,穆勒由于因皮肤炎而引起的高烧去世。
❖ 穆勒的主要著作: 《略论政治经济学中若干未解决的问题》(1844) 《政治经济学原理及其在社会哲学方面的应用》(1848) 《论自由》(1859) 《功利主义》(1863) 《孔德与实证主义》(1865)
❖ 西尼尔用主观唯心主义说明劳动和资本,证明在资本主义制 度下,雇佣工人和资本家之间的关系是完全平等的,他们各 自的收入是正当的、合理的。
六、最后一小时论
❖ 西尼尔在《论工厂法对棉纱制造业的影响的书信》一文中提 出,工厂主的利润是11个半小时劳动日的最后一小时创造出 来的。
工人每天劳动(小时) 每个劳动日生产的年产品价值(英镑) 花费的固定资本(英镑) 花费的流动资本(英镑) 得到的总利润(英镑) 每半小时工人生产棉纱(英镑) 工人20个半小时生产棉纱(英镑) 第21个半小时生产棉纱(英镑)
大学计算机第5章电子教案

TSP问题的算法策略设计:
当数学建模完成后,就要设计算法的策略或者说问题求解的策略。
求解TSP的遍历算法:列出每一条可供选择的路线,计算出每条
路线的总里程,最后从中选出一条最短的路线。
出现的问题是:组合爆炸
• 路径组合数目:(n-1)! • 20个城市,遍历总数1.216×1017 • 计算机以每秒检索1000万条路线的计算速度,需386年。
【例5-4】TSP问题(旅行商问题、货郎担问题)
TSP问题(Traveling Salesman Problem,旅行商问题),威廉 哈密尔顿爵士和英国数学家克克曼T.P.Kirkman于19世纪初提出。
有若干个城市,任何两个城市之间的距离都是确定的,现要求 一旅行商从某城市出发必须经过每一个城市且只能在每个城市逗 留一次,最后回到原出发城市,问如何事先确定好一条最短的路 线使其旅行的费用最少。
将现实世界的问题抽象成数学模型,就可能发现问题的本质及 其能否求解,甚至找到求解该问题的方法和算法。
(1) 百钱百鸡问题的数学模型:
x y z 100 5x 3y z / 3
(1) 100 (2)
且根据已知条件有:0≤x≤20,0≤y≤33,3≤z<100,z mod 3=0
(4) 阿基米德分牛问题
问题分析:引入数学变量,设白、黑、花、棕4种颜色的公牛、 母牛数量分别为x1、x2、x3、x4和y1、y2、y3、y4,这样可以 将要求的问题解表示成一个表格。
白色 黑色 花色 棕色 公牛 x1 x2 x3 x4
x1 x4 x2 1/ 2 1/ 3
x2
B
3
6
6
A
9
C
8
3
计算理论与算法

将问题分解为若干个子 问题,通过求解子问题 的最优解来得到原问题 的最优解的思想,适用 于具有重叠子问题和最 优子结构性质的问题。
03
复杂度理论
时间复杂度与空间复杂度
1 2
时间复杂度
评估算法执行时间随输入规模增长的速度,常用 大O表示法(如O(n), O(n^2), O(log n)等)来 描述。
广度优先搜索(BFS)
从某个顶点出发,逐层访问图中所有顶点,直到达到指定顶点或无 法再访问为止。
图的遍历应用
用于解决图的连通性问题、寻找图中的路径、生成拓扑排序等问题。
最小生成树与最短路径算法
01
最小生成树(MST)
对于连通的无向图,一个包含图中所有顶点的连通子图,且所有边的权
值之和最小。常用算法有Prim算法和Kruskal算法。
时间复杂度
动态规划和分治策略的时间复杂度通常取决于问题的规模 和子问题的数量。在某些情况下,动态规划可能比分治策 略更高效,因为它避免了重复计算子问题。
06
计算几何与算法
计算几何基本概念与性质
点、线、面的表示与性质
计算几何中的基本元素包括点、线、面等,它们在计算机中的表 示方式及其性质是研究计算几何的基础。
01
几何搜索
02
最近点对问题
03
应用场景
几何搜索是指在几何数据集中查找满 足特定条件的几何对象,如查找最近 的点、线、面等。常见的几何搜索算 法有KD树、四叉树、R树等。
最近点对问题是指在给定的点集中找 到距离最近的两个点。该问题可以通 过分治算法在O(nlogn)的时间复杂度 内解决。
几何搜索和最近点对问题在计算机图 形学、计算机视觉、机器人学等领域 有着广泛的应用,如三维模型检索、 图像特征匹配、机器人避障等。
金融理论第五章货币供给的内生性与外生性
是即非 否即中
n 货币供给内外生性的关给(果)
n
Ms = f (s I c i y)
否即外
金融理论第五章货币供给的内生性与 外生性
n 二、货币内外生性理论发展与变迁(王广谦43)
n 1、早期论述
n (1)货币本质观与货币的内生性、外生性
n 货币金属观(足额准备论):内生性
外生性
5.1货币供给的内生性与外生性理论概述
一、货币供给的内生性与外生性的基本范畴 1.内生性涵义
货币供给的内生性是指货币供给的变动,主要取 决于经济体系中的实际变量如收入、储蓄、投资、消 费等因素以及公众、商业银行等微观主体的经济行为, 而不是取决于货币当局的政策意愿,因而货币当局并 不能有效地控制货币供给量。
又当 MS V = Y = P•Q 中的MS V 不变, 则 Y 不变;P↑,必然Q↓,就业也下降,
(或P↑〉Y↑,Q↓) 结果有悖于中央银行银行的双重货币政策目标。 为了增加产量、降低失业,中央银行只有增加 MS↑ 因为: 在V不变时, MS↑V = Y = P↑Q
金融理论第五章货币供给的内生性与 外生性
n 货币名目观(管理通货论):外生性
n (2)传统货币数量论
n
M↑— P↑ 外生性
n (3)古典经济学家
n
W(G)↓—M↑— P↑ 内生性
n (4)“通货论争”中的银行主义
n 通货数量由社会交易的商品价格总额所决定 内生性
金融理论第五章货币供给的内生性与 外生性
n 2、凯恩斯的外生货币供给理论(一章3节三) n 3、货币学派对外生货币论的拓展
(五)货币的供需矛盾,宏观政策:国家可凭借权力创 造和增加货币供应
金融理论第五章货币供给的内生性与 外生性
计算方法课件 第五章 插值法
1 Ak ( xk x0 )( xk x1 ) ( xk xk 1 )( xk xk 1 ) ( xk xn )
( x x0 )( x x1 ) ( x xk 1 )( x xk 1 ) ( x xn ) lk ( x ) (k 0,1,, n) ( xk x0 )( xk x1 ) ( xk xk 1 )( xk xk 1 ) ( xk xn )
n n
上式是不超过n次的多项式,且满足所有的插值 条件,因而就是我们所需构造的插值多项式,称之 为Lagrange插值多项式。 当n=1时,有 当n=2时,有
n1 ( x) Ln ( x) f ( xi )li ( x) f ( xi ) ' ( x x ) i 0 i 0 i n 1 ( xi )
2 n , 即 P span 1 , x , x , , x 特别的取 = n
Pn ( x ) ( x ) a0 a1 x a 2 x 2 a n x n , ai R , 0 i n
五、插值多项式的存在唯一性
分析 对于多项式插值问题,插值条件(1)等价于 确定多项式的系数,使得满足如下的线性方程组
x x0 x x1 L1 ( x) y0 y1 x0 x1 x1 x0
( x x0 )( x x2 ) ( x x0 )( x x1 ) ( x x1 )( x x2 ) L2 ( x) y0 y1 y2 ( x0 x1 )( x0 x2 ) ( x1 x0 )( x1 x2 ) ( x2 x0 )( x2 x1 )
(n 1)
n 1
M n 1 R n (x ) n 1 (x ) (n 1) !
并行计算第五章并行算法与并行计算模型
并行计算第五章并行算法与并行计算模型在计算机领域中,并行计算是指同时进行多个计算任务的计算模式。
并行计算能够显著提高计算效率,加快计算速度,广泛应用于图像处理、数据挖掘、科学模拟等众多领域。
本文将重点介绍并行计算的背景和相关的并行算法与并行计算模型。
首先,我们来了解并行计算的背景。
随着计算机硬件的不断发展,单个处理器的计算能力已经达到了一个瓶颈,无法满足日益增长的计算需求。
为了充分利用硬件资源,提高计算效率,人们开始将多个处理器同时运行不同的任务,从而引入了并行计算的概念。
并行计算的基本思想是将计算任务分解为多个子任务,并将这些子任务分配给多个处理器并行执行。
在并行计算中,一个重要的问题是如何划分任务和调度子任务,以便充分利用处理器资源并减少通信开销。
为此,人们提出了各种并行算法和并行计算模型。
一种常用的并行算法是分治法,即将一个大问题分解为多个小问题,分别在不同的处理器上并行求解。
分治法通过递归地将子问题划分为更小的子问题,并组合子问题的解来获得原始问题的解。
分治法的优点是简单高效,适用于大规模问题的并行计算。
另一种常用的并行算法是图算法,主要应用于图论和网络分析等领域。
图算法通过将问题建模为图的形式,并用图上的顶点和边表示计算的对象和关系。
图算法的主要挑战是如何将计算任务划分为多个子任务,并通过合理的通信方式在多个处理器之间共享数据。
并行计算模型是指描述并行计算方式和通信机制的抽象模型。
其中,一种常用的并行计算模型是共享内存模型。
在共享内存模型中,所有的处理器共享同一块内存空间,并可以通过读写内存中的共享变量来实现进程间的通信。
共享内存模型的优点是简单易用,但需要额外的同步机制来确保数据的一致性。
另一种常用的并行计算模型是消息传递模型。
在消息传递模型中,各个处理器拥有自己的本地内存,并通过发送和接收消息来进行通信。
消息传递模型的优点是灵活性高,可以充分利用通信资源,但需要额外的编程工作来处理消息的发送和接收。
第五章 行为决策理论
案例二:
中国航空工业第一集团公司在2000年8月决定今后民用飞 机不再发展干线飞机,而转向发展支线飞机。这一决策立时引 起广泛争议和反弹。
该公司与美国麦道公司于1992年签订合同合作生产MD90 干线飞机。2019年项目全面展开,2019年双方合作制造的首架 飞机成功试飞,2000年第二架飞机再次成功试飞,并且两架飞 机很快取得美国联邦航空局颁发的单机适航证。这显示中国在 干线飞机制造和总装技术方面已达到90年代的国际水平,并具 备了小批量生产能力。
5.1.2 确定性效应的多种形式
我们再看一个与之相似的例子,下面这个例子较上面那 个例子更加简单,也许也更具代表性。 实验2 博彩1: 博彩A:80%的机会得到4000,20%的机会什么都得不到; 博彩B:100%的机会得到3000;
博彩2: 博彩C:20%的机会得到4000,80%的机会什么都得不到; 博彩D:25%的机会得到3000。
教学难点
确定性效应在实际中的表现形式,期望价值理论的基本原理与 应用。
课程引入
理性决策的规范模型在应用中出现一些和实 际行为相悖的现象,给人们带来许多启示。 决策科学研究,一方面沿着理性决策的轨道 发展,这包括对现有的期望效用值理论的改 进,也包括探索新的理性决策模型;另一方 面则朝着行为决策理论的轨道发展,即研究 人们的实际决策行为的机理。
博彩1
博彩A
20%
博彩B
80%*
博彩2
博彩C
65%*
博彩D
35%
注:1参加实验总人数为95人;2加*数据在 0.1的水平上是显著的。
