习题Ch1
通信原理习题课CH1-8

复习CH1-51. 如果在已知发送独立的符号中符号“X”出现的概率为0.125,则符号“X”所包含的信息量为C 。
A .1bitB .2bitC .3bitD .4bit2. 下列属于通信系统按调制方式分类的是 B 。
A. 模拟与数字通信B. 基带传输和频带传输C. 电报与数据通信D. 有线与无线通信3. 设某信息源由A,B,C 三个信息符号组成,发送A 的概率为1/2,发送其余符号的概率相同,且设每一符号的出现是相互独立的,则该符号集的平均信息量为 C bit/符号。
A .1.75B .1C .1.5D .24. 从信息传输角度来看,通信系统的主要质量指标可概括为 ___B___。
A .传输速率和差错率B .有效性和可靠性C .有效性和标准性D .可靠性和经济性5. 所谓门限效应,就是当检波器的 降低到一个特定的数值后,检波器输出 端出现的现象。
6. 如果通信仅在点—点之间进行,按照信号传输方向和时间的关系,电话的通信方式属于 ,而对讲机的通信方式属于 。
7. 八进制数字信号信息传输速率为300b/s ,其码元速率为__________,若传送1小时后,接收到 10个错误码元,其误码率为 。
8. 信道容量是指一个信道最大可能传输的 ;若某高斯信道带宽为4kHz ,输出信噪比为127倍,则信道容量为 。
9. 用10KHz 的正弦信号调制200MHz 的载波,若最大频偏为100KHz ,则产生FM 波的带宽为A 。
A .220KHzB .200KHzC .100KHzD .20KHz10. 一个频带限制在0到m f 以内的低通信号m(t),用s f 速率进行理想抽样,m s f f 2≥,若要不失真的恢复m(t),低通滤波器带宽B与m f 和s f 的关系应满足: D 。
A .m f B ≥ B .m m s f B f f ≥≥- C .m s f B f ≥≥ D .m f B 2≥11. 设x(t)为调制信号,调频波的表示式为:))(cos(⎰∞-+t f c d x k tττω,则FM 调制方式的瞬时相位偏差为 D : A .()t x k f B .⎰∞-+t f c d x k t ττω)( C .()t x k t f c +ω D .⎰∞-t f d x k ττ)(12. 以奈奎斯特速率进行抽样得到的以下抽样信号,仅用理想低通滤波器不可能将原始信号恢复出来的是 D 。
91543-网络技术与应用-ch1-2习题-214

A、80ms
B、80.08ms
C、80.16ms D、80.24ms
• 解答:分组大小为1000B,其中分组头大小 为20B,可以得出每个分组的数据部分 为 980B,所以大小为980000B 的文件应该分 为1000 个分组传送。
• 每一个分组1000B,而链路的数据传输速 度为100Mbps,所以主机H1 传送 完一个分 组所需的时间为 1000*8/100M=80*10-6(s)
最后一位在t=x/b时发送完毕,为到达目的 地,最后一个分组必须被中间的路由器重 发k-1次,每次重发花时间p/b, 分组交换总的时延:
t=x/b+(k-1)p/b+kd
电路交换时延: t=s时电路建立起来, t=s+x/b时报文最后一位发送完毕, t=s+x/b+kd时报文到达目的地,即为电路交
对总时延求p的导数,得到 (p-(p+h)) x/ p2 b+(k-1)/b 令(p-(p+h)) x/ p2 b+(k-1)/b=0, 得到hx/ p2=k-1 因为p>0,所以p= hx/(k-1)
考研试题
• (09-33)在OSI参考模型中,自下而上第 一个提供端到端服务的层次是 ( )
A、数据链路 B 、传输层 C 、会话层 D 、应用层 (B)
• H1发送完最后一个分组需要用的时间为: 80*10-6s*1000=80*10-3s=80ms
• 但此时恰好最后一个分组刚从主机H1出去, 还没有到达主机H2。
• 一个分组从主机H1需要经过2次存储转发才 能到达主机H2,在不考虑传 播时延及处理 时延的情况下,需要用时: 2*80*10-3ms=0.16ms
答:
(题)数据结构复习题_ch1

}
Key:
8、设n为正整数,分析下列各程序段中加下划线的语句的执行次数。
(1)for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
c[i][j]=0.0;
for(int k = 1;k <= n;k++)
算法效率的度量分为(②)和(③)。(②)主要通过在算法的某些部位插装时间函数来测定算法完成某一规定功能所需的时间。而(③)不实际运行算法,它是分析算法中语句的执行次数来度量算法的时间复杂性。
程序所需的存储空间包含两个部分(④)和(⑤)。(④)空间的大小与输入输出数据的个数多少,数值大小无关;(⑤)空间主要包括其大小与问题规模有关的成分变量所占空间,引用变量所占空间,以及递归栈所用的空间,还有在算法运行过程中动态分配和回收的空间。
s += a[i];
return s;
}
Key:2n+3
6、试计算以下递归求和程序中所有语句的总执行次数。
float rsum(float a[ ], int n)
{
if(n <= 0)return a[0];
else return rsum(a, n-1)+ a[n-1];
}
Key:
7、试用大O表示法给出下面程序的时间复杂性。
()数据结构是指相互之间存在一种或多种关系的数据元素的全体。
()从逻辑关系上讲,数据结构主要分为两大类:线性结构和非线性结构。
二级c语言程序设计习题及解答ch1-3

12)计算机能直接执行的程序是(B )。
A)源程序B)目标程序C)汇编程序D)可执行程序13)以下叙述中正确的是( D )A)程序设计的任务就是编写程序代码并上机调试B)程序设计的任务就是确定所用数据结构C)程序设计的任务就是确定所用算法D)以上三种说法都不完整例年真题:#include<stdio.h>main(){Int a;A=5; /*给A变量赋值5A+=3; 再赋值后再加3*/Printf(“%d”,a);}(11)以下叙述中正确的是( C )。
A)C 程序的基本组成单位是语句B)C 程序中的每一行只能写一条语句C)简单C 语句必须以分号结束D)C 语句必须在一行内写完(11)以下叙述中正确的是( C )A)C程序中的注释只能出现在程序的开始位置和语句的后面B)C程序书写格式严格,要求一行内只能写一个语句C)C程序书写格式自由,一个语句可以写在多行上D)用C语言编写的程序只能放在一个程序文件中(12)以下选项中,能用作用户标识符的是( C )A)voidB)8_8C)_0_D)unsigned【解析】A:关键字不可以B:不以数字开头C:正确D:关键字(13)以下选项中合法的标识符是( C )A)1-1 B)1—1C)-11D)1—【解析】A:不以数字开头,出现非法字符-而不是_ B:不以数字开头,非法字符C:正确D: 不以数字开头,出现非法字符(14)以下选项中不合法的标识符是( C )A)print B)FOR C)&a D)_00【解析】C:出现非法字符&(15)以下选项中,能用作数据常量的是( D )A)o115 B)0118 C)1.5e1.5D)115L【解析】A:八进制以0开头而不是以o开头B:八进制最大值为7,范围0-7 C:指数必须为整数D: 长整型正确(13)以下选项中不能作为C语言合法常量的是(A)。
A)'cd'B)0.1e+6 C)"\a" D)'\011'【解析】A:字符常量只能有一个字符(16)以下选项中不属于字符常量的是( B )A)'C'B)"C"C)'\xCC0' D)'\072'【解析】B:字符常量以单引号作为标志,其为字符串(14)表达式:4-(9)%2的值是( B )A)0B)3C)4D)5【解析】(9)%2=1(取余),4-1=3(14)设变量已正确定义并赋值,以下正确的表达式是 ( C )A)x=y*5=x+zB)int(15.8%5)C)x=y+z+5,++yD)x=25%5.0【解析】A:等号左边必须为变量,不可以为表达式,y*5是表达式B:%只适用于整型变量D: %只适用于整型变量(15)若有定义语句:int x=10;,则表达式x-=x+x的值为( B )A)-20B)-10C)0D)10【解析】先算右边得20,x-=20,则10-20=-10(14)设有定义:int x=2;,以下表达式中,值不为6的是 ( D )A) x*=x+1 x=x*(x+1)B) x++,2*xC)x*=(1+x)D)2*x,x+=2【解析】逗号表达式的最终结果看最后一个表达式,x+=2,结果为4(17)若变量均已正确定义并赋值,以下合法的C语言赋值语句是 (A)A)x=y==5;B)x=n%2.5;C)x+n=ID)x=5=4+1;【解析】等号左边必为变量,不能为常量或数字排除C 、D,%只能用于整数排除B第三章输入输出习题讲解(13)阅读以下程序#includemain(){ int case; float printF;printf(“请输入2个数:”);scanf(“%d %f”,&case,&pjrintF);printf(“%d %f\n”,case,printF);}该程序编译时产生错误,其出错原因是(A)A)定义语句出错,case是关键字,不能用作用户自定义标识符B)定义语句出错,printF不能用作用户自定义标识符C)定义语句无错,scanf不能作为输入函数使用D)定义语句无错,printf不能输出case的值(16)有以下程序#includemain(){ int a=1,b=0;printf(“%d,”,b=a+b);printf(“%d\n”,a=2*b);}程序运行后的输出结果是(D)A)0,0B)1,0C)3,2D)1,2【解析】b=a+b即b=1,a=2*b,a=2(15)程序段:int x=12;double y=3.141593; printf(“%d%8.6f”,x,y);的输出结果是(A )A)123.141593B)123.141593C)12,3.141593D)12 3.141593【解析】“%d%8.6f”原样输出,没有,也没有空格,所以x与y相连,小数总共8位,小数点之后6位#include <stdio.h>main(){double a=123.456;printf("%6.2f",a);}结果:123.46例题:int x;x=11/3;int y=5;printf("%%d,%%%d\n",x,y); 结果是:%d,%3【解析】"%%d,%%%d\n"原样输出,%%d中第一个%为转义字符,不是输出占位符,所以原样输出%d,然后%%转义只输出一个%,%d\n只有一个占位符,所以只输出x的值为3[3.5] 若变量已正确说明为int类型,要给a、b、c输入数据,以下正确的输入语句是( D )A)read(a,b,c); B)scanf(“ %d%d%d” ,a,b,c);C)scanf(“ %D%D%D” ,&a,%b,%c);D)scanf(“ %d%d%d”,&a,&b,&c);【解析】scanf中赋值必须用&(取地址符),即将输入的字符放在指定位置中[3.6] 若变量已正确说明为float类型,要通过以下赋值语句给a赋予10、b赋予22、c 赋予33,以下不正确的输入形式是( B )A)10 B)10.0,22.0,33.0 C)10.0 D)10 2222 22.0 33.0 3333scanf(“ %f %f %f” ,&a,&b,&c);【解析】输入时可以空格可以回车,但是不可以出现,复合语句:多个语句被{}括起来,当成一条语句来执行。
固体物理学习题课-1
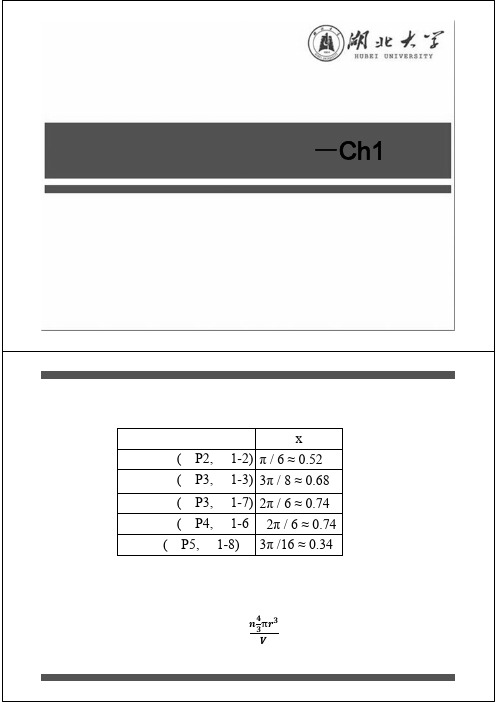
1.12 利用转动对称操作,证 明六角晶系介电常数矩阵为. 解:若 A是一旋转对称操作,则晶体的介电常数 满足 = AT A., 对六角晶系,绕x(即a)轴旋转180o和绕z(即c)轴旋转120o都 是对称操作,坐标变换矩阵分别为
假 设 六 角晶系统的介电常数为 x= Ax' Ax得
可见 即有
=
00 0 0
00 0 0
00
0
=
0
= Az' Az得
可见
,=
于是得到六角晶系的介电常数
=
1.12 比较面心立方晶格、金刚石晶格、闪锌矿晶格、N acl晶格 的晶系、布拉伐格子、点群、空间群。
补充习题 01 做出简单立方晶格、面心立方晶格和体心 立方晶格的维格纳 — 塞茨原胞 (Wingner-Seitz)
体心立方
面心立方
1.9 指出立方晶格(111)面与(100)面(111)面与(110)面的交线的晶 向
(111)面与(100)面的交线的AB
—— AB平移,A与O点重合
B点位矢 ⇀
⇀⇀
(111)面与(100)面的交线的晶向 ⇀ ⇀ —— 晶向指数
(111)面与(110)面的交线的AB
—— 将AB平移,A与原点O重合,B点位矢
⇀
⇀⇀
(111)面与(110)面的交线的晶向 ⇀⇀
—— 晶向指数 110
1.10 找出立方体中保持x 轴不变的所有对称操作,并指出他们中 任意两个操作乘积的结果 解:立方体中保持x轴不变,可有绕x轴转 , , ,加上不动 C1,所有对称操作构成群C4=(C1 C2 C3 C4),群中任意两 元素乘积仍是群中元。
a
3 2 –( )2= ( )2
气象习题ch1-2

第1章大气概况一.简答题1、简述大气的主要成分,并说明二氧化碳、臭氧和水汽的分布于作用。
2、简述大气的垂直分层概况。
3、简述对流层的主要特征。
二.选择题1.1 大气概述1.天气是指某一特定区域:A.在较短时间内各种气象要素的综合表现B.在较长时间内各种气象要素的综合表现C.气象要素的多年平均特征(包括极值)D.气象要素的一年平均特征(包括极值)2.表征大气状态的物理量和物理现象的气象术语称为:A.天气B.气候C.气象要素D.天气系统3.气候是指某一特定区域:A.在较短时间内各种气象要素的综合表现B.气象要素的多年平均特征(包括极值)C.气象要素的一年平均特征(包括极值)D.天气形势4.下列属于气象要素的是:A 风云雾霜沙尘暴B 气压高气压台风C 风云雨冷峰暖锋D 气温气压冷锋暖锋5.气象要素主要包括:I、气压、气温; II、雾、气团、锋面; III、相对湿度、沙尘暴; IV、风、云、能见度; V、温度、高压、低压;VI、雨、雪、雷暴A.I、III、IV、VI B. I、II、IV ~VI C.II~IV、VI D. II、IV~VI1.2 大气的组成1.大气的主要成分为:A.氮气、氧气、二氧化碳、惰性气体 B.干洁空气、水汽、气溶胶质粒C.氮气、氧气、二氧化、水汽 D. 氮气、氧气、二氧化碳、惰性气体、水汽2.干洁空气中的主要成分为:A.氮气、氧气、二氧化碳 B. 氮气、氧气、氩气C.氩气、氧气、二氧化 D. 氮气、氧气、氩气、二氧化碳、3.在气压相同的情况下,密度较小的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气4.在气压相同的情况下,密度较大的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气5.在气压相同的情况下,密度较小的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气6.在气压相同的情况下,密度较大的空气是:A.暖湿空气B.冷湿空气C.干热空气D.干冷空气7.影响天气及气候变化的主要大气成分包括:A.二氧化碳、臭氧和惰性气体B.氮气、二氧化碳和惰性气体C.二氧化碳、臭氧和水汽D.氧气、臭氧和惰性气体8.大气中能够透过太阳短波辐射、强烈吸收和放射长波辐射的主要气体成分为:A.臭氧B.氮气C.氧气D.二氧化碳9.在大气成分中,主要吸收太阳紫外线的气体成分为:A.臭氧B.二氧化碳C.氧气D.氮气10.在自然界的温度和压力条件下,哪种大气成份能在气态、液态和固态三者之间互相转化(即发生相变的唯一大气成份)?A.氮气B.氧气C.水汽D.二氧化碳11.在下列大气成分中,能产生温室效应的大气成分是:A.氧气 B.氮气 C.氩气 D.二氧化碳12.通常在90千米高度以下,可将干空气作为单一成分的理想气体处理,其平均分子量为:A.16摩尔B.18摩尔C.29摩尔D.32摩尔13.近地面层空气的平均密度为:A.1.01~1.03克/厘米3B.1.00克/厘米3C.1293克/厘米3D.0.86~0.92克/厘米314.从地面向上随着高度的增加,空气密度:A.缓慢递减B.迅速递减C.缓慢递增D.迅速递增15.从高空到地面向下随着高度的减小,空气密度:A.缓慢递减B.迅速递减C.缓慢递增D.迅速递增16.在自然条件下能发生相变的唯一大气成分是:A.氧 B.氮 C.水汽 D.氩17.一般而言,大气中的水汽分布A 低空多于高空B 海洋多于陆地,低纬多于高纬C 夏季多于冬季,白天多于夜间D ABC都对18.在水汽相变过程中,大气固体杂质可以充当:A.凝结核,不利于相变过程发生B.催化剂,不利于水汽凝结C.凝结核,有利于相变过程发生D.催化剂,有利于水汽凝结19.对大气温度有较大影响的大气成分:Ⅰ.氮气;Ⅱ.臭氧;Ⅲ.二氧化碳;Ⅳ.氧气;Ⅴ.水汽;Ⅵ.氢气。
一阶线性偏微分方程求解例题
一阶线性偏微分方程求解例题
CH1典型方程和定解条件
【内容提要】
方程的建立(步骤:确定物理量;微元法建立等式;化简得方程) 主要方法:微元法;
泛定方程:
波动方程(双曲型):
弦振动方程:
传输线方程:
电磁场方程:
热传导方程/扩散方程(抛物型):
导热杆(无热源),
导热片(无热源)
稳恒方程(椭圆型):
Poisson方程:
Laplace方程:
2.定解条件:初始条件及边界条件
边界条件(1)第一类边界条件(Dirichlet条件):
(2)第二类边界条件(Neumann条件):
(3)第三类边界条件(Robin条件):
3.定解问题的提法:
4.线性偏微分方程的基本性质
(1).线性迭加原理
(2.)齐次化原理(冲量原理)
Duhamel原理:设是方程的解,
(是方程的解。
【典型习题】
1:长为的均匀杆,侧面绝缘,一端温度为零,另一端有恒定热流进入(即单位时间内通过单位截面积流入的热量为),杆的初始温度分布是,试写出相应的定解问题
解:初始条件:,杆的初始温度分布是,
边界条件:由杆的一端温度为零
,杆的另一端有恒定热流q,)(Fourier实验定律
故定解问题为:
该定解问题为齐次方程第二类非齐次边界条件的混合问题
3:长为的弦两端固定,开始时在受冲量的作用,试写出相应的定解问题
解:设弦的两端为:,由题意有
弦的振动方程为
边界条件为:
初始条件为:
在点,取小段(是无穷小量),
由冲量定理有,(冲量=动量改变量);
∴
于是,
故定解问题为
该定解问题为齐次方程第一类齐次边界条件的混合问。
工程电磁场 (杨宪章 邹玲 樊亚东 著) 中国电力出版社 课后答案 题ch1
E2 ⋅ 2πR = E3 ⋅ 2πR =
τ1 τ1 , E2 = 2ε 0πR ε0
R > R2 :
S
课
后
v 仅 R2 中不填 ρ ,其内 E2 :
ρπr 2 E2 ⋅ 2πr = ε0
r v v v ρ v r ρa ∴ E = E1 − E2 = (R − r ) = 2ε 0 2ε 0
习题 1-17 解:任意半径 r 处 E: v v ∫ εEdS = q
v σ ⋅ 2πrdr ⋅ x v dE = i 3 2 2 2 4πε 0 r + x
网
P
x
(
故 r 从 R1 到 R2 积分即所有圆环产生的场强:
v R2 σ ⋅ 2πrdr ⋅ x v σx E=∫ i = 3 4ε 0 2 2 R1 4πε r + x 2 0
R2
(
)
d r 2 + x 2 v σx −2 i = 3 ∫ 4ε 0 2 R1 r 2 + x 2 2 r + x2
v E1 = q r r, 2 4πq0 (d + x )
-pq:
v E2 =
− pq v r 2 4πε 0 ( x )
两边开方取正值: x =
p 1− p
d
习题 1-11
A x q1 d q2
解:分析知,只可能是 A 点,Q q2 > q1 ,∴ A 点必须离 q1 近、离 q2 远才行 令 x 如图示,据题意有
σ ⎢ 1− E= 2ε 0 ⎢
⎣
⎡
(
⎤ ⎥ 1 2 2 2 ⎥ R2 + x ⎦ x
)
2)又
R2 →∞得 x
ch1习题1-2
Digital Signal Processing
主讲人:李艳凤
电子信息工程学院
利用数字系统处理模拟信号的框图如下图所示,抽样与重建间隔 T1=T2=0.01秒。试画出信号x[k],y[k]和y(t)的频谱。
x [k]
y[k]
x(t)
抽样
h[k]
重建
y(t)
X(j) 1
T1
T2
H(ej)
解:
x [k]
y[k]
x(t)
抽样
h[k]
重建
y(t)
T1
X(ej) 1/T1
T2
H(ej)
1
2
0.5 0 0.5
2
Y(ej) 1/T1
2
0.4 0 0.4
0.4 0.4
2
利用数字系统处理模拟信号的框图如下图所示,抽样与重建间隔 T1=T2=0.01秒。试画出信号x[k],y[k]和y(t)的频谱。
解:
x [k]
y[k]
x(t)
抽样
h[k]
重建
y(t)
T1
T2
Y(ej)
1/T1
2
0.4 0 0.4
2
Y(j) 1
/ T2
40 0 40
Hrec(j) T1
100
0
100
X(j)
1
50
0
50
谢谢
本课程所引用的一些素材为主讲老师多年的教学积累,来源 于多种媒体及同事和同行的交流,难以一一注明出处,特此说明 并表示感谢!
T1
1
T2
50
0Leabharlann 50 X (ej ) 1
原《数据挖掘》习题
ch11.讨论下列每项活动是否是数据挖掘任务:(fgh是)(a) 根据性别划分公司的顾客。
(b) 根据可赢利性划分公司的顾客。
(c) 计算公司的总销售额。
(d) 按学生的标识号对学生数据库排序。
(e) 预测掷一对骰子的结果。
(f) 使用历史记录预测某公司未来的股票价格。
(g) 监视病人心率的异常变化。
(h) 监视地震活动的地震波。
(i) 提取声波的频率。
2. (ch1)数据挖掘可以在很多数据源上进行,如关系数据库,空间数据库,多媒体数据库,文本数据库等。
3. (ch1)数据挖掘一定可以得到有趣的强关联规则。
4. (ch1)为了提高挖掘质量,通常要进行数据预处理,包括数据清理、集成、选择、变换等。
5. (ch5){发烧,上呼吸道感染}是(2)项集6.企业要建立预测模型,需准备建模数据集,以下四条描述建模数据集正确的是( B )。
A 数据越多越好B 尽可能多的适合的数据C数据越少越好D 以上三条都正确7. 数据挖掘算法以( D )形式来组织数据。
A 行 B列 C 记录 D 表格Ch28. (ch2)假定用于分析的数据包含属性age。
数据元组中age的值如下(按递增序):13,15,16,16,19,20,20,21,22,22,25,25,25,25,30,33,33,35,35,35,35,36,40,45,46,52,70,求:1)使用按箱平均值平滑对以上数据进行平滑,箱的深度是3。
解释你的步骤。
2)使用按箱边界值平滑对以上数据进行平滑,箱的深度是3。
解释你的步骤。
7、P98 3.4(ch3)假定大学的数据仓库包含4个维{student学生、course课程、semester学期、instructor教师},2个度量count和avg_grade。
在最低的概念层(例如对于给定的学生、课程、学期和教师组合),度量avg_grade存放学生的实际成绩。
为数据仓库画出雪花模式图8、P98 3.5(ch3)假定数据仓库包含4个维date,spectator,location和game,2个度量count和charge。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Exercise Ch. 11.1 Express each of the following complex numbers in Cartesian form (x+jy ):(3) e j π/2 = cos(π/2)+j sin(π/2)=j (6)2e j π/4 =2[cos(π/4)+j sin(π/4)]=1+j1.2 Express each of the following complex numbers in polar form (r e j θ, with -π< θ ≤ π):(6) (1-j)2 = 1-2j + j 2 = 1 + 2 e -j π/2- 1 = 2 e -j π/2(7) j(1-j) = j +1 = e j π/2 + 1 = e j π/4 ( e j π/4 + e -j π/4 ) = 2e j π/41.4 let x [n ] be a signal with x [n ] = 0 for n < -2, and n > 4. For each signal given below, determine thevalues of n for which it is guaranteed to be zero. (d) x [-n +2] Solution:(d) Since –n +2 < -2 ♑ n > 4; –n +2 > 4 ♑ n < -2, so, x [-n+2] will be zero for n < -2 and n > 4.1.11 Determine the fundamental period of the signal x[n]=1+e7/4n j π-e 5/2n j π.Solution: The period of e7/4n j π isN 1=7. The period of e5/2n j π isN 2=5. So N = N 1 N 2=351.12 Consider the discrete —time signal1[1][3kn n x k ---=∑∞=δDetermine the values of the integers M and 0n so that x[n] may be expressed as ].[][0n Mn u n x -=Solution: ∑∞=-=],[][k k n n u δ While ]4[]1[3-=--∑∞=n u k n k δSo, ]3[]4[]1[][]4[1][+-=---+-=--=n u n u n u n u n u n x we can find that easily: M = -1, 0n = -3.1.13 Consider the continuous-time signal )2()2()(--+=t t t x δδ.Calculate the value of ∞E for the signal ⎰∞-=td x t y .)()(ττSolution:Because )2()2()(--+=t t t x δδ)2()2()]2()2([)(-++=-++=⎰∞-t u t u d t y tττδτδ)2()2()2(2)2()(2-+-+-+=t u t u t u t u t y)2()2(2)2(-+--+=t u t u t u --+=t u t u ()2(2)So ⎰⎰+∞∞--∞===2224)(dt dt t y E1.14 Consider a periodic signal21,210,1{)(<<-≤≤=t t t xWith period T=2. The derivative of this signal is related to the ―impulse train ‖∑∞-∞=-=k k t t g )2()(δWith period T=2. It can be shown that)()()(2211t t g A t t g A dtt dx -+-=Determine the values of A 1, t 1, A 2, and t 2.Solution:We get the figure from the function,Then, in the interval of 20≤≤t ,)1(3)(3)(--=t t dtt dx δδ We getA 1=3,t 1=0,A 2=-3,t 2=1.)1.19 For each of the following input-output relationships, determine whether the corresponding system islinear, time invariant or both.(b) [][]22-=n x n y(i) Consider two arbitrary inputs x 1[n]and x 2[n] x 1[n] →y 1[n] = xı²[n - 2] x 2[n] → y 2[n] = x 2² [n - 2]Let x 3[n] be a linear combination of x 1[n] and x 2[n] That is,x 3[n] = a x 1[n] + b x 2[n]where a and b are arbitrary scalars. If x 3[n] is the input to the given system, then the corresponding output y 3[n] is[][][][]()[][][][][][]n by n ay n x n abx n xb n x a n bx n ax n x n y 212122221222123322222222+≠--+-+-=-+-=-=Therefore, the system is not linear.(ii)Consider an arbitrary input x 1[n]. Let [][]2211-=n x n yis th e corresponding output. Consider a second input x 2[n] obtained by shifting x 1[n] in time: [][]012n n x n x -=The output corresponding to this input is[][][][][][][]01202101021222222n n y n y n n x n n y n n x n x n y -=--=---=-=Also note that[][]021012n n xn n y --=-Therefore, [][]012n n y n y -=This implies that the system is time-invariant.1.31 In this problem we illustrate one of the most important consequences of the properties of linearity andtime invariance. Specifically, once we know the response of a linear system or a linear time-invariant (LTI) system to a single input or the responses to several inputs, we can directly compute the responses to many other input signals. Much of the remainder of this book deals with a thorough exploitation of this fact in order to develop results and techniques for analyzing and synthesizing LTI systems.(a) Consider an LTI system whose response to the signal x 1(t) in Figure P1.31 (a) is the signal y 1(t)illustrated in Figure P1.31(b). Determine and sketch carefully the response of the system to the input x 2(t) depicted in Figure 1.31(c).(b) Determine and sketch the response of the system considered in part (a) to the input x 3(t) shown inFigure P1.31 (d).x 2(t) x 3(t)Solution: ),2()()(112--=t x t x t x so, )2()()(112--=t y t y t y)()1()(113t x t x t x ++=, so, )()1()(113t y t y t y ++=。
