高考文科数学分类汇编 不等式
高考数学分项汇编 专题07 不等式(含解析)文

专题07 不等式一.基础题组1. 【2006高考陕西版文第7题】设x ,y 为正数, 则(x +y)(1x + 4y )的最小值为( )A . 6B .9C .12D .15 【答案】B考点:基本不等式,容易题.2. 【2007高考陕西版文第14题】已知实数x 、y 满足条件⎪⎩⎪⎨⎧≥≥≤--≥+-,0,0,033,042y x y x y x 则y x z 2+=的最大值为 . 【答案】8考点:线性规划,容易题.3. 【2009高考陕西版文第14题】设x ,y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z x y =+的最小值是 ,最大值为 . 【答案】1,11 【解析】 试题分析:考点:线性规划,容易题.4. 【2010高考陕西版文第14题】设x ,y 满足约束条件24,1,20,x y x y x +≤⎧⎪-≤⎨⎪+≥⎩,则目标函数z =3x -y的最大值为 .二.能力题组1. 【2011高考陕西版文第3题】设0a b <<,则下列不等式中正确的是 ( )(A ) 2a b a b ab +<<<(B )2a ba ab b +<<< (c )2a b a ab b +<<<2a bab a b +<<< 【答案】B考点:基本不等式.2. 【2011高考陕西版文第12题】如图,点(,)x y 在四边形ABCD 内部和边界上运动,那么2x y -的最小值为________.【答案】1考点:线性规划.3. 【2012高考陕西版文第10题】小王从甲地到乙地的时速分别为a 和b (a b <),其全程的平均时速为v ,则( )A .a v ab <<B .v ab =C ab v <<2a b+D .2a bv +=【答案】A考点:基本不等式.4. 【2013高考陕西版文第7题】若点(x,y)位于曲线y=|x|与y=2所围成的封闭区域,则2x-y的最小值是( ).A.-6 B.-2 C.0 D.2【答案】A.w.k.s.5考点:线性规划.5. 【2013高考陕西版文第14题】在如图所示的锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),则其边长x为__________(m).【答案】20.w考点:线性规划,容易题.6. 【2015高考陕西,文11】某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额表所示,如果生产1吨甲乙产品可获利润分别为3万元.4万元,则该企业每天可获得最大利润为()甲乙原料限额A(吨)3212B(吨)128A.12万元B.16万元C.17万元D.18万元【答案】D【考点定位】线性规划.。
2014高考真题+模拟新题 文科数学分类汇编:E单元 不等式 纯word版解析可编辑

数 学E 单元 不等式E1 不等式的概念与性质5.,[2014·山东卷] 已知实数x ,y 满足a x<a y(0<a <1),则下列关系式恒成立的是( )A .x 3>y 3B .sin x >sin yC .ln(x 2+1)>ln(y 2+1)D.1x 2+11y 2+15.A [解析] 因为a x <a y (0<a <1),所以x >y ,所以x 3>y 3恒成立.故选A. 5.[2014·四川卷] 若a >b >0,c <d <0,则一定有( ) A.a d >b c B.a d <b c C.a c >b d D.a c <b d5.B [解析] 因为c <d <0,所以1d <1c <0,即-1d >-1c>0,与a >b >0对应相乘得,-a d >-bc>0, 所以a d <bc ,故选B.E2 绝对值不等式的解法9.、[2014·安徽卷] 若函数f (x )=|x +1|+|2x +a |的最小值为3,则实数a 的值为( ) A .5或8 B .-1或5 C .-1或-4 D .-4或8 9.D [解析] 当a ≥2时, f (x )=⎩⎪⎨⎪⎧3x +a +1(x >-1),x +a -1⎝⎛⎭⎫-a2≤x ≤-1,-3x -a -1⎝⎛⎭⎫x <-a 2.由图可知,当x =-a 2时,f min (x )=f ⎝⎛-a 2=a2-1=3,可得a =8.当a <2时,f (x )⎩⎪⎨⎪⎧3x +a +1⎝⎛⎭⎫x >-a 2,-x -a +1⎝⎛⎭⎫-1≤x ≤-a 2,-3x -a -1(x <-1).由图可知,当x =-a 2时,f min (x )=f ⎝⎛⎭⎫-a 2=-a2+1=3,可得a =-4.综上可知,a 的值为-4或8.10.[2014·辽宁卷] 已知f (x )为偶函数,当x ≥0时,f (x )=⎩⎨⎧cos πx ,x ∈⎣⎡⎦⎤0,12,2x -1,x ∈⎝⎛⎭⎫12,+∞,则不等式f (x -1)≤12的解集为( )A.⎣⎡⎦⎤14,23∪⎣⎡⎦⎤43,74B.⎣⎡⎦⎤-34,-13∪⎣⎡⎦⎤14,23C.⎣⎡⎦⎤13,34∪⎣⎡⎦⎤43,74D.⎣⎡⎦⎤-34,-13∪⎣⎡⎦⎤13,34 10.A [解析] 由题可知,当x ∈⎣⎡⎦⎤0,12时,函数f (x )单调递减,由cos πx ≤12,得13≤x ≤12;当x ∈⎝⎛⎭⎫12,+∞时,函数f (x )单调递增,由2x -1≤12,得12<x ≤34.故当x ≥0时,由f (x )≤12,得13≤x ≤34.又因为f (x )为偶函数,所以f (x )≤12的解解集为⎣⎡⎦⎤-34,-13∪⎣⎡⎦⎤13,34,所以不等式f (x -1)≤12的解满足-34≤x -1≤-13或13≤x -1≤34,解得x ∈⎣⎡14,23∪⎣⎡⎦⎤43,74. 3.、[2014·全国卷] 不等式组⎩⎪⎨⎪⎧x (x +2)>0,|x |<1的解集为( )A .{x |-2<x <-1}B .{x |-1<x <0}C .{x |0<x <1}D .{x |x >1} 3.C [解析] 由⎩⎪⎨⎪⎧x (x +2)>0,|x |<1,得⎩⎪⎨⎪⎧x >0或x <-2,-1<x <1,即0<x <1.E3 一元二次不等式的解法3.、[2014·全国卷] 不等式组⎩⎪⎨⎪⎧x (x +2)>0,|x |<1的解集为( )A .{x |-2<x <-1}B .{x |-1<x <0}C .{x |0<x <1}D .{x |x >1} 3.C [解析] 由⎩⎪⎨⎪⎧x (x +2)>0,|x |<1,得⎩⎪⎨⎪⎧x >0或x <-2,-1<x <1,即0<x <1.E4 简单的一元高次不等式的解法 E5 简单的线性规划问题13.[2014·安徽卷] 不等式组⎩⎪⎨⎪⎧x +y -2≥0,x +2y -4≤0,x +3y -2≥0表示的平面区域的面积为________.13.4 [解析] 不等式组所表示的平面区域如图中阴影部分所示,S △ABD =S △ABD +S △BCD=12×2×(2+2)=4.13.[2014·北京卷] 若x ,y 满足⎩⎪⎨⎪⎧y ≤1,x -y -1≤0,x +y -1≥0,则z =3x +y 的最小值为________.13.1 [解析] 可行域如图,当目标函数线z =y +3x 过可行域内A 点时,z 有最小值,联立⎩⎪⎨⎪⎧y =1,x +y -1=0,得A (0,1),故z min =3×0+1×1=1.11.,[2014·福建卷] 已知圆C :(x -a )2+(y -b )2=1,平面区域Ω:⎩⎪⎨⎪⎧x +y -7≤0,x -y +3≥0,y ≥0.若圆心C ∈Ω,且圆C 与x 轴相切,则a 2+b 2的最大值为( )A .5B .29C .37D .4911.C [解析] 作出不等式组⎩⎪⎨⎪⎧x +y -7≤0,x -y +3≥0,y ≥0表示的平面区域Ω(如下图阴影部分所示,含边界),圆C :(x -a )2+(y -b )2=1的圆心坐标为(a ,b ),半径为1.由圆C 与x 轴相切,得b =1.解方程组⎩⎪⎨⎪⎧x +y -7=0,y =1,得⎩⎪⎨⎪⎧x =6,y =1,即直线x +y -7=0与直线y =1的交点坐标为(6,1),设此点为P .又点C ∈Ω,则当点C 与P 重合时,a 取得最大值, 所以,a 2+b 2的最大值为62+12=37,故选C.4.[2014·广东卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y ≤8,0≤x ≤4,0≤y ≤3,则z =2x +y 的最大值等于( )A .7B .8C .10D .114.D [解析] 作出不等式组所表示的平面区域,如图中阴影部分所示.作出直线l :2x +y =0,平移该直线,当直线经过点A (4,3)时,直线l 的截距最大,此时z =zx +y 取得最大值,最大值是11 .4.[2014·湖北卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤4,x -y ≤2,x ≥0,y ≥0,则2x +y 的最大值是( )A .2B .4C .7D .84.C [解析] 作出约束条件⎪⎨⎪⎧x +y ≤4,x -y ≤2,x ≥0,y ≥0表示的可行域如下图阴影部分所示.设z =2x +y ,平移直线2x x -y =2的交点A (3,1)处,z =2x +y 取得最大值7. 故选C.13.[2014·湖南卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤x ,x +y ≤4,y ≥1,则z =2x +y 的最大值为________.13.7 [解析] 依题意,画出可行域,如图所示. 由⎨⎪⎧x +y =4,得点B 的坐标为(3,1),则z =2x +y 在B (3,1)处取得最大值7.14.[2014·辽宁卷] 已知x ,y 满足约束条件⎩⎪⎨⎪⎧2x +y -2≥0,x -2y +4≥0,3x -y -3≤0,则目标函数z =3x +4y 的最大值为________.14.18 [解析] 不等式组表示的平面区域如图阴影部分所示,由z =3x +4y 得y =-34x+z4 ,当直线经过点C 时,z 取得最大值.由⎩⎪⎨⎪⎧x -2y +4=0,3x -y -3=0,得⎩⎪⎨⎪⎧x =2,y =3,故C 点坐标为(2,3),这时z =3×2+4×3=18.15.[2014·全国卷] 设x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0,x +2y ≤3,x -2y ≤1,则z =x +4y 的最大值为________.15.5 [解析] 如图所示,满足约束条件的可行域为△ABC 的内部(包括边界),z =x +4y 的最大值即为直线y =-14x +14z 的截距最大时z 的值.结合题意知,当y =-14x +14经过点A 时,z 取得最大值,联立x -y =0和x +2y =3,可得点A 的坐标为(1,1),所以z max =1+4=5.9.[2014·新课标全国卷Ⅱ] 设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -1≥0,x -y -1≤0,x -3y +3≥0,则z =x +2y 的最大值为( )A .8B .7C .2D .19.B [解析] 作出约束条件表示的可行域(略),可知该可行域为一三角形区域,当目标函数通过可行域的一个顶点(3,2)时,目标函数取得最大值,z max =3+2×2=7.11.[2014·全国新课标卷Ⅰ] 设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥a ,x -y ≤-1,且z =x +ay 的最小值为7,则a =( )A .-5B .3C .-5或3D .5或-311.B [解析] 当a <0时,作出相应的可行域,可知目标函数z =x +ay 不存在最小值.当a ≥0时,作出可行域如图,易知当-1a>-1,即a >1时,目标函数在A 点取得最小值.由A ⎝⎛⎭⎫a -12,a +12,知z min =a -12+a 2+a 2=7,解得a =3或-5(舍去).10.[2014·山东卷] 已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y -1≤0,2x -y -3≥0, 当目标函数z =ax +by (a >0,b >0)在该约束条件下取到最小值25时,a 2+b 2的最小值为( )A .5B .4C. 5 D .210.B [解析] 画出关于x ,y 的不等式组表示的可行域,如图阴影部分所示.显然当目标函数z =ax +by 过点A (2,1)时,目标函数z =ax +by 取得最小值,即25=2a +b ,所以25-2a =b ,所以a 2+b 2=a 2+(25-2a )2=5a 2-85a +20.构造函数m (a )=5a 2-85a +20(0<a <5),显然当a =455时,函数m (a )取得最小值4.故a 2+b 2的最小值为4.6.、[2014·四川卷] 执行如图1-2的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A .0B .1C .2D .36.C [解析] 题中程序输出的是在⎩⎪⎨⎪⎧x +y ≤1,x ≥0,y ≥0的条件下S =2x +y 的最大值与1中较大的数.结合图像可得,当x =1,y =0时,S =2x +y 取最大值2,2>1,故选C.2.[2014·天津卷] 设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -2≥0,x -y -2≤0,y ≥1,则目标函数z =x +2y 的最小值为( )A .2B .3C .4D .52.B [解析] 作出可行域,如图中阴影部分所示.联立⎩⎪⎨⎪⎧x +y -2=0,y =1,解得⎩⎪⎨⎪⎧x y =1,可得点A (1,1). 当目标函数线过可行域内A 点时,目标函数有最小值z =1×1+2×1=3.12.[2014·浙江卷] 若实数x ,y 满足⎩⎪⎨⎪⎧x +2y -4≤0,x -y -1≤0,x ≥1,则x +y 的取值范围是________.12.[1,3] [解析] 实数x ,y 满足的可行域如图中阴影部分(包括边界)所示,图中A (1,0),B (2,1),C ⎝⎛⎭⎫1,32.令z =x +y ,则y =-x +z .当直线y =-x +z 经过A 点时,z 取最小值1;经过B 点时,z 取最大值3.故x +y 的取值范围是[1,3].E6 2a b+≤9.、[2014·重庆卷] 若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( ) A .6+2 3 B .7+2 3 C .6+4 3 D .7+4 39.D [解析] 由log 4(3a +4b )=log 2ab ,得3a +4b =ab ,则4a +3b=1,所以a +b =(a+b )⎝⎛⎭⎫4a +3b =7+4b a +3a b ≥7+2 4b a ·3a b =7+4 3,当且仅当4b a =3a b ,即a =4+2 3,b =2 3+3时等号成立,故其最小值是7+4 3.16.[2014·湖北卷] 某项研究表明:在考虑行车安全的情况下,某路段车流量F (单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v (假设车辆以相同速度v 行驶,单位:米/秒)、平均车长l (单位:米)的值有关,其公式为F =76 000vv 2+18v +20l.(1)如果不限定车型,l =6.05,则最大车流量为________辆/小时;(2)如果限定车型,l =5,则最大车流量比(1)中的最大车流量增加________辆/小时. 16.(1)1900 (2)100 [解析] (1)依题意知,l >0,v >0,所以当l =6.05时,F =76 000v v 2+18v +121=76 000v +121v +18≤76 0002 v ·121v+18=1900,当且仅当v =11时,取等号.(2)当l =5时,F =76 000v v 2+18v +100=76 000v +100v+18≤2000,当且仅当v =10时,取等号,此时比(1)中的最大车流量增加100辆/小时. 14.、[2014·江苏卷] 若△ABC 的内角满足sin A +2sin B =2sin C ,则cos C 的最小值是______.14.6-24[解析] 设△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,则由正弦定理得a +2b =2c .故cos C =a 2+b 2-c22ab=a 2+b 2-⎝⎛⎭⎫a +2b 222ab=34a 2+122-22ab 2ab =342+12b 22ab -24≥234a 2·12b22ab -24=6-24,当且仅当3a 2=2b 2,即a b =23时等号成立.16.[2014·辽宁卷] 对于c >0,当非零实数a ,b 满足4a 2-2ab +b 2-c =0且使|2a +b |最大时,1a +2b +4c的最小值为________.16.-1 [解析] 因为4a 2-2ab +b 2-c =0,所以(2a +b )2-c =6ab =3×2ab ≤3×(2a +b )24(2a +b )2≤4c ,当且仅当b =2a ,c =4a 2时,|2a +b |取得最大值.故1a +2b +4c =2a +1a 2=⎝⎛⎭⎫1a+12-1,其最小值为-1. 21.,,[2014·山东卷] 在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,直线y =x 被椭圆C 截得的线段长为4105(1)求椭圆C 的方程.(2)过原点的直线与椭圆C 交于A ,B 两点(A ,B 不是椭圆C 的顶点).点D 在椭圆C 上,且AD ⊥AB ,直线BD 与x 轴、y 轴分别交于M ,N 两点.(i)设直线BD ,AM 的斜率分别为k 1,k 2,证明存在常数λ使得k 1=λk 2,并求出λ的值;(ii)求△OMN 面积的最大值.21.解:(1)由题意知,a 2-b 2a =32,可得a 2=4b 2.椭圆C 的方程可简化为x 2+4y 2=a 2. 将y =x 代入可得x =±5a 5. 因此2×25a 5=4105,即a =2,所以b =1, 所以椭圆C 的方程为x 24+y 2=1.(2)(i)设A (x 1,y 1)(x 1y 1≠0),D (x 2,y 2),则B (-x 1,-y 1).因为直线AB 的斜率k AB =y1x 1,且AB ⊥AD ,所以直线AD 的斜率k =-x1y 1.设直线AD 的方程为y =kx +m , 由题意知k ≠0,m ≠0.由⎩⎪⎨⎪⎧y =kx +m ,x 24+y 2=1,消去y ,得(1+4k 2)x 2+8mkx +4m 2-4=0, 所以x 1+x 2=-8mk 1+4k2,因此y 1+y 2=k (x 1+x 2)+2m =2m1+4k2.由题意知x 1≠-x 2, 所以k 1=y 1+y 2x 1+x 2=-14k =y14x 1.所以直线BD 的方程为y +y 1=y14x 1(x +x 1).令y =0,得x =3x 1,即M (3x 1,0). 可得k 2=-y12x 1.所以k 1=-12k 2,即λ=-12.因此,存在常数λ=-12使得结论成立.(ii)直线BD 的方程y +y 1=y14x 1(x +x 1),令x =0,得y =-341,即N ⎝⎛⎭⎫0,-34y 1.由(i)知M (3x 1,0),所以△OMN 的面积S =12×3|x 1|×34|y 1|=98|x 1||y 1|. 因为|x 1||y 1|≤x 214+y 21=1,当且仅当|x 1|2=|y 1|=22时,等号成立, 此时S 取得最大值98,所以△OMN 面积的最大值为98.E7 不等式的证明方法 20.、、[2014·天津卷] 已知q 和n 均为给定的大于1的自然数,设集合M ={0,1,2,…,q -1},集合A ={x |x =x 1+x 2q +…+x n q n -1,x i ∈M ,i =1,2,…,n }.(1)当q =2,n =3时,用列举法表示集合A .(2)设s ,t ∈A ,s =a 1+a 2q +…+a n q n -1,t =b 1+b 2q +…+b n q n -1,其中a i ,b i ∈M ,i =1,2,…,n .证明:若a n <b n ,则s <t .20.解:(1)当q =2,n =3时,M ={0,1},A ={x |x =x 1+x 2·2+x 3·22,x i ∈M ,i =1,2,3},可得A ={0,1,2,3,4,5,6,7}.(2)证明:由s ,t ∈A ,s =a 1+a 2q +…+a n q n -1,t =b 1+b 2q +…+b n q n -1,a i ,b i ∈M ,i =1,2,…,n 及a n <b n ,可得s -t =(a 1-b 1)+(a 2-b 2)q +…+(a n -1-b n -1)q n -2+(a n -b n )q n -1≤(q -1)+(q -1)q +…+(q -1)q n -2-q n -1=(q -1)(1-q n -1)1-q-q n -1=-1<0, 所以s <t .E8 不等式的综合应用16.[2014·浙江卷] 已知实数a ,b ,c 满足a +b +c =0,a 2+b 2+c 2=1,则a 的最大值是________.16.63[解析] 方法一:令b =x ,c =y ,则x +y =-a ,x 2+y 2=1-a 2,此时直线x +y =-a 与圆x 2+y 2=1-a 2有交点,则圆心到直线的距离d =|a |2≤1-a 2,解得a 2≤23,所以a 的最大值为63. 方法二:将c =-(a +b )代入a 2+b 2+c 2=1得2b 2+2ab +2a 2-1=0,此关于b 的方程有实数解,则Δ=(2a )2-8(2a 2-1)≥0,整理得到a 2≤23a 的最大值为63.9.、[2014·安徽卷] 若函数f (x )=|x +1|+|2x +a |的最小值为3,则实数a 的值为( ) A .5或8 B .-1或5C .-1或-4D .-4或8 9.D [解析] 当a ≥2时, f (x )=⎩⎪⎨⎪⎧3x +a +1(x >-1),x +a -1⎝⎛⎭⎫-a2≤x ≤-1,-3x -a -1⎝⎛⎭⎫x <-a 2.由图可知,当x =-a 2时,f min (x )=f ⎝⎛-a 2=a 2-1=3,可得a =8.当a <2时,f (x )⎩⎪⎨⎪⎧3x +a +1⎝⎛⎭⎫x >-a 2,-x -a +1⎝⎛⎭⎫-1≤x ≤-a 2,-3x -a -1(x <-1).由图可知,当x =-a 2时,f min (x )=f ⎝⎛⎭⎫-a 2=-a2+1=3,可得a =-4.综上可知,a 的值为-4或8.9.[2014·福建卷] 要制作一个容积为4 m 3,高为1 m 的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( ) A .80元 B .120元 C .160元 D .240元9.C [解析] 设底面矩形的一边长为x .由容器的容积为4 m 3,高为1 m .得另一边长为4xm. 记容器的总造价为y 元,则 y =4×20+2⎝⎛x +4x ×1×10 =80+20⎝⎛⎭⎫x +4x ≥80+20×2x ·4x=160,当且仅当x =4x,即x =2时等号成立.因此,当x =2时,y 取得最小值160,即容器的最低总造价为160元,故选C. 19.、、、[2014·江苏卷] 已知函数f (x )=e x +e -x ,其中e 是自然对数的底数. (1)证明:f (x )是R 上的偶函数.(2)若关于x 的不等式mf (x )≤e -x +m -1在(0,+∞)上恒成立,求实数m 的取值范围.(3)已知正数a 满足:存在x 0∈[1,+∞),使得f (x 0)<a (-x 30+3x 0)成立.试比较ea -1与ae -1的大小,并证明你的结论.19.解: (1)证明:因为对任意 x ∈R ,都有f (-x )=e -x +e -(-x )=e -x +e x =f (x ), 所以f (x )是R 上的偶函数.(2)由条件知 m (e x +e -x -1)≤e -x -1在(0,+∞)上恒成立. 令 t =e x (x >0),则 t >1,所以 m ≤-t -1t 2-t +1=-1t -1+1t -1+ 1对任意 t >1成立.因为t -1+1t -1+ 1≥2(t -1)·1t - 1+1=3, 所以 -1t -1+1t -1+ 1≥-13,当且仅当 t =2, 即x = ln 2时等号成立. 因此实数 m 的取值范围是⎝⎛⎦⎤-∞,-13.(3)令函数 g (x )=e x +1e x - a (-x 3+3x ),则g ′ (x ) =e x -1ex +3a (x 2-1).当 x ≥1时,e x -1ex >0,x 2-1≥0.又a >0,故 g ′(x )>0,所以g (x )是[1,+∞)上的单调递增函数, 因此g (x )在[1,+∞)上的最小值是 g (1)= e +e -1-2a .由于存在x 0∈[1,+∞),使e x 0+e -x 0-a (-x 30+ 3x 0 )<0 成立, 当且仅当最小值g (1)<0, 故 e +e -1-2a <0, 即 a >e +e -12.令函数h (x ) = x -(e -1)ln x -1,则 h ′(x )=1-e -1x. 令 h ′(x )=0, 得x =e -1.当x ∈(0,e -1)时,h ′(x )<0,故h (x )是(0,e -1)上的单调递减函数;当x ∈(e -1,+∞)时,h ′(x )>0,故h (x )是(e -1,+∞)上的单调递增函数. 所以h (x )在(0,+∞)上的最小值是h (e -1).注意到h (1)=h (e)=0,所以当x ∈(1,e -1)⊆(0,e -1)时,h (e -1)≤h (x )<h (1)=0; 当x ∈(e -1,e)⊆(e -1,+∞)时, h (x )<h (e)=0.所以h (x )<0对任意的x ∈(1,e)成立. 故①当a ∈⎝⎛⎭⎫e +e -12,e⊆(1,e)时, h (a )<0,即a -1<(e -1)ln a ,从而e a -1<ae -1;②当a =e 时,e a -1=a e -1;③当a ∈(e ,+∞)⊆(e -1,+∞)时,h (a )>h (e)=0,即a -1>(e -1)ln a ,故e a -1>ae -1.综上所述,当a ∈⎝⎛⎭⎫e +e -12,e 时,e a -1<a e -1;当a =e 时,e a -1=a e -1;当a ∈(e ,+∞)时,e a -1>a e -1. 12.、[2014·辽宁卷] 当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( )A .[-5,-3] B.⎣⎡⎦⎤-6,-98C .[-6,-2]D .[-4,-3]12.C [解析] 当-2≤x <0时,不等式可转化为a ≤x 2-4x -3x 3,令f (x )=x 2-4x -3x3(-2≤x <0),则f ′(x )=-x 2+8x +9x 4=-(x -9)(x +1)x 4,故函数f (x )在[-2,-1]上单调递减,在(-1,0)上单调递增,此时有a ≤f min (x )=f (-1)=1+4-3-1=-2.当x =0时,不等式恒成立.当0<x ≤1时,a ≥x 2-4x -3x 3,令g (x )=x 2-4x -3x 3(0<x ≤1),则g ′(x )=-x 2+8x +9x4,故函数g (x )在(0,1]上单调递增,此时有a ≥g max (x )=g (1)=1-4-31=-6. 综上,-6≤a ≤-2.21.、、[2014·陕西卷] 设函数f (x )=ln x +mx ,m ∈R .(1)当m =e(e 为自然对数的底数)时,求f (x )的极小值; (2)讨论函数g (x )=f ′(x )-x3零点的个数;(3)若对任意b >a >0,f (b )-f (a )b -a <1恒成立,求m 的取值范围.21.解:(1)由题设,当m =e 时,f (x )=ln x +ex ,则f ′(x )=x -e x 2,∴当x ∈(0,e)时,f ′(x )<0,f (x )在(0,e)上单调递减; 当x ∈(e ,+∞)时,f ′(x )>0,f (x )在(e ,+∞)上单调递增. ∴x =e 时,f (x )取得极小值f (e)=ln e +ee =2,∴f (x )的极小值为2.(2)由题设g (x )=f ′(x )-x 3=1x -m x 2-x3(x >0),令g (x )=0,得m =-13x 3+x (x >0),设φ(x )=-13x 3+x (x ≥0),则φ′(x )=-x 2+1=-(x -1)(x +1),当x ∈(0,1)时,φ′(x )>0,φ(x )在(0,1)上单调递增; 当x ∈(1,+∞)时,φ′(x )<0,φ(x )在(1,+∞)上单调递减.∴x =1是φ(x )的唯一极值点,且是极大值点,因此x =1也是φ(x )的最大值点, ∴φ(x )的最大值为φ(1)=23.又φ(0)=0,结合y =φ(x )的图像(如图所示),可知①当m >23时,函数g (x )无零点;②当m =23时,函数g (x )有且只有一个零点;③当0<m <23时,函数g (x )有两个零点;④当m ≤0时,函数g (x )有且只有一个零点. 综上所述,当m >23时,函数g (x )无零点;当m =23或m ≤0时,函数g (x )有且只有一个零点;当0<m <23时,函数g (x )有两个零点.(3)对任意的b >a >0,f (b )-f (a )b -a<1恒成立,等价于f (b )-b <f (a )-a 恒成立.(*) 设h (x )=f (x )-x =ln x +mx -x (x >0),∴(*)等价于h (x )在(0,+∞)上单调递减. 由h ′(x )=1x -mx 2-1≤0在(0,+∞)上恒成立,得m ≥-x 2+x =-⎝⎛⎭⎫x -122+14(x >0)恒成立,∴m ≥14⎝⎛⎭⎫对m =14,h ′(x )=0仅在x =12时成立, ∴m 的取值范围是⎣⎡⎭⎫14.E9 单元综合6.[2014·成都七中模拟] 若a >0,b >0,且a +b =4,则下列不等式恒成立的是( ) A.1ab >12 B.1a +1b≤1 C.ab ≥2 D.1a 2+b 2≤186.D [解析] 因为2=a +b 2≤a 2+b 22,所以a 2+b 2≥8,所以1a 2+b 2≤18.8.[2014·郑州联考] 已知a ,b ,c ∈R ,给出下列命题: ①若a >b ,则ac 2>bc 2;②若ab ≠0,则a b +ba ≥2;③若a >|b |,则a 2>b 2. 其中真命题的个数为( ) A .3 B .2 C .1 D .08.C [解析] 当c =0时,ac 2=bc 2=0,故①为假命题;当a 与b 异号时,a b <0,ba <0,故②为假命题;因为a >|b |≥0,所以a 2>b 2,故③为真命题.6.[2014·济南期末] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤1,x +y ≥0,x -y -2≤0,则z =x -3y 的最大值为( )A .4B .3C .2D .16.A [解析] 依题意画出可行域如图所示,由图可知,z =x -3y 在点(1,-1)处取得最大值4.8.[2014·长沙一中月考] 在关于x 的不等式x 2-(a +1)x +a <0的解集中恰有两个整数,则a 的取值范围是( ) A .(3,4)B .(-2,-1)∪(3,4)C .(3,4]D .[-2,-1)∪(3,4]8.D [解析] 由题意得,原不等式为(x -1)(x -a )<0.当a >1时,解得1<x <a ,此时解集中的整数为2,3,则3<a ≤4;当a <1时,解得a <x <1,此时解集中的整数为0,-1,则-2≤a <-1.故a ∈[-2,-1)∪(3,4].11.[2014·青岛二中月考] 已知x >0,y >0,lg 2x +lg 8y=lg 2,则1x +13y ( )A .2B .2 2C .4D .2 311.C [解析] 因为lg 2x +lg 8y =lg 2,所以x +3y =1,所以1x +13y =1x +13y (x +3y )=2+3y x +x 3y ≥4,当且仅当3y x =x 3y ,即x =12,y =16时,取等号. 17.[2014·西安模拟] 设OA →=(1,-2),OB →=(a ,-1),OC →=(-b ,0)(a >0,b >0,O 为坐标原点),若A ,B ,C 三点共线,则1a +2b的最小值是____________.17.8 [解析] 易知 AB →=(a -1,1),AC →=(-b -1,2).因为A ,B ,C 三点共线,所以2(a -1)-(-b -1)=0,即2a +b =1.又a >0,b >0,所以1a +2b =1a +2b (2a +b )=4+b a +4ab ≥4+4=8,当且仅当a =14,b =12时,取等号.。
2023年高考数学分类汇编不等式选讲

2012高考数学分类汇编-不等式选讲1000字不等式是高中数学中的一个重要知识点,也是高考难度较大的部分。
在不等式的学习中,我们需要掌握基本的不等式类型、不等式的解法、不等式的应用等知识点。
一、基本不等式类型1. 一元一次不等式:形如ax+b≤0或ax+b≥0的不等式,其中a、b为实数,x为未知数。
解法:将不等式分两种情况讨论,化简得出不等式的解集。
2. 一元二次不等式:形如ax²+bx+c≤0或ax²+bx+c≥0的不等式,其中a、b、c为实数,x为未知数。
解法:求出二次函数的零点,根据函数的变化性和不等式的符号,求出解集。
3. 绝对值不等式:形如|ax+b|≤c或|ax+b|≥c的不等式,其中a、b、c为实数,x为未知数。
解法:将绝对值符号去掉,分两种情况讨论,得到两个一元一次不等式,求解并合并。
4. 分式不等式:形如f(x)≤ 0或f(x)≥ 0的不等式,其中f(x)为一个分式函数。
解法:根据分式的零点和不等式的符号,分别求解不等式。
二、不等式的解法1. 图像解法:根据函数图像的性质,判断不等式的解集。
2. 化简法:将不等式转化为易于求解的形式。
3. 移项法:将未知数移至同一侧,化为一元不等式求解。
4. 差分法:构造一个新的不等式,使原不等式变为差分形式,进而求解。
5. 变形法:根据一些数学恒等式,将不等式进行变形,使得问题更易于解决。
三、不等式的应用1. 实际应用问题中的不等式:如周长不等式、面积不等式、三角形不等式、均值不等式等。
2. 理论应用问题中的不等式:如证明某个不等式成立或不成立,或者在定理证明中使用不等式来简化分析。
总之,掌握不等式的基本类型、解法和应用,对于高考数学的学习和考试都有很大的帮助。
十年(2012-2021)高考数学真题分项汇编(全国通用)-专题16 选修4-5不等式选讲(学生版)

专题16 选修4-5不等式选讲【2021年】1.(2021年全国高考乙卷数学(文)试题)已知函数()3f x x a x =-++.(1)当1a =时,求不等式()6f x ≥的解集;(2)若()f x a >-,求a 的取值范围.2.(2021年全国高考甲卷数学(理)试题)已知函数()2,()2321f x x g x x x =-=+--.(1)画出()y f x =和()y g x =的图像;(2)若()()f x a g x +≥,求a 的取值范围.3.(2021年全国新高考Ⅰ卷数学试题)已知函数()()1ln f x x x =-.(1)讨论()f x 的单调性;(2)设a ,b 为两个不相等的正数,且ln ln b a a b a b -=-,证明:112e a b<+<.【2012年——2020年】1.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))已知函数()|31|2|1|f x x x =+--.(1)画出()y f x =的图像;(2)求不等式()(1)f x f x >+的解集.2.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))已知函数2()|21|f x x a x a =-+-+. (1)当2a =时,求不等式()4f x ≥的解集;(2)若()4f x ≥,求a 的取值范围.3.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))设a ,b ,c ∈R ,a +b +c =0,abc =1. (1)证明:ab +bc +ca <0;(2)用max{a ,b ,c }表示a ,b ,c 中的最大值,证明:max{a ,b ,c .4.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))已知a ,b ,c 为正数,且满足abc =1.证明:(1)222111a b c a b c++≤++; (2)333()()()24a b b c c a +++≥++.5.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))已知()|||2|().f x x a x x x a =-+--(1)当1a =时,求不等式()0f x <的解集;(2)若(,1)x ∈-∞时,()0f x <,求a 的取值范围.6.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))设,,x y z ∈R ,且1x y z ++=.(1)求222(1)(1)(1)x y z -++++的最小值;(2)若2221(2)(1)()3x y z a -+-+-≥成立,证明:3a ≤-或1a ≥-. 7.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))已知()11f x x ax =+--. (1)当1a =时,求不等式()1f x >的解集;(2)若()0,1x ∈时不等式()f x x >成立,求a 的取值范围.8.(2018年全国普通高等学校招生统一考试理数(全国卷II ))设函数()52f x x a x =-+--. (1)当1a =时,求不等式()0f x ≥的解集;(2)若()1f x ≤恒成立,求a 的取值范围.9.(2018年全国卷Ⅰ理数高考试题)设函数()211f x x x =++-.(1)画出()y f x =的图像;(2)当[)0x +∞∈,,()f x ax b ≤+,求+a b 的最小值.10.(2017年全国普通高等学校招生统一考试文科数学(新课标1卷))已知函数2()4f x x ax =-++,()|1||1|g x x x =++-.(1)当1a =时,求不等式()()f x g x ≥的解集;(2)若不等式()()f x g x ≥的解集包含[–1,1],求a 的取值范围.11.(2017年全国普通高等学校招生统一考试理科数学(新课标2卷))已知0a >,0b >,332a b +=,证明:(1)()()554a b a b ++≥;(2)2a b +≤.12.(2017年全国普通高等学校招生统一考试文科数学(新课标3卷))已知函数()f x =│x +1│–│x –2│. (1)求不等式()f x ≥1的解集;(2)若不等式()f x ≥x 2–x +m 的解集非空,求实数m 的取值范围.13.(2016年全国普通高等学校招生统一考试文科数学(新课标1卷))(2016高考新课标Ⅰ,理24)选修4-5:不等式选讲已知函数f (x )=|x +1|−|2x −3|.(Ⅰ)画出y =f (x )的图象;(Ⅰ)求不等式|f (x )|>1的解集.14.(2016年全国普通高等学校招生统一考试文科数学(新课标2卷))选修4-5:不等式选讲已知函数11()22f x x x =-++,M 为不等式()2f x <的解集. (Ⅰ)求M ; (Ⅰ)证明:当a ,b M ∈时,1a b ab +<+.15.(2016年全国普通高等学校招生统一考试)已知函数()|2|f x x a a =-+.(1)当a=2时,求不等式()6f x ≤的解集;(2)设函数()|21|g x x =-.当x ∈R 时,()()3f x g x +≥,求a 的取值范围.16.(2015年全国普通高等学校招生统一考试理科数学(新课标))已知函数()|1|2||,0f x x x a a =+-->.(1)当1a =时,求不等式()1f x >的解集;(2)若()f x 的图象与x 轴围成的三角形面积大于6,求a 的取值范围.17.(2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ))选修4-5不等式选讲设a b c d ,,,均为正数,且a b c d +=+,证明:(Ⅰ)若ab cd >>;(Ⅰ>是a b c d -<-的充要条件.18.(2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ))若且 (I )求的最小值; (II )是否存在,使得?并说明理由.19.(2014年全国普通高等学校招生统一考试文科数学(全国Ⅰ卷))设函数1()|(0)f x x x a a a=++- (1)证明:()2f x ≥;(2)若(3)5f <,求a 的取值范围.20.(2013年全国普通高等学校招生统一考试理科数学(新课标1卷))选修4—5:不等式选讲 已知函数f (x )=|2x -1|+|2x +a|,g (x )=x +3.(1)当a =-2时,求不等式f (x )<g (x )的解集;(2)设a >-1,且当xⅠ1,22a ⎛⎫-⎪⎝⎭时,f (x )≤g (x ),求a 的取值范围.21.(2013年全国普通高等学校招生统一考试文科数学(新课标2卷))设a ,b ,c 均为正数,且a+b+c=1,证明:(Ⅰ)ab+bc+ac ≤13; (Ⅰ)2221a b c b c a++≥.22.(2012年全国普通高等学校招生统一考试文科数学(课标卷))已知函数()f x =2x a x ++-. (Ⅰ)当3a =-时,求不等式()f x ≥3的解集;(Ⅰ) 若()f x ≤4x -的解集包含[1,2],求a 的取值范围.(命题意图)本题主要考查含绝对值不等式的解法,是简单题.。
2021年高考数学分类汇编----不等式与线性规划

2021年高考数学分类汇编-----不等式与线性规划1.(2021全国乙卷文科)若,x y 满足约束条件4,2,3,x y x y y +≥⎧⎪-≤⎨⎪≤⎩则3z x y =+的最小值为( )A. 18B. 10C. 6D. 4【答案】C【解析】【分析】由题意作出可行域,变换目标函数为3y x z =-+,数形结合即可得解.【详解】由题意,作出可行域,如图阴影部分所示,由43x y y +=⎧⎨=⎩可得点()1,3A , 转换目标函数3z x y =+为3y x z =-+,上下平移直线3y x z =-+,数形结合可得当直线过点A时,z 取最小值,此时min 3136z =⨯+=.故选:C.2.(2021全国乙卷文科)下列函数中最小值为4的是( )A. 224y x x =++B. 4sin sin y x x=+ C. 222x x y -=+D. 4ln ln y x x=+ 【答案】C【解析】 【分析】根据二次函数的性质可判断A 选项不符合题意,再根据基本不等式“一正二定三相等”,即可得出,B D 不符合题意,C 符合题意.【详解】对于A ,()2224133y x x x =++=++≥,当且仅当1x =-时取等号,所以其最小值为3,A 不符合题意;对于B ,因为0sin 1x <≤,4sin 244sin y x x=+≥=,当且仅当sin 2x =时取等号,等号取不到,所以其最小值不为4,B 不符合题意;对于C ,因为函数定义域为R ,而20x >,242222442x x x x y -=+=+≥=,当且仅当22x =,即1x =时取等号,所以其最小值为4,C 符合题意;对于D ,4ln ln y x x =+,函数定义域为()()0,11,+∞,而ln x R ∈且ln 0x ≠,如当ln 1x =-,5y =-,D 不符合题意.故选:C .【点睛】本题解题关键是理解基本不等式的使用条件,明确“一正二定三相等”的意义,再结合有关函数的性质即可解出.3.(2021浙江)若实数x ,y 满足约束条件1002310x x y x y +≥⎧⎪-≤⎨⎪+-≤⎩,则12z x y =-的最小值是( ) A. 2-B. 32-C. 12-D. 110【答案】B【解析】【分析】画出满足条件的可行域,目标函数化为22y x z =-,求出过可行域点,且斜率为2的直线在y 轴上截距的最大值即可.【详解】画出满足约束条件1002310x x y x y +≥⎧⎪-≤⎨⎪+-≤⎩的可行域,如下图所示:目标函数12z x y =-化为22y x z =-,由12310x x y =-⎧⎨+-=⎩,解得11x y =-⎧⎨=⎩,设(1,1)A -, 当直线22y x z =-过A 点时,12z x y =-取得最小值为32-. 故选:B. 4.(2021上海春季高考)不等式2512x x +<-的解集为______. 【答案】(7,2)-【解析】【分析】移项通分后转化为一元二次不等式求解. 【详解】252571100(7)(2)072222x x x x x x x x x +++<⇒-<⇒<⇒+-<⇒-<<---. 故答案为:(7,2)-.5.(2021上海春季高考)已知函数()()3031x x a f x a =+>+的最小值为5,则a =______. 【答案】9【解析】【分析】配方得()()303113131x x x x a a f x a =+>=++-++,结合基本不等式即可求解 【详解】()()303111593131x x x x a a f x a a =+>=++-≥=⇒=++,当且仅当3log 2x =时等号满足,故答案为:96(2021上海).已知3220380x x y x y ≤⎧⎪--≥⎨⎪+-≥⎩,则z x y =-的最大值是_______.7(2021上海)已知112233,,,,,x y x y x y 满足112233,,,x y x y x y <<<112233111122,2x y x y x y x y x y x y +=+=+++=,下列哪个选项恒成立( )213.2A x x x <+ 213.2B x x x >+ 2213.C x x x < 2213.D x x x >8.(2021天津)。
2019年全国高考文科数学分类汇编---选考不等式

2019年全国高考文科数学分类汇编---选考不等式1.(2019全国1卷文科)已知a ,b ,c 为正数,且满足abc =1.证明:(1)222111a b c a b c++≤++; (2)333()()()24a b b c c a +++≥++.【答案】(1)见解析;(2)见解析【解析】【分析】(1)利用1abc =将所证不等式可变为证明:222a b c bc ac ab ++≥++,利用基本不等式可证得()2222222a b c ab bc ac ++≥++,从而得到结论;(2)利用基本不等式可得()()()()()()3333a b b c c a a b b c c a +++++≥+++,再次利用基本不等式可将式转化为()()()333a b b c c a +++++≥.【详解】(1)1abc = 111111a b c b c a c a ba b c a b c ⎛⎫∴++=++⋅=++ ⎪⎝⎭ ()()()()2222222222222a b c a b b c c a ab bc ac ++=+++++≥++当且仅当a b c ==时取等号 ()22211122a b c a b c ⎛⎫∴++≥++ ⎪⎝⎭,即:222111a b c a b c ++++≥ (2)()()()()()()3333a b b c c a a b b c c a +++++≥+++,当且仅当a b c ==时取等号又a b +≥b c +≥a c +≥a b c ==时等号同时成立)()()()3333a b b c c a ∴+++++≥⨯=又1abc = ()()()33324a b b c c a ∴+++++≥ 【点睛】本题考查利用基本不等式进行不等式的证明问题,考查学生对于基本不等式的变形和应用能力,需要注意的是在利用基本不等式时需注意取等条件能否成立.2.(2019全国2卷文科)已知()|||2|().f x x a x x x a =-+--(1)当1a =时,求不等式()0f x <的解集;(2)若(,1)x ∈-∞时,()0f x <,求a 的取值范围.【答案】(1)(,1)-∞;(2)[1,)+∞【解析】【分析】(1)根据1a =,将原不等式化为|1||2|(1)0x x x x -+--<,分别讨论1x <,12x ≤<,2x ≥三种情况,即可求出结果;(2)分别讨论1a ≥和1a <两种情况,即可得出结果.【详解】(1)当1a =时,原不等式可化为|1||2|(1)0x x x x -+--<;当1x <时,原不等式可化为(1)(2)(1)0x x x x -+--<,即2(10)x ->,显然成立,此时解集(,1)-∞;当12x ≤<时,原不等式可化为(1)(2)(1)0x x x x -+--<,解得1x <,此时解集为空集;当2x ≥时,原不等式可化为(1)(2)(1)0x x x x -+--<,即2(10)x -<,显然不成立;此时解集为空集; 综上,原不等式的解集为(,1)-∞;(2)当1a ≥时,因为(,1)x ∈-∞,所以由()0f x <可得()(2)()0a x x x x a -+--<,即()(1)0x a x -->,显然恒成立;所以1a ≥满足题意;当1a <时,2(),1()2()(1),x a a x f x x a x x a -≤<⎧=⎨--<⎩,因为1a x ≤<时, ()0f x <显然不能成立,所以1a <不满足题意;综上,a 的取值范围是[1,)+∞.【点睛】本题主要考查含绝对值的不等式,熟记分类讨论的方法求解即可,属于常考题型.3(2019全国3卷文科).设,,x y z R ∈,且1x y z ++=.(1)求222(1)(1)(1)x y z -++++的最小值;(2)若2221(2)(1)()3x y z a -+-+-≥成立,证明:3a -≤或1a ≥-. 【答案】(1)43;(2)见详解. 【解析】【分析】 (1)根据条件1x y z ++=,和柯西不等式得到2224(1)(1)(1)3x y z -++++≥,再讨论,,x y z 是否可以达到等号成立的条件.(2)恒成立问题,柯西不等式等号成立时构造的,,x y z 代入原不等式,便可得到参数a 的取值范围.详解】(1) 22222222[(1)(1)(1)](111)[(1)(1)(1)](1)4x y z x y z x y z -++++++≥-++++=+++=故2224(1)(1)(1)3x y z -++++≥等号成立当且仅当111x y z -=+=+而又因1x y z ++=,解得531313x y z ⎧=⎪⎪⎪=-⎨⎪⎪=-⎪⎩时等号成立所以222(1)(1)(1)x y z -++++的最小值为43. (2) 因为2221(2)(1)()3x y z a -+-+-≥,所以222222[(2)(1)()](111)1x y z a -+-+-++≥. 根据柯西不等式等号成立条件,当21x y z a -=-=-,即22321323a x a y a z a +⎧=-⎪⎪+⎪=-⎨⎪+⎪=-⎪⎩时有22222222[(2)(1)()](111)(21)(2)x y z a x y z a a -+-+-++=-+-+-=+成立所以2(2)1a +≥成立,所以有3a -≤或1a ≥-.【点睛】两个问都是考查柯西不等式,属于柯西不等式的常见题型.【.4.(2019江苏)设x ∈R ,解不等式||+|2 1|>2x x -. 【答案】1{|1}3x x x <->或.【解析】【分析】由题意结合不等式的性质零点分段即可求得不等式的解集.【详解】当x <0时,原不等式可化为122x x -+->,解得x <–13: 当0≤x ≤12时,原不等式可化为x +1–2x >2,即x <–1,无解; 当x >12时,原不等式可化为x +2x –1>2,解得x >1. 综上,原不等式的解集为1{|1}3x x x <->或.【点睛】本题主要考查解不等式等基础知识,考查运算求解和推理论证能力.。
高考文科数学不等式题型

高考文科数学不等式题型
在高考文科数学中,不等式是一种重要的题型,主要考察学生的数学思维和解决问题的能力。
以下是一些常见的不等式题型:
1. 基础不等式:考察学生对基本不等式的理解和应用,如AM-GM不等式、Cauchy-Schwarz不等式等。
2. 绝对值不等式:考察学生对绝对值不等式的理解和应用,如a ≤ b ≤ c等。
3. 线性规划问题:考察学生利用不等式表示的可行域,求目标函数的最值。
4. 函数不等式:考察学生对函数不等式的理解和应用,如f(x) > g(x)或f(x) < g(x),以及求解一些函数的不等式。
5. 序列不等式:考察学生对序列不等式的理解和应用,如an < bn或an > bn等。
6. 综合不等式:考察学生综合运用不等式的能力,如通过构造特定的函数或序列,利用不等式性质求解问题。
在解决不等式问题时,学生需要掌握一些基本的解题技巧和方法,如因式分解、配方、换元、放缩法等。
同时,还需要注意一些关键的细节,如不等式的定义域、取值范围等。
2012年高考文科数学试题分类汇编--不等式
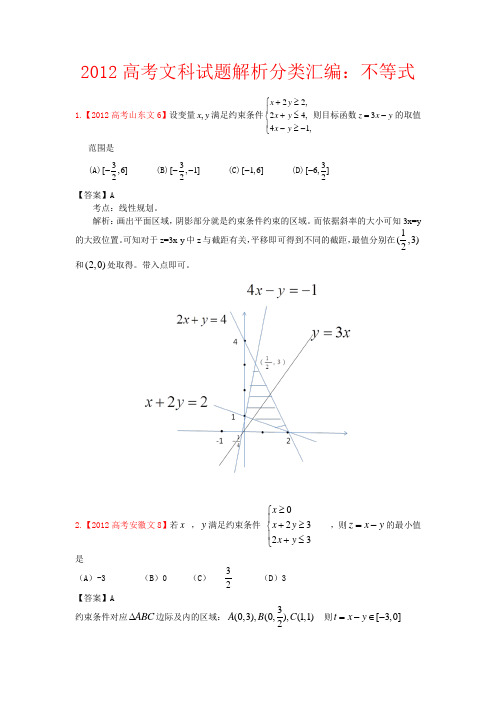
2012高考文科试题解析分类汇编:不等式1.【2012高考山东文6】设变量,x y 满足约束条件22,24,41,x y x y x y +≥⎧⎪+≤⎨⎪-≥-⎩则目标函数3z x y =-的取值范围是(A)3[,6]2- (B)3[,1]2--(C)[1,6]- (D)3[6,]2-【答案】A考点:线性规划。
解析:画出平面区域,阴影部分就是约束条件约束的区域。
而依据斜率的大小可知3x=y 的大致位置。
可知对于z=3x-y 中z 与截距有关,平移即可得到不同的截距,最值分别在1(,3)2和(2,0)处取得。
带入点即可。
2.【2012高考安徽文8】若x ,y 满足约束条件 02323x x y x y ≥⎧⎪+≥⎨⎪+≤⎩,则y x z -=的最小值是(A )-3 (B )0 (C ) 32(D )3【答案】A约束条件对应A B C ∆边际及内的区域:3(0,3),(0,),(1,1)2A B C 则[3,0]t x y =-∈-3.【2012高考新课标文5】已知正三角形ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x ,y )在△ABC 内部,则z=-x+y 的取值范围是(A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3) 【答案】A【命题意图】本题主要考查简单线性规划解法,是简单题.【解析】有题设知,作出直线0l :0x y -+=,平移直线0l ,有图像知,直线:l z x y =-+过B 点时,m ax z =2,过C 时,m in z =1-z x y =-+取值范围为(1-3,2),故选A.4.【2012高考重庆文2】不等式102x x -<+ 的解集是为(A )(1,)+∞ (B ) (,2)-∞- (C )(-2,1)(D )(,2)-∞-∪(1,)+∞ 【答案】C 【解析】:10(1)(2)0212x x x x x -<⇒-+<⇒-<<+【考点定位】本题考查解分式不等式时,利用等价变形转化为整式不等式解. 5.【2012高考浙江文9】若正数x ,y 满足x+3y=5xy ,则3x+4y 的最小值是 A.245B.285C.5D.6【答案】C【命题意图】本题考查了基本不等式证明中的方法技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数 学E 单元 不等式E1 不等式的概念与性质 1.,[2014·山东卷] 已知实数x ,y 满足a x <a y (0<a <1),则下列关系式恒成立的是( ) A .x 3>y 3 B .sin x >sin yC .ln(x 2+1)>ln(y 2+1) >1y 2+12.[2014·四川卷] 若a >b >0,c <d <0,则一定有( ) >b c <b c >b d <b dE2 绝对值不等式的解法 3.、[2014·安徽卷] 若函数f (x )=|x +1|+|2x +a |的最小值为3,则实数a 的值为( ) A .5或8 B .-1或5 C .-1或-4 D .-4或84.[2014·辽宁卷] 已知f (x )为偶函数,当x ≥0时,f (x )=⎩⎨⎧cos πx ,x ∈⎣⎡⎦⎤0,12,2x -1,x ∈⎝⎛⎭⎫12,+∞,则不等式f (x -1)≤12的解集为( )∪⎣⎡⎦⎤43,74 ∪⎣⎡⎦⎤14,23 ∪⎣⎡⎦⎤43,74 ∪⎣⎡⎦⎤13,34 E3 一元二次不等式的解法6.、[2014·全国卷] 不等式组⎩⎪⎨⎪⎧x (x +2)>0,|x |<1的解集为( )A .{x |-2<x <-1}B .{x |-1<x <0}C .{x |0<x <1}D .{x |x >1}E4 简单的一元高次不等式的解法 E5 简单的线性规划问题7.[2014·安徽卷] 不等式组⎩⎪⎨⎪⎧x +y -2≥0,x +2y -4≤0,x +3y -2≥0表示的平面区域的面积为________.8.[2014·北京卷] 若x ,y 满足⎩⎪⎨⎪⎧y ≤1,x -y -1≤0,x +y -1≥0,则z =3x +y 的最小值为________.9.9.,[2014·福建卷] 已知圆C :(x -a )2+(y -b )2=1,平面区域Ω:⎩⎪⎨⎪⎧x +y -7≤0,x -y +3≥0,y ≥0.若圆心C ∈Ω,且圆C 与x 轴相切,则a 2+b 2的最大值为( )A .5B .29C .37D .4910.[2014·广东卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y ≤8,0≤x ≤4,0≤y ≤3,则z =2x +y 的最大值等于( )A .7B .8C .10D .1111.[2014·湖北卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤4,x -y ≤2,x ≥0,y ≥0,则2x +y 的最大值是( )A .2B .4C .7D .812.[2014·湖南卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤x ,x +y ≤4,y ≥1,则z =2x +y 的最大值为________.13.[2014·辽宁卷] 已知x ,y 满足约束条件⎩⎪⎨⎪⎧2x +y -2≥0,x -2y +4≥0,3x -y -3≤0,则目标函数z =3x +4y 的最大值为________.14.[2014·全国卷] 设x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0,x +2y ≤3,x -2y ≤1,则z =x +4y 的最大值为________.15.[2014·新课标全国卷Ⅱ] 设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -1≥0,x -y -1≤0,x -3y +3≥0,则z =x +2y 的最大值为( ) A .8 B .7 C .2 D .116.[2014·全国新课标卷Ⅰ] 设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥a ,x -y ≤-1,且z =x +ay 的最小值为7,则a =( )A .-5B .3C .-5或3D .5或-317.[2014·山东卷] 已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y -1≤0,2x -y -3≥0, 当目标函数z =ax +by (a >0,b >0)在该约束条件下取到最小值25时,a 2+b 2的最小值为( )A .5B .4 D .2 18.、[2014·四川卷] 执行如图1-2的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )图1-2A .0B .1C .2D .319.[2014·天津卷] 设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -2≥0,x -y -2≤0,y ≥1,则目标函数z =x +2y 的最小值为( )A .2B .3C .4D .520.[2014·浙江卷] 若实数x ,y 满足⎩⎪⎨⎪⎧x +2y -4≤0,x -y -1≤0,x ≥1,则x +y 的取值范围是________.E6 2a b +≤21.、[2014·重庆卷] 若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( ) A .6+2 3 B .7+2 3 C .6+4 3 D .7+4 322.[2014·湖北卷] 某项研究表明:在考虑行车安全的情况下,某路段车流量F (单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v (假设车辆以相同速度v 行驶,单位:米/秒)、平均车长l (单位:米)的值有关,其公式为F =76 000vv 2+18v +20l.(1)如果不限定车型,l =,则最大车流量为________辆/小时;(2)如果限定车型,l =5,则最大车流量比(1)中的最大车流量增加________辆/小时. 23.、[2014·江苏卷] 若△ABC 的内角满足sin A +2sin B =2sin C ,则cos C 的最小值是______.24.[2014·辽宁卷] 对于c >0,当非零实数a ,b 满足4a 2-2ab +b 2-c =0且使|2a +b |最大时,1a +2b +4c的最小值为________.25.,,[2014·山东卷] 在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,直线y =x 被椭圆C 截得的线段长为4105. (1)求椭圆C 的方程.(2)过原点的直线与椭圆C 交于A ,B 两点(A ,B 不是椭圆C 的顶点).点D 在椭圆C 上,且AD ⊥AB ,直线BD 与x 轴、y 轴分别交于M ,N 两点.(i)设直线BD ,AM 的斜率分别为k 1,k 2,证明存在常数λ使得k 1=λk 2,并求出λ的值;(ii)求△OMN 面积的最大值.25.解:(1)由题意知,a 2-b 2a =32,可得a 2=4b 2.椭圆C 的方程可简化为x 2+4y 2=a 2. 将y =x 代入可得x =±5a5. 因此2×25a 5=4105,即a =2,所以b =1,所以椭圆C 的方程为x 24+y 2=1.(2)(i)设A (x 1,y 1)(x 1y 1≠0),D (x 2,y 2),则B (-x 1,-y 1).因为直线AB 的斜率k AB =y 1x 1,且AB ⊥AD ,所以直线AD 的斜率k =-x 1y 1.设直线AD 的方程为y =kx +m ,由题意知k ≠0,m ≠0. 由⎩⎪⎨⎪⎧y =kx +m ,x 24+y 2=1,消去y ,得(1+4k 2)x 2+8mkx +4m 2-4=0, 所以x 1+x 2=-8mk 1+4k 2,因此y 1+y 2=k (x 1+x 2)+2m =2m 1+4k 2. 由题意知x 1≠-x 2,所以k 1=y 1+y 2x 1+x 2=-14k =y 14x 1.所以直线BD 的方程为y +y 1=y 14x 1(x +x 1). 令y =0,得x =3x 1,即M (3x 1,0).可得k 2=-y 12x 1.所以k 1=-12k 2,即λ=-12.因此,存在常数λ=-12使得结论成立.(ii)直线BD 的方程y +y 1=y 14x 1(x +x 1),令x =0,得y =-34y 1,即N ⎝⎛⎭⎫0,-34y 1. 由(i)知M (3x 1,0),所以△OMN 的面积S =12×3|x 1|×34|y 1|=98|x 1||y 1|.因为|x 1||y 1|≤x 214+y 21=1,当且仅当|x 1|2=|y 1|=22时,等号成立, 此时S 取得最大值98,所以△OMN 面积的最大值为98.E7 不等式的证明方法 26.、、[2014·天津卷] 已知q 和n 均为给定的大于1的自然数,设集合M ={0,1,2,…,q -1},集合A ={x |x =x 1+x 2q +…+x n q n -1,x i ∈M ,i =1,2,…,n }.(1)当q =2,n =3时,用列举法表示集合A .(2)设s ,t ∈A ,s =a 1+a 2q +…+a n q n -1,t =b 1+b 2q +…+b n q n -1,其中a i ,b i ∈M ,i =1,2,…,n .证明:若a n <b n ,则s <t .26.解:(1)当q =2,n =3时,M ={0,1},A ={x |x =x 1+x 2·2+x 3·22,x i ∈M ,i =1,2,3},可得A ={0,1,2,3,4,5,6,7}.(2)证明:由s ,t ∈A ,s =a 1+a 2q +…+a n q n -1,t =b 1+b 2q +…+b n q n -1,a i ,b i ∈M ,i =1,2,…,n 及a n <b n ,可得s -t =(a 1-b 1)+(a 2-b 2)q +…+(a n -1-b n -1)q n -2+(a n -b n )q n -1≤(q -1)+(q -1)q +…+(q -1)q n -2-q n -1=(q -1)(1-q n -1)1-q-q n -1=-1<0, 所以s <t .E8 不等式的综合应用 27.[2014·浙江卷] 已知实数a ,b ,c 满足a +b +c =0,a 2+b 2+c 2=1,则a 的最大值是________.27 .6328.、[2014·安徽卷] 若函数f (x )=|x +1|+|2x +a |的最小值为3,则实数a 的值为( ) A .5或8 B .-1或5 C .-1或-4 D .-4或8 28.D [解析] 当a ≥2时,f (x )=⎩⎪⎨⎪⎧3x +a +1(x >-1),x +a -1⎝⎛⎭⎫-a 2≤x ≤-1,-3x -a -1⎝⎛⎭⎫x <-a 2.由图可知,当x =-a 2时,f min (x )=f ⎝⎛⎭⎫-a 2=a2-1=3,可得a =8.当a <2时,f (x )⎩⎪⎨⎪⎧3x +a +1⎝⎛⎭⎫x >-a2,-x -a +1⎝⎛⎭⎫-1≤x ≤-a 2,-3x -a -1(x <-1).由图可知,当x =-a2时,f min (x )=f ⎝⎛⎭⎫-a 2=-a 2+1=3,可得a =-4.综上可知,a 的值为-4或8.29.[2014·福建卷] 要制作一个容积为4 m 3,高为1 m 的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )A .80元B .120元C .160元D .240元30.、、、[2014·江苏卷] 已知函数f (x )=e x +e -x ,其中e 是自然对数的底数. (1)证明:f (x )是R 上的偶函数.(2)若关于x 的不等式mf (x )≤e -x +m -1在(0,+∞)上恒成立,求实数m 的取值范围.(3)已知正数a 满足:存在x 0∈[1,+∞),使得f (x 0)<a (-x 30+3x 0)成立.试比较e a -1与a e -1的大小,并证明你的结论.30.解: (1)证明:因为对任意 x ∈R ,都有f (-x )=e -x +e -(-x )=e -x +e x =f (x ), 所以f (x )是R 上的偶函数.(2)由条件知 m (e x +e -x -1)≤e -x -1在(0,+∞)上恒成立.令 t =e x (x >0),则 t >1,所以 m ≤-t -1t 2-t +1=-1t -1+1t -1+ 1对任意 t >1成立.因为t -1+1t -1+ 1≥2(t -1)·1t - 1+1=3, 所以 -1t -1+1t -1+ 1≥-13,当且仅当 t =2, 即x = ln 2时等号成立. 因此实数 m 的取值范围是⎝⎛⎦⎤-∞,-13. (3)令函数 g (x )=e x +1e x - a (-x 3+3x ),则g ′ (x ) =e x -1ex +3a (x 2-1).当 x ≥1时,e x -1e x >0,x 2-1≥0.又a >0,故 g ′(x )>0,所以g (x )是[1,+∞)上的单调递增函数, 因此g (x )在[1,+∞)上的最小值是 g (1)= e +e -1-2a .由于存在x 0∈[1,+∞),使e x 0+e -x 0-a (-x 30+ 3x 0 )<0 成立,当且仅当最小值g (1)<0, 故 e +e -1-2a <0, 即 a >e +e -12.令函数h (x ) = x -(e -1)ln x -1,则 h ′(x )=1-e -1x . 令 h ′(x )=0, 得x =e -1.当x ∈(0,e -1)时,h ′(x )<0,故h (x )是(0,e -1)上的单调递减函数;当x ∈(e -1,+∞)时,h ′(x )>0,故h (x )是(e -1,+∞)上的单调递增函数. 所以h (x )在(0,+∞)上的最小值是h (e -1).注意到h (1)=h (e)=0,所以当x ∈(1,e -1)?(0,e -1)时,h (e -1)≤h (x )<h (1)=0; 当x ∈(e -1,e)?(e -1,+∞)时, h (x )<h (e)=0.所以h (x )<0对任意的x ∈(1,e)成立. 故①当a ∈⎝⎛⎭⎫e +e -12,e ?(1,e)时, h (a )<0,即a -1<(e -1)ln a ,从而e a -1<a e -1;②当a =e 时,e a -1=a e -1;③当a ∈(e ,+∞)?(e -1,+∞)时,h (a )>h (e)=0,即a -1>(e -1)ln a ,故e a -1>a e -1. 综上所述,当a ∈⎝⎛⎭⎫e +e -12,e 时,e a -1<a e -1;当a =e 时,e a -1=a e -1;当a ∈(e ,+∞)时,e a -1>a e -1.31.、[2014·辽宁卷] 当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( )A .[-5,-3] C .[-6,-2] D .[-4,-3]32.、、[2014·陕西卷] 设函数f (x )=ln x +mx,m ∈R .(1)当m =e(e 为自然对数的底数)时,求f (x )的极小值; (2)讨论函数g (x )=f ′(x )-x3零点的个数;(3)若对任意b >a >0,f (b )-f (a )b -a <1恒成立,求m 的取值范围.32.解:(1)由题设,当m =e 时,f (x )=ln x +ex ,则f ′(x )=x -e x 2,∴当x ∈(0,e)时,f ′(x )<0,f (x )在(0,e)上单调递减;当x ∈(e ,+∞)时,f ′(x )>0,f (x )在(e ,+∞)上单调递增.∴x =e 时,f (x )取得极小值f (e)=ln e +ee =2, ∴f (x )的极小值为2.(2)由题设g (x )=f ′(x )-x 3=1x -m x 2-x 3(x >0),令g (x )=0,得m =-13x 3+x (x >0),设φ(x )=-13x 3+x (x ≥0),则φ′(x )=-x 2+1=-(x -1)(x +1),当x ∈(0,1)时,φ′(x )>0,φ(x )在(0,1)上单调递增;当x ∈(1,+∞)时,φ′(x )<0,φ(x )在(1,+∞)上单调递减.∴x =1是φ(x )的唯一极值点,且是极大值点,因此x =1也是φ(x )的最大值点, ∴φ(x )的最大值为φ(1)=23. 又φ(0)=0,结合y =φ(x )的图像(如图所示),可知①当m >23时,函数g (x )无零点;②当m =23时,函数g (x )有且只有一个零点;③当0<m <23时,函数g (x )有两个零点;④当m ≤0时,函数g (x )有且只有一个零点. 综上所述,当m >23时,函数g (x )无零点;当m =23或m ≤0时,函数g (x )有且只有一个零点;当0<m <23时,函数g (x )有两个零点.(3)对任意的b >a >0,f (b )-f (a )b -a <1恒成立,等价于f (b )-b <f (a )-a 恒成立.(*) 设h (x )=f (x )-x =ln x +mx -x (x >0),∴(*)等价于h (x )在(0,+∞)上单调递减. 由h ′(x )=1x -mx 2-1≤0在(0,+∞)上恒成立,得m ≥-x 2+x =-⎝⎛⎭⎫x -122+14(x >0)恒成立, ∴m ≥14⎝⎛⎭⎫对m =14,h ′(x )=0仅在x =12时成立,∴m 的取值范围是⎣⎡⎭⎫14,+∞.E9 单元综合答案:1.A 3.D4.A 5.C 6.C7.48.19. C10.D11.C12.713.18 14.515. B 16.B17.B 18.C19.B20.[1,3]21.D22.(1)1900 (2)100 [解析] (1)依题意知,l >0,v >0,所以当l =时,F =76 000v v 2+18v +121=76 000v +121v +18≤76 0002 v ·121v +18=1900,当且仅当v =11时,取等号.(2)当l =5时,F =76 000v v 2+18v +100=76 000v +100v +18≤2000,当且仅当v =10时,取等号,此时比(1)中的最大车流量增加100辆/小时.24.-1 29.C 31.C 16.、[2014·辽宁卷] 对于c >0,当非零实数a ,b 满足4a 2-2ab +4b 2-c =0且使|2a +b |最大时,3a -4b +5c 的最小值为________.16.-2。
