直角三角形三角函数公式
三角函数公式1113KB

sin 45o 1Touch2me;
22
cos 45o tan 45o
1Touch m2 e; 22 1Touch1me 1
1-1 直角三角形的邊角關係 4. 30° 的三角函數值
sin 30o cos30o tan30o
Tou1ch me ; 2
Tou3ch me ; 2
1-1 直角三角形的邊角關係
1.三角函數的定義
考慮一個直角三角形ABC,∠C 是直角, ∠A=θ,則角θ 的三個三角函數為
正弦函數sin
對邊 ; Touch me
斜邊
餘弦函數cos
Байду номын сангаас
鄰邊 ; Touch me
斜邊
tan 正切函數
對邊 Touch me
鄰邊
1-1 直角三角形的邊角關係
按小圖出現大圖 再按小圖
1-1 直角三角形的邊角關係 5. 15° 的三角函數值3-3
sin15o
T6ouch m2e ; 4
cos15o T6ouch m2 e ;
4
tan15o 1Touc=h2me 3
2 3
1-1 直角三角形的邊角關係 1.廣義角的三角函數定義(P2) 2.特殊角的三角函數值(P3) 3.商數關係(P4) 4.平方關係式(P4) 5.補角關係式(P5) 6.負角關係式(P6) 7.餘角關係式 (P7-P8) 8.直角坐標與極坐標的轉換(P9)
O
T(1,0)
輔助圖形
注意事項: θ 在不同象限的情形,可得到同樣的結論。
1-1 直角三角形的邊角關係
y
6.負角關係式
sin (-θ) = - sTionuθch me
初中直角三角形中的三角函数应用

初中直角三角形中的三角函数应用直角三角形是初中数学中常见的一个图形,通过对其各种角度的研究和计算,我们可以运用三角函数来解决与直角三角形相关的问题。
本文将探讨一些基本的三角函数应用,帮助初中学生更好地理解和运用三角函数。
一、正弦函数的应用在直角三角形中,我们可以通过对其角度的研究,运用正弦函数来计算其中的某些边长。
以直角三角形ABC为例,其中∠B为90°,AC为斜边,BC为邻边,AB为对边。
根据正弦函数的定义,我们可以得到以下公式:sin ∠B = 对边AB / 斜边AC如果已知∠B的度数和斜边AC的长度,我们可以通过这个公式来计算对边AB的长度。
同样地,如果已知∠B的度数和对边AB的长度,我们也可以通过这个公式来计算斜边AC的长度。
通过正弦函数的应用,我们可以解决类似于以下问题:已知直角三角形的一个角度和斜边的长度,求对边的长度。
或者已知直角三角形的一个角度和对边的长度,求斜边的长度。
二、余弦函数的应用除了正弦函数,余弦函数也是直角三角形中常用的三角函数之一。
在直角三角形ABC中,∠B为90°,AC为斜边,BC为邻边,AB为对边。
我们可以根据余弦函数的定义得到以下公式:cos ∠B = 邻边BC / 斜边AC与正弦函数相似,如果已知∠B的度数和斜边AC的长度,我们可以通过这个公式来计算邻边BC的长度。
同样地,如果已知∠B的度数和邻边BC的长度,我们也可以通过这个公式来计算斜边AC的长度。
通过余弦函数的应用,我们可以解决类似于以下问题:已知直角三角形的一个角度和斜边的长度,求邻边的长度。
或者已知直角三角形的一个角度和邻边的长度,求斜边的长度。
三、正切函数的应用正切函数是另一个常用的三角函数,它在直角三角形中的应用也非常广泛。
在直角三角形ABC中,∠B为90°,AC为斜边,BC为邻边,AB为对边。
我们可以根据正切函数的定义得到以下公式:tan ∠B = 对边AB / 邻边BC如果已知∠B的度数和对边AB的长度,我们可以通过这个公式来计算邻边BC的长度。
怎么解直角三角形角的度数

怎么解直角三角形角的度数直角三角形是指其中一个角为90度的三角形。
在解直角三角形角的度数时,我们可以利用三角函数的关系来求解。
主要涉及到正弦函数、余弦函数和正切函数。
我们来看正弦函数。
正弦函数是指一个角的对边与斜边的比值。
在直角三角形中,正弦函数的定义为:sinθ = 对边/斜边。
其中,θ代表角的度数。
通过这个公式,我们可以根据已知的对边和斜边来求解角的度数。
接下来,我们来看余弦函数。
余弦函数是指一个角的邻边与斜边的比值。
在直角三角形中,余弦函数的定义为:cosθ = 邻边/斜边。
同样地,通过已知的邻边和斜边,我们可以求解角的度数。
我们来看正切函数。
正切函数是指一个角的对边与邻边的比值。
在直角三角形中,正切函数的定义为:tanθ = 对边/邻边。
通过已知的对边和邻边,我们可以求解角的度数。
除了三角函数,我们还可以利用勾股定理来解直角三角形角的度数。
勾股定理指的是直角三角形中的两条直角边的平方和等于斜边的平方。
根据这个定理,我们可以通过已知的两条直角边的长度来求解角的度数。
我们还可以利用特殊直角三角形的知识来解直角三角形角的度数。
特殊直角三角形包括45度角和30度角的三角形。
在这些特殊情况下,我们可以直接得出角的度数而不需要进行计算。
在实际应用中,解直角三角形角的度数是非常重要的。
例如,在测量中,我们可以利用三角函数来确定不可直接测量的距离或高度。
此外,在建筑、导航等领域,解直角三角形角的度数也有着广泛的应用。
总结起来,解直角三角形角的度数可以通过三角函数、勾股定理和特殊直角三角形来进行。
通过这些方法,我们可以根据已知的边长或角度来求解未知的边长或角度。
在实际应用中,解直角三角形角的度数是非常常见和重要的操作。
sincostan度数公式以及常见角度数值

sincostan度数公式以及常见角度数值
锐角三角函数是以锐角为自变量,以此值为函数值的函数。
在直角三角形ABC 中,我们把锐角∠A的正弦、余弦、正切和余切都叫做∠A的锐角函数。
初中数学主要考察正弦(sin)、余弦(cos)和正切(tan)的计算公式。
正弦(sin)
在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA=∠A的对边/斜边。
sin30°=1/2 sin45°=√2/2 sin60°=√3/2
余弦(cos)
在直角三角形中,任意一锐角∠A的临边与斜边的比叫做∠A的余弦,记作cosA,即cosA=∠A的临边/斜边。
cos30°=√3/2 cos45°=√2/2 cos60°=1/2
正切(tan)
在直角三角形中,任意一锐角∠A的对边与临边的比叫做∠A的正切,记作tanA,即tanA=∠A的对边/临边。
tan30°=√3/3 tan45°=1 tan60°=√3
三角函数顺口溜
正弦对比斜,余弦邻比斜,正切对比邻,正弦余弦互逆运算。
sin30°=cos60°=1/2
sin60°= cos30°=√3/2
sin45°=cos45°=√2/2。
三角形及三角函数公式

三角形及三角函数公式三角形是最基本的几何图形之一,其研究成果对于数学和物理等学科都有重要的意义。
三角形的研究主要包括三角形的性质及其相关的三角函数公式。
三角形的性质:1.三角形是由三条边和三个内角组成的封闭图形。
2.三角形的两边之和大于第三边,任意两个内角之和小于180度。
3.在一个三角形中,外角等于其对应的非相邻内角之和。
4.三角形的内角和等于180度。
5.等腰三角形的两底角相等,而等边三角形的三个内角相等。
三角函数公式:在三角形中,我们经常使用三角函数来描述角度和边长之间的关系。
以下是一些常用的三角函数公式:1. 正弦定理(Sine Rule):在任意三角形ABC中,边长a、b、c与对应的角A、B、C之间有如下关系:sinA/a = sinB/b = sinC/c2. 余弦定理(Cosine Rule):在任意三角形ABC中,边长a、b、c与对应的角A、B、C之间有如下关系:c^2 = a^2 + b^2 - 2ab*cosC3. 正切定理(Tangent Rule):在任意三角形ABC中,角A、B、C的正切值与其对应边长之间有如下关系:tanA = a/b,tanB = b/a,tanC = c/a4. 正割公式(Secant Formula):在任意三角形ABC中,角A、B、C的正割值与其对应边长之间有如下关系:secA = c/a,secB = c/b,secC = a/c5. 余割公式(Cosecant Formula):在任意三角形ABC中,角A、B、C的余割值与其对应边长之间有如下关系:cscA = c/a,cscB = c/b,cscC = b/c6.直角三角形公式:对于直角三角形ABC(其中角C为直角),边长a、b和斜边c之间有如下关系:sinA = a/c,cosA = b/c,tanA = a/b这些三角函数公式可以应用于解决各种三角形问题,如求解边长、角度、三角形的面积等。
初中正弦余弦正切公式
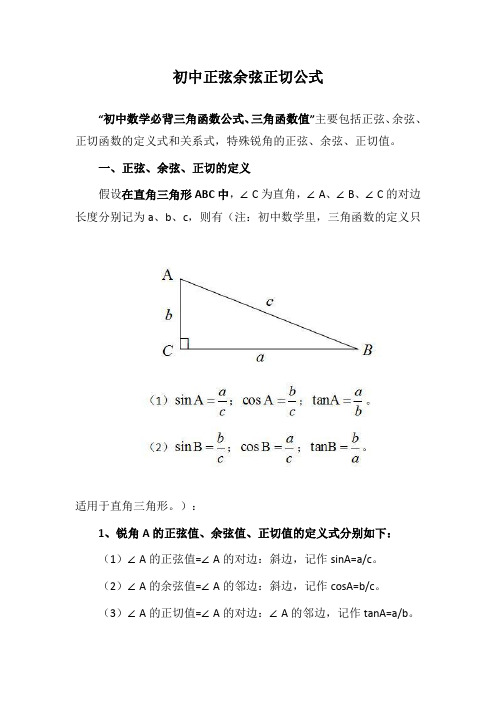
初中正弦余弦正切公式“初中数学必背三角函数公式、三角函数值”主要包括正弦、余弦、正切函数的定义式和关系式,特殊锐角的正弦、余弦、正切值。
一、正弦、余弦、正切的定义假设在直角三角形ABC中,∠C为直角,∠A、∠B、∠C的对边长度分别记为a、b、c,则有(注:初中数学里,三角函数的定义只适用于直角三角形。
):1、锐角A的正弦值、余弦值、正切值的定义式分别如下:(1)∠A的正弦值=∠A的对边:斜边,记作sinA=a/c。
(2)∠A的余弦值=∠A的邻边:斜边,记作cosA=b/c。
(3)∠A的正切值=∠A的对边:∠A的邻边,记作tanA=a/b。
2、锐角B的正弦值、余弦值、正切值的定义式分别如下:(1)∠B的正弦值=∠B的对边:斜边,记作sinB=b/c。
(2)∠B的余弦值=∠B的邻边:斜边,记作cosB=a/c。
(3)∠B的正切值=∠B的对边:∠B的邻边,记作tanB=b/a。
【注】正弦=“对比斜”、余弦=“邻比斜”、正切=“对比邻”。
3、互余的两个角间的正弦、余弦、正切值关系假设在直角三角形ABC中,∠C为直角,则∠A与∠B互余。
通过∠A和∠B的正弦、余弦、正切值的定义式的对比,我们不难发现:∠A的正弦值与∠B的余弦值相等,∠A的余弦值与∠B的正弦值相等,∠A的正切值与∠B的正切值互为倒数。
所以,当∠A与∠B互余时我们有以下3个同时成立的等式关系:(1)sinA=cosB;(2)sinB=cosA;(3)tanA·tanB=1。
二、同角的正弦值、余弦值、正切值间的关系式1、商数关系:tanA=sinA/cosA;tanB=sinB/cosB.2、平方关系:同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1,即(sinA)^2+(cosA)^2=1;(sinB)^2+(cosB)^2=1.3、倒数关系:tanA·cotA=1;tanB·cotB=1.【注】“cotA”称为为∠A的余切,它等于∠A的邻边比上∠A的对边。
直角三角形的边角关系三角函数的计算讲课课件

互余两角之间的三角函数关系: sinA=cosB,tanA*tanB=1.
同角之间的三角函数关系:
sin2A+cos2A=1.
sin A tan A . cos A
特殊角300,450,600角的三角函数值.
例1 小山顶上有一电视塔,在 山脚C处测得塔顶A、塔底B的 仰角分别为45°和30°. 若塔高AB = 40m,则山高BD ≈ m(精确到1m);
第一章 直角三角形的边角关系
1.3.1 三角函数的有关计算
回顾与思考
直角三角的边角关系
直角三角形三边的关系: 勾股定理 a2+b2=c2. A+B=900. 直角三角形两锐角的关系:两锐角互余
a sin A cos B , c
直角三角形边与角之间的关系:锐角三角函数
b cos A sin B , c
a sin A , c b cos A , c a tan A , b
a c sin A. b c cos A.
a b tan A.
a c . sin A b c . cos A a b . tan A
A
作业布置
习题1.4 1,2题;
A
B
C 图1-13
D
1 如图,根据图中已知数据,求△ABC其余各 边的长,各角的度数和△ABC的面积.
A
4cm
450 300
B
C
2 如图,根据图中已知数据,求△ABC其余 各边的长,各角的度数和△ABC的面积.
A
0 300 45 ┌ B 4cm C D
小结拓展 直角三角形中的边角关系
已知两边求角 已知一边一角 已知一边一角 及其三角函数 求另一边 求另一边 B c ┌ b C a
tanx cosx sinx度数表

tanx cosx sinx度数表tan cos sin数值表是什么?1、正弦在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA=∠A的对边/斜边。
2、余弦在直角三角形中,任意一锐角∠A的临边与斜边的比叫做∠A的余弦,记作cosA,即cosA=∠A的临边/斜边。
3、正切在直角三角形中,任意一锐角∠A的对边与临边的比叫做∠A的正切,记作tanA,即tanA=∠A的对边/临边。
扩展资料:相关公式1、平方和关系(sinα)^2+(cosα)^2=12、积的关系sinα=tanα×cosα(即sinα/cosα=tanα)cosα=cotα×sinα(即cosα/sinα=cotα)tanα=sinα×secα(即tanα/sinα=secα) 3、倒数关系tanα×cotα=1sinα×cscα=1cosα×secα=14、商的关系sinα/cosα=tanα=secα/cscαsin cos tan度数公式三角函数表sin cos tan度数公式三角函数表一、sin度数公式1、sin 30= 1/22、sin 45=根号2/23、sin 60= 根号3/2二、cos度数公式1、cos 30=根号3/22、cos 45=根号2/23、cos 60=1/2三、tan度数公式1、tan 30=根号3/32、tan 45=13、tan 60=根号31、三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
2、三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
