寒假复习第一讲三角形专题
三角形复习讲义(补课用)

三角形复习讲义(补课用)一、三角形相关概念1 .三角形的概念:由不在同一直线上的三条线段首尾顺次连结所组成的图形叫做三角形。
要点:①三条线段;②不在同一直线上;③首尾顺次相接.2 .三角形的表示:通常用三个大写字母表示三角形的顶点,如用A B、C表示三角形的三个顶点时,此三角形可记作△,其中线段、、是三角形的三条边,/ A、/ B、/ C分别表示三角形的三个内角。
3 .三角形中的三种重要线段:三角形的角平分线、中线、高线是三角形中的三种重要线段.(1)三角形的角平分线:三角形一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.①三角形的角平分线是一条线段,可以度量。
而角的平分线是经过角的顶点且平分此角的一条射线.②三角形有三条角平分线且相交于一点。
这一点一定在三角形的内部.③三角形的角平分线画法与角平分线的画法相同,可以用量角器画,也可通过尺规作图来画。
(2)三角形的中线:在一个三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线.注意:①三角形有三条中线,且它们相交三角形内部一点.②画三角形中线时只需连结顶点及对边的中点即可.(3 )三角形的高线:从三角形一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高.①三角形的三条高是线段②锐角三角形三条高线的交点在三角形内部,直角三角形的三条高线的交点在直角顶点上,钝角三角形三条高线的交点在三角形外部。
③画三角形的高时,只需要向对边或对边的延长线作垂线,连结顶点与垂足的线段就是该边上的高.(二)三角形三边关系定理:①三角形两边之和大于第三边。
故同时满足△三边长a、b、c的不等式有:>c, >a, >b.②三角形两边之差小于第三边。
故同时满足△三边长a、b、c的不等式有:a>, b>, c>.注意:判定这三条线段能否构成一个三角形,只需看两条较短的线段的长度之和是否大于第三条线段即可(三)三角形的稳定性:三角形的三边确定了,那么它的形状、大小都确定了,三角形的这个性质就叫做三角形的稳定性. 例如起重机的支架采用三角形结构就是这个道理.三角形内角和性质的推理方法有多种,常见的有以下几种: (四)三角形的内角:结论1 :三角形的内角和为180°.表示:在△中,/// 180°(1)构造平角①可过A点作// (如图)②可过一边上任一点,作另两边的平行线(如图)(2)构造邻补角,可延长任一边得邻补角(如图)构造同旁内角,过任一顶点作射线平行于对边(如图)结论2:在直角三角形中,两个锐角互余.表示:如图,在直角三角形中,/ 90 °,那么// 90° (因为ZZZ 180°)注意:①在三角形中,已知两个内角可以求出第三个内角女口:在△中,/ 180°-(ZZ B)②在三角形中,已知三个内角和的比或它们之间的关系,求各内角.如:△中,已知/ A:/ B:/ 2: 3: 4,求/ A、/ B、 / C的度数.(五)三角形的外角:1 .定义:三角形一边与另一边的延长线组成的角叫做三角形的外角.如图,/为△的一个外角,/也是△的一个外角,这两个角为对顶角,大小相等.2 .性质:①三角形的一个外角等于与它不相邻的两个内角的和.②三角形的一个外角大于与它不相邻的任何一个内角如图中,/// B , / >/ A , / >/ B.③三角形的一个外角与之相邻的内角互补3 .外角个数:过三角形的一个顶点有两个外角,这两个角为对顶角(相等), 可见一个三角形共有六个外角.(六)多边形1. 多边形的定义:在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
2020学而思教材讲义高一数学寒假(目标班、尖子班) 高一寒假 第1讲 我会解三角形你会么 教师版 目标班
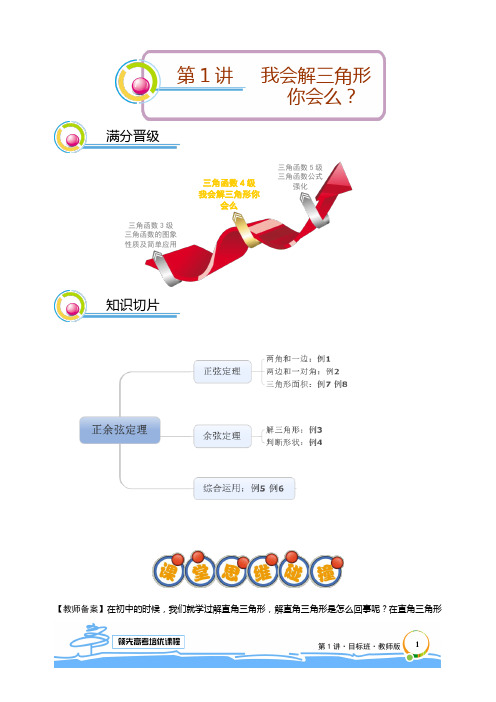
【教师备案】在初中的时候,我们就学过解直角三角形,解直角三角形是怎么回事呢?在直角三角形知识切片满分晋级第1讲 我会解三角形你会么?三角函数3级 三角函数的图象性质及简单应用三角函数4级 我会解三角形你会么三角函数5级 三角函数公式强化中,除了告诉我们直角外,还有5个要素,我们发现,如果解这个三角形,把要素都求出来,必须要知道至少2个要素,当然不能为2个角,换言之,解直角三角形就是知二求三的过程.当然,在我们学习了任意角的三角函数之后,我们的视野不能这么小,如果给我们一个一般的三角形,那我们应该如何解这个三角形呢?我们应该至少要知道几个量?我们先来回顾一下初中边和角相关的东西,我们在初中学过尺规作图,而且学过三角形全等的证明(SSS SAS ASA AAS,,,),只要给出上述条件我们就能把三角形确定,也就是全等. 那么,为什么我们知道2条边1个夹角就能求出其他要素呢?而知道两条边和一边的对角就无法证明三角形全等呢?三角形的边和角之间存在什么关系呢?尺规作图毕竟是定性的感受,在高中阶段,我们可以给出一个严格的证明,就是今天我们要讲的正余弦定理.正余弦定理的本质就是构造边与角之间的关系,由角就可以求出边,由边就可以求出角.下面我们就先来介绍正弦定理.在ABC△中的三个内角A,B,C的对边分别用a b c,,表示:1.正弦定理:在三角形中,各边的长和它所对的角的正弦的比相等,即sin sin sina b cA B C==.【教师备案】2sin sin sina b cRA B C===,其中R为ABC△的外接圆的半径.建议老师用三角形的外接圆给学生证明,因为板块1.4中讲三角形面积的时候还会用到三角形的外接圆,所以不如这时给学生讲了.利用三角形中的线段关系证明正弦定理:①在R t ABC△中(如图),有sin sina bA Bc c==,,因此sin sina bcA B==,又因为sin1C=,所以sin sin sina b cA B C==②在锐角ABC△中(如图),作CD AB⊥于点D,有sinCDAb=,即sinCD b A=;sinCDBa=,即sinCD a B=,因此sin sinb A a B=,即sin sina bA B=,同理可证sin sina cA C=,因此sin sin sina b cA B C==1.1正弦定理与其在解三角形中的应用知识点睛cb aDCBAC BAcba③在钝角ABC △中(如图),作CD AB ⊥,交AB 的延长线于点D ,则sin CDA b=,即sin CD b A =;()sin 180sin CDB B a=-=,即sin CD a B =,因此 sin sin b A a B =,即sin sin a b A B =,同理可证sin sin a cA C=,因此sin sin sin a b cA B C== 利用平面几何知识证明正弦定理:如图所示,设O 为ABC △的外接圆的圆心,连BO 并延长交O 于A ',连A C ',则A A '= 或πA A '=-,∴sin sin 2BC a A A A B R '===',即2sin aR A=,同理可证2sin sin b c R B C ==,故有2sin sin sin a b cR A B C=== 当ABC △是钝角三角形时,类似地得出上述结论. 利用向量知识证明正弦定理:①当ABC △是锐角三角形时,过A 点作单位向量i 垂直于AB , 如图,∵AC AB BC =+,∴()i AC i AB BC i AB i BC i BC ⋅=⋅+=⋅+⋅=⋅,∴()()cos 90cos 90b A a B -=-,得sin sin b A a B =,得sin sin a bA B= ②当ABC △为钝角三角形时,类似地得出上述结论2.利用正弦定理解三角形⑴解三角形:三角形的三个内角和它们的对边分别叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.⑵利用正弦定理可解下列两类型的三角形:①已知三角形的任意两个角与一边,求其它两边和另一角;【教师备案】有了正弦定理之后,我们可以简单的看出,任意的两个角与一边相当于AAS 和ASA 的条件,可以确定所有的角,然后可以确定所有的边,因此,三角形也随之确定.②已知三角形的两边与其中一边的对角,计算另一边的对角,进而计算出其它的边与角.【教师备案】1.已知三角形的两边和一边的对角,由正弦定理可以求得另一边的对角的正弦值,但是解三角形时,因为在(0,π)内,互补的角的正弦值相等,所以求得另一边所对的角的正弦值之后,可能对应有一个角或两个角,因此无法确定三角形的形状,这就是为什么SSA 无法证明三角形全等的原因.2.利用正弦定理证明三角形中“大边对大角”的结论:①当ABC △为锐角三角形时,若a b >,则sin sin A B >,又π02A B ⎛⎫∈ ⎪⎝⎭,,,正弦函数在此区间内单调递增,故A B >;i CA cba DCBAOA 'CA②当ABC△为钝角三角形时,若A为钝角,则由πA B+<得,πB A<-,又ππ02A B⎛⎫-∈ ⎪⎝⎭,,,故由正弦函数的单调性知:()sin sinπsinB A A<-=,从而由正弦定理知:b a<.对直角三角形,此结论显然成立,故综上知,在任意三角形中,均有大边对大角.3.此时,到底取一个角还是取两个角,关键保持一个原则“大边对大角”.具体讨论如下:已知,a b和角A,若B为钝角或直角,则C至多有一个解;若B为锐角,得分情况讨论,如图:无解的情况例如:3460b c B===︒,,,求C.由sin sinb cB C=sin4sin6023sin133c BCb︒⇒===>,∴C无解,从而满足此条件的三角形不存在.这就是sinc B b>的情况.【教师备案】在讲利用正弦定理解三角形时,对于边角互化和利用边角互化判断三角形形状的题型建议放到同步去讲,本板块只讲利用正弦定理解两种类型三角形,在讲完“已知两角和任一边解三角形”后就可以让学生做例1;在讲“已知两边和其中一边的对角解三角形”时一定要注意三角形的多解问题,具体的多解见考点2的【教师备案】,讲完多解问题后就可以让学生做例2的铺垫以及例2.考点1:已知两角和任一边解三角形【例1】已知两角和任一边解三角形⑴已知ABC△中,a b c,,分别是A B C、、的对边,3c=,60A=︒,45C=︒,则a=_______.⑵在ABC△中,30B=︒,45C=︒,1c=,则b=_______;三角形的外接圆半径R=_______.⑶在ABC△中,已知8a=,60B=,75C=,则b=_______.经典精讲b sin A<a<b , 两解a>b , 一解a<b sin A , 无解ba=b sin A , 一解CB【解析】⑴32⑵2;2已知30B =,45C =,1c =,由正弦定理得:2sin sin b cR B C==, 所以sin 1sin 302sin sin 45c B b C ⋅===,122sin sin 452c R C ====,2R =⑶46由60B =,75C =,知45A =,再由正弦定理有846sin 45sin 60bb =⇒=考点2:已知两边和其中一边的对角解三角形【铺垫】根据下列条件解三角形:①6031A a b ===,,;②3012A a b ===,,;③30610A a c ===,,; ④150105A a c ===,,,其中有唯一解的个数为( )A .1 B .2 C .3 D .4 【解析】C ①3sin 3b A =<,又31>∵,∴有唯一解;②sin 2sin301b A ==,∴有唯一解;③sin 10sin305610c A ==<<,∴有两解;④有唯一解.【例2】 已知两边和一边对角解三角形⑴在ABC △中,已知4522A a b ===,,B =_______.⑵已知ABC △中,a b c ,,分别是A B C 、、的对边,22345a b A ===︒, 则B =_______.⑶已知ABC △,三个内角A B C ,,的对边分别记为a b c ,,,若245c x b B ===︒,,,且这个 x 的取值范围. ⑷(目标班专用)(2010山东卷理数)在ABC △中,角A B C 、、所对的边分别为a b c 、、,若2a =,2b =,sin cos 2B B +A 的大小为 .【解析】⑴30 根据正弦定理得:sin sin a b A B =,∴sin 2sin 451sin 2b A B a ⋅===,b a <∵,B A <∴, B ∴为锐角,即30B =⑵60或120由正弦定理得,sin 23sin 453sin 22b A B a ===,∵sin b A a b <<,∴这个三角形有两组解,即60B =或120. ⑶ 由正弦定理可得:sin sin c b C B =,解得:2sin x C =,由于三角形有两解,又45B =︒, 则45135C <<︒且90C ≠2sin 1C <<221x<<,解得222x <<【点评】本题的⑶也可用以下方法解,当sinc B b c<<,即sin2x B x<<时,对应两个C的值,方程有两组解,解得222x<<.⑷π6由sin cos 2B B+=平方得12sin cos2B B+=,即sin21B=,因为0πB<<,所以π4B=.又因为22a b==,,所以在ABC△中,由正弦定理得:22sin B=,解得1sin2A=.又a b<∵,所以A B<,所以π6A=.【点评】易错点:忽略a b<A B⇒<的隐藏条件.多解.【教师备案】在正弦定理中,我们还有两种类型的全等没有讨论,SAS和SSS型,正弦定理处理的是对边对角的情形,仅仅用正弦定理是很难把三角形求解出来的,因此,我们需要一个新的工具,能够把边的条件化成角,就是下面所介绍的余弦定理.1.余弦定理:三角形任何一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦的积的两倍,即:2222222222cos,2cos,2cos.c a b ab Cb ac ac Ba b c bc A⎧=+-⎪=+-⎨⎪=+-它的变形为:222222222cos,2cos,2cos.2a b cCaba c bBacb c aAbc⎧+-=⎪⎪⎪+-=⎨⎪⎪+-=⎪⎩<教师备案> 余弦定理的推导可以由三角形的向量运算直接得到,比如:2222()()2a BC BA AC BA AC BA BA AC AC==+⋅+=+⋅+()22222cosπ2cosc bc A b c bc A b=+-+=-+.也可以通过坐标法及两点距离公式得到.建立合适的坐标系,如图,得()()()cos sin000A b C b CB a C,,,,,,从而有22(cos)(sin)AB c b C a b C==-+,1.2余弦定理及其在解三角形中的应用知识点睛bxyBCA(b cosC , b sinC)整理得:2222cos c a b ab C =+-. 也可以通过三角形中的线段关系证明:在ABC △中,已知边a b ,及C ∠(为了方便起见,假设C ∠为最大的角),求边c 的长证明:当90C ∠=时,那么222c a b =+当90C ∠≠时,如图,无论C ∠为锐角还是为钝角,都过A 点做边BC 的高,交BC (或延长线)于点D ,这时高AD 把ABC △分成两个直角三角形ADB 和ADC , 则sin AD b C =,cos BD a b C =-,在Rt ADB △中,运用勾股定理,得 ()222222sin cos c AD BD b C a b C =+=+-222cos a b ab C =+-2.余弦定理及其变形常用来解决这样两类解三角形的问题: ①已知两边和任意一个内角解三角形; ②已知三角形的三边解三角形.【教师备案】老师在讲完余弦定理后,可以就SSS 和SAS 型的全等证明做个简单讲解,这样子整个讲义的主线就串在一起.然后,可以让学生做【铺垫】,【铺垫】是直接套公式的,做完【铺垫】就可以做例3,例3是灵活的运用余弦定理解三角形,在解题过程中需要转化的;学生在能够灵活运用余弦定理后,就可以讲考点4,用余弦定理判断三角形形状,在三角形中,因为每个角都在()0π,内,所以一个角的正弦不能判断这个角是锐角还是钝角,但是余弦就能很快的判定是锐角还是钝角,在三角形中,当cos 0α>时,α为锐角;当cos 0α<时,α为钝角;当cos 0α=时,α为直角;考点4的【铺垫】是直接根据三角形的三条边判断三角形形状的,老师可以让学生先体会一下怎么样用余弦判定三角形形状,例4是已知三角形形状,求边的取值范围的,在解题过程中要注意用余弦定理和构成三角形的条件.考点3:用余弦定理解三角形【铺垫】⑴在ABC △中,5a =,8b =,60C =︒,则c =_______.⑵在ABC △中,222a b c bc =++,则A 等于( ).A . 60B . 45C .120 D . 30 【解析】⑴ 7 由余弦定理2222cos 25644049c a b ab C =+-=+-=,∴7c =. ⑵C∵2222222()1cos 222b c a b c b c bc A bc bc +-+-++===-经典精讲abcABCDD cbCBA∵0180A <<,∴120A =.【例3】 余弦定理解三角形⑴在ABC △中,5a =,8b =,7c =,则sin C =_______.⑵在ABC △中,已知3sin 5A =,sin cos 0A A +<,35a =,5b =,则c =______.⑶在ABC △中,若1378cos 14a b C ===,,,则最大角的余弦是( ). A .15- B .16- C .17- D .18-【解析】⑴3 由余弦定理2222cos c a b ab C =+-,∴1cos 2C =,3sin C =. ⑵∵sin cos 0A A +<,且3sin 5A =,24cos 1sin 5A A =--=-∴,又∵35a =,5b =,2222cos a b c bc A =+-,∴()2224355255c c ⎛⎫=+-⨯⨯⨯- ⎪⎝⎭,即28200c c +-=,解得2c =或10c =-(舍),∴2c = ⑶ C由2222cos c a b ab C =+-,∴3c =,则b a c >>,∴最大角为B ,∴2221cos 27a c b B ac +-==-考点4:用余弦定理判断三角形形状【教师备案】最大角定三角形的形状,由余弦定理易得,较小两边的平方和与最大边的平方的差可以定最大角是锐角、直角或钝角.注意:三角形三边关系应满足的为:较小两边的和大于 第三边.【铺垫】在ABC △中,已知5a =,6b =,7c =,则此三角形是一个 三角形. 【解析】锐角三角形 c b a >>∵,∴角C 为最大角,2221cos 025a b c C ab +-==>∴,∴角C 为锐角,∴三角形为锐角三角形【例4】判断三角形形状⑴ 若以34x ,,为三边组成一个直角三角形,则x 的值为 . ⑵ 若以34x ,,为三边组成一个锐角三角形,则x 的取值范围为 . ⑶ 若以34x ,,为三边组成一个钝角三角形,则x 的取值范围为 . 【追问】我们还可以考虑,当我们知道三角形两边的情况下,求某一个角的取值范围,例如下面这个问题:已知ABC △中,12AB BC ==,,则C ∠的取值范围是________________⑷ (目标班专用)已知三角形的三边长为三个连续自然数, 且最大角是钝角.求这个三角形三边的长.【解析】 ⑴ 5722234x +=或22234x +=.⑵)75依题意有:22217434x x x ⎧<<⎪>⎨⎪+>⎩或22217434x x x ⎧<<⎪⎨⎪+>⎩≤75x <.⑶ (()1757,∪, 解法一:依题意有:22217434x x x ⎧<<⎪>⎨⎪+<⎩或22217434x x x ⎧<<⎪⎨⎪+<⎩≤解得57x <<或17x <<.解法二:本题也可以由函数的图象来解决,如图,设圆的半径3OA =,4OB =,圆上任取一点与O B ,两点构成三角形,从图形上看出,当圆上的点在点D 和点E 上时,构成直角三角形;当点 在DE 上时,构成锐角三角形;当点在AD 和EG 上时,构成 钝角三角形.由此可以很快得出答案. 【追问】π06⎛⎤ ⎥⎝⎦,⑷设三角形三边的长为:()12n n n n *++∈N ,,最大角为α,∴222(1)(2)cos 2(1)n n n n n α++-+=+,∵α是钝角,∴cos 0α<,∴222(1)(2)02(1)n n n n n ++-+<+,2(1)0n n +>∵,∴222(1)(2)0n n n ++-+<∴2230n n --<,∴13n n *-<<∈N ,∵,1n =∴或2. 当1n =时,123,,不能构成三角形的三边,故舍去. 当2n =时,234,,即为所求三边的长.【拓展】⑴钝角三角形的三边分别是12a a a ++,,,其最大角不超过120,求a 的取值范围. ⑵在ABC △中,若三条边是三条连续的正整数,且最大角是最小角的2倍,求ABC △的三条边长.【解析】⑴∵钝角三角形的三边分别是12a a a ++,,,∴显然有210a a a +>+>>,设钝角三角形 的最大的(内)角为α,依题意,得90120α<≤, 由()()()()()()22212313cos 21212a a a a a a a a a a a α++-+-+-===++,可得13022a a--<≤, GFEDCBAO解得332a⎡⎫∈⎪⎢⎣⎭,⑵设最小内角为θ,三边长为11n n n-+,,,根据正弦定理得:11sin sin2n nθθ-+=,112cosnnθ+-=∴,()1cos21nnθ+=-∴,根据余弦定理得:()()()22211cos21n n nn nθ++--=+,()()()()2221112121n n nnn n n++--+=-+∴,解得5n=,从而得ABC△的三条边分别为456,,1.正弦定理灵活应用:①2sina R A=,2sinb R B=,2sinc R C=(其中R为ABC△的外接圆的半径);②sin2aAR=,sin2bBR=,sin2cCR=;③::sin:sin:sina b c A B C=.2.正余弦定理的综合应用已知条件应用定理一般解法一边和两角(如a B C,,)正弦定理由πA B C++=,求角A;由正弦定理求出b与c.两边和夹角(如a b C,,)余弦定理正弦定理由余弦定理求第三边c;由正弦定理求出小边所对的角(此角一定是锐角);再由πA B C++=,求剩下的角.三边(a b c,,)余弦定理正弦定理由余弦定理求出最大角,然后正弦计算剩余两角.两边和其中一边的对角(如a b A,,)正弦定理余弦定理由正弦定理求出角B;由πA B C++=,求出角C;再利用正弦定理或余弦定理求c.正弦定理可以得到三角形的边与角之间的关系,可以把角全部换成边,也可以把边全部换成角,【铺垫】就是根据正弦定理把边用角表示,例5是先要根据正弦定理把边角化掉再根据余弦定理解三角形,此类题型不属于边角互化题型,是正弦定理的灵活运用,边角互化的题型是比如“2sina b A=”类型的,对于这类题我们放到同步去讲;在讲完正余弦定理的灵活运用后就可以让学生体会一下正余弦定理在平面几何中的应用,因为在同步的时候不会讲此类题型,所以在预习的时候可以给学生介绍一下,具体见例6和目标班学案2,而对于三角形中()sin sinA B C+=的应用建议放到同步去讲.1.3正余弦定理在解三角形中的灵活应用经典精讲知识点睛【铺垫】在ABC △中,若::1:2:3A B C =,则::a b c =______.【解析】 由已知得306090A B C ===,,,::sin :sin :sin1:3:2a b c A B C ==∴【例5】 正余弦定理的综合运用⑴在ABC △中,若sin :sin :sin 3:2:4A B C =,则cos C 的值为( )A .14-B .14C .23-D .23⑵在ABC △中,若222sin sin sin A B C +<,则角C 为( )A .锐角B .钝角C .直角D .不确定【追问】在ABC △中,若cos cos cos a b cA B C==,则ABC △是( ) A .直角三角形 B .等边三角形C .钝角三角形D .等腰直角三角形⑶(2010天津理7)在ABC △中,内角A B C ,,的对边分别为a b c ,,,若223a b bc -=,sin 23sin C B =,则A =( )A .30B .60C .120D .150 【解析】⑴A 根据正弦定理sin 2a A R =,sin 2b B R =,sin 2cC R=,sin :sin :sin ::3:2:4A B C a b c ==∴,2223241cos 2324C +-==-⨯⨯∴⑵B222sin sin sin A B C +<∵,∴根据正弦定理得222a b c +<,222cos 02a b c C ab+-=<∴,∴角C 为钝角【追问】B ⑶A由sin 23sin C B =,根据正弦定理,得23c b =.所以22236a b bc b -==,即227a b =. 由余弦定理得2223cos 2b c a A bc +-==.所以30A =︒.【例6】 正余弦定理在平面几何中的应用⑴ 在平行四边形ABCD 中,3AB =,5BC =,6AC =,求BD⑵ 在ABC △中,已知4AB =,7AC =,BC 边上的中线7AD =,那么BC = .⑶ (目标班专用)在ABC △中,已知46AB =6cos ABC ∠=,AC 边上的中线5BD ,求sin A 的值【解析】 ⑴如图,在ABC △中,2222cos AC AB BC AB BC B =+-⋅,即222635235cos B =+-⋅⋅ ①在ABD △中,2222cos BD AB AD AB AD A =+-⋅, 即22235235cos BD A =+-⋅⋅ ②①+②得:()22226235BD +=+,即42BD =DCBA【点评】由本题可以得出平行四边形定理:平行四边形的对角线平方之和等于四条边长平方之和⑵解法一:如图:设BD x=,则2BC x=,DC x=,∵πADB ADC∠=-∠,cos cosADB ADC∠=-∠∴,由余弦定理,得222222774722772222x xx x⎛⎫⎛⎫+-+-⎪ ⎪⎝⎭⎝⎭=-⋅⋅⋅⋅,解得92x=,9BC=∴解法二:由平行四边形定理得:()2222247781BC=+-=,9BC=∴⑶如图:设E为BC的中点,连接DE,则DE AB∥,且1262DE AB==,设BE x=,在BDE△中利用余弦定理可得:2222cosBD BE ED BE ED BED=+-⋅∠,()()6cos cosπcosπcosBED DEC ABC ABC∠=-∠=-∠=-∠=-∵28266523x x=++⨯⨯∴,解得1x=或73x=-(舍),故2BC=,从而222282cos3AC AB BC AB BC ABC=+-⋅∠=,即221AC=,又30sin ABC∠=∵,故22123sin30A=,70sin A=∴【教师备案】因为三角形的面积和正余弦定理关系不是特别紧密,而且到本讲结束,三角形的面积公式已经全部讲完,所以把三角形的面积单独做一个板块,老师可以把所有的三角形面积公式给学生讲一下.1.4三角形的面积知识点睛DA72x745463DCA面积公式:()11111sin sin sin 222224a abcS ah a b c r ab C bc A ac B R ==++====.其中r 为ABC △内切圆半径,R 为外接圆半径.【教师备案】在求三角形的面积时,学生印象最深的就是12a ah ,那这个时候老师就可以根据12a ah 推导其它公式,并且老师可以在这里把三角形的面积公式全部给学生整理一下,但是本讲重点是介绍1sin 2S ab C =类型的三角形面积公式,如果学生的程度很好,老师可以介绍一下“海伦公式”和圆内接四边形面积公式.【选讲】海伦公式:()()()S p p a p b p c =---2a b cp ++=. 【推导】 ()2222222111sin 1cos 12224a b c S ab C C ab a b+-==--()()()2222222222221142244a b a b c ab a b c ab a b c -+-++---+()()()()()()22221144a b c c a b a b c a b c a c b b c a ⎡⎤⎡⎤+---+++-+-+-⎣⎦⎣⎦令()12p a b c =++,则()()()S p p a p b p c =---圆内接四边形面积:()()()()S p a p b p c p d ----2a b c dp +++=. 【推导】由()22222cos 2cos πa b ab c d cd θθ+-=+--,可得2222cos 22a b c d ab cd θ+--=+()()222222222sin 1cos ab cd a b c d θθ+-+---()()()()b c d a a c d b a b d c a b c d ++-++-++-++- (){}()11sin sin πsin 22S ab cd ab cd θθθ=+-=+ ()()()()()()()()142222b c d a a c d b a b d c a b c d a b c d a b c d a b c d a b c d a b c d p a p b p c p d ++-++-++-++-++++++++++++⎛⎫⎛⎫⎛⎫⎛⎫=---- ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=----【教师备案】老师在讲完三角形的面积后就可以让学生做【铺垫】,【铺垫】是直接利用公式求三角形面积的,例7不能够直接利用公式求三角形面积,需要先看在面积公式中缺少哪些变量,然后再根据题中的已知条件利用正余弦定理求出所需要的变量,最后再利用面积公式就CB A b aDC BAπ-θθd cba可以了.第三题放了一道关于圆内接四边形面积的题目,供老师选择使用;例8是已知三角形面积解三角形,在解题过程中会用到正余弦定理,对于求面积的最大值的问题建议放到同步,因为在求最大值的问题时大多数要用到均值定理,学生这时候还没学,所以建议以后再讲.【铺垫】在ABC△中,若5AB=,7BC=,33sin14B=,求ABC△的面积.【解析】∵5AB=,7BC=,33sin14B=,1133153sin5722144ABCS AB BC B=⋅⋅=⨯⨯⨯=△∴【例7】求面积⑴已知ABC△,三个内角,,A B C的对边分别记为a b c,,,43460b c B===︒,,,求ABCS△.⑵已知ABC△,三个内角,,A B C的对边分别记为a b c,,,若234a b c===,,,求ABCS△.⑶(目标班专用)已知:四边形ABCD内接于圆O,四边长依次为2,7,6,9,求圆直径. 【解析】⑴分析:三角形的已知条件为常见的SSA型.根据条件有两种思路求三角形的面积:11sin sin22ABCS bc A ac B∆=⋅=⋅.所以欲求三角形面积需要先求A或先求a.方法一:由正弦定理知sin sinb cB C=,sin1sin243c BCb︒===,因为C是三角形的一个内角,故30C︒=或150︒,又60B︒=,故30C︒=.180603090A︒︒︒︒=--=,从而1832ABCS bc∆==.方法二:由余弦定理得222cos2a c bBac+-=,即24320a a--=.()()480a a+-=.因为0a>,所以8a=.1sin832ABCS ac B∆=⋅=.⑵要求面积,先求一个角,已知三边,可以用余弦定理求一角:222416911cos21616a c bBac+-+-===,∴2315sin1cosB B=-=,经典精讲∴113153sin 241522164ABC S ac B ∆==⋅⋅⋅=.⑶ 85.【铺垫】已知ABC △的三边长分别为a b c ,,,且面积()22214ABC S b c a =+-△,则A 等于( ) A .45 B .30 C .120 D .15【解析】 A()2221112cos cos 442ABC S b c a bc A bc A =+-=⨯=△,又1sin 2ABC S bc A =△∵,sin cos A A =∴,45A =∴【例8】 已知三角形面积解三角形ABC △中,角A B C ,,的对边分别为a b c ,,,22sin 3cos C C =,7c =,又ABC △的面积为332, 求⑴角C 的大小;⑵a b +的值【解析】⑴由已知得()221cos 3cos C C -=,1cos 2C =∴或cos 2C =-(舍), ∴在ABC △中,60C =⑵133sin 22ABC S ab C ==△∵,133sin 6022ab =∴,6ab =∴,又2222cos c a b ab C =+-∵,()22272cos a b ab C =+-∴,227a b ab +-=∴,2213a b +=∴, 222255a b a b ab +=++==∴【演练1】 (2010北京卷文理10)在ABC △中,若2π133b c C ==∠=,,,则________a = 【解析】1 方法一: 由余弦定理222cos 2a b c C ab+-=得, 220a a +-=.∵0a >,∴1a =.方法二: 由正弦定理sin sin b c B C =得,1sin 2B =,π6B =或5π6,又因为b c <,即B C <, 所以π6B =,∴2ππππ366A =--=.∴1a b ==.实战演练【演练2】 在ABC △中,角A B C ,,的对边分别为a b c ,,,若()222tan 3a c b B ac +-,则角B 的值为( ).A . π6B . π3C .π6或5π6D . π3或2π3【解析】D 由余弦定理2222cos a c b ac B +-=及()222tan 3a c b B ac +-得, 3sin B =. 所以π3B =或2π3.【演练3】 在ABC △中,已知222sin sin sin 3sin sin B C A A C --,则角B 的大小为( )A .150︒B .30︒C .120︒D .60︒ 【解析】A 由222sin sin sin 3sin sinBC A A C --=及正弦定理可得2223b c a ac --=即得2223cos 2a c b B ac +-==,∴150B =︒.【演练4】 在ABC △中,角A B C ,,所对的边分别是a b c ,,,1tan 2A =,310cos B = 若ABC △最长的边为1,则最短边的长为( ).A 25B 35C 45D 5 【解析】D 由310cos B =B 为锐角,∴1tan 3B =,故()()tan tan πtan C A B A B =--=-+tan tan 11tan tan A BA B+=-=--⋅①, 由①知135C ∠=︒,故c 边最长,即1c =,又tan tan A B >,故b 边最短,∵10sin B =,2sin C =sin sin b c B C =, ∴sin 5sin c B b C =5.【演练5】(2011西城一模文15) 设ABC △的内角A ,B ,C 所对的边长分别为a ,b ,c ,且4cos 5B =,2b =. ⑴ 当30A =︒时,求a 的值;⑵ 当ABC △的面积为3时,求a c +的值.【解析】 ⑴ 因为4cos 5B =,所以3sin 5B =,由正弦定理sin sin a b A B =,可得10sin303a =︒,所以53a =.⑵ 因为ABC △的面积1sin 2S ac B =,3sin 5B =,所以3310ac =,10ac =.由余弦定理2222cos b a c ac B =+-,得222284165a c ac a c =+-=+-,即2220a c +=.所以2()220a c ac +-=,2()40a c +=,所以,210a c +=.1.正弦定理公式 ;余弦定理公式22a b +- = .2.三角形面积公式S = .盲人数学家——欧拉1783年9月18日,法国人蒙高尔费兄弟举行了第二次热气球升空试验。
第一章 三角形的初步知识复习(全等三角形)

找夹边(ASA) 已知两角
找对边(AAS)
5
一、全等三角形
知识结构
全 定义:能够 完全重合 的两个三角形
等 对应元素:对应_顶__点__、对应 边 、对应 角。
三 角 形
性质:全等三角形的对应边 相等 、对应角相等 。 判定: SSS 、 SAS 、 ASA 、AAS 。
6
练•习1、如图,已知AC=DB,∠ACB=∠DBC,则有
于当E,连结EG、EF;
A
(1)试说明BG=CF;
(2)请你判断BE+CF与EF的大小
关系,并说明理由。 F
E
B
C
D
G
16
例题7.如图所示,公路OA和公路OB相交于O,在∠AOB内部有 两个镇C、D,若要修建一大型农贸市场P,使P到OA,OB的距 离相等,且使PC=PD,用尺规作出农贸市场P的位置。
1、边边边(SSS) :三条边对应相等的两个三角形全等。 2、边角边(SAS):有两边及其夹角对应相等的两个三角形全等。 3、角边角 (ASA) :有两角及其夹边对应相等的两个三角形全等。 4、角角边(AAS):有两角及一角的对边对应相等的两个三角形全等。
7
3、如图,方格纸中△DEF的三个顶点分别在 小正方形的顶点(格点)上,请你在图中再画一个 顶点都在格点上的△ABC,且使△ABC≌△DEF。
3.兄弟齐心,其力断金;----小组合作,
摆拼出更多的图形来,并指出它们的对应边和对应角。
4
4.要判断两个三角形全等,我们是否需要知道多少条件? 怎样的三个条件呢?
找夹角(SAS) 已知两边
找另一边(SSS)
条 已知一角一边 件
边为角的对边,找任一角(AAS)
人教初三数学寒假A第1讲三角形

第1话: 三角形模块一:三角形的基本性质知识导入4.特殊线段、点① 中线:重心(平分三角形面积) ② 高:垂心(相似模型)③ 角平分线:内心(到三边距离相等,内切圆)、 ④ 外角平分线:旁心(到三边距离相等,旁切圆) ⑤ 中垂线:外心(到顶点距离相等,外接圆)5.周长:C a b c =++6.面积:111sin 222S ah ab pr θ===其中p 为三角形的周长)7.模型:(1)“五心”③重心:三边中线交点⑤垂心:三条高线交点①∠BHC+∠BAC=180°②HA HF HB HD HE HC⋅=⋅=⋅(2)折角模型、飞镖模型、8字模型能力提升例1 基本概念(1)下列六个命题中,结论正确的有()①三条线段组成的图形是三角形②三角形按角分可分为直角三角形和斜三角形③三角形按边分可分为不等边三角形和等腰三角形④三条线段能组成三角形,只需其中两条线段的长度和大于第三条线段的长度即可。
⑤任意三角形的最长边必然满足:l/3周长≤最长边<l/2周长A.2个B.3个C.4个D.5个【答案】B三边关系(2)如图,四边形ABCD 中,3AB =,4BC =,9CD =,AD a =,则a 的取值范围【答案】216a <<(3)已知ABC △的边长分别为21x +,3x ,5,则ABC △的周长L 的取值范围是( ) A .636L << B .1011L <≤ C .1136L ≤< D .1036L <<【答案】D例2 三条重要线段:(1)下列说法正确的是( )A .三角形的中线可能在三角形的外部B .三角形的三条角平分线不一定都在三角形内部C .三角形的三条高线中至少有一条在三角形内部D 只有一条高在三角形内部的三角形一定是钝角三角形【答案】C重要线段与面积关系(2)ABC ∆的边BC 上的高为AD ,如果AD=4,BD=6,CD=2,则=ABC S ∆_________ 【答案】16或8(3)如图,在ABC △中,点D E F ,,分别为边BC AD CE ,,的中点,且26ABC S cm =△,则S 阴影=__________【答案】1.5cm 2(4)如图,△ABC 中,AD 平分∠BAC ,求证:AB BDAC CD=C【答案】如图做辅助线,根据题意DE=DF ,此时易得ABD ACD S BD S CD ∆∆=,ABD ACD SAB S AC∆∆=,∴AB BDAC CD=.例3 “五心”(1)已知△ABC 中,PA=PB=PC ,则∠BPC 与∠BAC 之间的关系为_____________【答案】∠BPC=2∠BAC(2)(2015广东)如图,△ABC 三边的中线AD ,BE ,CF 的公共点G ,若12ABC S =△,则图中阴影部分面积是.BBCA【答案】4(3)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°-12αB.90°+12αC.12αD.360°﹣α【答案】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=12(∠ABC+∠BCD)=12(360°﹣α)=180°-12α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°-12α)=12α.故选:C.(4)如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACB的平分线CF相交于点F,与∠ACE的平分线CD 相交于点D,连接AD,以下结论:①∠BAC=70°;②∠BFC=125°③∠DOC=90°;④∠BDC=35°;⑤∠DAC=55°,其中正确的是___.(填写序号)。
初三寒假讲义

⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧不等腰三角形角形只有两边相等的等腰三等边三角形等腰三角形三角形⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧钝角三角形锐角三角形斜三角形直角三角形三角形第一节 三角形基础复习第一关 三角形的概念、分类 ★☆☆☆☆☆【识记】1.三角形概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形2.三角形分类:①按边分类:②按边分类:第二关 三角形三边关系、三角定理 ★★☆☆☆☆【初级理解】 过关指南:1.三角形三边关系:在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
2.三角形三角定理:三角形内角和为180度。
目标题目示例:【本节进步目标】★☆☆☆☆☆对三角形的概念、分类达到【识记】级别★★☆☆☆☆对三角形三边关系、三角定理达到【初级理解】级别 ★★★☆☆☆对等腰、直角、等边三角形达到【高级理解】级别 ★★★★☆☆对全等三角形达到【高级运用】级别1.如果三角形的两边长分别为3和5,则周长L 的取值范围是( ) A.6<L<15 B.6<L<16 C.11<L<13 D.10<L<162.三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为_______; 过关练习:1.如图,P 是△ABC 内一点,说明PA+PB+PC>21(AB+BC+AC).2.如图,C 岛在A 岛的北偏东50°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向。
从C 岛看A 、B 两岛的视角∠ACB 是多少度?第三关 等腰、直角、等边三角形 ★★★☆☆☆【高级理解】 过关指南:PCBA1. 等腰三角形60⎧⎧⎧⎪⎪⎨⎪⎪⎩⎨⎪⎧⎪⎪⎨⎪⎪⎩⎩⎪⎧⎪⎧⎨⎪⎨⎪⎩⎪⎪⎪︒⎧⎪⎪⎨⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩⎪⎩⎩等边对等角性质三线合一腰与底边不等的等腰三角形等角对等边判定定义三边相等性质三角都相等有一个角等于的等腰等边三角形三角形判定三边都相等(或三角都相等)的三角形 2. 直角三角形⎧⎪⎫⎨⎬⎪⎭⎩三边关系--勾股定理--应用直角三角形的性质---应用直角三角形的判别3. 等边三角形三条边都相等,三个角都相等且都为60度。
第一章三角形的初步认识总复习讲义

第⼀章三⾓形的初步认识总复习讲义龙⽂教育学科教师辅导讲义学员姓名:辅导课⽬:数学年级:七年级学科教师:汪⽼师授课⽇期及时段课题第⼀章三⾓形的初步认识总复习重点、难点、考点1、三⾓形的基本概念的应⽤2、三⾓形全等的证明学习⽬标1、理解三⾓形的相关概念2、会证明三⾓形的全等教学内容第⼀章三⾓形的初步认识总复习:1.1认识三⾓形①“△ABC”读作“三⾓形ABC”。
三⾓形任何两边的和⼤于第三边。
②三⾓形三个内⾓的和等于180°。
三⾓形的⼀个外⾓等于和它不相邻两个内⾓的和。
1.2三⾓形的平分线和中线在三⾓形中,⼀个内⾓的⾓平分线与它对边相交,这个⾓的顶点与交点之间的线段叫做三⾓形的三⾓形的平分线。
在三⾓形中,连结⼀个顶点与它对边中点的线段,叫做这个三⾓形的中线。
1.3三⾓形的⾼从三⾓形的⼀个顶点向它的对边所在的直线作垂线,顶点和垂⾜之间的线段叫做三⾓形的⾼。
锐⾓三⾓形的三条⾼在三⾓形的内部,垂⾜在相应顶点的对边上。
直⾓三⾓形的直⾓边上的⾼分别与另⼀条直⾓边重合,垂⾜都是直⾓的顶点。
⽽在钝⾓三⾓形中,夹钝⾓两边上的⾼都在三⾓形的外部,它们的垂⾜都在相应顶点的对边的延长线上。
1.4全等三⾓形能够重合的两个三⾓形称为全等三⾓形。
两个全等三⾓形重合时,能互相重合的顶点叫做全等三⾓形的对应顶点,互相重合的边叫做全等三⾓形的对应边,互相重合的⾓叫做全等三⾓形的对应⾓。
“全等”可⽤符号“≌”来表⽰。
全等三⾓形的性质:全等三⾓形对应边相等,对应⾓相等。
1.5三⾓形全等的条件①三边对应相等的两个三⾓形全等(简写成“边边边”或“SSS ”)。
当三⾓形三边长确定是,三⾓形的形状、⼤⼩完全被确定,这个性质叫做三⾓形的稳定性,这是三⾓形特有的性质。
②有⼀个⾓和夹这个⾓的两边对应相等的两个三⾓形全等(简写成“边⾓边”或“SAS ”)。
垂直于⼀条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。
线段垂直平分线上的点到线段两端点的距离相等。
专题01 与三角形有关的线段(知识串讲+10大考点)(原卷版)
专题01 与三角形有关的线段考点类型知识串讲(一)三角形的概念三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
三角形特性三角形用符号“”表示,顶点是A、B、C的三角形记作“ABC”,读作“三角形ABC”。
(二)三角形的分类三角形按边的关系分类如下:三角形按角的关系分类如下:(三)三角形的稳定性三角形的稳定性➢三角形具有稳定性➢四边形及多边形不具有稳定性要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了。
(四)三角形的三边关系三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边(1)三角形三边长分别是a,b,c,则a+b>c或c-b<a。
(2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b(五)三角形的相关线段(1)①高线概念:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
②高线性质:利用两个锐角互余(等量代换);利用等面积法求线段长度(2)①中线概念:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线。
②中线性质:线段中点性质求线段相等;三角形的中线可以将三角形分为面积相等的两个小三角形(3)①角平分线概念:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线②角平分线性质:角度相等求解角度考点训练考点1:三角形的识别与相关概念典例1:(2022秋·山东济宁·八年级校考阶段练习)如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是_____;在△ACD中,∠C所对的边是_____.【变式1】(2022·全国·八年级专题练习)如图,在△BCE中,边BE所对的角是________,∠CBE所对的边是________;在△AEC中,边AE所对的角是________,∠A为内角的三角形是________.【变式2】(2022·全国·八年级专题练习)如图所示,顶点是A、B、C的三角形,记作___________,读作___________.其中,顶点A所对的边为___________还可用___________表示;顶点B所对的边为___________还可用___________表示;顶点C所对的边为___________还可用___________表示.【变式3】(2021·八年级课前预习)由不在同一直线上的三条线段_______________所组成的图形叫做三角形.如图,线段_______ 、______、______是三角形的边.三角形的边有时也用小写字母abc来表示,a=________、b=________、c=________,点A、点B、点C是三角形的_______,________、______、________是相邻两边组成的角,叫做三角形的内角.图中三角形记作_______.考点2:三角形的个数问题典例2:(2022·全国·八年级专题练习)观察图形规律:(1)图①中一共有________个三角形,图②中共有________个三角形,图③中共有________个三角形.(2)由以上规律进行猜想,第n个图形共有________个三角形.【变式1】(2021秋·江西宜春·八年级上高中学校考期中)如图,以∠B为内角的三角形有_______个【变式2】(2022秋·八年级课时练习)已知:如图,试回答下列问题:(1)图中有_______个三角形,其中直角三角形是______.(2)以线段AC为公共边的三角形是___________.(3)线段CD所在的三角形是_______,BD边所对的角是________.(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于_______.【变式3】(2020秋·江西上饶·八年级校考阶段练习)北京冬季奥运会吉祥物冰墩墩落在n个三角形内,则n的值为________.考点3:三角形的分类典例3:(2022春·上海·七年级专题练习)在△ABC中,∠A=20°,∠B=60°,∠C=100°,那么△ABC是______三角形.(填“锐角”、“钝角”或“直角” )【变式1】(2022秋·八年级课时练习)在ΔABC中,若∠A:∠B:∠C=3:5:7,则该三角形是_________三角形.(填“锐角”“直角”或“钝角”)【变式2】(2022秋·八年级课时练习)已知a,b,c为三个正整数,如果a+b+c=12,那么以a,b,c为边能组成的三角形是:①等腰三角形,②等边三角形,③直角三角形,④钝角三角形.以上结论正确的是______.(只填序号)【变式3】(2020·全国·七年级假期作业)观察图中的三角形,把它们的标号填入相应横线上.锐角三角形_______,直角三角形________,钝角三角形________.考点4:三角形的三边关系典例4:(2021秋·甘肃武威·八年级校考阶段练习)若a ,b ,c 是△ABC 的三边的长,则化简|a ―b ―c|+|b ―c ―a|+|a +b ―c|=________.【变式1】(2023春·七年级课时练习)若等腰三角形的两边的长分别是5cm 、7cm ,则它的周长为___________cm .【变式2】(2022秋·全国·八年级专题练习)已知三角形三边长分别为2,9,x ,若x 为偶数,则这样的三角形有___________个.【变式3】(2022秋·广东广州·八年级校考阶段练习)已知△ABC 的三边长分别为a ,b ,c ,且a ,b 满足(a ―1)2+=0,则c 的取值范围是______.考点5:三角形三边关系的应用典例5:(2022秋·浙江·八年级专题练习)一个三角形的三边长均为整数.已知其中两边长为3和5,第三边长x 是不等式组x ―1⩽23x +25x ―7>2x +13的正整数解.则第三边的长为:______.【变式1】(2022秋·广东深圳·七年级统考期末)边长为1的小正方形组成如图所示的6×6网格,点A ,B ,C ,D ,E ,F ,G ,H 都在格点上.其中到四边形ABCD 四个顶点距离之和最小的点是_________.【变式2】(2022秋·八年级课时练习)如图,加油站A 和商店B 在马路MN 的同一侧,A 到MN 的距离大于B 到MN 的距离,AB =700米.一个行人P 在马路MN 上行走,当P 到A 的距离与P 到B 的距离之差最大时,这个差等于______米.【变式3】(2021秋·黑龙江佳木斯·八年级校联考期中)如图,填空:由三角形两边的和大于第三边,得AB+AD>____________,PD+CD>____________.将不等式左边、右边分别相加,得AB+AD+PD+CD>__________,即AB+AC>_________________.考点6:与三角形高线有关的计算问题典例6:(2023春·江苏盐城·七年级滨海县第一初级中学校考期中)如图,AD 是△ABC 的中线,BE 是△ABD 的中线,EF ⊥BC 于点F.若S=24,BD = 4 ,则EF 长为___________.△ABC【变式1】(2022秋·全国·八年级专题练习)如图,△ADF中,点B,C分别在AD,AF上,DC与BF交于点E,若DE:CE=2:1,S△DEF=6,S△DBE=4,则△ABC的面积=______.【变式2】(2022秋·福建厦门·八年级厦门市槟榔中学校考期末)如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为___________.【变式3】(2023秋·湖南邵阳·八年级统考期末)如图,在△ABC中,AB=AC=2,P是BC边上的任意一点,PE⊥AB于点E,PF⊥AC于点F.若S△ABC=PE+PF=______.考点7:三角形稳定性典例7:(2022秋·云南昆明·八年级云大附中校考期中)随着人们物质生活的提高,手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点.为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的______.【变式1】(2022秋·八年级课时练习)如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上 _____根木条.【变式2】(2019·全国·八年级统考假期作业)下列图中哪些具有稳定性?________.【变式3】(2023春·江苏扬州·七年级校联考阶段练习)如图,学校门口设置的移动拒马都用钢管焊接成三角形,这样做的数学原理是利用了三角形的_____(选填“稳定性”或“不稳定性”).考点8:与三角形角平分线有关的计算问题典例8:(2023春·七年级课时练习)如图所示,△ABC的两条角平分线相交于点D,过点D作EF∥BC,交AB于点E,交AC于点F,若△AEF的周长为30cm,则AB+AC=______cm.【变式1】(2022秋·海南省直辖县级单位·八年级统考期末)如图,(1)若AM是△ABC的中线,BC=12 cm,则BM=CM=______cm;(2)若AD是△ABC的角平分线,则∠BAD=∠DAC=______;若∠BAC=106°,则∠DAC=______;(3)若AH是△ABC的高,则△ABH是______三角形.【变式2】(2022春·山东菏泽·七年级校联考阶段练习)如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.CF⊥AD于H,交AB于F.下列说法:①线段AG是△ABE的角平分线;②线段AE是△ABG的边BG上的高;③BG是△ABD的中线;④△ABG与△DBG的面积相等;⑤∠1+∠ACF=90°.其中正确的有______ (填序号).【变式3】(2020秋·八年级课时练习)△ABC中,D为BC边上任意一点,DE、DF分别是△ADB和△ADC的角平分线,连接EF,则△DEF的形状为_________.考点9:与三角形中线有关的周长、面积问题典例9:(2022秋·浙江宁波·八年级统考阶段练习)如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为12,则△BCD的周长是_____.【变式1】(2022秋·福建厦门·八年级统考期末)如图,S△ABD=S△ACD,已知AB=8cm,AC=5cm,那么△ABD和△ACD的周长差是________cm.【变式2】(2023秋·广东广州·八年级统考期末)如图,BE是△ABC的中线,点D是BC边上一点,BD=2CD,BE、AD交于点F,若△ABC的面积为24,则S△BDF﹣S△AEF等于_____.【变式3】(2022春·江苏泰州·七年级校联考期中)已知在ΔABC中,已知点D、E、F分别为BC、AD、CE的中点,且SΔBEF=4cm2,则SΔABC的值为______cm2.考点10:利用网格求三角形的面积典例10:(2023秋·福建龙岩·八年级校考期末)如图所示的正方形网格,A、B、C、D是网格线交点,则△ABC的面积与△ABD的面积的大小关系为:S△ABC ______S△ABD.填“>”、“=”或“<”)【变式1】(2022秋·山东青岛·九年级统考期末)如图,△ABC与△DEF都是是正方形网格中的格点三角形(顶点在格点上),那么△ABC与△DEF的面积比为__________.【变式2】(辽宁省部分学校2022-2023学年九年级上学期期末数学试题)已知点A2,2,B5,6,C 4,8,那么S△ABC=__________.【变式3】(2022春·浙江杭州·七年级统考期末)如图,大长方形是由9个完全相同的小长方形组成,已知小长方形的长,宽分别为a,b,则图中连接三个格点围成的阴影部分图形的面积是______.(用a,b的代数式表示)同步过关一、单选题1.(2022秋·全国·八年级阶段练习)如图,线段BD是△ABC高的图形是()A.B.C.D.2.(2022春·云南保山·七年级统考期中)如图,AB⊥BC于点B,AC⊥CD于点C,连接AD.若AD=8,BC=6,则AC的长可能为().A.5B.6C.7D.93.(2022秋·江苏·八年级阶段练习)下列说法中,正确的个数有()①三角形具有稳定性;②如果两个角相等,那么这两个角是对顶角;③三角形的角平分线是射线;④直线外一点到这条直线的垂线段叫做这点到直线的距离;⑤任何一个三角形都有三条高、三条中线、三条角平分线;⑥三角形的三条角平分线交于一点,且这点在三角形内;A.2B.3C.4D.54.(2023春·七年级课时练习)图中,以DE为边的三角形有()A.2个B.3个C.4个D.5个5.(2022秋·辽宁葫芦岛·八年级校联考期中)下列各图中,正确画出△ABC中AC边上的高的是()A.①B.②C.③D.④6.(2022秋·广东珠海·八年级校考期中)如图,D,E,F分别是边BC,AD,AC上的中点,若S阴影的面积为3,则△ABC的面积是( )A.5B.6C.7D.87.(2022春·福建漳州·七年级漳州实验中学校考阶段练习)如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )A.DE是△BCD的中线B.BD是△ABC的中线C.AD=DC,BE=ECD.DE是△ABC的中线8.(2022秋·八年级课时练习)如图,有下列说法:①若∠1=∠3,AD//BC,则BD是∠ABC的平分线;②若AD//BC,则∠1=∠2=∠3;③若∠1=∠3,则AD//BC;④若∠C+∠3+∠4=180∘,则AD//BC.其中正确的有().A.1个B.2个C.3个D.49.(2023春·全国·八年级专题练习)若a、b、c+|b-a-c|=().A.2b-2c B.2a C.2(a+b―c)D.2a-2c10.(2022春·江苏南京·七年级校考阶段练习)如图,在△ABC中,D是AB中点,E是BC边上一点,且BE=4EC,CD与AE交于点F,连接BF.若四边形BEFD的面积是14,则△ABC的面积是()A.28B.32C.30D.29二、填空题11.(2023春·山东枣庄·七年级校联考阶段练习)超重机的底座、输电线路的支架、自行车的斜支架等,都是采用三角形结构,这样做的数学道理是利用了______________.12.(2022秋·全国·八年级专题练习)如图,∠CBD=∠E=∠F=90°,则线段______是△ABC中BC边上的高.13.(2023·全国·八年级专题练习)已知三角形的三边长均为偶数,其中两边长分别为6和8,则第三边长为________.14.(2021秋·四川资阳·九年级四川省安岳中学校考期中)在△ABC中,中线AD、BE相交于点O,若△BOD 的面积等于6,则△ABC的面积等于____.15.(2019·上海·七年级阶段练习)△ABC的三边长为a,b,c,且a,b b2―6b+9=0.则c的取值范围是_______.16.(2020春·江苏扬州·七年级校联考阶段练习)一个三角形的三边长都是整数,其中两条边的长度分别为3和8,第三边长为奇数,那么三角形的周长是__________.三、解答题17.(2022秋·全国·八年级专题练习)请你完成定理“三角形的任意两边之和大于第三边”的证明.已知:如图,△ABC.求证:AB+BC>AC,BC+CA>AB,CA+AB>BC.18.(2022秋·河北廊坊·八年级校考期末)画图并填空:如图,方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移,使点C移到点C'的位置.(1)请画出△A'B'C';(2)连接A A'、B B',则这两条线段的关系是______;(3)在方格纸中,画出△ABC的中线BD和高CE.19.(2021春·河北石家庄·七年级石家庄市第十九中学校考期末)(1)如图1,直线a∥直线b,点A、D 在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC 的面积(填“>”、“=”或“<”).(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则BDBC=.(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.20.(2023春·七年级单元测试)△ABC在如图所示的平面直角中,将其平移后得△A'B'C',若B的对应点B'的坐标是(―2,2).(1)在图中画出△A'B'C';(2)此次平移可看作将△ABC向____平移了______个单位长度,再向____平移了______个单位长度得△A'B' C';(3)△ABC的面积为______.21.(2023·陕西西安·校考三模)已知:a、b、c满足(a―2+|c―=0求:(1)a、b、c的值;(2)试问以a、b、c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.22.(2022春·黑龙江齐齐哈尔·七年级统考期中)在下列网格中建立平面直角坐标系,如图所示,每个小正方形的边长均为1个单位长度.已知A(1,1),B(3,4)和C(4,2).(1)在图中标出点A,B,C;(2)将点C向下平移3个单位到点D,将点A先向左平移3个单位,再向下平移1个单位到点E,在图中标出点D和点E;(3)求△EBD的面积.23.(2022春·福建福州·七年级福建省福州延安中学校考期末)若不等式组2x―a<1x―2b>―3的解集是―1<x<3,(1)求代数式(a+1)(b―1)的值;(2)若a,b,c为某三角形的三边长,试求|c―a―b|+|c―3|的值.24.(2022秋·山东泰安·七年级东平县实验中学校考阶段练习)等腰三角形一条腰上的中线将三角形的周长分成15和21两部分,求该三角形的腰长和底边的长.。
专题01_三角形的基础_(知识点串讲)(解析版)
专题01 三角形的基础 重点突破 三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。 三角形特性
三角形用符号“”表示,顶点是A、B、C的三角形记作“ABC”,读作“三角形ABC”。 三角形按边分类: 等腰三角形:有两条边相等的三角形叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的夹角叫做底角。 等边三角形:底边与腰相等的等腰三角形叫做等边三角形,即三边都相等。 三角形三边的关系(重点 (1)三角形的任意两边之和大于第三边。 三角形的任意两边之差小于第三边。(这两个条件满足其中一个即可) 用数学表达式表达就是:记三角形三边长分别是a,b,c,则a+b>c或c-b<a。 (2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b 三角形的分类: 三角形按边的关系分类如下:
三角形按角的关系分类如下: 三角形的稳定性 ➢ 三角形具有稳定性 ➢ 四边形及多边形不具有稳定性 要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了。 考查题型 考查题型一 三角形的个数问题 典例1.(2019·西林县期中)如图所示,其中三角形的个数是( )
A.2个 B.3个 C.4个 D.5个
【答案】D 【提示】根据三角形的定义解答即可,由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形. 【详解】图中的三角形有:△ABC,△BCD,△BCE,△ABE,△CDE共5个. 故选D. 【名师点拨】本题考查了三角形的概念,由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边,相邻边的公共端点叫做三角形的顶点.相邻两条边组成的角,叫做三角形的内角,简称为三角形的角. 变式1-1.(2017·秦皇岛市期中)图中三角形的个数是( )
A.3个 B.4个 C.5个 D.6个
《三角形》小结与复习-完整版PPT课件
内角、外角、高、角平分线、中线
性质
任意两边之和大于第三边
内角和定理及其推论
三
角 形
等腰(等边)三角形的性质与判定
线段的垂直平分线 全等三角形 用尺规作三角形
性质 判定(SAS、ASA、AAS、SSS)
逆命题
互 逆 命 题
命题
真命题
假命题 举反例
本课节内容
小结与复习
回顾
1 三角形的三边之间有怎样的关系? 2 什么叫三角形的高、角平分线、中线? 3 结合本章所学的知识,举出一个命题并写出 其逆命题,再判断它们的真假
4 等腰(等边)三角形具有哪些性质? 如何判定一个三角形是等腰(等边)三角形?
5 线段的垂直平分线的性质定理是什么? 如何作线段的垂直平分线?
结束
定义
基本事实 定理及其推论
证明 证明的依据
注意
1 一个命题是真命题,它的逆命题不一定是真命题
2 命题有真有假 要判断一个命题为真命题,需要 进行证明,并且证明的过程要言必有据要判断一 个命题为假命题,只需举一个反例
3 要证明某些线段或角相等时,可以考虑转化为证 明两个三角形全等
作业
P97 复习题2 A组
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一课时 三角形
一、知识点复习
1.三角形三边关系: 三角形两边之和_____第三边;三角形两边之差_____第三边;
2.三角形的高、角平分线、中线:
从三角形的一个顶点向它的对边所在直线作垂线,_____________间的线段叫做三角形的高.
三角形一个角的平分线与它的对边相交,这个角的_____________之间的线段叫做三角形的
角平分线。
连结三角形一个_________________的线段叫做三角形的中线。
3.三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形具有________,
而四边形没有_________。
4.三角形的角:
三角形的内角和等于_______;直角三角形的两个锐角_______;三角形的外角和等于_______.
三角形的一个外角等于与它不相邻的两个________的和.
三角形的一个外角大于与它不相邻的任何一个__________.
5.多边形内角和、外角和以及对角线:
n边形内角和为________;外角和为_________;过一个顶点的对角线条数________;分成三角
形的个数___________;所有的对角线条数__________;
二、经典例题
例1.如图,_____是△ACD外角,∠ADB= 115°,
∠CAD= 80°,则∠C = .
例2.下列条件中能组成三角形的是( )
A.5cm, 13cm, 7cm B.3cm, 5cm, 9cm
C.14cm, 9cm, 6cm D.5cm, 6cm, 11cm
例3.三角形的两边为7cm和5cm,则第三边x的范围是 __________ .
例4.已知等腰三角形的两边长分别为10 和6 ,则三角形的周长是 .
例5.如图,AD是BC边上高,BE是 △ABD的角平分线,
∠1=30°,∠2=40°, 则∠C=___, ∠BED= ______.
例6..如图,在△ABC中,AD⊥BC于点D,AE是∠BAC的角平分线,
∠B=36°,∠C=66°,(1)求∠DAE的度数?
(2)若题目把∠B=36°,∠C=66°改为∠C-∠B=20°,
你能发现∠DAE与∠B、∠C的关系吗?
A
B
C
D
1
2
E
A
B C
D
C
B
D
E
A
F
例7.如图, △ABC中, D是BC边上一点,∠1= ∠2,
∠3=∠4,∠BAC= 63°,求∠DAC的度数
例8.如图已知:AD是△ABC的中线,△ABC的面积为 60cm2 ,求△ABD的面积
例9..若△ABC的内角满足2∠A- ∠B= 60°, 4∠A+∠C=300°,则△ABC是( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.无法确定
例10.如图,∠1=∠2, ∠3=∠4, ∠A= 100°,求x的值。
例11.如图,在△ABC 中,∠ ABC ,∠ ACB 的平
分线BD,CE 交于点O.
变式1 若∠A =80°,则∠BOC = .
变式2 你能猜想出∠BOC 与∠A 之间的数量关系吗?
变式3 如图,若换成两外角平分线相交于O,则
∠BOC 与∠A 又有怎样的数量关系?
变式4 如图,若换成一内角与一外角平分线相交
于点O,则∠BOC与∠A 又有怎样的数量关系?
A
B
C
D
E
A
B
C
2
3
1
4
x
A
B
C
O
E
D
A
B
C
O
E
D
A
B
C
O
E
D
A
B
C
D
2
1
3
4
三、巩固练习
1.在△ABC中,(1)∠B=100°,∠A=∠C,则∠C=_______;
(2)2∠A=∠B+∠C,则∠A= _______。
2.已知两条线段的长分别是3cm、8cm ,要想拼成一个三角形,且第三条线段a的长为奇数,
问第三条线段应取多少长?
3.等腰三角形一边的长是5 cm,另一边的长是8cm,则它的周长为________.
4.五边形的五个内角度数之比为2︰3︰4︰5︰6,求这个五边形的最大的内角和它的外角的
度数.
5.小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得内角和1680° ,你
能否求得他漏掉的内角和多边形内角和的正确结果吗?
6.如图∠B=∠C,DE⊥BC于E,EF⊥AB于F,∠ADE=140°,求∠FED的度数
7.如图,在△ABC中,AD⊥BC于点D, AE是∠BAC的角平分线, DF⊥AE于点F,
∠B=38°,∠C=74°,求∠ADF的度数?
8.如图△ABC中AD是高,AE、BF是角平分线,它们相交于点O,∠A= 50°,
∠C = 70°求∠DAC,∠AOB 。
F
E
D
C
B
A
C
B
D E
A
D A B C E
F
O
9.如图, △ABC中,∠BAC=∠C=2∠B,AD是∠BAC的平分线,
求∠ADC的度数
10.在△ABC中,∠C比∠A+∠B 还大30°,则 这个三角形是 三角形.
11. 已知:P是△ABC内任意一点.
求证:∠BPC>∠A
12.已知△ABC的∠B、∠C的平分线交于点O。
求证:∠BOC=90°+ 21∠A
A
B C
P
A
B
C
D
0
A
B
C
