2019届一轮复习人教版 开普勒定律万有引力定律 学案
2019届一轮复习人教版 万有引力定律 课件(44张)

kg m 式中,质量的单位用 __________ ,距离的单位用 __________ ,力的单位用 引力常量 。 __________ ,G称为__________ N
返回导航
第六章 万有引力与航天
3.意义 万有引力定律清楚地向人们揭示,复杂运动的后面隐藏着简洁的科学规 完全相同 的科学法则,人类 律;它明确地向人们宣告,天上和地下都遵循着 __________ 认识自然界有了质的飞跃。
物 理 必 修 ② · 人 教 版
返回导航
第六章 万有引力与航天
『判一判』 (1)月球绕地球做匀速圆周运动是因为月球受力平衡。( × ) (2)万有引力不仅存在于天体之间,也存在于普通物体之间。( √ )
(3)引力常量是牛顿首先测出的。( × )
(4)物体间的万有引力与它们间的距离成反比。( × ) (5)根据万有引力表达式可知,质量一定的两个物体,若距离很近,它们间
物 理 必 修 ② · 人 教 版
返回导航
第六章 万有引力与航天
探究一
对万有引力定律的理解
如图甲所示,两个挨得很近的人之 间的万有引力是不是很大呢?如图乙所
示,设想将一个小球放到地球的中心,
小球受到的万有引力又是多少呢?
物 理质点,不能根据万有引力定律求他们间 的万有引力;物体放在地球的中心,地球的各部分对物体的吸引力是对称的,物 体受的万有引力是零。
物 理 必 修 ② · 人 教 版
返回导航
第六章 万有引力与航天
『想一想』 某个行星的质量是地球质量的一半,半径也是地球半径的一半。某运动员 在地球上能举起250kg的杠铃,在该行星上最多能举起质量为多少的杠铃? 答案:125kg
2019年高考物理总复习第16讲开普勒定律万有引力定律讲义word版本
第16讲开普勒定律万有引力定律弱项清单,1.不能正确理解开普勒第二定律;2.混淆动能和总能量的概念;3.不能将太阳系内的常见情景迁移到其他星系.知识整合一、开普勒定律1.开普勒第一定律又称轨道定律.2.开普勒第二定律又称面积定律.3.开普勒第三定律又称周期定律.该定律的数学表达式是:____________.4.开普勒行星运动定律,不仅适用于行星,也适用于其他卫星的运动.研究行星运动时,开普勒第三定律中的常量k与________有关;研究月球、人造地球卫星运动时,k 与____________有关.二、万有引力定律1.万有引力定律.其数学表达式是____________.万有引力定律的发现,证明了天体运动和地面上运动遵守共同的力学原理,实现了天地间力学的大综合,第一次揭示了自然界中的一种基本相互作用规律.2.____________实验证明了万有引力的存在及正确性,并使得万有引力定律可以定量计算,引力常量G=6.67×10-11N·m2/kg2.3.万有引力定律的应用计算中心天体的质量、密度若已知一个近地卫星(离地高度忽略,运动半径等于地球半径R)的运行周期是T.有:G MmR2=4π2mRT2,解得地球质量为____________;由于地球的体积为V=43πR3,可以计算地球的密度为:____________.当然同样的道理可以根据某行星绕太阳的运动计算太阳的质量.方法技巧考点1 开普勒定律的应用1.开普勒行星运动定律是对行星绕太阳运动的总结,实践表明该定律也适应于其他环绕天体,如月球或其他卫星绕行星运动.2.开普勒第二定律与第三定律的区别:前者揭示了同一行星在距太阳不同距离时运动的快慢,后者揭示了不同行星运动快慢的规律.【典型例题1】下列关于行星绕太阳运动的说法中,正确的是( )A.所有行星都在同一椭圆轨道上绕太阳运动B.行星绕太阳运动时,太阳位于行星轨道的中心处C.离太阳越近的行星运动周期越长D.所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等【典型例题2】(17年镇江模拟)飞船沿半径为R的圆周绕地球运动,其周期为T.如果飞船要返回地面,可在轨道上某点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运动,椭圆和地球表面在B点相切,如图所示.如果地球半径为R0,求飞船由A点运动到B点所需要的时间.1.如图是行星m绕恒星M运行的示意图,下列说法正确的是( )A.速率最大点是B点B.速率最小点是C点C.m从A点运动到B点做减速运动D.m从A点运动到B点做加速运动考点2 天体质量和密度的计算1.万有引力与重力的关系地球对物体的万有引力F 表现为两个效果:一是重力mg ,二是提供物体随地球自转的向心力F 向,如图所示.(1)在赤道上:G Mm R2=mg 1+m ω2R.(2)在两极上:G MmR2=mg 2.(3)在一般位置:万有引力G MmR2等于重力mg 与向心力F 向的矢量和.越靠近南北两极g 值越大,由于物体随地球自转所需的向心力较小,常认为万有引力近似等于重力,即GMmR2=mg.2.星体表面上的重力加速度(1)在地球表面附近的重力加速度g(不考虑地球自转): mg =G mM R2,得g =GM R2(2)在地球上空距离地心r =R +h 处的重力加速度为g ′ mg ′=GMm (R +h )2,得g ′=GM (R +h )2所以g g′=(R +h )2R2.3.天体质量和密度的计算(1)利用天体表面的重力加速度g 和天体半径R. 由于G Mm R2=mg ,故天体质量M =gR2G ,天体密度ρ=M V =M 43πR3=3g 4πGR.(2)通过观察卫星绕天体做匀速圆周运动的周期T 和轨道半径r.①由万有引力等于向心力,即G Mm r2=m 4π2T2r ,得出中心天体质量M =4π2r3GT2;②若已知天体半径R ,则天体的平均密度ρ=M V =M 43πR3=3πr3GT2R3;③若天体的卫星在天体表面附近环绕天体运动,可认为其轨道半径r 等于天体半径R ,则天体密度ρ=3πGT2.可见,只要测出卫星环绕天体表面运动的周期T ,就可估算出中心天体的密度.【典型例题3】 一行星绕恒星做圆周运动.由天文观测可得,其运行周期为T ,速度为v ,引力常量为G ,则下列关系式错误的是( )A .恒星的质量为v3T2πGB .行星的质量为4π2v3GT2C .行星运动的轨道半径为vT 2πD .行星运动的加速度为2πvT【典型例题4】 (17年盐城模拟)近年来,人类发射了多枚火星探测器,对火星进行科学探究,为将来人类登上火星、开发和利用火星资源奠定了坚实的基础.如果火星探测器环绕火星做“近地”匀速圆周运动,并测得该探测器运动的周期为T ,则火星的平均密度ρ的表达式为(k 是一个常数)( )A .ρ=kT B .ρ=kTC .ρ=kT 2D .ρ=k GT22.(17年盐城期中)2016年9月15日“天宫二号”空间实验室由长征二号FT 2火箭发射升空.这意味着,中国成功发射了真正意义上的空间实验室,即实现了载人航天工程“三步走”战略的第二步.10月19日凌晨神舟十一号载人飞船与“天宫二号”实施自动交会对接,近似把对接后一起运行看作以速度v 绕地球的匀速圆周运动,运行轨道距地面高度为h ,地球的半径为R.求:(1)“天宫二号”绕地球运转的角速度; (2)“天宫二号”在轨道上运行的周期; (3)地球表面上的重力加速度的计算表达式.当堂检测 1.在力学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法中不正确的是( )A .伽利略首先将实验事实和逻辑推理(包括数学推演)和谐地结合起来B .笛卡儿对牛顿第一定律的建立做出了贡献C .开普勒通过研究行星观测记录,发现了行星运动三大定律D .牛顿总结出了万有引力定律并用实验测出了引力常量 2.“嫦娥一号”和“嫦娥二号”两颗月球探测卫星,它们绕月的圆形轨道距月球表面分别约为200 km 和100 km .当它们在绕月轨道上运行时,两者相比,“嫦娥二号”的( )A .周期较小B .周期相同C .向心加速度相同D .向心加速度较小 3.“宜居”行星,是指适宜人类生存的行星,美国国家航天航空局2011年2月2日宣布,开普勒太空望远镜经过一年多的探寻,共发现了54颗“宜居”行星,可能存在支持生命的条件.若有一颗“宜居”行星,其质量为地球的a 倍,半径为地球的b 倍,则该行星卫星的最大环绕速度是地球卫星最大环绕速度的( )A .ab 倍B .a b倍 C .ba倍 D .ab3倍 4.(多选)在圆轨道运动的质量为m 的人造地球卫星,它到地面的距离等于地球半径R ,已知地面上的重力加速度为g ,则( )A .卫星运动的速度为2gRB .卫星运动的周期为4π2R gC .卫星运动的加速度为g2D .卫星的动能为mRg45.(多选)若宇航员在月球表面附近自高h 处以初速度v 0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R ,万有引力常量为G.则下列说法正确的是( )A .月球表面的重力加速度g 月=2hv20L 2B .月球的质量m 月=2hR2v20GL 2C .月球的自转周期T =2πRv0D .月球的平均密度ρ=3hv202πGL 2第16讲 开普勒定律 万有引力定律知识整合 基础自测一、3.a3T2=k 4.太阳质量 地球质量 二、1.F =G m1m2r22.卡文迪许扭秤 3.M =4πR3GT2 ρ=3πGT2方法技巧·典型例题1·D 【解析】 由开普勒行星运动定律可知所有行星轨道都是椭圆,太阳位于一个焦点上,行星在椭圆轨道上运动的周期T 和半长轴a 满足a3T2=k (常量),对于同一中心天体,k 不变,故A 、B 、C 都错误,D 正确.·典型例题2·()R +R0T4RR +R02R【解析】 飞船沿椭圆轨道返回地面,由题图可知,飞船由A 点到B 点所需要的时间刚好是沿图中整个椭圆运动周期的一半,椭圆轨道的半长轴为R +R02,设飞船沿椭圆轨道运动的周期为T ′.根据开普勒第三定律有R3T2=⎝ ⎛⎭⎪⎫R +R023T2.解得T ′=T⎝ ⎛⎭⎪⎫R +R02R 3= ()R +R0T2R R +R02R.所以飞船由A 点到B 点所需要的时间为 t =T 2=()R +R0T 4R R +R02R. ·变式训练1·C 【解析】 由开普勒第二定律知,行星与恒星的连线在相等的时间内扫过的面积相等;A 点为近地点,速率最大,B 点为远地点,速率最小,A 、B 错误;m 由A 点到B 点的过程中,离恒星M 的距离越来越远,所以m 的速率越来越小,C 正确,D 错误.·典型例题3·B 【解析】 因v =2πr T ,所以r =vT2π,选项C 正确;结合万有引力定律公式G Mmr2=m v2r,可解得恒星的质量M =v3T2πG,选项A 正确;因不知行星和恒星之间的万有引力的大小,所以行星的质量无法计算,选项B 错误;行星的加速度a =v2r =2πvT,选项D 正确.·典型例题4·D 【解析】 由万有引力定律知G Mm r2=m 4π2T2r ,联立M =ρ·43πR 3和r =R ,解得ρ=3πGT2,3π为一常数,设为k ,故D 正确. ·变式训练2·(1)v R +h (2) 2π()R +h v (3)g =(R +h )v2R2【解析】 (1)v =ωr r =R +h ω=vR +h;(2)由T =2πrv 得 T =2π()R +h v; (3)在地球表面,有G Mmr2=mg在距地面高h 处,有G Mm ()R +h 2=m v2R +h化简得g =(R +h )v2R2. 当堂检测 1.D2.A 【解析】 由万有引力充当向心力知F =G Mmr2=m 4π2T2r =ma 可知:T =2πr3GM,“嫦娥二号”的距月球表面越近,周期越小,故A 正确,B 错误;a =GMT2,“嫦娥二号”的距月球表面越近,向心加速度越大,故C 、D 错误.3.B 【解析】 由v =GMr,可知B 正确. 4.BD 【解析】 根据GMm (2R )2=ma =m v22R =m ·2R 4π2T2,解得v =GM2R ,T =4π2·8R3GM ,a =GM 4R2.又GM =gR 2,所以卫星的线速度v =gR 2,周期T =4π2R g,加速度a =g 4.则卫星的动能E k =12mv 2=mgR4.故B 、D 正确,A 、C 错误.5.AB 【解析】 根据平抛运动规律,L =v 0t ,h =12g 月t 2,联立解得g 月=2hv20L2,选项A 正确;由mg 月=Gmm 月R2解得m 月=2hR2v20GL2,选项B 正确;根据题目条件无法求出月球的自转周期,选项C 错误;月球的平均密度ρ=m 月43πR3=3hv202πGL 2R,选项D 错误.。
2019届高考物理一轮复习第11讲万有引力与天体运动课件

考
星和地球相比( )
向
互
行星 半径/m 质量/kg 轨道半径/m
动
地球 6.4×106 6.0×1024 1.5×1011
探 究
火星 3.4×106 6.4×1023 2.3×1011
A.火星的公转周期较小
B.火星做圆周运动的加速度较小
C.火星表面的重力加速度较大
D.火星的第一宇宙速度较大
返回目录
第11讲 万有引力与天体运动
(2)两物体间的距离趋近于零时,万有引力趋近于 无穷大.( )
(×)两物体间的距离趋近于零时,万有引力定律 不再适用.
返回目录
第11讲 万有引力与天体运动
教
易错判断
材
知
(3)行星在椭圆轨道上运行速率是变化的,离太阳
识 梳
越远,运行速率越小.( )
理
(√)
(4)近地卫星距离地球最近,环绕速度最小.( ) (×)近地卫星距离地球最近,环绕速度最大.过的面积等于木星与
究 太阳连线扫过的面积
返回目录
第11讲 万有引力与天体运动
C [解析] 本题考查了开普勒的三个行星运动定律.题目
中要求根据开普勒行星运动定律来判断,那么不能按照中学阶
段的近似处理来判断.太阳应位于行星运行轨道的一个焦点上,
考
而焦点不是圆心,A 错误.火星和木星绕太阳运行时是不在同
2.动力学分析:(1)万有引力提供_向__心__力___,即 F
向=GMr2m=ma=mvr2=mω2r=m2Tπ 2r.(2)在星球表面 附近的物体所受的万有引力近似等于__物__体__的__重__力____,
即 GMr2m=mg(g 为星球表面的重力加速度).
返回目录
[配套K12]2019年高考物理大一轮复习 第04章 曲线运动 万有引力定律 第4讲 万有引力与航天学案 新人教版
![[配套K12]2019年高考物理大一轮复习 第04章 曲线运动 万有引力定律 第4讲 万有引力与航天学案 新人教版](https://img.taocdn.com/s3/m/862e525d1ed9ad51f01df251.png)
第四讲 万有引力与航天1.开普勒第一定律:所有的行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上.2.开普勒第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积.3.开普勒第三定律:所有行星的轨道的半长轴的三次方跟周期的二次方的比值都相等,表达式:a 3T2=k .1.公式:F =Gm 1m 2R2,其中G =6.67×10-11 N·m 2/kg 2,叫引力常量. 2.适用条件:只适用于质点间的相互作用. 3.理解(1)两质量分布均匀的球体间的相互作用,也可用本定律来计算,其中r 为两球心间的距离.(2)一个质量分布均匀的球体和球外一个质点间的万有引力的计算也适用,其中r 为质点到球心间的距离.4.地球表面随地球自转的物体,其重力等于万有引力吗?如图所示,设地球的质量为M ,半径为R ,A 处物体的质量为m ,则物体受到地球的吸引力为F ,方向指向地心O ,由万有引力公式得F =G Mm R2.引力F 可分解为F 1、F 2两个分力,其中F 1为物体随地球自转做圆周运动的向心力F n ,F 2就是物体的重力mg .①赤道上,重力和向心力在一条直线上,写出万有引力与向心力和重力的关系式G Mm r2=m ω2r +mg .②地球的两极处:向心力为零,万有引力与重力的关系G Mmr2=mg .③其他位置:重力是万有引力的一个分力,重力的大小mg <G Mm R2,重力的方向偏离地心.(1)(2)若测出太阳的一个行星的周期T 和轨道半径r ,怎样计算太阳的质量?求解天体质量的基本思路是什么?要想估算太阳的密度还需知道什么物理量?(3)月球围绕地球做匀速圆周运动,能否求出月球的质量?怎样才能求出月球的质量?提示:(1)忽略地球自转的影响mg =G Mm R 2,M =gR 2G又ρ=M V ,V =43πR 3,得ρ=3g 4πRG.(2)根据万有引力充当向心力G Mm r 2=m ⎝ ⎛⎭⎪⎫2πT 2·r 得M =4π2r3GT 2.要想估算太阳的密度还需知道太阳的球半径.(3)不能.需知道月球的卫星的周期和轨道半径.1.三个宇宙速度速度g =9. 8 m/s 2.试用两种方法推导地球的第一宇宙速度?提示:方法一:由G Mm R 2=m v 21R 得v 1=GMR= 6.67×10-11×5.98×10246.4×106m/s =7.9×103m/s . 方法二:由mg =m v 21R得v 1=gR =9.8×6.4×106 m/s =7.9×103m/s .第一宇宙速度是发射人造卫星的最小速度,也是人造卫星的最大环绕速度,此时它的运行周期最短,T min =2πRg=5 075 s≈85 min.3.人造卫星(1)同步卫星是指相对地球表面静止的卫星,其绕地球运转的角速度与地球自转的角速度相同.试列式说明地球同步卫星离地面的高度一定,速率一定?提示:GMmR +h2=m ω2(R +h )得h =3Gmω2-R ,又v =ω(R +h )=GM R +h. (2)近地卫星、同步卫星和地球赤道上随地球自转的物体的三种圆周运动的比较.如图所示,a 为近地卫星,半径为r 1;b 为同步卫星,半径为r 2;c 为赤道上随地球自转的物体,半径为r 3.①试说明三种圆周运动的向心力来源?②如何比较a 和b 、b 和c 的角速度、线速度和向心加速度的大小关系?根据是什么? 提示:①a 、b 的向心力来源于地球的万有引力,c 的向心力是万有引力的一个分力.②对a 、b :万有引力充当向心力,则有G Mm r 2=m ω2r =m v 2r =ma ,可得ω1>ω2,v 1>v 2,a 1>a 2.对b 、c :因ω2=ω3根据v =ωr ,a =ωr 可得v 2>v 3,a 2>a 3. 综上所示:ω1>ω2=ω3,v 1>v 2>v 3,a 1>a 2>a 3.1.判断正误(1)地面上的物体所受地球引力的大小均由F =G m 1m 2r 2决定,其方向总是指向地心.( ) (2)只有天体之间才存在万有引力.( )(3)只要已知两个物体的质量和两个物体之间的距离,就可以由F =G Mm R2计算物体间的万有引力.( )(4)发射速度大于7.9 km/s ,小于11.2 km/s 时,人造卫星围绕地球做椭圆轨道运动.( )答案:(1)√ (2)× (3)× (4)√2.(2016·全国卷Ⅲ)关于行星运动的规律,下列说法符合史实的是( ) A .开普勒在牛顿定律的基础上,导出了行星运动的规律B .开普勒在天文观测数据的基础上,总结出了行星运动的规律C .开普勒总结出了行星运动的规律,找出了行星按照这些规律运动的原因D .开普勒总结出了行星运动的规律,发现了万有引力定律 答案:B3.(根据人教必修2相关内容改编)牛顿提出太阳和行星间的引力F =Gm 1m 2r 2后, 为证明地球表面的重力和地球对月球的引力是同一种力,也遵循这个规律,他进行了“月—地检验”.已知月球的轨道半径约为地球半径的60倍,“月—地检验”是计算月球公转的( )A .周期是地球自转周期的1602倍B .向心加速度是自由落体加速度的1602倍C .线速度是地球自转地表线速度的602倍 D .角速度是地球自转地表角速度的602倍解析:选B 已知月球绕地球运行轨道半径是地球半径的60倍,月球轨道上一个物体受到的引力与它在地面附近时受到的引力之比为1602,牛顿时代已经较精确的测量了地球表面的重力加速度g 、地月之间的距离和月球绕地球运行的公转周期,根据圆周运动的公式得月球绕地球运行的加速度a =4π2T 2r ,如果a g =1602,说明拉住月球使它围绕地球运动的力与地球上物体受到的引力是同一种力,故选项B 正确.4.静止在地面上的物体随地球自转做匀速圆周运动.下列说法正确的是( ) A .物体受到的万有引力和支持力的合力总是指向地心 B .物体做匀速圆周运动的周期与地球自转周期相等 C .物体做匀速圆周运动的加速度等于重力加速度 D .物体对地面压力的方向与万有引力的方向总是相同 答案:B5.(人教版必修2P 48第3题)金星的半径是地球的0.95倍,质量为地球的0.82倍,金星表面的自由落体加速度是多大?金星的第一宇宙速度是多大?答案:8.9 m/s 27.3 km/s1.2.开普勒第三定律a 3T2=k 中,k 值只与中心天体的质量有关,不同的中心天体k 值不同.1.(2018·浙江温州十校联考)2016年8月16日凌晨,被命名为“墨子号”的中国首颗量子科学实验卫星开启星际之旅,其运行轨道为如图所示的绕地球E 运动的椭圆轨道,地球E 位于椭圆的一个焦点上.轨道上标记了卫星经过相等时间间隔(Δt =T14,T 为运转周期)的位置.如果作用在卫星上的力只有地球E 对卫星的万有引力,则下列说法正确的是( )A .面积S 1>S 2B .卫星在轨道A 点的速度小于B 点的速度C .T 2=Ca 3,其中C 为常数,a 为椭圆半长轴 D .T 2=C ′b 3,其中C ′为常数,b 为椭圆半短轴解析:选C 根据开普勒第二定律可知,卫星与地球的连线在相等的时间内扫过的面积相等,故面积S 1=S 2,选项A 错误;根据开普勒第二定律可知,卫星在轨道A 点的速度大于在B 点的速度,选项B 错误;根据开普勒第三定律可知a 3T2=k ,其中k 为常数,a 为椭圆半长轴,选项C 正确,选项D 错误.2.(2017·课标Ⅱ)(多选)如图,海王星绕太阳沿椭圆轨道运动,P 为近日点,Q 为远日点,M 、N 为轨道短轴的两个端点,运行的周期为T 0.若只考虑海王星和太阳之间的相互作用,则海王星在从P 经M 、Q 到N 的运动过程中( )A .从P 到M 所用的时间等于T 0/4B .从Q 到N 阶段,机械能逐渐变大C .从P 到Q 阶段,速率逐渐变小D .从M 到N 阶段,万有引力对它先做负功后做正功解析:选CD 海王星绕太阳沿椭圆轨道运动,由开普勒第二定律可知,从P →Q 速度逐渐减小,故从P 到M 所用时间小于T 0/4,选项A 错误,C 正确;从Q 到N 阶段,只受太阳的引力,故机械能守恒,选项B 错误;从M 到N 阶段经过Q 点时速度最小,故万有引力对它先做负功后做正功,选项D 正确.1.地面上的物体所受地球的吸引力产生两个效果,其中一个分力提供了物体绕地轴做圆周运动的向心力,另一个分力等于重力.(1)在两极,向心力等于零,重力等于万有引力; (2)除两极外,物体的重力都比万有引力小;(3)在赤道处,物体的万有引力分解为两个分力F 向和mg 刚好在一条直线上,则有F =F向+mg ,所以mg =F -F 向=GMm R2-mR ω2自. 2.地球表面附近(脱离地面)的重力与万有引力物体在地球表面附近(脱离地面)时,物体所受的重力等于地球表面处的万有引力,即mg =GMmR2,R 为地球半径,g 为地球表面附近的重力加速度,此处也有GM =gR 2.3.距地面一定高度处的重力与万有引力 物体在距地面一定高度h 处时,mg ′=GMmR +h2,R 为地球半径,g ′为该高度处的重力加速度.(2018·河北重点中学联考)假设地球是一半径为R 、质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体的引力为零,不考虑地球自转的影响,则距离地球球心为r 处的重力加速度大小g 与r 的关系图象可能为( )解析:选A 当距地心距离r >R 时,根据GMm r 2=mg 得,g =GM r2,即g 与r 2成反比;当距地心距离r <R 时,地球对物体的万有引力等效为半径为r 的球和球壳对物体万有引力的合力,球壳对物体的引力为零,则物体受到的万有引力为GM 1m r 2=mg ,M 1=r 3M R 3,解得g =GMrR 3,即g 与r 成正比,故A 选项正确.(2015·海南单科)若在某行星和地球上相对于各自的水平地面附近相同的高度处、以相同的速率平抛一物体,它们在水平方向运动的距离之比为2∶7.已知该行星质量约为地球的7倍,地球的半径为R .由此可知,该行星的半径约为( )A .12R B .72R C .2RD .72R 解析:选C 在行星和地球上相对于各自的水平地面附近相同的高度处、以相同的速率平抛一物体,它们经历的时间之比即为在水平方向运动的距离之比,所以t 1t 2=27.竖直方向上做自由落体运动,重力加速度分别为g 1和g 2,因此g 1g 2=2h /t 212h /t 22=t 22t 21=74.设行星和地球的质量分别为7M 和M ,行星的半径为r ,由牛顿第二定律得G 7Mmr2=mg 1①G MmR2=mg 2② ①/②得r =2R因此选项A 、B 、D 错误,C 正确.3.(2018·山东潍坊模拟)如图所示,O 为地球球心,A 为地球表面上的点,B 为O 、A 连线间的点,AB =d ,将地球视为质量分布均匀的球体,半径为R .现挖掉以B 为圆心、以d2为半径的球.若忽略地球自转,则挖出球体后A 点的重力加速度与挖去球体前的重力加速度之比为( )A .4R -d4RB .8R -d 8RC .2R -d 2RD .R -dR解析:选B 地球对A 处质点的万有引力等于挖去的球体与剩余部分对A 处质点的万有引力之和.设地球质量为M ,剩余部分对A 处质点的万有引力为F ,挖去球体的质量M 1=(d 2)3MR3,有GMm R 2=F +GM 1m d 2,解得F :(GMm /R 2)=8R -d 8R,B 选项正确. 4.(2018·江西八校联考)据报道,科学家们在距离地球20万光年外发现了首颗系外“宜居”行星.假设该行星质量约为地球质量的6.4倍,半径约为地球半径的2倍.那么,一个在地球表面能举起64 kg 物体的人在这个行星表面能举起的物体的质量约为( )A .40 kgB .50 kgC .60 kgD .30 kg解析:选 A 根据地球表面物体的重力等于物体与地球的万有引力得,GMmR 2=mg ,则地球表面的重力加速度g =GM R 2,同理可得,行星表面的重力加速度g ′=G ·6.4MR 2=1.6g ,由力的平衡可知,人的举力F =mg =m ′g ′,则m ′=m1.6=40 kg ,A 正确.1.质量的估算(1)求得天体质量,即可由ρ=M V 、V =43πR 3求得密度;(2)当r =R 时,ρ=3πr 3GT 2R 3=3πGT2,只需测出近地卫星的运行周期即可求得.(2014·新课标全国卷Ⅱ)假设地球可视为质量均匀分布的球体.已知地球表面重力加速度在两极的大小为g 0,在赤道的大小为g ;地球自转的周期为T ,引力常量为G .地球的密度为( )A .3πGT 2·g 0-g g 0B .3πGT 2·g 0g 0-gC .3πGT2D .3πGT 2·g 0g解析:选B 设地球半径为R .质量为m 的物体在两极时有mg 0=G Mm R 2,在赤道时有G Mm R2-mg =mR ⎝⎛⎭⎪⎫2πT 2,又地球的密度ρ=M 43πR3.联立以上三式得ρ=3g 0πG g 0-g T 2,选项B 正确.本题是通过对天体表面上“两极”与“赤道”上的受力分析,联系向心力的来源,能写出“赤道”上万有引力与重力的关系式是解题的关键.(2018·湖北黄冈中学模拟)假定太阳系一颗质量均匀、可看成球体的小行星开始时不自转,若该星球某时刻开始自转,角速度为ω时,该星球表面的“赤道”上物体对星球的压力减为原来的23.已知引力常量为G ,则该星球密度ρ为( )A .9ω28πG B .3ω22πG C .9ω24πGD .ω23πG解析:选C 星球不自转时有G Mm R 2=mg ,自转角速度为ω时有G Mm R 2=23mg +m ω2R ,星球的密度ρ=M43πR 3,解得ρ=9ω24πG ,故选C .5.(2016·海南卷)(多选)通过观测冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量.这两个物理量可以是( )A .卫星的速度和角速度B .卫星的质量和轨道半径C .卫星的质量和角速度D .卫星的运行周期和轨道半径解析:选AD 根据线速度和角速度可以求出半径r =vω,根据万有引力提供向心力则有GMm r 2=m v 2r ,整理可得M =v 3G ω,故选项A 正确;由于卫星的质量m 可约掉,故选项B 、C 错误;若知道卫星的运行周期和轨道半径,则GMm r 2=m ⎝ ⎛⎭⎪⎫2πT 2r ,整理得M =4π2r3GT 2,故选项D 正确.6.对于环绕地球做圆周运动的卫星来说,它们绕地球做圆周运动的周期会随着轨道半径的变化而变化,某同学根据测得的不同卫星做圆周运动的半径r 与周期T 关系作出如图所示图象,则可求得地球质量为(已知引力常量为G )( )A .4π2a GbB .4π2bGaC .Ga4π2bD .Gb4π2a解析:选A 由G Mm r 2=mr ⎝ ⎛⎭⎪⎫2πT 2,得r 3=GMT 24π2,即r 3T 2=GM 4π2=a b ,求得地球的质量为M =4π2a Gb ,因此A 项正确.1.规律⎩⎪⎪⎨⎪⎪⎧G Mm r 2=r =R 地+h ⎩⎪⎪⎨⎪⎪⎧⎭⎪⎪⎬⎪⎪⎫m v 2r→v =GM r →v ∝1rm ω2r →ω=GM r 3→ω∝1r 3m 4π2T 2r →T =4π2r 3GM→T ∝r 3ma →a =GM r 2→a ∝1r2越高越慢mg =GMmR 2地近地时GM =gR2地2.极地卫星和近地卫星(1)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖. (2)近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s .(3)两种卫星的轨道平面一定通过地球的球心.(2017·江苏单科)(多选)“天舟一号”货运飞船于2017年4月20日在文昌航天发射中心成功发射升空.与“天宫二号”空间实验室对接前,“天舟一号”在距地面约380 km 的圆轨道上飞行,则其( )A .角速度小于地球自转角速度B .线速度小于第一宇宙速度C .周期小于地球自转周期D .向心加速度小于地面的重力加速度解析:选BCD C 对:由GMmR +h2=m (R +h )4π2T 2知,周期T 与轨道半径的关系为R +h3T2=k (恒量),同步卫星的周期与地球的自转周期相同,但同步卫星的轨道半径大于“天舟一号”的轨道半径,则“天舟一号”的周期小于同步卫星的周期,也就小于地球的自转周期.A 错:由ω=2πT知,“天舟一号”的角速度大于地球自转的角速度.B 对:由GMmR +h2=mv 2R +h知,线速度v =GMR +h ,而第一宇宙速度v ′= GMR ,则v <v ′. D 对:设“天舟一号”的向心加速度为a ,则ma =GMm R +h2,而mg =GMmR 2,可知a <g .利用万有引力定律解决卫星运动的技巧1.一个模型天体(包括卫星)的运动可简化为质点的匀速圆周运动模型. 2.两组公式G Mm r 2=m v 2r =m ω2r =m 4π2T2r =ma mg =GMmR2(g 为天体表面处的重力加速度)3.a 、v 、ω、T 均与卫星的质量无关,只由轨道半径和中心天体质量共同决定,所有参量的比较,最终归结到半径的比较.(2018·江西南昌二中月考)2016年2月1日,我国在西昌卫星发射中心成功发射了第五颗新一代北斗导航卫星.该卫星为地球圆轨道卫星,质量为m ,轨道离地面的高度约为地球半径R 的3倍.已知地球表面的重力加速度为g ,忽略地球自转的影响.则( )A .卫星的绕行速率大于7.9 km/sB .卫星的绕行周期约为8π2R gC .卫星所在处的重力加速度大小约为g4D .卫星的动能大小约为mgR8解析:选D 在地球表面附近飞行的卫星的绕行速度等于第一宇宙速度7.9 km/s ,对于卫星,根据万有引力提供向心力有GMm r 2=m v 2r,得v =GMr,半径越大,绕行速度越小,A 错误;地球表面万有引力近似等于重力,GMm R 2=mg ,重力加速度g =GMR2,卫星轨道离地面的高度约为地球半径R 的3倍,设绕行周期为T ,由GMm R 2=m 4π2T2·4R 得T =4π2R 3GM=16 πR 3GM ,B 错误;根据GMm R 2=mg ′,卫星所在处的重力加速度大小g ′=GM 16R 2=g16,C 错误;卫星的线速度v =GM 4R ,卫星的动能E k =12mv 2=mgR8,D 正确.7.(2018·四川资阳一诊)(多选)用m 表示地球的通信卫星(同步卫星)的质量,h 表示离地面的高度,用R 表示地球的半径,g 表示地球表面的重力加速度,ω表示地球自转的角速度,则通信卫星所受的地球对它的万有引力的大小为( )A .GMmR +h2B .mgR 2R +h2C .m ω2(R +h )D .m 3R 2g ω4解析:选BCD 地球同步卫星的角速度与地球自转的角速度ω相同,轨道半径为r =R +h ,则根据向心力公式得地球对卫星的引力大小为F =m ω2(R +h ).该卫星所受地球的万有引力为F =GMm R +h2,在地球表面有mg =GMm R 2,得到GM =gR 2,联立得F =mgR 2R +h 2.由F =m ω2(R +h )=mgR 2R +h2,解得R +h =3gR 2ω2,所以可得F =m ω2(R +h )=m ω23gR 2ω2=m 3gR 2ω4,由于地球的质量M 未知,故B 、C 、D 正确,A 错误.8.(2018·山东省实验中学一诊)地球赤道上的物体随地球自转的向心加速度为a 1,地球的同步卫星绕地球做匀速圆周运动的轨道半径为r ,向心加速度为a 2.已知引力常量为G ,地球半径为R .下列说法正确的是( )A .地球质量M =a 1R 2GB .地球质量M =a 2r 2GC .a 1、a 2的关系是a 1>a 2D .加速度之比a 1a 2=r 2R2解析:选B 根据G Mm r 2=ma 2得,地球的质量M =a 2r 2G ,在赤道上有G MmR2=mg +ma 1,故A错误,B 正确;地球赤道上的物体与同步卫星的角速度相等,根据a =rw 2知,a 1a 2=Rr,a 1<a 2,故C 、D 错误.。
2019届高三第一轮复习 第四章 第4节

体做圆周运动的向心力F向不断变化,因而
表面物体的重力随纬度的变化而变化,即
重力加速度g随纬度变化而变化,从赤道到
两极逐渐增大. (2)在地球表面附近:重力等于万有引力
g0地球表面附近的重力加速度 (3)在离地球表面h高处:重力等于万有引力
gh是离地球表面h高处的重力加速度 (4)在任一星球表面附近:
【例6】一宇航员在某一行星的极地着陆时 (行星可视为球体),发现自己在当地的重力是 在地球上重力的0.01倍,进一步研究还发现, 该行星一昼夜的时间与地球相同,而且物体 在该行星赤道上处于完全失重状态,试计算 这一行星的半径R.(结果保留两位有效数字, 地球表面重力加速度取g0=10m/s2,π2=10)
【例4】一宇宙飞船在离地面h的轨道上做 匀速圆周运动,质量为m的物块用弹簧秤 挂起,相对于飞船静止,则此物块所受的 合外力的大小为多大?(已知地球半径为 R,地面的重力加速度为g)
F合
R2 (R h)2
mg
【例5】某星球可视为球体,其自转周期
为T,在它的赤道上比在它的两极处,用
弹簧秤测得同一物体重量少10%,则该星 球的平均密度是多少? (已知万有引力常 量为G)
俗称“黄金代换式”
4.天体的运动
(1)运动模型:天体运动可看成是 匀速
圆周运动 ——其引力全部提供 向心力 .
G
Mm r2
=m
v2 r
=m 2 r=m
4 2
T2
r
(2)中心天体质量、密度的估算
天体的密度:=
M V
=
4
M
R3
=
3M
4 R3
3
【例2】2018年2月2日,我国成功将电磁
新课改瘦专用高考物理一轮复习第四章第5节开普勒行星运动定律和万有引力定律学案含解析

新课改瘦专用高考物理一轮复习第四章第5节开普勒行星运动定律和万有引力定律学案含解析一、开普勒行星运动定律1.第一定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2.第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积。
[注1]3.第三定律:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
二、万有引力定律[注2]1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比,与它们之间距离r 的二次方成反比。
2.表达式:F =Gm 1m 2r2,G 为引力常量,其值为G =6.67×10-11 N·m 2/kg 2。
3.适用条件(1)公式适用于质点间的相互作用。
当两个物体间的距离远远大于物体本身的大小时,物体可视为质点。
(2)质量分布均匀的球体可视为质点,r 是两球球心间的距离。
三、经典时空观和相对论时空观1.经典时空观[注3]空间、时间是独立于物体及其运动而存在的。
2.相对论时空观物体占有的空间以及物理过程、化学过程,甚至还有生命过程的持续时间,都与它们的运动状态有关。
[注解释疑][注1] 面积定律是对同一个行星而言的,不同的行星相等时间内扫过的面积不等。
由面积定律可知,行星在近日点的速度比它在远日点的速度大。
[注2] 万有引力定律的“三性”(1)普遍性:任何有质量的物体间都存在万有引力。
(2)相互性:两物体间的万有引力是一对作用力与反作用力。
(3)宏观性:只有质量巨大的天体间或天体与其附近物体间的万有引力才有实际的物理意义。
[注3] 经典力学——牛顿运动定律的适用范畴。
[深化理解]1.开普勒行星运动定律既适用于行星绕太阳运动,也适用于卫星绕地球运动。
2.不考虑地球自转时,地球表面上的重力加速度g =GM R 2。
3.地球赤道上的物体随地球自转的向心力由万有引力与支持力的合力提供,而地球表面附近做匀速圆周运动的卫星由万有引力提供向心力。
2019届高三物理第一轮复习第四章第五节《万有引力与航天1》教师版-word文档
第四章 直线运动第五节 万有引力与航天(一) 学案(1#)班别 姓名 学号一、学习目标1.能够解决水平面内和竖直面内圆周运动的临界问题.2.能够应用牛顿运动定律解决生活中的圆周运动问题.3.了解物体做离心运动的条件. 二、知识梳理考点一 万有引力定律的理解与应用(一)开普勒定律1.开普勒第一定律(轨道定律):所有的行星围绕太阳运行的轨道都是椭圆,太阳处在所有椭圆的一个 焦点上.2.开普勒第二定律(面积定律):对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的 面积.3.开普勒第三定律(周期定律):所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等,即 a 3T2=k(二)万有引力定律 内容自然界中任何两个物体都相互吸引,引力的方向在它们的 连线 上,引力的大小与物体的质量m 1和m 2的 乘积 成正比,与它们之间距离r 的 平方 成反比公式F =G m 1m 2r2 ,引力常量G =6.67×10-11N·m 2/kg 2,英国物理学家 卡文迪许 于1798并利用扭秤测出了G 值 适用条件(1)两质点间的作用(2)可视为质点的物体间的作用 (3)质量分布均匀的球体间的作用(三)万有引力与重力的关系地球对物体的万有引力F 表现为两个效果:一是重力mg,二是提供物体随地球自转的向心力F 向,如图所示.(1)在赤道上: G 2MmR =mg 1+ . (2)在两极上:G2MmR =mg 2. (3)在一般位置:万有引力G2MmR 等于重力mg 与向心力F 向的矢量和. 越靠近南北两极g 值越 ,由于物体随地球自转所需的向心力较大,常认为万有引力近似等于重力,即2GMmR = . (四)地球或其他天体表面及某一高度处的重力加速度的计算 设天体表面重力加速度为g,天体半径为R,忽略天体自转,则有mg=G2Mm R,得g=2GMR 或GM=gR 2;若物体距天体表面的高度为h,则重力mg′=G2()Mm R h +,得g′=2()GM R h +=22()R R h +g. 【典例1】(2019·课标卷Ⅱ,19)(多选)如图,海王星绕太阳沿椭圆轨道运动,P 为近日点,Q 为远日点,M 、N 为轨道短轴的两个端点,运行的周期为T 0.若只考虑海王星和太阳之间的相互作用,则海王星在从P 经M 、Q 到N 的运动过程中( )A .从P 到M 所用的时间等于T 04B .从Q 到N 阶段,机械能逐渐变大C .从P 到Q 阶段,速率逐渐变小D .从M 到N 阶段,万有引力对它先做负功后做正功【解析】 A 错:由开普勒第二定律可知,相等时间内,太阳与海王星连线扫过的面积都相等,由P到M 扫过面积小于S4.B 错:由机械能守恒定律知,从Q 到N 阶段,机械能守恒.C 对:从P 到Q 阶段,万有引力做负功,动能减小,速率逐渐变小.D 对:从M 到N 阶段,万有引力与速度的夹角先是钝角后是锐角,即万有引力对它先做负功后做正功. 【答案】 CD【即时训练1】(2019·课标卷Ⅰ,17)利用三颗位置适当的地球同步卫星,可使地球赤道上任意两点之间保持无线电通讯.目前,地球同步卫星的轨道半径约为地球半径的6.6倍.假设地球的自转周期变小,若仍仅用三颗同步卫星来实现上述目的,则地球自转周期的最小值约为( )A .1 hB .4 h C.8 h D .16 h【解析】 设地球的半径为R ,周期T =24 h ,当地球的自转周期变小时,三颗同步卫星A 、B 、C 的位置如图所示,所以此时同步卫星的半径r =2R ,由开普勒第三定律得:r 3T2=k ,可得T 1=T2R 36.6R3≈4 h ,故A 、C 、D 错误,B 正确.【答案】 B 【典例2】(2019·浙江卷,18)(多选)如图所示,三颗质量均为m 的地球同步卫星等间隔分布在半径为r 的圆轨道上,设地球质量为M,半径为R.下列说法正确的是( )A.地球对一颗卫星的引力大小为2()GMmr R - B.一颗卫星对地球的引力大小为2GMmr C.两颗卫星之间的引力大小为223Gm rD.三颗卫星对地球引力的合力大小为23GMmr 【即时训练2】 静止在地面上的物体随地球自转做匀速圆周运动.下列说法正确的是( ) A.物体受到的万有引力和支持力的合力总是指向地心 B.物体做匀速圆周运动的周期与地球自转周期相等 C.物体做匀速圆周运动的加速度等于重力加速度 D.物体对地面压力的方向与万有引力的方向总是相同【即时训练3】如图所示,有一个质量为M ,半径为R ,密度均匀的大球体.从中挖去一个半径为R2的小球体,并在空腔中心放置一质量为m 的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)( )A .G Mm R 2B .0C.4G Mm R 2D .G Mm 2R2【解析】 若将挖去的小球体用原材料补回,可知剩余部分对m 的吸引力等于完整大球体对m 的吸引力与挖去小球体对m 的吸引力之差,挖去的小球体球心与m 重合,对m 的万有引力为零,则剩余部分对m的万有引力等于完整大球体对m 的万有引力;以大球体球心为中心分离出半径为R 2的球,易知其质量为18M ,则剩余均匀球壳对m 的万有引力为零,故剩余部分对m 的万有引力等于分离出的球对其的万有引力,根据万有引力定律,F =G 18Mm ⎝⎛⎭⎫R 22=G Mm2R 2,故D 正确.【答案】 D【即时训练4】理论上已经证明:质量分布均匀的球壳对壳内物体的万有引力为零.现假设地球是一半径为R 、质量分布均匀的实心球体,O 为球心,以O 为原点建立坐标轴Ox,如图所示.一个质量一定的小物体(假设它能够在地球内部移动)在x 轴上各位置受到的引力大小用F 表示,则选项图所示的四个F 随x 的变化关系图像正确的是( )【即时训练5】 (2019·海南卷,5)已知地球质量为月球质量的81倍,地球半径约为月球半径的4倍.若在月球和地球表面同样高度处,以相同的初速度水平抛出物体,抛出点与落地点间的水平距离分别为s 月和s 地,则s 月∶s 地约为( )A.9∶4B.6∶1 C .3∶2 D.1∶1 考点二 宇宙速度 1.三种宇宙速度(1)由G 2MmR =m 2v R 得v= =7.9 km/s.(2)由mg=m 2v R得【典例3】 某人在一星球上以速率v 竖直上抛一物体,经时间t 物体以速率v 落回手中,已知该星球的半径为R,求该星球上的第一宇宙速度.【即时训练6】 (多选)下列关于三种宇宙速度的说法正确的是( )A.第一宇宙速度v 1=7.9 km/s,第二宇宙速度v 2=11.2 km/s,则人造卫星绕地球在圆轨道上运行时的速度大于等于v 1,小于v 2B.美国发射的“凤凰”号火星探测卫星,其发射速度大于第三宇宙速度C.第二宇宙速度是使物体可以挣脱地球引力束缚,成为绕太阳运行的小行星的最小发射速度D.第一宇宙速度7.9 km/s 是人造地球卫星绕地球做圆周运动的最大运行速度【即时训练7】 “伽利略”木星探测器,从1989年10月进入太空起,历经6年,行程37亿千米,终于到达木星周围.此后在t 秒内绕木星运行N 圈后,对木星及其卫星进行考察,最后坠入木星大气层烧毁.设这N 圈都是绕木星在同一个圆周上运行,其运行速率为v,探测器上的照相机正对木星拍摄整个木星时的视角为θ(如图所示),设木星为一球体.求:(1)木星探测器在上述圆形轨道上运行时的轨道半径; (2)木星的第一宇宙速度.考点三 中心天体的质量和密度的估算1.天体质量和密度的估算(1)“自力更生法”(g -R ):利用天体表面的重力加速度g 和天体的半径R由G Mm R 2=mg ,得M =R 2g G ,ρ=M V =M 43πR 3=3g 4πRG.(2)“借助外援法”(T -r ):利用天体的卫星,已知卫星的周期T (或线速度v )和卫星的轨道半径r 建立G Mm r 2=m v 2r =mr 4π2T 2,则M =⎩⎨⎧4π2r 3GT 2v 2rG测天体的密度:将天体的质量M 代入ρ=M43πR 3得:ρ=⎩⎨⎧3πr 3GR 3T 2 ――→表面卫星ρ= 3πGT 23v 2r4G πR 32.星体表面及其某一高度处的重力加速度的求法(1)设天体表面的重力加速度为g ,天体半径为R ,则mg =G Mm R 2,即g =GMR2(或GM =gR 2)(2)若物体距星体表面高度为h ,则重力mg ′=G Mm R +h 2,即g ′=GM R +h 2=R 2R +h 2g .【典例4】 (多选)假设航天员准备登陆木星,为了更准确了解木星的一些信息,到木星之前做一些科学实验,当到达与木星表面相对静止时,航天员对木星表面发射一束激光,经过时间t,收到激光传回的信号,测得相邻两次看到日出的时间间隔是T,测得航天员所在航天器的速度为v,已知引力常量G,激光的速度为c,则( )A.木星的质量M=32πv TGB.木星的质量M=2332π2c t GTC.木星的质量M=23324πc t GTD.根据题目所给条件,可以求出木星的密度【即时训练7】 (2019·海南卷,7)(多选)通过观察冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量,这两个物理量可以是( ) A.卫星的速度和角速度 B.卫星的质量和轨道半径 C.卫星的质量和角速度D.卫星的运行周期和轨道半径 【即时训练9】(2019·北京卷,17)利用引力常量G 和下列某一组数据,不能..计算出地球质量的是( ) A .地球的半径及重力加速度(不考虑地球自转)B .人造卫星在地面附近绕地球做圆周运动的速度及周期C .月球绕地球做圆周运动的周期及月球与地球间的距离D .地球绕太阳做圆周运动的周期及地球与太阳间的距离【解析】 A 能:根据G MmR2=mg 可知,已知地球的半径及重力加速度可计算出地球的质量.B 能:根据G Mm R 2=mv 2R 及v =2πRT可知,已知人造卫星在地面附近绕地球做圆周运动的速度及周期可计算出地球的质量.C 能:根据G Mm r 2=m 4π2T2r 可知,已知月球绕地球做圆周运动的周期及月球与地球间的距离,可计算出地球的质量.D 不能:已知地球绕太阳做圆周运动的周期及地球与太阳间的距离只能求出太阳的质量,不能求出地球的质量.【答案】 D 三、巩固训练1.(多选)已知甲、乙两行星的半径之比为2∶1,环绕甲、乙两行星表面运行的两卫星周期之比为4∶1,则下列结论中正确的是( )A .甲、乙两行星表面卫星的动能之比为1∶4B .甲、乙两行星表面卫星的角速度之比为1∶4C .甲、乙两行星的质量之比为1∶2D .甲、乙两行星的第一宇宙速度之比为2∶1【解析】 由GMm r 2=mrω2=mv 2r得ω=GMr 3,v = GM r ,E k =12mv 2, T =2πω=2π r 3GM,代入数据得M 甲∶M 乙=1∶2,ω甲∶ω乙=1∶4,v 甲∶v 乙=1∶2,卫星质量关系不知,不能比较动能大小.【答案】 BC 2.(多选)2019年10月19日3时31分,神舟十一号载人飞船与天宫二号空间实验室成功实现自动交会对接,此时天宫二号绕地飞行一圈时间为92.5 min ,而地球同步卫星绕地球一圈时间为24 h ,根据此两组数据我们能求出的是( )A .天宫二号与地球同步卫星受到的地球引力之比B .天宫二号与地球同步卫星的离地高度之比C .天宫二号与地球同步卫星的线速度之比D .天宫二号与地球同步卫星的加速度之比【解析】 由F =GMm r 2及GMm r 2=mrω2=m v 2r =ma 可知,ω=GM r 3,T =2π r 3GM ,a =GM r 2,v =GM r,已知周期关系可确定半径关系,进而确定线速度关系,加速度关系,但由于不知天宫二号和同步卫星的质量关系,故所受地球引力关系不确定,地球半径未知,所以离地高度关系不确定,C 、D 正确.【答案】 CD3.(多选)已知地球的半径为6.4×106 m ,地球自转的角速度为7.27×10-5rad/s ,地球表面的重力加速度为9.8 m/s 2,在地球表面发射卫星的第一宇宙速度为7.9×103 m/s ,第三宇宙速度为16.7×103 m/s ,月地中心间距离为3.84×108 m .假设地球上有一颗苹果树长到月球那么高,则当苹果脱离苹果树后,请根据此时苹果线速度的计算,判断苹果将不会( )A .落回地面B .成为地球的“苹果月亮”C .成为地球的同步“苹果卫星”D .飞向茫茫宇宙【解析】 地球自转的角速度为7.27×10-5rad/s ,月球到地球中心的距离为3.84×108 m ,地球上有一棵苹果树长到了接近月球那么高,根据v =rω得:苹果的线速度为v =2.8×104 m/s ,第三宇宙速度为16.7×103 m/s ,由于苹果的线速度大于第三宇宙速度,所以苹果脱离苹果树后,将脱离太阳系的束缚,飞向茫茫宇宙,故A 、B 、C 正确.【答案】 ABC4.随着人类航天事业的进步,太空探测越来越向深空发展,火星正在成为全球航天界的“宠儿”.我国计划于2020年发射火星探测器,一步实现绕、落、巡工程目标.假设某宇航员登上了火星,在其表面以初速度v 竖直上抛一小球(小球仅受火星的引力作用),小球上升的最大高度为h ,火星的直径为d ,引力常量为G ,则( )A .火星的第一宇宙速度为vd hB .火星的密度为3v 24πGhdC .火星的质量为v 2d 22GhD .火星的“近火卫星”运行周期为2πv dh【解析】 在火星表面竖直上抛的小球做匀减速直线运动,设火星表面的重力加速度为g ,第一宇宙速度为v 0,火星的自转周期为T ,则2gh =v 2,得g =v 22h ,在火星表面的物体的重力等于万有引力,也是在火星表面附近做圆周运动的向心力,mg =G Mm r 2=m (2πT )2r ,又r =d 2,M =43πr 3·ρ,得:v 0=vd 4h ,M =v 2d 28Gh,ρ=3v 24πGhd ,T =2πv dh2,故选B. 【答案】 B5.(中心天体密度的求解)(2019·全国Ⅱ卷,18)假设地球可视为质量均匀分布的球体.已知地球表面重力加速度在两极的大小为g 0,在赤道的大小为g;地球自转的周期为T,引力常量为G.地球的密度为( ) A.0203πg g GT g - B.0203πgGT g g - C.23πGT D.23πg GT g6.(估算问题)(2019·全国新课标卷,19)卫星电话信号需要通过地球同步卫星传送.如果你与同学在地面上用卫星电话通话,则从你发出信号至对方接收到信号所需最短时间最接近于(可能用到的数据:月球绕地球运动的轨道半径约为3.8×105km,运行周期约为27天,地球半径约为6 400 km,无线电信号的传播速度为3×108 m/s)( )A.0.1 sB.0.25 sC.0.5 sD.1 s。
第22天 开普勒定律和万有引力定律(人教版2019)(解析版)
第22天 开普勒定律和万有引力定律 (预习篇)1.理解开普勒定律,知道开普勒第三定律中k 值的大小只与中心天体有关.2.通过月—地检验等将太阳与行星间的引力推广为万有引力定律,理解万有引力定律的内容、含义及适用条件.3.认识引力常量测量的重要意义,能应用万有引力定律解决实际问题.一、开普勒定律1.开普勒第一定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上. 2.开普勒第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等.3.开普勒第三定律:所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等.其表达式为a 3T 2=k ,其中a 代表椭圆轨道的半长轴,T 代表公转周期,比值k 是一个对所有行星都相同的常量. 二、行星与太阳间的引力1.行星绕太阳的运动可以看作匀速圆周运动.行星受到一个指向圆心(太阳)的引力,这个引力提供行星做匀速圆周运动的向心力.2.若行星的质量为m ,行星到太阳的距离为r ,行星公转的周期为T ,则行星需要的向心力的大小F =4π2mr T 2,结合r 3T 2=k ,可知F =4π2k m r 2,即F ∝m r2.3.行星与太阳的引力在本质上和太阳与行星的引力地位完全相当,即F ′∝m 太r2.4.太阳与行星间的引力:根据牛顿第三定律知F =F ′,所以有F ∝m 太mr 2,写成等式就是F=G m 太m r 2.三、月—地检验1.检验目的:检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的吸引力是否为同一性质的力.2.检验方法:(1)假设地球与月球间的作用力和太阳与行星间的作用力是同一种力,它们的表达式也应该满足F =G m 月m 地r2,根据牛顿第二定律,月球绕地球做圆周运动的向心加速度a月=G m 地r2.(2)假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度a 苹=G m 地R 2.(3)a 月a 苹=R 2r 2,由于r ≈60R ,所以a 月a 苹=1602. (4)结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同的规律. 四、万有引力定律1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r 的二次方成反比. 2.表达式:F =G m 1m 2r 2,其中G 叫作引力常量.五、引力常量牛顿得出了万有引力与物体质量及它们之间距离的关系,但没有测出引力常量G 的值. 英国物理学家卡文迪什通过实验推算出引力常量G 的值.通常取G =6.67×10-11N·m 2/kg 2.一、开普勒定律的应用例题1. 某行星沿椭圆轨道绕太阳运行,如图所示,在这颗行星的轨道上有a 、b 、c 、d 四个对称点.若该行星运动的周期为T ,沿逆时针方向运行,则该行星( )A .从a 到b 的运动时间等于从c 到d 的运动时间B .从d 经a 到b 的运动时间等于从b 经c 到d 的运动时间C .a 到b 的时间t ab >T4D .c 到d 的时间t cd >T4答案 D解析 根据开普勒第二定律可知,A 、B 错误;在整个椭圆轨道上t ab =t da <T 4,t cd =t bc >T4,故C 错误,D 正确.解题归纳:1.当比较一个行星在椭圆轨道不同位置的速度大小时,选用开普勒第二定律;当比较或计算两个行星的周期问题时,选用开普勒第三定律.2.由于大多数行星绕太阳运动的轨道与圆十分接近,因此,在中学阶段的研究中我们可以按圆轨道处理,且把行星绕太阳的运动看作匀速圆周运动,写成r 3T 2=k .二、万有引力定律例题2. 如图所示,两质量均匀分布的小球半径分别为R 1、R 2,相距R ,质量为m 1、m 2,则两球间的万有引力大小为(引力常量为G )( )A .G m 1m 2R 12B .Gm 1m 2(R 1+R 2+R )2C .G m 1m 2(R 1+R 2)2D .G m 1m 2R 22答案 B解析 两质量均匀分布的小球均可看作质点,两球间的万有引力大小F =G m 1m 2(R 1+R 2+R )2,故选B. 解题归纳:1.万有引力定律的表达式:F =G m 1m 2r 2,其中G =6.67×10-11 N·m 2/kg 2,叫引力常量,由英国物理学家卡文迪什在实验中测出. 2.万有引力定律公式的适用条件 (1)两个质点间的相互作用.(2)一个质量分布均匀的球体与球外一个质点间的相互作用,r 为球心到质点的距离. (3)两个质量分布均匀的球体间的相互作用,r 为两球心间的距离.1. 太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动,其中火星轨道半长轴为1.524天文单位(地球到太阳的平均距离为1个天文单位).则火星公转一周约为( )A .0.8年B .2年C .3年D .4年 答案 B解析 由开普勒第三定律可得r 火3T 火2=r 地3T 地2,得T 火≈2年,故A 、C 、D 错误,B 正确.2. 关于万有引力及其计算公式F =G m 1m 2r 2,下列说法正确的是( )A .万有引力只存在于质量很大的两个物体之间B .根据公式知,r 趋近于0时,F 趋近于无穷大C .计算地球对卫星的引力时,r 是指卫星到地球表面的距离D .卡文迪什测出了引力常量G 答案 D解析 万有引力定律适用于任何两个可以看成质点的物体之间或均质球体之间的引力计算,故A 错误;当r 趋近于0时,两物体不能看成质点,万有引力公式不再适用,故B 错误;计算地球对卫星的引力时,r 是指卫星到地球球心的距离,故C 错误;卡文迪什测出了引力常量G ,故D 正确.(建议用时:30分钟)一、单选题1. 关于行星的运动,下列说法正确的是( )A .关于行星的运动,早期有地心说与日心说之争,日心说理论是完美无缺的B .所有行星围绕太阳运动的轨道都是椭圆,且近日点速度小,远日点速度大C .开普勒第三定律a 3T 2=k ,式中k 的值仅与中心天体的质量有关D .卫星围绕行星运动不满足开普勒第三定律 答案 C解析 不论是日心说还是地心说,在研究行星运动时都是有局限性的,A 错误;所有行星围绕太阳运动的轨道都是椭圆,且近日点速度大,远日点速度小,B 错误;开普勒第三定律a 3T2=k ,式中k 的值仅与中心天体的质量有关,C 正确;卫星围绕行星运动也满足开普勒第三定律,D 错误.2. 中国古代为区分季节有节气之说,如图所示,从现代物理学可知,地球沿椭圆形轨道绕太阳运动所处四个位置,分别对应我国的四个节气.下列说法正确的是( )A .地球沿椭圆轨道做匀速运动B .太阳在椭圆的一个焦点上C .冬至时地球公转速度最小D .秋分时地球公转速度最大 答案 B解析 地球在椭圆轨道上运动,根据开普勒第二定律可知,A 错误;根据开普勒第一定律可知,B 正确;冬至时,地球在近日点,根据开普勒第二定律可知,公转速度最大,故C 、D 错误.3. 要使相距较远的两物体间的万有引力增加到原来的4倍,下列方法不可行的是( )A .使两物体的质量各变成原来的2倍,距离不变B .使其中一个物体的质量增加到原来的4倍,距离不变C .使两物体间的距离减小为原来的12,质量不变D .使两物体间的距离和两个物体质量都减少为原来的12答案 D解析 根据F =Gm 1m 2r 2可知,使两物体的质量各变成原来的2倍,距离不变,两物体间的万有引力增加到原来的4倍,故A 可行;根据F =Gm 1m 2r 2可知,使其中一个物体的质量增加到原来的4倍,距离不变,两物体间的万有引力增加到原来的4倍,故B 可行;根据F =Gm 1m 2r 2可知,使两物体间的距离减小为原来的12,质量不变,两物体间的万有引力增加到原来的4倍,故C 可行;根据F =Gm 1m 2r 2可知,使两物体间的距离和两个物体质量都减少为原来的12,两物体间的万有引力不变,故D 不可行.4. 已知地球半径为R ,将一物体从地面发射至离地面高度为h 处时,物体所受万有引力减小到原来的一半,则h 为( ) A .R B .2R C.2R D .(2-1)R答案 D解析 在地面上有F =G Mm R 2,在高度为h 处有F ′=G Mm (R +h )2,因为F ′=12F ,所以(R +h )2R 2=21,所以h =(2-1)R ,故D 正确,A 、B 、C 错误. 二、多选题5.如图所示,P 、Q 是质量均为m 的两个质点,分别置于地球表面不同纬度上,如果把地球看成是一个质量分布均匀的球体,P 、Q 两质点随地球自转做匀速圆周运动,则下列说法正确的是( )A .P 、Q 所受地球引力大小相等B .P 、Q 做圆周运动的向心力大小相等C .P 、Q 做圆周运动的角速度大小相等D .P 、Q 两质点的重力大小相等 答案 AC解析 P 、Q 两质点所受地球引力都是F =G Mmr 2,故A 正确;P 、Q 都随地球一起转动,其角速度一样大,但P 的轨道半径大于Q 的轨道半径,根据F n =mω2r 可知P 的向心力大,故B 错误,C 正确;物体的重力为万有引力的一个分力,在赤道处最小,随着纬度的增加而增大,故D 错误.6. 在讨论地球潮汐成因时,地球绕太阳运行的轨道与月球绕地球运行的轨道均可视为圆轨道.已知太阳质量约为月球质量的2.7×107倍,地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍.关于太阳和月球对地球上相同质量海水的引力,下列说法正确的是( )A .太阳引力远大于月球引力B .太阳引力与月球引力相差不大C .月球对不同区域海水的引力大小相等D .月球对不同区域海水的引力大小有差异 答案 AD解析 根据F =G m 1m 2r 2,可得F 太阳F 月=M 太阳M 月·r 月2r 地2≈169,故A 正确,B 错误;由于月心到不同区域海水的距离不同,所以引力大小有差异,C 错误,D 正确.三、解答题7.如图所示,有一质量为m 的飞船,由静止开始从P 点在恒力F 的作用下,沿PD 方向做匀加速直线运动,一年(用字母T 表示,不考虑单位换算)后在D 点飞船掠过地球上空,再过三个月,又在Q 处掠过地球上空。
专题 开普勒三定律及万有引力定律 高一物理 (人教版2019)
专题6 开普勒三定律及万有引力定律(教师版)一、目标要求目标要求重、难点开普勒三定律重点万有引力定律的基本概念重点万有引力与重力的关系重难点1.开普勒三定律(1)开普勒第一定律:又称轨道定律,所有行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上.(2)开普勒第二定律:又称面积定律,对于每一个行星而言,太阳和行星的连线在相等的时间内扫过的面积相等S AB=S CD=S EK.(3)开普勒第三定律:又称周期定律,所有行星轨道半长轴的三次方跟公转周期的二次方的比值相等.用公式表示:32akT,其中比例常数k与行星无关只与太阳有关.(4)对开普勒三定律的理解①开普勒三定律是实验定律,都是从观察行星运动所取得的资料中总结出来的,主要是从运动学的角度描述了行星绕太阳的运动规律.②开普勒三定律否定了天体运行的圆轨道想法,建立了正确的行星轨道理论;它还指出行星绕太阳运行时远日点速率小,近日点速率大;开普勒第三定律提示了周期和轨道半径的关系,该定律具有普遍性,后面将学到的人造卫星也涉及相似的常数,此常数与卫星无关,只与地球质量有关.2.万有引力定律 (1)推导过程:①简化轨道:把实际的椭圆轨道看成是圆形轨道,天体做匀速圆周运动. ②圆周运动条件:引力向F F =,即2v F m r=.③开普勒定律的运用由于2π=r v T ,则2222π1()4π==⋅r rF m m T r T322'22224π()4π===r m m m k k T r r r ,其中32r k T =,'24π=k k ,所以2m F r∝=.④牛顿第三定律的结论:太阳对行星的引力与行星质量成正比,与距离平方成反比,而根据牛顿第三定律可知太阳对行星的引力与行星对太阳的引力大小相等,性质相同.因此行星对太阳的引力一定与太阳质量成正比,因此'122m m F r∝.(2)定律内容:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们距离的二次方成反比.把上面的结论写成等式122m m F Gr =,此式即为万有引力定律的公式表达形式. 公式中的G 叫做引力常量,116.6710G -=⨯N·m 2/kg 2.物理意义:对于任何物体来说,G 值都是相同的,它在数值上等于质量为1 kg 的两个物体,相距1 m 时的相互作用力.3.对万有引力定律的理解 (1)适用条件:①当两个物体间的距离远远大于每个物体的尺寸时,物体可以看成质点,直接使用万有引力定律计算.②当两物体是质量分布均匀的球体时,它们之间的引力也可直接用公式计算,但式中r 是指两球心间距离.③当研究物体不能看成质点时,可以把物体假想分割成无数个质点,求出两个物体上每个质点与另一物体上所有质点的万有引力,然后求合力.(2)万有引力的性质:①普遍性:万有引力存在于任何两个有质量的物体之间. ②相互性:万有引力的作用是相互的,符合牛顿第三定律.③一般物体之间虽然存在万有引力,但是很小,天体与物体之间或天体之间的万有引力才比较显著.(3)万有引力定律的意义:①万有引力定律的发现,是17世纪自然科学最伟大的成果之一,将天地间的规律统一起来,第一次提示了自然界中的一种基本相互作用的规律,在人类认识自然的历史上树立了一座里程碑.②消除了人们的迷信思想,使人们有信心、有能力理解天地间的各种事物,解放了思想,在科学文化的发展上起到了积极的推动作用.4.地球上的重力和万有引力的关系在地球表面上的物体所受的万有引力引F 可以分解成物体所受的重力mg 和随地球自转而做圆周运动的向心力F ,如图所示,其中2引MmF GR=,而2F mr ω=(1)当物体在赤道上时,引F 、mg 、F 三力同向,此时F 达到最大值2max F mR ω=,重力加速度达到最小值2min 2引F F Mg GR mRω-==-; (2)当物体在两极的极点时,0F =,引F mg =,此时重力等于万有引力,重力加速度达到最大值,此最大值为max 2M g G R =;因为地球自转角速度很小,22Mm G mR Rω,所以在一般情况下计算时认为2Mm mg GR =。
开普勒定律万有引力定律教案
开普勒定律与万有引力定律教案一、教学目标1. 让学生了解开普勒定律的发现过程和内容,理解开普勒定律在天文学上的重要意义。
2. 让学生掌握万有引力定律的发现过程、表达式及适用范围,了解万有引力定律在天体运动研究中的重要作用。
3. 培养学生运用物理知识解决实际问题的能力,提高学生的科学素养。
二、教学内容1. 开普勒定律:(1)开普勒定律的发现过程。
(2)开普勒定律的内容及意义。
(3)开普勒第三定律的应用。
2. 万有引力定律:(1)万有引力定律的发现过程。
(2)万有引力定律的表达式及适用范围。
(3)万有引力定律在天体运动中的应用。
三、教学重点与难点1. 教学重点:(1)开普勒定律的内容及意义。
(2)万有引力定律的表达式及适用范围。
2. 教学难点:(1)开普勒第三定律的应用。
(2)万有引力定律在天体运动中的应用。
四、教学方法1. 采用讲授法,讲解开普勒定律和万有引力定律的发现过程、内容及其应用。
2. 运用案例分析法,分析开普勒第三定律和万有引力定律在实际问题中的运用。
3. 引导学生进行讨论和思考,提高学生的科学素养。
五、教学安排1. 课时:本节课计划用2课时完成。
2. 教学过程:(1)第一课时:(1)介绍开普勒定律的发现过程。
(2)讲解开普勒定律的内容及意义。
(3)分析开普勒第三定律的应用。
(2)第二课时:(1)介绍万有引力定律的发现过程。
(2)讲解万有引力定律的表达式及适用范围。
(3)分析万有引力定律在天体运动中的应用。
六、教学活动1. 课堂讲解:教师通过多媒体课件,详细讲解开普勒定律和万有引力定律的发现过程、内容及其应用。
2. 案例分析:教师选取具有代表性的案例,分析开普勒第三定律和万有引力定律在实际问题中的运用。
3. 小组讨论:学生分组讨论开普勒定律和万有引力定律在现实生活中的应用,分享讨论成果。
4. 课后作业:布置有关开普勒定律和万有引力定律的练习题,巩固所学知识。
七、教学评价1. 课堂表现:评价学生在课堂讲解、案例分析和小组讨论中的参与程度和表现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第16讲 开普勒定律 万有引力定律 考情剖析 考查内容 考纲要求 考查年份 考查详情 能力要求 开普勒行星运动定律、万有引力定律及其应用 Ⅰ、Ⅱ
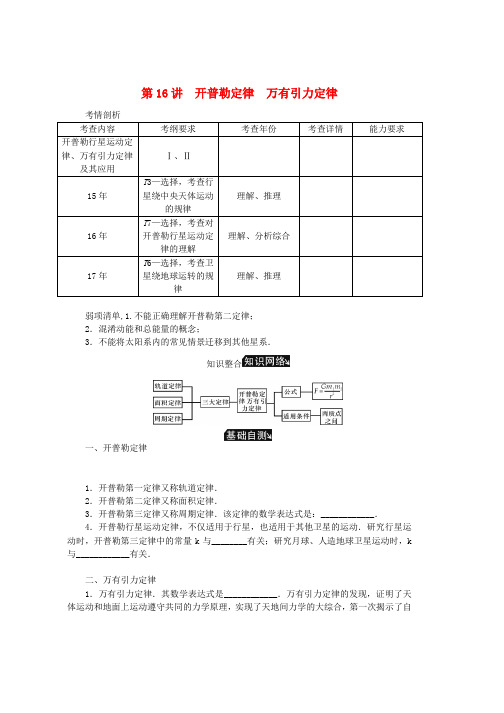
15年 T3—选择,考查行星绕中央天体运动的规律 理解、推理 16年 T7—选择,考查对开普勒行星运动定律的理解 理解、分析综合 17年 T6—选择,考查卫星绕地球运转的规律 理解、推理 弱项清单,1.不能正确理解开普勒第二定律; 2.混淆动能和总能量的概念; 3.不能将太阳系内的常见情景迁移到其他星系.
知识整合
一、开普勒定律 1.开普勒第一定律又称轨道定律. 2.开普勒第二定律又称面积定律. 3.开普勒第三定律又称周期定律.该定律的数学表达式是:____________. 4.开普勒行星运动定律,不仅适用于行星,也适用于其他卫星的运动.研究行星运动时,开普勒第三定律中的常量k与________有关;研究月球、人造地球卫星运动时,k与____________有关.
二、万有引力定律 1.万有引力定律.其数学表达式是____________.万有引力定律的发现,证明了天体运动和地面上运动遵守共同的力学原理,实现了天地间力学的大综合,第一次揭示了自然界中的一种基本相互作用规律. 2.____________实验证明了万有引力的存在及正确性,并使得万有引力定律可以定量计算,引力常量G=6.67×10-11 N·m2/kg2. 3.万有引力定律的应用 计算中心天体的质量、密度 若已知一个近地卫星(离地高度忽略,运动半径等于地球半径R)的运行周期是T. 有:
GMmR2=4π2mRT2,解得地球质量为____________;由于地球的体积为V=43πR3,可以计算地球的密度为:____________.当然同样的道理可以根据某行星绕太阳的运动计算太阳的质量. 方法技巧考点1 开普勒定律的应用 1.开普勒行星运动定律是对行星绕太阳运动的总结,实践表明该定律也适应于其他环绕天体,如月球或其他卫星绕行星运动.
2.开普勒第二定律与第三定律的区别:前者揭示了同一行星在距太阳不同距离时运动的快慢,后者揭示了不同行星运动快慢的规律. 【典型例题1】 下列关于行星绕太阳运动的说法中,正确的是( ) A.所有行星都在同一椭圆轨道上绕太阳运动 B.行星绕太阳运动时,太阳位于行星轨道的中心处 C.离太阳越近的行星运动周期越长 D.所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等 【典型例题2】 (17年镇江模拟)飞船沿半径为R的圆周绕地球运动,其周期为T.如果飞船要返回地面,可在轨道上某点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运动,椭圆和地球表面在B点相切,如图所示.如果地球半径为R0,求飞船由A点运动到B点所需要的时间.
1.如图是行星m绕恒星M运行的示意图,下列说法正确的是( ) A.速率最大点是B点 B.速率最小点是C点 C.m从A点运动到B点做减速运动 D.m从A点运动到B点做加速运动 考点2 天体质量和密度的计算 1.万有引力与重力的关系 地球对物体的万有引力F表现为两个效果:一是重力mg,二是提供物体随地球自转的向心力F向,如图所示. (1)在赤道上:GMmR2=mg1+mω2R. (2)在两极上:GMmR2=mg2. (3)在一般位置:万有引力GMmR2等于重力mg与向心力F向的矢量和. 越靠近南北两极g值越大,由于物体随地球自转所需的向心力较小,常认为万有引力近似等于重力,即GMmR2=mg. 2.星体表面上的重力加速度 (1)在地球表面附近的重力加速度g(不考虑地球自转):
mg=GmMR2,得g=GMR2 (2)在地球上空距离地心r=R+h处的重力加速度为g′ mg′=GMm(R+h)2,得g′=GM(R+h)2
所以gg′=(R+h)2R2. 3.天体质量和密度的计算 (1)利用天体表面的重力加速度g和天体半径R.
由于GMmR2=mg,故天体质量M=gR2G,
天体密度ρ=MV=M43πR3=3g4πGR. (2)通过观察卫星绕天体做匀速圆周运动的周期T和轨道半径r. ①由万有引力等于向心力,即GMmr2=m4π2T2r,得出中心天体质量M=4π2r3GT2; ②若已知天体半径R,则天体的平均密度 ρ=MV=M43πR3=3πr3GT2R3;
③若天体的卫星在天体表面附近环绕天体运动,可认为其轨道半径r等于天体半径R,则天体密度ρ=3πGT2.可见,只要测出卫星环绕天体表面运动的周期T,就可估算出中心天体的密度. 【典型例题3】 一行星绕恒星做圆周运动.由天文观测可得,其运行周期为T,速度为v,引力常量为G,则下列关系式错误的是( ) A.恒星的质量为v3T2πG
B.行星的质量为4π2v3GT2 C.行星运动的轨道半径为vT2π D.行星运动的加速度为2πvT 【典型例题4】 (17年盐城模拟)近年来,人类发射了多枚火星探测器,对火星进行科学探究,为将来人类登上火星、开发和利用火星资源奠定了坚实的基础.如果火星探测器环绕火星做“近地”匀速圆周运动,并测得该探测器运动的周期为T,则火星的平均密度ρ的表达式为(k是一个常数)( )
A.ρ=kT B.ρ=kT
C.ρ=kT2 D.ρ=kGT2 2.(17年盐城期中)2016年9月15日“天宫二号”空间实验室由长征二号FT2火箭发射升空.这意味着,中国成功发射了真正意义上的空间实验室,即实现了载人航天工程“三步走”战略的第二步.10月19日凌晨神舟十一号载人飞船与“天宫二号”实施自动交会对接,近似把对接后一起运行看作以速度v绕地球的匀速圆周运动,运行轨道距地面高度为h,地球的半径为R.求: (1)“天宫二号”绕地球运转的角速度; (2)“天宫二号”在轨道上运行的周期; (3)地球表面上的重力加速度的计算表达式. 当堂检测 1.在力学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法中不正确的是( )
A.伽利略首先将实验事实和逻辑推理(包括数学推演)和谐地结合起来 B.笛卡儿对牛顿第一定律的建立做出了贡献 C.开普勒通过研究行星观测记录,发现了行星运动三大定律 D.牛顿总结出了万有引力定律并用实验测出了引力常量 2.“嫦娥一号”和“嫦娥二号”两颗月球探测卫星,它们绕月的圆形轨道距月球表面分别约为200 km和100 km.当它们在绕月轨道上运行时,两者相比,“嫦娥二号”的( ) A.周期较小 B.周期相同 C.向心加速度相同 D.向心加速度较小 3.“宜居”行星,是指适宜人类生存的行星,美国国家航天航空局2011年2月2日宣布,开普勒太空望远镜经过一年多的探寻,共发现了54颗“宜居”行星,可能存在支持生命的条件.若有一颗“宜居”行星,其质量为地球的a倍,半径为地球的b倍,则该行星卫星的最大环绕速度是地球卫星最大环绕速度的( )
A.ab倍 B.ab倍
C.ba倍 D.ab3倍 4.(多选)在圆轨道运动的质量为m的人造地球卫星,它到地面的距离等于地球半径R,已知地面上的重力加速度为g,则( ) A.卫星运动的速度为2gR
B.卫星运动的周期为4π2Rg
C.卫星运动的加速度为g2 D.卫星的动能为mRg4 5.(多选)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
A.月球表面的重力加速度g月=2hv20L2
B.月球的质量m月=2hR2v20GL2 C.月球的自转周期T=2πRv0 D.月球的平均密度ρ=3hv202πGL2 第16讲 开普勒定律 万有 引力定律 知识整合 基础自测
一、3.a3T2=k 4.太阳质量 地球质量
二、1.F=Gm1m2r2 2.卡文迪许扭秤 3.M=4πR3GT2 ρ=3πGT2 方法技巧 ·典型例题1·D 【解析】 由开普勒行星运动定律可知所有行星轨道都是椭圆,太阳
位于一个焦点上,行星在椭圆轨道上运动的周期T和半长轴a满足a3T2=k(常量),对于同一中心天体,k不变,故A、B、C都错误,D正确. ·典型例题2·()R+R0T4RR+R02R 【解析】 飞船沿椭圆轨道返回地面,由题图可知,飞船由A点到B点所需要的时间刚好是沿图中整个椭圆运动周期的一半,椭圆轨道的半长轴为R+R02,设飞船沿椭圆轨道运动的周期为T′.
根据开普勒第三定律有R3T2=R+R023T2. 解得T′=TR+R02R3= ()R+R
0T2RR+R
0
2R.
所以飞船由A点到B点所需要的时间为 t=T2=()R+R0T4RR+R02R. ·变式训练1·C 【解析】 由开普勒第二定律知,行星与恒星的连线在相等的时间内扫过的面积相等;A点为近地点,速率最大,B点为远地点,速率最小,A、B错误;m由A点到B点的过程中,离恒星M的距离越来越远,所以m的速率越来越小,C正确,D错误.
·典型例题3·B 【解析】 因v=2πrT,所以r=vT2π,选项C正确;结合万有引力定
律公式GMmr2=mv2r,可解得恒星的质量M=v3T2πG,选项A正确;因不知行星和恒星之间的万有引力的大小,所以行星的质量无法计算,选项B错误;行星的加速度a=v2r=2πvT,选项D正确. ·典型例题4·D 【解析】 由万有引力定律知GMmr2=m4π2T2r,联立M=ρ·43πR3和r
