8-2安培环路定理
12.4安培环路定律

1、当 r R 1 时
L
B d 0I 0
R2
B 0
R1
r
I
2、当 R 1 r R 2 时
l
B d l 0I
B
0I
2π r
I
2 π rB 0 I
3、当 r R 2 时
L
B d 0I 0 B 0
例2 无限长载流圆柱体的磁场 解:对称性分析: 磁力线为同心圆,同一磁力线上 的B值相同,
取B 线为闭合回路L
I
R R
L
①、当 r R 时
2 π rB 0 I
l
B d l 0I
r
B
B
0I
2π r
②、当 r R 时
L
B d 0 I r 2 0
B 轴线上任一点的磁感应强度为:
的方向与轴线平行
0 nI
解: 1、管内任一点的磁场
L
B d 0
d
c
b
d
c
a
B b ab B c cd 0
++ ++++ ++ +++ ++ +
a
b
B b B c 0 nI
2、管外任一点磁场。
L
B d 0 n c d I
0 Ir
2
R2
B 2 r
0 Ir
R1
2
2
9.4安培环路定理
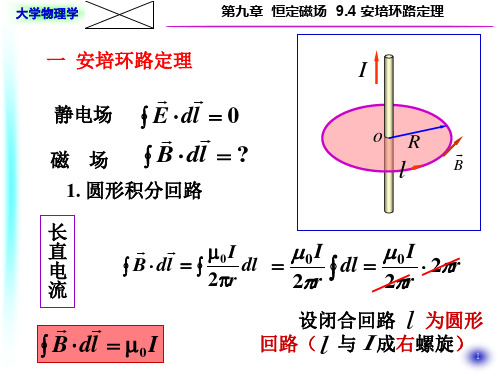
电流在回路之外
d
I
B1
r1
dl1
B2
dl2
r2
l
B1
0I
2π r1
,
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
3
大学物理学
第九章 恒定磁场 9.4 安培环路定理
多电流情况
I1
I2
I3
l
B B1 B2 B3
Bdl
l
0(I2
I3)
推广:
➢ 安培环路定理
n
B dl 0 Ii
i 1
4
大学物理学
第九章 恒定磁场 9.4 安培环路定理
安培环路定理
n
B dl 0 Ii
i 1
一闭合即路在径真的空积的分稳的恒值磁,场等中于,磁0感乘应以强该度闭合B 路沿径任
所包围的各电流的代数和.
注意
电流 I 正负的规定 :I 与 L 成右螺旋时, I 为正;反之为负.
➢ 分析对称性
电流分布 磁场分布
轴对称
I R
26
大学物理学
l
第九章 恒定磁场 9.4 安培环路定理
B 的方向判断如下:
r
dS1
O
dS2
dB
dB2 dB1
P
27
大学物理学
第九章 恒定磁场 9.4 安培环路定理
➢ 作积分环路并计算环流
如图 r R
B • dl Bdl 2rB
➢
利用安培环路定理求
说 明
B • dl 0 Ii 0 (I2 I3 )
安培环路定理

r R, B d l 0 I
l
第10章 稳恒磁场
10–2 安培环路定理
12
例10.2 如图所示,一无限大导体薄平板垂直于纸 面放置,其上有方向指向读者的电流,通过与电流 方向垂直的单位长度的电流大小为i,求其磁场分布 .
第10章 稳恒磁场
10–2 安培环路定理
13
解:
ab cd l
a b c d
b c d a B dl B dl B dl B dl B dl 0li
L
2Bl 0li
1 B 0i 2
以上结果说明:在无限大均匀平面电流两侧的磁场 是匀强磁场,且大小相等、方向相反.其磁感应线在 无限远处闭合,与电流亦构成右螺旋关系.
L L
2 rB 0 I
0 I B (r R ) 2 r
2)圆柱体内任一点Q
I 2 L B d l 2 rB 0 R2 r 0 Ir B (r R2 安培环路定理
10
B
的方向与
r R,
第10章 稳恒磁场
10–2 安培环路定理
B d l 0 ( I1 I1 I1 I 2 )
L
I1 I1
L
I2 I 3 I1
( 0 I1 I 2)
问 1) B是否与回路 L 外电流有关? 2)若 B d l 0 ,是否回路 L上各处 B 0? L 是否回路 L 内无电流穿过?
第10章 稳恒磁场
r R,
I
I 构成右手螺旋关系 0 Ir B 2 2 R 0 I B 2 r
0 I 2 R
大学物理稳恒磁场

B2
0
r
r2 R2
I
rR
I
0I rR p r
B20R I2r rR
rp
B 0I rR 2r
B
无限长圆柱导体电流外面的磁场与电流
都集中在轴上的直线电流的磁场相同
.
R
r
无限长通电柱面
B2r 0 rR
0I rR p r I
B0 rR
rp
B 0I rR 2r
B
思考:有人说:“环路不环绕
电流时,环路上磁场必处处为
o
( D ) 20I R
B
( E ) 20I 8R
.
[A]
5.如图所示,电流由长直导线 1 经 a 点流 入电阻均匀分布的正方形线框,再由 b 点 流出,经长直导线 2 返回电源(导线 1、2 的延长线均通过 o 点)。设载流导线 1、2 和正方形线框在框中心o 点产生的磁感应 强度分别用 B1、B2、B3 表示,则 o 点的感 应强度大小
单位长度的电流)到处均匀。大小为 j
解:视为无限多平行
长直电流的场。 B
p
分析场点p的对称性
B
因为电流平面是无限大,故与电流平面等距离的 各点B的大小相等。在该平面两侧的磁场方向相反。
.
作一安培回路如图: bc和 da两边被电流平 面等分。ab和cd 与电 流平面平行,则有
L B d lB 2 lojl
(A )BR2B r. (B)BRBr. (C )2BRB r. (D )BR4Br.
.
[B]
4.两半径为R的相同导体细圆环,互相垂直放 置,且两接触点A、B连线为环的直径,现有 电流1沿AB连线方向由A端流入,再由 B端流 出,则环中心处的磁感应强度大小为:
高斯定理 安培环路定律
b
c
d
a
B dl l
a B dl b B dl c B dl d B dl
Ba ab 0 Bd cd 0
由于环路内没有包围任何电流,按安培环路定理
B dl 0 l
Ba Bd Bb Bc
管内任一点的B与轴线上的B相同,即均匀场!
场强大小 选择安培环路如图所示: B沿闭合回路的环流为:
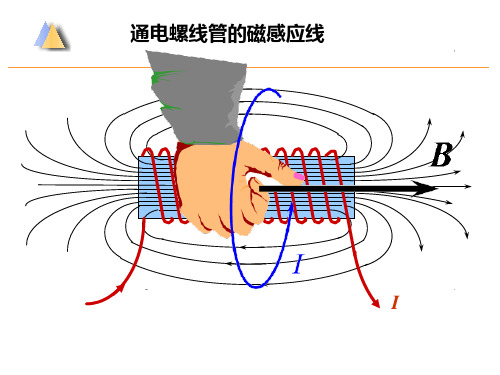
例题1 :长直密绕载流螺线管,单位长度上电流匝数 为 n ,求螺线管内的磁感应强度分布。
I B
解: 对称性分析 管内磁感应线平行于管轴 管外靠近管壁处磁场为零 原因:无漏磁!
性质:匀强磁场
螺线管内任取安培环 路如图,cd段位于轴 线上:
ab I
d
c
B
由于螺线管无限长,则 Ba = Bb,Bc = Bd 。
μ0 I
若电流方向相反
只要积分环路符合右手螺旋法
则,都有
I
B dl l
μ0 I
而当电流走向 和 环路方向与右手螺旋方向相背时
B dl l
μ0I
2. 无限长直线电流,任意积分回路
l B dl l B cosθdl
B方向的投影
0I1 cos dl
l 2 r
0I1 rd
l 2 r
得
B dl l
S B dS 0
磁感应线闭合 无自由“磁荷” 磁场是无源场
二 安培环路定理的应用
1. 条件 若电流分布具有高度对称性时,磁场分布也具有 高度对称性。此时才可以应用安培环路定理计算 磁感应强度的分布。
2. 关键
利用安培环路定理求磁感应强度的关健:根据磁 场分布的对称性,选取合适的闭合环路。
3. 环路选取原则
安培环路定理

第19讲 安培环路定理毕奥-萨伐尔定律的应用 毕奥 萨伐尔定律的应用 安培环路定理及其应用毕奥-萨伐尔定律毕奥—萨伐尔定律 一 毕奥 萨伐尔定律(给出了电流元在空间产生的磁场) 给出了电流元在空间产生的磁场 给出了电流元在空间产生的磁场v Idlv dBdB =µ0 Idl sin θ4π r2v dBP *v rθv IdlIv v v µ0 Idl × r dB = 3 4π rv r任意载流导线在点 P 处的磁感强度 磁感强度叠加原理v v v v µ0 I dl × r B = ∫ dB = ∫ 3 4π rA. 无限长载流长直导线的磁场B=µ0I2π rI BIXBB.半无限长载流长直导线的磁场 半无限长载流长直导线的磁场 半无限长BP =µ0I4π rIor* P圆形载流导线的磁场. 例2 圆形载流导线的磁场 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 的磁感强度的方向和大小. 电流 求其轴线上一点 p 的磁感强度的方向和大小v Idlrv Bv dBp *oRϕv BI 解 根据对称性分析4π r B = Bx = ∫ dB sin ϕdB =µ 0 Id l2xv IdlRrxoϕr 2 2 2 ϕ r =R +x α µ 0 I cos αdl *p x B= 4 π ∫l r 2v dBcosα = R4π r µ 0 I cos αdl dB x = 2 4π rdB =µ 0 Id l2B=B=µ0 IR4π r 2 µ0 IR2 23 0∫2π Rdl3(x + R )2 2IR o x *v BxB=B=µ0 IR22 2 3讨 论(x + R )2 2 v v 2)x < 0 B 的方向不变 I 和 B 成右螺旋关系) 的方向不变( 右螺旋关系 关系) ) µ 0I B = 3)x = 0 ) 2R 2 µ 0 IR µ 0 IS 4)x >> R ) B= , B= 3 3 2x 2π x2 21)若线圈有 N 匝 )(x + R )2 2 2 N µ 0 IR3(1) )I (2 )v R B x 0 µ0I o B0 = 2RI R o+(4) )BA =d *AR1µ0 I4π dB0 =µ0 I4R(5) ) IR2(3) I ) R o*oB0 =µ0 I8RB0 =µ0 I4 R2−µ0 I4 R1−µ0 I4π R1磁偶极矩(磁矩) 二 磁偶极矩(磁矩)v v m = IS e n圆电流磁感强度公式也可写成I Sv env mB=µ 0 IR2x32v µ0m v B= e 3 n 2π xv v µ0m B= 3 2π xv mv enI S说明:只有当圆形电流的面积S很小,或场点距 说明:只有当圆形电流的面积 很小, 很小 圆电流很远时,才能把圆电流叫做磁偶极子 磁偶极子. 圆电流很远时,才能把圆电流叫做磁偶极子三. 载流直螺线管的磁场 如图所示,有一长为l 半径为R的载流密绕直螺线 例 如图所示,有一长为 , 半径为 的载流密绕直螺线 管,螺线管的总匝数为N,通有电流I. 设把螺线管放 螺线管的总匝数为 ,通有电流 在真空中,求管内轴线上一点处的磁感强度. 在真空中,求管内轴线上一点处的磁感强度Ro* p xdxx++ ++++++ +++ ++ +解 由圆形电流磁场公式B=µ 0 IR22 2 3/ 2(x + R ) 2β1βx1o pβ2x2++ + + + + + + + + + + + + +xdB =µ02B = ∫ dB =µ 0 nI2(RR In d x22+xx2 x12 3/2)∫ (R3R 2 dx2x = R cot β 2 dx = − R csc βdβ+x22 3/ 2)R + x = R csc β2 2 2 2B=−µ 0 nI2∫ββ21R csc β d β µ0 nI β 2 =− 3 3 ∫β1 sin β d β 2 R csc β d β讨 论B=µ0 nI2(cos β 2 − cos β1 )β1 = π − β 2l/2点位于管内轴线中点 (1)P点位于管内轴线中点 ) 点位于管内cos β1 = − cos β 2B = µ0 nI cos β 2 =若cos β2 =(l / 2)l2+ R2µ0 nI2(l2/4+ R2 1/ 2)l >> RB = µ 0 nI(2) 无限长的螺线管 无限长的螺线管(3)半无限长螺线管 )半无限长螺线管B = µ 0 nI或由 β1 = π , β 2 = 0 代入π β1 = , β 2 = 0 21 B = µ 0 nI 2µ0nIxL/2B=µ0nI2(cos β2 − cos β1 )B1 µ 0 nI 2O-L/2安培环路定理一 安培环路定理 载流长直导线的磁感强度为 流长直导线的磁感强度为B=µ0IIov BR2π Rv dlv v µ0 I ∫l B ⋅ dl = ∫ 2π R dl v v µ0I ∫l B ⋅ dl = 2π R ∫l dl v v ∫ B ⋅ dl = µ0 Ill设闭合回路 l 为圆形 螺旋) 回路( 回路( l 与 I 成右螺旋)Iov BR若回路绕向化为逆时针时,则 回路绕向化为逆时针时,v dllv v µ0 I 2π ∫l B ⋅ d l = − 2π ∫0 dφ = −µ0 I对任意形状的回路dφv vB dlIrll与 I 成右螺旋v v µ0 I µ0 I B ⋅ dl = rdφ = dφ 2π r 2π v v B ⋅ dl = µ 0 I ∫l电流在回路之外dφv B1Ir1v , B2 = B1 = B2 2π r1 2π r2 v v v v v µ0 I v dl B1 ⋅ dl1 = −B2 ⋅ dl2 = − dφ 2 dl1 2π r2 v v v v B1 ⋅ dl1 + B2 ⋅ dl2 = 0 l v v ∫ B ⋅d l = 0lµ0 Iµ0 I多电流情况I1I2I3v v v v B = B1 + B2 + B3 v v ∫ B ⋅ d l = µ0 ( I 2 − I 3 )ll以上结果对任意形状 以上结果对任意形状 任意 的闭合电流( 的闭合电流(伸向无限远 的电流)均成立. 的电流)均成立n v v ∫ B ⋅ dl = µ 0 ∑ I i i =1安培环路定理安培环路定理n v v ∫ B ⋅ dl = µ 0 ∑ I i i =1一闭合路径的积分的值, 一闭合路径的积分的值,等于 所包围的各电流的代数和. 所包围的各电流的代数和 注意v 即在真空的稳恒磁场中, 即在真空的稳恒磁场中,磁感应强度 B 沿任µ 0 乘以该闭合路径I正负的规定 电流 I 正负的规定 :I 与 之为负 为正;反之为负.螺旋时, L 成右螺旋时,v v B⋅dl = µ0 (−I1 + I1 − I1 − I2 ) ∫LI1 I1LI2 I 3 I1= −µ0 I1 + I2) (问v 1) B 是否与回路 L 外电流有关? 外电流有关? ) v v v 2)若 ∫ B ⋅ d l = 0 ,是否回路 L上各处 B = 0? ) L 内无电流穿过? 是否回路 L 内无电流穿过?二 安培环路定理的应用举例 例1 求长直密绕螺线管内磁场解 1 ) 对称性分析螺旋管内为均匀场 , 方向沿 轴向, 轴向 外部磁感强度趋于零 ,即 B ≅ 0 .2 ) 选回路 电流L.M N +++ + + + ++++++ L O PNO OP PMv 磁场 B 的方向与右螺旋. I 成右螺旋v Bv v v v v v v v v v ∫ B ⋅ d l = ∫ B ⋅ d l + ∫ B ⋅ d l + ∫ B ⋅ d l +∫ B ⋅ d ll MNB ⋅ MN = µ 0 n MN IB = µ 0 nI无限长载流螺线管内部磁场处处相等 , 外部磁场 为零. 为零v 解 1) 对称性分析;环内 B ) 对称性分析; v 线为同心圆,环外 B 为零. 线为同心圆, 为零例2 求载流螺绕环内的磁场v v ∫l B ⋅ d l = 2π RB = µ0 NI µ0 NI B= 2π R令 当2)选回路 . )dRL = 2 πRB = µ0 NI L2R >> d 时,螺绕环内可视为均匀场 .例3 无限长均匀载流圆柱体的磁场 解 1)对称性分析 2)选取回路 ) )Ir>R2π rB = µ0 Iv v ∫ B ⋅ d l = µ0 IlR RLr2π r 2 v v πr 0 < r < R ∫ B ⋅ d l = µ0 2 I l πR 2 µ0r µ0 Ir 2π rB = 2 I B= 2 R 2π RB=µ0 II.v Bv dBdIv Bv B 的方向与 I 成右螺旋 µ 0 Ir B= 2 0 < r < R, 2π R µ0I r > R, B= 2π rIµ0I2π RBRo Rr例4 无限长载流圆柱面的磁场L1rRµ0 I2π RBIL2解ro R rB=0 µ0I2π rv v 0 < r < R, ∫ B ⋅ d l = 0lv v r > R, ∫ B ⋅ d l = µ 0 IlB=作业 作业:练习 作业:练习16。
安培环路定律
作积分回路如图
dB
b
a
ab、cd与导体板等距
.........
c
d
24 (下一页)
计算环流 b c B dl a Bdl cos 0 b Bdl cos 2 0 d a c Bdl cos 0 d Bdl cos 2 0 B ab B cd 利用安培环路定理求 B dl 0 n ab I
0 NI B 2r 0
内 外
. .
R1
N n 2R1
R1、R2 R2 R1
.. . . . ... B 0
R1 R2
..
R2
. .
.
.
.
B 0 nI
r
23
(下一页)
4. 无限大载流导体薄板
已知:导线中电流强度 I 单位长度导线匝数n
I
分析对称性
1 (下一页)
二、 毕奥---沙伐尔定律的应用 计算各种电流分布产生的磁场的磁感强度 基本步骤: 1)任取电流元, 求出其 dB p p = 在场点P产生的磁感 == 的大小与方向; r 2 ) 分 析 dB 方 向 是 否 变 化 : α ==若不变,直接积分; 若变化, ==则要将dB适当的分解, 对各 Idl ==分量分别积分, 然后再合成 ==起来.
a
d
b
c
I
20 (下一页)
计算环流 b c B dl a Bdl cos 0 b Bdl cos 0 2 d a c 0 cos d Bdl cos Bdl 02
利用安培环路定理求B . . . . . . . . . . . . . . .
普通物理学第七版 第八章 恒定电流的磁场
三、磁感应线和磁通量 1. 磁场的定性描述——磁感应线(磁感线) • 磁感线上各点的切线方向表示 此处磁场的方向 • 磁感线的疏密反映磁场的强弱
返回 退出
• 磁感应线的性质 磁感应线与闭合电流套连成无头无尾的闭合曲线 磁感应线绕行方向与电流成右手螺旋关系
返回 退出
2. 磁通量
磁通量:穿过磁场中任一给定曲面的磁感应线总数。
例:简单闭合电路
IR
a。
电路中有如图所示电流I。
Ri
绕行一周,各部分的电势变化总和为0。
。b
ε
ε UR Ui 0
ε I
R Ri
推广至多个电源和电阻组成的回路,有
I Σε j
闭合电路的欧姆定律
ΣRj ΣRij
注意式中电动势正负取值的规定。
返回 退出
例如计算如图闭合回路的电流。 I R1
Idl r2
方向:
(
Idl
r
)
各电流元产生的 dB方向各不相同,
分 解dB
垂 平直 行于 于zz轴 轴的 的ddBBz
返回 退出
由对称性,dB分量相互抵消。
B dB//
dB
sinθ
μ0 4π
Idl sinθ r2
μ0I sinθ 4πr 2
2 πR
电源把其它形式的能量转化为电势能。如化学电池、
发电机、热电偶、硅(硒)太阳能电池、核反应堆
等。
返回 退出
电动势 : ε dA dq
电动势 等于将单位正电荷从
电源负极沿内电路移到正极过
程中非静电场力做的功。
磁化强度
∑ p + ∑p M=
m
m
M = lim
V ∑Pm + ∑pm
V
V →0
磁化强度的单位: A/ m 磁化强度的单位:
磁化强度
注意:对顺磁质, 注意:对顺磁质, pm 可以忽略; ∑ 可以忽略; 对于真空, 对抗磁质 ∑pm = 0 ,对于真空,M = 0 。
外磁场为零,磁化强度为零。 外磁场为零,磁化强度为零。 外磁场不为零: 外磁场不为零:
I
取一长方形闭合回路ABCD,AB边在磁介质 取一长方形闭合回路 边在磁介质 内部,平行与柱体轴线,长度为l, 内部,平行与柱体轴线,长度为 ,而BC、AD两 两 边则垂直于柱面。 边则垂直于柱面。
l
B C
l M dl = ∫ M dl = M AB = M ∫
∵M =αs ∴∫ M d l = αsl = Is
在环内任取一点, 解:在环内任取一点, 过该点作一和环同心、 过该点作一和环同心、 r 的圆形回路。 半径为 的圆形回路。
r
∫ H dl = NI
式中 N为螺绕环上线圈 的总匝数。由对称性可知, 的总匝数。由对称性可知,在所取圆形回路上各 点的磁感应强度的大小相等,方向都沿切线。 点的磁感应强度的大小相等,方向都沿切线。
或
∫(
B
0
M) dl = ∑I
磁介质中的安培环路定理
定义 H =
B
0
为 M 磁场强度
∵
∫(
B
0
M) d = ∑I l
有磁介质时的 安培环路定理
则
∫ H dl = ∑I
磁介质中的安培环路定理: 磁场强度沿任 磁介质中的安培环路定理 :
意闭合路径的线积分等于穿过该路径的所有传导电 流的代数和,而与磁化电流无关。 流的代数和,而与磁化电流无关。 表明:磁场强度矢量的环流和传导电流 有关 有关, 表明:磁场强度矢量的环流和传导电流I有关, 而在形式上与磁介质的磁性无关。 而在形式上与磁介质的磁性无关。其单位在国际单 位制中是A/m. 位制中是
大学物理第八章恒定电流的磁场
Fe 2.磁性: 磁铁能吸引含有 Co 物质的性质。
Ni
3.磁极:磁铁上磁性最强的两端,分为
N S
北同 极,指向 方,
南异
斥 性相 。
吸
三.磁场
1.概念: 运动qυ电荷或电I流周围存在的物质,称为磁场。
2.对外表现
① qυ或 I 在磁场中受到力的作用。
②载流导线在磁场中移动,磁场力作功。
力的表现 功的表现
极。
然而,磁和电有很多相似之处。例如,同种电荷
互相推斥,异种电荷互相吸引;同名磁极也互相推
斥,异名磁极也互相吸引。用摩擦的方法能使物体带
上电;如果用磁铁的一极在一根钢棒上沿同一方向摩
擦几次,也能使钢棒磁化。但是,为什么正、负电荷 能够单独存在,而单个磁极却不能单独存在呢?多年 来,人们百思而不得其解。
dN B
dS
一些典型磁场的磁感线:
2.性质
①磁感线是无始无终的闭合曲线。
B
A
②任二条磁感线不相交。
B
③磁感线与电流是套合的,它们之间可用右手螺旋法 则来确定。
B
I
I
B
四.磁通量
1.定义:通过一给定曲面的磁感线的条数,称为通过该 曲面的磁通量。
电场强度通量:e S E dS
通过面元 dS的磁感线数: dN BdS BdS cos
3.电荷之间的磁相互作用与库仑相互作用的不同 ①电荷无论是静止还是运动的,它们之间都存在库仑 作用; ②只有运动的电荷之间才有磁相互作用。
四.磁感强度
电场 E 磁场 B
1.实验 在垂于电流的平面内放若干枚小磁针,发现:
①小磁针距电流远近不同,
N
受磁力大小不同。
②距电流等远处,小磁针受
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几种典型电流的B分布
一段载流直导线
B
0I 4a
(sin 2
sin 1)
无限长载流直导线 无限长均匀载流薄圆筒
B 0I 2 r
B内
0,B外
0I 2 r
无限长载流密绕直螺线管,细螺绕环
B内 0nI,B外 0
圆电流圈的圆心和轴线上
B中 心
0I
2R
B轴线 2
=B
.2π
r
=
μoI
2π r
2π
r
=μ oI
IB
r
安培环路定律:磁感应场强度矢量沿任 意闭合路径一周的线积分等于真空磁导率乘 以穿过闭合路径所包围面积的电流代数和。
l B .dl =μ oΣ I
电流和回路绕行方向 构成右旋关系的取正值
I
向 绕 行方
电流 I 取负值
I
向 方
绕行
I2
I1
I
I
I
l1
B
=
μ 0I
2π r
I R r
B
B
B
=
μ0
2π
Ir
R2
O
μ 0I
2π R
R
r
B
=
μ 0I
2π r
例. 求无限大载流平面的磁场分布
由俯视图:
无限大载流平面的磁场
分布如图示
dB'
dB
作闭合环路abcd如图 dB''
I
l p
d
c
dl' o dl''
a
b
b c d a
=abB .dl + 0 + 0 + 0 =abB dl cos00
.............
a
b
B
d
c
l B.dl =abB dl cos00 =B abdl
= B ab =μ 0n ab I
B =μ 0n I
(n:单位长度上的匝数)
2. 环形螺线管的磁场
l B.dl = l B dl cos00
1820年7月奥斯特发现了电流的磁效应.法国科 学家阿拉果8月在瑞士听到这一消息后,9月初回到 法国立即向法国科学院报告了这一最新发现.善于 接受新的研究成果的安培,怀着极大的兴趣,第二 天就重做了奥斯特的实验,并于9月18日向法国科学 院提交了第一篇论文,报告他的实验成果.接着又 在9月25日、10月9日提出了第二篇和第三篇实验报 告论文.
L dl
如图示的 I1 I2
电流分布
Ii内 代数和
i
与L绕行方向成右螺电流取正
如图示的电流 I1 取正
I
取负
2
选取环路原则
(1)环路要经过所研究的场点。
(2)环路的长度便于计算;
(3)要求环路上各点 B大小相等,B的方向与环路方向
一致.
目的是将:
B dl
L
0
I 写成
... .B
= B l dl =B 2π r
. .
= 0NI (N :匝数) ..
.
....
R1 R2
. . . . ..
.
r
.....
B = μ2π0 Nr I
B .. . . . . . . . ..
I
I
0
R1 R2
r
3. 均匀通电直长圆柱体的磁场
设电流 I 均匀分布在整个横截面上。
1. r < R
0 IS
R2 x2
3 / 2 ( 不 必 记)
无限大均匀平面电流的磁场,两侧为均匀磁场,方向相
反(右手定则)
B
j
大小为
B 0 j
2
j----面电流密度矢量的大小, 为通过垂直电流方向 的单位长度上的电流。
返回
B
I
l B .dl = l B dlcos00
R
Hale Waihona Puke =B 2π r =μ 0I ´
I ´=sδ .dS =sδ .dS cos00
=δ
s
dS =
π
I R
2π
r
2
=
Ir2 R2
(
或:II ´=ππ
r2 R2
I´)
得:
B
=
μ
2
0I r
R2
dS δ I´
r B
2. r >R
B 2π r =μ 0 I
或 B的方向与环路方向垂直,
B 0 I
dl
B dl , cos 0 B dl 0
§ 环路定律的应用 1. 直长通电螺线管内的磁场
.............
a
b
B
d
c
l B.dl =abB .dl + bc B .dl +cdB .dl+daB .dl
安培环路定律
法国物理学家
安培
A.M.Ampere (1775-1836)
安培(Andre-Marie Ampere, 1775-1836) 法国物理学家,电动力学的创始人。 12岁学习
了微积分,13岁发表关于螺旋线的论文.在化学方面 ,他最先预见了氯、氟、碘三种物质是元素,还独立 地发现了“阿伏伽德罗定律”.
B dl a B dl b B dl c B dl d B dl
b
d
a Bdl 0 c Bdl 0
b
d
a Bdl 0 c Bdl 0
2Bab 由安培环路定理0 jab
B
1 2
0
j
方向:平行于通电平面。与电流成右手螺旋。
(a)
l2
(b)
l3
(c)
(a)
. l
B
1
dl = μ o ( I 1
I2)
(b)
l
B
2
. dl
=
0
(c)
l
B
3
. dl
=μ
o
(
I
I )=0
B 空间所有电流共同产生的
L 在场中任取的一闭合线
I3
任意规定一个绕行方向 dl L上的任一线元
I内 与L套连的电流
I1
I2
在这三篇论文中,包括了电流方向和磁针偏转方 向关系的右手定则;同向直线电流间互相吸引,异 向直线电流间互相排斥;通电螺线管的磁性与磁针 等效,等等.
安培环路定律
Ampere circulation theorem
问题:
l E .dl = 0 l B .dl= ?
1. 圆形环路
l
l B .dl = l B dl cos0 0
