简谐运动的振动方程
简谐运动及其旋转矢量表示法简谐运动的能量

1 Hz , 2 6
T 2 1 6s, /4
(2)势能 总能
Epkx2/2, EkA 2/2
由题意, k2 x/2k2 A /4, xA/ 24.2 41 02m
(3)从平衡位置运动到 xA/ 2
的最短时间为 T / 8。
即为 6/80.75s
) )
O
A/2
x
(B)
A/2
O
x
A
x 10-2cos( t /3 - /4),(SI)
五、两个同频率简谐运动的相位关系
x 10-2cos( t /3 - /4),(SI)
x2 比 x1 超前
简谐运动及其旋转矢量表示法简谐运动的能量
五、两个同频率简谐运动的相位关系
(或 x1 比 x2 落后 ) 的最短时间为 T / 8。
x Acos( t )
半径
圆周运动小球 角速度
振幅
角频率 简谐振动物体
角坐标
相位
例:一物体做谐振动,振幅为 A,在起始
时刻质点的位移为 A/2 且向 x 轴的正方向
运动,代表此谐振动的旋转矢量图为:
质点运动的周期和振幅。
五、两个同频率简谐运动的相位关系
= 2 v = 2 /T
质点运动的周期和振幅。
A
,振幅A=1 cm. t=0时,速度具有负最O大值,求振动表达式.
(C ) x A/2
(D)
A/2
O
x
A
[D]
四、简谐运动的能量
1. 动能
Ek
1 mv 2
2
1 kA2 sin 2( t )
2
掌握
Ek max
简谐运动位移公式推导

简谐运动位移公式推导简谐运动是指具有周期性、振幅恒定、且运动方向与作用力方向相同的运动。
在简谐运动中,物体的位移可以用一个简单的数学公式来描述。
下面我将给出简谐运动位移公式的推导。
假设一个质点进行简谐运动,其运动方程可以表示为:x = X*sin(ωt + φ)其中,x表示质点的位移,X表示质点的振幅,ω表示角频率,t表示时间,φ表示初相位。
首先,我们知道简谐运动是一种周期性运动,即在一个周期内,物体的运动状态会重复出现。
一个周期的长度为T,即在时间T内,物体完成一次完整的往复运动。
因此,我们可以将角频率ω定义为:ω=2π/T接下来,我们考虑质点的初始运动状态。
初相位φ表示在t=0时刻质点的位移相对于振动的初始位置的差距。
当φ=0时,质点位于振动的初始位置;当φ=π/2时,质点位于振动的最大位移位置。
因此,我们可以得到:x = X*sin(ωt + φ)接下来,我们来推导简谐运动的位移公式。
我们将位移公式的形式写成以下形式:x = A*sin(ωt) + B*cos(ωt)其中,A和B是待定系数。
我们可以通过初始条件来确定这些系数。
当t=0时,由于质点的初始位移为X,所以我们有:x(0) = A*sin(ω*0) + B*cos(ω*0) = X由此可得B=X,即B的取值为振幅X。
当t=0时,由于质点的初始速度为0,所以我们有:v(0) = A*ω*cos(ω*0) - B*ω*sin(ω*0) = 0根据初中学的三角函数性质,sin(0) = 0,cos(0) = 1,所以我们有:v(0)=A*ω*1-B*ω*0=A*ω=0由此可得A=0,即A的取值为0。
综上所述,我们得到了简谐运动的位移公式:x = X*sin(ωt)简谐运动的位移公式中,位移与时间的关系是一个正弦函数关系。
其中,X表示振幅,表示质点的最大位移;ω表示角频率,表示单位时间内的相位改变量。
简谐运动具有周期性和重复性,其运动状态会在一个周期内周期性地发生变化。
简谐运动的图象和公式

• 图像绘制方法 1、描点法
第一个1/2周期: t 时间t(s) 0 第二个1/2周期: 7t 时间t(s) 6t
0
0
2t
0
3t
0
4t
0
5t
0
6t
0
位移x(cm) 20.0
-17.8
-10.1
0.1
10.3
17.7
20.0
0
8t
0
9t
0
10t
0
11t
0
12t
0
位移 x(cm)
20.0
17.7
10.3
以x代表质点对于平衡位置的位移,t代表时间,则
x A sint
(1)公式中的A 代表什么? A叫简谐运动的振幅。表示简谐运动的强弱。 (2)ω叫做什么?它和T、f之间有什么关系?
叫圆频率。表示简谐运动的快慢。 它与频率的关系: =2f
(3)公式中的相位用什么来表示?
“ t+” 叫简谐运动的相位。表示简谐运动所处的状态。
二、简谐运动的图象作用:
1.物理意义:简谐运动的振动图象表示某个振动物体 相对平衡位置的位移随时间变化的规律。 注意:振动图象不是振子运动的轨迹。 2. 从简谐运动的振动图象可以知道振动物体的运动情 况。 (1)从图象可以知道振幅。 (2)从图象可以知道周期(频率)。(曲线相邻两最 大值之间的时间间隔) (3)从图象可以知道任一时刻物体对平衡位置的位移, 从而确定此时刻物体的位置。 (4)从图象可以确定任一时刻物体的速度大小和方向, 以及某一段时间速度大小变化情况。
x
·
t = 0 A
x
参考圆
简谐运动的位移公式:
x A cos( t )
简谐运动微分方程推导

简谐运动微分方程推导
简谐运动是物理学中非常重要的一个概念,它描述了一种周期性的运动,如振动和波动等。
在数学上,简谐运动可以用微分方程来描述。
本文将介绍简谐运动微分方程的推导过程。
首先,我们需要了解简谐运动的定义。
一个物体进行简谐运动时,它的位移x可以表示为:
x = A sin(ωt + φ)
其中,A是振幅,ω是角频率,t是时间,φ是相位常数。
简谐运动的周期T等于2π/ω,频率f等于ω/2π。
我们现在要推导简谐运动的微分方程。
根据牛顿第二定律,物体的加速度a等于力F除以质量m:
a = F / m
对于简谐运动,力可以表示为弹性力和阻尼力的合力:
F = -kx - bv
其中,k是弹性系数,b是阻尼系数,v是速度。
我们可以通过对位移和速度的一阶导数进行求解,得到简谐运动的微分方程:
x'' + (k/m) x= 0
这个微分方程也可以表示为:
x'' + ωx = 0
其中,ω=k/m是简谐运动的角频率的平方。
这个微分方程描述了一个在没有外力作用下的简谐运动。
如果加入阻尼或强制外力,微分方程将会有所不同。
总之,简谐运动微分方程是描述简谐运动的重要数学工具。
通过推导,我们可以更好地理解简谐运动的本质。
振动方程简.ppt

解:1) 首先确定三个物理量ω, A, φ.
x Acos(t )
x
A
A/2
a
o
-A
Tt
振动曲线
已知A, T, ω=2π/T, 如何求φ? 方法1:解析法
将t=0, x0=A/2, t>0, v = -Aωsinφ>0代入方程
17
x A A/2
a
o
-A
cos 1
2
t Asin 0
3
T
代t 入 方
2. 周期、频率:
1
T 2π
x xt图
A
o
Tt
T
A
2
圆频率 2v 2
T
周期和频率仅与振动系 统本身的物理性质有关
弹簧振子周期
T 2π m k
6
3. 相位 t
相 位 (t) t
相位的意义:决定任意时刻物体的运动状态
1)相差 2nπ (n为整数)质点运动状态相同.
2)初相位 (t 0) 描述质点初始时刻的运动状态.
3
O
A x t 1 (s) 0.13s
18
v
x/m
0.05 0.025 o 0.025 0.05
15
3)若物体在x=0.05 m处时速度不为0,而是具有 向右的初速度v0=0.30 m•s-1 ,求其运动方程。
解:A和φ由初始条件x0 = 0.05m, v0 = 0.30 m•s-1定
O
1 2
kA2
1 2
kx02
1 2
m v02
A2
x02
m k
v02
2 k , k m2
m
A
x02
v02
第9章简谐振动

0
O
t
0t 0
t
0
描述:质点在各个时刻的偏离平衡位置的位移。
[例题4] 质点作简谐振动的曲线x t 如图所示,试根据图推
出该质点的振动式。
[解] 因 x Acos(t ),从图 得 A = 4,下面计算 和 。
x/cm 4
据图有 t 0 时,x 2 ,代 2
5.相位差:两振动相位之差 (1 2 ) 。
讨论下列几种情况:
(1)若(1 2 ) 是2k的整2数倍,则振动同相位; (2)若 (1 2) (2是k 1)的 奇数倍,则振动相位相反; (3)若 (1 ,2 )则 称0 超前1 ;2 (4)若2 (1 2,) 则称 落后1 ;2
x2 A2 cos(0t 2 )
A2 cos(0t 1 2nπ) A2 cos(0t 1 ) v2x 0 A2 cos(0t 2 ) 0 A2 cos(0t 1 )
二振动相位相同,即振动状态相同,同步调.
(2) 1 2 (2n 1)π (n 0,1,, n)
动,振动频率为
f 1 2 2
k1
m 2
k1k2 / (k1 k2 )m
讨论:斜面倾角对弹簧作简谐运动及振动的频率均不产 生影响。
§9.2 简谐振动的运动学
一、简谐振动的运动方程
解方程
d2x dt 2
02 x
简谐运动动力学方程
设初始条件为: t 0 时,x x0 ,v=v0
相位差的不同,表明二振动有不同程度的参差错落,振动步调不同。
例2 讨论振动的位移,速度和加速度之间的关系。
解:x Acos(0t )
物理-简谐振动

简谐振动:物体运动时,离开平衡位置的位移(或角 位移)按余弦(或正弦)规律随时间变化。
1.简谐振动的特征及其表达式
O
X
F
O
X
F
O
X
简谐振动的特征及其表达式
弹簧振子: 连接在一起的一个忽略了质量的弹簧和 一个不发生形变的物体系统。
简谐振动的特征及其表达式
回复力:作简谐运动的质点所受的沿位移方向的合 外力, 该力与位移成正比且反向。
A x02 (v0 )2
0
arctg
v0
x0
在到 之间,通常 存在0 两个值,可根据
v0 Asi进n 行0 取舍。
2.简谐振动的振幅、周期、频率和相位
(1)振幅: 物体离开平衡位置的最大位移的绝对值。
A x02 (v0 )2
由初始条件确定
(2)周期和频率
周期:物体作一次完全运动所经历的时间。
简谐振动的动力学特征:
F kx
据牛顿第二定律,得
a F k x mm
令
k 2
m
a
d2 x dt2
2 x
运动学特征
简谐振动的特征及其表达式
位移 x之解可写为: x Acos(t 0 )
或 x Aei(t 0 )
简谐振动的运动学特征:物体的加速度与位移成正 比而方向相反,物体的位移按余弦规律变化。
x2 A2 cos(t 20 )
二者的相位差为:
(t 20 ) (t 10 ) 20 10
简谐振动的振幅、周期、频率和相位
(t 20 ) (t 10 ) 20 10
讨论:
(a)当 时2,k称两个振动为同相; (b)当 (2k时,称1)两个振动为反相; (c)当 时 0,称第二个振动超前第一个振动 ; (d)当 时0,称第二个振动落后第一个振动 。
机械振动——简谐运动的基本概念
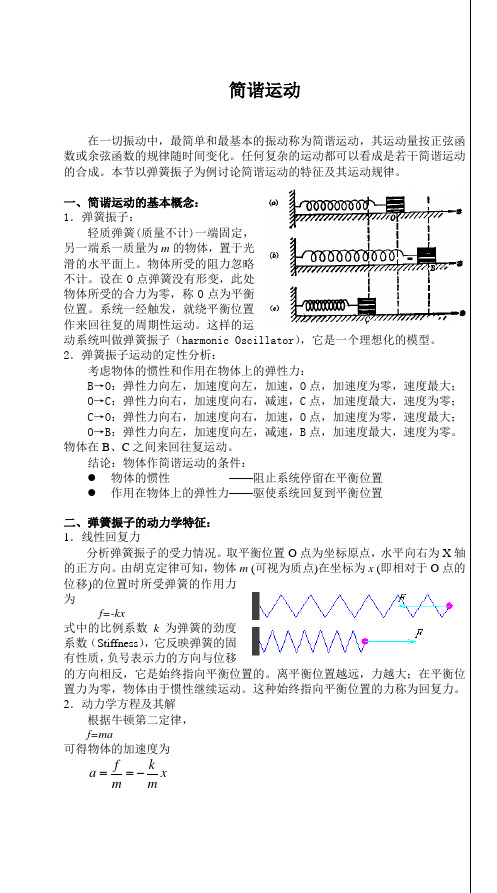
式中的比例系数k为弹簧的劲度系数(Stiffness),它反映弹簧的固有性质,负号表示力的方向与位移的方向相反,它是始终指向平衡位置的。离平衡位置越远,力越大;在平衡位置力为零,物体由于惯性继续运动。这种始终指向平衡位置的力称为回复力。
2.动力学方程及其解
根据牛顿第二定律,
f=ma
可得物体的加速度为
对于给定的弹簧振子,m和k均为正值常量,令
则上动的微分方程。
三、简谐运动的运动学特征:
1.简谐振动的表达式(运动学方程)
简谐运动的微分方程的解具有正弦、余弦函数或指数形式。我们采用余弦函数形式,即
这就是简谐运动的运动学方程,式中A和φ是积分常数。
说明:
1)简谐运动不仅是周期性的,而且是有界的,只有正弦函数、余弦函数或它们的组合才具有这种性质,这里我们采用余弦函数。
定义:物体在2π秒时间内所作的完全振动的次数,用ω表示,单位为弧度/秒(rad. s-1或s-1)。
说明:
1)简谐运动的基本特性是它的周期性;
2)周期、频率或圆频率均有振动系统本身的性质所决定,故称之为固有周期、固有频率或固有圆频率。
3)对于弹簧振子, , , 。
4)简谐运动的表达式可以表示为
三、相位(Phase)—反映振动的状态
物体在B、C之间来回往复运动。
结论:物体作简谐运动的条件:
物体的惯性——阻止系统停留在平衡位置
作用在物体上的弹性力——驱使系统回复到平衡位置
二、弹簧振子的动力学特征:
1.线性回复力
分析弹簧振子的受力情况。取平衡位置O点为坐标原点,水平向右为X轴的正方向。由胡克定律可知,物体m(可视为质点)在坐标为x(即相对于O点的位移)的位置时所受弹簧的作用力为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简谐运动的振动方程
简谐运动是一种特殊的周期性运动,其振幅在一个固定的周期内按照
正弦或余弦函数进行变化。
简谐运动在物理学中有着广泛的应用,如
弹簧振子、单摆等都属于简谐运动。
因此,了解简谐运动的振动方程
是非常重要的。
简谐运动的振动方程可以表示为:
x = A * sin(ωt + φ)
其中,x表示物体距离平衡位置的位移,A表示振幅,ω表示角频率,t表示时间,φ表示初相位。
角频率ω和周期T之间有以下关系:
ω = 2π/T
初相位φ是指物体在t=0时刻所处的相位。
如果物体在平衡位置右侧,则φ为正;如果物体在平衡位置左侧,则φ为负。
由于sin函数是周期性函数,在一个周期内它会不断地从0到1再到0
再到-1再回到0。
因此,在一段时间内完成若干个周期后,物体又回到了初始状态。
简谐运动还有另一种表达方式:x = A * cos(ωt + φ)。
这两种表达方式本质上是等价的,只是相位不同而已。
除了上述公式外,还有一些与简谐运动相关的公式。
例如,简谐运动的周期T和频率f之间有以下关系:
T = 1/f
简谐运动的角频率ω和频率f之间有以下关系:
ω = 2πf
简谐运动的周期T和振幅A之间有以下关系:
T = 2π√(m/k)
其中,m表示物体的质量,k表示弹簧的劲度系数。
总之,了解简谐运动的振动方程是非常重要的。
在物理学中,我们可以通过这个方程来计算物体在不同时间点处于什么位置、速度和加速
度等参数。
因此,掌握这个方程可以帮助我们更好地理解和应用简谐运动。
