《机器人学》课件 第9章 静态力
合集下载
机器人运动学PPT课件
2.1.2 机器人的坐标系
Ø手部坐标系——参考机器人手部的坐标系，也称机
器人位姿坐标系，它表示机器人手部在指定坐标系中
的位置和姿态。
Ø机座坐标系——参考机器人机座的坐标系，它是机
器人各活动杆件及手部的公共参考坐标系。
Ø杆件坐标系——参考机器人指定杆件的坐标系，它
是在机器人每个活动杆件上固定的坐标系，随杆件的
① 绕z轴旋转θ角——变换矩阵推导
技
若空间有一点p，则其
术
在坐标系{i}和坐标系{j}中 的坐标分量之间就有以下关系：
xi xj cos yj s in
ｏi θ ｏj
yi xj s in yj cos
zi zj
2021/3/7
ｘi
ｘj
CHENLI
*
ｙj ｙi
17
第2章 机器人运动学
2.2 齐次变换及运算
CHENLI
7
*
第2章 机器人运动学
2.1 机器人的位姿描述
机
2.1.1 机器人位姿的表示
器
例：右图所示两坐标
ｚ1
人
系的姿态为：
ｚ0
技 术
0 R01 1
1 0
0 0
ｏ0 ｘ0
ｘ1
ｏ1 ｙ1
ｙ0
0 0 1
2021/3/7
CHENLI
8
*
第2章 机器人运动学
机 器 人 技 术
2021/3/7
2.1 机器人的位姿描述
第2章 机器人运动学
机 运动学研究的问题：
器
手在空间的运动与各个关
人 节的运动之间的关系。
技 正问题：
术
已知关节运动，
求手的运动。
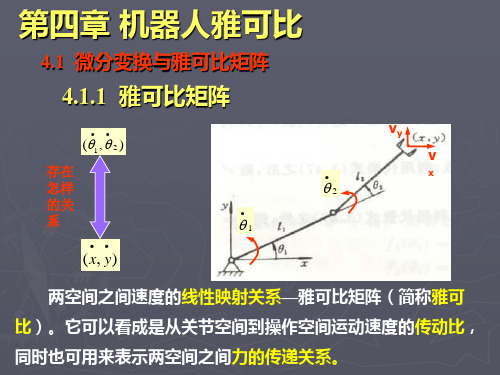
机器人学_机器人雅可比矩阵
0 0 0 1
若Rot（δx，δy，δz） 和Rot（δx‘，δy’，δz‘） 表示两
个不同的微分旋转，则两次连续转动的结果为：
1 (z z ' ) y y ' z z ' 1 (x x' ) Rot(x, y, z ) Rot(x' , y ' , z ' ) (y y ' ) x x' 1 0 0 0 0 0 0 1
Trans(d x , d y , d z )Rot(k , d ) I 44
于是得微分算子Δ
0 k d z k y d 0
k z d 0 k x d 0
k y d k x d 0 0
dx dy dz 0
四. 微分旋转的无序性 当θ→0 时，有sinθ→dθ，cosθ→1．若令δx=dθx，δy=dθy， δz=dθz，则绕三个坐标轴(p16)的微分旋转矩阵分别为
0 0 1 0
0 0 0 1
略去高 阶无穷 小量
0 y 1 xy 1 x Rot( x, x) Rot( y, y ) y x 1 0 0 0 1 xy y 0 1 x Rot( y, y ) Rot( x, x) y x 1 0 0 0
令 Trans(d x , d y , d z )Rot(k , d ) I 44 为微分算子
则相对基系有dT=Δ0T，相对i系有dT=TΔi 。这里Δ的下标不同是由 于微运动相对不同坐标系进行的。
三.微分平移和微分旋转 微分平移变换与一般平移 变换一样，其变换矩阵为:
1 0 Trans(dx, dy, dz) 0 0 0 1 0 0 0 dx 0 dy 1 dz 0 1
《机器人机构学课件》PPT课件
① 运动自由度的定义 ② 以自由度分类的机器人 ③ 自由度的分布
整理ppt
8
机器人自由度的定义
定义：用来确定手部相对于机身位置的每个独立
变化的参数，称为机器人的自由度。
整理ppt
9
以自由度分类的机器人
任一自由的空间物体，须有六个自由度描述 其在空间的位置和姿态，三个正交移动轴，决 定物体的位置；三个绕坐标轴 的转动，决定物 体的姿态变化。
⑴ 伸缩型 ⑵ 伸缩与旋转型 ⑶ 屈伸型 ⑷ 弹性手臂 ⑸ 柔性手臂
称六个自由度机器人为满自由度机器人， 少于六个自由度机器人为欠自由度机器人， 多于六个自由度机 器人为冗余自由度机器人。
整理ppt
第一节10
自由度的分布
一般机器人的机身和手臂构成前三个关节， 具有三个自由度，可确定手部在空间的位置，
所构成的机构称位置机构；
手腕和手部构成后三个关节，具有三个自 由度，可确定手部在空间的姿态，所构成的机
（1）直移型：直线运动 L 伸缩运动 E
（2）回转型：扭角运动 T 摆角运动 R
整理ppt
第一节14
3、 机器人工作空间
1）定义：
手腕部坐标系原点PW能在空间活 动的最大活动范围。又称可达空间 ，或总 工作空间，记W(PW) 。
整理ppt
15
直角坐标机器人的工作空间示意图
整理ppt
16
圆柱坐标机器人的工作空间示意图
第二节 机身和臂部机构
1、机身和臂部的作用 2、机身和臂部机构设计的特点 3、机身结构 4、臂部结构
整理ppt
24
ቤተ መጻሕፍቲ ባይዱ
1、机身和臂部的作用
1）机身定义：机身是连接、支承手臂及行走机构的部件 作用：臂部的驱动装置或传动装置安装在机身上。 类型：机身有固定式和行走式两种。
整理ppt
8
机器人自由度的定义
定义：用来确定手部相对于机身位置的每个独立
变化的参数，称为机器人的自由度。
整理ppt
9
以自由度分类的机器人
任一自由的空间物体，须有六个自由度描述 其在空间的位置和姿态，三个正交移动轴，决 定物体的位置；三个绕坐标轴 的转动，决定物 体的姿态变化。
⑴ 伸缩型 ⑵ 伸缩与旋转型 ⑶ 屈伸型 ⑷ 弹性手臂 ⑸ 柔性手臂
称六个自由度机器人为满自由度机器人， 少于六个自由度机器人为欠自由度机器人， 多于六个自由度机 器人为冗余自由度机器人。
整理ppt
第一节10
自由度的分布
一般机器人的机身和手臂构成前三个关节， 具有三个自由度，可确定手部在空间的位置，
所构成的机构称位置机构；
手腕和手部构成后三个关节，具有三个自 由度，可确定手部在空间的姿态，所构成的机
（1）直移型：直线运动 L 伸缩运动 E
（2）回转型：扭角运动 T 摆角运动 R
整理ppt
第一节14
3、 机器人工作空间
1）定义：
手腕部坐标系原点PW能在空间活 动的最大活动范围。又称可达空间 ，或总 工作空间，记W(PW) 。
整理ppt
15
直角坐标机器人的工作空间示意图
整理ppt
16
圆柱坐标机器人的工作空间示意图
第二节 机身和臂部机构
1、机身和臂部的作用 2、机身和臂部机构设计的特点 3、机身结构 4、臂部结构
整理ppt
24
ቤተ መጻሕፍቲ ባይዱ
1、机身和臂部的作用
1）机身定义：机身是连接、支承手臂及行走机构的部件 作用：臂部的驱动装置或传动装置安装在机身上。 类型：机身有固定式和行走式两种。
第1章 机器人控制技术绪论 机器人原理及控制技术 教学课件
1949-1953 美国麻省理工学院开始研制数控铣床
随 着 先 进 飞 机 制 造 的 需 要 ， 美 国 麻 省 理 工 学 院 辐 射 实 验 室 （ MIT Radiation Laboratory）开始研制数控铣床。
1953年研制成功能按照模型轨迹做切削动作的多轴数控铣床。
1954年 “可编程”“示教再现”机器人
美国国家标准局（NBS）的定义：机器人是一种能够进行编程并在自动 控制下执行某些操作和移动作业任务的机械装置。
美国机器人协会（RIA）的定义：机器人是一种用于移动各种材料、零 件、工具或专用装置的，通过可编程序动作来执行种种任务的，并具有 编程能力的多功能机械手。
日本工业机器人协会（JIRA）的定义：工业机器人是一种装备有记忆装 置和末端执行器的，能够转动并通过自动完成各种移动来代替人类劳动 的通用机器。
日本早稻田大学加藤一朗（日本机器人之父） 教授认为：机器人是由能 工作的手，能行动的脚和有意识的头脑组成的个体，同时具有非接触传 感器（相当于耳、目）、接触传感器（相当于皮肤）、固有感及平衡感 等感觉器官的能力。
2020/10/3
智能与控制工程研究所
12
也有一些组织和学者针对不同形式的机器人分别给出具体的解释 和定义，而机器人则只作为一种总称。例如，日本工业机器人协 会（JIRA）列举了6种型式的机器人：
2020/10/3
智能与控制工程研究所
8
80年代 开始进入智能机器人研究阶段
80年代，不同结构、不同控制方法和不同用途的工业机器人在工业发达国 家真正进入了实用化的普及阶段。
随着传感技术和智能技术的发展，开始进入智能机器人研究阶段。
机器人视觉、触觉、力觉、接近觉等项研究和应用，大大提高了机器人的 适应能力，扩大了机器人的应用范围，促进了机器人的智能化进程。
随 着 先 进 飞 机 制 造 的 需 要 ， 美 国 麻 省 理 工 学 院 辐 射 实 验 室 （ MIT Radiation Laboratory）开始研制数控铣床。
1953年研制成功能按照模型轨迹做切削动作的多轴数控铣床。
1954年 “可编程”“示教再现”机器人
美国国家标准局（NBS）的定义：机器人是一种能够进行编程并在自动 控制下执行某些操作和移动作业任务的机械装置。
美国机器人协会（RIA）的定义：机器人是一种用于移动各种材料、零 件、工具或专用装置的，通过可编程序动作来执行种种任务的，并具有 编程能力的多功能机械手。
日本工业机器人协会（JIRA）的定义：工业机器人是一种装备有记忆装 置和末端执行器的，能够转动并通过自动完成各种移动来代替人类劳动 的通用机器。
日本早稻田大学加藤一朗（日本机器人之父） 教授认为：机器人是由能 工作的手，能行动的脚和有意识的头脑组成的个体，同时具有非接触传 感器（相当于耳、目）、接触传感器（相当于皮肤）、固有感及平衡感 等感觉器官的能力。
2020/10/3
智能与控制工程研究所
12
也有一些组织和学者针对不同形式的机器人分别给出具体的解释 和定义，而机器人则只作为一种总称。例如，日本工业机器人协 会（JIRA）列举了6种型式的机器人：
2020/10/3
智能与控制工程研究所
8
80年代 开始进入智能机器人研究阶段
80年代，不同结构、不同控制方法和不同用途的工业机器人在工业发达国 家真正进入了实用化的普及阶段。
随着传感技术和智能技术的发展，开始进入智能机器人研究阶段。
机器人视觉、触觉、力觉、接近觉等项研究和应用，大大提高了机器人的 适应能力，扩大了机器人的应用范围，促进了机器人的智能化进程。
第9章Hopfield神经网络与联想记忆PPT课件
9.1 神经动力学
1989年Hirsch把神经网络看成是一种非线性动力学 系统，称为神经动力学（Neurodynamics）。
确定性神经动力学将神经网络作为确定性行为，在 数学上用非线性微分方程的集合来描述系统的行为， 方程解为确定的解。
统计性神经动力学将神经网络看成被噪声所扰动， 在数学上采用随机性的非线性微分方程来描述系统 的行为，方程的解用概率表示。
反馈神经网络是一个反馈动力学系统，具有更强的计 算能力。1982年J. Hopfield提出的单层全互连含有对 称突触连接的反馈网络是最典型的反馈网络模型。 Hopfield 用能量函数的思想形成了一种新的计算方法， 阐明了神经网络与动力学的关系，并用非线性动力学 的方法来研究这种神经网络的特性，建立了神经网络 稳定性判据，并指出信息存储在网络中神经元之间的 连接上，形成了所谓的离散Hopfield网络。
第9章 Hopfield神经网络与联想记忆
前言 神经动力学 Hopfield神经网络 Hopfield神经网络 联想记忆 最优化计算 仿真实例
1
机器人智能与神经计算实验室(B) (B) (B) (B) (B)
9.0 前言
d V(t的稳态或
平衡态。
7
机器人智能与神经计算实验室(B) (B) (B) (B) (B)
N维向量所处的空间称为状态空间， 状态空间通常 指的是欧氏空间，当然也可以是其子空间，或是类 似圆、球、圆环和其他可微形式的非欧氏空间。
3
机器人智能与神经计算实验室(B) (B) (B) (B) (B)
1984年，Hopfield设计与研制了Hopfield网络模型的 电路，指出神经元可以用运算放大器来实现，所有 神经元的连接可用电子线路来模拟，称之为连续 Hopfield网络。
《机器人学》教学大纲
《机器人学》课程教学大纲、课程基本信息二、课程目标（一）总体目标:机器人学是智能制造工程专业培养计划中一门高度交叉、前沿的重要专业必修课程，融合了运动学/动力学分析、机械学、控制理论与工程、计算机技术、人工智能等多学科内容的综合性新技术应用课程.通过该课程的学习，使学生了解并掌握机器人学相关的基本理论和方法，具有现代机器人系统设计、分析、应用等基本能力和以后从事相关科学研究和技术工作的能力。
本课程针对智能制造工程专业的特点，主要介绍机器人数学基础、工业机器人、服务机播人的基本机械结构设计、运动学与动力学分析，以及机器人传感器和控制技术等基础理论和技术基础知识，并以实际工程应用为背景，安排各类机器人实样参观、专题讲座、实验等内容。
通过本课程教学，不但使学生掌握机器人技术的基本理论知识，使学生对各类机器人技术和开发方法有所了解，同时通过课程设计等活动培养其在逻辑思维、科学研究和设计实践上的能力，从而培养学生综合运用机器人技术解决智能制造领域实际工程问题的能力。
（二）课程目标：课程目标1：学习并掌握现代机器人的基本理论及方法，具有应用机器人解决工程问题的创新意识和能力；（支撑毕业要求1）课程目标2：学习并掌握工业机器人、服务机器人的状态检测和控制技术，具有利用先进控制理论和方法进行机器人控制并完成具体工程应用的能力；（支撑毕业要求2）课程目标3：学习并掌握现代机器人的总体设计、技术设计和详细结构设计及控制系统设计等内容,具有根据实际工程问题设计相应机器人解决方案的能力：（支撑毕业要求3）课程目标4：评定方法包括课后作业（15%）、实验（20%）、项目研究（15%）和期末考试（50%）环节,总评成绩以百分计，满分100分，各考核环节所占分值比例和根据具体情况微调。
2.（三）评分标准通过机器人的实验，获得相关实验设计和实验技能的基本训练，具有应用相关实验方法解决实际工程问题的能力。
（支撑毕业要求5）（三）课程目标与毕业要求、课程内容的对应关系三、教学内容第1章：绪论（3学时）通过本章内容的教学，使学生了解机器人学的起源与发展，讨论机器人学的定义，分析机器人的特点、结构与分类。
第二章 机器人静力分析与动力学
式中：ri–1，i —坐标系{i}的原点相对于坐标系{i+1}的位置矢量； ri，ci —质心相对于坐标系{i}的位置矢量。
假如已知外界环境对机器人末杆的作用力和力矩，那么可 以由最后一个连杆向零连杆(机座)依次递推，从而计算出 每个连杆上的受力情况。
2.2.2 机器人力雅可比
为了便于表示机器人手部端点的力和力矩(简称为端点广义力F )，可 将 fn，n+1和nn，n+1合并写成一个6维矢量
Jli和J ai分别表示关节i的单位关节速度引起末端的线速度和角速度。
v J11 033 qu x w J 21 J 22 ql
v J11qu w J 21qu J 22 ql qu [q1 q2 q3 ] ql [q4 q5 q6 ]
定义如下变量： f i–1，I 及 ni–1，i ——i–1杆通过关节 i作用在i杆上的力和力矩； fi，i+1 及 ni，i+1——i杆通过关节i+1作用在i+1杆上的力和力矩； –fi，i+1 及 –ni，i+1——i+1杆通过关节i+1作用在i杆上的反作用力和反作 用力矩； fn，n+1及 nn，n+1——机器人最末杆对外界环境的作用力和力矩； –fn，n+1 及 –nn，n+1——外界环境对机器人最末杆的作用力和力矩； f0，1及n0，1——机器人机座对杆1的作用力和力矩； m g——连杆i的重量，作用在质心C 上。
Y 1 Y 2
dX dq J (q ) dt dt
第1列矢量和第2列矢量，则有 v J11 J 22 式中：右边第一项表示仅由第一个关节运动引起的端点速度；右边第 ， 二项表示仅由第二个关节运动引起的端点速度；总的端点速度为这两 个速度矢量的合成。因此，机器人速度雅可比的每一列表示其他关节 ， 不动而某一关节运动产生的端点速度。 2 f 2 (t ) 则可 1 f1 (t ) ， 假如已知的某一时刻的速度 v =f (t)，即手部瞬时速度。 反之，假如给定机器人手部速度，可解出相应的关节速度为 q J 1 v 式中：J–1称为机器人逆速度雅可比。
假如已知外界环境对机器人末杆的作用力和力矩，那么可 以由最后一个连杆向零连杆(机座)依次递推，从而计算出 每个连杆上的受力情况。
2.2.2 机器人力雅可比
为了便于表示机器人手部端点的力和力矩(简称为端点广义力F )，可 将 fn，n+1和nn，n+1合并写成一个6维矢量
Jli和J ai分别表示关节i的单位关节速度引起末端的线速度和角速度。
v J11 033 qu x w J 21 J 22 ql
v J11qu w J 21qu J 22 ql qu [q1 q2 q3 ] ql [q4 q5 q6 ]
定义如下变量： f i–1，I 及 ni–1，i ——i–1杆通过关节 i作用在i杆上的力和力矩； fi，i+1 及 ni，i+1——i杆通过关节i+1作用在i+1杆上的力和力矩； –fi，i+1 及 –ni，i+1——i+1杆通过关节i+1作用在i杆上的反作用力和反作 用力矩； fn，n+1及 nn，n+1——机器人最末杆对外界环境的作用力和力矩； –fn，n+1 及 –nn，n+1——外界环境对机器人最末杆的作用力和力矩； f0，1及n0，1——机器人机座对杆1的作用力和力矩； m g——连杆i的重量，作用在质心C 上。
Y 1 Y 2
dX dq J (q ) dt dt
第1列矢量和第2列矢量，则有 v J11 J 22 式中：右边第一项表示仅由第一个关节运动引起的端点速度；右边第 ， 二项表示仅由第二个关节运动引起的端点速度；总的端点速度为这两 个速度矢量的合成。因此，机器人速度雅可比的每一列表示其他关节 ， 不动而某一关节运动产生的端点速度。 2 f 2 (t ) 则可 1 f1 (t ) ， 假如已知的某一时刻的速度 v =f (t)，即手部瞬时速度。 反之，假如给定机器人手部速度，可解出相应的关节速度为 q J 1 v 式中：J–1称为机器人逆速度雅可比。
第二章-机器人静力分析与动力学PPT课件
机器人动力学主要研究机器人运动特性和受 力之间的关系，目的是对机器人进行控制、 优化设计和仿真。机器人动力学两类问题：
动力学正问题和动力学逆问题。
2021/6/7
2
动力学正问题：已知机械手各关节的作用 力或力矩，求各关节的位移、速度、加速 度、运动轨迹；
动力学逆问题：已知机械手的运动轨迹， 即各关节的位移、速度和加速度，求各关 节的驱动力和力矩。
度移动，杆长l1=l2=0.5 m。设在某瞬时θ1=30°，θ2=60°，求相应瞬时 的关节速度。 解：二自由度机械手速度雅可比为
Jl1l1cs11ll22cs1122
因此，逆雅可比为
l2s12
l2c12
J1l1l21 s2 l1cl2 1c 12l2c12
l2s12 l1s1lq2
末端微线位移和微小角位移(微小转动)组
Y
Y
成。有
q1
q 2
dX=J(q)dq
Z
Z
式中：J(q)是6×n维偏导数矩阵，称为
n自由度机器人速度雅可比。
J(q)
X qT
q1
X
q2 X
q1
q2
Y Y
q1
q2
2021/6/7
Z
Z
q 1
q2
X
qn
假如已知的 1 及 2 是时间的函数，即，1 f1(t) ，2 f2(t) 则可 求出该机器人手部在某一时刻的速度 v =f (t)，即手部瞬时速度。
反之，假如给定机器人手部速度，可解出相应的关节速度为
q J 1 v
2021/6/7式中：J–1称为机器人逆速度雅可比。
8
[例] 图示的二自由度机械手，手部沿固定坐标系X0轴正向以1.0 m/s的速
动力学正问题和动力学逆问题。
2021/6/7
2
动力学正问题：已知机械手各关节的作用 力或力矩，求各关节的位移、速度、加速 度、运动轨迹；
动力学逆问题：已知机械手的运动轨迹， 即各关节的位移、速度和加速度，求各关 节的驱动力和力矩。
度移动，杆长l1=l2=0.5 m。设在某瞬时θ1=30°，θ2=60°，求相应瞬时 的关节速度。 解：二自由度机械手速度雅可比为
Jl1l1cs11ll22cs1122
因此，逆雅可比为
l2s12
l2c12
J1l1l21 s2 l1cl2 1c 12l2c12
l2s12 l1s1lq2
末端微线位移和微小角位移(微小转动)组
Y
Y
成。有
q1
q 2
dX=J(q)dq
Z
Z
式中：J(q)是6×n维偏导数矩阵，称为
n自由度机器人速度雅可比。
J(q)
X qT
q1
X
q2 X
q1
q2
Y Y
q1
q2
2021/6/7
Z
Z
q 1
q2
X
qn
假如已知的 1 及 2 是时间的函数，即，1 f1(t) ，2 f2(t) 则可 求出该机器人手部在某一时刻的速度 v =f (t)，即手部瞬时速度。
反之，假如给定机器人手部速度，可解出相应的关节速度为
q J 1 v
2021/6/7式中：J–1称为机器人逆速度雅可比。
8
[例] 图示的二自由度机械手，手部沿固定坐标系X0轴正向以1.0 m/s的速
4、机器人静力学
B B ⎡d A ⎤ ⎡ A R − S ( BO P ) A R ⎤ ⎡d B ⎤ A =⎢ ⎥⎢ ⎥ ⎢δ ⎥ B ⎣ A⎦ ⎣ 0 AR ⎦ ⎣δ B ⎦
反 对 称 矩 阵
⎡ 0 ⎢ S ( P) = ⎢ p z ⎢− p y ⎣
− pz 0 px
py ⎤ ⎡ px ⎤ ⎥ − px ⎥ , P = ⎢ p y ⎥ ⎢ ⎥ ⎢ pz ⎥ 0 ⎥ ⎣ ⎦ ⎦
w = τ T ⋅ δq = τ 1δq1 + L + τ nδqn 各关节所做的虚功之和为
末端操作器所做的虚功为 ？
w = F T ⋅ D = f x dx + f y dy + f z dz + mxδ x + m yδ y + mzδ z
根据虚功原理，操作臂平衡情况下，由任意虚位移产 生的虚功和为零。即关节空间虚位移产生的虚功等于 操作空间虚位移产生的虚功
4.1 连杆的受力和平衡方程
机器人是由连杆和关节（低副机构）组成，这里将机器人的 连杆当成刚体，以其中一个连杆为对象对其进行静力分析， 连杆i及其相邻连杆之间的作用力和作用力矩关系如下图。
{i}
ci i
•
{i＋1}
Mi+1
r
i +1 i
•
-fi+1
•
Mi fi
P
fi+1
Hale Waihona Puke -Mi+1 mig
fi
：连杆i-1作用在连杆i上的力； ：连杆i-1作用在连杆i上的力矩；
关节空间 操作空间
q∈R
•
n
J映射
p ∈ Rm p=0
•
•
零空间N(J)
机械工程测试技术基础第9章应变、力与扭矩测量
拉（压）应变：
机械应变
i
指示应变
uy
1 4
u0
S
g
特点： 1、不能消除弯矩的影响
2、能补偿温度的影响
2、 试件受力状态图
电桥接法：
都受力，互为补偿
拉（压）应变：
i
1
电桥输出电压：
uy
1 4
u0
S
g
1
特点： 1、不能消除弯矩的影响 2、能补偿温度的影响
3、输出电压提高到（1+ ）
3、试件受力状态图
传感器的原边绕组（励磁绕组）和副边绕 组（测量绕组）互相垂直地安装在导磁体中， 原边绕组通过交流电。当不受力时，原边绕组 的磁力线呈对称分布，且不与副边绕组相交链， 此时副边绕组不产生感应电势（图8—7.b）。
当受力时，材料的导磁率发生变化，使磁力线 分布发生变化，磁力线与副边绕组相交链，在副 边绕组中感应电势，电势的大小正比于外力的大 小，测得该感应电势便知与之成比例的外力。
(4)
u0sg
i / 4
例8-2：如图3所示，悬臂梁弹性模 量 E 20 1010 Pa , 贴 片 处 的 抗 弯 截 面 系 数 W 2 106 m3 ，应变片 R1 R2，现用仪器
测得P力作用的指示应变为2000 ，求P力
的大小。
图3
（三）弯曲、拉（压）联合作用时的测量
测拉（压）
两个绕有线圈的铁心A和B相 互垂直放置，其开口端距被测轴表 面1~2mm间隙。A线圈通以交流电， 形成通过转轴的交变磁场。
转轴不受扭，磁力线与B线圈不交链；转 轴受扭矩作用后，应力的变化使部分磁力线 与B线圈交链，并在其中产生感应电势，该 感应电势与扭矩成正比关系。 特 点：