第10章 应力状态分析和强度理论【工程力学西南交大4学分】
工程力学电子教案2
工程力学电子教案
T
F
Q M
第十章 应力状态理论和强度理论
12
T T I
F
X
M y X IZ
QSZ X IZb
x
X
Y
X
X
工程力学电子教案
第十章 应力状态理论和强度理论
§10-2 平面应力状态分析
Y
X
X
Y
X X
Y Y
1. 求斜截面上的应力
x x
工程力学电子教案
第十章 应力状态理论和强度理论
18
作应力圆: (1) 注意截面的选取 (2) 注意应力的符号,特别是剪应力
求斜截面上的应力: (1) 找准起始点 (2) 角度的旋转以C为圆心 (3) 旋转方向相同 (4) 2倍角的关系 (5) 应力的符号
工程力学电子教案
第十章 应力状态理论和强度理论
工程力学电子教案
第十章 应力状态理论和强度理论
7
145 , min 45 , max
0, Y
3
45
4
21
45
0, X
根据对应力状态的分析,可以了解杆件中材料破坏的力学
因素,并建立强度条件。
工程力学电子教案
第十章 应力状态理论和强度理论
15
y
X
X
Y
Y
X
x
X
Y
Y
y
n
dA
X
p
x
X
Y
t
Y
t 0
dA ( xdAcos ) cos ( xdAcos ) sin ( ydAsin ) sin ( ydAsin ) cos 0
第十章 强度理论(习题解答)
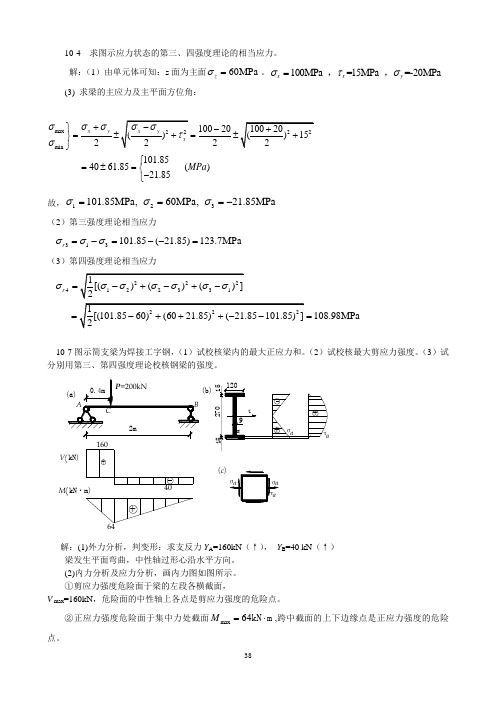
10-4 求图示应力状态的第三、四强度理论的相当应力。
解:(1)由单元体可知:z 面为主面60MPa z σ=。
100MPa =15MPa =-20MPa x x y στσ=,, (3) 求梁的主应力及主平面方位角:max min 1002022101.854061.85()21.85x y MPa σσσσ+⎫-=±=±⎬⎭⎧=±=⎨-⎩故,123101.85MPa,60MPa,21.85MPa σσσ===-(2)第三强度理论相当应力313101.85(21.85)123.7MPa r σσσ=-=--=(3)第四强度理论相当应力4108.98MPa r σ===10-7图示简支梁为焊接工字钢,(1)试校核梁内的最大正应力和。
(2)试校核最大剪应力强度。
(3)试分别用第三、第四强度理论校核钢梁的强度。
M kN ·m)64+V kN)(c )(b)解:(1)外力分析,判变形:求支反力Y A =160kN (↑), Y B =40 kN (↑)梁发生平面弯曲,中性轴过形心沿水平方向。
(2)内力分析及应力分析,画内力图如图所示。
①剪应力强度危险面于梁的左段各横截面,V max =160kN ,危险面的中性轴上各点是剪应力强度的危险点。
②正应力强度危险面于集中力处截面max 64M =⋅kN m ,跨中截面的上下边缘点是正应力强度的危险点。
③按第三、四强度理论,集中力处C 的左截面也可能是危险面,C 的左截面腹板和翼板的交界处为强度理论的危险点。
(3)求截面的几何性质:336512030055.5270287.9108.79101212z I -⨯⨯=-⨯=⨯=⨯44mm m4,30012015(7.5)256500 2.565102z a S *-=⨯⨯-==⨯33mm m 4,30013512015(7.5)1359338512.5 3.3851022z S *-=⨯⨯-+⨯⨯==⨯半33mm m m mm 135.0135==a y(4)对梁进行正应力校核[]3max max 564100.150109.21608.7910b zM y I σσ-⨯=⋅=⨯==⨯Pa MPa <MPa故,满足正应力强度。
《材料力学》第十章 强度理论

第十章 强度理论
Theory of Strength
§10-1 强度理论的概念
The Conception of Theory of Strength
材料力学所研究的最基本问题之一——构件的强度问题。
由§1-1我们知道:构件的强度是指构件承受荷载的能力或构件抵抗
破坏的能力。在前面各章中,我们得到:
圆簇的包络线(Envelope of the family of limiting stress circles)。
简化的莫尔包络线由简单拉伸极限 应力圆和简单压缩极限应力圆的公切线, 以及简单拉伸极限应力圆的切点间轴正 向侧部分曲线构成。
§10-3 莫尔强度理论及其相当应力
Mohr’s strength theory and its equivalent stresses
P
s
P A
4 50 103
0.12 106
6.37MPa
AA s t
t
T Wn
16 7 106
0.13 109
35.65MPa
s s
1 3
6.37 2
(6.37)2 35.652 38.98 MPa
2
32.61
s1 39.0MPa,s 2 0,s 3 32.6MPa
(2)最大伸长线应变理论(The maximum tension strain theory)
认为:最大伸长线应变是使材料发生断裂破坏的主要因素
破坏条件:
e1=ejx
强度条件: бr2=б1-μ(б2+б3)≤[б]---(10-2)
((10-2)式是由虎克定律得出的,因为:e1=[б1-μ(б2+б3)]/E;单向
(完整版)第10章应力应变分析及应力应变关系

第10章 应力应变分析 应力应变关系
本章主要内容
(1) 从静力学的角度给出应力的概念,一点处的应力状态的分析; (2) 从连续介质变形几何学的角度,给出应变的概念,一点处的应变状态
的分析; (3) 应力和应变的关系
将一点处的应力与应变联系起来的是材料本身所固有的力学性能,在 大量实验结果的基础上,本章给出常见工程材料的应力应变关系。
将直角坐标系作如下替换:x 1, y 2, z 3
11 12 13
i j 21
22
23
31 32 33
(i, j 1,2,3) (10.6)
11
剪应力互等定理
(1) 若将任意一点处的单元体看作从物体中切出来的一个分离体,则可 对单元体写出全部6个平衡方程
Fx 0 : ( xx yx zx ) ( xx yx zx ) 0 Fy 0 : ( xy yy zy ) ( xy yy zy ) 0
dx 2
( zxdxdy)
dy 2
( zydxdy)
dx 2
0
13
(2) 剪应力互等定理
在物体内任一点处互相垂直的两个截面上,剪应力总是同时存在, 且大小相等,两者的方向共同指向或共同背离这个两截面的交线。
用张量指标形式可表示为
i j ji
(10.9)
一点的应力状态
(1) 应力张量——二阶对称张量,9个分量中,6个独立分量。 (2) 一点处的应力张量可写为
y (dAsin )sin y (dAsin ) cos 0
Ft 0 : dA x (dAcos)sin x (dAcos) cos
y (dAsin ) cos y (dAsin )sin 0
考虑到 x y,仅数值相等
应力状态和强度理论

4
3
3
2 1
2 1
5 4
FP 2
S 截面
Mz FP l 4
5 4 3
3
2
1
2 1
1
x
2
1
2
2
x
3
2
3
取单元体示例二
l
y
S截面
FP
a
1
S 截面 4
z
2
3
x
忽略弯曲切应力
FSy
y
1
1
x
1
Mx Wp
1
Mx
Mz Wz
4
x
3
z
2
3
3
Mz
Mx Wp
x
3
Mz Wz
4
max (
min
x y
2
)2 x 2
——xy 面内的最大切应力
tan20 tan21 1
(1 0 45 )
将max 与max、min 画在原单元体上
tan 2 0 2 x x y
——主平面的位置 ——最大切应力 所在的位置
40 50 60
x x
x
0 67.50
主应力单元:
3
7.2.2 平面应力状态分析——应力圆
应力圆:
y
y
x y x y cos 2 x sin 2 2 2 x y sin 2 cos 2 x 2 消参数( 2 ),得:
3
Mx Wp
7-2 平面应力状态的应力分析 主应力 7.2.1 斜截面上的应力——解析法
y
材料力学第10章 强度理论

§10-2 四种常用的强度理论
一、关于断裂的强度理论
2.最大拉应变理论(第二强度理论、最大伸长线应变理论)
提出的假说:
最大拉应变是引起材料断裂破坏的原因 。
2
脆性断裂破坏的条件:
均处于弹性范围内 u 1 1 1 2 3 u
1 u
1
[ t ] 3 [ t ] [ c ]
当 [ t ] [ c ] [ ] 时,有
1 3 [ ]
莫尔强度理论可以看作是最大切应力理论的发展,考虑 了材料拉压强度不等的因素。
材料力学
第10章 强度理论
§10-3 莫尔强度理论 二、 莫尔强度理论简介与推导 按照材料在某些应力状态下破 坏时的主应力1,3可作出一组应力 圆——极限应力圆(如图),这组极限 应力圆有一条公共包络线(即极限包 络线,一般情况下为曲线,如图中 的曲线ABC和与它对称的另一曲线)。 莫尔强度理论认为,对于某一给 定的应力状态(1,2,3 )如果由1与 3所作应力圆与上述极限包络线相切 或相交,则表示材料要发生强度破坏。 在工程应用中,往往根据单轴拉伸和单轴压缩的强度试 验结果作两个极限应力圆定出公切线(直线)作为极限包络线。
2、按正应力条件选择截面 M max M max 84 103 6 3 ≤[ ] Wz≥ 494 10 m Wz [ ] 170 106 查型钢表选择28a工字钢。 4 I 3、切应力强度校核 I z 7114cm , z* =24.62,d =8.5cm Sz FQmax 200 103 max 2 3 Iz 24.62 10 8.5 10 d * Sz
②切应力强度条件
扭转
u
第十章强度理论(讲稿)
第十章强度理论同济大学航空航天与力学学院顾志荣一、教学目标掌握强度理论的概念。
了解材料的两种破坏形式(按破坏现象区分)。
了解常用的四个强度理论的观点、破坏条件、强度条件。
掌握常用的四个强度理论的相当应力。
了解莫尔强度理论的基本观点。
会用强度理论对一些简单的杆件结构进行强度计算。
二、教学内容讲解强度理论的概念及材料的两种破坏形式。
讲解常用的四个强度理论的基本观点,并推导其破坏条件从而建立强度计算方法。
介绍几种强度理论的应用范围和各自的优缺点。
简单介绍莫尔强度理论。
三、重点难点重点:强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。
难点:常用四个强度理论的理解;危险点的确定及其强度计算。
四、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
五、计划学时 2学时 六、实施学时 七、讲课提纲(一)为什么需要强度理论及强度理论的概念?1、为什么需要强度理论(回顾基本变形下强度条件的建立)2、复杂应力状态下的强度条件是什么?怎样建立?3、强度理论的概念4、四个强度理论及其相当应力 (二)四个强度理论第一强度理论——最大拉应力理论 第二强度理论——最大拉应变理论 第三强度理论——最大剪应力理论第四强度理论——⎪⎩⎪⎨⎧形状改变比能理论均方根剪应力理论 (三)相当应力11σσ=r-=12σσr μ)(32σσ+313σσσ-=r 2132322214)()()(21σσσσσσσ-+-+-=r (四)复杂应力状态下强度条件的表达式 σr ≤[σ](一)为什么需要强度理论?强度理论的概念1、回顾构件处于简单变形下的强度条件的建立 [拉、压] (单向)图10-1强度条件:[]nA F o N σσσ=≤=,b S oσσσ由试验得[扭转](双向)图10-2强度条件:[]nW M on n τττ=≤=max,b S o τττ由试验得[弯曲](二向)强度条件(上下边缘点):[]σσ≤=zW M maxmax 中性层处:[]ττ≤⋅=bI S F Z z Q *maxmax max ([]σ、[]τ由试验得)为什么可以这样来建立强度条件? 因为:⑴构件内的应力状态比较简单;⑵用接近这类构件受力情况的试验装置测定极限应力值比较容易实现。
第十章-强度理论精品文档
赠言
闻之而不见,虽博必谬;见之而不知,虽识必 妄;知之而不行,虽敦必困。
〈荀子 ·儒效〉 解释 知:理解; 妄:虚妄; 敦:敦厚; 困:困扰 可见,闻、见、知、行是一个深化的过程
〈 怎样引出---强度理论?〉 • 为了解决组合变形问题,导致应力状态理论 从一点应力状态的无穷个微元中,找到了主单元体
“豆腐渣”工程触目惊心
●2019年7月12日,浙江常山县城南开发区一幢5 层住宅楼突然发生中部坍塌,整栋楼内39人中 仅3人幸存
●1994年,青海沟后水库大坝垮塌,淹死下游居 民近300人,失踪几十人
●2019年12月,四川德阳旌湖开发区一栋7层综 合楼倒塌,造成17人死亡
工 程 力 学 部
工 程 力 学 部
《评价》
主应力有压应力时,当 3 1 ,理论接近实验
但不完全符合 其他情况下,不如第一强度理论
《结论》
除了 1,还有1, 2 的参与,似乎有理,但是
实验通不过——好看未必正确
三、莫尔强பைடு நூலகம்理论
第1-4强度理论都是同 [ t ](拉伸)比较,能否
把 [ c(] 压缩)考虑进去?
1773年,Coulomb提出 1882年到1900年 Mohr 用应力圆形式提出
u 0 f 1 6 Es2 0 2s2 2 (1 6 E )
2单向拉伸
s
则
e q 1 21-222-323-12s
强度条件
e q 1 21-2 2 2-3 2 3-1 2 []
《失效准则》
平面应力状态的拉应力 1 与压应力 3
第十章 强度理论
坏的条件是1=u= b
强度条件: 1≤[] (10-1)
该理论可以解释铸铁等脆性材料在轴向拉伸时断面为横截面,在扭 。 转时的断面为45 螺旋面,因为这些面都是最大拉应力所在平面, 这些破坏现象与该理论相符合。 缺点: (1)只考虑1、而未考虑2 、3对材料发生脆断的影响;
2 .7 6 8 1 0 m m
6 3
(kN.m)
m ax
m ax
FS , m ax S z ,m ax dI z
6 2 5 1 0 2 .7 6 8 1 0
3
3
10 10
3
2041 10
6
c
6 8 4 .8 1 0 P a 8 4 .8 M P a 1 0 0 M P a
s s
u
2
s
按此理论,材料发生屈服破坏的条件是
又 m ax
1 3
2
m ax u
s
2
1 3= s 屈雷斯卡(Tresca)
屈服准则
强度条件:
1- 3
(10-3)
注意:该理论只适用于拉、压屈服极限相同的塑性材料
2. 形状改变能密度理论(或称第四强度理论) 该理论假设:形状改变能密度nd是引起材料屈服的主要因素。即 不论材料处于何种应力状态,只要单元体中的形状改变能密度nd 达到了材料的极限形状改变能密度ndu,材料就会发生屈服破坏, 同样,材料的极限形状改变能密度ndu由单向拉伸试验测定。 形状改变能密度: P260(13-7)式
第10章强度理论与组合变形的强度计算
sx
A
sx
sx
tzx
B
txz
sx
平面应力状态分析——解析法 To applying analytic method to solve State of Stress at a Given Point
sy
y
sy sx
txy
z
sx
等价
y x O x
txy
主应力的计算公式 the formula of Principal Stress
2 t xy t
s 1t ;s 2 0;s 3 t
s x s y 2 2 t max ( )t xy t 2 t min
破坏分析 failure analysis mild steel
tg2 0
2t xy
s x s y
0 45
2t x tan 2 0 s x s y
4
0 1
, 即极值剪应力面与主面成450
The planes for maximum shear stress can be determined by orienting an element 45° from the position of an element that defines the planes of principal stress
此方程曲线为圆—应力圆(或莫尔圆,由德 国工程师:Otto Mohr引入)
s
sx
y
O
sy
x
txy
t
n
A graphical solution to analysis the plane stress transformation (MOHR’s circle)
