高考数学专题精讲之二项式定理全面优质讲义
高考江苏数学大一轮精准复习课件二项式定理

01
在复杂表达式中,先合并同类项,简化表达式,再求特定项的
系数。
提取公因子
02
提取表达式中的公因子,使得剩余部分变得简单,从而容易求
出特定项的系数。
分组转化法
03
将复杂表达式进行分组转化,使得每一组都容易求出特定项的
系数,再将各组的结果相加即可。
典型例题解析
例题1
解析
例题2
解析
求$(1 + x + x^2)^5$展开 式中$x^7$的系数。
解析
该数列可以看作等差数列与等比数列相乘得到的数列,可以采用错位 相减法进行求和。
06
创新思维拓展与高考真题模拟
创新思维在二项式定理中体现
灵活应用二项式定理
通过组合数性质、数列求和等方法,巧妙解决二项式定理中的复 杂问题。
创新解题思路
运用归纳、猜想、构造等创新思维方法,探索二项式定理的更深层 次应用。
利用通项公式求指定项系数
指定项系数求解方法
介绍如何利用通项公式,求出二项式 展开式中指定项的系数。
典型例题解析
通过具体例题,详细解析求指定项系 数的方法和步骤。
求解最大(小)值问题方法
最大(小)值问题概述
介绍二项式展开式中最大(小 )值问题的基本概念和求解思 路。
最大(小)值求解方法
详细讲解如何利用导数等数学 工具,求解二项式展开式的最 大(小)值。
放缩法
在保持不等式方向不变的前提下,对不等式两边进行适当的放大 或缩小处理。
变量替换法
通过变量替换简化不等式结构,进而利用二项式定理进行证明。
典型例题解析
例题1
证明对于任意正整数n,都有(1+1/n)^n < e < (1+1/n)^(n+1)。
第03讲二项式定理(十五大题型)(课件)高考数学一轮复习(新教材新高考)

CONTENTS
01
考情分析
02
网络构建
03
知识梳理 题型归纳
04
真题感悟
01
考情分析
考点要求
考题统计
考情分析
(1)能用多项式运算法则 和计数原理证明二项式定 理. (2)会用二项式定理解决 与二项展开式有关的简单问 题.
2023年北京卷第5题,4分
(1)今后在本节的考查形式依然以选择
2023年天津卷第11题,5分
或者填空为主,以考查基本运算和基
2023年上海卷第10题,5分
本方法为主,难度中等偏下,与教材相
2022年I卷第13题,5分
当.
(2)本节内容在高考中的比重可能会持
稿定PPT
续降低,但仍然是备考的重要内容.
稿定PPT,海量素材持续更
新,上千款模板选择总有一
款适合你
02
网络构建
03
知识梳理 题型归纳
1.二项式定理
二项式定理 (a+b)n=C__0na_n_+__C_1n_a_n_-_1b_1_+__…__+__C_kn_a_n_-_kb_k_+__…__+__C_nn_b_n (n∈N*)
二项展开式 的通项
二项式系数
Tk+1=_C_kn_a_n_-_kb_k_,它表示展开式的第__k_+__1_项 _C_kn_(k=0,1,…,n)
题型十五:杨辉三角
04
真题感悟
D B 64
常见结论
1.两个常用公式 (1)C0n+C1n+C2n+…+Cnn=2n. (2)C0n+C2n+C4n+…=C1n+C3n+C5n+…=2n-1. 2.二项展开式的三个重要特征 (1)字母a的指数按降幂排列由n到0. (2)字母b的指数按升幂排列由0到n. (3)每一项字母a的指数与字母b的指数的和等于n.
高考数学讲义二项式定理讲义(B级).学生版
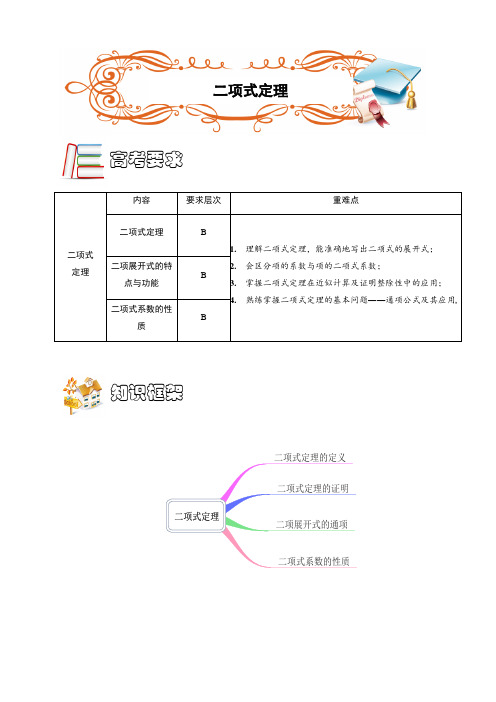
二项式定理内容要求层次重难点二项式定理 B1.理解二项式定理,能准确地写出二项式的展开式;2.会区分项的系数与项的二项式系数;3.掌握二项式定理在近似计算及证明整除性中的应用;4.熟练掌握二项式定理的基本问题――通项公式及其应用二项展开式的特点与功能B二项式系数的性质B二项式定理的定义二项式定理的证明二项展开式的通项二项式系数的性质二项式定理高考要求知识框架二项式定理一、定义:n nn r r n rn n n n n n n n b b a b a b a a b a C C C C C ++++++=+---ΛΛ22211)( )(*N n ∈,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做n b a )(+的二项展开式;上述二项展开式中各项的系数),,2,1,0(n r C rn Λ= 叫做二项式系数,第1+r 项叫做二项展开式的通项,用1+r T 表示;r r n rn r b a T C -+=1叫做二项展开式的通项公式. 二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共1+n (二项式的指数+1)项;指数:二项展开式各项的第一字母a 依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母b 依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数n ;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母b 的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a ,b 不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在b b a )(+的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据. 三、二项式系数的性质1. 对称性:在二项展开式中,与首末两项“等距离”的两项的二项式系数相等.2. 单调性:二项式系数(数列)在前半部分逐渐增大,在后半部分逐渐减小,在中间(项)取得最大值.其中,当n 为偶数时,二项展开式中间一项的二项式系数C n n2最大;当n 为奇数时,二项展开式中间两项的二项式系数Cn n21-,Cn n21+ 相等,且最大.3. 组合总数公式:n nn n n n C C C C 221=++++Λ 即二项展开式中各项的二项式系数之和等于n 2. 4. “一分为二”的考察:二项展开式中各奇数项的二项式系数之和等于各偶数项的二项式系数之和,即15314202-=+++=+++n n n n n n n C C C C C C ΛΛ.知识内容1. 二项式定理及其展开式【例1】 求5)1(x x +的展开式.【例2】 0.9915的近似值(精确到0.001)是【例3】 求证:(1)11--n n 能被2)1(-n 整除)3,(≥∈n N n ;2. 二项式系数【例4】 在8)1)(1(+-x x 的展开式中5x 的系数是( )A . –14B . 14C . –28D . 28【例5】 设1,2,3,4,5,k =则5)2(+x 的展开式中k x 的系数不可能是( )A . 10B . 40C . 50D . 80例题精讲【例6】 在8765)1()1()1()1(x x x x -+-+-+-的展开式中,3x 的项的系数为( )A . 74B . 121C . –74D . –121【例7】 已知n xx )21(3-)(*∈N n 的展开式中奇数项的二项式系数之和等于512,试求:(1)二项式系数最大的项; (2)系数的绝对值最大的项; (3)系数最大的项.【例8】 设2002002210200)14(x a x a x a a x ++++=-Λ ,求 ①展开式中各二项式系数的和;②展开式中各项系数的和; ③19931a a a +++Λ的值 ④20042a a a +++Λ的值 ⑤20021a a a +++Λ 的值3. 二项式展开式的通项公式【例9】 求9)1(xx -的二项展开式中3x 的系数.【例10】 求7)21(x +的二项展开式中,第4项的系数和第4项的二项式系数.【例11】 求10)1(xx +的二项展开式的第6项.【例12】 二项式6)1(xx +的展开式中常数项的值为______.【例13】 103)1(xx -展开式中的常数项是______.【例14】 (2010江西卷理6)8)2(x -展开式中不含4x 项的系数的和为( )A .-1B .0C .1D .24. 二项式定理在解决整除性问题中的应用【例15】 今天是星期一,再过n 8天后的那一天是星期几?【例16】 9291除以100的余数是( ).5. 信息迁移【例17】 若)()21(2004200422102004R x x a x a x a a x ∈++++=-Λ,)()()(200402010a a a a a a ++++++Λ= _______.(用数字作答)【例18】 已知函数1212)(+-=x x x f ,求证:对于任意不小于3的自然数n ,都有1)(+>n n n f .【例19】 求证:*12(1)3(2,)n n n N n <+<≥∈1. 在使用通项公式r r n rn r b a T C -+=1时,要注意:①通项公式是表示第r +1项,而不是第r 项②展开式中第r +1项的二项式系数C rn 与第r +1项的系数不同③通项公式中含有a ,b ,n ,r ,1+r T 五个元素,只要知道其中的四个元素,就可以求出第五个元素在有关二项式定理的问题中,常常遇到已知这五个元素中的若干个,求另外几个元素的问题,这类问题一般是利用通项公式,把问题归纳为解方程(或方程组)这里必须注意n 是正整数,r 是非负整数且r ≤n2. 证明组合恒等式常用赋值法3. 二项式定理应用通常有以下几类题型:①通项应用型:利用通项公式研究具体某一项系数的性质等问题②系数配对型:展开两因式乘积或可化为两因式乘积的三项式,求某项系数③系数性质型:灵活应用二项式系数性质或赋值求系数和④利用二项式定理求近似值,证明整除性或求余数问题,证明恒等式或不等式⑤在概率等方面的应用课堂总结【习题1】(2010全国Ⅰ卷理5)533)1()21(x x -+的展开式中x 的系数是( )A . -4B . -2C . 2D . 4【习题2】4)2(x x +的展开式中3x 的系数是( )A 6B 12C 24D . 48【习题3】73)12(xx -的展开式中常数项是( )A 14B -14C 42D -42【习题4】(2010陕西卷理4))(5R x x a x ∈⎪⎭⎫ ⎝⎛+展开式中3x 的系数为10,则实数a 等于( )A .-1B .0.5C .1D .2【习题5】若n xxx )1(3+的展开式中的常数项为84,则n =_____________【习题6】已知n x x )1(lg +展开式中,末三项的二项式系数和等于22,二项式系数最大项为20000,求x 的值【习题7】(2010安徽卷理12)6)(xy y x -展开式中,3x 的系数等于________.课后检测。
高考数学复习考点知识讲解课件64 二项式定理

则正整数n的最小值是(
)
A.3
B.4
答案:(1)C
C.5
D.6
-5
1 n
解析:(1)( x − 2 ) 的展开式的通项Tr+1 = · -1 · 2 ,r=0,1,2,
x
n−5r
3,…,n.令
=0,可得n=5r.因为展开式中含有常数项,所以n=5r能成立,
2
则正整数n的最小值为5.
x
·x
=C4−r
x
,取4-
r-3m=0,当m=0时,r=4,常数项为C44 ×C00 ×(-1)4=1;当m=1时,r=1,
常数项为C41 ×C31 ×(-1)1=-12.所以所求常数项为1-12=-11.
(2)[2023·山东五校调研]在(x2-2x-3)4的展开式中,含x6的项的系数
12
是________.
关的量的步骤
(1)根据二项式定理把(a+b)m与(c+d)n分别展开,并写出其通项公式;
(2)根据特定项的次数,分析特定项可由(a+b)m与(c+d)n的展开式中
的哪些项相乘得到;
(3)把相乘后的项合并即可得到所求特定项或相关量.
角度3 求解形如(a+b+c)n(n∈N*)的展开式中与特定项相关的量
+4x=7x,a4=C33 x0(-1)3+C44 x014=0,所以a2=3,a3=7,a4=0,所以a2+
a3+a4=10.
关键能力—考点突破
考点一
二项展开式中的项
[基础性、应用性]
角度1 求解形如(a+b)n(a∈N*)的展开式中与特定项相关的量
1 n
[例1] (1)[2023·四川成都模拟]若( x − 2 ) 的展开式中含有常数项,
高考数学一轮专项复习ppt课件-二项式定理(通用版)

第22页
高考一轮总复习•数学
第23页
解析:(1)x+mx x-1x5=xx-1x5+mx x-1x5.【会思考】x+mx 的每一项都要考虑,要注 意系数和符号因3页
重难题型 全线突破
高考一轮总复习•数学
题型
求展开式中的特定项的多维研讨
维度 1 利用通项公式求二项展开式的特定项
典例 1(1)(2024·天津南开中学第一次阶段测试)x-x326 展开式中的常数项是 方法一:通项;
方法二:凑:C46x4-x322.(
)
A.-135
B.135
+3-x3 的展开式中,x2 的系数是__2_0_2_3___.(用数字作答)
答案
高考一轮总复习•数学
第20页
解析:(1)2x-mx 6 的展开式的通项为 Tr+1=Cr6(2x)6-r-mx r=Cr6·26-r·(-m)r·x6-2r, 令 6-2r=0,得 r=3, 所以常数项为 C36·26-3·(-m)3=-20,解得 m=12. (2)用 1,2,3,4,5 组成没有重复数字的五位数中,满足个位小于百位且百位小于万位的五位 数有 C35A22=20(个),即 n=20. 当 n=20 时,不妨设 x≠0,则(1+x)3+(1+x)4+(1+x)5+…+(1+x)n+3-x3=(1+x)3+(1 +x)4+(1+x)5+…+(1+x)23-x3=1+x13-[1-1+1x+ x21]-x3=1+x3--x1+x24-x3=1+xx24 -1+x x3-x3,所以 x2 的系数是 C324-C33=2 024-1=2 023.
高考数学一轮总复习 专题11 计数原理 11.2 二项式定理

3.在二项式定理中,如果设a=1,b=x,则得到公式:(1+x)n=1+ C1n x+ C2n x2+ C3n x3 +…+ Cnn xn.如果设a=1,b=-x,则得到公式:(1-x)n=1+(-1)1 C1n x+(-1)2 C2n x2+…+(-
1)n Cnn xn. 4.二项式系数与项的系数是不同的,如(a+bx)n(a,b∈R)的展开式中,第r+1
考向突破
考Байду номын сангаас一 求指定项或指定项系数
例1
(2018浙江温州二模(3月),5)在
1 x
9
2x
的展开式中,常数项是
()
A. C39
B.- C92
C.8 C39
D.-8 C39
解析
1 x
9
2x
的展开式的通项为Tr+1= C9r
·
1 x
9r
·(-2x)r=(-2)r·C 9r
项的二项式系数是 Crn ,而第r+1项的系数为 Crn an-rbr. 5.通项公式主要用于求二项式的指数,求满足条件的项或系数,求展开式
的某一项或系数.在运用公式时要注意以下几点:
(1) Ckn an-kbk是第k+1项,而不是第k项; (2)运用通项公式Tk+1= Ckn an-kbk解题时,一般都需先转化为方程(组)求 出n、k,然后代入通项公式求解;
(3)求展开式的一些特殊项,通常都是由题意列方程求出k,再求所需的某 项;有时需要求n,计算时要注意n和k的取值范围及它们之间的大小关系. 6.在(a+b)n的展开式中,令a=b=1,得 C0n + C1n +…+ Cnn =2n;令a=1,b=-1,得 C0n - C1n + C2n - C3n +…=0,∴ C0n + C2n + C4n +…= C1n + C3n + C5n +…=2n-1. 7.对二项式系数性质的理解 (1)对称性:由组合数的性质“ Cmn = Cnnm ”,得从“ C0n = Cnn =1”开始,由左右 分别向中间靠拢,便有 C1n = Cnn1 , C2n = Cnn2 ,…… (2)最大值:当n为偶数时,(a+b)n的展开式共有n+1项,n+1是奇数,这时展 开式的形式是
高考数学《二项式定理》课件
解析 2x+1x-35表示五个2x+1x-3相乘,则展开式中的常数项由三种情况
产生,第一种是从五个2x+1x-3中分别抽取 2x,2x,1x,1x,-3,则此时的
常数项为 C25·C23·22·(-3)=-360; 第二种情况是从五个2x+1x-3中都抽取-3,则此时的常数项为(-3)5=-243; 第三种情况是从五个2x+1x-3中分别抽取 2x,x1,-3,-3,-3,则此时 的常数项为 C15·C14·21·(-3)3=-1 080,则展开式中常数项为-360-243- 1 080=-1 683.
索引
诊断自测 1.思考辨析(在括号内打“√”或“×”)
(1)Cknan-kbk 是二项展开式的第 k 项.( × ) (2)二项展开式中,系数最大的项为中间一项或中间两项.( × ) (3)(a+b)n 的展开式中某一项的二项式系数与 a,b 无关.( √ )
(4)(a+b)n 某项的系数是该项中非字母因数部分,包括符号等,与该项的二项
1=[1-(2-x)]100-1=(x-1)100-1, 即(x-1)100-1=a0+a1x+a2x2+…+a100x100. 令x=1,得a0+a1+a2+…+a100=-1. 令x=0,得a0=0. 又易知a100=1,所以a1+a2+a3+…+a99=-2.
索引
高考数学复习考点知识讲解课件54 二项式定理
(新教材) 高三总复习•数学
— 返回 —
考点二 二项式系数的性质与各项系数和——师生共研
【例 1】 (1)(多选)在二项式x13-3x2n 的展开式中,只有第 5 项的二项式系数最大, 则( BD )
A.n=10
B.展开式中没有常数项
C.展开式所有二项式系数和为 1024
D.展开式所有项的系数和为 256
知识梳理
1.二项式定理 (1)二项式定理:(a+b)n= C0nan+C1nan-1b+…+Cknan-kbk+…+Cnnbn (n∈N*). (2)通项公式:Tk+1= Cnkan-kbk ,它表示第 k+1 项. (3)二项式系数:二项展开式中各项的系数 C0n,C1n,…,Cnn.
— 4—
(新教材) 高三总复习•数学
+8=0,
解得 n=8 或 n=1(舍去).
所以二项式系数的最大项为 C48
x× 1 24
x4=385x.
设第 r+1 项的系数 ar+1 最大,
显然 ar+1>0,故有aar+r 1≥1 且aarr+ +21≤1,
— 22 —
(新教材) 高三总复习•数学
∵aar+r 1=C8rC-1r8··22--rr+1=9- 2r r,
解法二:二项式2
x+xa25 的展开式的常数项为 C15(2
x)4xa21=80a,所以 80a=16,
解得 a=15,故选 D.
— 14 —
(新教材) 高三总复习•数学
— 返回 —
3.(2023·河北保定期末)3x-
1 6 x
的展开式中,有理项共有___4____项.
[解析]
3x-
1 6 x
的展开式的通项公式为
高中数学完整讲义——二项式定理1二项展开式1求展开式中的指定项
1.二项式定理⑴二项式定理()()011222...nn n n n n n n n n a b C a C a b C a b C b n --*+=++++∈N这个公式表示的定理叫做二项式定理.⑵二项式系数、二项式的通项011222...nn n n n nnnnC a C a b C ab C b --++++叫做()na b +的二项展开式,其中的系数()0,1,2,...,r n C r n =叫做二项式系数,式中的r n r rnC a b -叫做二项展开式的通项,用1r T +表示,即通项为展开式的第1r +项:1r n r rr n T C a b -+=.⑶二项式展开式的各项幂指数二项式()na b +的展开式项数为1n +项,各项的幂指数状况是①各项的次数都等于二项式的幂指数n .②字母a 的按降幂排列,从第一项开始,次数由n 逐项减1直到零,字母b 按升幂排列,从第一项起,次数由零逐项增1直到n . ⑷几点注意①通项1r n r rr nT C a b -+=是()na b +的展开式的第1r +项,这里0,1,2,...,r n =. ②二项式()n a b +的1r +项和()nb a +的展开式的第1r +项r n r rnC b a -是有区别的,应用二项式定理时,其中的a 和b 是不能随便交换的.③注意二项式系数(r n C )与展开式中对应项的系数不一定相等,二项式系数一定为正,而项的系数有时可为负.④通项公式是()na b +这个标准形式下而言的,如()na b -的二项展开式的通项公式是()11rr n r rr n T C a b -+=-(只须把b -看成b 代入二项式定理)这与1r n r r r n T C a b -+=是不同的,在这里对应项的二项式系数是相等的都是r n C ,但项的系数一个是()1rr n C -,一个是r n C ,可看出,二项式系数与项的系知识内容求展开式中的指定项数是不同的概念.⑤设1,a b x ==,则得公式:()12211......nr r n nn n x C x C x C x x +=++++++. ⑥通项是1r T +=r n r rnC a b -()0,1,2,...,r n =中含有1,,,,r T a b n r +五个元素, 只要知道其中四个即可求第五个元素.⑦当n 不是很大,x 比较小时可以用展开式的前几项求(1)n x +的近似值.2.二项式系数的性质⑴杨辉三角形:对于n 是较小的正整数时,可以直接写出各项系数而不去套用二项式定理,二项式系数也可以直接用杨辉三角计算.杨辉三角有如下规律:“左、右两边斜行各数都是1.其余各数都等于它肩上两个数字的和.” ⑵二项式系数的性质:()na b +展开式的二项式系数是:012,,,...,n n n n n C C C C ,从函数的角度看r n C 可以看成是r 为自变量的函数()f r ,其定义域是:{}0,1,2,3,...,n . 当6n =时,()f r 的图象为下图:这样我们利用“杨辉三角”和6n =时()f r 的图象的直观来帮助我们研究二项式系数的性质. ①对称性:与首末两端“等距离”的两个二项式系数相等.事实上,这一性质可直接由公式m n m n n C C -=得到.②增减性与最大值如果二项式的幂指数是偶数,中间一项的二项式系数最大;如果二项式的幂指数是奇数,中间两项的二项式系数相等并且最大. 由于展开式各项的二项式系数顺次是 ()01211,,112n n n n n n C C C -===⋅,()()312123n n n n C --=⋅⋅,...,()()()()112...2123....1k n n n n n k C k ----+=⋅⋅⋅⋅-,()()()()()12...21123...1knn n n n k n k C k k---+-+=⋅⋅⋅-,...,1n n C =.其中,后一个二项式系数的分子是前一个二项式系数的分子乘以逐次减小1的数(如,1,2,...n n n --),分母是乘以逐次增大的数(如1,2,3,…).因为,一个自然数乘以一个大于1的数则变大,而乘以一个小于1的数则变小,从而当k 依次取1,2,3,…等值时,r n C 的值转化为不递增而递减了.又因为与首末两端“等距离”的两项的式系数相等,所以二项式系数增大到某一项时就逐渐减小,且二项式系数最大的项必在中间.当n 是偶数时,1n +是奇数,展开式共有1n +项,所以展开式有中间一项,并且这一项的二项式系数最大,最大为2n nC .当n 是奇数时,1n +是偶数,展开式共有1n +项,所以有中间两项. 这两项的二项式系数相等并且最大,最大为1122n n nnCC-+=.③二项式系数的和为2n ,即012......2r n n nn n n n C C C C C ++++++=. ④奇数项的二项式系数的和等于偶数项的二项式系数的和,即0241351......2n n n n n n n C C C C C C -+++=+++=.常见题型有:求展开式的某些特定项、项数、系数,二项式定理的逆用,赋值用,简单的组合数式问题.【例1】62⎛⎝的展开式中的第四项是 .【例2】6⎛⎫的展开式中,3x 的系数等于_ ___.【例3】((3511+-的展开式中x 的系数是A .4-B .2-C .2D .4典例分析【例4】 若9a x x ⎛⎫- ⎪⎝⎭的展开式中3x 的系数是84-,则a = .【例5】 5a x x ⎛⎫+ ⎪⎝⎭()x ∈R 展开式中3x 的系数为10,则实数a 等于A .1-B .12C .1D .2【例6】 若2012(12)n n n x a a x a x a x -=++++L ,则2a 的值是( )A .84B .84-C .280D .280-【例7】8()x -的展开式中62x y 项的系数是( )A .56B .56-C .28D .28-【例8】 若()554541031x a x a x a x a +=++⋅⋅⋅++,则2a 的值为( )A .270B .2702xC . 90D .902x【例9】 的展开式中的系数是_______(用数字作答).【例10】 在的展开式中,的系数为_______(用数字作答).64(1(1+x 25(42)x x ++x【例11】 在的展开式中,的系数为_______(用数字作答).【例12】 在的展开式中,的系数为_______(用数字作答).【例13】 求展开式中含项系数.【例14】 在的展开式中,项的系数是 .(用数字作答)【例15】 的展开式中的系数等于________.(用数字作答)【例16】展开式中的系数是_______(用数字作答).【例17】 在的展开式中的系数是( )25(42)x x ++2x 25(42)x x ++3x 294(31)(21)x x x +-+2x 26(1)(1)(1)x x x ++++++L 2x 2345(1)(1)(1)(1)(1)x x x x x ---+---+-2x 291()2x x-9x 8(1)(1)x x -+5xA .−14B .14C .−28D .28【例18】 在的展开式中,含的项的系数是( )A .15-B .85C .120-D .274【例19】 在的展开式中,含项的系数是 (用数字作答)【例20】 求展开式中的系数.【例21】 的展开式中的系数是_______(用数字作答).【例22】 在的展开式中,的系数为_______(用数字作答).【例23】 在的展开式中,的系数为_______(用数字作答).(1)(2)(3)(4)(5)x x x x x -----4x 56789(1)(1)(1)(1)(1)x x x x x -+-+-+-+-3x 26(1)x x +-5x 64(1(1+x 25(42)x x ++x 25(42)x x ++2x【例24】 在的展开式中,的系数为_______(用数字作答).【例25】 求展开式中含项系数.【例26】 在的展开式中,项的系数是 .(用数字作答)【例27】 的展开式中的系数等于________.(用数字作答)【例28】展开式中的系数是_______(用数字作答).25(42)x x ++3x 294(31)(21)x x x +-+2x 26(1)(1)(1)x x x ++++++L 2x 2345(1)(1)(1)(1)(1)x x x x x ---+---+-2x 291()2x x-9x【例29】 在的展开式中的系数是( )A .−14B .14C .−28D .28【例30】 在的展开式中,含的项的系数是( )(A )15- (B )85 (C )120- (D )274【例31】 在的展开式中,含项的系数是 (用数字作答)【例32】 求展开式中的系数.【例33】 在二项式的展开式中,含的项的系数是( )A .B .C .D .【例34】的展开式中的系数是______,的系数为______.8(1)(1)x x -+5x (1)(2)(3)(4)(5)x x x x x -----4x 56789(1)(1)(1)(1)(1)x x x x x -+-+-+-+-3x 26(1)x x +-5x 521x x ⎛⎫- ⎪⎝⎭4x 10-105-534(12)(1)x x +-x 2x【例35】 的展开中含的项的系数为( )A .B .C .D .【例36】 的展开式中的系数是( )A .B .C .3D . 4【例37】 求展开式中的系数;【例38】 在二项式的展开式中,含的项的系数是( )A .B .C .D .【例39】的展开式中的系数是( ) A .B .C .D .【例40】 在的展开式中,的系数为 (用数字作答)411(1)x x ⎛⎫++ ⎪⎝⎭2x 461012((6411+x 4-3-()()31011x x -+5x 521x x ⎛⎫- ⎪⎝⎭4x 10-105-56(2)x +3x 2040801604(1x【例41】 在的展开式中,的系数为 _____ (用数字作答)【例42】 的二项展开式中含的项的系数为( ) A .B .C .D .【例43】 若的二项展开式中的系数为则 .(用数字作答)【例44】 设常数,展开式中的系数为,则=_____.【例45】 已知(是正整数)的展开式中,的系数小于120,则 .((333(1)11x +++++x 91x x ⎛⎫- ⎪⎝⎭3x 36-84-3684261()x ax +3x 5,2a =0a>24(ax 3x 32a 26(1)kx +k 8x k =【例46】 已知的展开式中的系数与的展开式中的系数相等 .【例47】的二项展开式的第项的系数为() A .B .C .D .【例48】 若的二项展开式中的系数为则.(用数字作答)【例49】 若与的展开式中含的系数相等,则实数的取值范围是( )A .B .C .D .【例50】 已知,则二项式 展开式中含项的系数是 .【例51】 在的展开式中,的系数是的系数与的系数的等差中项,若实数,那么.5(cos 1)x θ+2x 45()4x +3x cos θ=106210-252-210252261()x ax +3x 5,2a =__________21()n x m ++2(1)(*0)n mx n m +∈≠N ,n x m 12(]23,2[1)3,(0)-∞,(0)+∞,()π0sin cos a x x dx =+⎰6⎛ ⎝2x 7(1)ax +3x 2x 4x 1a >_______a =【例52】 已知(是正整数)的展开式中,的系数小于,则______.【例53】的展开式中的系数为 .【例54】 若的展开式中,的系数是的系数的倍,求;【例55】的展开式中,的系数与的系数之和等于__________.【例56】 已知为实数,展开式中的系数是,则_______.26(1)kx +k 8x 120k=4(33x y (1)n x +3x x 7n 10()x y -73x y 37x y a 10()x a +7x 15-a =【例57】 二项式的展开式中第三项系数比第二项系数大,求第项的系数.【例58】 求的二项展开式中含的项的二项式系数与系数.【例59】 若的展开式中前三项的系数成等差数列,则展开式中项的系数为_______.【例60】 令为的展开式中含项的系数,则数列的前项和为.41nx ⎛⎫ ⎪⎝⎭44491x x ⎛⎫- ⎪⎝⎭3x 12nx x ⎛⎫+ ⎪⎝⎭4x n a 1()(1)n n f x x +=+1n x -1{}na 2009______【例61】 在的展开式中,的系数是的系数与的系数的等差中项,求的值.【例62】 已知,则 .【例63】 在展开式中,与的系数分别为,如果3ab =,那么的值为() A . B . C . D .【例64】 若的展开式中的系数是, 则实数的值是_______.7(1)ax +(1)a >3x 2x 4x a ()52551110ax x bx a x +=++++L b =()1n x +3x 2x a b ,b 706055405(1)ax -3x 80-a【例65】 设常数,展开式中的系数为,则 .【例66】 若展开式中含项的系数与含项的系数之比为,则等于( ) A .B .C .D .【例67】 设为的展开式中含项的系数,则数列的前项和为_____【例68】 已知展开式的第二项与第三项的系数比是,则________.【例69】 在的展开式中,如果第项和第项的二项式系数相等,则第项为______0a>42ax ⎛ ⎝3x 32a =12nx x ⎛⎫- ⎪⎝⎭21x 41x 5-n 46810n a 1()(1)n n f x x +=+1n x -1n a ⎧⎫⎨⎬⎩⎭n 12nx x ⎛⎫+ ⎪⎝⎭1:2n =220(1)x -4r 2r +4r【例70】 若在二项式的展开式中任取一项,则该项的系数为奇数的概率是.【例71】 已知展开式中最后三项的系数的和是方程的正数解,它的中间项是,求的值.【例72】 设数列是等比数列,,公比是的展开式的第二项. ⑴用表示通项与前项和;⑵若用表示10(1)x +_____lg lg 2(21)x n x ++2lg(7272)0y y --=410+x {}n a 311232C m m m a +-=Αq 421()4x x +n x ,n a n n S 1212C C C n n n n n n A S S S =+++L n x ,n A。
高中数学完整讲义——二项式定理1.二项展开式1求展开式中的指定项
求睁开式中的指定项知识内容1.二项式定理⑴二项式定理an0 n 1 n 1 2 n 2 2n nN b C n a C n a b C n a b... C n b n这个公式表示的定理叫做二项式定理.⑵二项式系数、二项式的通项0 n1n 1 2 n 2 2n nrn C n r 0, 1, 2, ..., n叫做二C n a C n a b C n a b ...C n b 叫做 a b的二项睁开式,此中的系数项式系数,式中的C n r a n r b r叫做二项睁开式的通项,用T r 1表示,即通项为睁开式的第r 1 项:T r 1C n r a n r b r.⑶二项式睁开式的各项幂指数二项式 a b nn 1 项,各项的幂指数情况是的睁开式项数为①各项的次数都等于二项式的幂指数n .②字母 a 的按降幂摆列,从第一项开始,次数由n 逐项减 1 直到零,字母b按升幂摆列,从第一项起,次数由零逐项增 1 直到 n .⑷几点注意①通项 T rr n r r是 a bn1 项,这里 r0, 1, 2,..., n .1C n a b的睁开式的第 ran1项和nr a r是有区其他,应用二项式定理时,其②二项式b的 r b a 的睁开式的第r 1项 C n r b n中的 a 和b是不可以随意互换的.③注意二项式系数(C n r)与睁开式中对应项的系数不必定相等,二项式系数必定为正,而项的系数有时可为负.④通项公式是n这个标准形式下而言的,如 a bna b的二项睁开式的通项公式是r r n r rb 当作 b 代入二项式定理)这与T r 1r n r rT r 11C n a b (只须把C n a b 是不一样的,在这里对应项的C n r r二项式系数是相等的都是,但项的系数一个是 1 C n r,一个是 C n r,可看出,二项式系数与项的系思想的挖掘能力的飞腾1数是不一样的观点.⑤设 a 1, b x ,则得公式:n...C n r x r... x n.1 x1 C n1 x C n2 x2⑥通项是 T r 1C n r a n r b r r0, 1, 2, ..., n 中含有 T r 1, a , b , n , r 五个元素,只需知道此中四个即可求第五个元素.⑦当 n 不是很大, x 比较小时能够用睁开式的前几项求(1x)n的近似值.2.二项式系数的性质⑴杨辉三角形:关于 n 是较小的正整数时,能够直接写出各项系数而不去套用二项式定理,二项式系数也能够直接用杨辉三角计算.杨辉三角有以下规律:“左、右两边斜行各数都是 1.其他各数都等于它肩上两个数字的和.”⑵二项式系数的性质:an睁开式的二项式系数是:012n,从函数的角度看r能够当作是r 为自变量的函数b C n, C n , C n , ..., C n C nf r,其定义域是: 0, 1, 2,3, ...,n.当n6时, f r 的图象为下列图:这样我们利用“杨辉三角”和n 6 时f r的图象的直观来帮助我们研究二项式系数的性质.①对称性:与首末两头“等距离”的两个二项式系数相等.事实上,这一性质可直接由公式C n m C n n m获得.②增减性与最大值假如二项式的幂指数是偶数,中间一项的二项式系数最大;假如二项式的幂指数是奇数,中间两项的二项式系数相等而且最大.因为睁开式各项的二项式系数按序是C n01, C n1n, C n2n n 1,1 1 22思想的挖掘能力的飞腾C n3n n1n2,...,1 23C n k 1n n 12n2... n k 2 ,C n k n n 1 n 2 ... n k2n k 1,...,1 3 ....k112 3...k 1 kC n n 1 .此中,后一个二项式系数的分子是前一个二项式系数的分子乘以逐次减小 1 的数(如n, n1, n 2,... ),分母是乘以逐次增大的数(如1, 2, 3,).因为,一个自然数乘以一个大于 1 的数则变大,而乘以一个小于 1 的数则变小,进而当k 挨次取1,2,3,等值时,r的值转变为不递加而递减了.又因为C n与首末两头“等距离”的两项的式系数相等,因此二项式系数增大到某一项时就渐渐减小,且二项式系数最大的项必在中间.当 n 是偶数时,n1是奇数,睁开式共有 n 1 项,因此睁开式有中间一项,而且这一项的二项式系数n最大,最大为C n2.当 n 是奇数时,n 1 是偶数,睁开式共有n 1项,因此有中间两项.n 1n1这两项的二项式系数相等而且最大,最大为C n2C n2.③二项式系数的和为012r...n n.2n,即C n C n C n ...C n C n2④奇数项的二项式系数的和等于偶数项的二项式系数的和,即024135n1C n C n C n ...C n C n C n... 2.常有题型有:求睁开式的某些特定项、项数、系数,二项式定理的逆用,赋值用,简单的组合数式问题.典例剖析16【例1】 2的睁开式中的第四项是.x3x y 6【例 2】的睁开式中,x3的系数等于____.y x35【例 3】 1 2 x13 x 的睁开式中 x 的系数是A .4B .2C. 2 D .4思想的挖掘能力的飞腾3a 9【例 4】若 x的睁开式中 x3的系数是84 ,则a.xa 5【例 5】 x( x R ) 睁开式中 x3的系数为10,则实数 a 等于xA .1B .1C.1D. 2 2【例 6】若 (1 2 x)n a0a1 x a2 x2L a n x n,则 a2的值是()A.84B.84C.280D.280【例 7】862项的系数是()( x2 y) 的睁开式中x yA.56 B .56C.28D.28【例8】若5a4 x4a1x a0,则 a2的值为(3x 1a5 x5)A .270B. 270 x2C. 90D. 90 x2【例 9】(1x )6 (1x)4的睁开式中x 的系数是_______(用数字作答).【例 10】在 (x2 4 x 2)5的睁开式中,x 的系数为_______(用数字作答).4思想的挖掘能力的飞腾【例 11】在 ( x24x 2)5的睁开式中,x2的系数为 _______(用数字作答).【例 12】在 ( x24x 2)5的睁开式中,x3的系数为 _______(用数字作答).294睁开式中含 x2项系数.【例 13】求 ( x3x 1) (2 x1)【例 14】在 (1 x) (1 x)2L(1 x)6的睁开式中,x2项的系数是.(用数字作答)【例 15】 ( x 1) (x 1)2( x 1)3( x 1)4(x 1)5的睁开式中x2的系数等于 ________.(用数字作答)1 )9睁开式中x9的系数是_______(用数字作答).【例 16】 (x22x【例 17】在 ( x 1)(x 1)8的睁开式中x5的系数是()思想的挖掘能力的飞腾5A .-14B. 14C. -28 D . 28【例 18】在 (x1)(x2)( x 3)( x4)( x 5) 的睁开式中,含x4的项的系数是()A .15B.85C.120 D .274【例 19】在 (1 x)5(1 x) 6(1 x)7(1 x)8(1 x)9的睁开式中,含x3 项的系数是(用数字作答)【例 20】求 (1 x x2 ) 6睁开式中x5的系数.【例 21】 (1x )6 (1x)4的睁开式中x 的系数是_______(用数字作答).【例 22】在 (x2 4 x 2)5的睁开式中,x 的系数为_______(用数字作答).【例 23】在 (x2 4 x 2)5的睁开式中,x2的系数为 _______(用数字作答).6思想的挖掘能力的飞腾【例 24】在 ( x 24x 2)5的睁开式中,3的系数为 _______(用数字作答).x【例 25】求 ( x23x 1)9 (2 x 1)4睁开式中含x2项系数.【例 26】在 (1 x) (1 x)2L(1 x)6的睁开式中,x2项的系数是.(用数字作答)【例 27】 ( x 1) (x 1)2( x 1)3( x 1)4(x 1)5的睁开式中x2的系数等于 ________.(用数字作答)【例 28】 (x21)9睁开式中 x9的系数是 _______(用数字作答).2x思想的挖掘能力的飞腾7【例 29】在 (x 1)(x 1)8的睁开式中x5的系数是()A .-14B. 14C. -28 D . 28【例 30】在 (x1)(x2)( x 3)( x 4)( x5) 的睁开式中,含x4的项的系数是()( A )15(B) 85( C)120( D )274【例 31】在 (1 x)5(1 x)6(1 x)7(1 x)8(1 x)9 的睁开式中,含x3项的系数是(用数字作答)【例 32】求 (1 x x2 ) 6睁开式中x5的系数.15【例 33】在二项式 x2的睁开式中,含x4的项的系数是()xA. 10B. 10C. 5 D . 5【例 34】 (1 2 x)3 (1 x)4的睁开式中x 的系数是______,x2的系数为______.8思想的挖掘能力的飞腾【例 35】 11(1x)4的睁开中含 x2的项的系数为()xA .4B . 6C. 10D.1264【例 36】 1x 1x 的睁开式中x的系数是()A .4B . 3C. 3 D . 4【例 37】求 1 x 3 1x 10睁开式中 x5的系数;【例 38】在二项式 x215的睁开式中,含x4的项的系数是()xA. 10B. 10C. 5D. 5【例 39】 (x 2)6的睁开式中x3 的系数是()A. 20B. 40C. 80D. 160【例 40】在 (1x)4的睁开式中,x 的系数为(用数字作答)思想的挖掘能力的飞腾9【例 41】在 (1 x)3313_____ (用数字作答)1x3 x 的睁开式中,x的系数为9【例 42】 x1的二项睁开式中含x3的项的系数为()xA .36B.84C.36D.84【例 43】若 (x216的二项睁开式中3的系数为5.(用数字作答)ax)x, 则a2【例 44】设常数 a2143的系数为3,则 a =_____.0 , (axx)睁开式中 x2【例 45】已知 (1 kx2 )6( k 是正整数)的睁开式中,x8的系数小于120,则 k.10思想的挖掘能力的飞腾【例 46】已知 ( xcos1)5 的睁开式中 x 2 的系数与 ( x 5 )4 的睁开式中 x 3 的系数相等4cos.1 10【例 47】的二项睁开式的第 6 项的系数为()xxA . 210B . 252C . 210D . 252【例 48】若 ( x 21 )6 的二项睁开式中 x 3 的系数为 5 , 则 a __________.(用数字作答)ax2【例 49】 若 ( x 2n 1 与 (mx 2 n0) 的睁开式中含 xn的系数相等,则实数 m 的取值范围m)1) (n N * ,m是()A . 1,22 , C . (,0)D . (0, )(B . [1)2 331 6【例 50】已知 a0πsin x cos x dx ,则二项式 a x睁开式中含 x 2 项的系数是.x【例 51】在 ( ax7的睁开式中,x 3 的系数是 x 2 的系数与 x 4 的系数的等差中项,若实数a 1 ,那么1) a _______ .【例 52】已知 (1 kx2 )6( k 是正整数)的睁开式中,x8的系数小于 120 ,则 k ______.【例 53】 ( x y y x)4的睁开式中x3 y3的系数为.【例 54】若 (1 x)n的睁开式中,x3的系数是x的系数的 7 倍,求n;【例 55】 ( x y)10的睁开式中,x7 y3的系数与x3 y7的系数之和等于__________ .【例 56】已知a为实数, ( x a)10睁开式中 x7的系数是15 ,则a_______.121n【例 57】二项式的睁开式中第三项系数比第二项系数大44,求第4项的系数.x x4x19【例 58】求 x的二项睁开式中含x3的项的二项式系数与系数.x1n【例 59】若 x的睁开式中前三项的系数成等差数列,则睁开式中x4项的系数为 _______.2x【例 60】令 a n为 f n (x)(1 x)n 1的睁开式中含x n 1项的系数,则数列{1} 的前 2009 项和为______.a n【例 61】在 (ax 1)7 (a 1) 的睁开式中,x3的系数是 x2的系数与 x4的系数的等差中项,求 a 的值.【例 62】已知 1 ax 52L a5 x5,则 b.1 10 x bx【例 63】在 1 x n的系数分别为 a ,b ,假如a3 ,那么 b 的值为()睁开式中, x3与 x2bA.70B.60C.55D.40【例 64】若 (ax 1)5的睁开式中x3的系数是80 ,则实数a的值是_______.142143【例 65】设常数 a0 , ax睁开式中 x3 的系数为,则 a.x21n12项的系数与含14项的系数之比为【例 66】若 2x睁开式中含 5 ,则n等于()x x xA . 4B.6C.8D.10【例 67】设 a n为 f n (x) (1 x)n 1的睁开式中含n 1项的系数,则数列1x的前 n 项和为_____a n1n【例 68】已知 x睁开式的第二项与第三项的系数比是1: 2 ,则n ________.2x【例 69】在 (1 x2 ) 20的睁开式中,假如第4r 项和第 r 2 项的二项式系数相等,则第4r 项为 ______【例 70】若在二项式 ( x 1)10的睁开式中任取一项,则该项的系数为奇数的概率是_____ .【例 71】已知 (2 x lg x lg21)n睁开式中最后三项的系数的和是方程lg( y272 y 72) 0 的正数解,它的中间项是 1042lg2,求 x 的值.【例 72】设数列 { a n } 是等比数列,3m1,公比是14的睁开式的第二项.1C2m3 m2q( x2 )aΑ4x⑴用 n,x 表示通项a n与前n项和S n;⑵若 A C1 S C2S L C n S 用n ,x 表示 An n 1n 2n n n 16。
