刚体的转动_2 - 武警学院精品课程建设
合集下载
刚体的转动
刚体的转动
4-1 刚体的转动
一. 刚体
1. 定义:不发生形变的物体。 说明: “刚体”是一理想模型。
2. 主要研究方法:质点系的定理、定律 + 刚体特点
刚体和质点系的关系:刚体是特殊的质点系。
例 1:质点系的动能定理:W外 W内 Ek 刚体特点:W内 0 刚体的动能定理:W外 Ek
4-1
二. 刚体的基本运动
(m2v2 )R (m1v1)R(末角动量)
(m2 0)R (m10)R (初角动量) 0 m2v2 m1v1 v1 v2
4-2 4-3
例 2 :如图,两人质量相同,初始高度相等,由静止
同时开始攀绳,忽略绳子质量、滑轮质量以及滑轮和
固定轴之间的摩擦。则以下关于两人到达滑轮顶端的
说法中正确的是
动量定理: I p
角动量定理:
t2
t1
Mdt
L
动能定理: W Ek
说明 1 :冲量、冲量矩和功为过程量(对应一段 时间),动量、角动量和动能为状态量(对应一 个时刻)。
说明 2 :三个定理的共同特点:用过程量反映状 态量的增量。
4-2 4-3
七. 角动量守恒定律
推导:由质点系的角动量定理: M外dt dL
任意设想一垂直于质点运 轴
动平面的轴,质点的运动
o
可看成是绕轴的转动(不
一定是圆周运动)。
F
v
m
4-2 4-3
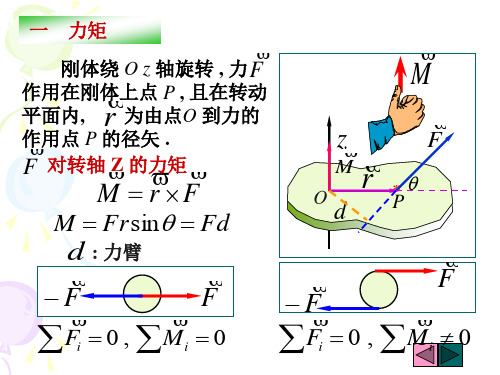
一. 力矩
M Fd F
d
F
:轴到力的距离,
即“力臂”
d
轴
F
o
二. 冲量矩
F
v
m
元冲量矩: Mdt (FdF )dt (Fdt)dF
4-1 刚体的转动
一. 刚体
1. 定义:不发生形变的物体。 说明: “刚体”是一理想模型。
2. 主要研究方法:质点系的定理、定律 + 刚体特点
刚体和质点系的关系:刚体是特殊的质点系。
例 1:质点系的动能定理:W外 W内 Ek 刚体特点:W内 0 刚体的动能定理:W外 Ek
4-1
二. 刚体的基本运动
(m2v2 )R (m1v1)R(末角动量)
(m2 0)R (m10)R (初角动量) 0 m2v2 m1v1 v1 v2
4-2 4-3
例 2 :如图,两人质量相同,初始高度相等,由静止
同时开始攀绳,忽略绳子质量、滑轮质量以及滑轮和
固定轴之间的摩擦。则以下关于两人到达滑轮顶端的
说法中正确的是
动量定理: I p
角动量定理:
t2
t1
Mdt
L
动能定理: W Ek
说明 1 :冲量、冲量矩和功为过程量(对应一段 时间),动量、角动量和动能为状态量(对应一 个时刻)。
说明 2 :三个定理的共同特点:用过程量反映状 态量的增量。
4-2 4-3
七. 角动量守恒定律
推导:由质点系的角动量定理: M外dt dL
任意设想一垂直于质点运 轴
动平面的轴,质点的运动
o
可看成是绕轴的转动(不
一定是圆周运动)。
F
v
m
4-2 4-3
一. 力矩
M Fd F
d
F
:轴到力的距离,
即“力臂”
d
轴
F
o
二. 冲量矩
F
v
m
元冲量矩: Mdt (FdF )dt (Fdt)dF
大学物理。刚体转动课件
解:杆上各质元均 受摩擦力作用, 受摩擦力作用,但 各质元受的摩擦阻 力矩不同, 力矩不同,靠近轴 的质元受阻力矩小, 的质元受阻力矩小, 远离轴的质元受阻 力矩大, 力矩大,
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
细杆的质量密度 m λ= l 质元质量 dm = λdx 质元受阻力矩
O
−l 2
O
l 2
r
dr
dr O´
O´
l
解 设棒的线密度为 λ ,取一距离转轴 OO´ 为 处的质量元 dm = λdr dJ = r 2 dm = λr 2 dr
r
1 3 J = 2λ ∫ r dr = λl 0 12 1 = ml 2 12
l/2 2
如转轴过端点垂直于棒
1 2 J = λ ∫ r dr = ml 0 3
4 –三 力矩 转动定律 转动惯量 2 转动惯量
2 j j j
第四章 刚体的转动
2
J = ∑ ∆m r , J = ∫ r dm
物理意义: 物理意义:转动惯性的量度 . 意义 转动惯性的计算方法 质量离散分布刚体的转动惯量
J = ∑ ∆m r = m r + m r + L
2 j j 2 11 2 2 2 j
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
3) 刚体内作用力和反作用力的力矩互相抵消 ) 刚体内作用力和反作用力的力矩互相抵消
v Mij
O
v rj
v Mji
d
v iF ri ij
j v Fji v
v v M ij = −M ji
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
《大学物理学》课件第04章 刚体的转动

刚d体A在力F作 用dr绕 轴F转F过c一o微s(小角位移)d| ,dr |
2
F sin | dr | F sin ds
z
ds F
o r d P
Frsind
Frsin M dA Md
F 力 使刚体由0转到 时,力矩的功为:
A Md 0
结论:刚体绕定轴转动时,力矩对转动物体做的功等于相应力矩和角位移的
12 12
J
A
JC
m(
L)2 2
例2.半径为 R 质量为 M 的圆环,绕垂直于圆环平面的质心轴转动,求转动 惯量J。
解:
分割质量元 dm圆环上各质量元到轴的距离相等,
M
J R2dm R2
M dm MR2
0
0
绕圆环质心轴的转动惯量为
M
J Mቤተ መጻሕፍቲ ባይዱ2
oR
讨论:若圆环绕其直径轴转动,再求此圆环的转动惯量。
at r
an
a r
an rω2
a r 2 rω2 2
e t v
at
质点直线运动或刚体平动 位移 速度 加速度
匀速直线运动 匀变速直线运动
刚体的定轴转动 角位移 角速度 角加速度 匀角速定轴转动 匀变角速定轴转动
4.2 刚体绕定轴转动的角动量和转动惯量
4.1定轴转动 刚体角动量
以角速度作定轴转动的刚体内取一质点mi,则其对轴的 角动量为:
计算力对某一转轴的力矩,若力的作用点不固定在同一处,则应当采取分小段 的办法,先计算每一小段上的作用力产生的矩,再求和。
4.3.2 刚体的角动量定理和转动定理
1M.则角 合i动外量力d定dL矩t理i :质d点(MdJmti受)合力d矩dMtM(im外 i(包ir括i2dMdti)外(、对M定mi轴内ir)i转2的)刚体d(dJt)
2
F sin | dr | F sin ds
z
ds F
o r d P
Frsind
Frsin M dA Md
F 力 使刚体由0转到 时,力矩的功为:
A Md 0
结论:刚体绕定轴转动时,力矩对转动物体做的功等于相应力矩和角位移的
12 12
J
A
JC
m(
L)2 2
例2.半径为 R 质量为 M 的圆环,绕垂直于圆环平面的质心轴转动,求转动 惯量J。
解:
分割质量元 dm圆环上各质量元到轴的距离相等,
M
J R2dm R2
M dm MR2
0
0
绕圆环质心轴的转动惯量为
M
J Mቤተ መጻሕፍቲ ባይዱ2
oR
讨论:若圆环绕其直径轴转动,再求此圆环的转动惯量。
at r
an
a r
an rω2
a r 2 rω2 2
e t v
at
质点直线运动或刚体平动 位移 速度 加速度
匀速直线运动 匀变速直线运动
刚体的定轴转动 角位移 角速度 角加速度 匀角速定轴转动 匀变角速定轴转动
4.2 刚体绕定轴转动的角动量和转动惯量
4.1定轴转动 刚体角动量
以角速度作定轴转动的刚体内取一质点mi,则其对轴的 角动量为:
计算力对某一转轴的力矩,若力的作用点不固定在同一处,则应当采取分小段 的办法,先计算每一小段上的作用力产生的矩,再求和。
4.3.2 刚体的角动量定理和转动定理
1M.则角 合i动外量力d定dL矩t理i :质d点(MdJmti受)合力d矩dMtM(im外 i(包ir括i2dMdti)外(、对M定mi轴内ir)i转2的)刚体d(dJt)
第四章 刚体的转动讲解

Δθ=ωt
4)角位置
=0+ t
2.匀变速转动(t=0,ω=ω0,θ=θ0)
1)角加速度 =const
2)角速度 =0 t
3)角位移 4)角位置
=
0
t
1 2
= 0+ 0
t
t2
1 2
t
2
四、角量与线量的关系
半径R,角位移
弧长 s R
线速度v: v lim
法向加速度:
an
t 0
v2
R
lim s
R
t t0 t
(R)2 R 2
R
R
切向加速度:
a
dv dt
d dt
(R)
R
d
dt
R
结论:刚体作定轴转动时,在某一时刻刚体上所有
各点的角位移、角速度和角加速度都是相同的;
而各点的线位移、线速度和线加速度均与r成正比。
M i
M F1r1 sin1 F2 r2 sin 2 F3r3 sin 3
单位: N.m
注意:力矩的单位和功的单位不是一回事,力矩的 单位不能写成焦耳。
与转动垂直但通过转轴的力对转动不产生力矩; 与转轴平行的力对转轴不产生力矩; 刚体内各质点间内力对转轴不产生力矩。 对于刚体的定轴转动,不同的力作用于刚体上的
轴的力矩。用M表示。
用矢量表示 M r F
或:
M=Fr sin
若力F不在垂直与转轴的平面内,则可把该力分解为两个
力,一个与转轴平行的分力,一个在垂直与转轴平面 内的分力,只有后者才对刚体的转动状态有影响。
物理刚体的转动

例题
均匀圆环 : m i
JC mi R R
2
2
m
i
C R
J C mR
2
例题
均匀圆盘:
m dm ds 2 R ds 2rdr
2 R 0
面密度rJ 源自 dm r 2 2 rdr R4
2
1 2 mR 2
半径为R质量为M的均匀圆盘联结一长为L质量为m 的均匀直棒,写出刚体对O轴的转动惯量。(O轴垂直 纸面)
J
r
2
dm
转动惯量与下列三个因素有关:
⑴形状、大小相同的均匀刚体总质量越大,转动惯量越大。 ⑵总质量相同的刚体,质量分布离轴越远,转动惯量越大。 ⑶同一刚体,转轴不同,质量对轴的分布就不同,因而转 动惯量不同。
4、转动惯量的计算 Calculation of moment of inertia 例题:三个质量为m的质点,A、B、C由三个长为L的 轻杆相联结。求该质点系通过A点和O点,且垂直于 三个质点所在平面的转轴的转动惯量。
4、刚体的一般运动
A r 1
A' B r 2
o1
o2
B'
刚体的一般运动可看作 是平动和转动的叠加
5、角速度矢量:
z
, α
v
angular velocity vector
刚体作定轴转动时,各质元 的线速度、角加速度一般是 不同的,但由于各质元的相 对位置保持不变,所以描述 各质元的角量,如角位移、 角速度、角加速度都是一样 的。因此描述刚体的整体运 动时,用角量最为方便
⑶ v R 78.5m s
1
a R an R 2
2 a a2 a n 6.16 m s 1
刚体的转动

平动 刚体的运动形式
转动 平动:刚体中所有点的运动轨迹都保持完全相同。
转动:刚体中所有的点都绕同一直线做圆周运动. 定轴转动
转动 非定轴转动
定轴转动: 转轴不动,刚体绕转轴运动。
非定轴转动: 转轴运动,刚体绕转轴运动。
垂直于转轴的平面叫转动平面.
二 描述刚体定轴转动的物理量
角坐标 (t)
一 角动量
1 质点的角动量
质量为 m 的质点以速度
v
在O的空位间矢运为动r,某,质时点刻相相对对于原原点点
的角动量
L
r
p
r
mv
大 小: L rmvsin
L 的方向符合右手法则.
L
z
v
rm
xo
y
L
v
r
z
2 刚体的角动量
L mi ri vi ( mi ri2 ) J
W ex
Md
而 EK
1 J 2 ,
2
0
EK 0
1 2
J02
得刚体定轴转动的动能定理
W
Md
0
1 2
J 2
1 2
J
2 0
刚体定轴转动的动能定理: 合外力矩对绕定轴转动的 刚体所作的功等于刚体转动动能的增量.
注意:
1 如果刚体在运动过程中还有势能的变化,可用质
点组的功能原理和机械能转换与守恒定律讨论.总之,
(b) 图4.4 均匀细棒的转动惯量
五 刚体定轴转动的动能定理
刚体是其内任两质点间距离不变的质点组,刚体做 定轴转动时,质点间无相对位移,质点间内力不作 功,外力功为其力矩的功,并且刚体无移动,动能 的变化只有定轴转动动能的变化.
转动 平动:刚体中所有点的运动轨迹都保持完全相同。
转动:刚体中所有的点都绕同一直线做圆周运动. 定轴转动
转动 非定轴转动
定轴转动: 转轴不动,刚体绕转轴运动。
非定轴转动: 转轴运动,刚体绕转轴运动。
垂直于转轴的平面叫转动平面.
二 描述刚体定轴转动的物理量
角坐标 (t)
一 角动量
1 质点的角动量
质量为 m 的质点以速度
v
在O的空位间矢运为动r,某,质时点刻相相对对于原原点点
的角动量
L
r
p
r
mv
大 小: L rmvsin
L 的方向符合右手法则.
L
z
v
rm
xo
y
L
v
r
z
2 刚体的角动量
L mi ri vi ( mi ri2 ) J
W ex
Md
而 EK
1 J 2 ,
2
0
EK 0
1 2
J02
得刚体定轴转动的动能定理
W
Md
0
1 2
J 2
1 2
J
2 0
刚体定轴转动的动能定理: 合外力矩对绕定轴转动的 刚体所作的功等于刚体转动动能的增量.
注意:
1 如果刚体在运动过程中还有势能的变化,可用质
点组的功能原理和机械能转换与守恒定律讨论.总之,
(b) 图4.4 均匀细棒的转动惯量
五 刚体定轴转动的动能定理
刚体是其内任两质点间距离不变的质点组,刚体做 定轴转动时,质点间无相对位移,质点间内力不作 功,外力功为其力矩的功,并且刚体无移动,动能 的变化只有定轴转动动能的变化.
第三章 刚体的转动.
定轴而言,刚体的转动惯量是一个常数。
由定义式求转动惯量的方法步骤:
1)在刚体上选取一个质元dm;
2)计算dm到转轴的距离r.
3) 求出积分:
I dI r 2 dm
R
x O x
R sin
d
dm dx
O
R
dm 2rdr
§3-3 力矩 转动定律
力矩
1、力对固定点的力矩 1)定义:作用于质点的力对 惯性系中某参考点的力矩, 等于力的作用点对该点的位 矢与力的矢积,即
F
F
Fi 0 , Mi 0
F
F
F
F
F 0 , M
i
i
0
(4)明确有心力对其力心的力矩恒为零 因为有心力对其力心的力臂为零,所以有心力对其 力心的力矩恒为零。
练习:试求作用在圆锥摆上的拉力T、重力mg和合力F对
o' 点、o 点、oo'
轴的力矩
L
r
mv
L
mv 是相对量: r
与参照系的选择有关, 与参考点的选择有关
2、质点对轴的角动量 ☆ 假定质点的动量就在转动平面内,且质点对轴的矢径为r, 则质点对z 轴的角动量为 ,方向沿 z 轴,可 L z r mv 正、可负
练习:在图示情况下,已知圆锥摆的质量为m,
(2)明确质点系内力矩的矢量和恒为零。
由于内力总是成对出现,作用力和反作用力 等大、反向、在同一直线上,所以对任何参考 点内力矩的矢量和恒为零。
(3)明确质点系的合外力矩不等于其外力矢量和 的力矩。
作用于系统的合外力为零时,合外力矩不一定为零; 系统的合外力矩为零时,其合外力也不一定为零。
大学物理课件-刚体转动
d M K
dt I I
K dt d
I
tK
0 d
0
I
dt 2 0
t I ln 2 k
[例題]一繩跨過定滑輪,一端系品質為m的物體, 滑輪的
品質為m,半徑為R,轉動慣量為J=mR2/2,可繞水準軸 自由轉動。繩與滑輪間無相對滑動. 求:物體的加速度和 繩的張力.
mg T ma TR J
O
任意質點i 的動能是
Eki
1 2
Dmii2
1 2
Dmi
ri2
2
剛體轉動動能是
Ek
i
Eki
1( 2
i
Dmi ri2 ) 2
Dmi
ri
i
Ek
1 2
I 2
m2>m1。滑輪可看作是品質均勻分佈的圓盤,品質為m,半徑為R, 轉動慣量為I=mR2/2,可繞水準軸自由轉動。繩與滑輪間無相對滑 動。 求:物體的加速度和繩的張力。
解:
T1
(2m2
1 2
m1 m2
m )m1 g 1m
2
T2
(2m1
1 2
m1 m2
m )m2 g 1m
2
T a
2m1m2 m1 m2 m2 m1
解:根據牛頓定律、轉動定律
m2 g T2 m2a T1 m1 g m1a
T2 R T1R I
a R
a (m2 m1 )g
m1
m2
1 2
m
m1
m2
T1 T2
m1 g m2 g T1 T2
例3.5 一 繩 跨 過 定 滑 輪 , 兩 端 分 別 系 品 質 為 m1 和 m2 的 物 體 ,
Lz ( Dmiri2) I
dt I I
K dt d
I
tK
0 d
0
I
dt 2 0
t I ln 2 k
[例題]一繩跨過定滑輪,一端系品質為m的物體, 滑輪的
品質為m,半徑為R,轉動慣量為J=mR2/2,可繞水準軸 自由轉動。繩與滑輪間無相對滑動. 求:物體的加速度和 繩的張力.
mg T ma TR J
O
任意質點i 的動能是
Eki
1 2
Dmii2
1 2
Dmi
ri2
2
剛體轉動動能是
Ek
i
Eki
1( 2
i
Dmi ri2 ) 2
Dmi
ri
i
Ek
1 2
I 2
m2>m1。滑輪可看作是品質均勻分佈的圓盤,品質為m,半徑為R, 轉動慣量為I=mR2/2,可繞水準軸自由轉動。繩與滑輪間無相對滑 動。 求:物體的加速度和繩的張力。
解:
T1
(2m2
1 2
m1 m2
m )m1 g 1m
2
T2
(2m1
1 2
m1 m2
m )m2 g 1m
2
T a
2m1m2 m1 m2 m2 m1
解:根據牛頓定律、轉動定律
m2 g T2 m2a T1 m1 g m1a
T2 R T1R I
a R
a (m2 m1 )g
m1
m2
1 2
m
m1
m2
T1 T2
m1 g m2 g T1 T2
例3.5 一 繩 跨 過 定 滑 輪 , 兩 端 分 別 系 品 質 為 m1 和 m2 的 物 體 ,
Lz ( Dmiri2) I
大学物理第四章 刚体的转动(3课时)讲解
c
2
t2
2 600π 3002
π 75
rad s3
1 ct 2 π t 2
2 150
4-1 刚体的定轴转动
由 dq π t 2
dt 150
得
q
dq
π
t t 2dt
0
150 0
q π t 3 rad
450
在 300 s 内转子转过的转数
N q π (300)3 3104
第四章 刚体的转动
物理学
第五版
4-0 教学基本要求
四 理解刚体定轴转动的转动动能概 念,能在有刚体绕定轴转动的问题中正确 地应用机械能守恒定律.
能运用以上规律分析和解决包括质点 和刚体的简单系统的力学问题.
第四章 刚体的转动
物理学
第五版
第一节
第四章 刚体的转动
4-1 刚体的定轴转动
刚体:在外力作用下,形状和大小都不 发生变化的物体.(任意两质点间距离保持 不变的特殊质点组.)
18 000 r·min-1 .转子的角加速度与时间成正
比.问在这段时间内,转子转过多少转?
解 令 ct,即 d ct ,积分
dt
t
d c tdt
得 1 ct 2
0
0
2
4-1 刚体的定轴转动
1 ct 2
2
当 t =300 s 时
18 000 r min 1 600 π rad s1
位置及方向 不变。
பைடு நூலகம்
该平面且通 过质心
刚体上 各质点都 以某一定 点为球心 的各个球 面上运动
复杂 的运动 与平动 的混合。
第四章 刚体的转动
细棒
J 1 ml2 12
球体
J 2 mr2 5
三.平行轴定理
zN
以质心C为坐标原点
设对Cz轴的转动
惯量为Jc
MN//Cz
O
d r
Or' 'dm
C
y
r'rd x
对MN
J
轴r的'2转dm动 惯量(为r:d)2dMm
m
m
r2 d m d 2 d m 2 r d d m
1J m C r dm m 2m 1 d2d (x m r im d ym j)dm
b
Y Y
d
X
o
a Y
X
C·
o’ Y
[例1]求半径为R质量为m的均匀圆环,对
于沿直径转轴的转动惯量。
解:圆环的质量密度为
m 2R
在环上取质量元dm, dm 距转轴r
rdm
d
R
dmdlRd rRcos
J r2dm22R2co2sRd
m
2
R3 1 mR 2
y
2
另解:
对过环心并与环垂直的 转轴的转动惯量
时惯性的大小。
讨论:转动惯量Jz的大小决定于
a.刚体的质量:同形状的刚体,ρ越大, Jz就越大; b.质量的分布:质量相同,dm分布在R 越大的地方,则Jz 越大;
c.刚体的转轴位置:同一刚体依不同的
转轴而有不同的Jz 。
常见刚体的转动惯量:
薄圆盘
J 1 mr2 r
2
细棒
J 1 ml 2 3
mm
1
m1m
xdim ydjm0
mm
mm
JJCmd2 ----平行轴定理
