三角函数_技巧
特殊三角函数的记忆技巧

特殊三角函数的记忆技巧
特殊三角函数包括正弦函数、余弦函数和正切函数。
记忆它们的一种简单方法是使用“东南西北”的方位词来帮助记忆。
1. 正弦函数(sin):
- 正弦函数在第一象限的值为正,可以记忆为“东正西正”。
- 正弦函数在第二象限的值为正,可以记忆为“东正北正”。
- 正弦函数在第三象限的值为负,可以记忆为“南负西负”。
- 正弦函数在第四象限的值为负,可以记忆为“南负北负”。
2. 余弦函数(cos):
- 余弦函数在第一象限的值为正,可以记忆为“东正北正”。
- 余弦函数在第二象限的值为负,可以记忆为“东负北负”。
- 余弦函数在第三象限的值为负,可以记忆为“南负西负”。
- 余弦函数在第四象限的值为正,可以记忆为“南正西正”。
3. 正切函数(tan):
- 正切函数在第一象限的值为正,可以记忆为“东正北正”。
- 正切函数在第二象限的值为负,可以记忆为“东负北负”。
- 正切函数在第三象限的值为正,可以记忆为“南正西正”。
- 正切函数在第四象限的值为负,可以记忆为“南负西负”。
通过以上的方位词记忆方法,可以帮助记忆特殊三角函数的正负性,从而更容易在计算中应用它们。
高考数学大二轮复习 微专题(三) 三角函数问题的解题技巧——“变角”“变式”

π
,
π
2
因此 sin
,所以
π
+4
所以 2sin
12
1
于是 t +t2
2
∈ -
π
+4
=
π
θ+4
∈
π
+
4
3π 5π
,
4 4
2 2
,
2 2
,
,
,
∈(-1,1),即 t∈(-1,1).
1
(t+1)2-1∈(-1,1).
2
故 sin θ+cos θ+sin θcos θ 的取值范围是(-1,1).
考查角度
角度一 变角
5π
12
[例 1—1](2021·山东淄博月考)已知 θ∈(0,π),cos 6 - =-13,则 tan +
π
=
6
.
5
答案
12
解析 由于
又因为 cos
π
θ∈(0,π),所以-6
5π
-
6
<
12
π
=- ,所以
13
2
因此 sin
5π
-
6
=
所以 tan
5π
-
6
5
=-12,
4
4
立联系.
,sin 2α,cos 2α等式子也都可以相互转化建
[例2-4](2021·山东潍坊月考)已知θ是钝角,则sin θ+cos θ+sin θcos θ的取值
范围是
.
答案 (-1,1)
2 -1
θ= ,于是
2
三角函数“角变换”的六种常用技巧

ʏ童昌立角变换 是三角变换的核心, 角变换 的六种常用技巧是:互余角或互补角的转化,非特殊角向特殊角的转化,半角与倍角的转化,复角与单角的转化,结论式中的角与条件式中的角的转化,引入辅助角㊂下面举例分析,供大家学习与提高㊂技巧一:互余角或互补角的转化例1 (1)已知c o s α-π4=45,αɪ0,π4,则c o s α+π4=㊂(2)已知s i n π3-α=14,则c o sπ3+2α=㊂(1)由αɪ0,π4,可得α-π4ɪ-π4,0 ㊂因为c o s α-π4 =45,所以s i n α-π4 =-35,所以s i n π4-α =35㊂故c o s α+π4 =s i n π2-α+π4 =s i n π4-α =35㊂(2)由s i n π3-α =14,可得c o s π6+α =c o s π2-π3-α=s i n π3-α =14,所以c o s π3+2α =c o s 2π6+α =2c o s 2π6+α -1=2ˑ116-1=-78㊂评注:利用π4+α=π2-π4-α,π3+α=π2-π6-α ,π6+α=π2-π3-α 的转化是解题的关键㊂技巧二:非特殊角向特殊角的转化例2 (多选题)下列式子结果为3的是( )㊂A .2s i n 35ʎc o s 25ʎ+c o s 35ʎc o s 65ʎB .1+t a n 15ʎ1-t a n 15ʎC .t a n 75ʎ1-t a n 275ʎD .t a n 25ʎ+t a n 35ʎ+3t a n 25ʎt a n35ʎ对于A ,2(s i n 35ʎc o s 25ʎ+c o s 35ʎc o s65ʎ)=2(s i n35ʎ㊃c o s 25ʎ+c o s 35ʎs i n 25ʎ)=2s i n 60ʎ=3㊂对于B ,1+t a n 15ʎ1-t a n 15ʎ=t a n 45ʎ+t a n 15ʎ1-t a n 45ʎt a n 15ʎ=t a n 60ʎ=3㊂对于C ,t a n 75ʎ1-t a n 275ʎ=12ˑ2t a n 75ʎ1-t a n 275ʎ=12ˑt a n150ʎ=-36㊂对于D ,t a n25ʎ+t a n 35ʎ+3t a n25ʎt a n35ʎ=t a n60ʎ(1-t a n 25ʎt a n 35ʎ)+3t a n25ʎt a n35ʎ=3-3t a n 25ʎt a n 35ʎ+3t a n 25ʎt a n 35ʎ=3㊂应选A B D ㊂评注:特殊角的三角函数值是同学们熟悉的㊂利用非特殊角向特殊角转化是解答本题的突破口㊂技巧三:半角与倍角的转化例3 (1)3c o s 15ʎ-4s i n 215ʎc o s15ʎ=( )㊂A.2 B .3C .6D .23(2)s i n 50ʎ(1+3t a n 10ʎ)=㊂(1)原式=3c o s15ʎ-2s i n 15ʎ㊃2s i n 15ʎc o s 15ʎ=3c o s 15ʎ-2s i n15ʎs i n30ʎ=3c o s15ʎ-01 知识结构与拓展 高一数学 2022年12月Copyright ©博看网. All Rights Reserved.s i n 15ʎ=2c o s (30ʎ+15ʎ)=2㊂应选A ㊂(2)原式=s i n 50ʎ(c o s 10ʎ+3s i n 10ʎ)c o s 10ʎ=s i n 50ʎ㊃2s i n 40ʎc o s 10ʎ=2s i n 50ʎc o s 50ʎc o s 10ʎ=s i n 100ʎc o s 10ʎ=c o s 10ʎc o s 10ʎ=1㊂评注:对于形如 c o s α,c o s 2α,c o s 4α的化简与求值问题,就要想到二倍角公式和辅助角公式的应用㊂技巧四:复角与单角的转化例4 已知s i n (2023π+θ)=13,则所给三角函数式:c o s (π+θ)c o s θ㊃[c o s (π-θ)-1]+c o s (θ-2π)s i n θ-3π2c o s (θ-π)-s i n 3π2+θ的值为㊂因为s i n (2023π+θ)=-s i n θ=13,所以s i n θ=-13㊂所以原式=-c o s θ-c o s θ㊃(1+c o s θ)+c o s θ-c o s 2θ+c o s θ=11+c o s θ+11-c o s θ=21-c o s 2θ=2s i n 2θ=2-132=18㊂评注:对于诱导公式2k π+α(k ɪZ ),πʃα,-α,π2ʃα的变换,每用一次公式,都要注意三角函数值的符号㊂技巧五:结论式中的角与条件式中的角的转化例5 已知α,β均为锐角,且c o s (α+β)=-513,s i n β+π3 =35,则c o s α+π6=( )㊂A.3365 B .6365C .-3365D .-6365因为α,β均为锐角,且c o s (α+β)=-513,s i n β+π3=35,所以α+βɪπ2,π ,β+π3ɪπ3,5π6,所以s i n α+β =1213,c o s β+π3 ɪ-32,12㊂易得c o s β+π3 =ʃ45,其中c o s β+π3 =45>12舍去㊂故c o s α+π6 =c o s (α+β)-β+π3 +π2 =-s i n (α+β)-β+π3 =-1213ˑ-45 +-513ˑ35=3365㊂应选A ㊂评注:三角公式中的角α,β可以是任意角,既能看成是单角,也能看成是复角㊂在运用公式时,要特别注意 条件角 与 结论角 之间可能存在的和差关系㊂常见的角的变换有15ʎ=45ʎ-30ʎ=60ʎ-45,α=(α+β)-β,α=α+β2+α-β2,2α=(α+β)+(α-β)=π4+α-π4-α,β=α+β2-α-β2等㊂技巧六:引入辅助角例6 已知函数f (x )=5s i n x -12c o s x ,当x =x 0时,f (x )有最大值13,则t a n x 0=㊂因为函数f (x )=5s i n x -12c o s x =13s i n (x -θ),其中θ由t a n θ=125确定㊂因为当x =x 0时,函数f (x )有最大值13,所以x 0-θ=π2+2k π(k ɪZ ),所以x 0=θ+π2+2k π(k ɪZ ),所以t a n x 0=t a n θ+π2+2k π=ta n θ+π2=s i n θ+π2 c o s θ+π2=c o s θ-s i n θ=-1t a n θ=-512㊂评注:形如a s i n x +b c o s x 的求值问题,可考虑利用辅助角公式来解决㊂a s i n x +b c o s x =a 2+b 2si n (x +θ),其中θ由t a n θ=ba确定㊂作者单位:湖北省恩施市第三高级中学(责任编辑 郭正华)11知识结构与拓展高一数学 2022年12月Copyright ©博看网. All Rights Reserved.。
三角函数解题思路与技巧

三角函数的解题思路与技巧如下:
1.直接法:直接进行正确的运算和公式变形,结合已知条件,得到正确的答案。
2.换元法:用变量代替一个函数或表达式,通过对变量进行代换,将问题转化为
更容易解决的问题。
3.比例法:通过比例关系,将三角函数值转化为其他函数值,从而解决问题。
4.构造法:通过对问题的分析,构造出符合条件的函数或表达式,从而解决问题。
5.倒推法:从目标结果倒推到起始条件,逐步解决问题。
以上仅为部分解题思路和技巧,实际解题中需要根据具体问题选择合适的思路和方法。
(完整版)三角函数化简求值证明技巧
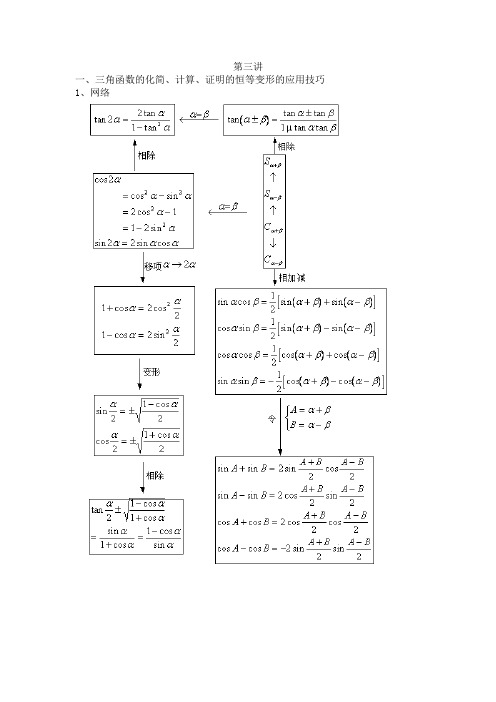
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
常用三角函数值有哪些表示方法和技巧

常用三角函数值有哪些表示方法和技巧三角函数是数学中重要的概念之一,在各个领域都有广泛的应用。
其中,常用三角函数包括正弦、余弦、正切等,它们在解决几何问题、物理问题以及工程问题时都会经常出现。
本文将介绍常用三角函数值的表示方法和一些计算技巧。
常用三角函数在解析几何中,最基本的三角函数有:•正弦(sin)•余弦(cos)•正切(tan)它们的定义如下:•对于任意角θ,正弦值sin(θ) 等于对边与斜边的比值;•余弦值cos(θ) 等于邻边与斜边的比值;•正切值tan(θ) 等于对边与邻边的比值。
这三个函数在数学中有广泛的用途,尤其在求解三角形各边、角的关系时常会用到。
表示方法常用三角函数值有多种表示方法,可以通过计算、计算器或查表得到。
其中常见的表示方法有:1.弧度制表示:以弧度为单位表示角度,对应的三角函数值一般是无理数,需要通过计算或查表得到;2.角度制表示:以度数为单位表示角度,通常在初等数学中使用,通过计算器或查表可以得到对应的三角函数值;3.函数图像表示:利用三角函数的图像特点,可以通过函数图像来理解和计算三角函数值;4.泰勒级数展开:三角函数在某些情况下可以通过泰勒级数展开来计算,尤其是在工程计算中会用到。
技巧在计算常用三角函数值时,有一些技巧可以帮助简化计算,提高效率:1.利用对称性:利用正弦、余弦、正切函数的偶函数性质简化计算过程;2.关系转化:利用三角函数之间的基本关系,如tanθ=sinθ/cosθ,可以将一个函数的值转化为另一个函数的值;3.特殊角的数值:熟记0°、30°、45°、60°、90°等特殊角的三角函数值,有助于快速计算其他角度的函数值;4.利用周期性:三角函数具有周期性,比如sin(θ+360°)=sinθ,可以利用这一性质简化计算。
总之,熟练掌握常用三角函数的表示方法和运算技巧,有助于提高数学计算的效率和准确度。
“三角函数放缩法技巧全总结”
“三角函数放缩法技巧全总结”昨天爱老师在高考数学文章中,承诺过大家今天要具体讲解一下不等式证明技巧——放缩法。
我来履行诺言啦!那为什么要单独挑出“放缩法”来讲呢?那是因为压轴题只要考到不等式证明,一般会用到这个方法,它属于压轴必备技巧哟!快点码起来~ 放缩法其实是在证明不等式成立时,通过放大或缩小,寻找一个中间量而已。
但是说起来简单,真正求解的话还是比较难的,因为中间变量不是直接可以找到的,有时候甚至给了答案我们都看不明白。
所以放缩的一些常见技巧大家还是要熟悉。
一般是裂项放缩,这个方法在数列的裂项相消里是经常用到的。
例如:求下图的值一看就是有分子分母的形式还要累加,对于这种形式我们最熟悉的莫过于数列中的裂项相消的方法。
但是对于这个题目并不是可以直接裂开的,所以我们要先去通过放缩法对其化简成可裂项相消的形式,再去累加求解。
所以本题解法为:其实这只是一个简单的放缩技巧,所以接下来重点来了,一些常见形式的放缩形式的总结如下(部分总结):对于姐妹不等式我们并不陌生,相反初中我们就已经熟悉这个形式了,只是当时我们是以假分数真分数的形式去记忆去理解,那到了高中我们还是用这个性质记忆口诀”小者小,大者大”。
例如:证明对于这个形式看上去没有好的方法去证明,所以想到放缩法去求解,实质就是根据咱们上边的不等式的基本性质。
一个不等式证明我们求解可能将其分为几部分,分别放缩求解,但是要注意我们放缩的方向是一致的,也就是要不都是放大,要不都是放小,切忌符号混乱。
例如:对于这个不等式,我们有很多项,所以放缩的话可以分别放缩这个方法更适合数列或者函数的形式去放缩,有迭代关系。
例如:对于这个题目,是数列的前n项和的形式,虽然不能转化为等差或者等比数列,但是我们要往这个形式去转化,去求解,去化简,然后又想到三角函数的值他是有范围的,肯定在[-1,1],所以从这可以开始放缩。
这个方法也是更适合数列或函数的形式去放缩。
例如:虽然仅仅只是总结了几个放缩的形式,但其实每个例题都是干货满满,并且需要大家消化和练习。
高中数学三角函数的诱导公式运用技巧详解
高中数学三角函数的诱导公式运用技巧详解高中数学中,三角函数是一个重要的概念,而诱导公式则是在解决三角函数问题中经常使用的工具。
本文将详细介绍高中数学中三角函数的诱导公式的运用技巧,并通过具体题目的举例,说明此题的考点以及解题思路。
一、正弦函数的诱导公式运用技巧正弦函数的诱导公式是指sin(A ± B)的展开式。
根据三角函数的性质,我们知道sin(A ± B)可以展开为sinAcosB ± cosAsinB,这就是正弦函数的诱导公式。
在解题过程中,我们经常会遇到需要将一个角度的正弦函数转化为两个角度的正弦函数之和或差的情况,这时就可以运用正弦函数的诱导公式。
例如,考虑以下题目:已知sinα = 3/5,且α为第二象限角,求sin(π - α)的值。
解析:根据题目中已知条件,我们可以得到cosα = -4/5,然后利用正弦函数的诱导公式sin(π - α) = sinπcosα - cosπsinα,代入已知的cosα和sinα的值,得到sin(π - α) = 0。
这个例子展示了如何利用正弦函数的诱导公式将一个角度的正弦函数转化为其他角度的正弦函数,从而解决问题。
二、余弦函数的诱导公式运用技巧余弦函数的诱导公式是指cos(A ± B)的展开式。
根据三角函数的性质,我们知道cos(A ± B)可以展开为cosAcosB ∓ sinAsinB,这就是余弦函数的诱导公式。
在解题过程中,我们经常会遇到需要将一个角度的余弦函数转化为两个角度的余弦函数之和或差的情况,这时就可以运用余弦函数的诱导公式。
例如,考虑以下题目:已知cosβ = 4/5,且β为第一象限角,求cos(π/2 + β)的值。
解析:根据题目中已知条件,我们可以得到sinβ = 3/5,然后利用余弦函数的诱导公式cos(π/2 + β) = cosπ/2cosβ - sinπ/2sinβ,代入已知的cosβ和sinβ的值,得到cos(π/2 + β) = -3/5。
cos函数使用技巧
cos函数使用技巧cos函数是数学中的三角函数之一,在计算机编程中非常常用。
下面我将介绍一些cos函数的使用技巧。
1. 弧度和角度的转换在计算机编程中,cos函数的参数一般是弧度而非角度。
弧度是以圆的半径为单位所划分的角度,记作rad。
而角度是我们常用的度数,记作degree。
要在两者之间进行转换,可以使用以下公式:rad = degree * π / 180degree = rad * 180 / π2. 角度值的范围在计算机编程中,角度值一般是在[0, 360)的范围内进行计算的。
如果角度值超过了这个范围,可以使用以下公式进行角度的规范化:angle = angle % 360这样可以将角度值限制在[0, 360)范围内。
3. cos函数的返回值在大多数编程语言中,cos函数的返回值是一个浮点数,表示给定角的余弦值。
余弦值的范围是[-1, 1],当输入的角度为0时,余弦值为1,当输入的角度为90度或270度时,余弦值为0,当输入的角度为180度时,余弦值为-1。
4. cos函数的应用cos函数在计算机图形学中常用于旋转、缩放和变形等操作。
例如,可以使用cos函数来计算物体在x轴上的缩放比例,假设物体的当前宽度为width,缩放因子为scale,则新的宽度可以通过以下公式计算:new_width = width * cos(angle)5. cos函数的实现在编程中,我们可以使用标准库或自己实现cos函数。
标准库中一般会提供cos函数的高效实现,可直接调用。
如果需要自己实现cos函数,可以使用泰勒级数或查表法等方法。
泰勒级数方法将cos函数表示为无穷级数的形式,可以通过截断级数来近似计算cos函数。
查表法通过事先计算并存储cos函数在一定间隔内的值,然后根据给定角度的近似值来查找对应的余弦值。
综上所述,cos函数在计算机编程中非常常用,掌握cos函数的使用技巧能够帮助我们更好地进行计算和图形操作。
三角函数诱导公式口诀
三角函数诱导公式口诀正弦角余弦角相互抒。
正弦角(sinθ)余弦角(cosθ)先来讲。
180°减去角度与这角个360°多,角度相等就像呼啦圈儿转向着方式相同。
不过值负号前加在正弦角上这你最好记牢。
认真数微多余度所以这点也要好好考。
180°异或角度是个性质,它并不负任何责任,180°-角度取其相抒正弦给余弦算。
对着45°看看你能明白,左加90°,又左旋90°,180°看见镜像都可以把余弦值记得夸。
上面是正弦余弦记得挺好离不开。
接下来我们来说正切这个大家伙。
余切的乙字旁方角只要把它变个样。
根号3往俩角度减,不加在这个方程里能变成样是猜得着。
它跟正切角度很相熟。
对两个角度的积微加,相减规律出来时可真不容易。
其实这三个也可以归一,就是去除分母的根号3,这就是技巧所在。
此时就别再纠结那个角度分子S型后平方根喽。
三角函数本质没变化,只是横坐标扩展或者还原。
若角在这区,可明白大小关系,节省记忆,提高效率。
三角函数进行计算之前,常需要一个0°-90°之间的锐角。
这时候就需要用到副函数呢。
余弦角互倒千万口诀记牢。
tan顶舵舵员,一驾车两个命名确保角度的后面焦。
就分母加个字母S变tan,横坐标倒在它前面,分母的倒数成除法,保证記得够牢。
试想正切角翻过机过渡,横纵线色彩相同还需刻画得足够细致。
副函数到此为止,同学们可以高兴发音啦。
从余切送回应正黏帝迈把右边再看一下。
我们来看看另一个重要的逆函数,这个函数叫做弧度函数。
简单点说,就是将角度转化为弧度。
弧度与角度成反而正,240°弧度报告单位不是固定也别固执。
单位直接乘以π一周两百三,这样加π/3逼的角也算的精确地道。
π加π/6真不是个难的数,抢着转弯就红头喜燕飞的精神强。
让我多对红弧代替黄弧向后转足百分之六。
π+3π/4,有折才美味。
一点减运算无难度,带了个弧后就剩这点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
希望辅导中心--------数学 1 浅论 三角函数的几种解题技巧
一、关于)2sin(cossincossin或与的关系的推广应用:
1、由于cossin21cossin2cossin)cos(sin222故知道)cos(sin,必可推出)2sin(cossin或,例如:
例1 已知33cossin,33cossin求。 分析:由于)coscossin)(sincos(sincossin2233 ]cossin3)cos)[(sincos(sin2 其中,cossin已知,只要求出cossin即可,此题是典型的知sin-cos,求sincos的题型。
解:∵cossin21)cos(sin2
故:31cossin31)33(cossin212 ]cossin3)cos)[(sincos(sincossin233 3943133]313)33[(332 2、关于tg+ctg与sin±cos,sincos的关系应用: 由于tg+ctg=cossin1cossincossinsincoscossin22 故:tg+ctg,cossin,sincos三者中知其一可推出其余式子的值。 例2 若sin+cos=m2,且tg+ctg=n,则m2 n的关系为( )。
A.m2=n B.m2=12n C.nm22 D.22mn 分析:观察sin+cos与sincos的关系: sincos=2121)cos(sin22m 希望辅导中心--------数学 2 而:nctgtgcossin1
故:1212122nmnm,选B。 例3 已知:tg+ctg=4,则sin2的值为( )。 A.21 B.21 C.41 D.41
分析:tg+ctg=41cossin4cossin1 故:212sincossin22sin。 答案选A。
例4 已知:tg+ctg=2,求44cossin 分析:由上面例子已知,只要44cossin能化出含sin±cos或sincos的式子,则即可根据已知tg+ctg进行计算。由于tg+ctg=2cossin1
21cossin,此题只要将44cossin化成含sincos的式子即可:
解:44cossin=44cossin+2 sin2cos2-2 sin2cos2 =(sin2+cos2)- 2 sin2cos2 =1-2 (sincos)2
=1-2)21(2
=211 =21 通过以上例子,可以得出以下结论:由于cossin,sincos及tg+ctg三者之间可以互化,知其一则必可知其余二。这种性质适合于隐含此三项式子的三角式的计算。但有一点要注意的;如果通过已知sincos,求含cossin的式子,必须讨论其象限才能得出其结果的正、负号。这是由于(cossin)2=1±2sincos,要进行开方运算才能求出cossin 二、关于“托底”方法的应用: 在三角函数的化简计算或证明题中,往往需要把式子添加分母,这常用在需把含tg(或ctg)与含sin(或cos)的式子的互化中,本文把这种添配分母的方法叫做“托底”法。方法如下:
例5 已知:tg=3,求cossin2cos3sin的值。
分析:由于cossintg,带有分母cos,因此,可把原式分子、分母各项除以cos,“造出”tg,即托出底:cos; 希望辅导中心--------数学 3 解:由于tg=30cos2k
故,原式=013233123coscoscossin2coscos3cossintgtg
例6 已知:ctg= -3,求sincos-cos2=? 分析:由于sincosctg,故必将式子化成含有sincos的形式,而此题与例4有所不同,
式子本身没有分母,为了使原式先出现分母,利用公式:1cossin22及托底法托出其分母,然后再分子、分母分别除以sin,造出ctg:
解:222222cossincoscossincoscossin1cossin
2sin,分母同除以分子
22
2
2
1)sincos(1)sincos(sincosctgctgctg
56)3(1)3(322 例7 (95年全国成人高考理、工科数学试卷) 设20,20yx,)6sin()3sin(sinsinyxyx且
求:)3)(33(ctgyctgx的值 分析:此题是典型已知含正弦函数的等式求含正切、余切的式子,故要用“托底法”,由于20,20yx,故0sin,0sinyx,在等式两边同除以yxsinsin,托出分母yxsinsin
为底,得: 解:由已知等式两边同除以yxsinsin得:
1sinsin6coscos6sinsinsin3coscos3sin1sinsin)6sin()3sin(yyyxxyxyx 希望辅导中心--------数学
4 334)3)(33(1)3)(33(431)3)(13(411sinsin3cossinsincos341ctgyctgxctgyctgxctgyctgxyyyxxx “托底”适用于通过同角的含正弦及余弦的式子与含正切、余切的式子的互化的计算。由于cossintg,sincosctg,即正切、余切与正弦、余弦间是比值关系,故它们间的互化需“托底”,通过保持式子数值不变的情况下添加分母的方法,使它们之间可以互相转化,达到根据已知求值的目的。而添加分母的方法主要有两种:一种利用1cossin22,把
22cossin作为分母,并不改变原式的值,另一种是通过等式两边同时除以正弦或余弦又
或者它们的积,产生分母。
三、关于形如:xbxasincos的式子,在解决三角函数的极值问题时的应用: 可以从公式)sin(sincoscossinxAxAxA中得到启示:式子xbxasincos与上述公式有点相似,如果把a,b部分变成含sinA,cosA的式子,则形如xbxasincos的式子都可以变成含)sin(xA的式子,由于-1≤)sin(xA≤1, 所以,可考虑用其进行求极值问题的处理,但要注意一点:不能直接把a当成sinA,b当成cosA,如式子:xxsin4cos3中,不能设sinA=3,cosA=4,考虑:-1≤sinA≤1,-1≤cosA≤1,可以如下处理式子:
xbabxbaa
baxbxasincossincos
222222
由于1)()(222222babbaa。 故可设:22sinbaaA,则AAsin1cos,即:22cosbabA ∴)sin()sincoscos(sinsincos2222xAbaxAxAbaxbxa 无论xA取何值,-1≤sin(A±x)≤1, 22ba≤)sin(22xAba≤22ba
即:22ba≤xbxasincos≤22ba 下面观察此式在解决实际极值问题时的应用: 例1(98年全国成人高考数学考试卷) 希望辅导中心--------数学 5 求:函数xxxycossincos32的最大值为(AAAA )
A.231 B.13 C.231 D.13 分析:xxxx2sin21cossin221cossin,再想办法把x2cos变成含xcso2的式子:212coscos1cos22cos22xxxx
于是:xxy2sin21212cos3
xx2sin21232cos23 23)2sin212cos23(xx 由于这里:1)21()23(,21,232222baba则 ∴23)2sin212cos23(1xxy
设:21cos,23123sin22AbaaA则 ∴232sincos2cossinxAxAy 23)2sin(xA 无论A-2x取何值,都有-1≤sin(A-2x)≤1,故231≤y≤231 ∴y的最大值为231,即答案选A。 例2 (96年全国成人高考理工科数学试卷) 在△ABC中,已知:AB=2,BC=1,CA=3,分别在边AB、BC、CA上任取点D、E、F,使△DEF为正三角形,记∠FEC=∠α,问:sinα取何值时,△EFD的边长最短?并求此最短边长。
