经济数学微积分第四章习题答案最新版

合集下载

(完整word版)微积分(经管类第四版)习题1-6答案(word文档良心出品)

习题1-61(1)错.无穷小是趋向于0，非常小是趋向于负无穷(2)对(3)对(4)错.，趋向于无穷大，则，设x x g x f xx g x x f ===)()(1)(1)(2 (5)错.，趋向于无穷小，则，设0)()()()(=+-==x g x f x x g x x f 2(1)无穷小 (2)无穷小 (3)无穷大 3，所以对任意给定的0,0-1sin >≤εx x x 时为无穷小为，即故时，就有则当，，要取要使01sin 01sin lim 0-1sin 00-1sin 0→==<<<=<→x xx y x x x x x xx x εδεδε 4(1)3)23(lim 23lim =+=+∞→∞→xx x x x (2)2)2(lim 24lim 020=+=--→→x x x x x (3)∞→→→→xx x x cos -110cos -11cos 0，，时，当 5存在极限，1lim lim 0/1==∞→∞→e e x x x不存在极限，+∞==∞→→e e x x x 0/10lim lim 6是有界函数，则假设x x y cos = ()，所以函数不是无穷大此时的情况，时，存在当内无界，在故函数所以假设不成立，，，使得显然不存在，00cos -cos cos cos ==∞→∞+∞=≤≤∴≤≤y x x x x y M x M Mx x x x M x x 7是有界量，时，)(0x g x x → 是无穷大即，则，时，恒有使得当，内无限增大，则存在在假设是无穷大，时，时，恒有使得当，内有界，则存在在假设)()(0)()(.)(000)()(.)(000)(222202*********x g x f M M x g x f M x f x x M x x x g x f x x M x g x x M x x x g ±=±≥±≥<-<><-<→≤<-<><-<δδδδ 8，内无限增大，则存在在假设’00)(0><-<M x x x g δ是无穷大即则时，恒有使得当’’)()(.)()(.)(00x g x f MM x g x f M x f x x ≥≥<-<δ。

(完整版)微观经济学第4章生产论习题与答案

第4章生产论【练习及思考】参考答案要点1．填空题(1)总产量曲线、平均产量曲线和边际产量曲线都呈现出先上升，而后达到最大值以后，再呈现出下降的趋势。

其中，边际产量最先达到最大值，而后开始下降并与平均产量的最大值相交。

(2)边际产量的变化随着可变要素投入的增加一般经历两个阶段，即递增和递减两个阶段。

(3)按照生产过程中使用的生产要素的搭配情况可将那生产函数分为两种类型固定比例生产函数和可变比例生产函数。

2．判断题（下列判断正确的在括号内打√，不正确的打×）1）（√）在一种可变投入生产函数中，可变要素合理投入区域应在AP＞MP＞0的阶段。

2）（×）在一种可变投入生产函数中，可变要素合理投入区域应在MP＞AP的第一阶段。

3）（√）生产理论中的短期是指未能调整全部生产要素的时期。

4）（×）AP曲线与MP曲线交于MP曲线的最高点。

5）（×）能提供相同效用的不同商品数量组合的点的连线即为等产量曲线。

6）（×）等产量曲线表示的是用同样数量劳动和资本生产不同的产量。

7）（√）当劳动的边际产量小于其平均产量时，平均产量肯定是下降的。

8）（×）边际产量递减，平均产量也递减。

9）（√）在生产的第Ⅱ阶段，AP是递减的。

3．选择题1）理性的生产者选择的生产区域应是（CD）。

A.MP＞AP阶段B.MP下降阶段C.AP＞MP＞0阶段D.MP与AP相交之点起至MP与横轴交点止2）下列说法中正确的是（AC）。

A.只要总产量减少，边际产量一定为负B.只要MP减少，总产量一定减少C.MP曲线必定交于AP曲线的最高点D.只要MP减少，AP 也一定减少3）最优生产要素组合点上应该有（ABD）。

A.等产量曲线和等成本线相切B.MRTS LK=w/rC.dk/dl=w/rD.MP L/MP k=w/r4）等产量曲线上任意两点的产量肯定是（A ）。

A.相等B.不等C.无关D.以上情况都存在5）若横轴代表劳动，纵轴表示资本，且劳动的价格为w，资本的价格为r，则等成本线的斜率为（C ）。

西方经济学(微观经济学)课后练习答案第四章

习题一、名词解释生产函数边际产量边际报酬递减规律边际技术替代率递规律等产量线等成本线规模报酬扩展线二、选择题1、经济学中，短期是指（）A、一年或一年以内的时期B、在这一时期内所有投入要素均是可以变动的C、在这一时期内所有投入要至少均是可以变动的。

D、在这时期内，生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的。

2、对于一种可变要素投入的生产函数QfL，所表示的厂商要素投入的合理区域为（D）A、开始于AP的最大值，终止于TP的最大值B、开始于AP与MP相交处，终止于MP等于零C、是MP递减的一个阶段D、以上都对3、当MP L AP L时，我们是处于（A）A、对于L的Ⅰ阶段B、对K的Ⅲ阶段C、对于L的Ⅱ阶段D、以上都不是4、一条等成本线描述了（）A、企业在不同产出价格下会生产的不同数量的产出B、投入要素价格变化时，同样的成本下两种投入要素的不同数量C、一定的支出水平下，企业能够买到的两种投入要素的不同组合D、企业能够用来生产一定数量产出的两种投入要素的不同组合5、当单个可变要素的投入量为最佳时，必然有：A.总产量达到最大B.边际产量达到最高C.平均产量大于或等于边际产量D.边际产量大于平均产量6、当平均产量递减时，边际产量是（）A、递减B、为负C、为零D、以上三种可能都有7、以下有关生产要素最优组合，也即成本最小化原则的描述正确的一项是（）．Ａ．MPL／r L＝MPK／r KＢ．MRTS LK＝r L/r KＣ．P MPr KKＤ．Ａ和Ｂ均正确8、等产量曲线上各点代表的是（）Ａ．为生产同等产量而投入的要素价格是不变的Ｂ．为生产同等产量而投入的要素的各种组合比例是不能变化的Ｃ．投入要素的各种组合所能生产的产量都是相等的Ｄ．无论要素投入量是多少，产量是相等的9、如果厂商甲的劳动投入对资本的边际技术替代率为13，厂商乙的劳动投入对资本的边际技术替代率为23，那么（D）Ａ．只有厂商甲的边际技术替代率是递减的Ｂ．只有厂商乙的边际技术替代率是递减的Ｃ．厂商甲的资本投入是厂商乙的两倍Ｄ．如果厂商甲用3单位的劳动与厂商乙交换2单位的资本，则厂商甲的产量将增加10、如果等成本曲线围绕它与纵轴的交点逆时针转动，那么将意味着（A）Ａ．横轴表示的生产要素的价格下降Ｂ．纵轴表示的生产要素的价格上升Ｃ．横轴表示的生产要素的价格上升Ｄ．纵轴表示的生产要素的价格下降11、若等成本曲线在坐标平面上与等产量曲线相交，那么该交点表示的产量水平（）Ａ．应增加成本支出Ｂ．应减少成本支出Ｃ．不能增加成本支出Ｄ．不能减少成本支出12、在规模报酬不变的阶段，若劳动的使用量增加5%，而资本的使用量不变，则（）Ａ．产出增加5%Ｂ．产出减少5%Ｃ．产出的增加少于5%Ｄ．产出的增加大于5%13、规模报酬递减是在下述哪种情况下发生的（）A、按比例连续增加各种生产要素B、不按比率连续增加各种生产要素C、连续地投入某种生产要素而保持其他生产要素不变D、上述都正确14、下列说法中正确的是（D）A、生产要素的边际替代率递减是规模报酬递减造成的B、边际收益递减是规模报酬递减规律造成的C、规模报酬递减是边际收益递减规律造成的D、生产要素的边际技术替代率递减是边际收益递减规律造成的15、当某厂商以最小成本生产出既定产量时（D）A、总收益为零B、获得最大利润C、没有获得最大利润D、无法确定是否获得了最大总利润三、判断题1、随着某种生产要素投入量的增加，边际产量和平均产量到一定程度将趋于下降，其中边际产量的下降一定先于平均产量。

微观经济学答案解析第四章生产论

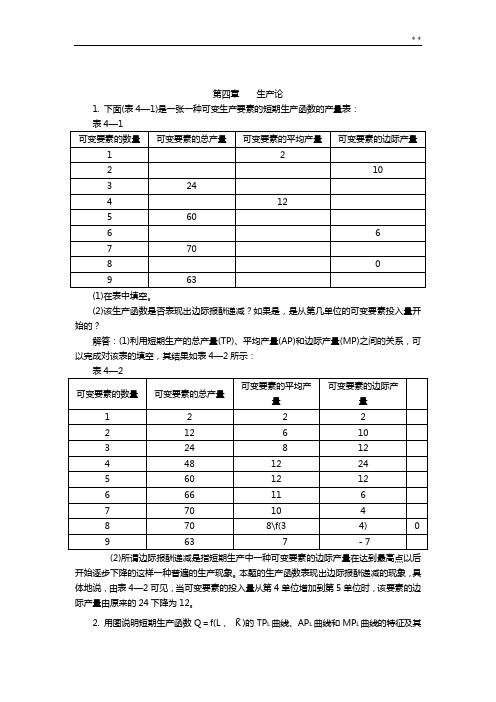
第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表：(2)该生产函数是否表现出边际报酬递减？如果是，是从第几单位的可变要素投入量开始的？解答：(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系，可以完成对该表的填空，其结果如表4—2所示：开始逐步下降的这样一种普遍的生产现象。

本题的生产函数表现出边际报酬递减的现象，具体地说，由表4—2可见，当可变要素的投入量从第4单位增加到第5单位时，该要素的边际产量由原来的24下降为12。

2. 用图说明短期生产函数Q＝f(L，K－)的TP L曲线、AP L曲线和MP L曲线的特征及其相互之间的关系。

解答：短期生产函数的TP L 曲线、AP L 曲线和MP L 曲线的综合图如图4—1所示。

图4—1由图4—1可见，在短期生产的边际报酬递减规律的作用下，MP L 曲线呈现出先上升达到最高点A 以后又下降的趋势。

从边际报酬递减规律决定的MP L 曲线出发，可以方便地推导出TP L 曲线和AP L 曲线，并掌握它们各自的特征及相互之间的关系。

关于TP L 曲线。

由于MP L ＝d TP L d L，所以，当MP L ＞0时，TP L 曲线是上升的；当MP L＜0时，TP L 曲线是下降的；而当MP L ＝0时，TP L 曲线达最高点。

换言之，在L ＝L 3时，MP L 曲线达到零值的B 点与TP L 曲线达到最大值的B ′点是相互对应的。

此外，在L ＜L 3即MP L ＞0的范围内，当MP ′L ＞0时，TP L 曲线的斜率递增，即TP L 曲线以递增的速率上升；当MP ′L ＜0时，TP L 曲线的斜率递减，即TP L 曲线以递减的速率上升；而当MP ′＝0时，TP L 曲线存在一个拐点，换言之，在L ＝L 1时，MP L 曲线斜率为零的A 点与TP L 曲线的拐点A ′是相互对应的。

关于AP L 曲线。

由于AP L ＝TP LL ，所以，在L ＝L 2时，TP L 曲线有一条由原点出发的切线，其切点为C 。

微观经济学第四章习题答案

第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表：可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量1 22 103 244 125 606 67 708 09 63(2)该生产函数是否表现出边际报酬递减？如果是，是从第几单位的可变要素投入量开始的？解答：(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系，可以完成对该表的填空，其结果如表4—2所示：可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量1 2 2 22 12 6 103 24 8 124 48 12 245 60 12 126 66 11 67 70 10 48 70 8\f(3 4) 09 63 7 －7开始逐步下降的这样一种普遍的生产现象。

2. 用图说明短期生产函数Q＝f(L，eq \o(K,\s\up6(－)))的TP L曲线、AP L曲线和MP L曲线的特征及其相互之间的关系。

解答：短期生产函数的TP L曲线、AP L曲线和MP L曲线的综合图如图4—1所示。

图4—1由图4—1可见，在短期生产的边际报酬递减规律的作用下，MP L曲线呈现出先上升达到最高点A以后又下降的趋势。

从边际报酬递减规律决定的MP L曲线出发，可以方便地推导出TP L曲线和AP L曲线，并掌握它们各自的特征及相互之间的关系。

关于TP L曲线。

由于MP L＝eq \f(d TP L,d L)，所以，当MP L＞0时，TP L曲线是上升的；当MP L＜0时，TP L曲线是下降的；而当MP L＝0时，TP L曲线达最高点。

换言之，在L＝L3时，MP L曲线达到零值的B点与TP L曲线达到最大值的B′点是相互对应的。

此外，在L＜L3即MP L＞0的范围内，当MP′L＞0时，TP L曲线的斜率递增，即TP L曲线以递增的速率上升；当MP′L＜0时，TP L曲线的斜率递减，即TP L曲线以递减的速率上升；而当MP′＝0时，TP L曲线存在一个拐点，换言之，在L＝L1时，MP L曲线斜率为零的A点与TP L 曲线的拐点A′是相互对应的。

大一微积分二至四章课后习题答案

第二章习题解答习题 2—11. 用定义求函数2y x =在1x =处的导数.解：(1）22(1)(1)(1)12()y f x f x x x ∆=+∆-=+∆-=∆+∆；（2）22()2y x x x x x∆∆+∆==+∆∆∆；（3）00limlim (2)2x x yx x ∆→∆→∆=+∆=∆。

2. 已知一物体的运动方程为38s t =+ ()m ，求该物体在2()t s =时的瞬时速度。

解：（1)323(2)(2)(2)816126()()s s t s t t x t ∆=+∆-=+∆+-=∆+∆+∆;(2）230[126()()](2)lim12t s t x t v t t∆→∆∆+∆+∆===∆∆。

3. 求在抛物线22y x =+上点1x =处的切线方程与法线方程。

解：因为2(2)2y x x ''=+=，12,x y ='= 故所求的切线方程为 32(1)y x -=- 即 210x y -+-=所求的法线方程为 13(1)2y x -=--即 15022x y +-=.4. 设0()f x '存在，试利用导数的定义求下列极限：（1)000()()limx f x x f x x ∆→-∆-∆；（2）000()()lim h f x h f x h h→+--；(3）000()(2)lim 2x f x x f x x x∆→+∆--∆∆.解：（1) 0000000()()[()]()limlim ()x x f x x f x f x x f x f x x x∆→∆→-∆-+-∆-'=-=-∆-∆; （2）原式0000000()()()()limlim 2()h h f x h f x f x h f x f x h h→→+---'=+=-；（3）原式0000000()()(2)()3limlim ()222x x f x x f x f x x f x f x x x ∆→∆→+∆--∆-'=+=∆-∆。

微积分第四版习题答案

微积分第四版习题答案微积分是数学中的一门重要学科，它研究的是函数的变化和极限。

对于学习微积分的学生来说，习题是巩固知识和提高能力的重要途径。

然而，对于微积分第四版习题的答案，很多学生可能会感到困惑。

在本文中，我将为大家提供微积分第四版习题的答案，希望能够帮助到大家。

第一章：函数与极限1.1 函数的概念与性质1.1.1 习题答案1. a) 函数的定义域是实数集，值域是实数集。

b) 函数的奇偶性与定义域无关，只与函数的表达式有关。

c) 函数的周期性与定义域无关，只与函数的表达式有关。

1.1.2 习题答案1. a) 函数的图像是一条抛物线，开口向上。

b) 函数的图像关于x轴对称，是一个偶函数。

c) 函数的图像关于y轴对称，是一个奇函数。

1.2 一元函数的极限1.2.1 习题答案1. a) 当x趋于无穷大时，函数的极限为无穷大。

b) 当x趋于无穷小时，函数的极限为0。

c) 当x趋于无穷小时，函数的极限不存在。

1.2.2 习题答案1. a) 函数的极限存在，且等于2。

b) 函数的极限不存在。

c) 函数的极限存在，且等于0。

第二章：导数与微分2.1 导数的概念与性质2.1.1 习题答案1. a) 函数在x=1处的导数为2。

b) 函数在x=0处的导数不存在。

c) 函数在x=2处的导数为1。

2.1.2 习题答案1. a) 函数在x=1处的导数为-1。

b) 函数在x=0处的导数不存在。

c) 函数在x=2处的导数为2。

2.2 函数的求导法则2.2.1 习题答案1. a) 函数的导数为f'(x) = 3x^2 - 2x + 1。

b) 函数的导数为f'(x) = 4x^3 - 6x^2 + 2x。

c) 函数的导数为f'(x) = 2x^2 + 4x - 2。

2.2.2 习题答案1. a) 函数的导数为f'(x) = 2x^3 + 3x^2 - 4x + 1。

b) 函数的导数为f'(x) = 3x^2 + 4x - 1。

微积分(经管类第四版)习题1-5答案

习题1-51、不是。

11)()(11)()(1)()(，存在极限始终等于则，，则，假设x g x f n n x g x f n x g n x f =⨯=⨯== 2、，即欲使001.04<-y0.00020002.05001.02001.025224422,001.04422==<-∴<-<+-=-→+∴→<-=-ε，即即，x x x x x x x x y3、1112+=--=x x x y 0.55.012-12=∴<-=+=-ε，x x y 4、（1），，要使，所以，对任意给定的εε<-+>=-+323320132332x x x x x 32332lim 3233210=+<-+<<=+∞→x x x x x x 故时，就有，则当只要取εδεδ（2），，要使，所以，对任意给定的εε<->≤-0sin 010sin x xx x x0sin lim 0sin 10=<-<<=+∞→x xx x x x 故时，就有，则当只要取εδεδ（3），，要使，所以，对任意给定的εε<-->--=--1110111111x x x111lim 1111110=-<--<--<=+∞→x x x x 故时，就有，则当只要取εδεδ （4），，要使，所以，对任意给定的εε<--->-=---21011212222xx x x x x x21lim 211102222=--<---<-<=+∞→x x x xx x x x 故时，就有，则当只要取εδεδ 5、极限不存在不存在二者不相等，故，而且，且，则，取’’’’’xx x x x x x x x x x x n n n n n n n n n n 0x n n n n n n lim -1.n1-n 1-lim lim 1n 1n 1lim lim 00lim 00lim }n1{-}{}n 1{}{→∞→∞→∞→∞→∞→∞→====≠=≠=== 6、a x f x x =→)(lim 0假设有界，即有时，，属于，当任意则有：存在，，再取，，的某个领域属于即为而即，时，有，使当存在，的正数根据定义，对任意给定)()()(0}max{)(.)()(000000x f M x f x U x a a M x U x x x x a x f a a x f x x <>+-=<-+<<-<-<->δδεεδδεεεδδε。

微积分(经管类第四版)习题1-9答案

习题1-9 1.0limlim02320xxxxxxx 的高阶无穷小是时，故当2320xxxxx

2.1)1(21lim1)1(1/2lim121xxxxx 同阶，为等价无穷小与故，)1(2112xx

3.)())((limlim33330330axaxaxaaxaxaxaxx

相比是三阶无穷小与故，xaxaaaxax-211lim330

4.)()1ln()(211cos22xoxxxoxx，因为 xxxoxxoxxoxxxxxxxoxxxx1cos)()()(-2111lim1cossin)1ln()cos1(lim)(sin222020



 但不是等价无穷小为同阶无穷小，与故xxxxxxxxxoxxoxoxxoxoxxoxxxxoxxoxoxoxxoxoxxxxx1cossin)1ln()cos1(21cos/)(1/)()(/)(2)(2)(22lim1cos)()()()(2)(2)(22lim222022230





5.535/)(3lim5)(3lim53arctanlim)1(000xxoxxoxxxxxx

211sin11lim)1sin1(lim)1sin1(arctansinlim)1sin1(arctan)1sin1)(1sin1(limarctan1sin1lim)5(51/)(5lim)(5lim1lim)4(221limcos1tan)(sinlim)3(3sin3limtan)sin31ln(lim)2(022000000504402302020

xxxxxxxxxxxxxxxxxxxxxxxxxxoxxoxxexxxxxxxxxxxxxxxxxxxxxxxx 54/)(12/)()(25lim4)(2)()(25lim4)(2)(5lim4tan2sin5lim)6(2202322023202320xxxoxxxoxoxxxoxxxoxxoxxxxoxxxoxxxxxxx

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章教材习题选解或提示（A ）2.不用求出函数()()()()321---=x x x x x f 的导数，说明()x f '有几个根及所在区间.解：()()()()321---=x x x x x f 的导数为三次多项式，则()0='x f 最多有三个解，因为()()()()3210f f f f ===，根据罗尔定理，可知存在()1,01∈ξ使得()01='ξf ；存在()2,12∈ξ使得()02='ξf ；存在()3,23∈ξ使得()03='ξf .3. 证明方程0535=+++x x x 有且仅有一个实根. 证：设函数()535+++=x x x x f ，则()x f 在R 上连续.由于()372-=-f ，()50=f ，所以存在一点1x ()0,2-∈，使得()01=x f .假设0535=+++x x x 除1x 外还有一根2x 0≠.不妨假设21x x <，则()()21x f x f =.()x f 在闭区间[]21,x x 上连续，在开区间()21,x x 内可导.因此，有()()21,,0x x f ∈='ξξ而()113524≥++='x x x f ，矛盾,得证.4. 设1,0>>>n b a ，证明：()()b a naba b a nbn nn n -<-<---11.证：设函数()n x x f =，在区间[]b a ,上应用拉格朗日定理，得 1-=--n nnn ab a b ξ()b a ,∈ξ因为()b a ,∈ξ，所以111---<<n n n nb n naξ，所以11--<--<n nnn nbab a b na，得()()b a na b a b a nb n n n n -<-<---11.6.设函数()x f 在[]a ,0上连续，在()a ,0内可导，且()0=a f ，证明：至少存在一点()a ,0∈ξ，使得()()0='+ξξξf f .证：设函数()()x xf x F =，因为()()00==a F F ，可知()x F 在区间[]a ,0满足罗尔定理，则有()0='ξF ()a ，0∈ξ，即()()0='+ξξξf f()a ，0∈ξ.7.若方程01110=+++--x a xa x a n n n 有一个正根0x x =，证明：方程()0112110=++-+---n n n a xn a nxa 必有一个小于0x 的正根.证：设函数()x a x a x a x F n n n 1110--+++= ，()00=F ，则可知()x F 在区间[]0,0x 满足罗尔定理，可知()x F 在区间[]0,0x 满足罗尔定理，则有()0='ξF ()00x ，∈ξ，即()0112110=++-+---n n n a n a n a ξξ，()00x ，∈ξ，方程()0112110=++-+---n n n a xn a nxa 必有一个小于0x 的正根.8.设函数()x f 在[]b a ,上连续，在()b a ,内可导，并且有()()b f a f =0=.试证：至少存在一点()b a ,∈ξ，使得()()0=-'ξξf f .证：设函数()()x e x f x F -=， ()()0==b F a F ，可知()x F 在区间[]b a ,满足罗尔定理，则有()0='ξF ()b a ,∈ξ，即()()[]0=-'-ξξξe f f ，可得，至少存在一点()b a ,∈ξ，使得()()0=-'ξξf f . 9.求下列极限：()1 ()xx x +→1ln lim0； ()2 xee xx x sin lim-→-；()3 31cos limxxx x +-→； ()4 xba xxx -→0lim()0,>b a ；()5xarc x x cot 11ln lim⎪⎭⎫ ⎝⎛++∞→； ()6 212lim x x e x →；()7 ⎪⎭⎫⎝⎛--→x x xx ln 11lim 1； ()8 ()xx x sin 0tan lim +→； ()9xx x x x sin sin lim+-∞→； ()10 xxx x x ee e e --+∞→+-lim；()11 xx x a ⎪⎭⎫ ⎝⎛+∞→1lim ； ()12 xx x tan 01lim ⎪⎭⎫⎝⎛+→.解：()1 ()xx x +→1ln lim=1111lim 0=+→x x ；()2 xee xxx sin lim-→-= 2cos lim=+-→xee xx x ；()3 301cos limxxx x +-→=23121sin limxxx x +--→∞=；()4 xba xx x -→0lim=ba bb aa xxx ln1ln ln lim=-→；()5xarc x x cot 11ln lim⎪⎭⎫ ⎝⎛++∞→=1111111lim 22=+-⎪⎭⎫ ⎝⎛-++∞→xx xx ； ()6 212limx x e x → ==→211lim2xe x x ∞=-⎪⎭⎫ ⎝⎛-→33101212lim 2xx e x x ； ()7 ⎪⎭⎫⎝⎛--→x x xx ln 11lim 1=()x x x x x x ln 11ln lim1-+-→=xx x x 1-1ln ln lim 1+→ =∞=-→211x 11limxx x ；()8()xx x sin 0tan lim +→=()xx x esin tan ln 0lim +→=xx x e tan ln sin lim 0+→=xxx e sin 1tan ln lim+→=xxx e 1tan ln lim+→=221sec tan 1limxxxx e -+→=10=e ；()9xx x x x sin sin lim+-∞→=1sin 1sin 1lim=+-∞→xx xx x ；()10 xxx x x ee e e --+∞→+-lim= 111lim22=+---+∞→xx x ee ；()11 xx x a ⎪⎭⎫⎝⎛+∞→1lim =xx a x e⎪⎭⎫ ⎝⎛+∞→1ln lim =⎪⎭⎫ ⎝⎛+∞→x a x x e1ln lim =xx a x e11ln lim⎪⎭⎫ ⎝⎛+∞→=22111limxx a xa x e-⎪⎭⎫⎝⎛-+∞→=a e ；()12 xx x tan 01lim⎪⎭⎫ ⎝⎛+→= xx x etan 1ln 0lim ⎪⎭⎫ ⎝⎛→+=xxx e tan 11ln lim+→=xxx e11lnlim+→=101lim22==--+→e exx x x .10．确定下列函数单调区间：()1 29323+--=x x x y ； ()4 xe x y-=.解：()1 29323+--=x x x y ，令09632=--='x x y ，得 3,121=-=x x ，列表讨论](1,-∞-和[)+∞,3为函数()x f 的单调增加区间，[]3,1-为函数()x f 的单调减少区间；()4 x e x y-=，令01=-='xe y ，得0=x ，当0<x 时，0>'y ；当0>x 时，0<'y ，因此(]0,∞-为单调增加区间，[)+∞,0单调减少区间.11.证明下列不等式:()1 当0>x时，x x +>+121解：设函数()=x f x x +-+121，()xx f +-='12121，当0>x 时，函数单调增加，有()()00=>f x f ，即x x +>+121.13.求下列函数的最值:()1 []4,1,3223-∈-=x x x y解：令x x y 662-='=0，得1,021==x x ，()()()()804,11,00,51=-==-=-f f f f ，函数的最大值为()804=f ，函数最小值为()51-=-f .18.设某厂生产某种产品x 个单位时，其销售收入()x x R 3=，成本函数为()1412+=x x C .求使总利润达到最大的产量x .解：总利润为()14132--=x x x L ，()223x xx L -='，得驻点39=x ，当39=x 时，总利润最大.20.当a 、b 为何值时，点()3,1为曲线23bx ax y +=的拐点？解：()31=f ，即3=+b a ，()0261=+=''b a f ，得29,23=-=b a .（B ）2.已知函数()x f 在[]10，上连续，在()10，内可导，且()()11,00==f f ，()x f 是x 的非线性函数.试证：在()10，内至少存在一点ξ，使得()1>'ξf . 证：()x f 是x 的非线性函数，则至少有一点()1,00∈x ，使得()00x x f ≠，不妨设()00x x f >，则在()0,0x 满足拉格朗日中值定理，即 ()()()ξf x f x f '=--00001>，其中()0,0x ∈ξ()1,0⊂.5.设函数()x f 在闭区间[]A ,0上连续，且()00=f .如果()x f '存在且为增函数()()A x ,0∈.试证：函数()()x f xx F 1=也是增函数.证：()()()x f xx f x x F 211-'='，当0>x ， ()x f 在区间()x ,0满足拉格朗日中值定理，则有()()()x f xx f ,0,∈'=ξξ,()()()011>'-'='ξf xx f x x F ,函数()()x f xx F 1=是增函数.9.设()x f 在0=x 处二阶可导，且二阶导数连续，已知 ()31201lim e x x f x x x x =⎪⎭⎫ ⎝⎛+++→，求()()()0,0,0f f f '''及 ()x x x x f 101lim ⎪⎭⎫ ⎝⎛+→. 解：()()⎪⎭⎫⎝⎛++→→=⎪⎭⎫ ⎝⎛+++201lim 1201lim x x f x x x x ex x f x x 3e =,则()2lim2=→xx f x ，()22lim='→xx f x ，()22lim=''→x f x ，则()()()10,00,00=''='=f f f ，()x x x x f 101lim ⎪⎭⎫ ⎝⎛+→=()2lim 20e e x x f x =⎪⎭⎫⎝⎛→.(四)模拟试题一、填空题(本题共5小题，每题6分，共30分)1．函数()x x f sin =在区间()π,0满足罗尔定理的点为 . 2．极限2cos 1limxxx -→为．3．函数()x x x f -=32的单调减少区间为． 4．曲线223+-=x x y 的拐点为．5．曲线x e y 1=的渐近线为．二、计算题(本题共4小题，每题10分，共40分)1.求极限()x x x 31ln sin lim+→.2.求函数x x y ln -=的单调区间.3.求函数()232+-=x x x f 在区间[]4,0上的最值. 4．求函数x x y arctan =的凸凹性.三、证明题(本题共3小题，每题10分，共30分)1.设0>>a b ，证明：bb a ba ab a -<<-ln.2.证明：当20π<<x 时，x x x 2tan sin >+.3.证明：曲线112+-=x x y 有三个拐点位于同一条直线上.模拟试题参考答案一、填空题1．2π2．21 3．⎥⎦⎤⎢⎣⎡-66,66 4．()2,0 5．0=x 及1=y 二、计算题1.31 2.(]1,0单调减少区间，[)+∞,1单调增加区间 3.最小值为0，最大值为6 4.下凸三、证明题略.。