【真题】18年湖北省鄂东南省级示范高中联盟联考高三(上)数学期中试卷含答案(理科)
数学---湖北省襄阳市四校联考2018届高三(上)期中试卷(理)(解析版)

湖北省襄阳市四校联考2018届高三(上)期中数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)命题“∃x0≤0,使得”的否定是()A.∀x>0,x2<0 B.C.∀x≤0,x2<0 D.2.(5分)设命题p:∃m∈R,使是幂函数,且在(0,+∞)上单调递减;命题q:∀x∈(2,+∞),x2>2x,则下列命题为真的是()A.p∧(¬q)B.(¬p)∧q C.p∧q D.(¬p)∨q3.(5分)下列函数中,既是偶函数,又在(0,+∞)上单调递增的是()A.y=ln|x﹣1| B.y=x2﹣|x| C.D.y=e x+e﹣x4.(5分)函数y=a x(a>0且a≠1)与函数y=(a﹣1)x2﹣2x﹣1在同一坐标系内的图象可能是()A.B.C.D.5.(5分)已知函数f(x)=f'(1)x2+x+2,则()A.B.C.D.6.(5分)等差数列{a n}中,已知|a7|=|a12|且公差d>0,则其前n项的和S n取得最小值时n 的值为()A.7 B.8 C.9 D.107.(5分)已知g(x)=[x],其中[x]表示不超过实数x的最大整数,x0是函数的零点,则g(x0)等于()A.1 B.2 C.3 D.48.(5分)点G为△ABC的重心(三边中线的交点).设,则等于()A.B.C.D.9.(5分)“a=2”是“∀∈(0,+∞),ax+”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10.(5分)已知函数的部分图象如图所示,f(x)的图象与x轴切于N点,则下列选项判断错误的是()A.B.C.D.|MN|=π11.(5分)设f(x)=|ax+b|+|cx+d|(x∈R),g(x)=|ax+b|﹣|cx+d|(x∈R)且都满足,则下列说法错误的是()A.f(x)有最小值而无最大值B.当|a|>|c|时,g(x)有最小值而无最大值C.当|a|<|c|时,g(x)有最小值而无最大值D.当|a|=|c|时,g(x)既有最小值又有最大值12.(5分)如图,直线y=ax+2与曲线y=f(x)交于A、B两点,其中A是切点,记h(x)=,g(x)=f(x)﹣ax,则下列判断正确的是()A.h(x)只有一个极值点B.h(x)有两个极值点,且极小值点小于极大值点C.g(x)的极小值点小于极大值点,且极小值为﹣2D.g(x)的极小值点大于极大值点,且极大值为2二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知集合A={1,2a},B={a,b},若A∩B={},则A∪B=.14.(5分)已知向量,且,则=.15.(5分)若函数在区间(﹣2,2)上有两个零点,则实数a 的取值范围为.16.(5分)在△ABC中,a,b,c分别为内角A,B,C的对边,若,且a=2,则△ABC的面积的最大值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)已知命题P:函数的定义域为R;命题q:∃x∈R,使不等式a>e2x﹣e x成立;命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.18.(12分)已知等差数列{a n}的前n项和为S n,其中a2=﹣2,S6=6.(1)求数列{a n}的通项;(2)求数列{|a n|}的前n项和为T n.19.(12分)设函数.(1)求函数f(x)的最小正周期和单调递增区间;(2)若f(α)=﹣1,且,求的值.20.(12分)已知函数f(x)=a(x+ln x)(a>0),g(x)=x2.(1)若f(x)的图象在x=1处的切线恰好也是g(x)图象的切线.求实数a的值;(2)对于区间[1,2]上的任意两个不相等的实数x1,x2且x1<x2,都有f(x2)﹣f(x1)<g(x2)﹣g(x1)成立.试求实数a的取值范围.21.(12分)在△ABC中,a,b,c分别为内角A,B,C的对边,,且.(1)试判断△ABC的形状;(2)若,求的取值范围.22.(12分)设f(x)=e x(e x﹣ax﹣1)且f(x)≥0恒成立.(1)求实数a的值;(2)证明:f(x)存在唯一的极大值点x0,且.【参考答案】一、选择题1.C【解析】∵命题“∃x0≤0,使得”是一个特称命题∴命题“∃x0≤0,使得”的否定是“∀x≤0,x2<0”故选C.2.A【解析】由m﹣1=1,解得:m=2,故f(x)=,在(0,+∞)上单调递减;故命题p是真命题;令x=4,则x2=2x;故命题q是假命题;故p∧(¬q)是真命题,故选:A.3.D【解析】函数y=ln|x﹣1|是非奇非偶函数,不满足条件;函数y=x2﹣|x|是偶函数,在(0,]是单调递减,在[,+∞)上单调递增,不满足条件;函数是偶函数,在(0,+∞)上,≥0不恒成立,故不满足条件;函数y=e x+e﹣x是偶函数,在(0,+∞)上单调递增,满足条件,故选:D4.C【解析】若0<a<1,则指数函数y=a x是减函数,二次函数y=(a﹣1)x2﹣2x﹣1开口向下,对称轴为x=<0,排除D;若a>1,则指数函数y=a x是增函数,二次函数y=(a﹣1)x2﹣2x﹣1开口向上,对称轴为x=>0,排除B;又二次函数y=(a﹣1)x2﹣2x﹣1与y轴交点为(0,﹣1),排除A;故选C.5.B【解析】∵f(x)=f'(1)x2+x+2,∴f′(x)=2f'(1)x+1,∴f′(1)=2f'(1)+1,∴f′(1)=﹣1,∴f(x)=﹣x2+x+2,∴=═(﹣x3+x2+2x)=,故选B.6.C【解析】∵等差数列{a n}中,|a7|=|a12|且公差d>0,∴|a1+6d|=|a1+12d|,∴a1=﹣9d<0,∴S n=na1+==(n﹣)2﹣.∴其前n项的和S n取得最小值时n的值为9.故选:C.7.B【解答】解;f(2)=ln2﹣1<0,f(3)=ln3﹣>0,则x0是(2,3)上的一个值,∴g(x0)=[x0]=2,故选B.8.B【解析】如图所示:点G为△ABC的重心(三边中线的交点).则:,设,则:,,=.故选:B.9.A【解析】“∀∈(0,+∞),ax+”⇔“∀∈(0,+∞),a≥”⇔“a ≥2”,故“a=2”是“∀∈(0,+∞),ax+”的充分不必要条件,故选:A10.B【解析】由函数的部分图象知,1+ω=2,解得ω=1,∴f(x)=cos(x﹣)+1;当x=时,f(x)=2,为最大值,∴f(x)的图象关于直线x=对称,有f(﹣x)=f(+x),∴A正确;由于f(x)+f(﹣x)=cos(x﹣)+1+[cos(﹣x﹣)+1]=2+cos(x﹣)+sin x=2+cos x+sin x=2+sin(x+)≠2,∴B错误;由于f()=cos(﹣)+1=cos+1=1,∴C正确;由于|MN|=T=×2π=π,∴D正确.故选:B.11.C【解析】∵f(x)=|ax+b|+|cx+d|(x∈R),g(x)=|ax+b|﹣|cx+d|(x∈R)且都满足,不妨令a,b均为正,则由ax+b=0得:x=﹣,由cx+d=0得:x=﹣,则当x=﹣,或x=﹣时,函数f(x)有最小值而无最大值,故A正确;当|a|>|c|时,g(x)有最小值而无最大值,故B正确;当|a|<|c|时,g(x)有最大值而无最小值,故C错误;当|a|=|c|时,g(x)既有最小值又有最大值,故D正确;故选:C.12.D【解析】∵直线y=ax+2与曲线y=f(x)交于A、B两点,∴ax+2=f(x)有两个解,设f(x)的极大值点为m,∴f′(m)=a,x<m,f′(x)>a,x>m,f′(x)<a.g(x)=f(x)﹣ax,g′(x)=f′(x)﹣a,∴g′(m)=f′(m)﹣m,∴g′(m)=0,x>m,g′(x)<0,x<m,g′(x)>0,∴x=m是函数的极大值点,且g(m)=f(m)﹣am=2,同理g(x)有极小值,故选:D.二、填空题13.{﹣1,,1}【解析】由A∩B={}得,2a=⇒a=﹣1,b=,∴A={1,},B={﹣1,},∴A∪B={1,﹣1,}故答案为:{﹣1,,1}.14.【解析】向量,且,∴6×3=﹣2m,解得m=﹣9,∴﹣=(6,﹣2)﹣(3,﹣9)=(3,7),∴|﹣|==,故答案为:.15.[0,1+ln2)【解析】当x≤0时,y=x2﹣a≥﹣a,函数是减函数,x>0时,y=x﹣a+ln x是增函数,函数在区间(﹣2,2)上有两个零点,可知分段函数,两个区间各有一个零点,可得,解得a∈[0,1+ln2).故答案为:[0,1+ln2).16.+1【解析】△ABC中,a,b,c分别为内角A,B,C的对边,若,利用正弦定理:,即:,所以:,且a=2.则:sin A=cos A.解得:A=.利用余弦定理:a2=b2+c2﹣2bc cos A,,整理得:bc,=,故三角形面积的最大值为:.故答案为:三、解答题17.解:若命题p为真命题,则在x∈R恒成立,当a=0时显然不成立,当a≠0时,;若命题q为真命题,则,由命题“p∨q”为真命题,“p∧q”为假命题知p,q一真一假,若p真q假,则,无解,若p假q真,则,综上所述,.18.解:(1)设等差数列{a n}的首项为a1,公差为d,由已知得:,∴a n=﹣4+(n﹣1)×2=2n﹣6;(2),当n<3时,a n<0,此时,当n≥3时,a n≥0,此时T n=﹣a1﹣a2+a3+a4+…+a n=,综上:.19.解:(1)∵,∴f(x)的最小正周期为.由,得,k∈Z.∴f(x)的单调递增区间为;(2)由,得,∵,∴,∴.∴==.20.解:(1)函数f(x)=a(x+ln x)(a>0),,∴x=1,f'(1)=2a,切点为(1,a),∴切线方程为y﹣a=2a(x﹣1),即y=2ax﹣a,又联立,消去y,可得x2﹣2ax+a=0,△=4a2﹣4a=0,∴a=1;(2)由条件可知:f(x2)﹣g(x2)<f(x1)﹣g(x1)(x1<x2),设F(x)=f(x)﹣g(x),即F(x)=a(x+ln x)﹣x2,∴F(x)在[1,2]上单调递减,∴在[1,2]上恒成立,即在[1,2]上恒成立,∵,∴a≤1,又由条件知a>0,0<a≤1从而即为所求.21.解:(1)由条件及正弦定理,得:(sin C﹣sin2A)sin B=(sin C﹣sin B)sin2A,即sin C sin B﹣sin2A sin B=sin C sin2A﹣sin B sin2A,∴sin C sin B=sin C sin2A,又sin C≠0,∴sin B=sin2A,∴B=2A,或B+2A=π,①当B=2A时,∵,∴B+A=3A>π导出矛盾,则B=2A应舍去.②当B+2A=π时,又A+B+C=π,∴A=C合理,综上判断△ABC为等腰三角形;(2)在等腰△ABC中,取AC的中点D,由得|BD|=3,又由(1)知,则=.22.(1)解:f(x)=e x(e x﹣ax﹣1)≥0,因为e x>0,所以e x﹣ax﹣1≥0恒成立,令φ(x)=e x﹣ax﹣1,x∈R,问题等价φ(x)≥0恒成立,∴φ'(x)=e x﹣a,当a≤0时,φ(x)在x∈R单调递增,又φ(0)=0当x∈(﹣∞,0)时,φ(x)<0矛盾,当a>0时,φ(x)在(﹣∞,ln a)单调递减,在(ln a,+∞)单调递增,∴φ(x)≥0恒成立,等价为φ(ln a)=e ln a﹣a ln a﹣1≥0,即a﹣a ln a﹣1≥0,又令g(a)=a﹣a ln a﹣1,(a>0),g'(a)=1﹣ln a﹣1=﹣ln a,∴g(a)在(0,1)单调递增,在(1,+∞)单调递减,而g(1)=0,所以不等式a﹣a ln a﹣1≥0的解为a=1,综上a=1.(2)证明:f'(x)=e x(2e x﹣x﹣2),令h(x)=2e x﹣x﹣2,h'(x)=2e x﹣1,所以h(x)在单调递减,在单调递增,∵由零点存在定理及h(x)的单调性知,方程h(x)=0在有唯一根,设为x0且,从而h(x)有两个零点x0和0,所以f(x)在(﹣∞,x0)单调递增,在(x0,0)单调递减,在(0,+∞)单调递增,从而f(x)存在唯一的极大值点x0即证,由得,∴取等不成立,所以得证,又∵在(﹣∞,x0)单调递增所以得证,从而且成立.。
湖北省鄂东南省级示范高中教育教学改革联盟学校2023-2024学年高三上学期期中联考物理试题答案

2023年秋季鄂东南省级示范高中教育教学改革联盟学校期中联考高三物理参考答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案DACDDDCADADBCD11.(1)A 距地面的高度h ,A 、B 的质量m A 、m B (3分)(每个物理量1分)(2)()A A B A m h m m s m h µ=+− (3分)或者 s m h s m h m B A A +−=)(µ,hm h s m hm B B A A +−+=))(m (µ12.(1) B (2分)(2)① C (2分) ②(2分) ③ 1.54v (1.51—1.58)v 均可以(2分)0.58Ω (0.51—0.63)Ω均可以 (2分)13.解:(1)对A 、B 、C 中的气体,初状态有:P 1=P 0 = 76cmHg V 1=V AC +V B末状态有:P 2=P 0+9.5cmHg=85.5cmHg V 2=V AC =1000cm 3 (2分)根据玻意耳定律得 1122PV PV = (2分) 解得 V B =125cm 3 (1分)末状态有: P 4=P 0+10cmHg=86cmHg V 4=V AC - V x(2分)根据玻意耳定律得 3344PV PV =(2分)解得被测固体的体积为 350cm x V =(1分)14C 点离地高度为1.2cos 3R R R R θ++= (1分) 解得 1.75h m = (1分)由题可知,滑块到达摆渡车右端时刚好与摆渡车共速,速度大小设为v 根据动量守恒定律可得2G mv mv = (1分)综合解得 2.5L m = (1分) (3)滑块从滑上摆渡车到与摆渡车共速过程,若恰好碰到IJ0 3.75L m = (2分)滑块凹槽GHIJ 底面HI 长度0L 至少3.75m15.解:(1)小球由A 点进入第一象限后,所受电场力与重力平衡:E 1q=mg ,E 1=40N/C (2分)由几何关系得: r+√rr 2−1=OA ,r=2m (2分) 小球做匀速圆周运动:qV 0B 1==mV 02r,v 0=2m/s (2分)(2)由几何关系得:BC 与竖直方向夹角为θ=30° (1分)小球由B 到C 做直线运动,则电场力与重力的合力与v B 均沿BC 方向,当电场力与BC 垂直时,电场力有最小值:qE 2min =mgsinθ E 2min =20N/C (2分) 对小球有:mgcosθ=ma (1分) x BC =OBcosθ=2√33m (1分)v C 2-v 02=2ax BC , (1分)代入数据得:a=5√3m/s 2 v C =2√6m/s (1分)(3)小球进入第三象限后,在重力、洛伦兹力作用下做变加速曲线运动,把初速度v C 分解为v 1和v 2,其中v 1满足:Bqv 1=mg ,v 1=mgB 2q =2√6m/s ,方向水平向左 (1分)则v 2=2√6m/s ,方向与x 轴正方向夹角为60° (1分)小球的实际运动可以分解为:运动一:速度为v 1=2√6m/s ,水平向左,合力为B 2qv 1-mg=0的匀速直线运动运动二:速度为v 2=2√6m/s ,顺指针旋转,合力为F 洛=B 2qv 2的匀速圆周运动 (1分) 当v 1和v 2的方向相同时合运动的速度最大,最大速度v m =v 1+v 2=4√6m/s (1分)方向水平向左 (1分)。
湖北省鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高三上学期期中考试 化学试题

2024年秋季鄂东南省级示范高中教育教学改革联盟学校期中联考高三化学试卷考试时间:2024年11月5日下午14:30-17:05 试卷满分:100分可能用到的相对原子质量:H-1 C-12 N-14 O-16 Mg-24 S-32 Cl-35.5 Cu-64 Ga-70一、选择题:(本题共15小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.化学是人类进步的阶梯,科技的发展与化学密切相关。
下列说法错误的是( )A.人民币使用的防伪磁性油墨中含有B.巴黎奥运会金牌是含的银、镀有的金、其余为铜的金属合金材质C.天津大学研发的石墨烯芯片将引领电子行业新革命,石墨烯属于新型烯烃D.是我国在月壤中发现的新型矿物,Y 是金属元素2.下列化学用语或图示表达错误的是( )A.乙炔的结构简式:B.基态Si 原子的价层电子轨道表示式:C.顺丁烯的分子结构模型:D.的电子式:3.下列说法正确的是( )A.二氧化碳不支持燃烧,故泡沫灭火器可用于金属钠着火后灭火B.和纯碱在高温条件下反应生成,该反应利用的是较强酸制较弱酸的原理C.氯气可使湿润的有色布条褪色,说明氯气具有漂白性D.工业上采用“吹出法”进行海水提溴,该方法利用溴易挥发的性质4.设为阿伏加德罗常数的值。
下列说法正确的是( )A.和的混合物中,所含中子数为B.与过量的和混合气体充分反应后,放出的为C.常温常压下,晶体中有个键D.用惰性电极电解溶液一段时间后,若加入能使溶液复原,则电解过程中转移电子数目为34Fe O 92.5% 1.34%()()847Ca Y Fe PO HC CH ≡2--22Na O 2Na [:O :O :]Na+-+2SiO 2CO A N 18218gH O 22H O A9N 220.1molNa O 2CO 2H O 2O A 0.2N 21molSiO A 2N Si O -4CuSO 229.4gCu(OH)A0.9N5.下列离子方程式书写正确的是()A.用惰性电极电解溶液:B.泡沫灭火器原理:C.向溶液中加入足量溶液:D.实验室制备乙酸甲酯:6.我国科研团队在嫦娥五号带回的月球样本中,发现了一种富含水分子和铵的未知矿物晶体。
湖北省鄂州市鄂州高中2018-2019学年上学期期中高考数学模拟题
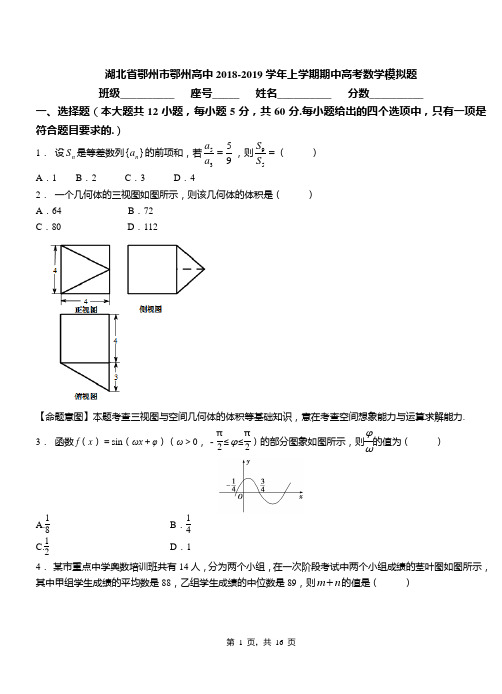
湖北省鄂州市鄂州高中2018-2019学年上学期期中高考数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 设n S 是等差数列{}n a 的前项和,若5359a a =,则95SS =( ) A .1 B .2 C .3 D .42. 一个几何体的三视图如图所示,则该几何体的体积是( )A .64B .72C .80D .112【命题意图】本题考查三视图与空间几何体的体积等基础知识,意在考查空间想象能力与运算求解能力. 3. 函数f (x )=sin (ωx +φ)(ω>0,-π2≤φ≤π2)的部分图象如图所示,则φω的值为( )A.18 B .14C.12D .14. 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m n +的值是( )A .10B .11C .12D .13【命题意图】本题考查样本平均数、中位数、茎叶图等基础知识,意在考查识图能力和计算能力. 5. 一个几何体的三个视图如下,每个小格表示一个单位, 则该几何体的侧面积为( )A.4πB.C. 5πD. 2π+【命题意图】本题考查空间几何体的三视图,几何体的侧面积等基础知识,意在考查学生空间想象能力和计算能力.6. 已知函数()cos (0)f x x x ωωω+>,()y f x =的图象与直线2y =的两个相邻交点的距离等于π,则()f x 的一条对称轴是( )A .12x π=-B .12x π=C .6x π=-D .6x π=7. 某几何体的三视图如下(其中三视图中两条虚线互相垂直)则该几何体的体积为( )A.83 B .4 C.163D .2038. 已知曲线2:4C y x =的焦点为F ,过点F 的直线与曲线C 交于,P Q 两点,且20FP FQ +=,则OPQ ∆的面积等于( )A .22B .32C .322 D .3249. 已知平面向量(12)=,a ,(32)=-,b ,若k +a b 与a 垂直,则实数k 值为( ) A .15- B .119 C .11 D .19【命题意图】本题考查平面向量数量积的坐标表示等基础知识,意在考查基本运算能力. 10.设集合{|12}A x x =<<,{|}B x x a =<,若A B ⊆,则的取值范围是( ) A .{|2}a a ≤ B .{|1}a a ≤ C .{|1}a a ≥ D .{|2}a a ≥11.已知全集U R =,{|239}x A x =<≤,1{|2}2B y y =<≤,则有( ) A .A ØB B .A B B =C .()R A B ≠∅ðD .()R A B R =ð12.在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若2cos a b C =,则此三角形一定是( ) A .等腰直角三角形 B .直角三角形C .等腰三角形D .等腰三角形或直角三角形二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.已知函数2()ln log 1f x a x b x =++,(2016)3f =,则1()2016f =___________. 14.在ABC ∆中,角A B C 、、的对边分别为a b c 、、,若1cos 2c B a b ⋅=+,ABC ∆的面积312S c =,则边c 的最小值为_______.【命题意图】本题考查正弦定理、余弦定理、三角形面积公式、基本不等式等基础知识,意在考查基本运算能力.15.已知M N 、为抛物线24y x =上两个不同的点,F 为抛物线的焦点.若线段MN 的中点的纵坐标为2,||||10MF NF +=,则直线MN 的方程为_________.16.如图,在三棱锥P ABC -中,PA PB PC ==,PA PB ⊥,PA PC ⊥,PBC △为等边三角形,则PC 与平面ABC 所成角的正弦值为______________.【命题意图】本题考查空间直线与平面所成角的概念与计算方法,意在考查学生空间想象能力和计算能力.三、解答题(本大共6小题,共70分。
湖北省鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高一上学期开学起点联考数学 含解析

2024年秋季鄂东南省级示范高中教育教学改革联盟学校起点考试高一数学试题命题学校:黄冈中学命题教师考试时间:2024年10月14日上午8:00—10:00试卷满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,0,1,2,3},{12}A B xx =-=-<≤∣,则A B ⋂=()A.{1,0}- B.{1,0,1}- C.{0,1}D.{0,1,2}2.命题“2[1,3],320x x x ∀∈--+≤”的否定为()A.2000[1,3],320x x x ∃∈--+≥ B.2[1,3],320x x x ∃∈--+>C.2[1,3],320x x x ∀∈--+≥ D.2000[1,3],320x x x ∃∉--+≥3.已知集合86A x x ⎧⎫⎨⎬⎩⎭=∈∈-N N ,则集合A 的所有非空子集的个数为()A.5个B.6个C.7个D.8个4.下列各组函数表示相同函数的是()A.()1,()|1|f x x g x x =+=+B.0()1,()f x g x x ==C.2()()f m g n == D.32(),()1x xf xg x xx +==+5.设x ∈R ,则“|32|3x -≤”是“(2)0x x -≤”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知1,c a b >==,则正确的结论是()A.a b <B.a b>C.a b= D.a 与b 的大小不确定7.已知关于x 的不等式20ax bx c ++>的解集为{23}xx <<∣,则关于x 的不等式20bx ax c ++<的解集为()A.615x x ⎧⎫-<<⎨⎬⎩⎭B.{1xx <-∣,或6}5x >C.213x x ⎧⎫-<<⎨⎬⎩⎭D.213x x x ⎧⎫<->⎨⎬⎩⎭,或8.若正实数,x y 满足24x y +=,不等式212131m m x y +>++有解,则m 的取值范围是()A.4,13⎛⎫-⎪⎝⎭B.4,(1,)3⎛⎫-∞-⋃+∞ ⎪⎝⎭C.41,3⎛⎫- ⎪⎝⎭D.4(,1),3⎛⎫-∞-⋃+∞ ⎪⎝⎭二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.图中阴影部分用集合符号可以表示为()A.()U ()B A C ⋂⋃ð B.U (()())A B B C ⋂⋃⋂ðC.()()U A C B⋃⋂ð D.()()()()U UA BC B ⋂⋃⋂ðð10.若0,0a b >>,且41a b +=,则下列说法正确的是()A.ab 有最大值116+有最大值2C.1aa b+有最小值5 D.2216a b +有最小值2211.下列命题正确的有()A.若方程2210ax x -+=有两个根,一个大于1另一个小于1,则实数a 的取值范围为(0,1)B.设,a b ∈R ,若12a b -且24a b +,则54210a b -C.设,a b ∈R ,命题:p a b >是命题:||||q a a b b >的充分不必要条件D.若集合{}{}2220,220,A xx x a B x x ax A =+-==++=∣∣和B 至少有一个集合不是空集,则实数a 的取值范围是a 或1a -三、填空题:本题共3小题,每小题5分,共15分.12.已知函数()y f x =的定义域为[3,2]-,则函数(21)1f x y x +=+的定义域为______.13.已知()f x 为二次函数,满足2()(1)2f x f x x ++=,则函数()f x =______.14.设集合[0,1),[1,3]M N ==,函数21,()63,x x Mf x x x N+∈⎧=⎨-∈⎩,已知a M ∈,且(())f f a M ∈,则a 的取值范围为______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知集合{68},{123}A xx B x m x m =-<=++∣∣.(1)若1m =,求()A B ⋂R ð;(2)若A B A ⋃=,求实数m 的取值范围.16.(15分)设命题p :对任意[0,1]x ∈,不等式2234x m m --恒成立,命题q :存在[1,1]x ∈-使得不等式2210x x m -+-成立.(1)若p 为真命题,求实数m 的取值范围;(2)若命题p 与命题q 一真一假,求实数m 的取值范围.17.(15分)已知关于x 的不等式31,1ax x a x +->∈-R .(1)若不等式的解集为{1xx <∣或2}x >,求a 的值;(2)求关于x 的不等式的解集.18.(17分)某公司销售甲、乙两种产品,根据市场调查和预测,甲产品的利润y (万元)与投资额x (万元)成正比,其关系如图(1)所示;乙产品的利润y (万元)与投资额x (万元)的算术平方根成正比,其关系式如图(2)所示,(1)分别将甲、乙两种产品的利润表示为投资额的函数;(2)若该公司投资(0)a a >万元资金,并全部用于甲、乙两种产品的营销,问:怎样分配这a 万元投资,才能使公司获得最大利润?其最大利润为多少?19.(17分)设22()21,()41f x x tx g x x tx =-+=-++,其中0t >,记()min{(),()}F x f x g x =.(1)若1t =,求()F x 的值域;(2)若0t >,记函数2()()1h x f x tx t =+-+对任意1,x t t ⎡⎤∈⎢⎥⎣⎦,总存在1,22m t t ⎡⎤∈⎢⎥⎣⎦,使得()h x m =成立,求实数t 的取值范围;(3)若13[0,3],()22x F x ∀∈-≤,求实数t 的取值范围.2024年秋季鄂东南省级示范高中教育教学改革联盟学校起点考试高一数学参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】D【详解】因为{1,0,1,2,3),{12}A B xx =-=-<≤∣,所以{}0,1,2A B ⋂=.故选:D.2.【答案】B【详解】由全称命题的否定为特称命题知:原命题的否定为:2000[1,3],320x x x ∃∈--+>故选:B 3.【答案】C 【详解】由题设,86x∈-N ,即8可被6x -整除且60,x x ->∈N ,{2,4,5},A ∴=故集合A 的所有非空子集的个数为3217-=4.【答案】D【解答】解:()1f x x =+与()1g x x =+的对应关系不同,不是同一函数:0()1,()f x g x x ==定义域不同,不是同一函数:()f m =R ,2()g n =而的定义域为[0,)∞+,不是同一函数:32()1x xf x x +=+与()g x x =的定义域都为R ,对应关系相同,是同一函数.故途:D.5.【答案】D【解答】根据题意,不等式323x -,则3323x --,即1533x -≤≤,解集为15,33⎤-⎥⎦不等式()20x x -,即02x ,解集为[]0,2,因为[]15,0,233-⊂且[]150,2,33⎤⊄-⎥⎦,所以“324x -”是“()20x x -”的既不充分也不必要条件,故选:D.6.【解新】方法一:特值法取特殊值,令2c =,则1a b ==易知a b <,排除B ,C ,还不能排除D ,猜测选A.方法二:作差法,分析法a b -=-=+-要比较,a b+⇔比较2+与4c 的大小(遇到二次根式可考虑平方去掉恨号)⇔比较2c +4c 的大小⇔与c 的大小.c <.<,故a b <.故选:A.方法三:有理化法==1100.c c ∴+>->⇒>⇒>>1.c ∀><a b <,故选A.7.【答案】A【解答】因为不等式20ax bx c ++>的解集为{23}xx <<∣,所以2和3是方程20ax bx c ++=的两个实数解,且0a <;由根和系数的关系知,2323b ac a ⎧+=-⎪⎪⎨⎪⨯=⎪⎩所以5,6b a c a =-=;所以不等式20bx ax c ++<可化为2560ax ax a -++<,叫2560x x --<,解得615x -<<,所求不等式的解集为615x x ⎧⎫-<<⎨⎬⎩⎭故选:A.8.【答栥】B 【详解】由()()4121121114214421616163y x x y x y x y x y ⎡⎡⎤+⎛⎫⎡⎤⎢+=+++=⨯++≥⨯+=⎢⎥ ⎪⎣⎦+++⎢⎝⎭⎣⎦⎣,仅当()411y x x y +=+,即13,2x y ==时等号成立.要使不等式212131m m x y +>++有解,只需()()221434341033m m m m m m +>⇒+-=+->.所以()4,1,3m ∞∞⎛⎫∈--⋃+ ⎪⎝⎭.故选:B二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.【答案】AD【解答】解:图中阴影部分用集合符号可以表示为()()U B A C ⋂⋃ð或()()()()U UA B C B ⋂⋃⋂痧.故选:AD.10.【答案】AC【解答】解:对于A ,211(4)1444416a b ab ab +=⨯≤⨯=,当且仅当4a b =且41a b +=,当11,82b a ==时取等号,不以ab 有最大值1,16故A 正确,对于B.因为24442a b a b a b +=+++++=.+≤,当且仅当142a b ==时取等号,+,故B 错误对于C ,144115a a b a b a a b a b a b ++=+=++≥+=,当且仅当4b a a b =且41,a b +=叫2a b =且41a b +=,即11,36a b ==时取等号,所以1aa b+有最小值5,故C 正确对于D.因为221624a b ab +⨯.所以()222222161624(4)a ba b ab a b +++⨯=+,所以222(4)11622a b a b ++≥=,当且仅当4a b =且41a b +=,即11,82b a ==时取等号,所以2216a b +有最小值12,故D 错误.故选:AC 11.【答案】ABD 【解答】选项A : 函数()()221f x x x x α=-+∈R 有两个两点,0a ∴≠,而且一个大于1另一个小于1.则()01210a f a >⎧⎨=-+<⎩或()01210a f a <⎧⎨=-+>⎩,解得01a <<.∴实数a 的取值范围为()0,1,故A 正确;选项B :令,a b u a b v +=-=,则24,12u v .由a b u a b v +=⎧⎨-=⎩解得22u v a u v b +⎧=⎪⎪⎨-⎪=⎪⎩所以424222322u v u v a b u v u v u v +--=⋅-⋅=+-+=+.因为24,336u v ,所以5310u v +,则54210a b -.故B 正确;选项C :若220,a b a b >≥>既有a a b b >;若0,a b ≥>显然有0a a b b >>;若0a b >>,则22a b <,而22,a a a b b b =-=-,所以a a b b >,故a b >可以推出||||a ab b >若a a b b >,当0b <时,如果0a ≥,不等式显然成立,此时有1a b >如果0a <,则有22a b ->-,因而1a b >当0b ≥时,0a >,此时有22a b >.因而a b >,敬a a b b >可以推出a b >,综合知p 是q 的充要条件故C 不正确;选项D :假设两个方程无实根(即,A B 均是空集),则有1221Δ440Δ480a a a a ⎧<-⎧=+<⎪⎪⇒⎨⎨=-<<<⎪⎪⎩⎩1a <<-.所以当a ≤或1a -时,两个方程至少有一个方程有实根,即两个集合至少有一个不是空集.故填a ≤或1a ≥-,故D 正确三、填空题:本题共3小题,每小题5分,共15分.12.【答案】[)12,11,2⎛⎤--⋃- ⎥⎝⎦【详解】由题意得:3212x -≤+≤,解得:122x -≤≤,由10+≠x ,解得:1≠-x ,故函数的定义域是[)12,11,2⎛⎤--⋃- ⎥⎝⎦.13.【答案】()2f x x x=-【解答】解:设()2f x ax bx c =++,满足()()212f x f x x ++=,所以()()()2221(1)12f x f x ax bx c a x b x c x ++=+++++++=,解得2212201200a a ab b a bc c ⎧==⎧⎪⎪+=⇒=-⎨⎨⎪⎪++==⎩⎩则函数()2f x x x =-.14.【答案】11,32⎛⎤ ⎥⎝⎦【解答】解:因为a M ∈.所以()[)211,3f a a =+∈,则()()()632136f f a a a =-+=-,由()()ff a M ∈,可得0361a -<,解得1132a <≤.故答案为:11,32⎛⎤⎥⎝⎦.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)【解答】解:(1)1m =时,{25}B xx =<∣,则{2R B x x =<∣ð或5}x >,则(){62A A B xx ⋂=-<<∣ð或58}x <(2)A B A ⋃=,等价于B A ⊆,当B =∅,则123m m +>+,船得2m <-,符合题意当B ≠∅.则12316238m m m m +≤+⎧⎪+>-⎨⎪+≤⎩,解得522m -≤≤.综上,实数m 的取值范围为5,2∞⎛⎤- ⎥⎝⎦16.(15分)【解析】(1)因为p 为真命题,所以对任意[0,1],x ∈不等式2234x m m --恒成立,所以2min (23)4x m m -≥-其中[]0,1x ∈,所以234m m --,解得13m ,有以m 的取值范围[]1,3,(2)若q 为真命题,即存在[]1,1x ∈-.使得不等式2210x x m -+-成立,则()2min210x x m -+-,其中[1x ∈-,1],而()2min212x x m m -+-=-+,所以20m -+,故2m :因为.p q 一真一假.所以p 为真命题,q 为假命题或p 为假命题,q 为真命题,若p 为真命题,q 为假命题,则132m m ≤≤⎧⎨>⎩,所以23m <≤;若p 为假命题,q 为真命题.则12m m <⎧⎨≤⎩或32m m >⎧⎨≤⎩,所以1m <.综上,1m <或23m <,所以m 的取值范围为()(],12,3∞-⋃.17.(15分)【解答】解:(1) 不等式311ax x x +->-可化为()()210ax x -->,原不等式的解集为{1xx <∣或2}x >.故1a =;(2)①当0a =时,不等式为220x -+>,解得1x <:②当0a ≠时,方程()2220ax a x -++=的两根分别为21,a,(i )当0a <时,21a <,故不等式的解为21x a <<:(ii )当0a >时,若21a >,即02a <<时,不等式的解为1x <或2x a>.若21a=,即2a =时,不等式的解为1x ≠;考21a <,即2a >时,不等式得解为2x a<或1x >.综上可知,当0a <时,不等式的解集为21xx a ⎧⎫<<⎨⎬⎩⎭;当0a =时,不等式的解集为{}|1x x <当02a <<时,不等式的解集为{1xx <∣或2}x a >;当2a =时,不等式的解集为{}1xx ≠∣,当2a >时,不等式的解集为{1xx >∣或2}x a <.18.(17分)【解答】解:(1)由题知,甲产品的利润函数为()(0)f x kx x =乙产品的利润函数为())0g x x =>.由题知,函数()f x 经过d 点()1.8,0.45,有10.45 1.8,4k k ==,所以()()104f x x x =.函数()g x 经过点()9,3.75,有3.75=由54k =,所以())0g x x =.(2)设乙产品的投资金额为(0)x x a <万元,则甲产的投资金额为()a x -万元.所获得总利润为y 万元,则()1,(0)4y a x x a =+-<,令t =,则2x t =,()2251151.44444y t a t t t a =+-=-++函数图象开口问上,对称轴为5541224t=-=-⨯,所以当52<时,函数在⎡⎣上单调递增,当t=,即x a=时,y.52>时,函数在50,2⎡⎤⎢⎥⎣⎦上递增,在52⎛⎝上递减,当52t=,即254x=时,y有最大值42516a+.综上得:52>时,乙产品投资254万元,甲产品投资254a⎛⎫-⎪⎝⎭万元,该公司可获得最大利润,最大利润为42516a+万元.52时,乙产品投资a万元:52>时,乙产品投资254万元,印产品投资254a⎛⎫-⎪⎝⎭万元,该公司可获得最大利润,最大利润为42516a+万元19.【解答】(1)()()2221,41f x x xg x x x=-+=-++,()()()22623,f xg x x x x x∴-=-=-()()(),03,,3,f x xF xg x x⎧≤≤⎪∴=⎨>⎪⎩即()[]()()2221,0,3,41,,03,.x x xF xx x x∞∞⎧-+∈⎪=⎨-++∈-⋃+⎪⎩作图可知,函数()F x的最大值为()()3 4.F F x=值域为(],4∞-.(2)由题意,只需()h x在1,x tt⎡⎤∈⎢⎥⎣⎦上的值域为1,22tt⎡⎤⎢⎥⎣⎦的子集即可,因为0t>,所以()2222324th x x tx t x t⎛⎫=-+=-+⎪⎝⎭,对称轴为2tx=,由1,x tt⎡⎤∈⎢⎥⎣⎦得1t>,①当12tt≤,即1t<≤()h x在1,tt⎡⎤⎢⎥⎣⎦的图象可知,2221()1,h x r tt⎡⎤∈+-⎢⎥⎣⎦,由题意得22211122t t t t t ⎧≤+-⎪⎨⎪≥⎩由221111t t +-≥=(1t =时取等号.放第一个式子成立,由第二个式子得02t <故此时1t <≤②当12t t >,即1>时,()h x 在1,2t t ⎡⎫⎪⎢⎣⎭递减,在,2t t ⎡⎤⎢⎥⎣⎦上递增.此时最小值为2324t t h ⎛⎫= ⎪⎝⎭,最大值为2()h t t =,所以2231422t t t t ⎧≥⎪⎨⎪≤⎩2t ≤≤2t <≤,综上,所求t 的范围为(1,2].(3)()()131222F x F x -≤⇔-≤≤.()()()22623,f xg x x tx x x t -=-=- ∴①当01t <≤时,()()[]()(]()()()1,,0,3,32,,3,3.31,f t f x x t F x f t g x x t g ⎧⎧≥-∈⎪⎪=∴≤⎨⎨∈⎪⎪≥-⎩⎩无解,②当13t <<时,()()[]()()1,,0,3,32,f t F x f x x f ⎧≥-⎪=∈∴⎨≤⎪⎩解得43t ≤≤.③当3t ≥时,()()[](),0,3,31F x f x x f =∈∴≥-,解得116t ≤,舍去.综上,413≤≤。
湖北省颚东南省级示范高中2019届高三上-期中文科数学试卷(pdf版,有答案)(精选)

21.解:(1) f ( x) a(1 ln x) x 2 2
f (1) a 1 2 0 ∴a=1
∴ f ( x) ln x x 2 1
当 x>1 时, f ( x) ln x x 2 1 ln x 0
鄂东南省级示范高中教育教学改革联盟学校 2018 年秋季期中联考 高三数学(文科)参考答案(共 4 页)第 2页
题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C A B A D C D B A D C
13. 9 ; 2
14. 5 ; 5
15.丙;
16. 1 2
17.解:命题 p 等价于 m<- 2 ……………………………………………………3 分
命题 q 等价于 m>2 或 m<-2…………………………………………… 6 分
C.f(x)=(ex-e-x)cos x 2
B.f(x)= ( x 1 ) ·cos2x x
D.f(x)= x ln | x | |x|
鄂东南省级示范高中教育教学改革联盟学校 2018 年秋季期中联考高三数学(文科)试卷(共 4 页)第 1页
9.关于函数 f(x)=3cos(2x- )+1 ,x∈R,下列命题正确的( ) 3
物不在我这儿”,丙说:“礼物不在乙处”,如果三人中只有一人说的是假的,请问
获
得了礼物(填“甲”或“乙”或“丙”).
16.已知 x∈(0,+∞),a∈R,则(x-a)2+(lnx-a)2 的最小值为
.
鄂东南省级示范高中教育教学改革联盟学校 2018 年秋季期中联考 高三数学(文科)试卷(共 4 页)第 2页
B.p
是假命题,┓p: x0
2018年最新 湖北省部分重点中学2018届高三第一次联考(数学) 精品
湖北省部分重点中学2018届高三第一次联考数 学 试 卷本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.全集=-∞=+∞==)(),2,(),,1(,B A C B A R U U 则( )A .),2()1,(+∞-∞B .),2[)1,(+∞-∞C .),2[]1,(+∞-∞D .),2(]1,(+∞-∞2.下列函数中,在区间)0,(-∞上为增函数的是( )A .)(log 21x y --=B .2)1(+-=x yC .xxy -=1D .|1|+=x y3.)(x f y =是以π2为周期的周期函数,其图象的一部分如图所示,则)(x f y =的解析式 可能是( )A .)1sin(3+=x yB .)1sin(3+-=x yC .)1sin(3-=x yD .)1sin(3--=x y4.已知向量与向量互相垂直且||||=,若==则),1,2( ( )A .(1,-2)B .(-2,1)C .(-2,1)或(2,-1)D .(1,-2)或(-1,2)5.设)))(((3)(x f f f x x f ,则-==( )A .)(x fB .)(1x f C .)(x f -D .)(3x f6.在△ABC 中,用a 、b 、c 和A 、B 、C 分别表示它的三条边和三条边所对的角,若a =2、 2=b 、4π=A ,则B=( )A .12π B .6π C .656ππ或D .121112ππ或7.等比数列}{n a 中,28,410987654321=++++=++++a a a a a a a a a a ,则 =++++1514131211a a a a a( )A .196B .224C .728D .2288.设a 、R b ∈,则“)1lg()1lg(22+<+b a ”是“b a <”的 ( ) A .充分必要条件B .充分不必要条件C .必要不充分条件D .既不充分又不必要条件9.函数)2(log )(221++=kx x x f 的值域为R ,则实数k 的取值范围为( )A .)22,22(-B .]22,22[-C .),22()22,(+∞-∞D .),22[]22,(+∞--∞10.已知-9,a 1,a 2,-1成等差数列,-9,b 1,b 2,b 3,-1成等比数列,则212)(b a a -等于 ( )A .±8B .8C .-8D .89±11.方程)10)(log (23log 222≠>++=+++a a x a x x a x a xa ax a 且其中的实根个数是 ( )A .0B .1C .2D .312.若βααβα2222sin sin ,sin 2sin 2sin3+=+则的取值范围是( )A .)21,23(-B .]94,0[C .]21,0[D .]41,0[第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上. 13.函数)65(log 221+-=x x y 的单调递增区间为 .14.等差数列3,}{1=a a n 中,前n 项和为S n ,且S 3=S 12则a 8= . 15.函数||sin sin 2x x y -=的值域为 . 16.下列结论中是真命题的有 (填上所有真命题的序号)①“)()(C B C A ⊇”是“B A ⊇”的必要不充分条件.②向量与向量共线,向量与向量共线,则向量与向量共线. ③函数)1lg(2++=x x y 是奇函数.④函数)1(2112xx y x x y +=-+=与函数互为反函数. 三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或演变步骤.17.(本题满分12分)设向量a 、7|23|1||||=-==及满足. (1)求、所成的角的大小. (2)求|3|b a +的值.18.(本题满分12分)如图:在正四棱柱ABCD—A1B1C1D1中,底面边长为1,侧棱长为2,E、F分别是侧棱AA1、CC1的中点.(2)求四棱锥A1—EBFD1的体积.19.(本题满分12分)(文科)函数c bx ax x x f +++=23)(的图象在点(1,f(1))处切线的斜率为O. (1)求a 、b 的关系式.(2)若)(x f y =在R 上是增函数,求a 、b 的值.(理科)有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数 较大者获胜.(1)分别求出两只骰子投掷所得点数的期望. (2)投掷蓝色骰子者获胜的概率是多少?20.(本题满分12分)求函数xx xx x x y cos sin 2sin sin cos 2cos +--=的值域.21.(本题满分12分)已知函数.||1)(x a x f -= (1)求证:函数),0()(+∞=在x f y 上是增函数.(2)若),1(2)(+∞<在x x f 上恒成立,求实数a 的取值范围.(3)若函数],[)(n m x f y 在=上的值域是)](,[n m n m ≠,求实数a 的取值范围.22.(本题满分14分)已知数列}{n a 的前n 项和为S n ,且满足)(11+∈+-=N n S tt a n n ,其中t 为常数, .lg ),2,21(n n a b t =∈(1)求数列}{n b 的通项公式.(2)当1≠t 时,设)(2)(212+++∈++=N n b x b x b x f n n n 的图象在x 轴上截得的线段长为n c ,求).2(1433221≥++++-n c c c c c c c c n n(理科)(3)若)1(21nn n a a d +=,数列}{n d 的前n 项和为T n ,求证n n n T )22(2-<湖北省部分重点中学2018届高三第一次联考数学试卷参考答案一、C C D D A B A D D C A B二、13.)2,(-∞ 14.0 15.[-3,3] 16.①③ 三、17.解(1)7)23(2=-b a 712||4||922=⋅-+b a b a 而1||||== 21=⋅∴…………4分a b a ∴=⋅∴21||||、所成的角为3π…………6分 (2)13|3|13139||6||9)3(222=+∴=++=+⋅+=+……12分18.(1)解2||||||||||11=====EF EB E D FD BF故31=E BFD S …………3分设平面D 1EBF 与平面ABCD 所成的角为θ. 则33arccos3331cos 1=∴===θθE BFD ABCD S S …………6分 (2)由(1)四边形BFD 1E 为菱形.11111122ED A F EFD A EBFD A V V V ---==………………9分点F 到平面ADD 1A 1的距离为1. 而2111=∆E D A S 3112131211=⋅⋅⋅=∴-EBFD A V ………………12分19.(文科)(1)0230)1(23)(2=++='++='b a f bax x x f 得由032=++∴b a …………4分(2)由条件0)(≥'x f 在R 上恒成立. 即0232≥++b ax x 在R 上恒成立.……6分0≤∆…………8分 而0)3(0322≤+∴=++a b a⎩⎨⎧=-=∴33b a ……………………12分 (理科)(1)红色骰子投掷所得点数1ξ是随机变量,其分布列如下:432381=⋅+⋅=ξE ………………3分蓝色骰子投掷所得点数2ξ是随机变量,其分布如下421272=⋅+⋅=ξE …………6分 (2)332=⋅…………12分20.解:原式xx xx x x x x x x x x 2sin 22cos 21cos sin 3sin 2cos 2cos sin 2sin cos cos sin 22222+=+--++=……6分 )54cos ,53sin ()2cos(52)2sin 532cos 54(251==-=+=ϕϕϕ其中x x x而0)2cos(11)2cos(0<-≤-≤-<ϕϕx x 或…………10分故函数值域为),52[]52,(+∞--∞ ………………12分21.解:(1)当.1)(,),0(x a x f x -=+∞∈时用定义或导数证明单调性均可…………3分 (2)),1(21+∞<-在x xa 上恒成立. 设),1()(12)(+∞<+=在则x h a xx x h 上恒成立. 可证),1()(+∞在x h 单调增……………5分 故3)1(≤≤a h a 即a ∴的取值范围为]3,(-∞…………6分(3))(x f 的定义域为0},0|{>∴∈≠mn R x x x …………7分当),0()()1(,0+∞>>在知由时x f m n 上单调增 )(),(n f n m f m ==∴ 故012=+-ax x 有两个不相等的正根m ,n , 200>∴⎩⎨⎧>∆>∴a a ………………9分当0<<n m 时,可证)0,()(-∞在x f 上是减函数.01,)(),(==≠==∴a mn n m m f n n f m 此时故而…………11分 综上所述,a 的取值范围为),2(}0{+∞ …………12分22.解:(1)1)11(1)11(111+-==∴+-=n n S t a ta a t a n n n n n a ta a n S t a )11()2(1)11(111-=-∴≥+-=--- t nb t a n ta a n n n n n lg ,)2(1==∴≥=∴-…………(文科6分)(理科4分) (2)由(1)知}{n b 为等差数列,故212+++=n n n b b b0,1)1)(()(2≠∴≠++=∴+n n n b t x b x b x f1,0)(2--=∴+n n b b x f 的两根分别为 nb b C n n n 2|1|2=-=∴+……(文科10分)(理科6分) ))1(1431321211(41433221nn c c c c c c c c n n -++⋅+⋅+⋅=++++∴- )11(4)1113121211(4nn n -=--++-+-= …………(文科14分)(理科8分) (3))1(21n n n t t d +=而))2(11)(2(21)1212(21n n n n n n n t t t t --=--+ )212(211)2(,22,21n n n n n n d t t t +<∴>>∴∈ …………(理科11分) )212(21)212(21)212(2122n n n T ++++++< )211(212)211(2112)212121(21)222(2122n n n n n n +-=-+-=+++++++= 又n n n n n n T )22(2)22(21)211(21-<∴=>+…………(理科14分)。
湖北省鄂东南省级示范高中教育教学改革联盟学校2025届高三上学期期中联考语文试卷(含答案)
湖北省鄂东南省级示范高中教育教学改革联盟学校2025届高三期中联考语文试卷考试时间: 2024年11月4日上午09: 00——11: 30 试卷满分: 150分一、现代文阅读 (35 分)(一) 现代文阅读Ⅰ (本题共5小题,19分)阅读下面的文字,完成1~5小题。
材料一:2024年7月10日,“萝卜快跑”连然登上热搜。
武汉市交通运输局向媒体表示,“萝卜快跑”在武汉投放了400多辆无人车。
支持者为AI技术的运用欢呼,反对者则对无人车的高歌猛进表现出不安和抵触情绪,有出租车司机联名求助“给一条活路”。
10公里3.9元、L4级自动驾驶技术、不拒载、车内无异味……“萝卜快跑”着实不简单。
但随着时间的推移,在出租车司机或网约车司机群体里,嘲讽“萝卜快跑”无人车不善“变通”的声音也高了起来,甚至盖过了最初的“恐惧感”。
7月16日前后,网传“萝卜诀跑”停运,但官方回应称,武汉系订单被自动取消,而合肥系技术原因需要调整。
短短十几天工夫,情绪的落差之大,观点的纷繁复杂,也折射着“萝卜快跑”无人车在极速发展过程中的一丝“震颤”。
但显然,当无人车恪守规则意识“不争不抢”“安全第一”却让不少人类司机感到不适应时,我们应该展开的思考显然超越了技术层面。
首先,无人车是新质生产力的典型代表。
不必讳言,它在一定程度上直接冲撞了传统产业,对于传统产业的劳动者形成直接的“威胁”。
有人说,对于新技术,就该无条件地欢迎,“有什么好嚎的?”理由是,火车和汽车代替马车时,人的感受并不重要。
这当然是一种事实,但另一个事实是,被類覆的传统产业的劳动者在短暂的病苦之后,从各个方面适应了残酷的现实,并重新找到了生存所需要的岗位。
争议开启的思考是有益的:发自传统产业深处的痛感,是在“呼唤”一种良性的关系。
这就是:在新技术力量“攻城掠地”之时,也要允许和倡导温情的力量进行某种改善和修补。
具体而言,关键是在政策层面保持开放和引导的态度。
既要允许“先行先试”,从基础设施建设等方面提供帮助,也要抓紧完善相关规则,加强监管,让无人车在公共交通领域里规范地发挥作用,不至于“裸奔”。
(新)湖北省武汉市2018届高三数学上学期期中试题理
2017-2018学年度上学期高三年级期中检测数学(理)试题第I 卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知复数2z1i,则下列命题中正确的个数为①2=z ②i z -=1 ③z 的虚部为i ④z 在复平面上对应点在第一象限 A .1 B .2 C .3 D .4 2.下列函数为偶函数且在(0,+∞)上为增函数的是A .20()(cos )x f x tdt B .223()f x x x C .21()2f x x x D .()()xx f x x e e3.已知集合2lg 2x A x y x ⎧-⎫==⎨⎬+⎩⎭,集合{}21B y y x ==-,则集合{x x A B 且}x A B 为A .[]()2,12,-+∞ B .()()2,12,-+∞C .()[),21,2-∞-D .(](),21,2-∞-4.下列说法正确的是 A .“,x yR ,若0xy,则1x且1y ”是真命题B .在同一坐标系中,函数(1)y f x =+与(1)y f x =-的图象关于y 轴对称.C .命题“x R ,使得2230x x ”的否定是“x R ,都有2230x x ”D .aR ,“11a”是“1a ”的充分不必要条件5.如图,在ABC 中,13AN NC ,P 是BN 上的一点, 若29AP mABAC ,则实数m 的值为 A .19 B .13C .1D .3 6.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织七匹三丈(1匹=40尺,一丈=10尺),问日益几何?”第5题图其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了七匹三丈,问每天增加多少尺布?”若这一个月有31天,记该女子一个月中的第n 天所织布的尺数为n a ,则132931242830a a a a a a a a ++⋅⋅⋅++++⋅⋅⋅++的值为A .2930 B .1615 C .13D .15 7.若13tan ,(,)tan 242ππααα-=∈,则sin(2)4πα+的值为 A .2±B .25C .2D .2±8.某食品的保鲜时间y (单位:小时)与储存温度x (单位:C )满足函数关系bkx ey +=( 718.2=e 为自然对数的底数,,k b 为常数),若该食品在0C 的保鲜时间是192小时,在22C 的保鲜时间是48小时,则该食品在33C 的保鲜时间是( )小时.A .22B .23C .24D .33 9.已知函数()sin()(0,)2f x x πωϕωϕ=+><的部分图像如所示,为了得到()y f x 的图像需将cos 2yx 的图像A .向右平移3π个单位长度 B .向左平移3π个单位长度 C .向右平移6π个单位长度D .向左平移6π个单位长度 10.已知定义在R 上的偶函数)(x f ,满足)()4(x f x f =+,且]2,0[∈x 时,()sin 2sin f x x xππ=+,则方程0lg )(=-x x f 在区间[0,10]上根的个数是A .18B .19C .10D .9 11.在ABC 和AEF 中,B 是EF 的中点,1633ABEF BC CA ,,,若2AB AEAC AF ,则EF 与BC 的夹角的余弦值为A .12 B .23 C .34 D .13第9题图12.设函数()()x x f x e x ae (其中e 为自然对数的底数)恰有两个极值点12,x x 12()x x ,则下列说法中正确的是A .103aB .201x C .1(0)02f -<< D .12()()0f x f x第II 卷二、填空题(每题5分,共20分,将答案填在答题纸上)13.函数2lg(23)y x x =--+的单调递增区间是________.14.已知向量(6,2)a =-,(1,)b m =,且a b ⊥,则2a b -= . 15.已知数列{}n a 的通项公式为219104na n n,当123234a a a a a a 345a a a12n n n a a a 取得最大值时,n 的值为_________.16.若函数()y f x =满足b x a f x a f 2)()(=-++(其中220ab ),则称函数)(x f y =为“中心对称函数”,称点),(b a 为函数()f x 的“中心点”.现有如下命题:①函数()sin 1f x x =+是“中心对称函数”;②若“中心对称函数”()y f x =在R 上的“中心点”为()(),a f a ,则函数()()()F x f x a f a =+-是R 上的奇函数;③函数()32362f x x x x =-+-是“中心对称函数”,且它的“中心点”一定为()1,2;④函数x x x f cos 2)(-=是“中心对称函数”,且它的“中心点”一定为(,)2ππ.其中正确的命题是___ _____.(写出所有正确命题的序号)三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)已知向量(,cos())a sinx x π=-,(2cos ,2cos )b x x ,函数()1f x a b .(Ⅰ)求()f x 的对称中心; (Ⅱ)求函数()f x 在区间[0,]2π上的最大值和最小值,并求出相应x 的值.18.(本小题满分12分)已知函数()f x =4log (41)x++kx (k R ∈).(Ⅰ)当12k时,若方程()f x -m =0有解,求实数m 的取值范围; (Ⅱ)试讨论()f x 的奇偶性.19.(本小题满分12分)已知数列{}n a ,{}n b ,n S 为数列{}n a 的前n 项和,且满足214a b =,22n n S a =-,21(1)n n nb n b n n +-+=+(*n N ∈).(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)试问{}nb n能否为等差数列,请说明理由; (III )若数列{}n c 的通项公式为,24n n n n n a b n c a b n ⎧-⎪⎪=⎨⎪⎪⎩为奇数,为偶数,令n T 为{}n c 的前n 项的和,求2n T .20.(本小题满分12分)已知函数()-xf x e ax =(a R ∈,e 为自然对数的底数).(Ⅰ)讨论函数()f x 的单调性;(Ⅱ)若1a =,函数()()()2xg x x m f x e x x =--++在()2,+∞上为增函数,求实数m 的取值范围.21.(本小题满分12分)如图所示,某住宅小区一侧有一块三角形空地ABO ,其中3,OA km 33,OBkm90AOB .物业管理拟在中间开挖一个三角形人工湖OMN ,其中,M N 都在边AB 上(,M N 不与,A B 重合,M 在,A N 之间),且30MON .(Ⅰ)若M 在距离A 点2km 处,求点,M N 之间的距离;(Ⅱ)为节省投入资金,三角形人工湖OMN 的面积要尽可能小.试确定M 的位置,使OMN 的面积最小,并求出最小面积.22.(本小题满分12分)已知数列{}n a 满足1n na t =+(,,3,)n t N t t n t *∈≥≤,为常数. (Ⅰ)设1121111nni inS a a a a ,*n N ,证明:(1)ln(1)nS t n ;(Ⅱ)证明:1n a na e -<(e 为自然对数底数);(Ⅲ)设1231()=()()()()nttt t t n kn k T a a a a a ==+++∑ ,*nN ,试比较与n T 与1的大小关系,并说明理由.第21题图1. C 2. D 3. D 4. B 5. A 6. B 7. C 8. C 9. A 10. B 11. B 12. C第II 卷二、填空题:每题5分,满分20分,将答案填在答题纸上. 13. (3,1]或(3,1) 14. 45 15. 9n16.①②③三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.解:(I )因为()1f x a b =2sin cos cos(π)2cos 1x x x x +-⋅+22sin cos 2cos 1x x x =-+=sin 2cos2x x -=2sin(2)4x………4分所以()f x 的对称中心为(,0)()28k k Z ππ+∈ ……………5分 (II )由(I )得,()f x =sin 2cos2x x -=2sin(2)4x π-, …………7分因为π0,2x ⎡⎤∈⎢⎥⎣⎦,所以π3π2,444x π⎡⎤-∈-⎢⎥⎣⎦, 所以当242x ππ-=时,即8x 3π=时,()f x 的最大值是2;当244x ππ-=-时,即0x =时,()f x 的最小值是1-. …………10分 18.(本小题满分12分)解:(Ⅰ)由m =()f x =4log (41)x+-12x ,∴m =441log 2x x +=41log (2)2xx+. ∵1222xx ,∴m ≥12. ……………………………………6分(Ⅱ)依题意得定义域为R ,关于原点对称∵()f x 4log (41)x ++kx ,()f x 4log (41)x -+-kx ,令()()f x f x ,得441log 41x x-++=2kx -,即4log 4x=2kx -, ∴2x kx 对一切k R ∈恒成立.∴12k时()()f x f x ,此时函数()f x 是偶函数……………………9分∵0441(0)log (41)0log 22f k =+-⨯==,∴函数()f x 不是奇函数, 综上,当12k时,函数()f x 是偶函数;当12k 时,函数()f x 是非奇非偶函数. …………12分 19、(本小题满分12分)解:(Ⅰ)当1n =时,111222S a a =-⇒=,当2n ≥时,由112222n n n n S a S a --=-⎧⎨=-⎩,得:122n n n a a a -=-,则12n n a a -=,综上,{}n a 是公比为2,首项为2的等比数列,2nn a =;………………3分(Ⅱ){}nb n是等差数列,理由如下: ∵214a b =,∴11b =,∵21(1)n n nb n b n n +-+=+,∴111n nb b n n+-=+ 综上,{}n b n 是公差为1,首项为1的等差数列,且211n n bn b n n=+-⇒=;…7分 (Ⅲ)令212n n n p c c -=+22122221(21)2(2)2(41)2(41)424n nn n n n n n ----⋅⋅=-+=-⋅=-⋅01212123123474114(41)443474114(45)4(41)4n n n nn T n T n n --⎧=⨯+⨯+⨯++-⨯⎪⎨=⨯+⨯+⨯++-⨯+-⨯⎪⎩ ①②①-②,得:012121644334444444(41)43(41)414nn nnn T n n --⋅-=⋅+⋅+⋅++⋅--⋅=+--⋅- 所以27127499nn n T -=+⋅. ……………… ………12分20.(本小题满分12分)解:(Ⅰ)函数()f x 的定义域为R ,()xf x e a '=-.当0a ≤时,()0f x '>,∴()f x 在R 上为增函数; 当0a >时,由()0f x '=得ln x a =,当(),ln x a ∈-∞时,()0f x '<,∴函数()f x 在(),ln a -∞上为减函数, 当()ln ,x a ∈+∞时,()0f x '>,∴函数()f x 在()ln ,a +∞上为增函数……4分 (Ⅱ)当1a =时,()()()2x x g x x m e x e x x =---++,∵()g x 在()2,+∞上为增函数;∴()10xxg x xe me m '=-++≥在()2,+∞上恒成立,即11x x xe m e +≤-在()2,+∞上恒成立, …………………………6分令()11xx xe h x e +=-,()2,x ∈+∞,则()()()2221x x xxe xe e h x e --'==-()()221x x xe e x e---,令()2xL x e x =--,()10xL x e '=->在()2,+∞上恒成立,即()2xL x e x =--在()2,+∞上为增函数,即()()2240L x L e >=->,∴()0h x '>,即()11x x xe h x e +=-在()2,+∞上为增函数,∴()()222121e h x h e +>=-,∴22211e m e +≤-,所以实数m 的取值范围是2221,1e e ⎛⎤+-∞ ⎥-⎝⎦. ………………12分21.(本小题满分12分)解:(Ⅰ)在ABO 中,因为33390OAOB AOB ,,,所以60OAB ,在OAM 中,由余弦定理得:2222cos 7OM AO AM AO AM A ,所以7OM,所以22227cos 2OA OM AM AOM AO AM, 在OAN 中,sin sin()sin(90)ONA A AON AOM 27cos 7AOM, 在OMN 中,由sin 30sin MN OMONA,得7172427MN;… ………6分 (Ⅱ)解法1:设,060AOM,在OAM 中,由sin sin OM OAOAB OMA ,得332sin(60)OM,在OAN 中,由sinsin ONOA OABONA ,得90)2cos ON ==, 所以11sin 22OMNSOM ONMON 60)⋅12cos 2θ⋅ =2716sin(60)cos θθ+6060)4θ<<+.当26090θ+=,即15θ=时,OMN S的最小值为27(23)4.所以应设计15AOM ,可使△OMN 的面积最小,最小面积是27(23)4km 2…12分解法2:设AM =x ,0<x <3.在△OAM 中,由余弦定理得OM 2=AO 2+AM 2-2AO ·AM ·cos A =x 2-3x +9,所以OM =x 2-3x +9,所以cos∠AOM =OA 2+OM 2-AM 22OA ·OM =6-x2x 2-3x +9, 在△OAN 中,sin∠ONA =sin(∠A +∠AON )= sin(∠AOM +90°)=cos∠AOM =6-x 2x 2-3x +9,由ON sin ∠OAB =OAsin ∠ONA,得ON =36-x2x 2-3x +9·32=33x 2-3x +96-x, 所以S △OMN=12OM ·ON ·sin∠MON =12·x 2-3x +9·33x 2-3x +96-x ·12=33(x 2-3x +9)4(6-x ),0<x <3,令6-x =t ,则x =6-t ,3<t <6,则:S △OMN=33(t 2-9t +27)4t =334(t -9+27t )≥334·(2t ·27t-9)=27(2-3) 4.当且仅当t =27t ,即t =33,x =6-33时等号成立,S △OMN 的最小值为27(2-3)4, 所以M 的位置为距离A 点6-3 3 km 处,可使△OMN 的面积最小,最小面积是27(2-3) 4km 2.22.(本小题满分12分) 解:(Ⅰ)即证:12111ln(1)(1)(1)(1)nn t a t a t a +++>++++,即证:1111ln(1)23n n++++>+, 设()ln(1)g x x x =-+,1()111xg x x x '=-=++, ∵当0x >时,()0g x '>,()g x 在(0,)+∞上单调递增, 当10x -<<时,()0g x '<,()g x 在(1,0)-上单调递减, ∴()ln(1)(0)0g x x x g =-+≥=(当且仅当0x =时等号成立), 即0x >时,有ln(1)x x >+, ∴1113411ln 2ln ln lnln(1)2323n n n n+++++>++++=+, ∴12111(1)ln(1)n t n a a a +++>++ ……………………………4分(用数学归纳法给分)(Ⅱ)由(Ⅰ)知:当1x >-且0x ≠时,有ln(1)x x >+,即当0x >且1x ≠时,有1ln x x ->,因为0111n n t a t t <=≤<++,所以 1ln n n a a ->, 即1n a na e -<………………………………………8分(Ⅲ)1231()=()()()()1nt t t t tnk n k T a a a a a ,理由如下:解法一:由(Ⅱ)知:123()()()()t t tt n a a a a ++++3121111()()()()n a a a a t t t t e e e e 3121111()()()()n a a a a t t t t e e e e2111(1)1t tn t t t t ee e-+++-=-22211111(1)111t t t t t t t t t t ee ee e--+++++--≤=--,设 1t t eq +=,因为3142t t q ee +=≥>,21111t t t t ee-++-∴=-1111111t t q q q q q ----=<<---, 所以1231()=()()()()1nttt t t n kn k T a a a a a ==++++<∑ ………………12分解法二:因为,*n t N ∈, 且n t ≤,所以1231231()=()()()()()()()()nt t t t t t t t t nk n t k T a a a a a a a a a12()()()111tt t t t t t下面用数学归纳法证明:*3,t tN 时,12()()()1111tt t t t t t,即12(1)tt t t t t ,①当3t时,左边333312336(13),即当3t 时不等式成立;②假设当(3)t k k时不等式成立,即12(1)kkkk k k ,则当1tk时,111112(1)k kkk k k 11122(1)k k k k k k k 1(1)(12)(1)k k k k k k k11(1)(1)(1)2(1)kkk kkkk,11111112111()(1)1()()1111k k k k k k k C C k kkk111121kC k ,11(2)2(1)k k k k,11111112(1)2(1)(2)kkkkkk k kkk,所以当1t k时,不等式也成立;综合①②*3,t tN 时,12(1)tttt t t ,即12()()()1111tt t t tt t成立,所以1231()=()()()()1nt t t t t n kn k T a a a a a ==++++<∑.。
2021届湖北省鄂东南省级示范高中高三上学期期中联考数学试题(解析版)
附:
0.050
0.010
0.001
3.841
6.635
10.828
【答案】(1)分布列答案见解析,数学期望: ;(2)没有 以上的把握认为教师、学生对该食堂的评价有差异.
【分析】(1)设教师对食堂服务满意为事件A,学生对食堂服务满意为事件B,即可求得 ,再得出抽取人员中学生人数 的取值为 ,求得相应的概率,得出分布列,利用公式求得期望.
13.已知向量 ,若 ,则 在 方向上的投影为___________.
【答案】
【分析】先利用 求出 ,再利用 可得 在 方向上的投影.
【详解】由 可得 ,
又因为 ,
所以 ,
所以 .
所以 在 方向上的投影为 .
故答案为: .
14.有8个座位连成一排,现有5人就坐,则恰有两个空座位相邻的不同坐法有___________(用数字作答).
A. B.数列 是等比数列
C. D.
【答案】AB
【分析】化简得到 ,根据 三点共线,得到 ,即 ,计算 ,依次判断每个选项得到答案.
【详解】由 得
因为 三点共线,所以 ,则
又 ,所以 是以4为首项,公比为2的等比数列,
所以 ,故 .
则 , ,
所以AB正确,CD错误.
故选:AB
【点睛】关键点点睛:本题的关键在于运用平面向量共线定理的推论来解题,即由 三点共线,得到 .
选条件②:由 ,可得 ,结合分组求和法,即可求解;
选条件③:由 ,可得 ,结合乘公比错位相减法,即可求解.
【详解】(1)由题意,等差数列 中 且 ,
可得 ,解得 ,所以 .
(2)选条件①: ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年湖北省鄂东南省级示范高中教育教学改革联盟联考高三(上)期中数学试卷(理科)一、选择题1.(3分)设全集I是实数集R,M={x|x≥3}与N={x|(x﹣3)(x﹣1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为()A.{x|1<x<3}B.{x|1≤x<3}C.{x|1<x≤3}D.{x|1≤x≤3}2.(3分)下列函数中,既是偶函数又在区间(1,2)上单调递增的是()A.y=log2|x|B.y=cos2xC.D.3.(3分)已知a=21.2,b=()﹣0.2,c=2log52,则a,b,c的大小关系为()A.b<a<c B.c<a<b C.c<b<a D.b<c<a4.(3分)设角A,B,C为锐角△ABC的三个内角,则点P(sinA﹣cosB,cosA ﹣sinC)在()A.第一象限B.第二象限C.第三象限D.第四象限5.(3分)已知△ABC是边长为4的等边三角形,P为平面ABC内一点,则的最小值为()A.﹣3 B.﹣6 C.﹣2 D.6.(3分)我国古代数学名著《算法统宗》中有如下问题:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏 B.3盏 C.5盏 D.9盏7.(3分)如图曲线y=x2和直线x=0,x=1,y=所围成的图形(阴影部分)的面积为()A.B.C.D.8.(3分)如果对于任意实数x,[x]表示不超过x的最大整数,那么“[x]=[y]”是“[x﹣y]<1”成立的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件9.(3分)将函数y=sin(2x+)图象上的点M(θ,)(0<θ<)向右平移t(t>0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则()A.θ=,t的最小值为B.θ=,t的最小值为C.θ=,t的最小值为D.θ=,t的最小值为10.(3分)已知A(1,0),点B在曲线G:y=lnx上,若线段AB与曲线M:y=相交且交点恰为线段AB的中点,则称B为曲线G关于曲线M的一个关联点.那么曲线G关于曲线M的关联点的个数为()A.0 B.1 C.2 D.411.(3分)如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:原点处标0点(1,0)处标1,点(1,﹣1)处标2,点(0,﹣1)处标3,点(﹣1,﹣1)处标4,点(﹣1,0)点标5,点(﹣1,1)处标6,点(0,1)处标7,以此类推,则标签20172的格点的坐标为()A.(1009,1008)B.(1008,1007)C.(2017,2016)D.(2016,2015)12.(3分)函数f(x)=e x+x2+x+1与g(x)的图象关于直线2x﹣y﹣3=0对称,P,Q分别是函数f(x),g(x)图象上的动点,则|PQ|的最小值为()A.B.C.D.2二、填空题13.(3分)已知,则sin2α+sin2α=.14.(3分)对于任意两集合A,B,定义A﹣B={x|x∈A且x∉B},A*B=(A﹣B)∪(B﹣A)记A={y|y≥0},B={x|﹣3≤x≤3},则A*B=.15.(3分)若[x]表示不超过x的最大整数(如:等等),则=.16.(3分)方程(x2018+1)(1+x2+x4+…+x2016)=2018x2017的实数解的个数为.三、解答题17.在△ABC中,角A,B,C所对应的边分别为a,b,c,且a2﹣(b﹣c)2=bc,cosAcosB=.(1)求角A和角B的大小;(2)若f(x)=sin(2x+C),将函数y=f(x)的图象向右平移个单位后又向上平移了2个单位,得到函数y=g(x)的图象,求函数g(x)的解析式及单调递减区间.18.已知数列{a n}满足a1=1,S n=2a n+1,其中S n为{a n}的前n项和(n∈N+).(1)求S1,S2及数列{S n}的通项公式;(2)若数列{b n}满足,且{b n}的前n项和为T n,求|T n|的最大值和最小值.19.如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=,PD=BC=CD=AD,AP⊥PD.(1)若E为AP的中点,求证:BE∥平面PCD;(2)求二面角P﹣AB﹣C的余弦值.20.如图,在平面直角坐标系xOy中,椭圆的焦距为2,且过点.(1)求椭圆E的方程;(2)若点A,B分别是椭圆E的左、右顶点,直线l经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,直线AP交l于点M.(ⅰ)设直线OM的斜率为k1,直线BP的斜率为k2,求证:k1k2为定值;(ⅱ)设过点M垂直于PB的直线为m.求证:直线m过定点,并求出定点的坐标.21.已知函数f(x)=lnx,g(x)=(m>0).(Ⅰ)若函数y=f(x)与y=g(x)在x=1处有相同的切线,求m的值;(Ⅱ)若函数y=f(x)﹣g(x)在定义域内不单调,求m﹣n的取值范围;(Ⅲ)若∀x>0,恒有|f(x)|≥|g(x)|成立,求实数m的最大值.22.在平面直角坐标系xOy中,曲线C1的参数方程为(α为参数).以平面直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.(Ⅰ)求曲线C1的普通方程和曲线C2的直角坐标方程;(Ⅱ)求曲线C1和C2公共弦的长度.23.设函数f(x)=|x+2|+|x﹣1|.(1)求f(x)的最小值及取得最小值时x的取值范围;(2)若集合{x|f(x)+ax﹣1>0}=R,求实数a的取值范围.2017-2018学年湖北省鄂东南省级示范高中教育教学改革联盟联考高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题1.(3分)设全集I是实数集R,M={x|x≥3}与N={x|(x﹣3)(x﹣1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为()A.{x|1<x<3}B.{x|1≤x<3}C.{x|1<x≤3}D.{x|1≤x≤3}【解答】解:由题意M={x|x≥3}与N={x|(x﹣3)(x﹣1)≤0}={x|1≤x≤3}由图知阴影部分所表示的集合为N∩(C I M)∴N∩(C I M)={x|1≤x<3}故选:B.2.(3分)下列函数中,既是偶函数又在区间(1,2)上单调递增的是()A.y=log2|x|B.y=cos2xC.D.【解答】解:y=log2|x|有f(﹣x)=f(x),为偶函数,当x∈(1,2)时,函数y=log2x递增,符合题意;y=cos2x为偶函数,在(1,)递减,在(,2)递增,不符题意;y=,有f(﹣x)==﹣f(x),函数为奇函数;y=log2(﹣2<x<2),有f(﹣x)=log2=﹣log2,函数为奇函数.故选:A.3.(3分)已知a=21.2,b=()﹣0.2,c=2log52,则a,b,c的大小关系为()A.b<a<c B.c<a<b C.c<b<a D.b<c<a【解答】解:∵b=()﹣0.2=20.2<21.2=a,∴a>b>1.∵c=2log52=log54<1,∴a>b>c.故选:C.4.(3分)设角A,B,C为锐角△ABC的三个内角,则点P(sinA﹣cosB,cosA ﹣sinC)在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:由△ABC为锐角三角形,则0<A,B,C<,即0<﹣B<A<,即有sinA>sin(﹣B)=cosB,即sinA﹣cosB>0,同理sinC>cosA,cosA﹣sinC<0,∴点P(sinA﹣cosB,cosA﹣sinC)在第四象限,故选:D.5.(3分)已知△ABC是边长为4的等边三角形,P为平面ABC内一点,则的最小值为()A.﹣3 B.﹣6 C.﹣2 D.【解答】解:以BC中点为坐标原点,建立如图所示的坐标系,则A(0,2),B(﹣2,0),C(2,0),设P(x,y),则=(﹣x,2﹣y),=(﹣2﹣x,﹣y),=(2﹣x,﹣y),所以则的最=﹣x•(﹣2x)+(2﹣y)•(﹣2y)=2x2﹣4y+2y2 =2[x2+2(y﹣)2﹣3];所以当x=0,y=时,取得最小值为2×(﹣3)=﹣6,故选:B.6.(3分)我国古代数学名著《算法统宗》中有如下问题:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏 B.3盏 C.5盏 D.9盏【解答】解:设塔顶的a1盏灯,由题意{a n}是公比为2的等比数列,∴S7==381,解得a1=3.故选:B.7.(3分)如图曲线y=x2和直线x=0,x=1,y=所围成的图形(阴影部分)的面积为()A.B.C.D.【解答】解:由于曲线y=x2(x>0)与y=的交点为(),而曲线y=x2和直线x=0,x=1,y=所围成的图形(阴影部分)的面积为S=,所以围成的图形的面积为S==(x﹣x3)|+(x3﹣x)|=.故选:D.8.(3分)如果对于任意实数x,[x]表示不超过x的最大整数,那么“[x]=[y]”是“[x﹣y]<1”成立的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:若“[x]=[y]”,设[x]=a,[y]=a,x=a+b,y=a+c其中b,c∈[0,1)∴x﹣y=b﹣c∴|x﹣y|<1即“[x]=[y]”成立能推出“|x﹣y|<1”成立反之,例如x=1.2,y=2.1满足|x﹣y|<1但[x]=1,[y]=2即|x﹣y|<1成立,推不出[x]=[y]故“[x]=[y]”是“|x﹣y|<1”成立的充分不必要条件故选:A.9.(3分)将函数y=sin(2x+)图象上的点M(θ,)(0<θ<)向右平移t(t>0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则()A.θ=,t的最小值为B.θ=,t的最小值为C.θ=,t的最小值为D.θ=,t的最小值为【解答】解:将函数y=sin(2x+)图象上的点M(θ,)(0<θ<)向右平移t(t>0)个单位长度得到点M′,故有sin(2θ+)=,∴θ=,点M′(θ+t,),即M′(+t,).若M′位于函数y=sin2x的图象上,则=sin2(+t),∴t的最小值为,故选:A.10.(3分)已知A(1,0),点B在曲线G:y=lnx上,若线段AB与曲线M:y=相交且交点恰为线段AB的中点,则称B为曲线G关于曲线M的一个关联点.那么曲线G关于曲线M的关联点的个数为()A.0 B.1 C.2 D.4【解答】解:如图所示:设线段AB与曲线y=的交点为C,如图所示,令点B(x,lnx),则点C(,lnx).由于点C在函数y=lnx的图象上,故有lnx=,即lnx=.故曲线G关于曲线M的关联点的个数,即为函数y=lnx 和曲线y=的交点的个数.在同一个坐标系中,画出函数y=lnx 和曲线y=的图象,数形结合可得函数y=lnx 和曲线y=的交点的个数为1,故选:B.11.(3分)如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:原点处标0点(1,0)处标1,点(1,﹣1)处标2,点(0,﹣1)处标3,点(﹣1,﹣1)处标4,点(﹣1,0)点标5,点(﹣1,1)处标6,点(0,1)处标7,以此类推,则标签20172的格点的坐标为()A.(1009,1008)B.(1008,1007)C.(2017,2016)D.(2016,2015)【解答】解:观察已知中点(1,0)处标1,即12,点(2,1)处标9,即32,点(3,2)处标25,即52,…由此推断点(n+1,n)处标(2n+1)2,当2n+1=2017时,n=1008,故标签20172的格点的坐标为(1009,1008).故选:A.12.(3分)函数f(x)=e x+x2+x+1与g(x)的图象关于直线2x﹣y﹣3=0对称,P,Q分别是函数f(x),g(x)图象上的动点,则|PQ|的最小值为()A.B.C.D.2【解答】解:∵f(x)=e x+x2+x+1,∴f′(x)=e x+2x+1,∵函数f(x)的图象与g(x)关于直线2x﹣y﹣3=0对称,∴函数f(x)到直线的距离的最小值的2倍,即可|PQ|的最小值.直线2x﹣y﹣3=0的斜率k=2,由f′(x)=e x+2x+1=2,即e x+2x﹣1=0,解得x=0,此时对于的切点坐标为(0,2),∴过函数f(x)图象上点(0,2)的切线平行于直线y=2x﹣3,两条直线间距离d就是函数f(x)图象到直线2x﹣y﹣3=0的最小距离,此时d=,由函数图象的对称性可知,|PQ|的最小值为2d=2.故选:D.二、填空题13.(3分)已知,则sin2α+sin2α=.【解答】解:∵,可得sinα=2cosα,即tanα=2,∴sin2α+sin2α====.故答案为:.14.(3分)对于任意两集合A,B,定义A﹣B={x|x∈A且x∉B},A*B=(A﹣B)∪(B﹣A)记A={y|y≥0},B={x|﹣3≤x≤3},则A*B=[﹣3,0)∪(3,+∞).【解答】解:有题意知:A﹣B={x|x>3},B﹣A={x|﹣3≤x<0},A*B=(A﹣B)∪(B﹣A)=[﹣3,0)∪(3,+∞).故答案为:[﹣3,0)∪(3,+∞).15.(3分)若[x]表示不超过x的最大整数(如:等等),则=2017.【解答】解:∵===1+,∴[]=[1+]=1,∴=1+1+…+1=2017.故答案为:2017.16.(3分)方程(x2018+1)(1+x2+x4+…+x2016)=2018x2017的实数解的个数为1.【解答】解:显然(x2018+1)(1+x2+x4+…+x2016)>0,∴方程(x2018+1)(1+x2+x4+…+x2016)=2018x2017的解为正数.∵(x2018+1)(1+x2+x4+…+x2016)=2018x2017,∴(x+)(1+x2+x4+…+x2016)=2018,∴x+x3+x5+…+x2017+++…+=2018,又x+≥2,x3+≥2,…,x2017+≥2,当且仅当x=1时取等号.∴x+x3+x5+…+x2017+++…+≥2018,当且仅当x=1时取等号.∴原方程的解为x=1.故答案为:1.三、解答题17.在△ABC中,角A,B,C所对应的边分别为a,b,c,且a2﹣(b﹣c)2=bc,cosAcosB=.(1)求角A和角B的大小;(2)若f(x)=sin(2x+C),将函数y=f(x)的图象向右平移个单位后又向上平移了2个单位,得到函数y=g(x)的图象,求函数g(x)的解析式及单调递减区间.【解答】解:(1)△ABC中,∵a2﹣(b﹣c)2=bc,∴a2﹣b2﹣c2=﹣bc,∴cosA==,∴A=.∵cosAcosB=,∴2cosAcosB=sinA+cosC,∴cosB=+cos(﹣B),即cosB=+cos•cosB+sin sinB,即cosB=1+sinB,∴B=.综上可得,.(2)∵C=﹣B=,∴f(x)=sin(2x+)=cos2x,∴,令2kπ≤2x﹣≤2kπ+π,求得kπ+≤x≤kπ+,故函数g(x)的单调减区间为[kπ+,kπ+],k∈Z.18.已知数列{a n}满足a1=1,S n=2a n+1,其中S n为{a n}的前n项和(n∈N+).(1)求S1,S2及数列{S n}的通项公式;(2)若数列{b n}满足,且{b n}的前n项和为T n,求|T n|的最大值和最小值.【解答】解:(1)∵数列{a n}满足a1=1,S n=2a n+1,∴S n=2(S n+1﹣S n),化为:S n+1=S n.∴S1=a1=1,S2==.∴数列{S n}是等比数列,首项为1,公比为,可得:S n=.(2)数列{b n}满足=(﹣1)n•.∴{b n}的前n项和为T n==﹣.n为奇数时,|T n|=∈,n为偶数时,|T n|=∈.∴最大值为1,最小值为.19.如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=,PD=BC=CD=AD,AP⊥PD.(1)若E为AP的中点,求证:BE∥平面PCD;(2)求二面角P﹣AB﹣C的余弦值.【解答】(1)证明:取PD的中点F,连接EF,CF,∵E,F分别是PA,PD的中点,∴EF∥AD且EF=AD;∵BC=AD,BC∥AD,∴EF∥BC且EF=BC;∴BE∥CF.又BE⊄平面PCD,CF⊂平面PCD,∴BE∥平面PCD;(2)解:方法一、以P为坐标原点,PD,PA所在直线分别为x轴和y轴,建立如图所示的空间直角坐标系,不妨设BC=1,则P(0,0,0),A(0,,0),D(1,0,0),C(1,0,1),B(,,1),=(0,,0),=(,﹣,1),=(1,﹣,0).设平面PAB的一个法向量为n=(x,y,z),则,取x=2,得=(2,0,﹣1).同理可求平面ABD的一个法向量为=(3,,0).cos<>==.平面ABD和平面ABC为同一个平面,∴二面角P﹣AB﹣C的余弦值为;方法二、以D为坐标原点,DA,DC所在直线分别为x轴和z轴,建立如图所示的空间直角坐标系,不妨设BC=1,则P(,,0),A(2,0,0),D(0,0,0),C(0,0,1),B(1,0,1),=(,﹣,0),=(﹣1,0,1),设平面PAB的一个法向量为=(x,y,z),则,取y=,得=(1,,1).易知平面ABC的一个法向量为=(0,1,0).∴cos<>==.∴二面角P﹣AB﹣C的余弦值为.20.如图,在平面直角坐标系xOy中,椭圆的焦距为2,且过点.(1)求椭圆E的方程;(2)若点A,B分别是椭圆E的左、右顶点,直线l经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,直线AP交l于点M.(ⅰ)设直线OM的斜率为k1,直线BP的斜率为k2,求证:k1k2为定值;(ⅱ)设过点M垂直于PB的直线为m.求证:直线m过定点,并求出定点的坐标.【解答】解:(1)由题意得2c=2,∴c=1,又,a2=b2+1.消去a可得,2b4﹣5b2﹣3=0,解得b2=3或(舍去),则a2=4,∴椭圆E的方程为.(2)(ⅰ)设P(x1,y1)(y1≠0),M(2,y0),则,,∵A,P,M三点共线,∴,∴,∵P(x1,y1)在椭圆上,∴,故为定值.(ⅱ)直线BP的斜率为,直线m的斜率为,则直线m的方程为,====,即.所以直线m过定点(﹣1,0).21.已知函数f(x)=lnx,g(x)=(m>0).(Ⅰ)若函数y=f(x)与y=g(x)在x=1处有相同的切线,求m的值;(Ⅱ)若函数y=f(x)﹣g(x)在定义域内不单调,求m﹣n的取值范围;(Ⅲ)若∀x>0,恒有|f(x)|≥|g(x)|成立,求实数m的最大值.【解答】解:(I)函数y=f(x)在x=1处的切线方程为y=x﹣1,由g(1)=0得n=﹣1,由g'(1)=1得m=2;(II)y'=f'(x)﹣g'(x)=,因为y=f(x)﹣g(x)在定义域内不单调,所以h(x)=x2+[2﹣m(1﹣n)]x+1 在(0,+∞)内有至少一个实根且曲线与x不相切.因为h(0)=1>0,于是[2﹣m(1﹣n)]2﹣4>0;∴m(1﹣n)>4或m(1﹣n)<0;由m(1﹣n)>4知m+(1﹣n)≥2>,所以m﹣n>3;(III)当x=1时,由|f(1)|≥|g(1)|得n=1,当x>1时,f(x)>0,g(x)>0;当0<x<1时,f(x)<0,g(x)<0;令k(x)=f(x)﹣g(x),则问题转化为:当x>1时,k(x)≥0恒成立,当0<x<1时,k(x)≤0恒成立;而k(x)=,当x≥1时,函数y=x+2﹣2m+是单调函数,最小值为4﹣2m,为使k(x)≥0恒成立,注意到k(1)=0,所以4﹣2m≥0,即m≤2;同理,当0<x<1时,m≤2;综上:m≤2.22.在平面直角坐标系xOy中,曲线C1的参数方程为(α为参数).以平面直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.(Ⅰ)求曲线C1的普通方程和曲线C2的直角坐标方程;(Ⅱ)求曲线C1和C2公共弦的长度.【解答】解:(I)曲线C1的参数方程为(α为参数),消去参数α可得普通方程:(x﹣1)2+y2=4,即x2+y2﹣2x=3.曲线C2的极坐标方程为ρ=4sinθ,即ρ2=4ρsinθ,可得直角坐标方程:x2+y2=4y,配方为x2+(y﹣2)2=4.(II)x2+y2﹣2x=3与x2+y2=4y相减可得公共弦所在的直线方程:2x﹣4y+3=0.圆心C1(1,0)到公共弦所在的直线的距离d==.∴公共弦长=2=.23.设函数f(x)=|x+2|+|x﹣1|.(1)求f(x)的最小值及取得最小值时x的取值范围;(2)若集合{x|f(x)+ax﹣1>0}=R,求实数a的取值范围.【解答】解:(1)∵函数f(x)=|x+2|+|x﹣1|≥|x+2﹣(x﹣1)|=3,故函数f (x)=|x+2|+|x﹣1|的最小值为3,此时,﹣2≤x≤1.(2)函数f(x)=|x+2|+|x﹣1|=,而函数y=﹣ax+1表示过点(0,1),斜率为﹣a的一条直线,如图所示:当直线y=﹣ax+1过点A(1,3)时,3=﹣a+1,∴a=﹣2,当直线y=﹣ax+1过点B(﹣2,3)时,3=2a+1,∴a=1,故当集合{x|f(x)+ax﹣1>0}=R,函数f(x)>﹣ax+1恒成立,即f(x)的图象恒位于直线y=﹣ax+1的上方,数形结合可得要求的a的范围为(﹣2,1).赠送—高中数学知识点【1.3.1】单调性与最大(小)值 (1)函数的单调性②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()u g x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则yxo[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质 ()f x分别在(,-∞、)+∞上为增函数,分别在[、上为减函数.(3)最大(小)值定义①一般地,设函数()y f x =的定义域为I ,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M ≤;(2)存在0x I ∈,使得0()f x M =.那么,我们称M 是函数()f x 的最大值,记作max ()f x M =.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.。
