利用matlab进行仿真的案例
matlab中Simulink 的仿真实验报告
Simulink 的仿真实验报告1.实验目的:熟悉使用Simulink的各种使用方法及仿真系统2.数学建模:假设系统的微分方程为:r''(t)+3r'(t)+2r(t)=e(t) , 其中e(t)=u(t)求该系统的零状态响应令等式右边为零,则可求得方程的两个特征根为:r1=-1, r2=-2所以设该系统的零状态响应为:r(t)=Ae^-t+Be^-2t+C其中C为方程的一个特解,由微分方程可知,等式右边没有冲激函数及冲激函数的微分,故系统在零负到零正的过程中没有发生跳变,则C为一个常数。
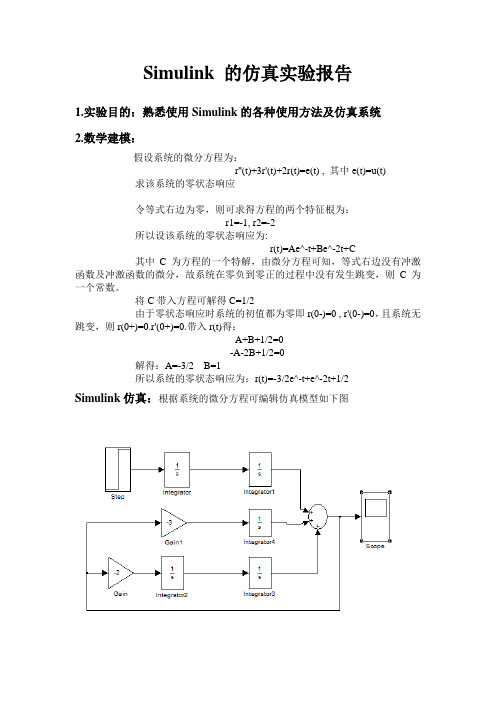
将C带入方程可解得C=1/2由于零状态响应时系统的初值都为零即r(0-)=0 , r'(0-)=0,且系统无跳变,则r(0+)=0.r'(0+)=0.带入r(t)得:A+B+1/2=0-A-2B+1/2=0解得:A=-3/2 B=1所以系统的零状态响应为:r(t)=-3/2e^-t+e^-2t+1/2Simulink仿真:根据系统的微分方程可编辑仿真模型如下图打开开始按键,可以得到波形图:验证仿真结果:由前面得到的系统零状态响应结果:r(t)=-3/2e^-t+e^-2t+1/2可编辑仿真模型:>> t=(0:0.1:10);>> plot(t,((-3)/2)*exp((-1)*t)+exp((-2)*t)+1/2)实验结论:Simulink仿真结果和函数仿真结果基本一致,所以simulink仿真是正确的。
实验心得:1.此实验是利用matlab对一个微分方程进行建模求解,既要求我们掌握对微分方程的求解,又要求掌握用matlab对微分方程进行建模,所以要求我们对软件得熟悉。
2.信号与系统的实验主要是用matlab分析或验证书上的东西,前提当然是学好书本上的知识,再学好matlab这个软件。
3.用simulink仿真的时候,对函数用积分器较好,不知为什么用微分器做不出来,报错显示不出图形。
matlab电路仿真教程

matlab电路仿真教程Matlab是一种功能强大的软件,用于进行电路仿真和分析。
通过Matlab,用户可以轻松地进行电路分析、验证和优化。
在本教程中,我将介绍如何使用Matlab进行电路仿真,并提供一些实例来帮助您更好地理解。
首先,我们需要了解Matlab中的电路仿真工具。
Matlab提供了许多函数和工具箱,用于电路建模和仿真。
其中最常用的是Simulink和Circuits工具箱。
Simulink是一个可视化的仿真环境,用于建立和模拟电路系统。
Circuits工具箱则提供了一些基本电路元件和函数,用于电路建模和分析。
要开始使用Matlab进行电路仿真,首先需要安装Matlab和Simulink软件,并确保您具有有效的许可证。
然后,打开Matlab并导航到Simulink库。
在Simulink库中,您将找到许多电路元件,例如电阻器、电容器和电感器,以及电压源和电流源。
将合适的元件拖放到工作区域中,然后连接它们以构建您的电路。
在电路建模完成后,您需要为电路设置适当的参数。
例如,您可以指定电阻、电容和电感的值,以及电压源和电流源的值。
您还可以添加信号源和观察点,以便在仿真期间监视电路的行为。
一旦您完成了电路建模和参数设置,接下来就可以对其进行仿真了。
在Simulink工具箱中,有几种不同类型的仿真可用,例如时域仿真和频域仿真。
通过选择合适的仿真类型,并设置仿真时间和步长,您可以开始执行仿真并观察电路的响应。
在仿真完成后,您可以使用Matlab绘图工具箱中的一些函数来绘制和分析电路响应。
例如,您可以绘制电压随时间的变化曲线,或者计算电源输出和负载电流之间的关系。
通过使用Matlab的分析工具,您还可以进行降阶、优化和参数估计等进一步分析。
让我们通过一个简单的示例来说明如何使用Matlab进行电路仿真。
假设我们有一个简单的RC电路,其中包括一个电阻器和一个电容器。
我们想要了解电容器的电压如何随时间变化。
基于Matlab的光学实验仿真

基于Matlab的光学实验仿真一、本文概述随着科技的快速发展,计算机仿真技术已成为科学研究、教学实验以及工程应用等领域中不可或缺的一部分。
在光学实验中,仿真技术能够模拟出真实的光学现象,帮助研究者深入理解光学原理,优化实验设计,提高实验效率。
本文旨在探讨基于Matlab的光学实验仿真方法,分析Matlab在光学实验仿真中的优势和应用,并通过具体案例展示其在光学实验仿真中的实际应用效果。
通过本文的阐述,读者将能够了解Matlab在光学实验仿真中的重要作用,掌握基于Matlab的光学实验仿真方法,从而更好地应用仿真技术服务于光学研究和实验。
二、Matlab基础知识Matlab,全称为Matrix Laboratory,是一款由美国MathWorks公司出品的商业数学软件,主要用于算法开发、数据可视化、数据分析以及数值计算等领域。
Matlab以其强大的矩阵计算能力和丰富的函数库,在光学实验仿真领域具有广泛的应用。
Matlab中的变量无需预先声明,可以直接使用。
变量的命名规则相对简单,以字母开头,后面可以跟字母、数字或下划线。
Matlab支持多种数据类型,包括数值型(整数和浮点数)、字符型、逻辑型、结构体、单元数组和元胞数组等。
Matlab的核心是矩阵运算,它支持多维数组和矩阵的创建和操作。
用户可以使用方括号 [] 来创建数组或矩阵,通过索引访问和修改数组元素。
Matlab还提供了大量用于矩阵运算的函数,如矩阵乘法、矩阵转置、矩阵求逆等。
Matlab具有强大的数据可视化功能,可以绘制各种二维和三维图形。
在光学实验仿真中,常用的图形包括曲线图、散点图、柱状图、表面图和体积图等。
用户可以使用plot、scatter、bar、surf和volume 等函数来创建这些图形。
Matlab支持多种控制流结构,如条件语句(if-else)、循环语句(for、while)和开关语句(switch)。
这些控制流结构可以帮助用户编写复杂的算法和程序。
如何利用Matlab进行模拟和仿真实验

如何利用Matlab进行模拟和仿真实验Matlab是一种功能强大的数学计算和数据可视化软件。
它不仅可以进行数学模拟和仿真实验,还可以处理数据、绘制图表和实施算法。
在工程、物理学、生物学等领域,Matlab被广泛用于解决各种实际问题。
本文将介绍如何利用Matlab进行模拟和仿真实验,并探讨其在实验设计和结果分析中的应用。
一. Matlab的基本功能Matlab具有很多基本功能,如矩阵操作、数值计算、符号计算等。
这些功能使得Matlab成为进行模拟和仿真实验的理想选择。
在Matlab中,可以定义和操作矩阵,进行线性代数运算,如求解方程组、矩阵求逆等。
此外,Matlab还提供了许多内置函数,可以进行数值计算和符号计算,如求解微分方程、积分、数值优化等。
二. 模拟实验的设计在进行模拟实验之前,首先需要设计实验方案。
实验设计包括选择合适的模型和参数设置,确定实验变量和观测指标等。
在Matlab中,可以使用函数或脚本来定义模型和参数,通过修改参数值来观察实验结果的变化。
比如,可以使用Matlab的模型库来选择合适的模型,然后使用函数传入参数值进行求解。
此外,Matlab还提供了绘图功能,可以绘制实验结果的图表,以便更直观地分析数据。
三. 仿真实验的实施在设计好实验方案后,就可以开始进行仿真实验了。
在Matlab中,可以使用已定义的模型和参数进行仿真计算。
可以通过Matlab的编程功能来实现计算过程的自动化。
比如,可以使用循环语句来迭代计算,以观察参数变化对结果的影响。
此外,Matlab还提供了随机数生成和统计分析函数,可以用于生成随机变量和分析实验数据。
四. 实验结果的分析在完成仿真实验后,需要对实验结果进行分析。
Matlab提供了丰富的数据处理和分析工具,可以对实验数据进行统计分析、绘图和可视化展示。
可以使用Matlab的数据处理函数来计算均值、标准差、相关系数等统计指标。
此外,Matlab还可以通过绘图函数来绘制直方图、散点图、线图等图形,以便更好地理解和展示数据。
应用MATLAB设计电磁场与电磁波模拟仿真实验

应用MATLAB设计电磁场与电磁波模拟仿真实验在当今科技飞速发展的时代,电磁场与电磁波在通信、电子工程、无线电技术等众多领域中发挥着至关重要的作用。
为了更深入地理解和研究电磁场与电磁波的特性和行为,借助先进的工具进行模拟仿真是一种极为有效的方法。
其中,MATLAB 凭借其强大的数学计算和图形处理能力,成为了设计电磁场与电磁波模拟仿真实验的理想选择。
一、MATLAB 简介MATLAB 是一种广泛应用于科学计算、数据分析和可视化的高级编程语言和交互式环境。
它提供了丰富的函数库和工具箱,使得用户能够轻松地进行数值计算、矩阵运算、信号处理、图像处理等各种复杂的任务。
对于电磁场与电磁波的研究,MATLAB 中的数值计算和绘图功能尤为重要。
二、电磁场与电磁波基础在开始设计模拟仿真实验之前,我们需要先了解一些电磁场与电磁波的基本概念和理论。
电磁场是由电荷和电流产生的物理场,包括电场和磁场。
电磁波则是电磁场的一种运动形式,它以光速在空间中传播,具有电场分量和磁场分量,并且两者相互垂直。
电磁波的特性可以用频率、波长、波速、振幅等参数来描述。
不同频率的电磁波在传播过程中会表现出不同的特性,例如在介质中的折射、反射、吸收等。
三、设计思路在利用 MATLAB 进行电磁场与电磁波模拟仿真实验时,我们的设计思路通常包括以下几个步骤:1、问题定义:明确要研究的电磁场与电磁波现象,例如电磁波在自由空间中的传播、在介质中的折射和反射等。
2、数学模型建立:根据电磁学理论,建立描述该现象的数学方程。
这可能涉及到麦克斯韦方程组的应用以及边界条件的设定。
3、数值求解:使用 MATLAB 提供的数值计算方法,如有限差分法、有限元法等,对数学方程进行求解,得到电磁场的数值解。
4、结果可视化:将求解得到的数值结果通过图形的方式展示出来,以便直观地观察和分析电磁场与电磁波的特性。
四、具体实验案例下面我们通过一个简单的例子来展示如何使用 MATLAB 设计电磁场与电磁波的模拟仿真实验。
MATLAB实验电磁实验仿真

实验四 电磁实验仿真 —点电荷电场分布的模拟一. 实验目的电磁场是一种看不见摸不着但又客观存在的物质,通过使用Matlab 仿真电磁场的空间分布可以帮助我们建立场的图景,加深对电磁理论的理解和掌握。
按照矢量分析,一个矢量场的空间分布可由其矢量线(也称力线)来形象表示。
点电荷的电场就是一个矢量场,模拟其电力线的分布可以得到电场的空间分布。
通过本次上机实验希望达到以下目的:1. 学会使用MATLAB 绘制电磁场力线图和矢量图的方法;2. 熟悉二维绘图函数contour 、quiver 的使用方法。
二. 实验原理根据库仑定律,真空中的一个点电荷q 激发的电场3r E q r=v v (高斯制) (1) 其中r 是观察点相对电荷的位置矢量。
考虑相距为d 的两个点电荷q 1和q 2,以它们的中点建立坐标(如图),根据叠加原理,q 1和q 2激发的电场为:12123312r r E q q r r =+v v v (2) 由于对称性,所有包含电荷的平面上,电场的分布一样,所以只需要考虑xy 平面上的电场分布,故121233331212(/2)(/2)ˆˆˆˆ()[]x y E E q x q x q y d q y d E j j r r r r i i -+==++++v (3)其中12 r r ==。
根据电动力学知识(参见谢处方,《电磁场与电磁波》,1.4.1节),电场矢量线(或电力线)满足微分方程: yx E dydx E = (4) 代入(3)式解得电力线满足的方程 1212(/2)(/2)q y d q y d r r C -++= (5) 其中C 是积分常数。
每一个C 值对应一根电力线。
电场的分布也可以由电势U 的梯度(gradient ,为矢量)的负值计算,根据电磁学知识,易知两点电荷q 1和q 2的电势1212q q U r r =+(6)那么电场为 E gradU U =-=-∇v (7)或者 ()(),x y x y E U E U =-∇=-∇ (8)在Matlab 中,提供了计算梯度的函数gradient()。
llc电路的 闭环控制matlab仿真

一、概述LLC电路是一种常见的电源拓扑结构,具有高效、稳定和输出调节范围广等特点。
闭环控制可以有效地提高LLC电路的性能,降低输出波动和响应时间。
本文将利用MATLAB软件进行闭环控制的仿真研究,以探讨LLC电路在不同控制策略下的性能表现。
二、LLC电路的工作原理LLC电路是由电感、电容和开关器件组成的拓扑结构,能够实现高效率的能量转换。
在工作过程中,LLC电路通过周期性地开关控制,将输入直流电压转化为输出交流电压,同时滤波器承担了输出的交流电平平滑工作。
其工作原理复杂,但是通过闭环控制可以实现输出电压和电流的精准调节。
三、MATLAB仿真环境的搭建1. MATLAB软件简介MATLAB是一种用于算法开发、数据可视化和数值计算的高级技术计算语言和交互式环境。
在电路仿真领域,MATLAB具有强大的仿真性能和丰富的工具箱,能够快速准确地搭建电路模型和进行闭环控制仿真。
2. LLC电路模型的建立在MATLAB中,我们可以利用电路建模工具箱来建立LLC电路的等效模型。
通过对电感、电容和开关管等元件的参数建模,可以快速搭建出一个与实际电路性能相近的仿真模型。
3. 闭环控制算法的设计在进行仿真之前,我们需要设计闭环控制算法。
常见的闭环控制算法包括PID控制、模糊控制、自适应控制等。
针对LLC电路的特性和需求,我们需要选择适合的控制策略,并在MATLAB中进行算法实现。
四、闭环控制仿真实验1. 参数设置在进行仿真实验之前,我们需要对LLC电路的参数进行设置。
包括输入电压、输出电压、开关频率、电感和电容数值等。
这些参数设置将直接影响到仿真结果的准确性和有效性。
2. 仿真结果分析通过MATLAB进行闭环控制的仿真实验后,我们可以得到输出电压和电流随时间的波形图。
同时还可以获得系统的稳定性、过渡过程、调节时间和超调量等性能指标。
通过对这些仿真结果的分析,可以评估闭环控制策略的有效性和稳定性。
五、不同闭环控制策略下的LLC电路性能对比1. PID控制PID控制是一种经典的闭环控制策略,它通过比例、积分和微分三个环节来调节电路的输出。
基于MATLAB的新能源汽车仿真实例

在电池管理系统的章节中,作者详细阐述了如何利用MATLAB对电池的充放电 过程进行模拟。通过调整不同的参数,如电流、电压和温度,读者可以深入了解 电池性能的变化,为实际的新能源汽车设计提供有力支持。
书中还重点介绍了电动汽车的电机和控制系统。电机作为新能源汽车的心脏, 其性能直接影响到车辆的整体表现。通过MATLAB的电机仿真模型,我们可以预测 在不同工况下电机的性能表现,从而优化设计。
内容摘要
该书还介绍了如何使用MATLAB进行实车试验数据的处理和分析,以及如何使用MATLAB进行模型 的可视化和优化等方面的内容。这些内容都是实际研发过程中不可或缺的重要环节。 《基于MATLAB的新能源汽车仿真实例》这本书是一本非常实用的书籍,适合于从事新能源汽车研 发的工程师和技术人员阅读和使用。通过学习这本书,读者可以快速掌握使用MATLAB进行新能源 汽车仿真的方法和技巧,提高研发效率和质量。
除了硬件部分,书中还涵盖了新能源汽车的能量管理策略。如何有效地分配 电能,使得车辆在保证性能的同时,实现更长的续航里程,是能量管理策略的核 心问题。通过MATLAB的仿真,我们可以对不同的策略进行比较和优化,为实际应 用提供最佳方案。
书中一个特别引人注目的是关于充电基础设施的仿真部分。除了电池和电机, 充电设施同样是新能源汽车发展中不可或缺的一环。通过仿真,我们可以模拟不 同类型的充电设施在不同场景下的性能表现,为充电网络的规划和建设提供决策 依据。
作者简介
作者简介
这是《基于MATLAB的新能源汽车仿真实例》的读书笔记,暂无该书作者的介绍。
感谢观看
仿真方法是实现新能源汽车仿真的关键技术。在仿真方法这一章节中,目录 列举了多种常用的仿真软件和工具,并对其优缺点进行了比较分析。还介绍了如 何根据实际需求选择合适的仿真软件和工具,为读者在实际操作中提供了指导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用matlab进行仿真的案例
利用Matlab进行仿真可以涉及多个领域的案例,下面列举10个案例:
1. 汽车碰撞仿真:利用Matlab中的物理仿真库,可以模拟汽车碰撞的过程,分析碰撞时车辆的变形、撞击力等参数。
可以根据不同的碰撞角度和速度,评估不同碰撞条件下的安全性能。
2. 电力系统仿真:利用Matlab中的电力系统仿真工具,可以模拟电力系统的运行情况,包括电压、电流、功率等参数的变化。
可以用于分析电力系统的稳定性、短路故障等问题,并进行相应的优化设计。
3. 通信系统仿真:利用Matlab中的通信系统仿真工具箱,可以模拟无线通信系统的传输过程,包括信号的发送、接收、调制解调等环节。
可以用于评估不同调制方式、编码方式等对通信系统性能的影响。
4. 智能控制仿真:利用Matlab中的控制系统仿真工具,可以模拟各种控制系统的运行情况,包括PID控制、模糊控制、神经网络控制等。
可以用于设计、优化和评估各种控制算法的性能。
5. 雷达系统仿真:利用Matlab中的雷达仿真工具,可以模拟雷达系统的工作原理和性能,包括发射、接收、信号处理等过程。
可以
用于评估雷达系统的探测能力、跟踪精度等指标,并进行系统参数的优化设计。
6. 气候变化模拟:利用Matlab中的气候模型,可以模拟气候系统的变化过程,包括温度、降水、风速等参数的变化。
可以用于研究气候变化对生态环境、农业生产等方面的影响,以及制定相应的应对策略。
7. 人体生理仿真:利用Matlab中的生理仿真工具箱,可以模拟人体的生理过程,包括心血管系统、呼吸系统、神经系统等。
可以用于研究不同疾病、药物对人体的影响,以及评估各种治疗方案的效果。
8. 金融市场仿真:利用Matlab中的金融工具箱,可以模拟金融市场的价格变化过程,包括股票、期货、汇率等。
可以用于研究不同投资策略、风险管理方法等对投资收益的影响,并进行相应的决策分析。
9. 电子器件仿真:利用Matlab中的电子器件仿真工具,可以模拟各种电子器件的工作原理和性能,包括二极管、晶体管、集成电路等。
可以用于设计、优化和评估各种电子器件的性能,并进行相应的工艺改进。
10. 空气动力学仿真:利用Matlab中的空气动力学仿真工具,可以
模拟飞行器的飞行过程,包括气动力、飞行稳定性等参数的变化。
可以用于研究飞行器的设计、性能评估和飞行控制等问题。
总结起来,利用Matlab进行仿真可以涉及汽车、电力、通信、控制、雷达、气候、生理、金融、电子、空气动力学等多个领域,为工程技术、科学研究和决策分析等提供了强大的工具和平台。
通过仿真分析,可以更好地理解和预测系统行为,优化设计方案,提高工作效率,减少实验成本,推动科技创新和应用发展。
