冲刺2020年高考满分数学30复数的计算(学生版)理科

合集下载

2020年高考数学(理科)终极冲刺卷全国卷I(模拟三)(练习)

2020年高考数学(理科) 终极冲刺卷全国卷I （模拟三）1.已知集合21A x x ⎧⎫=≤⎨⎬⎩⎭，{}3,2,1,1,2,3B =---，则AB =（）A ．{}3,2,1,2,3---B ．{}2,1--C ．{}1,1,2,3-D ．{}3,2--2.若复数z 满足i 24i z -=，则z 的虚部是( ) A.4B.-4C.2D.-23.已知“命题:p x R ∃∈，使得2210ax x ++<成立”为真命题，则实数a 满足( ) A.[)0,1B.(1),-∞C.[1,)+∞D.(1],-∞4.已知平面向量,a b 的夹角为π3，且12a b ==，，则()2a b b +⋅=（） A ．64B ．36C ．8D ．65.已知等差数列{}n a ，若18102,36a a a =+=，则11a =( ) A.22B.24C.26D.286.()()()342111n x x x +++++⋅⋅⋅++的展开式中2x 的系数是( )A. 33n C +B. 32n C + C. 321n C +-D. 331n C +-7.某几何体的三视图如图所示，图中的四边形都是边长为1的正方形，其中正视图、侧视图中的两条虚线互相垂直，则该几何体的体积是( ) A. 56B.34C.12D.168.已知12,F F 是双曲线()2222:10,0x y C a b a b -=>>的左、右焦点，若直线3y x =与双曲线C 在第一象限交于点P ，过P 向x 轴作垂线，垂足为D ，且D 为2OF (O 为坐标原点)的中点，则该双曲线离心率为( ) A.2B.3C.21+D.31+9.古希腊数学家毕达哥拉斯在公元前六世纪发现了”完全数，”6和28，后人进一步研究发现后续3个“完全数”分别为496，8 128，33 550 336，现将这5个“完全数”随机分为两组，一组2个，另一组3个，则6和28恰好在同一组的概率为( ) 123110.已知函数()cos sin f x x m x =+的图象过点π(,2)3，若函数()f x 在区间[,]a a -上单调递增，则a 的取值范围为( ) A.π(0,]6B.ππ(,]63C.π(0,]3D.ππ(,]6411.已知点P 在圆224x y +=上，()()2,0,2,0A B -，M 为BP 中点，则sin BAM ∠的最大值为（） A.12B.13C.10 D.1412.已知函数()ln e (0)x a f x x a x x a -=++-<，若()0f x ≥在[2,)x ∈+∞上恒成立，则实数a 的最小值为( ) A.2e -B.e -C.e -D.e 2-13.若实数,x y 满足条件0230260x y x y x y -⎧⎪+-⎨⎪+-⎩，则z x y =+的最小值为_________.14.已知函数321,0,()2,0,x x f x x x ⎧+≥=⎨+<⎩若()1f x =，则x =_________.15.已知等比数列{}n a 的前n 项和为n S ，且131,3a S ==，则5S =_________。

2020届全国高考理科数学模拟冲刺卷三(含答案)

(3)依据条形统计图中的数据，把频率视为概率.从节约成本的角度考虑该工厂选择.种方案更合适请说明理由. 19、如图,在直四棱柱 ABCD A1B1C1D1 中,底面 ABCD 为等腰梯形, AB CD, AA1 AD 2BC,DAB 60o , M , N 分别为 A1D, CD1 的中点
13、已知an 为等差数列，若 a2 2a3 1, a4 2a3 7, 则 a3 ________.
14、设 m, n 是两条不同的直线, 是两个不同的平面，且直线 m 平面直线 n 平面给
出下列说法:①” m n ”是” n ”必要条件 ②“ m / /n ”是” m / / ”的必要条件 ③” m / /n ”是” / / ”充要条件 ④” m n ”是” ”的充分条件,其中所有正确说法的序号是_________.
y M
D
A
O
Bx
E
N
(1).求椭圆 C 的离心率；
(2).若 a 3 时，点 D 为 x 轴上一点，过 D 作 x 轴的垂线交椭圆 C 于不同的两点 M , N ,过 D 作
AM 的垂线交 BN 于点 E ，求△BDE 与△BDN 的面积之比.
2x 1
21、已知 f (x) a x ln x x2 , a R .
（1）讨论 f (x) 的单调性;
（2）当 a 1时,证明 f (x) f ' x 3 对于任意的 x 1, 2 成立.
2 请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分.做答
时，用 2B 铅笔在答题卡把所选题目对应的标号涂黑.
1
22、在平面直角坐标系 xOy
x 1 2 t 中,已知直线 l 的参数方程为
（2）证明： a2 b2 ab 1 .

2020年高考数学(理)冲刺模拟卷(十)(全国版含答案解析)

2020年高考数学（理）冲刺模拟卷10（本试卷满分150分，考试用时120分钟）第I 卷（选择题)一、单选题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知复数z 满足()13z i i -=+（i 为虚数单位),则复数z =（）A ．12i +B ．12i-C ．2i+D ．2i-【答案】B 【解析】【分析】运用复数的除法运算法则求出复数z ,在根据共轭复数的定义求出复数z .【详解】由题意()13z i i -=+,可变形为()()()()31324121112i i i iz i i i i ++++====+-+-.则复数12z i =-.故选：B.【点睛】本题考查了复数的除法运算法则和共轭复数的定义,属于基础题.2．已知：1:12p a -<<，[]:1,1q x ∀∈-，220,x ax --<则p 是q 成立的（）A ．充分但不必要条件B ．必要但不充分条件C ．充分必要条件D ．既不是充分条件也不是必要条件【答案】A 【解析】【分析】构造函数()22f x x ax =--，先解出命题q 中a 的取值范围，由不等式()0f x <对[]1,1x ∀∈-恒成立，得出()()1010f f ⎧-<⎪⎨<⎪⎩，解出实数a 的取值范围，再由两取值范围的包含关系得出命题p 和q 的充分必要性关系。

【详解】构造函数()22f x x ax =--，对[]1,1x ∀∈-，()0f x <恒成立，则()()110110f a f a ⎧-=-<⎪⎨=--<⎪⎩，解得11a -<<，()1,11,12⎛⎫-- ⎪⎝⎭Q Ü，因此，p 是q 的充分但不必要条件，故选：A.【点睛】本题考查充分必要条件的判断，一般利用集合的包含关系来判断两条件的充分必要性：（1）A B Ü，则“x A ∈”是“x B ∈”的充分不必要条件；（2）A B Ý，则“x A ∈”是“x B ∈”的必要不充分条件；（3）A B =，则“x A ∈”是“x B ∈”的充要条件；（4）A B ⊄，则“x A ∈”是“x B ∈”的既不充分也不必要条件。

高考冲刺2020年高考数学(理)全真模拟演练三(解析word版)

高考冲刺2020年高考数学（理）全真模拟演练（三）数学试卷一、单选题 1．已知集合1,0,1A，{|11}Bxx，则AB（）

A．0 B．1,0 C．0,1 D．1,0,1 答案：B 因为1,0,1,BBB所以1,0AB.

【考点定位】集合的表示，集合的运算. 2．已知,abR，i是虚数单位，若ai与2bi互为共轭复数，则ab（） A．0 B．1 C．2 D．3 答案：D 分析：由条件利用共轭复数的定义求得,ab的值，即可得到ab的值. 详解：因为ai与2bi互为共轭复数，则2,1ab，所以3ab，故选：D. 点睛：该题考查的是有关共轭复数的概念，属于基础题目. 3．2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式．孪生素数猜想是希尔伯特在1900年提

出的23个问题之一，可以这样描述：存在无穷多个素数p，使得p+2是素数，素数对(p，p+2)称为孪生素数．在不超过30的素数中，随机选取两个不同的数，其中能够组成孪生素数的概率是 A．115 B．215 C．245 D．445 答案：D 分析：由题意明确不超过30的素数有10个，满足题意的孪生素数对有4个，利用古典概型公式可得结果. 详解：不超过30的素数有2,3,5,7,11,13,17,19,23,29，共10个，根据素数对(p，p+2)称为孪生素数，则由不超过30的素数组成的孪生素数对为(3,5),(5,7),(11,13),(17,19)，

共有4组，能够组成孪生素数的概率为2104445PC，故选D 点睛：本题考查古典概型概率公式，考查组合知识的应用，考查分析问题解决问题的能力. 4．已知向量2,4ar，1,1br，则2abrr（） A．5,7 B．5,9 C．3,7 D．3,9 答案：A 因为2(4,8)ar，所以2(4,8)(1,1)abrr=（5，7），故选A. 考点：本小题主要考查平面向量的基本运算，属容易题.

2020年高考理科数学之高频考点解密29 算法、复数、推理与证明(解析版)

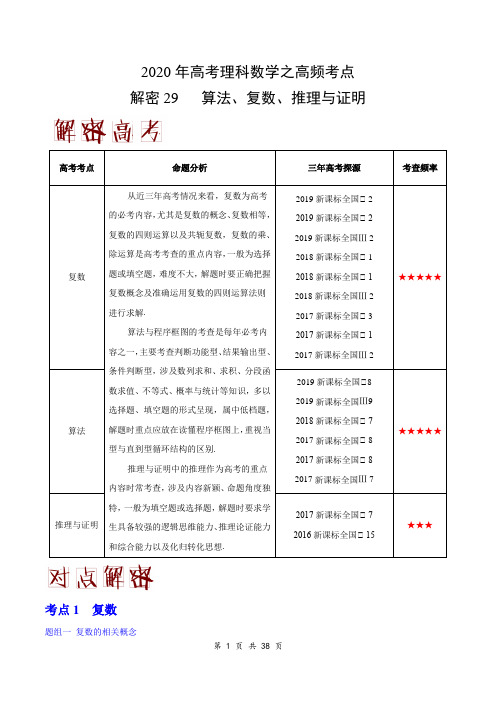
2020年高考理科数学之高频考点解密29算法、复数、推理与证明考点1 复数题组一复数的相关概念调研1 若复数z ＝（3﹣6i ）（1+9i ），则 A ．复数z 的实部为21B ．复数z 的虚部为33C ．复数z 的共轭复数为57﹣21iD ．复数z 所对应的点位于第二象限【答案】C【解析】∵复数z ＝（3﹣6i ）（1+9i ）＝57+21i ，∴复数z 的实部为57，虚部为21，复数z 的共轭复数为57−21i ，在复平面内，复数z 所对应的点的坐标为（57，21），位于第一象限．故选C ．【名师点睛】本题考查复数代数形式的乘除运算，考查复数的基本概念.利用复数代数形式的乘除运算化简，再由复数的基本概念逐一核对四个选项得答案．调研2 若复数(1)(1)i z m m m =-+-是纯虚数，其中m 是实数，则1z= A ．iB ．i -C ．2iD ．2i -【答案】A【解析】因为复数z =m(m −1)+(m −1)i 是纯虚数，所以{m(m −1)=0m −1≠0，则m =0，所以z =−i ，则1z =1−i =i .题组二复数的计算调研3 已知复数z 满足i 21i z z +=-，则z = A ．12i + B ．12i - C ．1i +D ．1i -【答案】C【解析】设i(,)z a b a b =+∈R ，则i z a b =-，故i 2(i)i 2(i)(2)(2)i 1i z z a b a b b a a b +=++-=-++-=-，故2121b a a b -+=⎧⎨-=-⎩，解得11a b =⎧⎨=⎩.所以1i z =+.故选C.调研4 若复数23201834i 1i i i i34iz -=++++++-L ，则z 的共轭复数z 的虚部为A ．15- B ．95-C ．95D ．9i 5-【答案】B【解析】因为23201834i 5391i i i i i i 34i34i 55z -=++++++=+=+--L ，所以z 的共轭复数为39i 55z =-，虚部为95-，故选B ．题组三复数的几何意义调研5 复数5(12i)i-在复平面内对应的点的坐标为A ．()21，B ．()21-，C ．()12，D ．()12-，【答案】B 【解析】∵()()()()52i 552i 12i i 2i 2i 2i -===--++-，∴复数()512i i -在复平面内对应的点的坐标为（2，﹣1）．故选B ．【名师点睛】本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．由复数代数形式的乘除运算化简即可得答案．调研6 在复平面内表示复数iim m +-的点位于第一象限，则实数m 的取值范围是 A ．(),1-∞- B ．(),0-∞ C ．()0,+∞D ．()1,+∞【答案】D【解析】()()()2222i i 12i i i i 11m m m m m m m m m ++-==+--+++，因为对应的点22212(,)11m m m m -++在第一象限内，所以满足222201101mm m m ⎧>⎪⎪+⎨-⎪>⎪+⎩，所以()1,m ∈+∞，故选D.【名师点睛】本道题结合复数的四则运算化简该复数，结合复数的几何意义建立不等式即可. 调研7 “复数ii3a z -=在复平面内对应的点在第三象限”是“0≥a ”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【答案】A 【解析】3i (3i)i3i i i ia a z a --⋅===--⋅，对应的点为(,3)a --在第三象限，所以0a -<，所以0a >，所以复数ii3a z -=在复平面内对应的点在第三象限是0≥a 的充分不必要条件.故选A ．☆技巧点拨☆ 常用结论：（1）()21i 2i ±=±；1＋i 1－i =i ；1－i 1＋i =.（2）i i(i)b a a b -+=+．（3）4414243*i1i i i 1i (i )nn n n n ===-=-∈N ＋＋＋,,,，4414243*i i i i 0()n n n n n ++++++=∈N ．（4）模的运算性质：①22||||z z z z ==⋅；②1212z z z z ⋅=；③1122||||||z z z z =. （5）设ω＝－12＋32i ，则①|ω|＝1；②1＋ω＋ω2＝0；③ω＝ω2.注意点：1．判定复数是实数，仅注重虚部等于0是不够的，还需考虑它的实部是否有意义．2．对于复系数(系数不全为实数)的一元二次方程的求解，判别式不再成立．因此解此类方程的解，一般都是将实根代入方程，用复数相等的条件进行求解． 3．两个虚数不能比较大小．4．利用复数相等a ＋b i ＝c ＋d i 列方程时，注意a ，b ，c ，d ∈R 的前提条件．5．注意不能把实数集中的所有运算法则和运算性质照搬到复数集中来．例如，若z 1，z 2∈C ，z 21＋z 22＝0，就不能推出z 1＝z 2＝0；z 2<0在复数范围内有可能成立．i -考点2 算法调研1 执行如图所示的程序框图，如果输入53n m ==、，则输出的p 等于A ．3B ．12C ．60D ．360【答案】C【解析】模拟执行程序，可得5n =，3m =，1k =，1p =，3p =，满足条件k m <，执行循环体，2k =，12p =，满足条件k m <，执行循环体，3k =，60p =，不满足条件k m <，退出循环，输出p 的值为60．故选C ．调研2 执行下面的程序框图，如果输出的S 为1112，则判断框中填写的内容可以是A ．5?n <B ．5?n ≤C ．6?n <D ．6?n ≤【答案】D【解析】运行程序，0,2S n ==，判断是，1,42S n ==，判断是，11,624S n =+=，判断是，11111,824612S n =++==，判断否，输出1112S =，故选D. 【名师点睛】本小题主要考查程序框图，考查已知程序框图的输出结果求判断框填写的内容，属于基础题.运行程序，当1112S =时退出程序，由此判断出所填写的内容. 调研 3 元朝时，著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒，携着游春走，与店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒?”用程序框图表达如图所示，即最终输出的0x =时，问一开始输入的x =A ．34 B ．78 C ．1516D ．3132【答案】B【解析】第一次运行，输入x ，1i =，21x x =-，23i =<；第二次运行，()221143x x x =--=-，3i =；第三次运行，()243187x x x =--=-，43i =>，输出87x -，令870x -=，解得78x =.故选B ．【名师点睛】本题考查算法框图，解答本题的关键是根据所给的框图，得出函数关系，然后通过解方程求得输入的值，当程序的运行次数不多或有规律时，可采用模拟运行的办法解答．解决本题时，根据流程图，求出对应的函数关系式，根据题设条件输出的0x =，由此关系建立方程求出自变量的值即可．调研4 若执行如图所示的程序框图后，输出的27S =，则判断框内的条件应为A ．3?i >B ．4?i >C ．4?i <D ．5?i <【答案】A【解析】当S =0，i =1时，应不满足退出循环的条件，故S =1，i =2；当S =1，i =2时，应不满足退出循环的条件，故S =6，i =3；当S =6，i =3时，应不满足退出循环的条件，故S =27，i =4；当S =27，i =4时，应满足退出循环的条件，故判断框内的条件应为i ＞3？，故选A ．【名师点睛】本题主要考查程序框图的循环结构流程图，属于中档题.解决程序框图问题时一定注意以下几点：(1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构； (3)注意区分当型循环结构和直到型循环结构； (4)处理循环结构的问题时一定要正确控制循环次数； (5)要注意各个框的顺序；(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.调研5 执行如图所示的程序框图，若输入的m =1，则输出数据的总个数为A．5 B．6C．7 D．8【答案】B【解析】模拟程序的运行，可得：m=1.满足条件m∈（0，100），执行循环体，n=3，输出n的值为3，m=3；满足条件m∈（0，100），执行循环体，n=7，输出n的值为7，m=7；满足条件m∈（0，100），执行循环体，n=15，输出n的值为15，m=15；满足条件m∈（0，100），执行循环体，n=31，输出n的值为31，m=31；满足条件m∈（0，100），执行循环体，n=63，输出n的值为63，m=63；满足条件m∈（0，100），执行循环体，n=127，输出n的值为127，m=127，此时，不满足条件m∈（0，100），退出循环，结束．可得输出数据的总个数为6．故选B．【名师点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．☆技巧点拨☆高考中对程序框图的考查，主要是顺序结构、条件结构、循环结构，其中循环结构为重点，考查程序运行后的结果，或考查控制循环的条件，主要以选择题或填空题的形式出现.(1)顺序结构顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的． (2)条件结构利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足． (3)循环结构①已知程序框图，求输出的结果．可按程序框图的流程依次执行，最后得出结果．②完善程序框图问题，结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．③对于辨析程序框图功能问题，可将程序执行几次，即可根据结果作出判断.考点3 推理与证明调研 1 对大于1的自然数的三次幂可以分解成几个奇数的和，比如3235,=+337911,=++3413151719,=+++L 以此规律，则345的分解和式中一定不含有A ．2069B ．2039C ．2009D ．1979【答案】D【解析】由规律得3n 中有n 项，而333234，，中第一项分别为()2212412221⨯-⨯-=⨯+-，，()27122231⨯-=⨯++-，所以345的分解和式中第一项为()222344411981⨯+++++-=L ，所以一定不含有1979，故选D ．调研 2 中国有个名句“运筹帷幄之中，决胜千里之外”，其中的“筹”原意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图所示），表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位、百位、万位数用纵式表示，十位、千位、十万位用横式表示，以此类推．例如8455用算筹表示就是，则以下用算筹表示的四位数正确的为A ．B ．C ．D ．【答案】C【解析】根据“各位数码的筹式需要纵横相间，个位、百位、万位数用纵式表示，十位、千位、十万位用横式表示”的原则，只有C 符合，故选C.【名师点睛】本题主要考查合情推理，属于基础题型.根据题意直接判断即可.调研 3 分形理论是当今世界十分风靡和活跃的新理论、新学科.其中，把部分与整体以某种方式相似的形体称为分形.分形是一种具有自相似特性的现象、图象或者物理过程.标准的自相似分形是数学上的抽象，迭代生成无限精细的结构.也就是说，在分形中，每一组成部分都在特征上和整体相似，只仅仅是变小了一些而已，谢尔宾斯基三角形就是一种典型的分形，是由波兰数学家谢尔宾斯基在1915年提出的，按照如下规律依次在一个黑色三角形内去掉小三角形，则当=6n 时，该黑色三角形内共去掉( )个小三角形A ．81B ．121C ．364D ．1093【答案】C【解析】由图可知，每一个图形中小三角形的个数等于前一个图形小三角形个数的3倍加1，所以，1n =时，11a =；2n =时，2314a =+=；3n =时，334113a =⨯+=；4n =时，4313140a =⨯+=；5n =时，53401121a =⨯+=；6n =时，631211364a =⨯+=，故选C ．【名师点睛】常见的归纳推理分为数的归纳和形的归纳两类：(1)数的归纳包括数的归纳和式子的归纳，解决此类问题时，需要细心观察，寻求相邻项及项与序号之间的关系，同时还要联系相关的知识，如等差数列、等比数列等； (2)形的归纳主要包括图形数目的归纳和图形变化规律的归纳.调研4 有甲、乙、丙、丁四位歌手参加比赛，其中只有一位获奖.有人走访了四位歌手，甲说：“是乙或丙获奖”，乙说：“甲、丙都未获奖”，丙说：“我获奖了”，丁说：“是乙获奖”.已知四位歌手有且只有一位说了假话，则获奖的歌手是______________．【答案】乙【解析】由题意，乙与丙的说法是相互矛盾的，所以乙与丙的说法中一对一错，又甲说：“是乙或丙获奖”，是正确；丁说“是乙获奖”是正确，由此可知获奖的歌手是乙，且乙说的也对.【名师点睛】本题主要考查了简单的合情推理的应用，其中解答中正确理解题意，合理利用已知条件合情推理进行，逐一判定是解答的关键，着重考查了推理与论证能力，属于基础题.根据乙、丙的说法是相互矛盾的，得出乙与丙说法一对一错，再根据甲、丁的说法都准确，推出获奖的歌手是乙即可.调研5 学校艺术节对A B C D 、、、四件参赛作品只评一件一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四件参赛作品预测如下：甲说：“是C 或D 作品获得一等奖”；乙说：“是B 作品获得一等奖”；丙说：“A D 、两件作品未获得一等奖”；丁说：“是C 作品获得一等奖”．评奖揭晓后，发现这四位同学中只有两位说的话是对的，则获得一等奖的作品是______________．【答案】B【解析】若A 为一等奖，则甲、丙、丁的说法均错误，不满足题意；若B 为一等奖，则乙、丙的说法正确，甲、丁的说法错误，满足题意；若C 为一等奖，则甲、丙、丁的说法均正确，不满足题意；若D 为一等奖，则乙、丙、丁的说法均错误，不满足题意. 综上所述，故B 获得一等奖.【名师点睛】本题属于信息题，可根据题目所给信息来找出解题所需要的条件并得出答案，在做本题的时候，可以采用依次假设A B C D 、、、为一等奖并通过是否满足题目条件来判断其是否正确.首先根据“学校艺术节对A B C D 、、、四件参赛作品只评一件一等奖”，故假设A B C D 、、、分别为一等奖，然后判断甲、乙、丙、丁四位同学的说法的正确性，即可得出结果.1．（北京市西城区北京师范大学第二附属中学2019-2020学年高三上学期期中）若复数z 满足11i z -=+，则z 的共轭复数的虚部是 A ．i B ．1 C ．i -D ．1-【答案】B【分析】先由复数的加减运算求出i z =-，得到共轭复数，即可得出结果．【解析】因为11i z -=+，所以i z =-，因此其共轭复数为i z =，所以虚部为1．故选B ．【名师点睛】本题主要考查复数的虚部，熟记复数的概念，复数的加减运算，以及复数的共轭复数即可，属于基础题型．2．（湖北省黄冈市2019-2020学年高三上学期11月月考）复数z 满足25i(1i)iz ++=，则复数z 的共轭复数的虚部为A ．72B ．7i 2- C ．72-D ．7i 2【答案】A【分析】利用复数的乘除运算求出复数z 的代数形式，再求出其共轭复数，确认其虚部即可．【解析】因为()()25i (1i)25i 25i 7i 337i i(1i)i 1i 1(1i)222z ++++-=====-+--+-，所以37i 22z =+，其虚部为72．故选A ．【名师点睛】本题考查复数的乘除运算，以及对共轭复数的认识，是基础题．3．（湖北省荆州中学、宜昌一中、龙泉中学三校2019-2020学年高三联考）复数z 满足：(2)i z z -⋅=（i 为虚数单位），z 为复数z 的共轭复数，则下列说法正确的是 A ．22i z = B ．2z z ⋅= C ．||2z =D ．0z z +=【答案】B【分析】由已知求得z ，然后逐一核对四个选项得答案．【解析】由（z ﹣2）•i ＝z ，得z i ﹣2i ＝z ，∴z 2i 2i(1i)1i 1i (1i)(1i)--+===---+，∴z 2＝（1﹣i ）2＝﹣2i ，2||2z z z ⋅==，z =，2z z +=．故选B ．【名师点睛】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．4．（云南省曲靖市第一中学2019-2020学年高三高考复习质量监测三）若i 为虚数单位，复数z 在复平面中对应的点为1(2-，则2019z 的值是 A ．-1 B ．-i C ．iD ．1【答案】D【分析】由题意得的12z =-，根据31z =，即可得到结果．【解析】∵复数z 在复平面中对应的点为1(22-，∴12z =-，又31z =，∴()673201931zz ==，故选D ．【名师点睛】本题考查复数的几何意义与乘方运算，考查计算能力，属于常考题型．5．（陕西省汉中市2019-2020学年高三上学期第五次质量检测）我们常用的数是十进制数，如4657=3210410610510710⨯+⨯+⨯+⨯，数要用10个数码（又叫数字）：0、1、2、3、4、5、6、7、8、9，在电子计算机中用的二进制，只要两个数码：0和1，如二进制中210110121202=⨯+⨯+⨯等于十进制的数6，543210110101121202120212=⨯+⨯+⨯+⨯+⨯+⨯等于十进制的数53．那么十二进制数66用二进制可表示为 A ．1001110 B ．1000010 C ．101010D ．111000【答案】A【分析】先将十二进制数66化为十进制数78，再将十进制数78化为二进制即可．【解析】十二进制数1066612612=⨯+⨯等于十进制的数78．十进制的数65432107812+02+02+12+12+12+02=⨯⨯⨯⨯⨯⨯⨯．故十进制的数78等于二进制的数1001110．故选A ．【名师点睛】本题考查k 进制化二进制，其方法是，先将k 进制化十进制，再将其化为二进制．属于基础题．6．（湖南省三湘名校教育联盟2019-2020学年高三上学期第一次大联考）若复数z 满足()1i 12i z -=+，则z 在复平面内对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【分析】先由复数的除法得13i 22z =-+，再求其共轭复数即可得解．【解析】由(1i)12i z -=+，可得12i (12i)(1i)13i 213i 1i 2222z ++++-====-+-． 13i 22z =--在复平面内对应的点为13(,)22--位于第三象限．故选C ．【名师点睛】本题主要考查了复数的除法运算及共轭复数的概念，属于基础题．7．（河南省郑州市第一中学2019-2020学年高三上学期期中）如果执行下边的程序框图，且输入6n =，4m =，则输出的p =A ．240B ．120C ．720D ．360【答案】D【分析】根据题中的程序框图，模拟运行，依次计算k 和p 的值，利用条件k m <进行判断是否继续运行，直到k m ≥则结束运行，输出p 的值即为答案．【解析】根据题中的程序框图，模拟运行如下：输入6,4,1,1n m k p ====，1(641)3,14p k ∴=⨯-+==<，符合条件，112,3(642)12,24k p k ∴=+==⨯-+==<，符合条件， 213,12(643)60,34k p k ∴=+==⨯-+==<，符合条件， 314,60(644)360,44k p k ∴=+==⨯-+===，不符合条件，故结束运行，输出360p =．故选D ．【名师点睛】本题考查了程序框图，主要考查了循环语句和条件语句的应用．其中正确理解各变量的含义并根据程序功能的需要合理的分析是解答的关键．属于基础题．8．（贵州省安顺市2019-2020学年高三上学期第一次联考）执行下面的程序框图，若输入的1A =，则输出的A 的值为A ．7B ．-17C ．31D ．-65【答案】C【解析】1,1A k ==；5,2A k =-=；7,3A k ==；17,4A k =-=；31,5A k ==．结束，输出答案31，故选C ．【名师点睛】本题考查了程序框图，根据程序框图依次计算是一种常用的方法，需要同学们熟练掌握．9．（湖北省黄冈市2019-2020学年高三上学期11月月考）鸡兔同笼，是中国古代著名的趣味题之一．《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如右图的算法来解决这个问题，则判断框中应填入的是A ．94m >B ．94m =C ．35m =D ．35m ≤【答案】B【分析】由题意知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意可得出判断条件．【解析】由题意可知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意知，在程序框图中，当计算足的数量为94时，算法结束，因此，判断条件应填入“94m =”．故选B ．【名师点睛】本题考查算法程序框图中判断条件的填写，考查分析问题和解决问题的能力，属于中等题． 10．（福建省晋江市南侨中学2019-2020学年高三上学期第一阶段考试）A 4纸是生活中最常用的纸规格．A系列的纸张规格特色在于：①A 0、A 1、A 2、…、A 5，所有尺寸的纸张长宽比都相同．②在A 系列纸中，前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后，可以得到两张后面序号大小的纸，比如1张A 0纸对裁后可以得到2张A 1纸，1张A 1纸对裁可以得到2张A 2纸，依此类推．这是因为A 系：1这一特殊比例，所以具备这种特性．已知A 0纸规格为84.1厘米×118.9厘米．，那么A 4纸的长度为 A ．14.8厘米 B ．21.0厘米 C ．29.7厘米D ．42.0厘米【答案】C【解析】由题意，A 0纸的长与宽分别为118.9厘米，84.1厘米，则A 1A 2= A 3=，A 4==29.7（厘米）．故选C ．11．（内蒙古自治区赤峰市赤峰二中、呼市二中2019-2020学年高三上学期10月月考）观察下列等式：332123+=，33321236++=，33332123410+++=，记()3333123f n n =+++⋅⋅⋅+．根据上述规律，若()225f n =，则正整数n 的值为 A ．8 B ．7 C ．6D ．5【答案】D【分析】由规律得()()()22211234n n f n n +=+++⋅⋅⋅+=再解方程即可【解析】由已知等式的规律可知()()()22211234n n f n n +=+++⋅⋅⋅+=，当()225f n =时，可得5n =．故选D ．【名师点睛】本题考查归纳推理，熟记等差数列求和公式是关键，考查观察转化能力，是基础题． 12．（黑龙江省大庆市2019-2020学年高三上学期第一次教学质量检测）现有甲、乙、丙、丁四人参加数学竞赛，其中只有一位获奖．有人走访了四人，甲说：“乙、丁都未获奖”，乙说：“是甲或丙获奖”，丙说：“是甲获奖”，丁说：“是乙获奖”，四人所说话中只有一位是真话，则获奖的人是 A ．甲 B ．乙 C ．丙D ．丁【答案】B【分析】结合题意分类讨论甲乙丙丁获奖的情况，然后考查说真话的人的个数即可确定获奖的人．【解析】结合题意分类讨论：若甲获奖，则说真话的人为：甲乙丙，说假话的人为：丁，不合题意；若乙获奖，则说真话的人为：丁，说假话的人为：甲乙丙，符合题意；若丙获奖，则说真话的人为：甲乙，说假话的人为：丙丁，不合题意；若丁获奖，则说假话的人为：甲乙丙丁，不合题意；综上可得，获奖人为乙．故选B ．13．（2019年10月山西省吕梁市高三阶段性测试）我们在求高次方程或超越方程的近似解时常用二分法求解，在实际生活中还有三分法．比如借助天平鉴别假币．有三枚形状大小完全相同的硬币，其中有一假币（质量较轻），把两枚硬币放在天平的两端，若天平平衡，则剩余一枚为假币，若天平不平衡，较轻的一端放的硬币为假币．现有27枚这样的硬币，其中有一枚是假币（质量较轻），如果只有一台天平，则一定能找到这枚假币所需要使用天平的最少次数为 A ．2 B ．3 C ．4D ．5【答案】B【分析】根据提示三分法，考虑将硬币分为3组，然后将有问题的一组再分为3组，再将其中有问题的一组分为3，此时每组仅为1枚硬币，即可分析出哪一个是假币．【解析】第一步将27枚硬币分为三组，每组9枚，取两组分别放于天平左右两侧测量，若天平平衡，则假币在第三组中；若天平不平衡，假币在较轻的那一组中；第二步把较轻的9枚金币再分成三组，每组3枚，任取2组，分别放于天平左右两侧测量，若天平平衡，则假币在第三组，若天平不平衡则假币在较轻的一组；第三步再将假币所在的一组分成三组，每组1枚，取其中两组放于天平左右两侧测量若天平平衡，则假币是剩下的一个；若天平不平衡，则较轻的盘中所放的为假币．因此，一定能找到假币最少需使用3次天平．故选B ．【名师点睛】本题考查类比推理思想的应用，难度一般．处理该类问题的关键是找到题干中的提示信息，由此入手会方便很多．14．（江苏省苏州市2019-2020学年高三上学期期中）已知复数z 满足i 2iz=+（i 为虚数单位），则复数z 的实部为______________．【答案】1-【分析】把已知等式变形，再由复数代数形式的乘除运算化简得答案．【解析】由i 2iz=+，得i(2i)12i z =+=-+，∴复数z 的实部为−1，故答案为1-．【名师点睛】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．15．（2019年上海市高三上学期一模冲刺练习）已知复数11i z =-，121i z z ⋅=+，则复数2z =______________．【答案】1【分析】根据复数的四则运算以及复数的模求法公式即可求解．【解析】因为11i z =-，121i z z ⋅=+，所以221i (1i)2ii 1i (1i)(1i)2z ++====-+-，21z ==，故答案为1．16．（辽宁省葫芦岛市六校协作体2019-2020学年高三上学期11月月考）复数()i 14i z =+的实部为______________．【答案】4-【分析】先利用复数代数形式的运算法则求出z ．即可由复数的定义知z 的实部．【解析】因为4i z =-+，所以z 的实部为－4．故答案为－4．【名师点睛】本题主要考查复数代数形式的运算法则和复数的定义的应用．17．（2019年贵州省贵阳市高三8月摸底）数式1111++L中省略号“L ”代表无限重复，但该式是一个固定值，可以用如下方法求得：令原式=t ，则11+t t=，则210t t --=，取正值得12t =．用类似方法=______________．【答案】4【分析】通过已知得到求值方法：先换元，再列方程，解方程，求解（舍去负根），再运用该方法，注意两边平方，得到方程，解出方程舍去负的即可．【解析】由已知代数式的求值方法：先换元，再列方程，解方程，求解（舍去负根），(0)m m =>，则两边平方得212m =，即122m m +=，解得4m =（-3舍去）故答案为4．【名师点睛】本题考查类比推理的思想方法，考查从方法上类比，是一道基础题．18．（江西省新余第四中学2020届高三9月月考）执行如图所示的程序框图，则输出S 的值为______________．【答案】2【解析】①1i =，3273log 2i s ≤−−→=+=−−→2i =，②2i =，327log 2i s ≤−−→=+−−→3i =，③3i =，3227log log 42i s ≤−−→=+=−−→4i =， ④4i =，32log 42i s >−−→==，输出2s =．【名师点睛】本题考查程序框图，注意每一步运行成立的条件即可，属于基础题．19．（2019年湖南省怀化市高三二模）甲、乙、丙、丁四人进行一项益智游戏，方法如下：第一步：先由四人看着平面直角坐标系中方格内的16个棋子（如图所示），甲从中记下某个棋子的坐标；第二步：甲分别告诉其他三人：告诉乙棋子的横坐标．告诉丙棋子的纵坐标，告诉丁棋子的横坐标与纵坐标相等；第三步：由乙、丙、丁依次回答．对话如下：“乙先说我无法确定．丙接着说我也无法确定．最后丁说我知道”．则甲记下的棋子的坐标为______________．【答案】(5,5)【分析】根据题意，得出乙棋子必落在横坐标为2，5，6，7上，丙棋子必落在纵坐标为0，1，3，4，5，7上，再根据横纵坐标相等，即可求解，得到答案．【解析】由题意，乙只知道棋子的横坐标，又无法确定，所以棋子必落在横坐标为2，5，6，7上，接下来丙知道棋子的纵坐标，又无法确定，所以棋子必落在纵坐标为0，1，3，4，5，7上，这些横纵坐标相等的点只有(5,5)，所以丁说棋子的坐标为(5,5)．【名师点睛】本题主要考查了合情推理的应用，其中解答中认真审题，合理确定乙棋子必落在横坐标为2，5，6，7上，丙棋子必落在纵坐标为0，1，3，4，5，7上是解答的关键，着重考查了推理与运算能力，属于基础题．20．（2019年上海市高三上学期一模冲刺练习）根据高一课本基本不等式章节知识所学，我们知道基本不等式,)a b a b ++≥∈R ，那么类比可得,,)x y z x y z +++≥∈R ，那么根据上述结论，则32124(04)4y t t t t =-+<<的最大值为______________．【答案】6427【分析】由,)a b a b ++≥∈R 可得2()2a b ab +≤，类比可得3()3x y z xyz ++≤(,,)x y z +∈R ，再求解即可．【解析】由已知,)a b a b ++≥∈R 可得2()2a b ab +≤，又,,)x y z x y z +++≥∈R ，则类比可得3()3x y z xyz ++≤(,,)x y z +∈R ，又04t <<，所以40t ->，则32231112(4)4)6424(2)(4)[]488327t t t t t t t t +-+--+=-≤=，当且仅当24t t =-，即43t =时取等号，故答案为6427． 21．（辽宁省沈阳市东北育才学校2019-2020学年高三上学期10月月考）甲、乙、丙、丁四名同学组成一个4⨯100米接力队，老师要安排他们四人的出场顺序，以下是他们四人的要求：甲：我不跑第一棒和第二棒；乙：我不跑第一棒和第四棒；丙：我也不跑第一棒和第四棒；丁：如果乙不跑第二棒，我就不跑第一棒．老师听了他们四人的对话，安排了一种合理的出场顺序，满足了他们的所有要求，据此我们可以断定在老师安排的出场顺序中跑第三棒的人是______________．【答案】丙【分析】由题意知乙、丙均不跑第一棒和第四棒，则跑第三棒的人只能是乙、丙中的一个，讨论两种情况，验证是否符合要求即可．【解析】由题意知乙、丙均不跑第一棒和第四棒，则跑第三棒的人只能是乙、丙中的一个，当丙跑第三棒时，乙只能跑第二棒，这时丁是第一棒，甲是第四捧，符合题意，当乙跑第三棒时，丙只能跑第二棒，丁只能跑第四棒，甲跑第一捧，不符合题意，故跑第三棒的人是丙，故答案为丙．【名师点睛】本题主要考查推理案例，属于难题．推理案例的题型是高考命题的热点，由于条件较多，做题时往往感到不知从哪里找到突破点，解答这类问题，一定要仔细阅读题文，逐条分析所给条件，并将其引伸，找到各条件的融汇之处和矛盾之处，多次应用假设、排除、验证，清理出有用“线索”，找准突破点，从而使问题得以解决．22．（湖北部分重点中学2020届高三年级新起点考试）将正奇数按如图所示的规律排列：1 3 57911 13 15 1719 21 23 25 27 29 31 ……则2019在第______________行，从左向右第______________个数．【答案】32 49【分析】先找到每一行的数字个数的规律，再将2019转化为第1010个奇数，即可得解．【解析】根据排列规律可知，第一行有1个奇数，第2行有3个奇数，第3行有5个奇数……。

2020高考数学冲刺精选新题好题真题精练【精】第11章算法复数推理与证明第5讲 Word版含解析

2020高考数学冲刺精选新题好题真题精练第5讲数学归纳法[考纲解读] 1.了解数学归纳法的原理，能用数学归纳法证明一些简单的命题．(重点)2.数学归纳法的主要作用是证明与自然数有关的不等式及数列问题．(难点)[考向预测]从近三年高考情况来看，对本讲并没有直接涉及，当遇到与正整数n 有关的不等式的证明，且其他方法不易证时，可以考虑用数学归纳法进行证明求解.数学归纳法的定义一般地，证明一个与正整数n有关的命题，可按下列步骤进行：1．(归纳奠基)证明当n取第一个值n0(n0∈N*)时命题成立；2．(归纳递推)假设n＝k(k≥n0，k∈N*)时命题成立，证明当n＝□01k＋1时命题也成立．只要完成这两个步骤，就可以断定命题对从n0开始的所有正整数n都成立，上述证明方法叫做数学归纳法．1．概念辨析(1)用数学归纳法证明问题时，第一步是验证当n＝1时结论成立．()(2)不论是等式还是不等式，用数学归纳法证明时，由n＝k到n＝k＋1时，项数都增加了一项．()(3)用数学归纳法证明问题时，归纳假设可以不用．()(4)用数学归纳法证明等式“1＋2＋22＋…＋2n＋2＝2n＋3－1”，验证n＝1时，左边式子应为1＋2＋22＋23.()答案(1)×(2)×(3)×(4)√2．小题热身(1)下列结论能用数学归纳法证明的是()A．x>sin x，x∈(0，π)B ．e x ≥x ＋1(x ∈R )C ．1＋12＋122＋…＋12n －1＝2－⎝ ⎛⎭⎪⎫12n －1(n ∈N *)D ．sin(α＋β)＝sin αcos β＋cos αsin β(α，β∈R ) 答案 C解析数学归纳法是用来证明与自然数有关的命题的一种方法，由此可知C 符合题意．(2)用数学归纳法证明1＋a ＋a 2＋…＋a n ＋1＝1－a n ＋21－a(a ≠1，n ∈N *)，在验证n＝1时，等式左边的项是( )A ．1B ．1＋aC ．1＋a ＋a 2D ．1＋a ＋a 2＋a 3答案 C解析验证n ＝1时，等式左边的项是1＋a ＋a 2.(3)用数学归纳法证明“当n 为正奇数时，x n ＋y n 能被x ＋y 整除”，当第二步假设n ＝2k －1(k ∈N *)命题为真时，进而需证n ＝________时，命题亦真．答案 2k ＋1解析由于步长为2，所以2k －1后一个奇数应为2k ＋1.题型一用数学归纳法证明恒等式设i 为虚数单位，n 为正整数，θ∈[0,2π)．用数学归纳法证明：(cos θ＋isin θ)n ＝cos nθ＋isin nθ.证明 ①当n ＝1时，左边＝右边＝cos θ＋isin θ，所以命题成立； ②假设当n ＝k 时，命题成立，即 (cos θ＋isin θ)k ＝cos kθ＋isin kθ，则当n ＝k ＋1时，(cos θ＋isin θ)k ＋1＝(cos θ＋isin θ)k ·(cos θ＋isin θ) ＝(cos kθ＋isin kθ)(cos θ＋isin θ)＝(cos kθcosθ－sin kθsinθ)＋i(sin kθcosθ＋cos kθsinθ)＝cos(k＋1)θ＋isin(k＋1)θ，所以当n＝k＋1时，命题成立．综上，由①和②可得，(cosθ＋isinθ)n＝cos nθ＋isin nθ.数学归纳法证明等式的思路和注意点(1)思路：用数学归纳法证明等式问题，要“先看项”，弄清等式两边的构成规律，等式两边各有多少项，初始值n0是多少．(2)注意点：由n＝k时等式成立，推出n＝k＋1时等式成立，一要找出等式两边的变化(差异)，明确变形目标；二要充分利用归纳假设，进行合理变形，正确写出证明过程．提醒：归纳假设就是证明n＝k＋1时命题成立的条件，必须用上，否则就不是数学归纳法.用数学归纳法证明：12 1×3＋223×5＋…＋n2(2n－1)(2n＋1)＝n(n＋1)2(2n＋1)(n∈N*)．证明①当n＝1时，左边＝121×3＝13，右边＝1×(1＋1)2×(2×1＋1)＝13，左边＝右边，等式成立．②假设n＝k(k≥1，k∈N*)时，等式成立．即12 1×3＋223×5＋…＋k2(2k－1)(2k＋1)＝k(k＋1)2(2k＋1)，当n＝k＋1时，左边＝121×3＋223×5＋…＋k2(2k－1)(2k＋1)＋(k＋1)2(2k＋1)(2k＋3)＝k (k ＋1)2(2k ＋1)＋(k ＋1)2(2k ＋1)(2k ＋3)＝k (k ＋1)(2k ＋3)＋2(k ＋1)22(2k ＋1)(2k ＋3)＝(k ＋1)(2k 2＋5k ＋2)2(2k ＋1)(2k ＋3)＝(k ＋1)(k ＋2)2(2k ＋3)，右边＝(k ＋1)(k ＋1＋1)2[2(k ＋1)＋1]＝(k ＋1)(k ＋2)2(2k ＋3)，左边＝右边，等式成立．由①②知，对n ∈N *，原等式成立．题型二用数学归纳法证明不等式用数学归纳法证明：对一切大于1的自然数，不等式⎝ ⎛⎭⎪⎫1＋13⎝ ⎛⎭⎪⎫1＋15·…·⎝ ⎛⎭⎪⎫1＋12n －1>2n ＋12均成立．证明 ①当n ＝2时，左边＝1＋13＝43，右边＝52. ∵左边>右边，∴不等式成立．②假设当n ＝k (k ≥2，且k ∈N *)时不等式成立．即⎝ ⎛⎭⎪⎫1＋13⎝ ⎛⎭⎪⎫1＋15·…·⎝ ⎛⎭⎪⎫1＋12k －1>2k ＋12.则当n ＝k ＋1时，⎝ ⎛⎭⎪⎫1＋13⎝ ⎛⎭⎪⎫1＋15·…·⎝ ⎛⎭⎪⎫1＋12k －1·⎣⎢⎡⎦⎥⎤1＋12(k ＋1)－1>2k ＋12·2k ＋22k ＋1＝2k ＋222k ＋1＝4k 2＋8k ＋422k ＋1>4k 2＋8k ＋322k ＋1＝2k ＋32k ＋122k ＋1＝2(k ＋1)＋12.∴当n ＝k ＋1时，不等式也成立．由①②知对于一切大于1的自然数n ，不等式成立．应用数学归纳法证明不等式应注意的问题(1)适用范围：当遇到与正整数n 有关的不等式证明时，应用其他办法不容易证，则可考虑应用数学归纳法．(2)关键：用数学归纳法证明不等式的关键是由n ＝k 成立，推证n ＝k ＋1时也成立，证明时用上归纳假设后，可采用分析法、综合法、求差(求商)比较法、放缩法等证明.求证：当n ≥1(n ∈N *)时，(1＋2＋…＋n )⎝ ⎛⎭⎪⎫1＋12＋13＋…＋1n ≥n 2.证明 (1)当n ＝1时，左边＝右边，命题成立．当n ＝2时，左边＝(1＋2)⎝ ⎛⎭⎪⎫1＋12＝92>22，命题成立．(2)假设当n ＝k (k ≥2)时命题成立，即 (1＋2＋…＋k )⎝ ⎛⎭⎪⎫1＋12＋…＋1k ≥k 2.则当n ＝k ＋1时，有左边＝[(1＋2＋…＋k )＋(k ＋1)]·⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1＋12＋…＋1k ＋1k ＋1 ＝(1＋2＋…＋k )⎝ ⎛⎭⎪⎫1＋12＋…＋1k ＋(1＋2＋…＋k )·1k ＋1＋(k ＋1)⎝ ⎛⎭⎪⎫1＋12＋…＋1k ＋1≥k 2＋k 2＋1＋(k ＋1)⎝ ⎛⎭⎪⎫1＋12＋…＋1k . ∵当k ≥2时，1＋12＋…＋1k ≥1＋12＝32，∴左边≥k 2＋k 2＋1＋(k ＋1)×32＝k 2＋2k ＋1＋32≥(k ＋1)2.这就是说当n ＝k ＋1时，命题成立．由(1)(2)可知当n ≥1(n ∈N *)时原命题成立．题型三归纳—猜想—证明如图，P 1(x 1，y 1)，P 2(x 2，y 2)，…，P n (x n ，y n )(0<y 1<y 2<…<y n )是曲线C ：y 2＝3x (y ≥0)上的n 个点，点A i (a i,0)(i ＝1,2,3，…，n )在x 轴的正半轴上，且△A i －1A i P i 是正三角形(A 0是坐标原点)．(1)写出a 1，a 2，a 3；(2)求出点A n (a n,0)(n ∈N *)的横坐标a n 关于n 的表达式．解 (1)设P 1(x 1，y 1)，A 1(a 1,0)，则x 1＝a 12，即a 1＝2x 1，由y 2＝3x 得y 1＝3x 1，由|A 0P 1|＝|OA 1|得，x 21＋y 21＝a 1，即a 214＋32a 1＝a 21，即a 1>0，所以a 1＝2，同理可得a 2＝6，a 3＝12.(2)依题意，得x n ＝a n －1＋a n 2，y n ＝3·a n －a n －12，由此及y 2n ＝3x n 得⎝⎛⎭⎪⎫3·a n －a n －122＝32(a n －1＋a n )，即(a n －a n －1)2＝2(a n －1＋a n )．由(1)可猜想：a n ＝n (n ＋1)(n ∈N *)．下面用数学归纳法予以证明： ①当n ＝1时，命题显然成立；②假设当n ＝k 时命题成立，即有a n ＝k (k ＋1)，则当n ＝k ＋1时，由归纳假设及(a k ＋1－a k )2＝2(a k ＋a k ＋1)得 [a k ＋1－k (k ＋1)]2＝2[k (k ＋1)＋a k ＋1]，即a 2k ＋1－2(k 2＋k ＋1)a k ＋1＋[k (k －1)]·[(k ＋1)(k ＋2)]＝0，解得a k ＋1＝(k ＋1)(k ＋2)或a k ＋1＝k (k －1)<a k (不符合题意，舍去)．即当n ＝k ＋1时，命题成立．由①②知，命题成立.归纳—猜想—证明的应用策略一般思路是：通过观察有限个特例，猜想出一般性的结论，然后用数学归纳法证明．这种方法在解决探索性问题、存在性问题或与正整数有关的命题中有着广泛的应用．其关键是归纳、猜想出公式.已知数列{a n }的前n 项和S n 满足S n ＝a n 2＋1a n－1且a n >0，n ∈N *.(1)求a 1，a 2，a 3，并猜想{a n }的通项公式； (2)证明通项公式的正确性．解 (1)当n ＝1时，由已知得a 1＝a 12＋1a 1－1，a 21＋2a 1－2＝0.所以a 1＝3－1(a 1>0)．当n ＝2时，由已知得a 1＋a 2＝a 22＋1a 2－1，将a 1＝3－1代入并整理得a 22＋23a 2－2＝0. 所以a 2＝5－3(a 2>0)．同理可得a 3＝7－ 5. 猜想a n ＝2n ＋1－2n －1(n ∈N *)．(2)证明：①由(1)知，当n ＝1,2,3时，通项公式成立． ②假设当n ＝k (k ≥3，k ∈N *)时，通项公式成立，即a k ＝2k ＋1－2k －1.由a k ＋1＝S k ＋1－S k ＝a k ＋12＋1a k ＋1－a k 2－1a k ，将a k ＝2k ＋1－2k －1代入上式并整理，得a 2k ＋1＋22k ＋1a k ＋1－2＝0，解得a k ＋1＝2k ＋3－2k ＋1(负值舍去)．即当n ＝k ＋1时，通项公式也成立．由①和②，可知对所有n ∈N *，a n ＝2n ＋1－2n －1都成立．。

2020年高考冲刺数学(理)全真模拟演练(解析版)

冲刺2020年高考数学（理）全真模拟演练（八）一、单选题1．设集合2{|90}A x x =->，则RC A = （） A ．(3,)+∞B ．(,3)-∞-C ．[3-，3]D ．()3,3-【答案】C【解析】【分析】先求出集合A ，由此能求出C A R．【详解】Q 集合2{|90}{|3A x x x x =->=<-或3}x >，C {|33}[33]R A x x ∴=-≤≤=-，，故选：C ．【点睛】本题考查补集的求法，考查补集定义等基础知识，考查运算求解能力，是基础题．2．已知i 是虚数单位，复数21i i +=-（） A ．132i + B ．132i - C ．134i + D ．134i - 【答案】A【解析】【分析】根据复数的除法运算，即可求解.【详解】()()()()212131112i i i i z i i i ++++===-+- 故选：A【点睛】本题考查复数的除法运算，属于基础题.3．齐王有上等、中等、下等马各一匹，田忌也有上等、中等、下等马各一匹．田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马．现在从双方的马匹中随机各选一匹进行一场比赛，若有优势的马一定获胜，则齐王的马获胜得概率为（）A ．49B ．59C ．23D ．79【答案】C【解析】【分析】现从双方的马匹中随机各选一匹进行一场比赛 ,利用列举法求出基本事件有9种，齐王的马获胜包含的基本事件有6种，利用古典概型概率公式可求出齐王的马获胜的概率.【详解】设齐王上等、中等、下等马分別为,,A B C ，田忌上等、中等、下等马分别为,,a b c ，现从双方的马匹中随机各选一匹进行一场比赛,基本事件有：()()()()()()()()(),,,,,,,,,,,,,,,,,A a A b A c B a B b B c C a C b C c ，共9种，有优势的马一定获胜，齐王的马获胜包含的基本事件有：()()()()()(),,,,,,,,,,,A a A b A c B b B c C c ，共 6种,∴齐王的马获胜的概率为6293P ==，故选C. 【点睛】本题主要考查古典概型概率公式的应用，属于中档题，利用古典概型概率公式求概率时，找准基本事件个数是解题的关键，基本亊件的探求方法有 (1)枚举法：适合给定的基本事件个数较少且易一一列举出的；(2)树状图法：适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时，一定要按顺序逐个写出：先11(,)A B ，12(,)A B …. 1(,)n A B ，再21(,)A B ，22(,)A B …..2(,)n A B 依次31(,)A B 32(,)A B ….3(,)n A B … 这样才能避免多写、漏写现象的发生.4．已知向量(1,0)m =r ，n =r ，)y ，若m r 与n r 的夹角为3π，则(y = ) A ．0 B ．±1 C ．2± D ．3± 【答案】D【解析】【分析】由题意利用两个向量的数量积的定义和公式，求得y 的值．【详解】Q 向量(1,0)m =r，n =r ，)y ，若m r 与n r 的夹角为3π，∴101cos 3m n y π=⨯==r r g 求得3=±y ，故选：D ．【点睛】本题主要考查两个向量的数量积的定义和公式，属于基础题．5．设等比数列{}n a 的前n 项和为n S ，且639S S =，764a =，则1(a = )A ．1B ．2C ．3D ．4【答案】A【解析】【分析】利用等比数列前n 项和公式和通项公式列出方程组，能求出1a ．【详解】Q 等比数列{}n a 的前n 项和为n S ，且639S S =，764a =， ∴631161(1)9(1)1164a q a q q q a q ⎧--=⎪--⎨⎪=⎩，解得11a =，2q =．故选：A ．【点睛】本题考查等比数列的首项的求法，考查等比数列的性质等基础知识，考查运算求解能力，是基础题． 6．已知()f x 是定义在R 上的偶函数，且(5)(3)f x f x +=-，如果当[0,4)x ∈时，2()log (2)f x x =+，则(766)f =（）A ．3B ．-3C ．2D ．-2【答案】C【解析】【分析】根据()()53f x f x +=- 得()()8f x f x += 即f （x ）的周期为8，再根据x ∈[0，4）时，()()2f x log 2x =+及f （x ）为R 上的偶函数即可求出f （766）=f （2）=2．【详解】由()()53f x f x +=-，得()()8f x f x +=，所以()f x 是周期为8的周期函数，当[)0,4x ∈时，()()2log 2f x x =+，所以()()()76696822f f f =⨯-=-，又()f x 是定义在R 上的偶函数所以()()222log 42f f -===.【点睛】本题考查函数的周期性，奇偶性与求值，考查运算求解能力.7．函数422x x cosx y -=+的图象大致为（） A ．B ．C ．D ．【答案】B【解析】【分析】判断函数的奇偶性，排除选项，利用特殊值以及函数的图象的变化趋势判断即可【详解】解：令函数f （﹣x ）()422x x cos x --==+f （x ），所以函数f （x ）是偶函数，故排除选项C ，D ，又f （0）411==+2，故排除A ，故选B ．【点睛】本题考查函数的图象的判断，函数的奇偶性以及函数的特殊点的位置，变化趋势是常用方法．8．一个几何体的三视图如图所示，则该几何体的表面积为( )A ．324π+B ．4323π+C ．244π+D ．4243π+ 【答案】A【解析】【分析】首先把三视图转换为几何体，进一步求出几何体的表面积．【详解】根据几何体的三视图，转换为几何体为：该几何体为上面为一个半径为1的球体，下面为一个底面为边长为2的正方形，高为3的长方体．∴241222423324S ππ=⋅+⨯⨯+⨯⨯=+表．故选：A ．【点睛】本题考查的知识要点：三视图和几何体之间的转换，几何体的体积和表面积公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题．9．如图是一个程序框图，则输出k 的值为（）A ．6B ．7C ．8D ．9【答案】B【解析】【分析】根据程序框图，模拟计算过程即可求解.【详解】程序框图的执行过程如下：1S =，10k =；1011S =，9k =； 911S =，8k =； 811S =，7k =，循环结束.故选B.【点睛】本题主要考查了程序框图，算法结构，属于中档题.10．已知抛物线22(02)y px p =<<的焦点为F ，以(42p M +，0)为圆心，||MF 长为半径画圆，在第一象限交抛物线于A 、B 两点，则||||AF BF +的值为( )A ．4B ．5C ．6D ．8【答案】D【解析】【分析】求得抛物线的焦点，可得圆的半径和方程，联立圆的方程和抛物线的方程可得x 的二次方程，运用韦达定理和抛物线的定义，计算可得所求和．【详解】抛物线22(02)y px p =<<的焦点为(2p F ，0)，(42p M +，0)，即有||4MF =，可得圆M 的方程为22(4)162p x y --+=，联立抛物线22y px =，可得222(4)4024p p x x p +-++=，可得△224((4)4(4)024p p p =--+>，解得02p <<，设1(A x ，1)y ，2(B x ，2)y ，可得128x x p +=-，则12||||88AF BF x x p p p +=++=-+=．故选：D ．【点睛】本题考查抛物线的定义、方程和性质，考查圆的方程和抛物线的方程联立，运用韦达定理，考查方程思想和运算能力，属于基础题．11．已知函数11,20()ln 1,0x x f x x x ⎧+--≤≤=⎨->⎩若()()g x f x kx =-恰有4个零点，则k 的取值范围是（） A ．210,e ⎛⎫ ⎪⎝⎭ B ．21,1e ⎛⎫ ⎪⎝⎭ C ．221,e e ⎛⎫ ⎪⎝⎭D ．)20,e ⎡⎣ 【答案】A【解析】【分析】由零点定义可知()f x kx =恰有4个不同交点，画出函数()f x 的图像；利用导数求得直线()f x kx =与()f x 相切时的斜率，再将直线()f x kx =绕原点旋转，即可判断出有4个交点时的斜率取值范围.【详解】根据零点定义可知()()0g x f x kx =-=，即()f x kx =恰有4个不同交点，画出函数11,20()ln 1,0x x f x x x ⎧+--≤≤=⎨->⎩的图像如下图所示：当0x >时，()ln 1f x x =-，则1()f x x'=，设()f x kx =与()ln 1f x x =-相切于(),m km ，由导数几何意义及切点在()ln 1f x x =-上，则满足1ln 1k m km m ⎧=⎪⎨⎪=-⎩解得221k e m e⎧=⎪⎨⎪=⎩，将直线()f x kx =绕原点旋转，当恰有4个交点时满足210k e <<，即k 的取值范围为210,e ⎛⎫ ⎪⎝⎭，故选：A【点睛】本题考查了函数零点与方程根的关系，利用导数的几何意义求得相切的斜率，利用数形结合法求参数的取值范围，综合性强，属于难题.12．正方体1111ABCD A B C D -的棱长为4，点M 在棱AB 上，且1AM =，点P 是正方体下底面ABCD 内（含边界）的动点，且动点P 到直线11A D 的距离与点P 到点M 的距离的平方差为16，则动点P 到B 点的最小值是（）．A ．72 B．CD【答案】C【解析】【分析】作PQ AD ⊥，11QR A D ⊥，PR 即为P 到直线11A D 的距离，从而可得PM PQ =，即点P 的轨迹是以AD 为准线，点M 为焦点的抛物线，然后建立平面直角坐标系求解.【详解】如图所示，作PQ AD ⊥，Q 为垂足，则PQ ⊥面11ADD A过点Q 作11QR A D ⊥，则11A D ⊥面PQR所以PR 即为P 到直线11A D 的距离因为22216PR PQ RQ -==，2216PR PM -=所以PM PQ =所以点P 的轨迹是以AD 为准线，点M 为焦点的抛物线如图建立直角坐标系，则点P 的轨迹方程是(22022y x y =≤≤ 点7,02B ⎛⎫ ⎪⎝⎭,设2,2y P y ⎛⎫ ⎪⎝⎭所以22422754922424y y y PB y ⎛⎫=-+=-+ ⎪⎝⎭所以当25y =，PB 6故选：C【点睛】本题考查的是立体几何中的垂直关系、解析几何中抛物线的定义及最值问题，属于较难题.二、填空题13．在ABC V 中，角A 、B 、C 的对边分别为a 、b 、c，若b =3c =，2B C =，则cos 2C 的值为____________．【答案】59【解析】【分析】根据正弦定理、二倍角的正弦公式、余弦公式直接进行求解即可.【详解】由正弦定理可得：sin sin b c B C =，即sin sin 22sin cos 2cos cos sin sin sin b B C C C C C c C C C =====⇒∴275cos22cos 12199C C =-=⨯-=．故答案为：59【点睛】本题考查了正弦定理的应用，考查了二倍角的正弦公式和余弦公式，考查了数学运算能力.14．已知x ，y 满足约束条件202010x y x y y ++≥⎧⎪--≤⎨⎪+≤⎩，则目标函数2z x y =-的最大值为__________________。

2020年高考数学(理科)最后冲刺指导选择填空

的建系（直角三角形、等腰、等边、矩形、正方形、直角梯形等）、投影问题记牢运算方法
b
c os
a b
。通过三角形法则和平行四边形法则转化也很重要；单位向量要看清，模为
1 ；向量
a
夹角为锐角，数量积大于 0 且向量不能同向（夹角为 0）；向量夹角为钝角，数量积小于 0 且向量
例 6、命题“ xR ， x2 x 1 0 ”的否定是 ( B )
A． xR ， x2 x 1 0
B． x0 R ，
C． x0 R ， x02 x0 1 0
D． x0 R ， x02 x0 1 0
例 7、设 a ， b ， c 为正数，则“ a b c ”是“ a2 b2 c2 ”的 ( B )
A． (,0) 例 29、已知函数
B． ( ,0) 12
C． ( 5 , 1) 6
D． ( , 1) 6
的部分图象如图所示，则函数
图象的一个对称中心可能为（ C ）
A． (2,0)
例 30、已知 A． (0 ， 2]
3
B． (1,0)
C． (10,0)
D． (14,0)
在区间
[
,
]
上单调递增，则
D．6 上，则| PQ | 的取值范围是 ( D )
A．[ 5 1 ， 10 1] B．[ 5 1 ， 10 1] C．[ 10 1， 5]
D．[ 5 1 ， 5]
例 22、已知 x 0 ， y 0 ，且 1 2 1，则 xy x y 的最小值为 7 4 3 ． xy
5、三角函数小题
A．
B． (3, 4)
C． (2,1)
D． (4, )

2020年高考数学(理科)模拟冲刺卷(一)

第1页共8页第2页共8页 2020年高考数学（理科）模拟冲刺卷（一）考生注意事项： 1．答题前，先将自己的姓名、考号填写在试题卷和答题卡上。 2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。 4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合

2160Axx

，lg20Bxx，则ABI（）

A．[4,1)(3,4]U B．[4,3)(1,4]U C．(4,1)(3,4)U D．(4,3)(1,4)U 2．设复数

z满足(1i)2iz，则复数z

（）

A．

1i

B．1i C．1i D．1i

3．

1()2xx的展开式中的常数项为（）

A．

1516 B．1516 C．2116 D．21

4．“cos0A”是“

为锐角”的（）

A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既非充分又非必要条件

5．若双曲线

2214xym的离心率为2，则双曲线的标准方程为（）

A．

221416xy B．221412xy C．22148xy D．22144xy

6．设函数

π()cos(2)6fxx，则下列结论正确的是（）

A．

()fx的一个周期为π2 B．()fx

的图象关于直线对称

12x

C．

()fx的一个零点是π12 D．()fx

在ππ(,)22单调递增

7．一个算法的程序框图如图所示，若该程序输出的结果是

4，则判断框中应填入的条件是

（）

A．5?i B．5?i C．4?i D．4?i 8．已知正三棱柱的高为23，它的六个顶点都在一个直径为

2020届数学(理)高考二轮专题复习课件：第三部分考前冲刺三溯源回扣八复数、程序框图、推理与证明

2．复数的四则运算法则． (a＋bi)±(c＋di)＝(a±c)＋(b±d)i (a＋bi)(c＋di)＝(ac－bd)＋(bc＋ad)i (a＋bi)÷(c＋di)＝acc2＋＋bdd2 ＋bcc2－＋add2 i(a，b，c，d∈R，c ＋di≠0)． 3．算法的三种基本逻辑结构． (1)顺序结构；(2)条件结构；(3)循环结构． 4．合情推理包括归纳推理与类比推理：演绎推理的一般模式是“三段论”，包括：(1)大前提；(2)小前提；(3) 结论．
考前冲刺三考前提醒回扣溯源
溯源回扣八复数、程序框图、推理与证明
环节一：牢记概念公式，避免卡壳 1．复数 z＝a＋bi(a，b∈R)概念． (1)分类：当 b＝0 时，z∈R；当 b≠0 时，z 为虚数；当 a＝0，b≠0 时，z 为纯虚数． (2)z 的共轭复数－z ＝a－bi. (3)z 的模|z|＝ a2＋b2.
解析：结论的否定：方程 x2＋ax＋b＝0 一个实根都没有，所以假设应是“若 a，b 为实数，则方程 x3＋ax＋b＝0 没有实根”．
答案：若 a，b 为实数，则方程 x3＋ax＋b＝0 没有实根
5．控制循环结构的是计数变量和累加变量的变化规律以及循环结束的条件．在解答这类题目时，易混淆两变量的变化次序，且容易错误判定循环体结束的条件．
出 S，结果为 8.
答案：B
6．用数学归纳法证明时，易盲目认为 n0 的起始取值 n0＝1，另外注意证明传递性时，必须用 n＝k 成立的归纳假设．
[回扣问题 6] 设数列{an}的前 n 项和为 Sn，且方程 x2－anx－an＝0 有一根为 Sn－1(n∈N*)．
(1)求 a1，a2； (2)猜想数列{Sn}的通项公式，并给出证明．解：(1)当 n＝1 时，方程 x2－a1x－a1＝0 有一根为 S1 －1＝a1－1，所以(a1－1)2－a1(a1－1)－a1＝0，解得 a1＝12.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

冲刺满分·备战高考
精品资源·战胜高考
专题30 复数的计算（原卷版）

易错点1：误认为21i；
易错点2：对复数整数指数幂的运算法则理解不到位而致错；
易错点3：计算失误；
易错点4：弄错相等复数的条件。
题组一：复数的运算
1.（2019全国III理2）若,则z=（）
A． B． C． D．
2．（2013新课标2）设复数满足,则=（）
A． B． C． D．
3．(2018全国卷Ⅲ)(1i)(2i)=
A．3i B．3i C．3i D．3i
4．(2018全国卷Ⅱ)12i12i（）
A．43i55 B．43i55 C．34i55 D．34i55
5．（2017新课标Ⅱ）
3i1i




A．1+2i B．1-2i C．2+i D．2-i

6．（2014新课标1）32(1)(1)ii=

(1i)2iz
1i1+i1i1+i
z12iziz
1i1i1i1i
冲刺满分·备战高考

精品资源·战胜高考
A．1i B．1i C．1i D．1i
7．（2014新课标2）
131ii




A．12i B．12i C．1-2i D．1-2i
题组二：复数的模
8．(2018全国卷Ⅰ)设1i2i1iz,则||z
A．0 B．12 C．1 D
．

9．（2017新课标Ⅲ）设复数z满足(1i)2zi,则||z=
A．12 B．22 C．2 D．2
10．(2016年全国I)设(1)1ixyi,其中,xy是实数,则
A．1 B．2 C． D．2
11．（2015新课标1）设复数z满足11ziz,则||z=
A．1 B．2 C．3 D．2
12．（2014新课标1）设iiz11,则||z

A． 21 B． 22 C． 23 D． 2
13．（2013新课标1）若复数z满足(34i)|43i|z,则z的虚部为

i=xy
3
冲刺满分·备战高考

精品资源·战胜高考
A．－4 B．
45 C．4 D．4
5

14.（2019全国I理2）设复数z满足,z在复平面内对应的点为(x,y),则

A． B．
C． D．
题组三：共轭复数
14．(2016年全国III)若12zi,则41izz
A．1 B．1 C． i D．i
15．（2012新课标）复数z＝
32ii

的共轭复数是

A．2i B．2i C．1i D．1i
16．(2011新课标)复数的共轭复数是

A． B． C． D．
17．（2010新课标）已知复数23(13)izi,z是z的共轭复数,则zz=
A．14 B．12 C．1 D．2
18．（2014新课标2）设复数
1z,2z在复平面内的对应点关于虚轴对称,12zi,则12
zz

A．5 B．5 C．4i D．4i
19．（2017新课标Ⅰ）设有下面四个命题

1
p
：若复数z满足1zR,则zR；

=1iz
22+11()xy22
1(1)xy

22(1)1yx22
(+1)1yx

212ii


3
5
i
3

5
i
i
i
冲刺满分·备战高考

精品资源·战胜高考
2
p
：若复数z满足2zR,则zR；

3
p
：若复数1z,2z满足12zzR,则12zz；

4
p
：若复数zR,则zR．

其中的真命题为
A．
1p,3p B．1p,4p C．2p,3
p

D．2p,4p

A．1 B．2 C． D．2
题组四：复平面坐标
20.（2019全国II理2
）设z=-3+2i,则在复平面内对应的点位于

A．第一象限 B．第二象限
C．第三象限 D
．第四象限

21．(2016年全国II)
已知

(3)(1)izmm

在复平面内对应的点在第四象限,则实数m的取

值范围是

A．31， B．13， C．1,+ D．3-，

3
z