初高中数学衔接教材

合集下载

初高中数学衔接教材(已整理精品)

初高中数学衔接教材之袁州冬雪创作我们在初中已经学习过了下列一些乘法公式：（1）平方差公式 22()()a b a b a b +-=-；（2）完全平方公式222()2a b a ab b ±=±+．我们还可以通过证明得到下列一些乘法公式：（1）立方和公式2233()()a b a ab b a b +-+=+；（2）立方差公式2233()()a b a ab b a b -++=-；（3）三数和平方公式2222()2()a b c a b c ab bc ac ++=+++++；（4）两数和立方公式 33223()33a b a a b ab b +=+++；（5）两数差立方公式 33223()33a b a a b ab b -=-+-．对上面列出的五个公式，有兴趣的同学可以自己去证明．例1 计算：22(1)(1)(1)(1)x x x x x x +--+++．解法一：原式=2222(1)(1)x x x ⎡⎤-+-⎣⎦=242(1)(1)x x x -++=61x -．解法二：原式=22(1)(1)(1)(1)x x x x x x +-+-++=33(1)(1)x x +-=61x -．例2 已知4a b c ++=，4ab bc ac ++=，求222a b c ++的值．解：2222()2()8a b c a b c ab bc ac ++=++-++=．练习1．填空：（1）221111()9423a b b a -=+（）；（2）(4m +22)164(m m =++)；(3 ) 2222(2)4(a b c a b c +-=+++)．2．选择题：（1）若212x mx k ++是一个完全平方式，则k 等于（）（A ）2m （B ）214m （C ）213m （D ）2116m （2）不管a ，b 为何实数，22248a b a b +--+的值（）（A ）总是正数（B ）总是负数（C ）可以是零（D ）可以是正数也可以是负数2．因式分解因式分解的主要方法有：十字相乘法、提取公因式法、公式法、分组分解法，别的还应懂得求根法及待定系数法．1．十字相乘法例1 分解因式：（1）x2－3x ＋2；（2）x2＋4x －12；（3）22()x a b xy aby -++；（4）1xy x y -+-．解：（1）如图1．1－1，将二次项x2分解成图中的两个x 的积，再将常数项2分解成－1与－2的乘积，而图中的对角线上的两个数乘积的和为－3x ，就是x2－3x ＋2中的一次项，所以，有x2－3x ＋2＝(x －1)(x －2)．说明：此后在分解与本例近似的二次三项式时，可以直接将图1．1－1中的两个x 用1来暗示（如图1．1－2所示）．（2）由图1．1－3，得x2＋4x －12＝(x －2)(x ＋6)．（3）由图1．1－4，得22()x a b xy aby -++＝()()x ay x by --（4）1xy x y -+-＝xy ＋(x －y)－1 ＝(x －1) (y+1) （如图1．1－5所示）．讲堂操练一、填空题：1、把下列各式分解因式：（1）=-+652x x __________________________________________________.（2）=+-652x x __________________________________________________.（3）=++652x x __________________________________________________.（4）=--652x x __________________________________________________.（5）()=++-a x a x 12__________________________________________________.（6）－1 －2 x x 图1．1－1 －1 －2 1 1 图1．1－2 －2 6 1 1 图1．1－3 －ay －by xx 图1．1－4 －1 1x y 图1．1－5=+-18112x x __________________________________________________.（7）=++2762x x __________________________________________________.（8）=+-91242m m __________________________________________________.（9）=-+2675x x __________________________________________________.（10）=-+22612y xy x __________________________________________________.2、()() 3 42++=+-x x x x3、若()()422-+=++x x b ax x 则 =a ， =b .二、选择题：（每小题四个答案中只有一个是正确的）1、在多项式（1）672++x x （2）342++x x （3）862++x x （4）1072++x x（5）44152++x x 中，有相同因式的是（）A 、只有（1）（2）B 、只有（3）（4）C 、只有（3）（5）D 、（1）和（2）；（3）和（4）；（3）和（5）2、分解因式22338b ab a -+得（）A 、()()3 11-+a aB 、()()b a b a 3 11-+C 、()()b a b a 3 11--D 、()()b a b a 3 11+-3、()()2082-+++b a b a 分解因式得（）A 、()()2 10-+++b a b aB 、()()4 5-+++b a b aC 、()()10 2-+++b a b aD 、()()5 4-+++b a b a4、若多项式a x x +-32可分解为()()b x x --5，则a 、b 的值是（）A 、10=a ，2=bB 、10=a ，2-=bC 、10-=a ，2-=bD 、10-=a ，2=b5、若()()b x a x mx x ++=-+ 102其中a 、b 为整数，则m 的值为（）A 、3或9B 、3±C 、9±D 、3±或9±三、把下列各式分解因式1、()()3211262+---p q q p2、22365ab b a a +-3、6422--y y4、8224--b b2．提取公因式法例2 分解因式：（1）()()b a b a -+-552 （2）32933x x x +++解：（1）．()()b a b a -+-552=)1)(5(--a b a（2）32933x x x +++=32(3)(39)x x x +++=2(3)3(3)x x x +++=2(3)(3)x x ++．或32933x x x +++＝32(331)8x x x ++++＝3(1)8x ++＝33(1)2x ++＝22[(1)2][(1)(1)22]x x x +++-+⨯+ ＝2(3)(3)x x ++讲堂操练：一、填空题：1、多项式xyz xy y x 42622+-中各项的公因式是_______________.2、()()()•-=-+-y x x y n y x m __________________.3、()()()•-=-+-222y x x y n y x m ____________________.4、()()()•--=-++--z y x x z y n z y x m _____________________.5、()()•--=++---z y x z y x z y x m ______________________.6、523623913x b a x ab --分解因式得_____________________.7．计算99992+=二、断定题：（正确的打上“√”，错误的打上“×” ）1、()b a ab ab b a -=-24222………………………………………………………… （）2、()b a m m bm am +=++…………………………………………………………… （）3、()5231563223-+-=-+-x x x x x x …………………………………………… （）4、()111+=+--x x x x n n n ……………………………………………………………… （）3：公式法例3分解因式：（1）164+-a （2）()()2223y x y x --+解：(1)164+-a =)2)(2)(4()4)(4()(4222222a a a a a a -++=-+=-(2)()()2223y x y x --+=)32)(4()23)(23(y x y x y x y x y x y x ++=+-+-++讲堂操练一、222b ab a +-，22b a -，33b a -的公因式是______________________________.二、断定题：（正确的打上“√”，错误的打上“×” ）1、()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=-⎪⎭⎫ ⎝⎛=-1.032 1.0321.03201.094222x x x x …………………………（）2、()()()()b a b a b a b a 43 4343892222-+=-=-………………………………… （）3、()()b a b a b a 45 4516252-+=-………………………………………………… （）4、()()()y x y x y x y x -+-=--=-- 2222………………………………………… （）5、()()()c b a c b a c b a +-++=+- 22……………………………………………… （）五、把下列各式分解1、()()229n m n m ++--2、3132-x 3、()22244+--x x 4、1224+-x x4．分组分解法例4 （1）x y xy x 332-+- （2）222456x xy y x y +--+-．（2）222456x xy y x y +--+-=222(4)56x y x y y +--+-=22(4)(2)(3)x y x y y +----=(22)(3)x y x y -++-．或222456x xy y x y +--+-=22(2)(45)6x xy y x y +----=(2)()(45)6x y x y x y -+---=(22)(3)x y x y -++-．讲堂操练：用分组分解法分解多项式（1）by ax b a y x 222222++-+-（2）91264422++-+-b a b ab a5．关于x 的二次三项式ax2+bx+c(a≠0)的因式分解．若关于x 的方程20(0)ax bx c a ++=≠的两个实数根是1x 、2x ，则二次三项式2(0)ax bx c a ++≠便可分解为12()()a x x x x --.例5 把下列关于x 的二次多项式分解因式：（1）221x x +-；（2）2244x xy y +-．解：（1）令221x x +-=0，则解得11x =-21x =-，∴221x x +-=(1(1x x ⎡⎤⎡⎤----⎣⎦⎣⎦ =(11x x ++．（2）令2244x xy y +-=0，则解得1(2x y =-+，1(2x y =--，∴2244x xy y +-=[2(1][2(1]x y x y ++．练习1．选择题：多项式22215x xy y --的一个因式为（）（A ）25x y - （B ）3x y - （C ）3x y + （D ）5x y -2．分解因式：（1）x2＋6x ＋8；（2）8a3－b3；（3）x2－2x －1；（4）4(1)(2)x y y y x -++-．习题1．21．分解因式：（1） 31a +；（2）424139x x -+；（3）22222b c ab ac bc ++++；（4）2235294x xy y x y +-++-．2．在实数范围内因式分解：（1）253x x -+ ；（2）2223x x --；（3）2234x xy y +-；（4）222(2)7(2)12x x x x ---+．3．ABC ∆三边a ，b ，c 知足222a b c ab bc ca ++=++，试断定ABC ∆的形状．4．分解因式：x2＋x －(a2－a)．5. （测验测验题）已知abc=1，a+b+c=2，a ²+b ²+c ²=，求1-c ab 1++1-a bc 1++1-b ca 1+的值. 1、一元二次方程、一元二次不等式与二次函数的关系2、一元二次不等式的解法步调一元二次不等式()00022≠<++>++a c bx ax c bx ax 或的解集：设相应的一元二次方程()002≠=++a c bx ax 的两根为2121x x x x ≤且、，ac b 42-=∆，则不等式的解的各种情况如下表：0>∆ 0=∆ 0<∆二次函数 c bx ax y ++=2（0>a ）的图象c bx ax y ++=2c bx ax y ++=2 c bx ax y ++=2一元二次方程()的根002>=++a c bx ax 有两相异实根)(,2121x x x x < 有两相等实根 ab x x 221-== 无实根的解集)0(02>>++ac bx ax {}21x x x x x ><或 ⎭⎬⎫⎩⎨⎧-≠a b x x 2 R的解集)0(02><++a c bx ax {}21x x x x << ∅ ∅例1解不等式：（1）x2＋2x －3≤0；（2）x －x2＋6＜0；（3）4x2＋4x ＋1≥0；（4）x2－6x ＋9≤0；（5）－4＋x －x2＜0．例2 解关于x 的不等式0)1(2>---a a x x解：原不等式可以化为：0))(1(>--+a x a x若)1(-->a a 即21>a 则a x >或a x -<1 若)1(--=a a 即21=a 则0)21(2>-x R x x ∈≠,21 若)1(--<a a 即21<a 则a x <或a x ->1 例3已知不等式20(0)ax bx c a ++<≠的解是2,3x x <>或求不等式20bx ax c ++>的解．解：由不等式20(0)ax bx c a ++<≠的解为2,3x x <>或，可知0a <，且方程20ax bx c ++=的两根分别为2和3，∴5,6b c a a-==，即 5,6b c a a=-=．由于0a <，所以不等式20bx ax c ++>可变成20b c x x a a++< ，即－2560,x x ++<整理，得所以，不等式20bx ax c +->的解是x ＜－1，或x ＞65．说明：本例操纵了方程与不等式之间的相互关系来处理问题．练习1．解下列不等式：（1）3x2－x －4＞0；（2）x2－x －12≤0；（3）x2＋3x －4＞0；（4）16－8x ＋x2≤0．2.解关于x 的不等式x2＋2x ＋1－a2≤0（a 为常数）．作业：1.若0<a<1,则不等式(x －a)(x －a1)<0的解是 ( )A.a<x<a 1B.a1<x<a C.x>a 1或x<a D.x<a1或x>a 2.如果方程ax2＋bx ＋b ＝0中，a ＜0，它的两根x1，x2知足x1＜x2，那末不等式ax2＋bx ＋b ＜0的解是______.3．解下列不等式：（1）3x2－2x ＋1＜0；（2）3x2－4＜0；（3）2x －x2≥－1；（4）4－x2≤0．(5)4+3x －2x2≥0;(6)9x2－12x>－4;4．解关于x 的不等式x2－(1＋a)x ＋a ＜0（a 为常数）．5．关于x 的不等式02<++c bx ax 的解为122x x <->-或求关于x 的不等式02>+-c bx ax 的解．4.三角形的“四心”1.“四心”的概念及性质心坎：性质：外心：性质：重心：性质：垂心：例 1 求证：三角形的三条中线交于一点，且被该交点分成的两段长度之比为2：1.已知D、E 、F 分别为△ABC 三边BC 、CA 、AB 的中点，求证AD 、BE 、CF 交于一点，且都被该点分成2： 1.证明保持DE ，设AD 、BE 交于点G ，D 、E 分别为BC 、AE 的中点，则DE//AB ，且12DE AB ， GDE ∽GAB ，且相似比为1：2，2,2AG GD BG GE . 设AD 、CF 交于点'G ，同理可得，'2','2'.AG G D CG G F则G 与'G 重合， AD 、BE 、CF 交于一点，且都被该点分成2:1.例2 已知ABC 的三边长分别为,,BC a AC b AB c ，I 为ABC 的心坎，且I 在ABC 的边BC AC AB 、、上的射影分别为D E F 、、，求证：2b c a AE AF . 证明作ABC 的内切圆，则D E F 、、分别为内切圆在三边上的切点，,AE AF 为圆的从同一点作的两条切线，AE AF ，同理，BD=BF ，CD=CE. 即2b c a AE AF . 例 3 若三角形的心坎与重心为同一点，求证：这个三角形为正三角形.已知O 为三角形ABC 的重心和心坎.求证三角形ABC 为等边三角形.证明如图，连AO 并延长交BC 于 D. O 为三角形的心坎，故AD 平分BAC ， AB BD AC DC（角平分线性质定理） O 为三角形的重心，D 为BC 的中点，即BD=DC. 1AB AC ，即AB AC . 同理可得，AB=BC. ABC 为等边三角形.例4 求证：三角形的三条高交于一点.已知ABC 中，,AD BC D BE AC E 于于，AD 与BE 交于H 点.求证CH AB . 证明以CH 为直径作圆，D E 、在以CH 为直径的圆上，FCB DEH .同理，E 、D 在以AB 为直径的圆上，可得BED BAD .BCH BAD ，又ABD 与CBF 有公共角B ，90o CFB ADB。

初高中数学衔接教材6

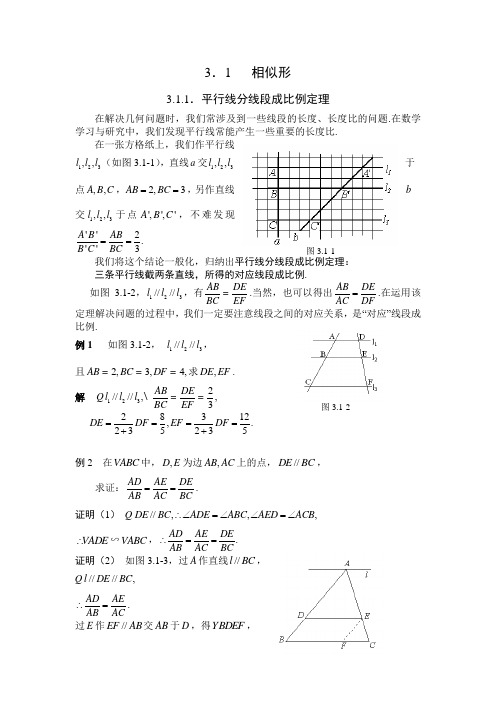
3．1 相似形3.1.1．平行线分线段成比例定理在解决几何问题时，我们常涉及到一些线段的长度、长度比的问题.在数学学习与研究中，我们发现平行线常能产生一些重要的长度比.在一张方格纸上，我们作平行线123,,l l l （如图3.1-1），直线a 交123,,l l l 于点,,A B C ，2,3AB BC ==，另作直线b交123,,l l l 于点',','A B C ，不难发现''2.''3A B A B B C B C == 我们将这个结论一般化，归纳出平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例.如图 3.1-2，123////l l l ，有AB DE BC EF =.当然，也可以得出AB DEAC DF=.在运用该定理解决问题的过程中，我们一定要注意线段之间的对应关系，是“对应”线段成比例.例1 如图3.1-2， 123////l l l ，且2,3,4,AB BC DF ===求,DE EF . 解 1232////,,3A B D E l l l B C E F \==Q 28312,.235235DE DF EF DF ====++例2 在ABC 中，,D E 为边,AB AC 上的点，//DE BC ，求证：AD AE DEAB AC BC==. 证明（1） //,,,DE BC ADE ABC AED ACB ∴∠=∠∠=∠ADE ∴ ∽ABC ，.AD AE DEAB AC BC∴== 证明（2）如图3.1-3，过A 作直线//l BC ，////,l DE BC AD AEAB AC∴=. 过E 作//EF AB 交AB 于D ，得BDEF ，图3.1-1图3.1-2因而.DE BF =//,.AE BF DE EF AB AC BC BC∴== .AD AE DE AB AC BC ∴==从上例可以得出如下结论：平行于三角形的一边的直线截其它两边（或两边的延长线），所得的对应线段成比例.平行于三角形的一边，并且和其它两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例.例3 已知ABC ，D 在AC 上，:2:1AD DC =，能否在AB 上找到一点E ，使得线段EC 的中点在BD 上. 解假设能找到，如图3.1-4，设EC 交BD 于F ，则F 为EC 的中点，作//EG AC 交BD 于G .//,EG AC EF FC = ，∴EGF CDF ≅ ，且EG DC =，1//,2EG AD BEG BAD ∴ ，且1,2B E E G B A A D == E ∴为AB 的中点. 可见，当E 为AB 的中点时，EC 的中点在BD 上.我们在探索一些存在性问题时，常常先假设其存在，再解之，有解则存在，无解或矛盾则不存在.例4 在ABC V 中，AD 为BAC Ð的平分线，求证：AB BDAC DC=. 证明过C 作CE //AD ，交BA 延长线于E ，//,.BA BDAD CE AE DC\=QQ AD 平分,,BAC BAD DAC 衆?由//AD CE 知,,BADE DAC ACE ?行=,,EACE AE AC \??即AB BDAC DC\=. 例4的结论也称为角平分线性质定理，可叙述为角平分线分对边成比例（等于该角的两边之比）.练习11．如图 3.1-6，123////l l l，下列比例式正确的是图3.1-3 图3.1-4 图3.1-5（）A ．ADCE DF BC = B ．ADBCBE AF = C ．CEAD DF BC = D.AFBEDF CE= 2．如图 3.1-7，//,//,DE BC EF AB 5,AD cm =3,2,DB cm FC cm ==求BF .3．如图，在ABC V 中，AD 是角BAC 的平分线，AB =5cm,AC =4cm,BC =7cm,求BD 的长.4．如图，在ABC V 中，BAC Ð的外角平分线AD 交BC 的延长线于点D ，求证：A B B DA C D C =.5．如图，在ABC V 的边AB 、AC 上分别取D 、E 两点，使BD =CE ，DE 延长线交BC 的延长线于F .求证：DF ACEF AB=.3.1．2．相似形我们学过三角形相似的判定方法，想一想，有哪些方法可以判定两个三角形相似？有哪些方法可以判定两个直角三角形相似？例5 如图3.1-11，四边形ABCD 的对角线相交于点O ，BAC CDB ? ，求证：图3.1-6图3.1-7 图3.1-8 图3.1-9 图3.1-10DAC CBD ? .证明在OAB V 与ODC V 中，,,AOB DOC OAB ODC ?行=\OAB V ∽ODC V ， OA OB OD OC \=，即OA OD OB OC =. 又OAD V 与OBC V 中，AOD BOC ? ，\OAD V ∽OBC V ， \DAC CBD ? .例6 如图3.1-12,在直角三角形ABC 中，BAC Ð为直角，AD BC D ^于.求证：（1）2AB BD BC = ，2AC CD CB = ；（2）2AD BD CD =证明（1）在Rt BAC V 与Rt BDA V 中，B B ? ，BAC \V ∽BDA V ，2,.BA BCAB BD BC BD BA \== 即同理可证得2AC CD CB = .（2）在Rt ABD V 与Rt CAD V 中，90o CCADBAD ?-? ，Rt ABD \V ∽Rt CAD V ，2,.AD DCAD BD DC BD AD\== 即我们把这个例题的结论称为射影定理，该定理对直角三角形的运算很有用.例7 在ABC V 中，,,AD BC D DE AB E DF AC F ^^^于于于，求证：A E AB A F AC ? . 证明 AD B C ^Q ，\ADB V 为直角三角形，又DE AB ^，由射影定理，知2AD AE AB = . 同理可得2AD AF AC = .AE AB AF AC \? . 例8 如图3.1-14，在ABC V 中，D 为边BC 的中点，E 为边AC 上的任意一点，BE 交AD 于点O .某学生在研究这一问题时，发现了如下的事实：图3.1-11图3.1-12图3.1-13（1）当11211AE AC ==+时，有22321AO AD ==+.（如图3.1-14a ）（2）当11312AE AC ==+时，有22422AO AD ==+.（如图3.1-14b ）（3）当11413AE AC ==+时，有22523AO AD ==+.（如图3.1-14c ）在图3.1-14d 中，当11AE AC n=+时，参照上述研究结论，请你猜想用n 表示AOAD的一般结论，并给出证明（其中n 为正整数）. 解：依题意可以猜想：当11AE AC n =+时，有22AO AD n=+成立. 证明过点D 作DF //BE 交AC 于点F ，Q D 是BC 的中点，\F 是EC 的中点，由11AE AC n =+可知1AE EC n =，22,.2AE AE EF n AF n\==+. 2.2AO AE AD AF n\==+ 想一想，图3.1-14d 中，若1AO AD n =，则?AEAC= 本题中采用了从特殊到一般的思维方法.我们常从一些具体的问题中发现一些规律，进而作出一般性的猜想，然后加以证明或否定 .数学的发展史就是不断探索的历史.练习21．如图3.1-15，D 是ABC V 的边AB 上的一点，过D 点作DE //BC 交AC 于E .已知AD ：DB =2：3，则:A D E B C D ES S V 四边形等于（）图3.1-14A ．2:3B ．4:9C ．4:5D ．4:212．若一个梯形的中位线长为15，一条对角线把中位线分成两条线段.这两条线段的比是3:2，则梯形的上、下底长分别是__________.3．已知：ABC V 的三边长分别是3，4，5，与其相似的'''A B C V 的最大边长是15，求'''A B C 的面积'''A B C S V .4．已知：如图3.1-16，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点.（1）请判断四边形EFGH 是什么四边形，试说明理由；（2）若四边形ABCD 是平行四边形，对角线AC 、BD 满足什么条件时，EFGH 是菱形？是正方形？5．如图3.1-17,点C 、D 在线段AB 上，PCD V 是等边三角形，（1）当AC 、CD 、DB 满足怎样的关系时，ACP V ∽PDB V ？（2）当ACP V ∽PDB V 时，求APB Ð的度数.习题3.1 A 组1．如图3.1-18，ABC V 中，AD =DF =FB ，AE =EG =GC ，FG =4，则（）A ．DE =1，BC =7B ．DE =2，BC =6 C ．DE =3，BC =5D ．DE =2，BC =82．如图3.1-19，BD 、CE 是ABC V 的中线，P 、Q 分别是BD 、CE 的中点，则:PQ BC 等于（） A ．1：3 B ．1：4 C ．1：5 D ．1：6图3.1-15 图3.1-16 图3.1-17 图3.1-183．如图3.1-20，ABCD Y 中，E 是A B 延长线上一点，DE 交BC 于点F ，已知BE ：AB =2：3，4BEF S =V ，求CDF S V .4．如图3.1-21，在矩形ABCD 中，E 是CD 的中点，BE AC ^交AC 于F ，过F 作FG //AB 交AE 于G ，求证：2AG AF FC = .B 组1．如图3.1-22，已知ABC V 中，AE ：EB =1：3，BD ：DC =2：1，AD 与CE 相交于F ，则EF AFFC FD+的值为（） A ．12 B ．1 C ．32 D ．22．如图3.1-23，已知ABC V 周长为1，连结ABC V 三边的中点构成第二个三角形，再连结第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（） A ．12002 B ．12003 C ．200212 D ．2003123．如图3.1-24，已知M 为ABCD Y 的边AB 的中点，CM 交BD 于点E ，则图中阴影部分的面积与ABCD Y 面积的比是（） A ．13 B ．14 C ．16 D ．5124．如图3.1-25，梯形ABCD 中，AD //BC ，EF 经过梯形对角线的交点O ，且EF //AD .图3.1-19 图3.1-20图3.1-22 图3.1-23 图3.1-24 图3.1-21（1）求证：OE =OF ；（2）求OE OEAD BC+的值；（3）求证：112AD BC EF+=.C 组1．如图3.1-26，ABC V 中，P 是边AB 上一点，连结CP . （1）要使A C P V ∽ABC V ，还要补充的一个条件是____________.（2）若ACP V ∽ABC V ，且:2:A PP B =，则:B C P C =_____.2．如图 3.1-27，点E 是四边形ABCD 的对角线BD 上一点，且B AC BD C D A ?? . （1）求证：BE AD CD AE ? ；（2）根据图形的特点，猜想BCDE可能等于那两条线段的比（只须写出图中已有线段的一组比即可）？并证明你的猜想.3．如图3.1-28，在Rt ABC V 中，AB =AC ，90o A?，点D 为BC 上任一点，DF AB ^于F ，DE AC ^于E ，M 为BC 的中点，试判断MEF V 是什么形状的三角形，并证明你的结论.4．如图3.1-29a ，,,AB BD CD BD ^^垂足分别为B 、D ，AD 和BC 相交于E ，EF BD ^于F ，我们可以证明111AB CD EF+=成立. 图3.1-25图3.1-26 图3.1-27 图3.1-28若将图3.1-29a 中的垂直改为斜交，如图3.1-29 b ，//,AB CD AD BC 、相交于E ，EF//AB 交BD 于F ，则：（1） 111AB CD EF +=还成立吗？如果成立，请给出证明；如果不成立，请说明理由；（2）请找出,ABD BCD S S V V 和EBD S V 之间的关系，并给出证明.第二讲三角形与圆3.1 相似形练习11．D2．设510,,,283DE AD x BF x x BC AB x ==∴==+ ，即103BF =. 3．535,.49AB BD BD cm AC DC ==∴=4．作//CF AB 交AD 于F ，则A B B DC FD C=，又A F C F A EF A ∠=∠=∠得,AC CF =AB BDAC DC∴=. 5．作//EG AB 交BC 于G ，,,EG CECEG CAB AB AC∴= 即,AC CE DB AB EG EG ==DF ACEF AB∴=.练习2 1．C2．12，183．2'''115346,()654.25ABC A B C S S =⨯⨯=∴=⨯= 4．（1）因为1////,2EH BD FG 所以EFGH 是平行四边形；（2）当A C B D =时，EFGH 为菱形；当,AC BD AC BD =⊥时，EFGH 为正方形.5．（1）当2CD AC BD =⋅时，ACP PDB ；（2）120oAPB ∠=.图3.1-29习题3.1 A 组1．B 2.B 3.9CDF S =4．BF 为直角三角形ABC 斜边上的高，2BF AF FC =⋅，又可证,AG BF =2AG AF FC ∴=⋅.B 组1．C 2.C 3.A4．（1）//,,EO AE DE OF AD BC EO OF BC AB DC BC ∴==== .（2） 1.OE OE AE BEAD BC AB AB +=+=（3）由（2）知1112.AD BC OE EF+== C 组1.(1)2AC AP AB =⋅或ACP B ∠=∠.(2):BC PC =2．（1）先证AEB ADC ，可得BE AE CD AD =；（2）,BC AB ADADE ACB DE AE AC∴== . 3．连AD 交EF 于O ，连OM ，ABC 为等腰直角三角形，且AEDF 为矩形，OM ∴为Rt AMD 斜边的中线，11,22OM AD EF ==MEF ∴ 为直角三角形.又可证BMF AME ≅ ，得MF ME =，故MEF 为等腰直角三角形.4．（1）成立，1111,.EF EF FD BF AB CD BD BD AB CD EF +=+=∴+= （2）111ABD BCD EBDS S S += ，证略.。

初高中数学衔接教材已整理

初高中数学衔接教材已整理近年来，我国教育体制改革不断深化，对于初高中数学教学也提出了更高的要求。

初高中数学衔接教材的整理成为了一个重要的课题。

本文将从初高中数学教学的需求出发，探讨初高中数学衔接教材的整理方法和教学实践。

一、初高中数学教学的需求随着初高中的衔接程度越来越紧密，初中数学教学要求学生打下坚实的数学基础，为高中的学习打下良好的基础。

因此，初高中数学教学需要有一套科学合理的教材体系，使学生在初中阶段就能够逐步接触和掌握高中数学的知识和方法。

二、初高中数学衔接教材的整理方法初高中数学衔接教材的整理方法有多种，下面将介绍其中两种常用的方法。

1. 由梳理知识点出发初高中数学教材的整理可以从梳理知识点的角度出发。

可以将初中数学和高中数学的知识点进行对比，将初中的知识点补充和扩展到高中的要求。

同时，还可以将一些高中中的难点知识通过适当的方式向初中生进行引导，提前进行铺垫，以便他们更好地适应高中数学的学习。

2. 由编写教材章节出发另一种整理初高中数学衔接教材的方法是从编写教材章节的角度出发。

可以将每个章节的核心知识点进行归纳总结，并配以一定的习题和例题，以帮助学生巩固和掌握知识。

同时，还要注意章节之间的衔接，使学生在学习过程中能够理解数学知识的发展脉络，形成良好的数学思维方式和解题习惯。

三、初高中数学衔接教材的教学实践初高中数学衔接教材的整理还需要通过教学实践来验证和完善。

可以通过以下几个方面来实践教学：1. 设计合理的课堂教学环节在教学中，可以针对初高中数学衔接的难点和疑惑，设计一些小组合作、讨论和展示等形式的环节，激发学生的学习兴趣和主动性。

通过合作学习的方式，使学生之间相互交流、互相启发，更好地理解和掌握数学知识。

2. 提供多样化的学习资源在教学过程中，可以利用多媒体、网络等现代化教育手段，为学生提供多样化的学习资源。

可以通过教育软件、教学视频等方式，让学生在课后进行更加深入的学习和巩固。

3. 注重学生的实际应用能力培养在教学中，要注重引导学生将所学的数学知识应用到实际问题中去，培养学生的实际应用能力。

初高中数学衔接教材(已整理精品)

初高中数学衔接教材之羊若含玉创作我们在初中已经学习过了下列一些乘法公式：（1）平方差公式 22()()a b a b a b +-=-；（2）完全平方公式222()2a b a ab b ±=±+．我们还可以通过证明得到下列一些乘法公式：（1）立方和公式2233()()a b a ab b a b +-+=+；（2）立方差公式2233()()a b a ab b a b -++=-；（3）三数和平方公式2222()2()a b c a b c ab bc ac ++=+++++；（4）两数和立方公式 33223()33a b a a b ab b +=+++；（5）两数差立方公式 33223()33a b a a b ab b -=-+-．对上面列出的五个公式，有兴趣的同学可以自己去证明．例1 盘算：22(1)(1)(1)(1)x x x x x x +--+++．解法一：原式=2222(1)(1)x x x ⎡⎤-+-⎣⎦=242(1)(1)x x x -++=61x -．解法二：原式=22(1)(1)(1)(1)x x x x x x +-+-++=33(1)(1)x x +-=61x -．例2 已知4a b c ++=，4ab bc ac ++=，求222a b c ++的值．解：2222()2()8a b c a b c ab bc ac ++=++-++=．练习1．填空：（1）221111()9423a b b a -=+（）；（2）(4m +22)164(m m =++)；(3 ) 2222(2)4(a b c a b c +-=+++)．2．选择题：（1）若212x mx k ++是一个完全平方法，则k 等于（）（A ）2m （B ）214m （C ）213m （D ）2116m （2）不管a ，b 为何实数，22248a b a b +--+的值（）（A ）总是正数（B ）总是负数（C ）可以是零（D ）可以是正数也可以是负数2．因式分化因式分化的主要办法有：十字相乘法、提取公因式法、公式法、分组分化法，别的还应懂得求根法及待定系数法．1．十字相乘法例1 分化因式：（1）x2－3x ＋2；（2）x2＋4x －12；（3）22()x a b xy aby -++；（4）1xy x y -+-．解：（1）如图1．1－1，将二次项x2分化成图中的两个x 的积，再将常数项2分化成－1与－2的乘积，而图中的对角线上的两个数乘积的和为－3x ，就是x2－3x ＋2中的一次项，所以，有x2－3x ＋2＝(x －1)(x －2)．说明：往后在分化与本例相似的二次三项式时，可以直接将图1．1－1中的两个x 用1来暗示（如图1．1－2所示）．（2）由图1．1－3，得x2＋4x －12＝(x －2)(x ＋6)．（3）由图1．1－4，得22()x a b xy aby -++＝()()x ay x by -- （4）1xy x y -+-＝xy ＋(x －y)－1 ＝(x －1) (y+1) （如图1．1－5所示）．教室演习一、填空题：1、把下列各式分化因式：（1）=-+652x x __________________________________________________.（2）=+-652x x __________________________________________________.（3）=++652x x __________________________________________________.（4）=--652x x __________________________________________________.（5）()=++-a x a x 12__________________________________________________.（6）=+-18112x x __________________________________________________.（7）=++2762x x __________________________________________________.（8）－1 －2 x x 图1．1－1 －1 －2 1 1 图1．1－2 －2 6 11 图1．1－3 －ay －by x x 图1．1－4 －11x y 图1．1－5=+-91242m m __________________________________________________.（9）=-+2675x x __________________________________________________.（10）=-+22612y xy x __________________________________________________. 2、()() 3 42++=+-x x x x3、若()()422-+=++x x b ax x 则 =a ， =b .二、选择题：（每小题四个答案中只有一个是正确的）1、在多项式（1）672++x x （2）342++x x （3）862++x x （4）1072++x x（5）44152++x x 中，有相同因式的是（）A 、只有（1）（2）B 、只有（3）（4）C 、只有（3）（5）D 、（1）和（2）；（3）和（4）；（3）和（5）2、分化因式22338b ab a -+得（）A 、()()3 11-+a aB 、()()b a b a 3 11-+C 、()()b a b a 3 11--D 、()()b a b a 3 11+- 3、()()2082-+++b a b a 分化因式得（）A 、()()2 10-+++b a b aB 、()()4 5-+++b a b aC 、()()10 2-+++b a b aD 、()()5 4-+++b a b a4、若多项式a x x +-32可分化为()()b x x --5，则a 、b 的值是（）A 、10=a ，2=bB 、10=a ，2-=bC 、10-=a ，2-=bD 、10-=a ，2=b5、若()()b x a x mx x ++=-+ 102其中a 、b 为整数，则m 的值为（）A 、3或9B 、3±C 、9±D 、3±或9±三、把下列各式分化因式1、()()3211262+---p q q p2、22365ab b a a +-3、6422--y y4、8224--b b2．提取公因式法例2 分化因式：（1）()()b a b a -+-552 （2）32933x x x +++解：（1）．()()b a b a -+-552=)1)(5(--a b a（2）32933x x x +++=32(3)(39)x x x +++=2(3)3(3)x x x +++=2(3)(3)x x ++．或32933x x x +++＝32(331)8x x x ++++＝3(1)8x ++＝33(1)2x ++＝22[(1)2][(1)(1)22]x x x +++-+⨯+ ＝2(3)(3)x x ++教室演习：一、填空题：1、多项式xyz xy y x 42622+-中各项的公因式是_______________.2、()()()•-=-+-y x x y n y x m __________________.3、()()()•-=-+-222y x x y n y x m ____________________.4、()()()•--=-++--z y x x z y n z y x m _____________________.5、()()•--=++---z y x z y x z y x m ______________________.6、523623913x b a x ab --分化因式得_____________________.7．盘算99992+=二、断定题：（正确的打上“√”，错误的打上“×” ）1、()b a ab ab b a -=-24222………………………………………………………… （）2、()b a m m bm am +=++…………………………………………………………… （）3、()5231563223-+-=-+-x x x x x x …………………………………………… （）4、()111+=+--x x x x n n n ……………………………………………………………… （）3：公式法例3分化因式：（1）164+-a （2）()()2223y x y x --+解：(1)164+-a =)2)(2)(4()4)(4()(4222222a a a a a a -++=-+=-(2)()()2223y x y x --+=)32)(4()23)(23(y x y x y x y x y x y x ++=+-+-++ 教室演习一、222b ab a +-，22b a -，33b a -的公因式是______________________________.二、断定题：（正确的打上“√”，错误的打上“×” ）1、()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=-⎪⎭⎫ ⎝⎛=-1.032 1.0321.03201.094222x x x x …………………………（）2、()()()()b a b a b a b a 43 4343892222-+=-=-………………………………… （）3、()()b a b a b a 45 4516252-+=-………………………………………………… （）4、()()()y x y x y x y x -+-=--=-- 2222………………………………………… （）5、()()()c b a c b a c b a +-++=+- 22……………………………………………… （）五、把下列各式分化1、()()229n m n m ++--2、3132-x3、()22244+--x x4、1224+-x x4．分组分化法例4 （1）x y xy x 332-+- （2）222456x xy y x y +--+-．（2）222456x xy y x y +--+-=222(4)56x y x y y +--+-=22(4)(2)(3)x y x y y +----=(22)(3)x y x y -++-．或222456x xy y x y +--+-=22(2)(45)6x xy y x y +----=(2)()(45)6x y x y x y -+---=(22)(3)x y x y -++-．教室演习：用分组分化法分化多项式（1）by ax b a y x 222222++-+-（2）91264422++-+-b a b ab a5．关于x 的二次三项式ax2+bx+c(a≠0)的因式分化．若关于x 的方程20(0)ax bx c a ++=≠的两个实数根是1x 、2x ，则二次三项式2(0)ax bx c a ++≠就可分化为12()()a x x x x --.例5 把下列关于x 的二次多项式分化因式：（1）221x x +-；（2）2244x xy y +-．解：（1）令221x x +-=0，则解得11x =-21x =-，∴221x x +-=(1(1x x ⎡⎤⎡⎤----⎣⎦⎣⎦=(11x x ++．（2）令2244x xy y +-=0，则解得1(2x y =-+，1(2x y =--， ∴2244x xy y +-=[2(1][2(1]x y x y ++．练习1．选择题：多项式22215x xy y --的一个因式为（）（A ）25x y - （B ）3x y - （C ）3x y + （D ）5x y -2．分化因式：（1）x2＋6x ＋8；（2）8a3－b3；（3）x2－2x －1；（4）4(1)(2)x y y y x -++-．习题1．21．分化因式：（1） 31a +；（2）424139x x -+；（3）22222b c ab ac bc ++++；（4）2235294x xy y x y +-++-．2．在实数规模内因式分化：（1）253x x -+ ；（2）23x --；（3）2234x xy y +-；（4）222(2)7(2)12x x x x ---+． 3．ABC ∆三边a ，b ，c 知足222a b c ab bc ca ++=++，试剖断ABC ∆的形状．4．分化因式：x2＋x －(a2－a)．5. （测验测验题）已知abc=1，a+b+c=2，a²+b²+c²=，求1-c ab 1++1-a bc 1++1-b ca 1+的值. 1、一元二次方程、一元二次不等式与二次函数的关系2、一元二次不等式的解法步调一元二次不等式()00022≠<++>++a c bx ax c bx ax 或的解集：设相应的一元二次方程()002≠=++a c bx ax 的两根为2121x x x x ≤且、，ac b 42-=∆，则不等式的解的各类情况如下表： 0>∆ 0=∆ 0<∆二次函数 c bx ax y ++=2（0>a ）的图象c bx ax y ++=2c bx ax y ++=2 c bx ax y ++=2一元二次方程()的根002>=++a c bx ax 有两相异实根)(,2121x x x x < 有两相等实根 a b x x 221-== 无实根的解集)0(02>>++a c bx ax {}21x x x x x ><或 ⎭⎬⎫⎩⎨⎧-≠a b x x 2 R 的解集)0(02><++a c bx ax {}21x x x x << ∅ ∅例1（1）x2＋2x －3≤0；（2）x －x2＋6＜0；（3）4x2＋4x ＋1≥0；（4）x2－6x ＋9≤0；（5）－4＋x －x2＜0．例2 解关于x 的不等式0)1(2>---a a x x解：原不等式可以化为：0))(1(>--+a x a x若)1(-->a a 即21>a 则a x >或a x -<1 若)1(--=a a 即21=a 则0)21(2>-x R x x ∈≠,21 若)1(--<a a 即21<a 则a x <或a x ->1 例3已知不等式20(0)ax bx c a ++<≠的解是2,3x x <>或求不等式20bx ax c ++>的解．解：由不等式20(0)ax bx c a ++<≠的解为2,3x x <>或，可知0a <，且方程20ax bx c ++=的两根分离为2和3， ∴5,6b c a a -==，即 5,6b ca a =-=．由于0a <，所以不等式20bx ax c ++>可变成20b cx x a a ++< ，即－2560,x x ++<整理，得所以，不等式20bx ax c +->的解是x ＜－1，或x ＞65 ．说明：本例应用了方程与不等式之间的相互关系来解决问题．练习1．解下列不等式：（1）3x2－x －4＞0；（2）x2－x －12≤0；（3）x2＋3x －4＞0；（4）16－8x ＋x2≤0．2.解关于x 的不等式x2＋2x ＋1－a2≤0（a 为常数）．作业：1.若0<a<1,则不等式(x －a)(x －a 1)<0的解是 ( )A.a<x<a 1B.a 1<x<aC.x>a 1或x<a D.x<a 1或x>a2.如果方程ax2＋bx ＋b ＝0中，a ＜0，它的两根x1，x2知足x1＜x2，那么不等式ax2＋bx ＋b ＜0的解是______.3．解下列不等式：（1）3x2－2x ＋1＜0；（2）3x2－4＜0；（3）2x －x2≥－1；（4）4－x2≤0．(5)4+3x －2x2≥0;(6)9x2－12x>－4;4．解关于x 的不等式x2－(1＋a)x ＋a ＜0（a 为常数）．5．关于x 的不等式02<++c bx ax 的解为122x x <->-或求关于x 的不等式02>+-c bx ax 的解．4.三角形的“四心”1.“四心”的概念及性质心坎：性质：外心：性质：重心：性质：垂心：例1 求证：三角形的三条中线交于一点，且被该交点分成的两段长度之比为2：1.已知D 、E 、F 分离为△ABC 三边BC 、CA 、AB 的中点，求证AD 、BE 、CF 交于一点，且都被该点分成2：1.证明贯穿连接DE ，设AD 、BE 交于点G ，D 、E 分离为BC 、AE 的中点，则DE//AB ，且12DE AB ， GDE ∽GAB ，且相似比为1：2，2,2AG GD BG GE . 设AD 、CF 交于点'G ，同理可得，'2','2'.AG G D CG G F 则G 与'G 重合， AD 、BE 、CF 交于一点，且都被该点分成2:1.例 2 已知ABC 的三边长分离为,,BC a AC b AB c ，I 为ABC 的心坎，且I 在ABC 的边BC AC AB 、、上的射影分离为D E F 、、，求证：2bc a AE AF . 证明作ABC 的内切圆，则D E F 、、分离为内切圆在三边上的切点，,AE AF 为圆的从同一点作的两条切线，AE AF ，同理，BD=BF ，CD=CE. 即2b c a AE AF . 例3 若三角形的心坎与重心为同一点，求证：这个三角形为正三角形. 已知O 为三角形ABC 的重心和心坎.求证三角形ABC 为等边三角形.证明如图，连AO 并延长交BC 于 D. O 为三角形的心坎，故AD 平分BAC ， ABBD AC DC （角平分线性质定理）O 为三角形的重心，D 为BC 的中点，即BD=DC. 1AB AC ，即AB AC .同理可得，AB=BC. ABC 为等边三角形.例4 求证：三角形的三条高交于一点. 已知ABC 中，,AD BC D BE AC E 于于，AD 与BE 交于H 点.求证CH AB .证明以CH 为直径作圆， D E 、在以CH 为直径的圆上， FCB DEH .同理，E 、D 在以AB 为直径的圆上，可得BED BAD . BCH BAD ，又ABD 与CBF 有公共角B ，90o CFB ADB。

初高中数学衔接校本教材(Word版)

《初高中数学衔接教材》序言童永奇高一新生，你们好，祝贺大家考入临潼区马额中学！进入我校，同学们必须努力学好《初高中数学衔接教材》，理由如下：一方面，由于我校是普通农村高中学校，生源质量相对较差；另一方面，由于高中数学是初中数学的延伸与拓展，初中我们学到的知识、方法在高中会经常使用。

既然学习《初高中数学衔接教材》如此重要，那么我们应该如何学习呢提几点建议：一、“信心”是源泉。

人缺乏信心，就丧失了驱动力，终将一事无成。

二、“恒心”是保障。

人缺乏恒心，将“三天打鱼，两天晒网”。

:三、“巧心”是支柱。

人无巧心，就缺乏灵气和创造力。

最后，衷心祝愿同学们在《初高中数学衔接教材》的学习中获得成功，请将那么成功的经验及时告诉我们，以便让更多的朋友分享你们成功的喜悦！}$临潼区马额中学高一数学校本教材童永奇结合我校学生的实际情况——基础知识较差，能力较差，没有掌握较好的学习方法，特设计适合我校高一学生使用的校本教材。

主要包括以下两个内容：一是《怎样学好数学》，二是《初高中数学衔接》。

怎样学好数学。

A.要学好数学，就应该了解数学本身具有的三大特点。

（一）抽象性：数学的抽象性是无条件的，它的概念一经产生和定义之后，就稳定下来并且被看作是已知的，它们与现实的比较不是数学本身，而是它的应用问题。

（二）严谨性：由于数学的严谨性，人们往往认为数学是一种“冷而严肃的美”。

罗素说：“数学，如果正确地看它，不但拥有真理，而且也是具有至高的美，正像雕刻的美，是一种冷而严肃的美，这种美不是投合我们天性的微弱的方面，这种美没有绘画或音乐的那些华丽的装饰，它可以纯净到崇高的地步，能够达到严格的只有最伟大的艺术才能显示的那种完美的境地。

”（三）应用的广泛性：在任何一个领域，只要能从数学的角度提出问题，数学就能给出与所提问题的精确度相符合的答案，数学的这种威力恰恰是来源于它的抽象性。

B.要学好数学，就应该重视数学思想方法的学习。

数学思想方法的学习是一个潜移默化的过程，是在多次领悟、反复应用的基础上形成的，所以一道题做完后，就应该进行反思，回味解题中所使用的思想方法。

职业中学数学初高中衔接教材(共4课时)

职业中学数学初高中衔接教材（共4课时）第1课时因式分解(1)课标导航：1.熟悉常见的乘法公式,会用乘法公式分解因式;2.了解方程的根与对应的代数式的因式分解之间的关系,体会因式分解的求根法和待定系数法 . 课堂实录：1.分解因式的方法主要有: 提取公因式法、公式法、十字相乘法、分组分解法、解求根法及待定系数法.2.常见的乘法公式有:(1)平方差公式 :22a b -= ；(2)立方差公式: 33a b -= ;(3)立方和公式: 33a b += ;(4)完全平方公式:2()a b ±= ;(5) 完全立方公式:3()a b ±= .思维点击：【例1】分解因式:338x y -【例2】把下列关于x 的二次多项式分解因式：(1)221x x +- (2)2244x xy y +-【例3】解方程: (1) 61x = (2) 3223830x x x +-+=随堂训练：1.分解下列因式(1)223x x --(2) 2()2x y x y +++-(3) 26m -(4) 3223272791a a b ab b -+--2.解列三次方程:(1)329330x x x +++=(2) (1)(1)(2)240x x x x -⋅⋅++-=课后作业:1.分解下列因式:(1)253x x -+(2) 23x --(3)2234x xy y +-(4)222(2)7(2)12x x x x ---+(5)22244x z xy y --+(6)31a +(7)424139x x -+(8)2235294x xy y x y +-++-．2.解下列方程:(1)320x x ++=; (2)4310x x x --+=3. 已知331,3x y a b x y xy +=+=++且,求333a b ab ++的值.4.化简:3343341111()()[(1)()]a a a a a a a a+-÷++-5. 化简333211111x x x x x x x x -+-+-+++-,并求当28x =时,此式的值.第2课时因式分解(2)课标导航：1.掌握十字相乘法、分组分解法;2.能根据问题,灵活运用各种方法分解因式.课堂实录：1.十字相乘法:设ax 2＋bx ＋c ＝(cx ＋d)(ex ＋f)，其中a ≠0．∵(cx ＋d)(ex ＋f)＝cex 2＋dex ＋cfx ＋df ＝cex 2＋(de ＋cf)x ＋df ，∴a ＝ce,b ＝de ＋cf,c ＝df;可以将以上三式表示为思维点击：【例1】用十字相乘法分解下列各因式:(1) 2832--x x (2) 212176a a -+-(3) 2()2x y x y +++-【例2】分解因式(1) x y y x 2222--+ (2) x 2＋x －(a 2－a)c ed f(3) 22222a b ac bc ab ++++【例3】分解因式:222456x xy y x y +--+-【例4】已知23a b +=,求2224443a a b b ab ++++-的值.随堂训练：分解因式:(1)2310b b +-= ; (2)268y y -+= ；(3)256x x --= ;(4)2712a a -+-= ；(5)33bc bd += ;(6)2216x x+-= ;(7)()(3)2x y x y ---+= ;(8)22(33)(34)8x x x x +-++-=课后作业:1.分解因式：(1)x 2＋6x ＋8＝ ; (2)x 2－2x －1＝ ;(3)242025x x -+= ;(4)256x x -+-= ;(5)2232x xy y +-= ; (6)22710a b ab -+= ;(7)26(6)2x x -+= ;(8) 3245a b ab a b --= ；(9)2222x a a x ---= ;(10)4x 2－8x －12y －9y 2 ＝ ;2.分解因式:(1) a(a ＋3)2－a(a －b)2 (2) 2235294x xy y x y +-++-(3)4(1)(2)x y y y x -++- (4)4b 2－10b ＋c 2－5c ＋4bc ＋6(5)1322+-+-y x xy x (6)222222a c ab b d cd -++--3.已知210x y ++=，求222332x xy y x y +-+++的值.第3课时一元二次方程课标导航：1.熟练掌握一元二次方程的求解方法;2.掌握一元二次方程根与系数的关系—韦达定理,能熟练应用韦达定理解决相关问题 . 课堂实录：1、一元二次方程20(0)ax bx c a ++=≠的求解方法：（1）公式法：判别式△＝若，则方程无实数根。

初高中数学衔接教材已整理.doc

初高中数学衔接教材1.乘法公式我们在初中已经学习过了下列一些乘法公式：（ 1）平方差公式(a b)(a b) a2 b2；（ 2）完全平方公式(a b)2 a2 2ab b2．我们还可以通过证明得到下列一些乘法公式：（ 1）立方和公式(a b)(a2 ab b2 ) a3 b3；（ 2）立方差公式(a b)( a2 ab b2 ) a3 b3；（ 3）三数和平方公式(a b c)2 a2 b2 c2 2(ab bc ac) ；（ 4）两数和立方公式(a b)3 a3 3a2b 3ab2 b3；（ 5）两数差立方公式(a b)3 a3 3a2b 3ab 2 b3．对上面列出的五个公式，有兴趣的同学可以自己去证明．例 1 计算：( x 1)(x 1)(x2 x 1)(x2 x 1) ．解法一：原式 = ( x2 1) ( x2 1)2 x2= ( x2 1)(x4 x2 1)= x6 1．解法二：原式 = ( x 1)( x2 x 1)(x 1)(x2 x 1)=( x3 1)(x3 1)=x6 1．例 2 已知 a b c 4 ， ab bc ac 4 ，求a2 b2 c2 的值．解： a2 b2 c2 ( a b c) 2 2(ab bc ac) 8 ．练习1．填空：（ 1）1a2 1 b2 (1b1a) （）；9 4 2 3（ 2）(4 m )2 16m2 4m ( ) ；(3 ) (a 2b c)2 a2 4b2 c2 ( ) ．2．选择题：（ 1）若x2 1mx k 是一个完全平方式，则k 等于（）2（ B）1m2 （ C）1m2 （D ）1m2（ A ）m24 3 16（ 2）不论a，b为何实数，a2 b2 2a 4b 8的值（）（A ）总是正数（B ）总是负数（ C）可以是零（D ）可以是正数也可以是负数2．因式分解因式分解的主要方法有：十字相乘法、提取公因式法、公式法、分组分解法，另外还应了解求根法及待定系数法．1．十字相乘法例1 分解因式：（1） x2－3x＋ 2；2（ 3）x(a b) xy aby2；（2）x2＋ 4x－12；（4）xy 1 x y ．。

初升高衔接教材数学

初升高衔接教材数学初升高衔接教材数学是针对初中升高中阶段编写的数学教材，旨在帮助学生适应高中数学的难度和深度，掌握高中数学的基础知识和基本技能，提高数学思维能力。

以下是初升高衔接教材数学的一些重点内容：1. 函数：函数是高中数学的重要概念之一，也是初升高衔接的重点之一。

学生需要了解函数的定义、性质、图像和基本运算，掌握一次函数、二次函数、指数函数、对数函数等常见函数的性质和图像，为后续学习打下基础。

2. 代数：高中代数相对于初中代数更加深入和复杂，需要学生掌握更高级的代数知识和技能，如解一元二次方程、因式分解、分式运算等。

学生需要适应高中数学的符号运算和代数表达方式，提高代数思维能力。

3. 平面几何：平面几何是初中数学的重要内容之一，但高中数学的平面几何更加深入和复杂。

学生需要掌握基本的几何知识和技能，如三角形的性质、全等三角形、相似三角形、解直角三角形等。

同时，还需要了解一些基本的几何定理和证明方法，为后续学习打下基础。

4. 解析几何：解析几何是高中数学的重要内容之一，也是初升高衔接的重点之一。

学生需要了解平面直角坐标系、点的坐标、直线的方程等基本概念，掌握一次函数、二次函数、圆的方程等解析几何的应用。

同时，还需要了解一些解析几何的基本定理和证明方法，为后续学习打下基础。

5. 数学思想方法：高中数学注重培养学生的数学思想方法，如数形结合、分类讨论、转化与化归等。

学生需要了解这些数学思想方法的基本概念和应用，掌握这些方法在解题中的应用技巧，提高数学思维能力。

总之，初升高衔接教材数学需要注重培养学生的数学基础知识和基本技能，提高学生的数学思维能力和解决问题的能力。

通过系统的学习和练习，学生可以更好地适应高中数学的难度和深度，为后续的学习打下坚实的基础。

初高中数学衔接教材 §2.1 一元二次方程(含答案)

初高中数学衔接教材 2.1 一元二次方程2.1.1根的判别式{情境设置：可先让学生通过具体实例探索二次方程的根的求法，如求方程的根： (1)0322=-+x x ；(2)0122=++x x ；(3)0322=++x x 。

} 用配方法可把一元二次方程ax 2＋bx ＋c ＝0（a ≠0）变为2224()24b b ac x a a -+=①a ≠0，∴4a 2＞0。

于是（1）当b 2－4ac ＞0时，方程①的右端是一个正数，因此，原方程有两个不相等的实数根x 1，2＝2b a-±；（2）当b 2－4ac ＝0时，方程①的右端为零，因此，原方程有两个等的实数根x 1＝x 2＝－2b a；（3）当b 2－4ac ＜0时，方程①的右端是一个负数，而方程①的左边2()2b x a+一定大于或等于零，因此，原方程没有实数根。

由此可知，一元二次方程ax 2＋bx ＋c ＝0（a ≠0）的根的情况可以由b 2－4ac 来判定，我们把b 2－4ac 叫做一元二次方程ax 2＋bx ＋c ＝0（a ≠0）的根的判别式，通常用符号“Δ”来表示。

综上所述，对于一元二次方程ax 2＋bx ＋c ＝0（a ≠0），有（1）当Δ＞0时，方程有两个不相等的实数根，x 1，2（2）当Δ＝0时，方程有两个相等的实数根，x 1＝x 2＝－2ba；（3）当Δ＜0时，方程没有实数根。

例1 判定下列关于x 的方程的根的情况（其中a 为常数），如果方程有实数根，写出方程的实数根。

（1）x 2－3x ＋3＝0；（2）x 2－ax －1＝0；（3） x 2－ax ＋(a －1)＝0；（4）x 2－2x ＋a ＝0。

解：（1）∵Δ＝32－4×1×3＝－3＜0，∴方程没有实数根。

（2）该方程的根的判别式Δ＝a 2－4×1×(－1)＝a 2＋4＞0，所以方程一定有两个不等的实数根12a x +=，22a x -=（3）由于该方程的根的判别式为Δ＝a 2－4×1×(a －1)＝a 2－4a ＋4＝(a －2)2，所以，①当a ＝2时，Δ＝0，所以方程有两个相等的实数根x 1＝x 2＝1； ②当a ≠2时，Δ＞0，所以方程有两个不相等的实数根x 1＝1，x 2＝a －1。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018初高中数学衔接教材目录第一章数与式 1.1 数与式的运算 1.1.1 绝对值 1.1.2 乘法公式 1.1.3 二次根式 1.1.4 分式 1.2 分解因式第二章二次方程与二次不等式 2.1 一元二次方程 2.1.1 根的判别式 2.1.2 根与系数的关系

2.2 二次函数 2.2.1 二次函数y=ax2+bx+c的图像和性质 2.2.2 二次函数的三种表达方式 2.2.3 二次函数的应用

2.3 方程与不等式 2.3.1 二元二次方程组的解法第三章相似形、三角形、圆 3.1 相似形 3.1.1 平行线分线段成比例定理 3.1.2 相似三角形形的性质与判定

3.2 三角形 3.2.1 三角形的五心 3.2.2 解三角形：钝角三角函数、正弦定理和余弦定理及其应用

3.3 圆 3.3.1 直线与圆、圆与圆的位置关系：圆幂定理 3.3.2 点的轨迹 3.3.3 四点共圆的性质与判定 3.3.4 直线和圆的方程（选学） 1.1 数与式的运算 1.１.1．绝对值绝对值的代数意义：正数的绝对值是它的本身，负数的绝对值是它的相反数，零的绝对值仍是零．即 ,0,||0,0,,0.aaaaaa





绝对值的几何意义：一个数的绝对值，是数轴上表示它的点到原点的距离．两个数的差的绝对值的几何意义：ba表示在数轴上，数a和数b之间的距离．

例1 解不等式：13xx＞4．解法一：由01x，得1x；由30x，得3x； ①若1x，不等式可变为(1)(3)4xx，即24x＞4，解得x＜0，又x＜1， ∴x＜0； ②若12x，不等式可变为(1)(3)4xx，即1＞4， ∴不存在满足条件的x； ③若3x，不等式可变为(1)(3)4xx，即24x＞4，解得x＞4．又x≥3， ∴x＞4．综上所述，原不等式的解为 x＜0，或x＞4．解法二：如图1．1－1，1x表示x轴上坐标为x的点P到坐标为1的点A之间的距离|PA|，即|PA|＝|x－1|；|x－3|表示x轴上点P到坐标为2的点B之间的距离|PB|，即|PB|＝|x－3|．所以，不等式13xx＞4的几何意义即为 |PA|＋|PB|＞4．由|AB|＝2，可知点P 在点C(坐标为0)的左侧、或点P在点D(坐标为4)的右侧． x＜0，或x＞4．练习 1．填空：（1）若5x，则x=_________；若4x，则x=_________.

（2）如果5ba，且1a，则b＝________；若21c，则c＝________. 2．选择题：下列叙述正确的是（）（A）若ab，则ab （B）若ab，则ab

1 3 A B x 0 4 C D x P

|x－1|

|x－3|

图1．1－1 （C）若ab，则ab （D）若ab，则ab 3．化简：|x－5|－|2x－13|（x＞5）． 1.1.2. 乘法公式

我们在初中已经学习过了下列一些乘法公式：（1）平方差公式 22()()ababab；（2）完全平方公式 222()2abaabb．我们还可以通过证明得到下列一些乘法公式：（1）立方和公式 2233()()abaabbab；（2）立方差公式 2233()()abaabbab；（3）三数和平方公式 2222()2()abcabcabbcac；（4）两数和立方公式 33223()33abaababb；（5）两数差立方公式 33223()33abaababb．对上面列出的五个公式，有兴趣的同学可以自己去证明．例1 计算：22(1)(1)(1)(1)xxxxxx．解法一：原式=2222(1)(1)xxx =242(1)(1)xxx =61x．解法二：原式=22(1)(1)(1)(1)xxxxxx =33(1)(1)xx =61x．例2 已知4abc，4abbcac，求222abc的值．解： 2222()2()8abcabcabbcac．练习 1．填空：

（1）221111()9423abba（）；（2）(4m 22)164(mm )； (3 ) 2222(2)4(abcabc )． 2．选择题：

（1）若212xmxk是一个完全平方式，则k等于（）

（A）2m （B）214m （C）213m （D）2116m （2）不论a，b为何实数，22248abab的值（）（A）总是正数（B）总是负数（C）可以是零（D）可以是正数也可以是负数

1.1.3．二次根式一般地，形如(0)aa的代数式叫做二次根式．根号下含有字母、且不能够开得尽方的式子称为无理式. 例如 232aabb，22ab等是无理式，而22212xx，222xxyy，2a等是有理式．

1．分母（子）有理化把分母（子）中的根号化去，叫做分母（子）有理化．为了进行分母（子）有理化，需要引入有理化因式的概念．两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式互为有理化因式，例如2与2，3a与a，36与36，2332与2332，等等．一般地，ax与x，axby与axby，axb与

axb互为有理化因式．

分母有理化的方法是分母和分子都乘以分母的有理化因式，化去分母中的根号的过程；而分子有理化则是分母和分子都乘以分母的有理化因式，化去分子中的根号的过程在二次根式的化简与运算过程中，二次根式的乘法可参照多项式乘法进行，运算中要运用公式(0,0)ababab；而对于二次根式的除法，通常先写成分式的形式，然后通过分母有理化进行运算；二次根式的加减法与多项式的加减法类似，应在化简的基础上去括号与合并同类二次根式．

2．二次根式2a的意义 2aa

,0,,0.aaaa



例1 将下列式子化为最简二次根式：

（1）12b；（2）2(0)aba；（3）64(0)xyx．解：（1）1223bb；（2）2(0)abababa；（3）633422(0)xyxyxyx．例2 计算：3(33)．

解法一： 3(33)＝333

＝3(33)(33)(33) ＝33393 ＝3(31)6 ＝312．解法二： 3(33)＝333 ＝33(31) ＝131＝31(31)(31)＝312．例3 试比较下列各组数的大小：（1）1211和1110；（2）264和226－.

解：（1）∵1211(1211)(1211)11211112111211， 1110(1110)(1110)11110111101110

，

又12111110， ∴1211＜1110．（2）∵226(226)(226)2226,1226226－－+－++ 又 4＞22， ∴6＋4＞6＋22，

∴264＜226－.

例4 化简：20042005(32)(32)．解：20042005(32)(32)

＝20042004(32)(32)(32)＝2004(32)(32)(32) ＝20041(32)＝32．例 5 化简：（1）945；（2）2212(01)xxx．解：（1）原式5454 22(5)22522(25)2552．（2）原式=21()xx1xx， ∵01x，∴11xx，所以，原式＝1xx．例 6 已知3232,3232xy，求22353xxyy的值．解： ∵223232(32)(32)103232xy， 323213232xy

，

∴22223533()1131011289xxyyxyxy．练习 1．填空：

（1）1313＝__ ___；（2）若2(5)(3)(3)5xxxx，则x的取值范围是_ _ ___；（3）4246543962150__ ___；

（4）若52x，则11111111xxxxxxxx______ __． 2．选择题：等式22xxxx成立的条件是（）（A）2x （B）0x （C）2x （D）02x 3．若22111aaba，求ab的值． 4．比较大小：2－3 5－4（填“＞”，或“＜”）．

1.1.４．分式

初高中数学衔接教材

初高中数学衔接教材(已整理精品)

初高中数学衔接教材6

初高中数学衔接教材已整理

初高中数学衔接教材(已整理精品)

初高中数学衔接校本教材(Word版)

最新初高中数学衔接教材[新课标人教A版](学生版)(适用黑龙江)名师优秀教案

职业中学数学初高中衔接教材(共4课时)

初高中数学衔接教材已整理.doc

初升高衔接教材数学

初高中数学衔接教材 §2.1 一元二次方程(含答案)