2.4 电阻的Y形联接与△形联接的等效变换
电阻星形连接与三角形连接的等效变换

公正处法人授权委托书范本一、前言为了明确公正处法人的授权范围和内容,确保代理人能够合法、合规地代表法人行事,特制定本授权委托书。
本授权委托书旨在规范法人授权行为,保障法人及其代理人的合法权益,维护社会经济秩序。
二、授权主体1. 授权单位:×××公正处2. 法定代表人:×××3. 授权人:×××三、授权范围1. 代理人代表公正处参加各类法律诉讼活动,包括但不限于起诉、应诉、举证、质证、调解、和解等。
2. 代理人代表公正处与各类当事人进行法律事务谈判、协商,并签署相关法律文件。
3. 代理人代表公正处处理各类法律事务,包括但不限于合同审查、起草、签订、变更、解除等。
4. 代理人代表公正处参加各类行政复议、行政诉讼活动,维护公正处的合法权益。
5. 代理人代表公正处处理各类法律咨询、法律培训、法律宣传等活动。
6. 代理人代表公正处与各类政府部门、企事业单位、社会团体等进行法律事务往来。
7. 代理人代表公正处处理其他各类法律事务,包括但不限于知识产权、劳动关系、交通事故等。
四、授权期限本授权委托书的有效期为自授权人之签名或盖章之日起至法定代表人书面声明本授权作废之日止。
五、授权方式1. 法定代表人签字或盖章。
2. 公正处盖章。
六、注意事项1. 代理人应当在授权范围内行事,不得超出授权范围进行任何活动。
2. 代理人不得转委托授权,不得将授权事项转让给他人。
3. 代理人不得以公正处名义从事任何非法活动,不得损害公正处的合法权益。
4. 代理人应当严格遵守国家法律法规,合规行事。
5. 代理人应当保持与当事人的良好沟通,确保授权事项的顺利进行。
6. 代理人应当及时向法定代表人报告授权事项的进展情况。
七、法律后果1. 代理人依据本授权委托书行事,其法律后果由公正处承担。
2. 代理人超出授权范围行事,其法律后果由代理人自行承担。
3. 代理人违反国家法律法规、本授权委托书约定,给公正处造成损失的,应当承担赔偿责任。
2电路的等效变换

Δ形→ Y形
Y形→Δ形
R1R2 + R2 R3 + R3 R1 R12 R3 R1R2 + R2 R3 + R3 R1 R23 R1 R1R2 + R2 R3 + R3 R1 R31 R2
Y电阻
相邻两电阻之积 电阻之和
Y两两电阻乘积之和 电阻 Y形不相邻那个电阻
2015-4-23
a iS
b
注意:iSk前符号的取法。
串连:
a
iS1
iS2
iSN
b
a
iS
b
当仅当电源极性、电流大小相同串联才有意义。
2015-4-23 23
§2-6 实际电源的两种模型及其等效变换
一、实际电源的伏安特性
实际 直流 电源
u(V)
ቤተ መጻሕፍቲ ባይዱUOC
线性区 非线性区
u
-
+ A +
-
i +
V
-
R u(V)
UOC
i(A)
R31 ( R12 + R23 ) R23 R31 U13 I1 + I2 R12 + R23 + R31 R12 + R23 + R31
R23 R31 R23 ( R12 + R31 ) U 23 I1 + I2 R12 + R23 + R31 R12 + R23 + R31
2015-4-23
一、Y形(T形)连接
1
I1
R3 R1
可相互等效,进行 某些电路的化简
二、∆形(Π形)连接
1
I1
R31 R12 R23
电路课件——电路等效变换

R
R
d
Rab R
§2-4 电阻的星形联接与三角形联接的
等效变换 (—Y 变换)
c
1. 电阻的 ,Y连接
R1
R2
包含
1
a
b
R3
R4
1d
R12
R31
R1
R2
R3
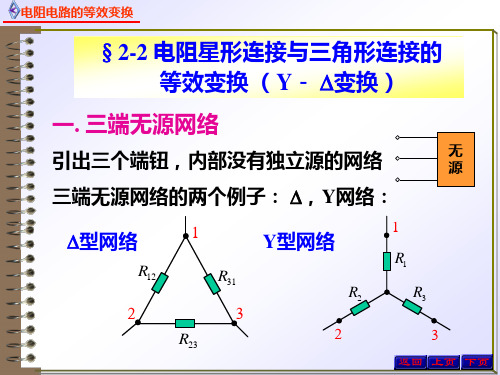
三端 网络
2
R23
3
2
3
型网络
Y型网络
,Y 网络的变形:
型电路 ( 型)
T 型电路 (Y、星 型)
这两个电路当它们的电阻满足一定的关系时,能够相互等效
开路的电流源可以有电流流过并联电导Gi 。
电压源短路时,电阻中Ri有电流; 电流源短路时, 并联电导Gi中无电流。
(3) 理想电压源与理想电流源不能相互转换。
应用:利用电源转换简化电路计算。
例1.
5A
3
I=?
+ 15v_
7
_
2A
4
8v
+
例2. U=?
7 I
7
I=0.5A
5 10V 10V 6A
+ u
-
-
§2-3 电阻的串联、并联和串并联
1. 电阻串联( Series Connection of Resistors )
(1) 电路特点
R1
Rk
Rn
i
+ u1 _ + U k _ + un _
+
u
_
(a) 各电阻顺序连接,流过同一电流 (KCL);
(b) 总电压等于各串联电阻的电压之和 (KVL)。
i
+ uS _
第二章 电阻电路的等效变换

Ib Ic
c
将Y形联接等效变换为∆形联结时 形联接等效变换为∆ 3R 若 Ra=Rb=Rc=RY 时,有Rab=Rbc=Rca= R∆ = 3RY; 将∆形联接等效变换为Y形联结时 形联接等效变换为Y 若 Rab=Rbc=Rca=R∆ 时,有Ra=Rb=Rc=RY =R∆/3
总目录 章目录 返回 上一页 下一页
总目录 章目录 返回 上一页 下一页
+ U –
2.3.2 电阻的并联
I + I1 U – I2 R1 R2 特点: 特点: (1)各电阻联接在两个公共的结点之间; (1)各电阻联接在两个公共的结点之间 各电阻联接在两个公共的结点之间; (2)各电阻两端的电压相同; (2)各电阻两端的电压相同; 各电阻两端的电压相同 (3)等效电阻的倒数等于各电阻倒数之和; (3)等效电阻的倒数等于各电阻倒数之和; 等效电阻的倒数等于各电阻倒数之和 1 1 1 = + Req R1 R2 (4)并联电阻上电流的分配与电阻成反比。 (4)并联电阻上电流的分配与电阻成反比 并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式: 两电阻并联时的分流公式: Req
R R ab ca R = a R +R +R ab bc ca R R bc ab R = b R +R +R ab bc ca R R ca bc R = c R +R +R ab bc ca
总目录 章目录 返回 上一页 下一页
Ia a Ra Ib Ic b Rb Rc c 等效变换
Ia
a Rab RbcRca b
第2章 电阻电路的等效变换 章
2.1 引言 2.2 电路的等效变换 2.3 电阻的串联和并联 2.4 电阻星型联结与三角型联结的等效变换 电阻星型联结与三角型联结的等效变换 2.5 电压源、电流源的串联和并联 电压源、 2.6 实际电源的两种模型及其等效变换 实际电源的两种模型及其等效变换 2.7 输入电阻
第二章 等效变换

例2:
求图2-9a电路中电流 I1, I2, I3 , I4。
I
I2 I1
解: 思路
Δ→Y
Req
I
Rb
48 2, 同理, 求得 : Rc 2, Rd 1, Req (1 Rb ) //(5 Rd ) Rc 4 4 48 1 Rb 18 I 3 A, 由分流公式, 可得: I1 I 1A, I 2 I I1 2 A 2 Req 1 Rb 5 Rd U db 5 I1 1 I 2 I3 0.75 A, I 4 I1 I 3 1.75 A 4 4
根据电路的对称性, 可知 c, d, e三点等电位, 故可用导线短接。
8 2 8 2 3 3 2 16 Req [( 2 // 1) 2] //(2 // 1) 2 // 2 8 2 3 3 15 3 3
§2-4电阻的Y-Δ 等效变换
R1, R2, R3 Y(星)形连接 R3, R4, R5 R1, R3, R4 Δ(三角)形连接 R2, R3, R5
②
'' Req R1 Req 6 6 12 ③
15 10 6 ②R R2 R34 15 10
'' eq ' R2 Req
Req R1 R2 //(R3 R4 ) R1
R2 ( R3 R4 ) 15(5 5) 6 12 R2 R3 R4 15 5 5
6 9 54 断开时,Req 2+4) 3 6) ( //( 3.6 6 9 15
结论:若电路中两点电位相等,则: ①可将这两点短路 ② 可将这两点之间连接的支路断开 对某些对称性电路可采用此方法处理
电路原理2.2.1电阻的星形联结和三角形联结的等效变换 - 电阻星形连接与三角形连接的等效变换
返回 上页 下页
电阻电路的等效变换
由式(2)解得:
i1Y
u12Y R3 u31Y R2 R1R2 R2 R3 R3 R1
i2Y
u23Y R 1 u12Y R1R2 R2 R3
R3 R3
R1
(3)
i3Y
u31Y R2 u23Y R1 R1R2 R2 R3 R3 R1
G12
G1
G1G2 G2 G3
G23
G1
G2G3 G2 G3
G31
G1
G3G1 G2
G3返回
上页
下页
电阻电路的等效变换
由Y接 接的变换结果:
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
4
35 R1 3 2 5 1.5
32 R2 3 2 5 0.6
R3
3
2 2
5
5
1
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
1.5
0.6 1
2
3
1.4
1
再用电阻串联和 并联公式,求出连接 到电压源两端单口的 等效电阻:
4
R 1.5 (0.6 1.4)//(1 1)
5 )
17
R23
(5
2+2 1+1 5
5 )
3.4;
R31
(
5
2+2 1+1 2
5 )
8.5
电阻的星形与三角形的等效变换
电阻的星形与三角形的等效变换
电阻的星形与三角形等效变换是指将一个电阻网络的星形连接转化为相应的等效三角形连接,或者将一个电阻网络的三角形连接转化为相应的等效星形连接。
这种变换可以使电阻网络更易于分析和计算。
将星形电阻连接转化为等效三角形电阻连接的方法如下:
1. 将三个电阻连接在一起,形成一个三角形。
2. 对于每一个电阻,通过连接其两个端点和三角形的第三个顶点来连接它们。
3. 删除原来的星形连接。
这样得到的等效三角形电阻网络与原来的星形电阻网络在电阻值等效的情况下具有相同的电流分布和电压分布。
将三角形电阻连接转化为等效星形电阻连接的方法如下:
1. 将三个电阻的一个共享节点连接在一起,形成一个星形。
2. 对于每一个电阻,通过连接其两个端点和星形的共享节点来连接它们。
3. 删除原来的三角形连接。
这样得到的等效星形电阻网络与原来的三角形电阻网络在电阻值等效的情况下具有相同的电流分布和电压分布。
通过这种等效变换,我们可以简化复杂的电阻网络,使得分析和计算更加容易和方便。
大学物理 电阻电路的等效变换ppt课件
以上两条等效都是对外电路而言
最新课件
31
例:
us1
a
us2 is2
a
us2 is2
is1
is1
b
b
a
us2 is
a
is
is = is2 - is1
b
最新课件
b
32
§2.6 实际电源的两种模型及其等效变换
1. 实际电压源的电路模型
实际直流电压源实测的端纽伏安关系并不是一条与i 轴平 行的直线,而是一条稍微向下倾斜的直线。如图所示:
Y接: 用电流表示电压
i1 =u12 /R12 – u31 /R31
u12Y=R1i1Y–R2i2Y
i2 =u23 /R23 – u12 /R12 (1)
u23Y=R2i2Y – R3i3Y (2)
i3 =u31 /R31 – u23 /R23
i1Y+i2Y+i3Y = 0
最新课件
18
由式(2)解得:
+
u
_
结论:串联电路的总电阻等于各分电阻之和。
最新课件
+
Req
u
_
8
串联电阻上电压的分配
uk
Rk u, Req
k1,2,n
例:两个电阻分压, 如下图
i
++
u
u1 +
R1
_
u2
R2
u1
R1 R1 R2
u
u2
R2 R1 R2
u
功率关系
p1=R1i2, p2=R2i2,, pn=Rni2
p u i R eiq 2 最新课件R k i2
第二章 电阻电路的等效变换
电阻网络中的三角形星形等效变换
电阻网络中的三角形星形等效变换在电路中,电阻网络是一个由电阻器连接而成的结构,用于控制电流和电压的传输。
在电阻网络中,基本的电路元件是电阻器,可以通过不同方式进行连接和变换,以达到不同的电流分布和电压分配的目的。
本文将介绍电阻网络中的三角形星形等效变换,以及其在电路设计和分析中的应用。
一、三角形到星形等效变换三角形到星形等效变换指的是将一个由三个电阻器连接而成的三角形电路转化为一个由三个电阻器连接而成的星形电路。
在三角形到星形等效变换中,需要满足以下条件:1. 三个电阻器的连接点形成一个等边三角形;2. 三角形的每个顶点连接一个电阻器;3. 三角形的一个顶点作为星形电路的中心连接点。
通过三角形到星形等效变换,可以改变电路的结构和性质,并简化电路的分析和计算。
二、星形到三角形等效变换星形到三角形等效变换是三角形到星形等效变换的逆过程,即将一个由三个电阻器连接而成的星形电路转化为一个由三个电阻器连接而成的三角形电路。
在星形到三角形等效变换中,需要满足以下条件:1. 三个电阻器连接到一个中心节点,形成一个星形电路;2. 两个相邻的电阻器连接到一个顶点,形成一个等腰三角形;3. 三个电阻器的连接点形成一个等边三角形。
通过星形到三角形等效变换,可以将星形电路转化为三角形电路,使得电路的分析更加简单和方便。
三、等效电阻的计算方法在电阻网络中,等效电阻是指将一个复杂的电路转化为一个简单的电阻网络,使得该电阻网络具有与原电路相同的电流-电压特性。
在三角形星形等效变换中,可以计算出等效电阻。
1. 三角形到星形等效变换中,等效电阻的计算公式为:Rt = R1 * R2 + R2 * R3 + R1 * R3其中,R1、R2、R3分别代表三个电阻器的阻值。
2. 星形到三角形等效变换中,等效电阻的计算公式为:Rt = R1 + R2 + R3其中,R1、R2、R3分别代表三个电阻器的阻值。
通过计算等效电阻,可以将复杂的电阻网络简化为一个等效电阻器,便于电路的计算和分析。
电路理论 电阻电路的等效变换
例Leabharlann 桥 T 电路 1kΩ 1kΩ 1kΩ 1kΩ R E
1/3kΩ
1/3kΩ 1/3kΩ R 1kΩ
E
1kΩ 3kΩ i E 3kΩ 3kΩ R
例
1Ω + 20V 1Ω + 20V -
计算90Ω 计算90Ω电阻吸收的功率 90 4Ω 9Ω 90Ω 1Ω 4Ω 3Ω 3Ω 90Ω 1Ω 9Ω 3Ω 9Ω 9Ω 9Ω 1Ω
(3) 串联电阻的分压
u R u =Ri =R = k u<u k k k Rq Rq e e
说明电压与电阻成正比, 说明电压与电阻成正比,因此串联电阻电路可作分压电路
例 i
两个电阻的分压: 两个电阻的分压:
º + + u1 R1 u u2 R2 _ + º
R 1 u u= 1 R+R 1 2 −R 2 u= u 2 R+R 1 2
2 +
i1∆ =i1Y , ∆
i2 ∆ =i2Y ,
i3 ∆ =i3Y ,
u12∆ =u12Y , u23∆ =u23Y , u31∆ =u31Y ∆ ∆ ∆
1 + i1∆ ∆ u12∆ ∆ – i2 ∆ 2 + R12 R23 u23∆ ∆ – R31 u31∆ ∆ i3 ∆ + – 3 u12Y – i2Y R2 + i1Y
i1∆ =u12∆ /R12 – u31∆ /R31 ∆ ∆ ∆ i2∆ =u23∆ /R23 – u12∆ /R12 ∆ ∆ ∆ i3∆ =u31∆ /R31 – u23∆ /R23 ∆ ∆ ∆ (1)
根据等效条件,比较式(3)与式(1), →∆型的变换条件: 根据等效条件,比较式(3)与式(1),得Y型→∆型的变换条件: (3)与式(1) 型的变换条件 RR G 2 G R2 =R +R + 1 2 1 1 1 2 G = 1 2 R 3 G+ 2 + 3 G G 1 RR GG 2 3 R3 =R +R + 2 3 G3 = 2 2 3 或 2 R G+ 2 + 3 G G 1 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题的引入
求等效电阻 RAB = ?
2Ω 3Ω 3Ω 5Ω B
3Ω 3Ω A
二、星形联接和三角形联接的等效变换的条件
要求它们的外部性能相同, 要求它们的外部性能相同, 即当它们对应端子间的电压相同时, 即当它们对应端子间的电压相同时, 流入对应端子的电流也必须分别相等。 流入对应端子的电流也必须分别相等。
R1 = R2 = R3 = RY
则等效的三角形电路的电阻也相等
R∆ = R12 =之,则RY = R∆ 3
D 3Ω 3Ω A C 3Ω E A D 1Ω 3Ω A C 1Ω E 5Ω 1Ω 2Ω B E 3Ω 5Ω B D 2Ω
×
3Ω
2Ω B 5Ω
R=3+1+(1+2)∥(1+5) ∥ =6Ω
1
1
R1
R31
R3
3 星接
R12
R2
2 3
R23
三角接
2
△→Y
R31 R12 R1 = R12 + R23 + R31
R12 R23 R2 = R12 + R23 + R31
R23 R31 R3 = R12 + R23 + R31
1
1
R1
R31
R3
3 星接
R12
R2
2 3
R23
三角接
2
特别若星形电路的3 特别若星形电路的 个电阻相等
1 1
R1
R31
R3
3
R12
R2
2 3
R23
2
星接( 接 星接(Y接)
三角接( 三角接(△接)
1
1
R1
R31
R12
R3
3
R2
2 3
R23
2
星接( 接 星接(Y接) Y→△ △
三角接( 三角接(△接)
R1 R2 R12 = R1 + R2 + R3
R2 R3 R23 = R2 + R3 + R1
R3 R1 R31 = R1 + R3 + R2
