反比例函数与几何的综合应用及答案
反比例函数的应用经典习题(含答案)

反比例函数的应用反比例函数应用——跨学科的综合性问题:解答该类问题的关键是确定两个变量之间的函数关系(常应用物理公式),然后利用待定系数法求出它们的关系式.常见模型:1.压力与压强、受力面积的关系2.电压、电流与电阻的关系3.水池中水的体积、排水量与所需时间的关系 4、气体的气压P(千帕)与气体体积V(立方米)的关系例1、某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)将如何变化?如果人和木板对湿地地面的压力合计600 N,那么(1) 用含S的代数式表示p,并求木板面积为0.2 m2时.压强是多少?解:P=F/S=600/S ,S=0.2 m2 ,P=600/0.2=1200(Pa)(2)如果要求压强不超过6000 Pa,木板面积至少要多大?方法一:P=600/S≤6000,S≥600/6000=0.1,故面积至少0.1 m2方法二:已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线P=6000下方的图象上(3) 在直角坐标系中,作出相应的函数图象.注意:只需要坐第一象限的图,因为S>0.例2.蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R( )之间的函数关系如图所示。
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?解:因为电流I与电压U之间的关系为IR=U(U为定值),把图象上的点A的坐标(9,4)代入,得U=36.所以蓄电池的电压U=36V.这一函数的表达式为:I=36/R(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?R(Ω) 3 4 5 6 7 8 9 10I(A) 4解:当I≤10A时,解得R≥3.6(Ω).所以可变电阻应不小于3.6Ω.试一试1.某蓄水池的排水管每时排水8m 3 ,6h 可将满池水全部排空。
中考反比例函数与几何综合
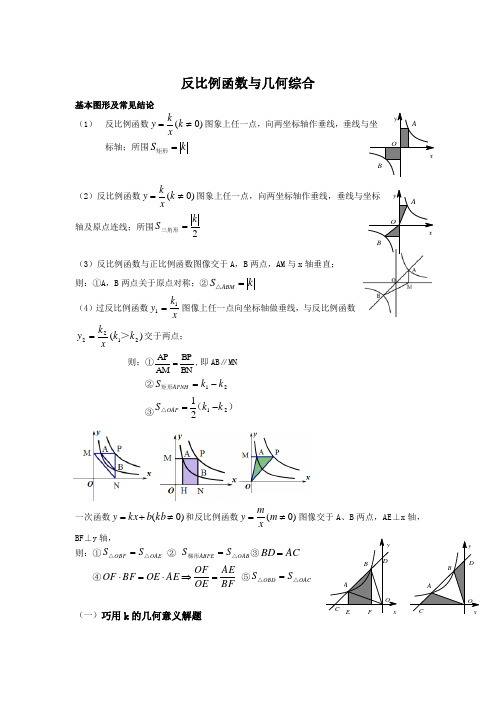
Oy xBAABxy O反比例函数与几何综合基本图形及常见结论 (1) 反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴;所围k S =矩形(2)反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴及原点连线;所围2k S =三角形(3)反比例函数与正比例函数图像交于A ,B 两点,AM 与x 轴垂直; 则:①A ,B 两点关于原点对称;②k S ABM =△(4)过反比例函数xk y 11=图像上任一点向坐标轴做垂线,与反比例函数)(2122k k xk y >=交于两点; 则:①BNBP AM AP =,即AB ∥MN②21k k S APNH -=矩形③)(△2121k k S OAP -=一次函数)0(≠+=kb b kx y 和反比例函数)0(≠=m xmy 图像交于A 、B 两点,AE ⊥x 轴,BF ⊥y 轴,则:①OAE OBF S S △△= ② OAB ABFE S S △梯形=③AC BD =④BFAEOE OF AE OE BF OF =⇒⋅=⋅ ⑤OACOBD S S △△=(一)巧用k 的几何意义解题y x ABO CDy xDC F EO B A例1.函数y=和y=在第一象限内的图象如图,点P 是y=的图象上一动点,PC ⊥x 轴于点C ,交y=的图象于点B .给出如下结论:①△ODB 与△OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA=AP .其中所有正确结论的序号是________。
迁移练习1(1).如图,双曲线)0x (k>=xy 经过Rt △OAB 斜边OB 的中点D ,与AB 交于点C .若△OBC 面积为3,则k =_______迁移练习1(2)..双曲线)0x (k>=xy 经过矩形OABC 边AB 的中点F ,交BC 于点E ; 若梯形OEBA 的面积为9,则k=________。
人教版九年级数学下册作业课件 第二十六章 反比例函数 专题课堂(二) 反比例函数的综合应用

n=-2,
得 b=6,
∴直线 AC 的解析式为:y=-2x+6
二、反比例函数与二次函数的综合应用
【例 2】(2022·绥化)已知二次函数 y=ax2+bx+c 的部分函数图象如图所示,则一
次函数
y=ax+b2-4ac
与反比例函数
4a+2b+c y= x
在同一平面直角坐标系中的图象
大致是( B )
[对应训练] 4.抛物线 y=ax2+bx+c(a<0)与双曲线 y=kx 相交于点 A,B,且抛物线经过坐 标原点,点 A 的坐标为(-2,2),点 B 在第四象限内,过点 B 作直线 BC∥x 轴,点 C 为直线与抛物线的另一交点,已知直线 BC 与 x 轴之间的距离是点 B 到 y 轴的距离 的 4 倍.记抛物线顶点为 E. (1)求双曲线和抛物线的解析式; (2)计算△ABC 与△ABE 的面积.
b=-4,
的解析式为 y=-x-4 (2)如图,过点 B 作 BM⊥OP,垂足为 M,由题意可知,
OM=1,BM=3,AC=1,MC=OC-OM=3-1=2,∴S 四边形 ABOC=S△BOM+S 梯 形 ACMB=32 +12 (1+3)×2=121
[对应训练] 1.一次函数 y=kx+b(k≠0)与反比例函数 y=kx (k≠0)在同一平面直角坐标系上的 大致图象如图所示,则 k,b 的取值范围是( C ) A.k>0,b>0 B.k<0,b>0 C.k<0,b<0 D.k>0,b<0
解:(1)由点 A(-2,2)在双曲线上得双曲线的解析式为 y=-4x ,设点 B 的坐标为
(m,-4m)且 m>0,代入 y=-4x ,得 m=1,∴B(1,-4),由题意知 c=0,把 A,B
4a-2b=2,
反比例函数k的几何意义专项训练及答案

反比例函数K 的几何意义专项训练及答案(中考复习)1、如图(1)所示,已知反比例函数 y =x k 和 y =x 1分别过点 A 和点 B ,且 AB // x 轴, S ABC △ =23,点C 是 x 轴上任意一点,则 k =____________. 2、如图(2)所示,矩形ABOC 的顶点B ,C 分别在x 轴,y 轴上,顶点A 在第二象限,点B 的坐标为(-2,0),将线段OC 绕点O 逆时针旋转60°至线段0D,若反比例函数y=xk (k ≠0)的图像经过A ,D 两点,则k 的值为_____________. 3、如图(3)所示,面积为25的Rt △OAB 的斜边OB 在x 轴上,∠ABO=30°,反比例函数y=xk 的图象恰好经过点A ,则k 的值为______________.4、如图(4)所示,A ⎪⎭⎫ ⎝⎛1y 21,,B ()2y 2,为反比例数y=x 2图象上的两点,动点P(x,0)在x 轴上运动,当|AP-BPI 的值最大时,连接OA ,则△AOP 的面积为_________.5、如图(5)所示,反比例函数y=x12在第一象限内的分支经过菱形OACB 的顶点A,B,且点A,B 的横纵坐标都为正整数,则点C 的坐标为__________________.6、如图(6)所示,在反比例函数y=xk 的图象上有A,B 两点,过点A 作AC ⊥x 轴,交x 轴于点C ,连接BC 并延长交y 轴于点D,连接AB,AD,若BD=4CD,ABD S △=8,则k 的值为__________________.(1)(2) (3)7、如图(7)所示,直线y=3x-6分别交x ,y 轴于点A ,B ,M 是反比例函数y=xa (x>0)的图象上位于直线AB 上方的一点,MC//x 轴交AB 于点C,MD ⊥MC 交AB 于点D,若AC ·BD=43则a 的值为__________.8如图(8)所示,正方形ABCD 的顶点A.B 分别在x ,y 轴上,tan ABO=3,正方形的面积为10,反比例函数y=xk 的图象经过点D,则k 的值是_______________. 9如图(9)所示,在平面直角坐标系中,△OAB 的顶点A 在反比例函数y=x 1上,顶点B 在反比例函数y=xk 上,AB ∥x 轴,△OAB 的面积是3,则k 的值为____________. 10、如图(10)所示,在平面直角坐标系中,等边三角形的顶点 A 在反比例函数y=x 1(x>0)上,顶点B,C 在反比例函数y=xk (x>0)上,且点B,C 关于直线y=x 对称.若等边三角形的边长为62,则k 的值为________________.(4) (5) (6) (7) (8) (9) (10)参考答案1、-22、3316-3、5-4、55、(13,13)或(8,8)或(7,7)6、-47、-38、-69、7 10、13。
(江西人教)数学中考专题突破【专题4】反比例函数与几何图形综合题(20页)

本的途径,预计2015年仍会延续此命题方式.
考点探究
专题四
反比例函数与几何图形综合题
考向互动探究
【点拨交流】
1.本题考查了哪些知识?解题的关键是什么?
2.∠BCO与∠BPD有怎样的数量关系?
3.tan∠BCO的值是多少?怎样求线段OC的长?
4.要求点D的坐标,需要求出哪两条线段的长?怎样求?
5.怎样确定反比例函数的解析式?
考点探究
专题四
反比例函数与几何图形综合题
【解题思路】
考点探究
专题四
反比例函数与几何图形综合题
例 1 [2014·南昌] 如图 T4-1,在平面直角坐标系中,Rt△ 1 PBD 的斜边 PB 落在 y 轴上,tan∠BPD= .延长 BD 交 x 轴于点 C, 2 过点 D 作 DA⊥x 轴,垂足为 A,OA=4,OB=3. (1)求点 C 的坐标; k (2)若点 D 在反比例函数 y= (k>0)的图象上,求反比例函数 x 的解析式.考点探究专题四来自反比例函数与几何图形综合题
图T4-3
考点探究
专题四
反比例函数与几何图形综合题
解:(1)过点 C 作 CE⊥AB 于点 E. ∵四边形 ABCD 是梯形,AD=BC ∴DO=CE, ∴△AOD≌△BEC,∴AO=BE=2. ∵BO=6,∴DC=OE=4, ∴C(4,3). k 设反比例函数的解析式为 y= (k≠0), x k 根据题意,得 3= , 4
【点拨交流】
1.本题考查了哪些知识?
2.B,C,D三点的坐标可以看作由点A(2,6)通过怎样的平
移得到?
3.在将矩形向下平移的过程中,哪两点能同时落在函数图 象上? 4.将矩形向下平移 a个单位后点A,C对应的点A′,C′的 坐标怎样表示?
(完整版)应用反比例函数中k的几何意义解题举例

反比例图像上的点与坐标轴围成图形的面积一般地,如图1,过双曲线上任一点A 作x 轴、y 轴的垂线AM 、AN ,,所得矩形AMON 的面积为:S=AM×AN=|x|×|y|=|xy|. 又∵y=xk,∴xy=k. ∴AMON S 矩形=|k|.∴||21k S AOM=∆. 这就是说,过双曲线上任一点,做X 轴、Y 轴的垂线,所得矩形的面积为|k|,这是系数k 的几何意义,明确了k 的几何意义会给解题带来许多方便,请思考下列问题: 1、求函数的解析式例1如图2所示,在平面直角坐标系中,一次函数1y kx =+的图象与反比例函数9y x=的图象在第一象限相交于点A .过点A 分别作x 轴、y 轴的垂线,垂足为点B 、C .如果四边形OBAC 是正方形,求一次函数的关系式.解析 四边形OBAC 是正方形及反比例函数9y x=的图象在第一象限相交于点A ,则正方形OBAC 的面积为:S =xy =9,所以正方形的边长为3,即点A 的坐标(3,3,)。
将点A (3,3,)代入直线得y=32x+1。
2.特殊点组成图形的面积例2如图3,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,若1S =阴影,则12S S += .解析 由A,B 分别向两坐标轴作垂线围成图形的面积相等, ∴S 1+S 阴影=S 2+S 阴影=xy =3. ∵1S =阴影,∴12S S +=2+2=4。
例3如图4,A 、B 是函数2y x=的图象上关于原点对称的任意 AN MXY O ACOBx图2xyABO1S 2S 图3两点,BC ∥x 轴,AC ∥y 轴,△ABC 的面积记为S ,则( ) A .2S = B .4S = C .24S << D .4S >解析 ∵A 、B 是函数2y x=的图象上关于原点对称的任意两点, ∴△ABC 的面积记为S =4S △AOD =4×21xy=4.3、求字母的值例4如图5,直线y=mx 与双曲线y=xk交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM,若ABM S ∆=2,则k 的值是( ) A .2 B 、m-2 C 、m D 、4 解析 ∵直线y=mx 与双曲线y=xk交于A 、B 两点,已知A,B 两点关于原点O 对称,所以ABM S ∆=2S △AOM =2×21xy=xy=2 ∴k=2。
八年级反比例函数综合(含答案)
反比例函数的综合要点一、确定反比例函数的关系式确定反比例函数关系式的方法仍是待定系数法,由于反比例函数中y=kx,只有一个待定系数k,因此只需要知道一对x,y的对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.用待定系数法求反比例函数关系式的一般步骤是:(1)设所求的反比例函数为:y=kx(k≠0);(2)把已知条件(自变量与函数的对应值)代入关系式,得到关于待定系数的方程;(3)解方程求出待定系数k的值;(4)把求得的k值代回所设的函数关系式y=kx中.要点二、反比例函数的图象和性质1.反比例函数的图象特征:反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限;反比例函数的图象关于原点对称,永远不会与x轴、y轴相交,只是无限靠近两坐标轴.要点诠释:(1)若点(a,b)在反比例函数y=kx的图象上,则点(-a,-b)也在此图象上,所以反比例函数的图象关于原点对称;(2)在反比例函数y =k x(k 为常数,k ≠0)中,由于x ≠0且y ≠0,所以两个分支都无限接近但永远不能达到x 轴和y 轴.2.反比例函数的性质(1)如图1,当k >0时,双曲线的两个分支分别位于第一、三象限,在每个象限内,y 值随x 值的增大而减小.(2)如图2,当k <0时,双曲线的两个分支分别位于第二、四象限,在每个象限内,y 值随x 值的增大而增大.要点诠释:反比例函数的增减性不是连续的,它的增减性都是在各自的象限内的增减情况,反比例函数的增减性都是由反比例系数k 的符号决定的;反过来,由双曲线所在的位置和函数的增减性,也可以推断出k 的符号.要点三、反比例函数y =k x(k ≠0)中的比例系数k 的几何意义过双曲线y =k x (k ≠0)上任意一点作x 轴、y 轴的垂线,所得矩形的面积为|k|.过双曲线y =k x (k ≠0)上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为||2k .要点诠释:只要函数式已经确定,不论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.例1.两个反比例函数y =3x ,y =6x在第一象限内的图象如图所示,点P 1,P 2,P 3……P 2020在反比例函数y =6x 图象上,它们的横坐标分别是x 1,x 2,x 3……x 2020,纵坐标分别是1,3,5,…,共2020个连续奇数,过点P 1,P 2,P 3……P 2020分别作y 轴的平行线,与反比例函数y =3x的图象交点依次是Q 1(x 1,y 1),Q 2(x 2,y 2),Q 3(x 3,y 3)……Q 2020(x 2020,y 2020),则y 2020等于()A .2019.5B .2020.5C .2019D .4039例2.如图,直线y =k 1x +b 与双曲线y =2k x A ,B 两点,其横坐标分别为1和5,则不等式k 1x <2k x +b 的解集是.1.一次函数y 1=k 1x +b 和y 2=2k x (k 2>0)相交于A (1,m ),B (3,n )两点,则不等式k 1x +b >2k x的解集为()A.1<x<3B.x<1或x>3C.x<0或x>3D.1<x<3或x<02.反比例函数y=kx和正比例函数y=mx的图象如图.由此可以得到方程kx=mx的实数根为()A.x=﹣2B.x=1C.x1=2,x2=﹣2D.x1=1,x2=﹣2例3.如图,点A在双曲线y=kx的第一象限的那一支上,AB垂直y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.1.如图,在反比例函数y=4x的图象上有一点A向x轴作垂线交x轴于点C,B为线段AC的中点,又D点在x轴上,且OD=3OC,则△OBD的面积为.例4.在平面直角坐标系xOy中,反比例函数y=kx(k≠0,x>0)的图象经过点A(1,-4),直线y=-2x+m与x轴交于点B(1,0).(1)求k,m的值;(2)已知点P(n,-2n)(n>0),过点P作平行于x轴的直线,交直线y=-2x+m于点C,过点P作平行于y轴的直线交反比例函数y=kx(k≠0,x>0)的图象于点D,当PD=2PC时,结合函数的图象,求出n的值.1.如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=kx的图象在同一直角坐标系中,若y3>y2>y1,则自变量x的取值范围是()A.x<﹣1B.﹣1<x<0或x>1.6C.﹣1<x<0D.x<﹣1或0<x<12.设函数y1=kx,y2=kx (k>0),当2≤x≤3时,函数的y1最大值是a,函数y2的最小值是a﹣4,则ak=()A.4B.6C.8D.103.已知反比例函数y=8x和y=3x在第一象限内的图象如图所示,则△AMN的面积为.4.如图,P1是反比例函数y=kx(k>0)图象在第一象限上的一点,点A1的坐标为(2,0).(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?逐渐减少.(2)若点P2在反比例函数图象上,点A2在x轴上,△P1OA1与△P2A1A2均为等边三角形,①求次反比例函数的解析式;②求点A2的坐标.5.如图,反比例函数y=kx图象和一次函数y=ax+b经过M(1,6)和N(2,a).(1)求一次函数解析式;(2)一次函数y=ax+b与x轴交于点B,与y轴交于点A,求证:AM=BN.6.已知:A (a ,y 1).B (2a ,y 2)是反比例函数y =k x (k >0)图象上的两点.(1)比较y 1与y 2的大小关系;(2)若A 、B 两点在一次函数y =43x+b 第一象限的图象上(如图所示),分别过A 、B 两点作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,且S △OAB =8,求a 的值;(3)在(2)的条件下,如果3m =-4x +24,3n =32x ,求使得m >n 的x 的取值范围.7.如图,在平面直角坐标系xOy 中,函数y =k x(x <0)的图象经过点A (﹣1,6),直线y =mx ﹣2与x 轴交于点B (﹣1,0).(1)求k ,m 的值;(2)过第二象限的点P (n ,﹣2n )作平行于x 轴的直线,交直线y =mx ﹣2于点C ,交函数y =k x(x <0)的图象于点D .①当n =﹣1时,判断线段PD 与PC 的数量关系,并说明理由;②若PD ≥2PC ,结合函数的图象,直接写出n 的取值范围.8.在平面直角坐标系xOy中,函数y=mx(x>0)的图象G与直线l:y=kx-4k+1交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.(1)求m的值;(2)横、纵坐标都是整数的点叫做整点.记图象G与直线l围成的区域(不含边界)为W.①当n=5时,求k的值,并写出区域W内的整点个数;②若区域W内恰有5个整点,结合函数图象,求k的取值范围.【经典例题1】A【解析】解:∵P n 的纵坐标为:2n -1,∴P 2020的纵坐标为2×2020-1=4039.∵y =与y =在横坐标相同时,y =的纵坐标是y =的纵坐标的2倍,∴y 2020=×4039=2019.5.∴A 答案正确.【经典例题2】-5<x <-1或x >0【解析】解:根据一次函数平移和反比例函数的对称性可得,直线y =k 1x -b 与双曲线y =2k x 交于第三象限点的坐标为(-5,-1)和(-1,-5),如下图所示,∴不等式k 1x <2k x +b ,即k 1x -b <2k x 的解集,即当直线y =k 1x -b 的图象在反比例函数y =2k x 图象的下方对应的自变量x 的取值范围为:-5<x <-1或x >0.【举一反三1】D【解析】解:如图,由图象可得:不等式k 1x +b >2k x 的解集是1<x <3或x <0.故选:D .【举一反三2】C【解析】解:如图,反比例函数y =和正比例函数y =mx 相交于点A (﹣2,1),∴另一个交点为:(2,﹣1),∴方程=mx 的实数根为:x 1=2,x 2=﹣2.故选:C .【经典例题3】163【解析】解:连DC ,∵AE =3EC ,S △ADE =3,∴S △CDE =1.∴S △ADC =4.设A (a ,b ),则AB =a ,OC =2AB =2a .∵D 为OB 的中点,∴BD =OD =12b .∵S 梯形OBAC =S △ABD +S △ADC +S △ODC ,12(a +2a )·b =12a ·12b +4+12·2a ·b ,∴ab =163.把A (a ,b )代入y =,得k =ab =163.【举一反三1】3【解析】解:设A (x 、y ),由反比例函数y =4x可知xy =4,BC =AC =y ,OD =3OC =3x ,∴S △OBD =BC ×OD =×y ×3x =xy =×4=3.故答案为:3.【经典例题4】【解析】解:(1)把A(1,-4)代入y=k x,得k=1×(-4)=-4;把B(1,0)代入y=-2x+m,得-2+m=0,解得m=2;(2)反比例函数解析式为y=-(x>0),一次函数解析式为y=-2x+2,如图,当y=-2n时,-2x+2=-2n,解得x=n+1,则C(n+1,-2n),∴PC=n+1-n=1,当y=-2n时,y=-=,∴D(n,-),∴PD=|-2n+|,∵PD=2PC,∴|-2n+|=2,当-2n+=2时,解得n1=-2(舍去),n2=1,当-2n+=-2时,解得n1=-1(舍去),n2=2,综上所述,当PD=2PC时,n=1或n=2.【自我检测1】B【解析】解:由图象可知,当﹣1<x<0或x>1.6时,双曲线y3落在直线y2上方,且直线y2落在直线y1上方,即y3>y2>y1,所以若y3>y2>y1,则自变量x的取值范围是﹣1<x<0或x>1.6.故选:B.【自我检测2】C【解析】解:∵k>0,2≤x≤3,∴y1随x的增大而减小,y2随x的增大而增大,∴当x=2时,y1取最大值,最大值为=a①;当x=2时,y2取最小值,最小值为﹣=a﹣4②;由①②得a=2,k=4,∴ak=8,故选:C.【自我检测3】25 16【解析】解:设A(a,),则M(a,),N(,),∴AN=a﹣=,AM=﹣=,∴△AMN的面积=AN×AM=××=25 16,故答案为:25 16.【自我检测4】【解析】解:(1)△P1OA1的面积逐渐减少;(2)作P1C⊥OA1于C,∵△P1OA1为等边三角形,A1(2,0),∴OC=1,P1C3P1(1,3).∴反比例函数的解析式为y=3 x.(3)作P2D⊥A1A2于D,如上图,设A1D=x,则OD=2+x,P2D3x,∴P2(2+x3x).将点P2代入y=3x,得y332x=+.x2+2x-1=0,解得x1=-2,x2=-12<0(舍).∴x=-2,OA2=2+x+x=2+2x=2+2(-2)=22.∴A2(22,0).【自我检测5】【解析】解:(1)∵点M(1,6)在反比例函数y=图象上,∴k=1×6=6,∴反比例函数的关系式为y=,把N(2,a)代入得,a==3,∴N(2,3).∵点M(1,6)和N(2,3)在一次函数y=ax+b的图象上,∴a+b=6,2a+b=3,解得a=﹣3,b=9,∴一次函数的关系式为y=﹣3x+9;(2)过点M、N分别作MC⊥OA,ND⊥OB,垂足分别为C、D,当x=0时,y=9,当y=0时,x=3,∴一次函数y=﹣3x+9与x轴的交点B(3,0),与y轴的交点A(0,9),由于A(0,9),B(3,0),M(1,6),N(2,3),∴MC=1,AC=9﹣6=3,ND=3,BD=3﹣2=1,∴MC=BD=1,AC=ND=3,又∵∠ACM=∠NDB=90°,∴△ACM≌△NDB(SAS),∴AM=BN.【自我检测6】【解析】解:(1)∵A、B是y=kx(k>0)图象上的两点,∴a≠0.当a>0时,A、B在第一象限,a<2a,∴此时y1>y2,同理,a<0时,y1<y2.(2)∵A(a,y1)、B(2a,y2)在y=kx(k>0)图象上,∴AC=y1=,BD=y2=.∴y1=2y2.又A (a ,y 1)、B (2a ,y 2)在y =a +b 图象上,∴y 1=a +b ,y 2=a +b .∴a +b =2(a +b ),得b =4a .∵S △AOC +S 梯形ACDB =S △AOB +S △BOD ,又S △AOC =S △BOD ,∴S 梯形ACDB =S △AOB ,即[(a +b )+(a +b )]•a =8.∴a 2=4,由a >0,得a =2.(3)由(2)知,一次函数y =x +8,反比例函数y =.∵A 、B 两点的横坐标分别为2,4,且m =x +8,n =,∴使得m >n 的x 的范围,是反比例函数的图象在一次函数图象下方的点的横坐标取值范围.∴由图可知,2<x <4或x <0.【自我检测7】【解析】解:(1)∵函数y =k x (x <0)的图象经过点A (﹣1,6),∴k =﹣6.∵直线y =mx ﹣2与x 轴交于点B (﹣1,0),∴m =﹣2.(2)①判断:PD =2PC .理由如下:当n =﹣1时,点P 的坐标为(﹣1,2),∵y =﹣2x ﹣2交于于点C ,且点P (﹣1,2)作平行于x 轴的直线,∴点C 的坐标为(﹣2,2),∵函数y =k x(x <0)的图象于点D ,且点P (﹣1,2)作平行于x 轴的直线,点D 的坐标为(﹣3,2).∴PC =1,PD =2.∴PD =2PC .②当PD=2PC时,有两种情况,分别为:y=2,或者y=6.若PD≥2PC,0<y≤2,或y≥6即0<﹣2n≤2,或﹣2n≤6解得﹣1≤n<0.或n≤﹣3【自我检测8】【解析】(1)解:把A(4,1)代入y=mx(x>0),得m=4×1=4;(2)①当n=5时,把B(1,5)代入直线l:y=kx-4k+1得,5=k-4k+1,解得k=4 3-,如图所示,区域W内的整点有(2,3),(3,2),有2个;(3)直线l:y=kx-4k+1过(1,6)时,k=53-,区域W内恰有4个整点,直线l:y=kx-4k+1过(1,7)时,k=-2,区域W内恰有5个整点,∴区域W内恰有5个整点时,k的取值范围是-2≤k<5 3-.。
2023成都各区二诊复习——反比例函数综合解答题(解析版)
1.(2021-2022七中育才二诊模拟·18)(10分)如图,在平面直角坐标系中,直线3y x b =+经过点(1,0)A -,与y 轴正半轴交于B 点,与反比例函数(0)k y x x=>交于点C ,且3AC AB =,//BD x 轴交反比例函数(0)k y x x =>于点D .(1)求b 、k 的值;(2)如图1,若点E 为线段BC 上一点,设E 的横坐标为m ,过点E 作//EF BD ,交反比例函数(0)k y x x=>于点F .若13EF BD =,求m 的值.(3)如图2,在(2)的条件下,连接FD 并延长,交x 轴于点G ,连接OD ,在直线OD 上方是否存在点H ,使得ODH D 与ODG D 相似(不含全等)?若存在,请求出点H 的坐标;若不存在,请说明理由.【考点】反比例函数综合题【专题】存在型;反比例函数及其应用;推理能力【分析】(1)将点A 代入一次函数求出b 的值,然后根据3AC AB =求出点C 的坐标,即可求出反比例函数的解析式;(2)将E 点横坐标代入33y x =+,求出纵坐标,根据//EF BD 即可知道F 的纵坐标,代入反比例函数的解析式,求出F 的横坐标,即可表示出EF 的长度,同理将B 点纵坐标代入反比例函数求出D 点横坐标,从而表示出BD 的长,根据13EF BD =列方程即可求解m 的值;(3)根据相似三角形的性质可知,需要分三种情况,当HOD DOG Ð=Ð时,当HOD DGO Ð=Ð时,当HOD ODG Ð=Ð时三种情况,分别画出图形,列出等式求解即可.【解答】解:(1)作CM x ^轴于M ,如图1:BOA CMA Ð=ÐQ ,BAO CAM Ð=Ð,BOA CMA \D D ∽,Q 直线3y x b =+经过点(1,0)A -,30b \-+=,解得3b =,\直线解析式为:33y x =+,(0,3)B \,3AC AB =Q ,39CM BO \==,33AM OA ==,C \点坐标为(2,9),\将C 点坐标代入k y x=,得18k =.(2)//BD x Q 轴,D \点的纵坐标为3,代入18y x=,得6x =,D \点坐标为(6,3),将E 点横坐标代入33y x =+,得33y m =+,//EF BD Q ,F \点纵坐标为33m +,代入18y x =,得61x m =+,F \点坐标为6(1m +,33)m +,13EF BD =Q ,\,解方程得1m =或4-(舍),1m \=.(3)存在,理由如下:如图2,过点D 作DQ x ^轴于点Q ,由(2)知(3,6)F ,(6,3)D ,\直线FD 的解析式为:9y x =-+,6OQ =,3DQ =,9OG \=,:3DQ GQ \=,45QGD QDG \Ð=Ð=°.OD \=DG =Ⅰ、当HOD DOG Ð=Ð时,如图2所示,设BD 与OH 交于点P ,由(2)知,//BD x 轴,BDO DOG \Ð=Ð,BDO HOD \Ð=Ð,OP PD \=,设OP m =,则6BP m =-,在Rt OBP D 中,由勾股定理可得,2223(6)m m =+-,解得154m =;94BP \=;9(4P \,3),\直线OP 的解析式为:43y x =;①若ODG ODH D D ∽,则::1OD OD OG OH ==,不符合题意,舍去;②若ODG OHD D D ∽,::OD OH OG OD \=,即9:OH =,解得5OH =,设(3,4)H t t ,222(3)(4)5t t \+=,解得1t =,负值舍去,(3,4)H \;Ⅱ、当HOD DGO Ð=Ð时,①若ODG DHO D D ∽,如图4,DOG ODH \Ð=Ð,::DG OH OG DO =,//DH OG \,即点H 在BD 上,9:OH =OH \=1BH \=,(1,3)H \,直线OH 的解析式为:3y x =;②若ODG HDO D D ∽,::DG OD OG OH \=,即9:OH =,解得OH =,设(,3)H t t ,222(3)t t \+=,解得92t =,负值舍去,9(2H \,272;Ⅲ、当HOD ODG Ð=Ð时,//OH EG ,\直线OH 的解析式为:y x =-;①若ODG DOH D D ∽,则::1OD OD OG DH ==,不符合题意,舍去;②若ODG HOD D D ∽,如图5,::OD OH DG OD \=,即OH =,解得OH =,设(,)H t t -,222()t t \+-=,解得152t =-,正值舍去,15(2H \-,15)2;综上,符合题意的点H的坐标为:(3,4)或(1,3)或9(2,272或15(2-,15)2.【点评】本题属于反比例函数综合问题,涉及待定系数法求函数解析式,相似三角形的性质与判定,分类讨论思想;用坐标表示线段长度,然后列方程是解决这类试题的关键.2.(2021-2022七中育才二诊·18)(10分)直线2y x=与双曲线2yx=交于A,B两点,C是第一象限内的双曲线上A点右侧任意一点;(1)如图1,求A,B两点坐标;(2)如图2,连接BC,若45ABCÐ=°,求点C的坐标;(3)如图3,设直线AC,BC分别与x轴相交于D,E两点,且AC mCD=,BC nCE=,求n m-的值.【考点】反比例函数综合题【专题】代数几何综合题;推理能力【分析】(1)当22x x=时,解方程可得点A 、B 的横坐标,从而得出答案;(2)过点A 作AD AB ^,交直线BC 于D ,过A 作x 轴的平行线HG ,作DG HG ^于G ,BH HG ^于H ,利用AAS 证明ABH DAG D @D ,得4AG BH ==,2DG AH ==,则(5,0)D ,利用待定系数法求出直线BD 的解析式为1533y x =-,从而求出交点C 的坐标;(3)作AG x ^轴于G ,CH AG ^于H ,BQ CH ^,交CH 的延长线于Q ,设2(,C a a,利用平行线分线段成比例定理得222222AC AH a a m CD HG a --====,同理得,222222BC BQ a a n CE PQ a++====,即可得出答案.【解答】解:(1)当22x x=时,解得1x =±,(1,2)A \,(1,2)B --;(2)过点A 作AD AB ^,交直线BC 于D ,过A 作x 轴的平行线HG ,作DG HG ^于G ,BH HG ^于H ,45ABD Ð=°Q ,AB AD \=,90ABH HAB Ð+Ð=°Q ,90BAH DAG Ð+Ð=°,ABH DAG \Ð=Ð,H G Ð=ÐQ ,()ABH DAG AAS \D @D ,4AG BH \==,2DG AH ==,(5,0)D \,\直线BD 的解析式为1533y x =-,\15233x x-=,解得16x =,21x =-(舍去),当6x =时,13y =,1(6,3C \;(3)作AG x ^轴于G ,CH AG ^于H ,BQ CH ^,交CH 的延长线于Q ,设2(,)C a a,//CH DG Q ,\222222AC AH a a m CD HG a--====,同理得,222222BC BQ a a n CE PQ a++====,2222222a a n m +-\-=-=.【点评】本题是反比例函数综合题,主要考查了反比例函数与一次函数交点问题,全等三角形的判定与性质,平行线分线段成比例定理等知识,利用平行线分线段成比例表示出m 和n 是解题的关键.3.(2021-2022成华区二诊·18)(10分)如图,直线2y x =与反比例函数1(0)k y x x=>的图象交于点(,6)A m ,以OA 为边作Rt ABO D ,使点B 在第二象限,90AOB Ð=°,2AO BO =.(1)求反比例函数1(0)k y x x=>的表达式;(2)求直线AB 的表达式;(3)过点B 的反比例函数2(0)k y x x=<与直线AB 的另一个交点为C ,求BOC D 的面积.【考点】反比例函数综合题【专题】代数几何综合题;推理能力【分析】(1)将(,6)A m 代入2y x =得:26m =,可得点A 的坐标,再将点A 的坐标代入1k y x=,可得答案;(2)过点A 作AD x ^轴于D ,过点B 作BE x ^轴于E ,利用BOE OAD D D ∽,可得BE 和OE 的长,则得出点B 的坐标,再利用待定系数法求出直线AB 的解析式即可;(3)设直线AB 与y 轴的交点为F ,可得点F 的坐标,将3(3,)2B -代入2(0)k y x x =<得2k 的值,联立方程组可得点C 的坐标,则BOC BOF COF S S S D D D =-,代入即可解决问题.【解答】解:(1)将(,6)A m 代入2y x =得:26m =,3m \=,(3,6)A \,将(3,6)A 代入1k y x =得:13618k =´=,18y x\=,\反比例函数1(0)k y x x =>的表达式为18(0)y x x =>;(2)如图,过点A 作AD x ^轴于D ,过点B 作BE x ^轴于E ,AD x ^Q 轴,6AD \=,3OD =,90ODA Ð=°,BE x ^Q 轴,90BEO ODA \Ð=Ð=°,90EBO BOE \Ð+Ð=°,90AOB Ð=°Q ,18090BOE AOD AOB \Ð+Ð=°-Ð=°,EBO AOD \Ð=Ð,BOE OAD \D D ∽,\BO OE BE AO AD OD==,2AO BO =Q ,\1632OE BE ==,3OE \=,32BE =,Q 点B 在第二象限,3(3,2B \-,设直线AB 的表达式为:(0)y m x n m ¢¢=+¹,代入(3,6)A ,3(3,)2B -,得:36332m n m n ¢+=ìïí¢-+=ïî,解得34154m n ì¢=ïïíï=ïî,31544y x \=+,\直线AB 的表达式为31544y x =+;(3)如图,设直线AB 与y 轴的交点为F ,31544y x =+Q ,\当0x =时,1515044y =+=,15(0,4F \,154OF \=,将3(3,2B -代入2(0)k y x x=<得:239322k =-´=-,9(0)2y x x-\=<,联立9231544y x y x -ì=ïïíï=+ïî,解得332x y =-ìïí=ïî(不符合题意,舍去)或294x y =-ìïí=ïî,9(2,)4C \-,BOC BOF COFS S S D D D \=-11||||22B C OF x OF x =×-×115115322424=´´-´´158=,BOC \D 的面积为158.【点评】本题是反比例函数综合题,主要考查了函数图象上点的坐标的特征,待定系数法求函数解析式,函数与方程的关系,相似三角形的判定与性质等知识,构造相似三角形求出点B 的坐标是解题的关键.4.(2021-2022高新区二诊·18)(10分)在平面直角坐标系xOy 中,直线12y x b =-+与反比例函数6y x=的图象交于(2,)A m ,B 两点.(1)求直线AB 的函数表达式;(2)如图1,过点A 的直线分别与x 轴,y 轴交于点M ,N ,若AM MN =,连接BM ,求ABM D 的面积;(3)如图2,以AB 为边作平行四边形ABCD ,点C 在y 轴负半轴上,点D 在反比例函数(0)k y k x=<的图象上,线段AD 与反比例函数(0)k y k x =<的图象交于点E ,若12DE AE =,求k 的值.【分析】(1)将(2,)A m 代入直线12y x b =-+与反比例函数6y x=,可得答案;(2)首先求出交点B 的坐标,过点A 作AP y ^轴于P ,利用NOM NPA D D ∽,可得OM 的长,从而得出MD 的长,再计算ABM ADM BDM S S S D D D =-即可;(3)设(0,)C a ,利用平行四边形的性质可得(4,2)D a -+,过D 作x 轴的平行线l ,过点A 、E 作l 的垂线,垂足分别为G ,H ,根据DEG DAH D D ∽,表示出点E 的坐标,从而得出方程解决问题.【解答】解:(1)当2x =时,反比例函数632y ==,(2,3)A \,将点(2,3)A 代入12y x b =-+得,4b =,\一次函数的解析式为142y x =-+;(2)联立1426y x y x ì=-+ïïíï=ïî,\23x y =ìí=î或61x y =ìí=î,(6,1)B \,当0y =时,1402x -+=,8x \=,(8,0)D \,过点A 作AP y ^轴于P ,//OM AP Q ,NOM NPA \D D ∽,\OM MN AP AN =,\122OM =,1OM \=,7MD \=,17(31)72ABM ADM BDM S S S D D D \=-=´´-=;(3)设(0,)C a ,Q 四边形ABCD 是平行四边形,//AB CD \,AB CD =,(4,2)D a \-+,过D 作x 轴的平行线l ,过点A 、E 作l 的垂线,垂足分别为G ,H ,AHD EGD \Ð=Ð,EDG ADH Ð=Ð,DEG DAH \D D ∽,\13DG EG DE DH AH AD ===,123DG DH \==,111333EG AH a ==-,\点27(2,)33E a -+,Q 点D 、E 都在反比例函数k yx 上,272(4(2)33a a \-´+=-+,解得54a =-,54(2)4(2)34k a \=-+=-´-+=-.【点评】本题是反比例函数综合题,主要考查了函数图象上点的坐标的特征,反比例函数图象与一次函数图象的交点问题,平行四边形的性质,相似三角形的判定与性质等知识,作辅助线构造相似三角形是解题的关键.5.(2021-2022高新区二诊·18)(10分)如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA ,OC 分别在x 轴和y 轴上,顶点B 的坐标为(4,2),反比例函数(0)k y x x=>的图象经过对角线OB 的中点E ,与矩形的边BC ,BA 分别交于点F ,G ,设直线FG 的函数表达式为y ax b =+.(1)求k ,a ,b 的值;(2)利用图象,直接写出当k ax b x+…时x 的取值范围;(3)若点P 在矩形的边OA 上,且PFG D 为等腰三角形,求点P 的坐标.【考点】反比例函数综合题【专题】综合题;分类讨论;图形的相似;等腰三角形与直角三角形;应用意识;反比例函数及其应用;一次函数及其应用【分析】(1)过点E 作EM OC ^于点M ,由OME OCB D D ∽,点E 为对角线OB 的中点,可得(2,1)E ,用待定相似法即得2y x =,设(,2)F m ,(4,)G n ,根据反比例函数图象上点坐标特征可得1m =,12n =,(1,2)F ,1(4,)2G ,用待定系数法即得12a =-,52b =;(2)由图象直接可得01x <…或4x …;(3)设(,0)P m ,有222145(14)(224FG =-+-=,22(1)4PF m =-+,221(4)4PG m =-+,分三种情况:当GF PF =时,245(1)44m -+=,P ,0);当PF PG =时,221(1)4(4)4m m -+=-+,15(8P ,0);当GF PG =时,(4P -,0).【解答】解:(1)过点E 作EM OC ^于点M ,如图:90OME OCB \Ð=Ð=°,MOE COB Ð=Ð,OME OCB \D D ∽,Q 点E 为对角线OB 的中点,\12OE ME OM OB BC OC ===,(4,2)B Q ,112OM OC \==,122EM BC ==,(2,1)E \,Q 反比例函数(0)k y x x =>的图象经过点E ,12k \=,即2k =,2y x\=,Q 点F ,G 分别在矩形的边BC ,BA 上,\设(,2)F m ,(4,)G n ,Q 点F ,G 在2y x =上,22m \=,24n =,1m \=,12n =,(1,2)F \,1(4,2G ,将(1,2)F ,1(4,2G 分别代入y ax b =+得:2142a b a b +=ìïí+=ïî,解得1252a b ì=-ïïíï=ïî,1522y x \=-+,2k \=,12a =-,52b =;(2)由图象可知:当01x <…或4x …时,k ax b x+…;(3)设(,0)P m ,(1,2)F Q ,1(4,2G ,222145(14)(224FG \=-+-=,22(1)4PF m =-+,221(4)4PG m =-+,当GF PF =时,245(1)44m -+=,m =(此时P 不在边OA 上,舍去),P \当PF PG =时,221(1)4(4)4m m -+=-+,解得158m =,15(8P \,0),当GF PG =时,2145(4)44m -+=,解得4m =(此时P 不在边OA 上,舍去)或4m =(4P \-,0),综上,点P 的坐标为,0)或15(8,0)或(4-0).【点评】本题考查一次函数、反比例函数综合应用,涉及矩形性质与应用,等腰三角形性质及应用,相似三角形判定与性质等知识,解题的关键是作辅助线,构造相似三角形求出点E 的坐标及分类讨论思想的应用.6.(2021-2022金牛区二诊·18)(10分)如图,一次函数2y x =-+的图象与两坐标轴分别交于A ,B 两点,与反比例函数k y x=交于点C 、D ,且点C 坐标为(2,)m -.(1)求反比例函数的解析式;(2)若点M 在y 轴正半轴上,且与点B ,C 构成以BC 为腰的等腰三角形,求点M 的坐标.(3)点P 在第二象限的反比例函数图象上,若tan 3OCP Ð=,求点P 的坐标.【考点】反比例函数综合题【专题】反比例函数及其应用;代数几何综合题;推理能力【分析】(1)先确定C 点的坐标,再代入反比例函数解析式中,即可得出结论;(2)分两种情况,利用等腰三角形的性质,即可得出结论;(3)作OQ PC ^于Q ,过Q 作HG x ^轴于G ,////CH x 轴,交HG 于H ,利用CHQ QGO D D ∽,且tan 3OCP Ð=,得13CQ OQ =,设CH x =,则3GQ x =,43HQ x =-,可得方程31292OG HQ x x ==-=+,求出点Q 的坐标,求出CQ 的解析式,从而解决问题.【解答】解:(1)Q 点(2,)C m -在一次函数2y x =-+的图象上,(2)2m \=--+,解得:4m =,(2,4)C \-,将(2,4)C -代入k y x=,得8k =-,\反比例函数为8y x =-;(2)如图1,过点C 作CH y ^轴于H ,在直线2y x =-+中,当0x =时,则2y =,(0,2)B \,由(1)知,(2,4)C -,BC \==,当BM BC ==时,2OM =,(0M \,2),当BC MC =时,点C 在BM 的垂直平分线,(0,6)M \,综上所述,点M 的坐标为(0,2)+或(0,6)(3)作OQ PC ^于Q ,过Q 作HG x ^轴于G ,////CH x 轴,交HG 于H ,则CHQ QGO D D ∽,\CQCHHQOQ QG OG ==,tan 3OCP Ð=Q ,\13CQOQ =,设CH x =,则3GQ x =,43HQ x =-,31292OG HQ x x \==-=+,解得1x =,(3,3)Q \-,\直线CQ 的解析式为6y x =+,86x x\+=-,解得12x =-,24x =-,Q 点P 与B 不重合,(4,2)P \-.【点评】本题是反比例函数综合题,主要考查了函数图象上点的坐标的特征,等腰三角形的性质,相似三角形的判定与性质,三角函数,待定系数法求函数解析式等知识,构造相似三角形求出点Q 的坐标是解题的关键.7.(2021-2022锦江区二诊·18)(10分)如图,点B 坐标为(5,2),过点B 作BA y ^轴于点A ,作BC x ^轴于点C ,点D 在第一象限内.(1)如图1,反比例函数1(0)m y x x =>的图象经过点B ,点D ,且直线OD 的表达式为52y x =,求线段OD 的长;(2)将线段OD 从(1)中位置绕点O 逆时针旋转得到OD ¢(如图2),反比例函数2(0)n y x x =>的图象过点D ¢,交AB 于点E ,交BC 于点F ,连接OE ,OF ,EF .①若AE CF EF +=,求n 的值;②若90OEF Ð=°时,设D ¢的坐标为(,)a b ,求2()a b +的值.【考点】反比例函数综合题【专题】反比例函数及其应用【分析】(1)先求得反比例函数的解析式,然后可求得点D 的坐标,从而可求得OD 的值;(2)①由反比例函数k 的几何意义可知OA AE OC CF n ×=×=,然后将AE ,CF 的长度代入AE CF EF +=得到52n BE =-,25n BF =-,710n EF =,然后在Rt △EF 中,依据勾股定理可求得n 的值;②易证AOE BEF D D ∽,根据相似三角形的性质可得2:(5):(2)225n n n =--,可求出n 的值,进一步根据完全平方公式和勾股定理即可求值.【解答】解:(1)Q 反比例函数1(0)m y x x =>的图象经过点B ,点B 坐标为(5,2),2510m \=´=,\反比例函数的解析式为:110y x=,Q 点D 在双曲线110y x =和直线52y x =上,联立110y x =和52y x =,解得2x =或2x =-,Q 点D 在第一象限内,\点(2,5)D ,OD \==;(2)①Q 函数2n y x=的图象经过点E ,F ,OA AE OC CF n \×=×=,5OC =Q ,2OA =,52CF AE n \==,5n CF \=,2n AE =,52n BE AB AE \=-=-,25n BF BC CF =-=-,AE CF EF +=Q ,75210n n n EF \=+=,在Rt BEF D ,由勾股定理得:222EF BE BF =+,2227((5(2)1025n n n \=-+-,整理得20=解得n =或n =),n \=②90OEF Ð=°Q ,90AEO BEF \Ð+Ð=°,BA y ^Q 轴,BC x ^轴,90ABC \Ð=°,90BEF BFE \Ð+Ð=°,AEO BFE \Ð=Ð,AOE BEF \D D ∽,::OA AE BE BF \=,5n CF =Q ,2n AE =,52n BE =-,25n BF =-,2:(5:(2225n n n \=--,解得10n =(舍)或85n =,D ¢Q 的坐标为(,)a b ,85ab \=,由(1)得OD =OD \¢=2229a b \+=,28161()29255a b \+=+´=.【点评】本题主要考查的是反比例函数的综合应用,涉及反比例函数k 的几何意义、勾股定理、两点间的距离公式、相似三角形的性质和判定等,本题综合性较强.8.(2021-2022郫都区二诊·18)(10分)如图,一次函数4y kx k =-的图象与x 轴、y 轴分别交于点B 、点A ,与反比例函数2(0)y x x=>的图象交于点C 、点D .(1)直接写出点B 的坐标;(2)作CE y ^轴于E ,作DF x ^轴于F .连接EF ,求证://EF CD ;(3)若点N 在x 轴上,且满足90CND Ð=°的N 点有且只有一个,求k 的值.【考点】反比例函数综合题【专题】代数几何综合题;推理能力【分析】(1)令0y =时,得4x =,可得点B 的坐标;(2)连接CF ,DE ,根据1122CEF S CE OE k D =´=,1122DEF S DF OF k D =´=,得CEF DEF S S D D =,可证明结论;(3)联立两个函数解析式,设C 、D 两点的横坐标为m 、n ,则4m n +=,2mn k =-,再根据CPN NQD D D ∽,得CP PN NQ DQ=,设(,0)N x ,若要存在唯一的N ,则当△240b ac =-=时,从而得出答案.【解答】(1)解:当0y =时,40kx k -=,4x \=,(4,0)B \;(2)证明:连接CF ,DE ,1122CEF S CE OE k D =´=Q ,1122DEF S DF OF k D =´=,CEF DEF S S D D \=,//CD EF \;(3)解:Q 直线4y kx k =-与双曲线2(0)y x x=>的交点为C ,D 点,24kx k x \-=,2420kx kx \--=,设C 、D 两点的横坐标为m 、n ,则4m n +=,2mn k=-,作CP x ^轴于P ,DQ x ^轴于Q ,90CPN NQD \Ð=Ð=°,当90CND Ð=°时,90PCN DNQ CNP Ð=Ð=°-Ð,CPN NQD \D D ∽,\CP PN NQ DQ=,设(,0)N x ,则PN x m =-,2CP m=,NQ n x =-,DQ n =,\22x m m n xn-=-,22420x x k k\---=,当△224164(2)0b ac k k =-=---=,1k \=-时,存在唯一的点N ,满足90CND Ð=°.【点评】本题是反比例函数综合题,主要考查了反比例函数与一次函数的交点问题,反比例函数k 的几何意义,相似三角形的判定与性质,一元二次方程等知识,利用代数方法解决几何问题是解决问题(3)的关键.9.(2021-2022青羊区树德中学二诊·18)(10分)如图,点A 是反比例函数12(0)y x x =>图象上的任意一点,过点A 作//AB x 轴,交y 轴于点C ,交另一个反比例函数2(0,0)k y k x x=<<的图象于点B .(1)若A 点坐标为(,4)a ,且3BC AC =,求a ,k 的值;(2)若8k =-,且90AOB Ð=°,求A 点的坐标;(3)若不论点A 在何处,反比例函数2(0,0)k y k x x =<<图象上总存在一点D ,使得四边形AOBD 为平行四边形,求k 的值.【考点】反比例函数综合题【专题】反比例函数及其应用;代数几何综合题;推理能力【分析】(1)根据点(,4)A a 在反比例函数12y x=的图象上求出a ,根据题意求出点B 的坐标,进而求出k ;(2)过点A 作AE x ^轴于点E ,过点B 作BF x ^轴于点F ,根据勾股定理列出方程,解方程得到答案;(3)根据平行四边形的性质用n 表示出点D 的坐标,根据反比例函数图象上点的坐标特征列式计算即可.【解答】解:(1)Q 点(,4)A a 在反比例函数12y x=的图象上,42a \=,解得:12a =,则点A 的坐标为1(2,4),//AB x Q 轴,\点B 的纵坐标为4,3BC AC =Q ,\点B 的横坐标为32-,3462k \=-´=-,综上所述,12a =,6k =-;(2)过点A 作AE x ^轴于点E ,过点B 作BF x ^轴于点F ,设点A 的坐标为2(,)n n ,则点B 的坐标为2(4,n n-,(4)5AB n n n \=--=,由勾股定理得:OA =,OB =,90AOB Ð=°Q ,222OA OB AB \+=,即2222222((4)()(5)n n n n n++-+=,解得:11n =,21n =-(不合题意,舍去),\点A 的坐标为(1,2);(3)由题意可知,当四边形AOBD 为平行四边形时,点D 在点B 的上方,设点A 的坐标为2(,)n n ,则点B 的坐标为(2nk ,2n,Q 四边形AOBD 为平行四边形,//BD OA \,BD OA =,\点D 的坐标为(2nk n +,4n,Q 点D 在反比例函数2k y x =的图象上,4()2nk n k n\+´=,解得:4k =-.【点评】本题考查的是反比例函数的图象和性质、平行四边形的性质,掌握反比例函数图象上点的坐标特征是解题的关键.10.(2021-2022青羊区二诊·18)(10分)如图1,一次函数312y x =-+的图象与反比例函数(0)k y k x=>的图象相交于A ,B 两点(A 在B 的左侧),与x 轴和y 轴分别交于E ,F 两点.(1)当9k =时,求A ,B 两点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P ,使PAB D 是以点B 为直角顶点的直角三角形?若存在,求出点P 的坐标,若不存在,请说明理由;(3)如图2,连接AO 并延长交反比例函数(0)k y k x =>图象的另一支于点C ,连接BC 交y 轴于点G .若2BG CG =,求反比例函数的表达式.【考点】反比例函数综合题【专题】待定系数法;一次函数及其应用;反比例函数及其应用;等腰三角形与直角三角形;应用意识【分析】(1)当9k =时,反比例函数为9y x =,解9312y x y x ì=ïíï=-+î得(1,9)A ,(3,3)B ;(2)设9(,)P m m ,又(1,9)A ,(3,3)B ,可得222(13)(93)40AB =-+-=,2229(1)(9)AP m m=-+-,2229(3)(3)BP m m =-+-,根据PAB D 是以点B 为直角顶点的直角三角形,可得222299(1)(9)40(3)(3)m m m m-+-=+-+-,解得(9,1)P --;(3)过B 作BT y ^轴于T ,过C 作CK y ^轴于K ,由A 、B 在直线312y x =-+上,设(,312)A a a -+,(,312)B b b -+,可得(,312)C a a --,||CK a a =-=,||BT b b ==,又CKG BTG D D ∽,得2BG BT CG CK ==,2BT CK =,即2b a =①,又(,312)A a a -+,(,312)B b b -+都在k y x=图象上,有(312)(312)a a b b -+=-+②,联立①②可解得4(3A ,8),8(3B ,4),即得反比例函数的表达式为323y x=.【解答】解:(1)当9k =时,反比例函数为9y x=,解9312y x y x ì=ïíï=-+î得19x y =ìí=î或33x y =ìí=î,(1,9)A \,(3,3)B ;(2)存在一点P ,使PAB D 是以点B 为直角顶点的直角三角形,理由如下:如图:设9(,)P m m,又(1,9)A ,(3,3)B ,222(13)(93)40AB \=-+-=,2229(1)(9)AP m m =-+-,2229(3)(3)BP m m =-+-,PAB D Q 是以点B 为直角顶点的直角三角形,222AP AB BP \=+,即222299(1)(9)40(3)(3)m m m m -+-=+-+-,整理化简得:26270m m +-=,解得9m =-或3m =(不符合题意,舍去),(9,1)P \--;(3)过B 作BT y ^轴于T ,过C 作CK y ^轴于K ,如图:由A 、B 在直线312y x =-+上,设(,312)A a a -+,(,312)B b b -+,由已知可得A 、C 关于原点对称,(,312)C a a \--,||CK a a \=-=,||BT b b ==,CGK BGT Ð=ÐQ ,90BTG CKG Ð=°=Ð,CKG BTG \D D ∽,\2BG BT CG CK==,2BT CK \=,2b a \=①,又(,312)A a a -+,(,312)B b b -+都在k y x=图象上,(312)(312)a a b b \-+=-+②,联立①②可解得00a b =ìí=î(不符合题意,舍去)或4383a b ì=ïïíï=ïî,4(3A \,8),8(3B ,4),把4(3A ,8)代入k y x =得:432833k =´=,\反比例函数的表达式为323y x=.【点评】本题考查反比例函数及一次函数的综合应用,涉及待定系数法,求反比例函数及一次函数图象的交点、直角三角形性质及应用、相似三角形等知识,解题的关键是数形结合、方程思想等重要数学思想的应用.11.(2021-2022双流区二诊·18)(10分)如图,点(1,)A m 和点B 是反比例函数1(0,0)k y k x x=>>图象上的两点,一次函数22(0)y ax a =+¹的图象经过点A ,与y 轴交于点C ,过点B 作BD x ^轴,垂足为D ,连接OA ,OB .已知OAC D 与OBD D 的面积满足:2:3OAC OBD S S D D =.(1)求OAC D 的面积和k 的值;(2)求直线AC 的表达式;(3)过点B 的直线MN 分别交x 轴和y 轴于M ,N 两点,2NB MB =,若点P 为MON Ð的平分线上一点,且满足2OP OM ON =×,请求出点P 的坐标.【考点】反比例函数综合题【专题】代数几何综合题;推理能力【分析】(1)首先可知C 的坐标,从而得出OAC D 的面积,再根据:2:3OAC OBD S S D D =.得32OBD S D =,可得k 的值;(2)由点(1,)A m 在反比例函数3y x=上,可得3m =,再将点A 的坐标代入反比例解析式即可;(3)设(,)B a b ,分点N 在y 轴正半轴上或点N 在y 轴负半轴两种情形,分别根据相似三角形的判定与性质求出OM 和ON 的长,从而得出OP 的长,即可得出答案.【解答】解:(1)Q 一次函数22y ax =+与y 轴交于C ,(0,2)C \,2OC \=,12112OAC S D \=´´=,:2:3OAC OBD S S D D =Q .32OBD S D \=,Q 点B 在反比例函数1k y x =上,3232k \=´=;(2)Q 点(1,)A m 在反比例函数3y x=上,3m \=,(1,3)A \,将(1,3)A 代入一次函数22y ax =+得,23a+=,1a\=,\一次函数22y x=+;(3)设(,)B a b,当点N在y轴正半轴上时,作BH y^轴于H,//BH OM\,NBH NMO\D D∽,\BH BN NH OM MN NO==,2NB MB=Q,\23 BNMN=,32 OM a\=,3ON b=,2OP OM ON=×Q,OP\====,Q点P为MONÐ90=°,\点P到x轴和y,P\,当点N在y轴负半轴上时,如图,同理可得,1122OM BH a==,ON OH b==,OP\====Q点P为MONÐ90=°,\点P到x轴和yP\,,当点M在x轴负半轴上时,不合题意,舍去.综上:P或,.【点评】本题是反比例函数综合题,主要考查了反比例函数图象上点的坐标的特征,k的几何意义,相似三角形的判定与性质等知识,表示出OM和ON的长是解题的关键,同时渗透了分类讨论的数学思想.12.(2021-2022天府新区二诊·18)(10分)如图,在平面直角坐标系xOy中,点A,B在反比例函数1(0)y xx=>的图象上(点B在点A右侧),过点A作x轴的平行线,过点B作y轴的平行线,两线相交于点C,OC交AB于点E,过点B作//BD x轴交OC于点D,连接AD.设点A的横坐标为1,点B的横坐标为m.(1)求点A的坐标及直线OC的表达式(直线OC表达式用含m的式子表示);(2)求证:四边形ACBD为矩形;(3)若2AOC ACOÐ=Ð,求m的值.【考点】反比例函数综合题【专题】反比例函数及其应用【分析】(1)将点A的横坐标代入反比例函数解析式,即可求出A的纵坐标,先求出B点坐标,然后根据平行线的性质求出点C坐标,即可求出直线OC的解析式;(2)先证四边形ACBD是平行四边形,再证90ACBÐ=°,即可得证;(3)根据矩形的性质,可得2AEO ACOÐ=Ð,E的坐标,进一步可知OA EA=,用两点之间的距离公式,列方程,即可求出m的值.【解答】解:(1)Q点A的横坐标为1,将A点横坐标代入反比例函数1yx =,得1y=,(1,1)A\,BQ的横坐标为m,代入反比例函数1yx =,得1ym =,1 (,) B mm\,//AC xQ轴,//BC y轴,(,1)C m\,设OC 的解析式:y kx =,代入C 点坐标,得1mk =,解得1k m=,\直线OC 的解析式:1y x m =;(2)//AC x Q 轴,//BD x 轴,//AC BD \,1(1,)D m,1AC m \=-,1BD m =-,AC BD \=,\四边形ACBD 是平行四边形,又//AC x Q 轴,//BC y 轴,90ACB \Ð=°,\四边形ACBD 为矩形;(3)Q 四边形ACBD 为矩形,\点E 是CD 的中点,2AEO ACO Ð=ÐQ ,1(2m E +\,1)2m m+,2AOC ACO Ð=ÐQ ,AOC AEO \Ð=Ð,AO AE \=,即22221111(1)(1)22m m m+++=-+-,解方程,得1m =-或2m =+或2m =,B Q 在点A 右侧,2m \=【点评】本题考查了反比例函数得综合,涉及待定系数法求解析式,矩形的判定与性质,中点坐标公式,两点之间的距离公式,等腰三角形的性质等,综合性很强.13.(2021-2022温江区二诊·18)(10分)在平面直角坐标系xOy 中,一次函数y kx b =+的图象由正比例函数2y x =的图象向下平移3个单位长度得到,一次函数y kx b =+与反比例函数m y x=的图象交于A ,B 两点,与x 轴、y 轴分别交于点C ,D ,且23AC CD =.(1)求一次函数和反比例函数的表达式;(2)点E 在x 轴上,连接AE ,DE ,90AED Ð=°,直线AE 与反比例函数m y x=的图象交于另一点F ,求ADF D 的面积.【考点】反比例函数综合题【专题】代数几何综合题;推理能力【分析】(1)根据平移规律可得一次函数表达式为:23y x =-,作AH x ^轴于H ,利用23AC CD =,可得AH 的长,从而得出点A 的坐标,代入反比例函数解析式可得答案;(2)设(,0)E t ,根据90AED Ð=°,利用勾股定理列出t 的方程,可得t 的值,从而得出点E 的坐标,分别利用待定系数法求出直线AE 的表达式,从而得出点F 的坐标,即可解决问题.【解答】解:(1)Q 一次函数y kx b =+的图象由正比例函数2y x =的图象向下平移3个单位长度得到,\一次函数表达式为:23y x =-,令0x =,则3y =-,(0,3)D \-,作AH x ^轴于H ,Q 23AC CD =,2AH \=,5(,2)2A \,Q 反比例函数m y x =的图象经过点5(,2)2A ,252m \=,5m \=,\反比例函数表达式为5y x=;(2)点E 在x 轴上,设(,0)E t ,90AED Ð=°Q ,5(,2)2A ,(0,3)D -,222AE DE AD \+=,22222255()23(522t t \-+++=+,32t \=-或4,当32t =-时,即3(2E -,0),设直线AE 的函数表达式为11y k x b =+,则1111522302k b k b ì+=ïïíï-+=ïî,解得112k =.134b =,\直线AE 的解析式为1324y x =+,当13524x x +=时,4x =-或52,5(4,)4F \--,Q 直线1324y x =+与y 轴交点3(0,)4G ,1135195|||3||4|224216ADF A F S DG x x D \=´´-=´+´+=,当(4,0)E 时,同理可得310(,)23F ,256ADF S D =,综上:ADF D 的面积为19516或256.【点评】本题的反比例函数综合题,主要考查了函数图象上点的坐标的特征,勾股定理,相似三角形的判定与性质,铅垂高求三角形的面积等知识,求出交点F的坐标是解题的关键.14.(2021-2022武侯区二诊·18)(10分)如图,在平面直角坐标系xOy 中,一次函数24y x =-+的图象与反比例函数(0)k y x x=<的图象相交于点(,6)A a ,与y 轴相交于点B .(1)求点A 的坐标及反比例函数的表达式;(2)点P 是反比例函数(0)k y x x=<的图象上一点,连接PA ,PB ,若PAB D 的面积为4,求点P 的坐标;(3)在(2)的条件下,取位于A 点下方的点P ,将线段PA 绕点P 逆时针旋转90°得到线段PC ,连接BC .点M 是反比例函数(0)k y x x=<的图象上一点,连接MB ,若90PCB MBO Ð+Ð=°,求满足条件的点M 的坐标.【考点】反比例函数综合题【专题】代数几何综合题;推理能力【分析】(1)将点(,6)A a 代入24y x =-+,可得点A 的坐标,从而得出答案;(2)首先求出点B 的坐标,在点B 下方的y 轴上取点C ,使8BC =,则4ABC S D =,过点C 作//CP AB ,交双曲线于P ,得出直线CP 的解析式为24y x =--,与双曲线求交点即可得出点P 的坐标,当点P 在点A 上方时,同理可求;(3)过点P 作//HG x 轴,作GH HG ^与H ,AG HG ^于G ,连接BC ,利用()PHC AGP AAS D @D ,得2CH PG ==,4PH AG ==,则(7,4)C -,可知//BC x 轴,从而解决问题.【解答】解:(1)将点(,6)A a 代入24y x =-+得,1a =-,(1,6)A \-,166k \=-´=-,\反比例函数解析式6y x=-;(2)Q 直线24y x =-+与y 轴交于B ,(0,4)B \,在点B 下方的y 轴上取点C ,使8BC =,则4ABC S D =,过点C 作//CP AB ,交双曲线于P ,\直线CP 的解析式为24y x =--,624x x\--=-,解得13x =-,21x =(舍),(3,2)P \-,当点P 在点A 上方时,同理可得(3P -,6+,综上:(3,2)P -或(3-,6+;(3)过点P 作//HG x 轴,作GH HG ^与H ,AG HG ^于G ,连接BC ,AP PC =Q ,90APC Ð=°,90APG CPH \Ð+Ð=°,90APG PAG Ð+Ð=°,CPH PAG \Ð=Ð,H G Ð=ÐQ ,()PHC AGP AAS \D @D ,2CH PG \==,4PH AG ==,(7,4)C \-,//BC x \轴,90PCB MBO Ð+Ð=°Q ,MBO HCP \Ð=Ð,tan tan 2MBO HCP \Ð=Ð=,设直线BM 交x 轴于Q ,8OQ \=,\直线BQ 的解析式为142y x =+,\1642x x+=-,解得2x =-或6-,(2,3)M \-或(6,1)-.【点评】本题是反比例函数综合题,主要考查了待定系数法求函数解析式,三角形的面积,全等三角形的判定与性质,三角函数等知识,利用平行线转化三角形的面积是求点P 坐标的关键.15.(2021-2022武侯区西川中学二诊·18)(10分)如图,已知反比例函数(0)m y x x=>的图象经过点(4,2)A ,过A 作AC y ^轴于点C .点B 为反比例函数图象上的一动点,过点B 作BD x ^轴于点D ,连接AD .直线BC 与x 轴的负半轴交于点E .(1)求反比例函数的表达式;(2)若3BD OC =,求BDE D 的面积;(3)是否存在点B ,使得四边形ACED 为平行四边形?若存在,请求出点B 的坐标;若不存在,请说明理由.【考点】GB :反比例函数综合题【专题】152:几何综合题;69:应用意识【分析】(1)利用待定系数法即可解决问题.(2)求出直线BC 的解析式,可得E 点坐标,求出DE ,BD 即可解决问题.(3)设8(,)B a a,由平行四边形的性质可得BCF BED D D ∽,利用相似三角形的性质可求得a 的值,则可求得B 点坐标.【解答】解:(1)Q 反比例函数(0)m y x x =>的图象经过点(4,2)A ,8m \=,\反比例函数8(0)y x x=>.(2)AC y ^Q 轴,(4,2)A ,2OC \=,3BD OC =Q ,6BD \=,BD x ^Q 轴,4(3B \,6),(0,2)C Q ,设直线BC 的解析式为y kx b =+,则有2463b k b =ìïí+=ïî,解得32k b =ìí=î,\直线BC 的解析式为32y x =+,2(3E \-,0),24233DE \=+=,162BED S DE BD D \=´´=.(3)存在.如图,设BD 交AC 于F .设8(,B a a,(4,2)A Q 4AC \=,Q 四边形ACED 是平行四边形,4DE AC \==,且//CF DE ,BCF BED \D D ∽,\CF BF DE BD=,即8284a a a-=,解得2a =,(2,4)B \.【点评】本题为反比例函数的综合应用,涉及待定系数法、相似三角形的判定和性质、平行四边形的性质、方程思想等知识.在(1)中用待定系数法,在(3)中由平行四边形的性质得到相似三角形,从而得到关于a的方程是解题的关键.本题考查知识点较多,综合性较强,难度适中.。
中考数学:反比例函数的图象与性质综合问题真题+模拟(原卷版北京专用)
中考数学反比例函数的图象与性质综合问题【方法归纳】(1)双曲线kyx=与坐标轴没有交点,当k>0时,图象的两支分别位于一、三象限;在每个象限内,y随x的增大而减小;当k<0时,图象的两支分别位于二、四象限;在每个象限内,y随x的增大而增大.(2)对称性图象关于原点对称,即若(a,b)在双曲线的一支上,则(-a,-b)在双曲线的另一支上.图象关于直线y=±x对称,即若(a,b)在双曲线的一支上,则(b,a)和(-b,-a)在双曲线的另一支上.(3)k的几何意义如图1,设点P(a,b)是双曲线kyx=上任意一点,作PA⊥x轴于A点,PB⊥y轴于B点,则矩形PBOA的面积是|k|(三角形PAO和三角形PBO的面积都是12|k|).如图2,由双曲线的对称性可知,P关于原点的对称点Q也在双曲线上,作QC⊥PA的延长线于C,则有三角形PQC的面积为2|k|.图1 图22.反比例函数的应用(1)利用反比例函数解决实际问题①能把实际的问题转化为数学问题,建立反比例函数的数学模型.②注意在自变量和函数值的取值上的实际意义.③问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.(2)跨学科的反比例函数应用题要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式.同时体会数学中的转化思想.(3)反比例函数中的图表信息题正确的认识图象,找到关键的点,运用好数形结合的思想.(4)数形结合类综合题利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.【典例剖析】(x>0)的图象【例1】(2017·北京·中考真题)如图,在平面直角坐标系xOy中,函数y=kx与直线y=x−2交于点A(3,m).(1)求k、m的值;(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x-2于点M,过点P作平(x>0)的图象于点N.行于y轴的直线,交函数y=kx①当n=1时,判断线段PM与PN的数量关系,并说明理由;②若PN≥PM,结合函数的图象,直接写出n的取值范围.(x>0)的图象G经【例2】(2018·北京·中考真题)在平面直角坐标系xOy中,函数y=kxx+b与图象G交于点B,与y轴交于点C.过点A(4,1),直线l∶y=14(1)求k的值;(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC 围成的区域(不含边界)为W.①当b=−1时,直接写出区域W内的整点个数;②若区域W内恰有4个整点,结合函数图象,求b的取值范围.【真题再现】1.(2011·北京·中考真题)如图,已知反比例函数y1=k1x(k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 . (1)求出反比例函数与一次函数的解析式;(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值.2.(2012·北京·中考真题)如图,在平面直角坐标系xoy中,函数y=4x(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).(1)求一次函数的解析式;(2)设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是4,直接写出点P的坐标.3.(2011·北京·中考真题)如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y=kx的图象的一个交点为A(﹣1,n).(1)求反比例函数y=kx的解析式;(2)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.4.(2014·北京·中考真题)对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足−M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(x>0)和y=x+1(−4<x≤2)是不是有界函数?若是有界函数,(1)分别判断函数y=1x求其边界值;(2)若函数y=−x+1(a⩽x⩽b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数y=x2(−1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值≤t≤1?是t,当m在什么范围时,满足34【模拟精练】1.(2022·北京市广渠门中学模拟预测)在平面直角坐标系xOy中,一次函数y=k(x−1)+4(k>0)(m≠0)的图象的一个交点的横坐标为1.的图象与反比例函数y=mx(1)求这个反比例函数的解析式;(2)当x<−4时,对于x的每一个值,反比例函数y=m的值大于一次函数y=k(x−1)+x4(k>0)的值,直接写出k的取值范围.2.(2022·北京西城·二模)在平面直角坐标系xOy中,一次函数y=−x+b的图象与x轴交的图象在第四象限的交点为(n,−1).于点(4,0),且与反比例函数y=mx(1)求b,m的值;<y p<4,连接OP,结(2)点P(x p,y p)是一次函数y=−x+b图象上的一个动点,且满足mx p合函数图象,直接写出OP长的取值范围.(k≠0)与一次函数3.(2022·北京·二模)图,在平面直角坐标系xOy中,反比例函数y1=kxy2=ax+4(a≠0)的图像只有一个公共点A(2,2),直线y3=mx(m≠0)也过点A.(1)求k、a及m的值;(2)结合图像,写出y1>y2>y3时x的取值范围.4.(2022·北京东城·二模)如图,在平面直角坐标系xOy中,双曲线y=k(k≠0)经过点xA(2,−1),直线l:y=−2x+b经过点B(2,−2).(1)求k,b的值;(2)过点P(n,0)(n>0)作垂直于x轴的直线,与双曲线y=k(k≠0)交于点C,与直线l交于点xD.①当n=2时,判断CD与CP的数量关系;②当CD≤CP时,结合图象,直接写出n的取值范围.5.(2022·北京顺义·二模)在平面直角坐标系xOy中,直线l:y=kx−k+4与函数y=mx(x>0)的图象交于点A(1,4).(1)求m的值;(2)横、纵坐标都是整数的点叫做整点.记直线l与函数y=mx(x>0)的图象所围成的区域(不含边界)为W.点B(n,1)(n≥4,n为整数)在直线l上.①当n=5时,求k的值,并写出区域W内的整点个数;②当区域W内恰有5个整点时,直接写出n和k的值.6.(2022·北京市十一学校模拟预测)在平面直角坐标系xOy中,直线l1:y=−x+b与双曲线G:y=−12x的一个交点为A(−3,n).(1)求n和b的值;(2)若直线l2:y=kx(k≠0)与双曲线G:y=−12x有两个公共点,它们的横坐标分别为x1,x2(x1<x2).直线l1与直线l2的交点横坐标记为x3,若x1<x3<x2,请结合函数图象,求k的取值范围.7.(2022·北京海淀·二模)在平面直角坐标系xOy中,一次函数y=k(x−1)+6(k>0)的图象与反比例函数y=mx(m≠0)的图象的一个交点的横坐标为1.(1)求这个反比例函数的解析式;(2)当x<﹣3时,对于x的每一个值,反比例函数y=mx的值大于一次函数y=k(x−1)+6(k> 0)的值,直接写出k的取值范围.8.(2022·北京东城·一模)在平面直角坐标系xOy中,一次函数y=x−2的图象与x轴交于点A,与反比例函数y=kx (k≠0)B(3,m),点P为反比例函数y=kx(k≠0)的图象上一点.(1)求m,k的值;(2)连接OP,AP.当S△OAP=2时,求点P的坐标.9.(2022·北京市十一学校二模)在平面直角坐标系xOy中,已知点P(1,2),Q(−2,2),函数y=mx.(1)当函数y=mx的图象经过点Q时,求m的值并画出直线y=-x-m.(2)若P,Q两点中恰有一个点的坐标(x,y)满足不等式组{y>mxy<−x−m(m<0),求m的取值范围.10.(2022·北京师大附中模拟预测)如图,一次函数y=-2x-2的图象分别交x轴、y轴于点B、A,与反比例函数y=mx(m≠0)的图象在第二象限交于点M,△OBM的面积是1.(1)求反比例函数的解析式;(2)若x轴上的点P与点A,M是以AM为直角边的直角三角形的三个顶点,求点P的坐标.11.(2022·北京·东直门中学模拟预测)如图,在平面直角坐标系xOy中,点A(1,4),B(3,m).(1)如果点A,B均在反比例函数y1=k的图象上,求m的值;x(2)如果点A,B均在一次函数y2=ax+b的图象上,①当m=2时,求该一次函数的表达式;②当x≥3时,如果不等式mx−1>ax+b始终成立,结合函数图象,直接写出m的取值范围.12.(2022·北京一七一中一模)在平面直角坐标系xOy中,直线l与双曲线y=k(k≠0)的两x个交点分别为A(−3,−1),B(1,m).(1)求k和m的值;(2)求直线l的解析式;(3)点P为直线l上的动点,过点P作平行于x轴的直线,交双曲线y=k(k≠0)于点Q.当点Q位x于点P的左侧时,求点P的纵坐标n的取值范围.13.(2022·北京市第一六一中学分校一模)如图,在平面直角坐标系中,A(a,2)是直线l:(x>0)的图像G的交点.y=x−1与函数y=kx(1)①求a的值;(x>0)的解析式.②求函数y=kx(2)过点P(n,0)(n>0)且垂直于x轴的直线与直线l和图像G的交点分别为M,N,当S△OPM> S△OPN时,直接写出n的取值范围.14.(2022·北京通州·一模)已知一次函数y1=2x+m的图象与反比例函数y2=k(k>0)的x图象交于A,B两点.(1)当点A的坐标为(2,1)时.①求m,k的值;②当x>2时,y1______y2(填“>”“=”或“<”).(2)将一次函数y1=2x+m的图象沿y轴向下平移4个单位长度后,使得点A,B关于原点对称,求m的值15.(2022·北京十一学校一分校一模)在平面直角坐标系xOy中,函数y=k的图象与直线yx=mx交于点A(2,2).(1)求k,m的值;(2)点P的横坐标为n,且在直线y=mx上,过点P作平行于x轴的直线,交y轴于点M,交(x>0)的图象于点N.函数y=kx①n=1时,用等式表示线段PM与PN的数量关系,并说明理由;②若0<PN≤3PM,结合函数的图象,直接写出n的取值范围.16.(2022·北京·模拟预测)如图,在平面直角坐标系xOy中,直线l:y=x﹣1的图象与反(x>0)的图象交于点A(3,m).比例函数y=kx(1)求m、k的值;(2)点P(xp,0)是x轴上的一点,过点P作x轴的垂线,交直线l于点M,交反比例函数y=kx (x>0)的图象于点N.横、纵坐标都是整数的点叫做整点.记y=kx(x>0)的图象在点A,N之间的部分与线段AM,MN围成的区域(不含边界)为W.①当xp=5时,直接写出区域W内的整点的坐标为_____;②若区域W内恰有6个整点,结合函数图象,求出xp的取值范围.17.(2022·北京·中国人民大学附属中学分校一模)有这样一个问题:探究函数y=2x−1−3的图象与性质.小亮根据学习函数的经验,对函数y=2x−1−3的图象与性质进行了探究.下面是小亮的探究过程,请补充完整:(1)函数y=2x−1−3中自变量x的取值范围是;(2)表格是y与x的几组对应值.直接写出m的值;(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(4)根据画出的函数图象,发现下列特征:①该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线越来越靠近而永不相交.②请再写出此函数的一条性质:.(5)已知不等式kx+b<2−3的解集为1<x<2或x>4,则k+b的值为.x−118.(2020·北京·模拟预测)如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.标为(2,4),双曲线y=kx(1)求k的值及点E的坐标;(2)若点F是边OC上一点,当△FBC~△DEB时,求直线FB的解析式.19.(2022·北京四中模拟预测)在平面直角坐标系xOy中,直线l1:y=x+b与双曲线G:y=2x 的一个交点为A(2,n).(1)求n和b的值;(2)若直线l2:y=kx(k≠0)与双曲线G:y=2有两个公共点,它们的横坐标分别为x1,x2x(x1<x2),直线l1与直线l2的交点横坐标为x3,若x1<x3<x2,请结合函数图象,求k的取值范围.20.(2022·北京朝阳·模拟预测)已知:一次函数y1=x﹣2﹣k与反比例函数y2=−2k(k≠0).x(1)当k=1时,①求出两个函数图象的交点坐标;②根据图象回答:x取何值时,y1<y2;(2)请说明:当k取任何不为0的值时,两个函数图象总有交点;(3)若两个函数图象有两个不同的交点A、B,且AB=5√2,求k值.21.(2022·北京·北理工附中模拟预测)在平面直角坐标系xOy中已知双曲线y=k过点A(1,x1),与直线y=4x交于B,C两点(点B的横坐标小于点C的横坐标).(1)求k的值;(2)求点B,C的坐标;(3)若直线x=t与双曲线y=k,交于点D(t,y1),与直线y=4x交于点E(t,y2).当y1<y2x时,直接写出t的取值范围.22.(2022·北京朝阳·模拟预测)如图,一次函数y=kx+b的图象交反比例函数y=m的图x象于A(2,−4),B(a,−1)两点.(1)求反比例函数与一次函数解析式.(2)连接OA,OB,求ΔOAB的面积.(3)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?23.(2022·北京·二模)一次函数y=kx+b(k≠0)的图像与反比例函数y=m的图象相交于A(2,x3),B(6,n)两点(1)求一次函数的解析式(2)将直线AB沿y轴向下平移8个单位后得到直线l,l与两坐标轴分别相交于M,N,与的值反比例函数的图象相交于点P,Q,求PQMN24.(2022·北京·模拟预测)如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)经过点A(0,-1)和点B(3,2).(1)求直线y=kx+b(k≠0)的表达式;(m≠0).(2)已知双曲线y=mx(m≠0)经过点B时,求m的值;①当双曲线y=mx②若当x>3时,总有kx+b>m直接写出m的取值范围.x(x>0)的图象上.25.(2021·北京·二模)如图,A、B两点在函数y=mx(1)求m的值及直线AB的解析式;(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出函数y=m(x>0)的图象与直线AB围出的封闭图形中(不包括边界)所含格点的坐标.x26.(2021·北京朝阳·二模)在平面直角坐标系xOy中,过点A(2,2)作x轴,y轴的垂线,(k<4)的图象分别交于点B,C,直线AB与x轴相交于点D.与反比例函数y=kx(1)当k=−4时,求线段AC,BD的长;(2)当AC<2BD时,直接写出k的取值范围.27.(2021·北京顺义·二模)在平面直角坐标系xOy中,反比例函数y=m与一次函数y=kx+xb相交于A(3,2)、B(-2,n)两点.(1)求反比例函数和一次函数的表达式;(2)过P(p,0)(P≠0)作垂直于x轴的直线,与反比例函数y=m交于点C,与一次函数xy=kx+b交于点D,若SΔCOP=3SΔDOP,直接写出p的值.28.(2021·北京门头沟·二模)在平面直角坐标系xOy中,反比例函数y=k的图象过点P(2 , 2 ).x(1)求k的值;(2)一次函数y=x+a与y轴相交于点M,与反比例函数y=k(x > 0)的图象交于点N,x≤S△MNQ≤2时,过点M作x轴的平行线,过点N作y轴的平行线,两平行线相交于点Q,当12通过画图,直接写出a的取值范围.29.(2021·北京丰台·二模)在平面直角坐标系xOy中,直线y=kx+b(k≠0)与反比例函数(m≠0)的图象交于点A(−1,n),B(2,−1)两点.y=mx(1)求m,n的值;(2)已知点P(a,0)(a>0),过点P作x轴的垂线,分别交直线y=kx+b(k≠0)和反比例(m≠0)的图象于点M,N,若线段MN的长随a的增大而增大,直接写出a的取值范函数y=mx围.30.(2021·北京西城·二模)在平面直角坐标系xOy中,直线l:y=kx−k+2(k>0),函数y=2k(x>0)的图象为F.x(x>0)的图象F上,求直线l对应的函数解析式:(1)若A(2,1)在函数y=2kx(2)横、纵坐标都是整数的点叫做整点.记直线l:y=kx−k+2(k>0),图象F和直线y=12围成的区域(不含边界)为图形.①在(1)的条件下,写出图形G内的整点的坐标;②若图形G内有三个整点,直接写出k的取值范围.。
专题 反比例函数与几何小综合
专题 反比例函数与几何小综合1、如图,直线122y x =-+交x 轴于A 点,交y 轴于B 点,点P 为双曲线()0ky x x=>上一点,且P A =PB ,90APB ∠=︒,求k 的值.2、如图,直线122y x =--与坐标轴交于A 、B 两点,与双曲线()0ky x x=<交于C 点,且AC =AB ,求k 的值.3、如图,55y x =-+与坐标轴交于A 、B 两点,△ABC 为等腰直角三角形,BC =AC ,双曲线()0ky x x=<过C 点,求k 的值.4、双曲线ky x=经过1P 、2P 二点,1AOP △为等腰直角三角形,1AP x ⊥轴且21AP =,求k 的值.5、如图,直线115y x =-与x 轴、y 轴分别相交于B 、A ,点M 为双曲线()0ky x x=>上一点,若△AMB 是以AB 为底的等腰直角三角形,求k 的值.6、如图,1P 是反比例函数()0ky k x=>在第一象限图象上的一点,点1A 的坐标为(2,0).(1)当点1P 的横坐标逐渐增大时,11POA △的面积将如何变化?(2)若11POA △与212P A A △均为等边三角形,求此反比例函数的解析式及2A 点的坐标.7、如图,直线24y x =-分别交x 轴、y 轴于B 、A 二点,交双曲线()0ky x x=>于点C ,且8AOC S =△.(1)求双曲线的解析式;(2)在C 点右侧的双曲线上是否存在点P ,使45PBC ∠=︒?若存在,求P 点坐标;若不存在,请说明理由.8、如图所示,已知()4,A m ,()1,B n -在反比例函数8y x=的图象上,直线AB 与x 轴交于C ,如果点D 在y 轴上,且DA =DC . (1)求C 点的坐标; (2)求D 点的坐标.9、如图1,A (-2,0)、B (10,0),点D 在第一象限,且DA =DB ,90ADB ∠=︒,双曲线ky x=经过D 点. (1)求k 的值;(2)如图2,已知C (0,-4),点M 为双曲线上一点,CM 交x 轴于N ,若y 轴平分△ACM 的面积,求MNCN.10、已知点A (-1,0)、C (0,-3),双曲线()80y x x =->. (1)如图1,点M 为双曲线上一点,且5=2ACM S △,求点M 的坐标;(2)如图2,点N 为y 轴上一点,将线段AN 沿线段AC 的垂直平分线折叠,使点N 的对应点P 恰好落在双曲线上,求直线AP 的解析式.11、如图1,直线4y x =-+交x 轴、y 轴于B 、C ,点A 为x 轴正半轴上一点,16=5ABC S △,CA 的延长线交双曲线()0ky x x=>于E ,且CA =4AE . (1)求点A 的坐标及k 的值;(2)如图2,正方形OMKN 的顶点M 、N 分别在双曲线及线段BC 上,求出点M 、N 的坐标.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. 可编辑 专训1 反比例函数与几何的综合应用 名师点金:解反比例函数与几何图形的综合题,一般先设出几何图形中的未
知数,然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标,再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组),解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值. 反比例函数与三角形的综合 1.如图,一次函数y=kx+b与反比例函数y=x6(x>0)的图象交于A(m,6),B(3,n)两点. (1)求一次函数的解析式; (2)根据图象直接写出使kx+b(3)求△AOB的面积.
(第1题) 2.如图,点A,B分别在x轴、y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=xk(k>0)的图象过CD的中点E. (1)求证:△AOB≌△DCA; (2)求k的值; (3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由. .
可编辑 (第2题) 反比例函数与四边形的综合 反比例函数与平行四边形的综合 3.如图,过反比例函数y=x6(x>0)的图象上一点A作x轴的平行线,交双曲线y=-x3(x<0)于点B,过B作BC∥OA交双曲线y=-x3(x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
(第3题) 反比例函数与矩形的综合 4.如图,矩形OABC的顶点A,C的坐标分别是(4,0)和(0,2),反比例函数y=xk(x>0)的图象过对角线的交点P并且与AB,
(第4题) BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为________. 5.如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,. 可编辑 且BE∥AC,AE∥OB. (1)求证:四边形AEBD是菱形; (2)如果OA=3,OC=2,求出经过点E的双曲线对应的函数解析式.
(第5题) 反比例函数与菱形的综合
6.如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=x3的图象
(第6题) 经过A,B两点,则菱形ABCD的面积为( ) A.2 B.4
C.2 D.4
7.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=xk(k>0,x>0)的图象上,点D的坐标为(4,3). (1)求k的值; . 可编辑 (2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在反比例函数y=xk
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(第7题) 反比例函数与正方形的综合 8.如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(2,2),反比例函数y=xk(x>0,k≠0)的图象经过线段BC的中点D (1)求k的值; (2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的函数解析式并写出x的取值范围.
(第8题) 反比例函数与圆的综合 .
可编辑 (第9题) 9.如图,双曲线y=xk(k>0)与⊙O在第一象限内交于P,Q两点,分别过P,Q两点向x轴和y轴作垂线,已知点P的坐标为(1,3),则图中阴影部分的面积为________. 10.如图,反比例函数y=xk(k<0)的图象与⊙O相交.某同学在⊙O内做随机扎针试验,求针头落在阴影区域内的概率.
(第10题) 专训2 全章热门考点整合应用 名师点金:反比例函数及其图象、性质是历年来中考的热点,既有与本学科知识的综合,也有与其他学科知识的综合,题型既有选择、填空,也有解答类型.其热门考点可概括为:1个概念,2个方法,2个应用及1个技巧. 1个概念:反比例函数的概念 1.若y=(m-1)x|m|-2是反比例函数,则m的取值为( ) . 可编辑 A.1 B.-1
C.±1 D.任意实数
2.某学校到县城的路程为5 km,一同学骑车从学校到县城的平均速度v(km/h)与所用时间t(h)之间的函数解析式是( ) A.v=5t B.v=t+5
C.v=t5 D.v=5
t
3.判断下面哪些式子表示y是x的反比例函数: ①xy=-31;②y=5-x;③y=5x-2;④y=x2a(a为常数且a≠0). 其中________是反比例函数.(填序号) 2个方法: 画反比例函数图象的方法 4.已知y与x的部分取值如下表:
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 … y … 1 1.2 1.5 2 3 6 -6 -3 -2 -1.5 -1.2 -1 … (1)试猜想y与x的函数关系可能是你学过的哪类函数,并写出这个函数的解析式; (2)画出这个函数的图象.
求反比例函数解析式的方法 .
可编辑 5.已知反比例函数y=xk的图象与一次函数y=x+b的图象在第一象限内相交于点A(1,-k+4).试确定这两个函数的解析式.
6.如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=xm的图象的两个交点.求: (1)反比例函数和一次函数的解析式; (2)直线AB与x轴的交点C的坐标及△AOB的面积; (3)方程kx+b-xm=0的解(请直接写出答案); (4)不等式kx+b-xm<0的解集(请直接写出答案).
(第6题) 2个应用 反比例函数图象和性质的应用 7.画出反比例函数y=x6的图象,并根据图象回答问题: (1)根据图象指出当y=-2时x的值; (2)根据图象指出当-2(3)根据图象指出当-3. 可编辑 反比例函数的实际应用 8.某厂仓库储存了部分原料,按原计划每小时消耗2吨,可用60小时.由于技术革新,实际生产能力有所提高,即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位:吨),库存的原料可使用的时间为y(单位:小时). (1)写出y关于x的函数解析式,并求出自变量的取值范围. (2)若恰好经过24小时才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
1个技巧:用k的几何性质巧求图形的面积 9.如图,A,B是双曲线y=xk(k≠0)上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )
A.34 B.38 C.3 D.4
(第9题) .
可编辑 (第10题) 10.如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=x2和y=-x4的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________. 11.如图是函数y=x3与函数y=x6在第一象限内的图象,点P是y=x6的图象上一动点,PA⊥x轴于点A,交y=x3的图象于点C,PB⊥y轴于点B,交y=x3的图象于点D. (1)求证:D是BP的中点; (2)求四边形ODPC的面积.
(第11题)
答案 1.解:(1)∵A(m,6),B(3,n)两点在反比例函数y=x6(x>0)的图象上, ∴m=1,n=2,即 A(1,6),B(3,2). . 可编辑 又∵A(1,6),B(3,2)在一次函数y=kx+b的图象上,
∴2=3k+b,6=k+b,解得b=8,k=-2,
即一次函数解析式为y=-2x+8.
(第1题) (2)根据图象可知使kx+b3. (3)如图,分别过点A,B作AE⊥x轴,BC⊥x轴,垂足分别为E,C,设直线AB交x轴于D点. 令-2x+8=0,得x=4,即D(4,0). ∵A(1,6),B(3,2),∴AE=6,BC=2. ∴S△AOB=S△AOD-S△ODB=21×4×6-21×4×2=8. 2.(1)证明:∵点A,B分别在x轴,y轴上,点D在第一象限内,DC⊥x轴于点C,∴∠AOB=∠DCA=90°. 在Rt△AOB和Rt△DCA中,∵AB=DA,AO=DC,∴Rt△AOB≌Rt△DCA. (2)解:在Rt△ACD中,∵CD=2,DA=, ∴AC==1.∴OC=OA+AC=2+1=3. ∴D点坐标为(3,2). ∵点E为CD的中点,∴点E的坐标为(3,1).∴k=3×1=3. (3)解:点G在反比例函数的图象上. 理由如下:∵△BFG和△DCA关于某点成中心对称, . 可编辑 ∴△BFG≌△DCA. ∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°. ∵OB=AC=1,∴OF=OB+BF=1+2=3.∴G点坐标为(1,3). ∵1×3=3,∴点G(1,3)在反比例函数的图象上. 3.解:∵BC∥OA,AB∥x轴,∴四边形ABCO为平行四边形. ∴AB=OC=3. 设Aa6,则Ba6, ∴(a-3)·a6=-3.∴a=2. ∴A(2,3),B(-1,3). ∵OC=3,C在x轴负半轴上,∴C(-3,0), 设直线BC对应的函数解析式为y=kx+b, 则-k+b=3,-3k+b=0,解得.9
∴直线BC对应的函数解析式为y=23x+29. 解方程组,3得y1=3,x1=-1,.3
∴D23. 设直线AD对应的函数解析式为y=mx+n,
则,3解得.9
∴直线AD对应的函数解析式为y=83x+49. ∴E49.∴OE=49. 4.415 点拨:因为C(0,2),A(4,0),由矩形的性质可得P(2,1),把P点坐标代入反比例函数解析式可得k=2,所以反比例函数解析式为y=x2.因为D点的横坐标为4,所以AD=42=21.因为点E的纵坐标为2,所以2=CE2,所以CE
