反比例函数与几何图形的综合
中考反比例函数与几何综合
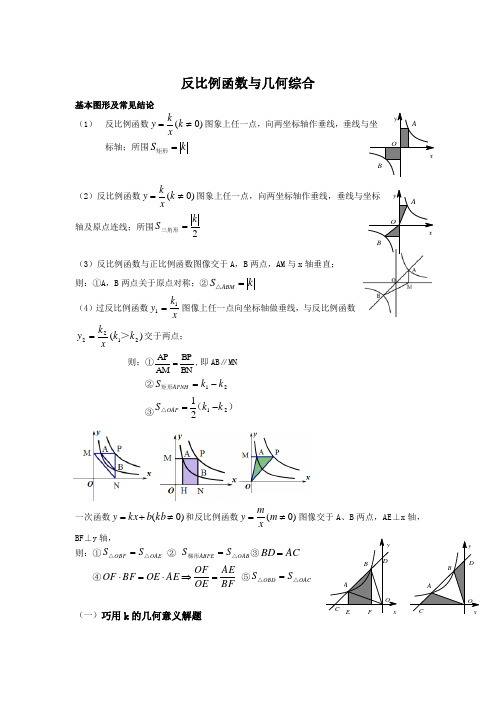
Oy xBAABxy O反比例函数与几何综合基本图形及常见结论 （1） 反比例函数)0(≠=k xky 图象上任一点，向两坐标轴作垂线，垂线与坐标轴；所围k S =矩形（2）反比例函数)0(≠=k xky 图象上任一点，向两坐标轴作垂线，垂线与坐标轴及原点连线；所围2k S =三角形（3）反比例函数与正比例函数图像交于A ，B 两点，AM 与x 轴垂直； 则：①A ，B 两点关于原点对称；②k S ABM =△（4）过反比例函数xk y 11=图像上任一点向坐标轴做垂线，与反比例函数)(2122k k xk y ＞=交于两点； 则：①BNBP AM AP =,即AB ∥MN②21k k S APNH -=矩形③）（△2121k k S OAP -=一次函数)0(≠+=kb b kx y 和反比例函数)0(≠=m xmy 图像交于A 、B 两点，AE ⊥x 轴，BF ⊥y 轴，则：①OAE OBF S S △△= ② OAB ABFE S S △梯形=③AC BD =④BFAEOE OF AE OE BF OF =⇒⋅=⋅ ⑤OACOBD S S △△=（一）巧用k 的几何意义解题y x ABO CDy xDC F EO B A例1．函数y=和y=在第一象限内的图象如图，点P 是y=的图象上一动点，PC ⊥x 轴于点C ，交y=的图象于点B ．给出如下结论：①△ODB 与△OCA 的面积相等；②PA 与PB 始终相等；③四边形PAOB 的面积大小不会发生变化；④CA=AP ．其中所有正确结论的序号是________。
迁移练习1（1）.如图，双曲线)0x (k>=xy 经过Rt △OAB 斜边OB 的中点D ，与AB 交于点C ．若△OBC 面积为3，则k ＝_______迁移练习1（2）..双曲线)0x (k>=xy 经过矩形OABC 边AB 的中点F ，交BC 于点E ； 若梯形OEBA 的面积为9，则k=________。
反比例函数的图像和性质的综合应用
解析
根据题意，将点 A（-2 ，3）和点 B（3，-2 ）分别代入两个函数中 ，得到关于 m、k、b 的方程组，解方程组求 得 m、k、b 的值，即 可得到两个函数的解析
式。
05
反比例函数在几何图形中应用
相似三角形判定定理推广
预备定理
平行于三角形的一边，并且和 其他两边相交的线段，所截得 的三角形的三边与原三角形三 边对应成比例。
反比例函数图像在平面直角坐标系中 ，沿y轴方向平移，函数表达式不变， 图像沿y轴平移。
伸缩变换规律
01
当k>0时，图像分别位于第一、三象限，每一个象限内，从 左往右，y随x的增大而减小；
02
当k<0时，图像分别位于第二、四象限，每一个象限内，从 左往右，y随x的增大而增大。
03
k>0时，函数在x<0上同为减函数、在x>0上同为减函数； k<0时，函数在x<0上为增函数、在x>0上同为增函数。
3
平行四边形面积问题
通过已知相邻两边及其夹角求解面积，或已知面 积和一边长度及夹角求解另一边长度，应用反比 例函数进行求解。
速度、时间、距离关系分析
匀速直线运动问题
通过已知速度和时间求解距离，或已 知距离和时间求解速度，利用反比例 关系建立方程。
变速直线运动问题
曲线运动问题
通过已知速度和方向的变化规律，求 解某时刻的速度或某段时间内的平均 速度及运动轨迹，结合反比例函数进 行综合分析。
解析
根据题意，将点（-2， -1）代入两个函数中， 得到关于 k、m、n 的 方程组，解方程组求得 k、m、n 的值，即可 得到两个函数的解析式 。再将 x = 3 代入两个 函数中，得到关于 k、 m、n 的另一个方程， 与前面的方程组联立求 解，即可得到最终的解
专题21反比例函数的图象与性质(3个知识点5种题型2种中考考法)(原卷版-初中数学北师大版9年级上册
专题21反比例函数的图象与性质（3个知识点5种题型2种中考考法）【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.反比例函数图象的画法（重点）知识点2.反比例函数的图象与性质（重点）知识点3.反比例函数表达式中比例系数k 的几何意义（难点）【方法二】实例探索法题型1.反比例函数的图象与性质的应用题型2.反比例函数与图形面积问题题型3.利用反比例函数图象的对称性解题题型4.创新题题型5.反比例函数与几何图形的综合【方法三】仿真实战法考法1.反比例函数的比例系数k 的几何意义考法2.利用反比例函数的性质比较函数值大小【方法四】成果评定法【学习目标】1.能画出反比例函数的图象，知道反比例函数的图象是双曲线。
2.理解反比例函数的性质，并能运用其性质解决相关的问题。
3.理解反比例函数)0(≠=k xky 中的比例系数k 的几何意义，并能运用其意义求与反比例函数图象有关的图形面积问题。
【知识导图】【倍速学习四种方法】【方法一】脉络梳理法知识点1.反比例函数图象的画法（重点）（1）列表：自变量的取值应以0为中心，在0的两侧取三对（或三对以上）互为相反数的值，填写y 值时，只需计算右侧的函数值，相应左侧的函数值是与之对应的相反数；（2）描点：描出一侧的点后，另一侧可根据中心对称去描点；（3）连线：按照从左到右的顺序连接各点并延伸，连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线.注意双曲线的两个分支是断开的，延伸部分有逐渐靠近坐标轴的趋势，但永远不与坐标轴相交；（4）反比例函数图象的分布是由k 的符号决定的：当0k >时，两支曲线分别位于第一、三象限内，当0k <时，两支曲线分别位于第二、四象限内．知识点2.反比例函数的图象与性质（重点）1、反比例函数的图象特征：反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限；反比例函数的图象关于原点对称，永远不会与x 轴、y 轴相交，只是无限靠近两坐标轴.注意：（1）若点(a b ，)在反比例函数ky x=的图象上，则点(a b --，)也在此图象上，所以反比例函数的图象关于原点对称；（2）在反比例函数(k 为常数，0k ≠)中，由于，所以两个分支都无限接近但永远不能达到x 轴和y 轴．2.反比例函数的性质（1）如图1，当0k >时，双曲线的两个分支分别位于第一、三象限，在每个象限内，y 值随x 值的增大而减小；（2）如图2，当0k <时，双曲线的两个分支分别位于第二、四象限，在每个象限内，y 值随x 值的增大而增大；注意：（1）反比例函数的增减性不是连续的，它的增减性都是在各自的象限内的增减情况，反比例函数的增减性都是由反比例系数k 的符号决定的；反过来，由双曲线所在的位置和函数的增减性，也可以推断出k 的符号.（2）反比例的图像关于原点的对称【例2】（2022秋•南华县期末）反比例函数与一次函数y ＝kx +1在同一坐标系的图象可能是（）A ．B ．C．D．【变式】（2022秋•大渡口区校级期末）在同一坐标系中，函数和y＝kx﹣2的图象大致是（）A．B．C．D．【例3】（2023•瑞安市开学）对于反比例函数，当﹣1＜y≤2，且y≠0时，自变量x的取值范围是（）A．x≥1或x＜﹣2B．x≥1或x≤﹣2C．0＜x≤1或x＜﹣2D．﹣2＜x＜0或x≥1【变式】（2023•西湖区校级开学）若点A（x1，y1），B（x2，y2），C（x3，y3），都在反比例函数（k为常数，k＞0）的图象上，其中y2＜0＜y1＜y3，则x1，x2，x3的大小关系是（）A．x1＜x2＜x3B．x2＜x3＜x1C．x1＜x3＜x2D．x2＜x1＜x3知识点3.反比例函数表达式中比例系数k的几何意义（难点）通过反比例函数上一点向一条坐标轴作垂线，这个点与垂足和原点所构成的三角形面积为12k，与两条坐标轴围成矩形面积为k，注意加绝对值时，有正负两个答案．【例4】（2023•和平区校级三模）如图，点A在双曲线上，AB ⊥x 轴于B ，且△AOB 的面积S △AOB ＝2，则k 的值为（）A ．2B ．4C ．﹣2D ．﹣4【变式】如图，矩形ABCD 的边CD 在x 轴上，顶点A 在双曲线1y x =上，顶点B 在双曲线3y x=上，求矩形ABCD 的面积．A B CDE Oxy【方法二】实例探索法题型1.反比例函数的图象与性质的应用1．（2023•株洲）下列哪个点在反比例函数的图象上？（）A ．P 1（1，﹣4）B ．P 2（4，﹣1）C ．P 3（2，4）D ．2.（2023•西湖区校级开学）若点A （x 1，y 1），B （x 2，y 2），C （x 3，y 3），都在反比例函数（k 为常数，k＞0）的图象上，其中y 2＜0＜y 1＜y 3，则x 1，x 2，x 3的大小关系是（）A ．x 1＜x 2＜x 3B ．x 2＜x 3＜x 1C ．x 1＜x 3＜x 2D ．x 2＜x 1＜x 33.（2023春•东阳市期末）已知反比例函数的图象的一支如图所示，它经过点（3，﹣2）．（1）求此反比例函数的表达式，并补画该函数图象的另一支．（2）求当y ≤4，且y ≠0时自变量x 的取值范围．4.（1）平面直角坐标系中，点A (725)m m --，在第二象限，且m 为整数，求过点A 的反比例函数解析式；（2）若反比例函数3k y x -=的图像位于第二、四象限内，正比例函数2(1)3y k x =-过一、三象限，求整数k 的值．5.已知反比例函数(0)k y k x =≠，当自变量x 的取值范围为84x ≤≤--时，相应的函数取值范围是12y ≤≤--1，求这个反比例函数解析式．题型2.反比例函数与图形面积问题6.（1）若P是反比例函数3kyx=图像上的一点，PQ⊥y轴，垂足为点Q，若2POQs∆=，求k的值；（2）已知反比例函数kyx=的图像上有一点A，过A点向x轴，y轴分别做垂线，垂足分别为点B C，，且四边形ABOC的面积为15，求这个反比例函数解析式．7.（2022秋•朝阳期末）如图，一次函数y＝k1x+b与反比例函数y＝（x＞0）的图象交于A（1，6），B（3，n）两点．（1）求反比例函数的解析式和n的值；（2）根据图象直接写出不等式k1x+b的x的取值范围；（3）求△AOB的面积．题型3.利用反比例函数图象的对称性解题8．（2023•福建）如图，正方形四个顶点分别位于两个反比例函数y＝和y＝的图象的四个分支上，则实数n的值为（）A．﹣3B．﹣C．D．39．（2023•广西）如图，过的图象上点A，分别作x轴，y轴的平行线交的图象于B，D 两点，以AB，AD为邻边的矩形ABCD被坐标轴分割成四个小矩形，面积分别记为S1，S2，S3，S4，若，则k的值为（）A．4B．3C．2D．1(1)若点A（1，1），分别求线段(2)对于任意的点A（a，b），试探究线段14．（2022秋·安徽滁州·九年级统考期中）如图，已知1A，2A，3A，…，n A…是x轴上的点，且15．（2021秋·河北石家庄每个台阶凸出的角的顶点记作（1）若L 过点1T ，则k =（2）若曲线L 使得1T T ～16．（2022秋·全国·九年级期末）如图，已知反比例函数题型5.反比例函数与几何图形的综合17.过原点作直线交双曲线(0)ky k x=>于点A 、C ，过A 、C 两点分别作两坐标轴的平行线，围成矩形ABCD ，如图所示．（1）已知矩形ABCD 的面积等于8，求双曲线的解析式；（2）若已知矩形ABCD 的周长为8，能否由此确定双曲线的解析式?如果能，请予求出；如果不能，说明理由．y ABCDOx18.正方形OAPB 、ADFE 的顶点A 、D 、B 在坐标轴上，点E 在AP 上，点P 、F 在函数(0)ky k x=>的图像上，已知正方形OAPB 的面积是16．（1）求k 的值和直线OP 的函数解析式；（2）求正方形ADEF 的边长．yABPFOxED19.如图，已知正方形OABC 的面积是9，点O 为坐原点，A 在x 轴上，C 在y 轴上，B 在函数(00)ky k x x=>>，的图像上，点P （m ，n ）在(00)ky k x x=>>，的图像上异于B 的任意一点，过点P 分别作x 轴，y 轴的垂线，垂足分别是E 、F ．设矩形OEPF 和正方形OABC 不重合部分的面积是S ．（1）求点B 的坐标；（2）当92S =时，求点P 的坐标；（3）写出S 关于m 的函数解析式．A BC PE FyOx【方法三】仿真实战法考法1.反比例函数的比例系数k 的几何意义1．（2023•福建）如图，正方形四个顶点分别位于两个反比例函数y ＝和y ＝的图象的四个分支上，则实数n 的值为（）A ．﹣3B．﹣C．D ．32．（2023•湘西州）如图，点A 在函数y＝（x ＞0）的图象上，点B 在函数y＝（x ＞0）的图象上，且AB ∥x 轴，BC ⊥x 轴于点C ，则四边形ABCO 的面积为（）A ．1B ．2C ．3D ．4考法2.利用反比例函数的性质比较函数值大小3．（2023•镇江）点A（2，y1）、B（3，y2）在反比例函数y＝的图象上，则y1y2（用“＜”、“＞”或“＝”填空）．4．（2022•广东）点（1，y1），（2，y2），（3，y3），（4，y4）在反比例函数y＝图象上，则y1，y2，y3，y4中最小的是（）A．y1B．y2C．y3D．y45．（2021•广安）若点A（﹣3，y1），B（﹣1，y2），C（2，y3）都在反比例函数y＝（k＜0）的图象上，则y1，y2，y3的大小关系是（）A．y3＜y1＜y2B．y2＜y1＜y3C．y1＜y2＜y3D．y3＜y2＜y1【方法四】成果评定法一、单选题A．1 43．（2022·福建福州·校考模拟预测）如图，在x轴于B、D两点，连结A ．4B ．65．（2022秋·福建厦门·九年级校考期中）如图，过双曲线上任意一点交x 轴、y 轴于点M 、N ，所得矩形A ．4B ．4-6．（2021秋·河北石家庄·九年级校联考期中）关于反比例函数A ．函数图像分别位于第一、三象限C ．函数图像过()(23A mB n -，、，A．4 10．（2023·江苏宿迁图像上，点E在yA．1B 二、填空题11．（2022秋·湖南永州13．（2022秋·黑龙江大庆的大小关系是14．（2023·安徽滁州15．（2023秋·重庆沙坪坝比例函数()0ky k x=≠上两点，平行线，两直线交于点16．（2023秋·福建泉州·九年级校考专题练习）如图，已知直线(00)a y x a x =>>，和b y x =象于点D ，过点C 作CE ∥17．（2022秋·贵州铜仁·九年级统考期中）如图，点112232021OA A A A A A ==== 图象分别交于点123,,,B B B 18．（2023·浙江·九年级专题练习）如图，点所示，分别过点A ，C 作x 轴与构成的阴影部分面积为2，则矩形三、解答题19．（2023秋·陕西榆林·九年级校考期末）已知反比例函数(1)函数的图象在第二、四象限？(1)求k的值；(2)请用无刻度的直尺和圆规作出(3)设（2）中的角平分线与⊥．证：DE OA(1)如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；(2)研究函数并结合图象与表格，回答下列问题：①点()121,7552,,,,2A y B y C x ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭②当函数值2y =时，求自变量x 的值；(1)求点A 的坐标；(2)求反比例函数的解析式：(1)点D的坐标为______，点E的坐标为______；(2)动点P在第一象限内，且满足12PBO ODE S S∆∆=。
(江西人教)数学中考专题突破【专题4】反比例函数与几何图形综合题(20页)
本的途径，预计2015年仍会延续此命题方式．
考点探究
专题四
反比例函数与几何图形综合题
考向互动探究
【点拨交流】
1．本题考查了哪些知识？解题的关键是什么？
2．∠BCO与∠BPD有怎样的数量关系？
3．tan∠BCO的值是多少？怎样求线段OC的长？
4．要求点D的坐标，需要求出哪两条线段的长？怎样求？
5．怎样确定反比例函数的解析式？
考点探究
专题四
反比例函数与几何图形综合题
【解题思路】
考点探究
专题四
反比例函数与几何图形综合题
例 1 [2014·南昌] 如图 T4－1，在平面直角坐标系中，Rt△ 1 PBD 的斜边 PB 落在 y 轴上，tan∠BPD＝ .延长 BD 交 x 轴于点 C， 2 过点 D 作 DA⊥x 轴，垂足为 A，OA＝4，OB＝3. (1)求点 C 的坐标； k (2)若点 D 在反比例函数 y＝ (k＞0)的图象上，求反比例函数 x 的解析式．考点探究专题四来自反比例函数与几何图形综合题
图T4－3
考点探究
专题四
反比例函数与几何图形综合题
解：(1)过点 C 作 CE⊥AB 于点 E. ∵四边形 ABCD 是梯形，AD＝BC ∴DO＝CE， ∴△AOD≌△BEC，∴AO＝BE＝2. ∵BO＝6，∴DC＝OE＝4， ∴C(4，3)． k 设反比例函数的解析式为 y＝ (k≠0)， x k 根据题意，得 3＝ ， 4
【点拨交流】
1．本题考查了哪些知识？
2．B，C，D三点的坐标可以看作由点A(2，6)通过怎样的平
移得到？
3．在将矩形向下平移的过程中，哪两点能同时落在函数图 象上？ 4．将矩形向下平移 a个单位后点A，C对应的点A′，C′的 坐标怎样表示？
专题九-反比例函数与几何的综合应用
在物理学中，一些物理量之间可能存在反比例关系，如电阻与电流、压力与面积等。通过运用反 比例函数的性质，可以更好地理解和解决这些物理问题。
反比例函数在经济学中的应用
在经济学中，一些经济指标之间可能存在反比例关系，如价格与需求量、成本与产量等。通过运 用反比例函数的性质，可以对这些经济指标进行更准确的预测和分析。
如长度、面积等。
利用反比例函数性质建立关系
02
根据反比例函数的性质，结合几何图形的特点，建立所求最值
与相关量之间的关系。
求解最值
03
通过求解反比例函数的最值，得到所求几何量的最值。
判定存在性问题
根据题意列出方程或不等式
01
根据题目条件，列出与几何图形相关的方程或不等式
。
利用反比例函数性质分析解的情况
反比例关系在圆中的应用
在圆中，当一个圆的半径增加时，其 面积会按平方比例增加，但其周长只 会按线性比例增加。这种关系虽然不 是严格的反比例关系，但也可以用于 解决一些与圆相关的问题。
解题技巧与实例分析
通过利用圆的性质和上述关系， 可以求解一些与圆相关的问题。 例如，已知一个圆的半径和另一 个圆的面积或周长，可以求解未 知圆的半径或面积等。
仔细阅读题目要求，明确题意 ，避免答非所问。
合理安排答题顺序
先做易做的题目，确保会做的 题目不丢分，再攻克难题。
控制答题时间
每道题目分配合理的时间，避 免时间不够用或浪费过多时间
。
检查答案
做完题目后要认真检查答案， 确保没有遗漏或错误。
THANKS FOR WATCHING
感谢您的观看
解题技巧与实例分析
对于其他几何图形中的反比例关系问题，可以通过设定未知数、利用几何图形的性质和反比例关系来求解。 需要注意的是，在解题过程中要仔细分析题目条件和数据特点，选择合适的解题方法和思路。
专题：反比例函数与几何图形结合
专题4：反比例函数与几何图形结合方法点睛反比例函数与几何图形结合常涉及以下几个方面：1．求反比例函数与一次函数的解析式：(1)找到或求出反比例函数图象上一点的坐标，利用待定系数法求解；(2)找到或求出一次函数图象上两点的坐标，再利用待定系数法求解．注：当已知一次函数与反比例数函数图象上的一个交点A的坐标及交点B的横(纵)坐标，确定两个函数的解析式时，先利用点A的坐标求得反比例函数解析式，再由反比例函数解析式求得点B的坐标，再利用A，B两点的坐标确定一次函数解析式．2、(1)给出图形面积求点的坐标：根据解析式用只含一个参数的代数式表示该点的坐标，列出关于该图形面积的等式进行求解．(2)点的存在性问题：涉及线段和面积的关系，图形的判定等，对这类题应观察图形，结合问题，建立数学模型，按照题意列出等量关系式进行求解．典例分析例1：（2022达州中考）如图，一次函数1y x =+与反比例函数k y x=的图象相交于(,2)A m ，B 两点，分别连接OA ，OB ．（1）求这个反比例函数的表达式；（2）求AOB 的面积；（3）在平面内是否存在一点P ，使以点O ，B ，A ，P 为顶点的四边形为平行四边形？若存在，请直接写出点P专题过关1.（2022西宁中考）如图，正比例函数4y x =与反比例函数()0k y x x=>的图象交于点(),4A a ，点B 在反比例函数图象上，连接AB ，过点B 作BC x ⊥轴于点()2,0C ．（1）求反比例函数解析式；（2）点D 在第一象限，且以A ，B ，C ，D 为顶点的四边形是平行四边形，请直接写出．．．．点D 的坐标．2.（2022绵阳中考）如图，一次函数1y k x b =+与反比例函数2k y x=在第一象限交于(2,8)M 、N 两点，NA 垂直x 轴于点A ，O 为坐标原点，四边形OANM 的面积为38．（1）求反比例函数及一次函数的解析式；（2）点P 是反比例函数第三象限内的图象上一动点，请简要描述使PMN 的面积最小时点P 的位置（不需证明），并求出点P 的坐标和PMN3.（2022眉山中考）已知直线y x =与反比例函数k y x=的图象在第一象限交于点(2,)M a ．（1）求反比例函数的解析式；（2）如图，将直线y x =向上平移b 个单位后与k y x=的图象交于点(1,)A m 和点(,1)B n -，求b 的值；（3）在（2）的条件下，设直线AB 与x 轴、y 轴分别交于点C ，D ，求证：AOD BOC ≌△△．4.（2022衡阳中考）如图，反比例函数myx=的图象与一次函数y kx b=+的图象相交于()3,1A，()1,B n-两点．（1）求反比例函数和一次函数的关系式；（2）设直线AB交y轴于点C，点M，N分别在反比例函数和一次函数图象上，若四边形OCNM是平行四边形，求点M的坐标．A，B两点．5.（2022常德中考）如图，已知正比例函数1y x=与反比例函数2y的图象交于()2,2y y<时x的取值范围；（1）求2y的解析式并直接写出12（2）以AB为一条对角线作菱形，它的周长为，在此菱形的四条边中任选一条，求其所在直线的解析式．6.（2022绥化中考）在平面直角坐标系中，已知一次函数11y k x b =+与坐标轴分别交于()5,0A ，50,2B ⎛⎫ ⎪⎝⎭两点，且与反比例函数22k y x =的图象在第一象限内交于P ，K 两点，连接OP ，OAP △的面积为54．（1）求一次函数与反比例函数的解析式；（2）当21y y >时，求x 的取值范围；（3）若C 为线段OA 上的一个动点，当PC KC +最小时，求PKC 的面积．7.（2022大庆中考）已知反比例函数k y x =和一次函数1y x =-，其中一次函数图象过(3,)a b ，31,3k a b ⎛⎫++ ⎪⎝⎭两点．（1）求反比例函数的关系式；（2）如图，函数1,33y x y x ==的图象分别与函数(0)k y x x =>图象交于A ，B 两点，在y 轴上是否存在点P ，使得ABP △周长最小？若存在，求出周长的最小值；若不存在，请说明理由．8.（2022湘潭中考）已知()3,0A 、()0,4B 是平面直角坐标系中两点，连接AB ．（1）如图①，点P 在线段AB 上，以点P 为圆心的圆与两条坐标轴都相切，求过点P 的反比例函数表达式；（2）如图②，点N 是线段OB 上一点，连接AN ，将AON 沿AN 翻折，使得点O 与线段AB 上的点M 重合，求经过A 、N 两点的一次函数表达式．9.（2022成都中考）如图，在平面直角坐标系xOy 中，一次函数26y x =-+的图象与反比例函数ky x=的图象相交于(),4A a ，B 两点．（1）求反比例函数的表达式及点B 的坐标；（2）过点A 作直线AC ，交反比例函数图象于另一点C ，连接BC ，当线段AC 被y 轴分成长度比为1:2的两部分时，求BC 的长；（3）我们把有两个内角是直角，且一条对角线垂直平分另一条对角线的四边形称为“完美筝形”．设P 是第三象限内的反比例函数图象上一点，ABPQ 是完美筝形时，求P ，Q 两点的坐标．10.（2022河南西华二模）如图，反比例函数(0)my x x=>的图象与一次函数y kx b =+的图象交于(14)B ，和(1)C n ，两点．（1）求反比例函数与一次函数的解析式；（2）根据图象直接写出不等式(0)mkx b x x+> 的解集；（3）将直线BC 向下平移5个单位长度得到直线l ，已知点P ，Q 分别为x 轴、直线l 上的动点，当PC PQ +的值最小时，请直接写出点P 的坐标．11.（2022河南西华一模）在平面直角坐标系xOy 中，函数()0ky x x=>的图象经过点()2,3A ，()6,B a ，直线l ：y ＝mx ＋n 经过A ，B 两点，直线l 分别交x 轴，y 轴于D ，C 两点．（1）求反比例函数与一次函数的解析式；（2）在y 轴上是否存在一点E ，使得以A ，C ，E 为顶点的三角形与△CDO 相似？若存在，请求出点E 的坐标；若不存在，请说明理由．12.（2022河南长垣一模）如图，在平面直角坐标系中，直线y x =与反比例函数1y x=（x ＞0）的图象交于点A ，将直线y x =沿y 轴向上平移k 个单位长度，交y 轴于点B ，交反比例函数图象于点C ，且13BC OA =．AD ⊥y 轴于点D 、CE ⊥y 于点E ．（1）求证：△BCE ∽△OAD ；（2）求点A 和点C 的坐标；（3）求k 值．13.（2022河南虞城二模）如图，点A 为直线y ＝3x 上位于第一象限的一个动点，过点A 作AB ⊥x 轴于点B ，将点B 向右平移2个单位长度到点C ，以AB ，BC 为边构造矩形ABCD ，经过点A 的反比例函数()0ky x x=>的图象交CD 于点M ．（1）若B(1，0)，求点M 的坐标；（2）连接AM ，当AM ⊥OA 时，求点A 的坐标．14.（2022河南商城二模）如图，一次函数2y x =与反比例函数(0)ky k x=>的图象交于点A ，B ，点P 在以点(2,0)C -为圆心，1为半径的C 上，Q 是AP 的中点，OQ 长的最大值为32时．（1）试确定反比例函数ky x=的表达式．（2）C 与x 轴在点C 的左侧交于点M ，请直接写出劣弧MP 的长是___________．（sin 310.52︒≈，sin 400.64︒≈，sin530.8︒≈．）15.（2022新乡二模）如图，在平面直角坐标系中，正比例函数为11y k x =和反比例函数22k y x=图像交于A ，B 两点，矩形OAEC 的边EC 交x 轴于点D ，AD ⊥x 轴，点D 的坐标为（2，0），且AE=ED ．（1）求这两个函数的解析式；（2）点P 为y 轴上的一个动点，当PE-PA 的值最大时，求点P 的坐标．16.（2022河南西平一模）如图，一次函数11y k x b =+经过点()4,0A ，()0,4B ，与反比例函数()220k y x x=>的图象交于点()1,C n ，D 两点．（1）求反比例函数和一次函数的解析式；（2）结合函数图象，直接写出当210k k x b x<+≤时x 的取值范围；（3）点P 在x 轴上，是否存在PCD 是以CD 为腰的等腰三角形，若存在，请直接写出点P 的坐标；若不存在，说明理由．17.（2022河南天一大联考）如图，一次函数y ＝k 1x+b 的图象与反比例函数y 2k x=的图象交于点A （m ，2），B （﹣1，4），与y 轴交于点C ，连接OA ，OB ．（1）求反比例函数和一次函数的解析式；（2）求△OAB 的面积；（3）若点P 在y 轴上，且BP 12=OA ，请直接写出点P 的坐标．18.（2022河南实验中学一模）如图，在矩形OABC中，AB＝2，BC＝4，D是AB边的中点，反比例函数yk x（x＞0）的图象经过点D，与BC边交于点E．（1）求反比例函数的表达式及点E的坐标；（2）若点P在y轴上，当△PDE的周长最小时，求出此时点P的坐标．19.（2022河南虞城二模）如图，一次函数142y x=-+交反比例函数(0)ky xx=>于A，B两点，过点A作AC x⊥轴于点C，AOC△的面积为3．（1）求反比例函数的解析式；（2）D为y轴上一个动点，当DA DB+有最小值时，求点D的坐标．20.（2022河南夏邑一模）在平面直角坐标系xOy 中，函数(0)k y x x=>的图象经过点(2,3),(6,)A B a ，直线:l y mx n =+经过A ，B 两点．（1）求反比例函数与一次函数的解析式，并在下面的平面直角坐标系中描绘出一次函数的大致图象．（2）当直线l 向下平移b 个单位时，与(0)k y x x=>的图象有唯一交点，求b 的值．（3）若直线AB 分别交x 轴，y 轴于D ，C 两点，在y 轴上是否存在一点Q ，使得ACQ 与CDO 相似？若存在，请求出点Q 的坐标；若不存在，请说明理由．21.（2022南阳方城二模）如图，在矩形OABC 中，2,4AB BC ==，点D 是边AB 的中点，反比例函数1(0)k y x x=>的图象经过点D ，交BC 边于点E ，直线DE 的解析式为2(0)y mx n m =+≠．（1）求反比例函数1(0)k y x x=>的解析式和直线DE 的解析式；（2）在y 轴上找一点P ，使PDE △的周长最小，求出此时点P 的坐标；（3）在（2）的条件下，PDE △的周长最小值是______．22.（2022洛阳一模）如图，反比例函数()0k y k x =≠的图象与正比例函数32y x =-的图象相交于(),3A a ，B 两点．（1）求k 的值及点B 的坐标；（2）请直接写出不等式32k x x >-的解集；（3）已知AD x ∥轴，以AB 、AD 为边作菱形ABCD ，求菱形ABCD 的面积．23.（2022开封二模）如图，平面直角坐标系中，反比例函数()0n y n x=≠与一次函数()0y kx b k =+≠的图像相交于点()1,A m ，()3,1B --两点．（1）求反比例函数与一次函数的解析式；（2）直接写出n kx b x+>的解集．（3）已知直线AB 与y 轴交于点C ，点(),0P t 是x 轴上一动点，作PQ ⊥x 轴交反比例函数图像于点Q ，当以C ，P ，Q ，O 为顶点的四边形的面积等于2时，求t 的值．24.（2022鹤壁一模）如图，在矩形ABCO 中，84AB BC ==，，点D 是边AB 的中点，反比例函数11(0)k y x x=<的图象经过点D ，交BC 边于点E ，直线DE 的解析式为()2220y k x b k =+≠．（1）求反比例函数和直线DE 的解析式．（2）在x 轴上找一点P ，使PDE △的周长最小，求出此时点P 的坐标．（3）在（2）的条件下，PDE △的周长最小值是_________．25.（2022周口扶沟一模）如图，正比例函数y x =的图象与反比例函数k y x=（0x >）的图象交于点()1,A a ，在ABC 中，90ACB ∠=︒，CA CB =，点C 坐标为()2,0-．（1）求k 的值；（2）求AB 所在直线的解析式．26.（2022信阳一模）如图，直线y=-2x+b与x轴、y轴分别相交于点A，B，以线段AB为边在第一象限作正方形ABCD，已知（1）求直线AB的解析式；（2）求点D的坐标，并判断点D是否在双曲线y=12x，说明理由.27.（2022雅安中考）如图，在平面直角坐标系中，等腰直角三角形ABO的直角顶点A的坐标为（m，2），点B在x轴上，将△ABO向右平移得到△DEF，使点D恰好在反比例函数y＝8x（x＞0）的图象上．（1）求m的值和点D的坐标；（2）求DF所在直线的表达式；（3）若该反比例函数图象与直线DF的另一交点为点G，求S△EFG．28.（2022盘锦中考）如图，平面直角坐标系xOy 中，四边形OABC 是菱形，点A 在y 轴正半轴上，点B 的坐标是(4,8)-，反比例函数(0)k y x x=<的图象经过点C ．（1）求反比例函数的解析式；（2）点D 在边CO 上，且34CD DO =，过点D 作DE x 轴，交反比例函数的图象于点E ，求点E 的坐标．29．（2022天门中考）（7分）如图，OA＝OB，∠AOB＝90°，点A，B分别在函数y＝（x＞0）和y＝（x ＞0）的图象上，且点A的坐标为（1，4）．（1）求k1，k2的值；（2）若点C，D分别在函数y＝（x＞0）和y＝（x＞0）的图象上，且不与点A，B重合，是否存在点C，D，使得△COD≌△AOB．若存在，请直接写出点C，D的坐标；若不存在，请说明理由．30.（2022恩施中考）如图，在平面直角坐标系中，O 为坐标原点，已知∠ACB=90°，A(0，2)，C(6，2)．D 为等腰直角三角形ABC 的边BC 上一点，且S △ABC =3S △ADC ．反比例函数y 1=kx(k≠0)的图象经过点D ．（1）求反比例函数的解析式；（2）若AB 所在直线解析式为()20y ax b a =+≠，当12y y >时，求x 的取值范围．31.（2022河南中考）如图，反比例函数()0ky x x=>的图像经过点()2,4A 和点B ，点B 在点A 的下方，AC 平分OAB ∠，交x 轴于点C ．（1）求反比例函数的表达式．（2）请用无刻度的直尺和圆规作出线段AC 的垂直平分线．（要求：不写作法，保留作图痕迹，使用2B 铅笔作图）（3）线段OA 与（2）中所作的垂直平分线相交于点D ，连接CD ．求证：CD AB ∥．32.（2022荆州中考）小华同学学习函数知识后，对函数()()2410410x x y x x x⎧-<≤⎪=⎨-≤->⎪⎩或通过列表、描点、连线，画出了如图1所示的图象．x…－4－3－2－134-12-14-01234…y (1)4324941140－4－243-－1…请根据图象解答：（1）【观察发现】①写出函数的两条性质：______；______；②若函数图象上的两点()11,x y ，()22,x y 满足120x x +=，则120y y +=一定成立吗？______．（填“一定”或“不一定”）（2）【延伸探究】如图2，将过()1,4A -，()4,1B -两点的直线向下平移n 个单位长度后，得到直线l 与函数()41y x x=-≤-的图象交于点P ，连接PA ，PB ．①求当n ＝3时，直线l 的解析式和△PAB 的面积；②直接用含．．．．n ．的代数式表示．．．．．．△PAB 的面积．33.（2022牡丹江中考）如图，在平面直角坐标系中，四边形ABCD ，A 在y 轴的正半轴上，B ，C 在x 轴上，AD//BC ，BD 平分ABC ∠，交AO 于点E ，交AC 于点F ，CAO DBC ∠=∠．若OB ，OC 的长分别是一元二次方程2560x x -+=的两个根，且OB OC >．请解答下列问题：（1）求点B ，C 的坐标；（2）若反比例函数()0ky k x=≠图象的一支经过点D ，求这个反比例函数的解析式；（3）平面内是否存在点M ，N （M 在N 的上方），使以B ，D ，M ，N 为顶点的四边形是边长比为2:3的矩形？若存在，请直接写出在第四象限内点N 的坐标；若不存在，请说明理由．34.（2022驻马店六校联考三模）如图，在平面直角坐标系中，反比例函数kyx(x>0)的图象和矩形ABCD在第一象限，AD平行于x轴，且AB=2，AD=4，点A的坐标为(2，6)．（1）直接写出B、C、D三点的坐标；（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式．35.（2022周口川汇区一模）如图，正方形ABCD的边AB在x轴上，点D的坐标为（2，2），点M是AD的中点，反比例函数ykx的图象经过点M，交BC于点N．（1）求反比例函数的表达式；（2）若点P是x轴上的一个动点，求PM+PN的最小值．36.（2022郑州外国语一模）如图，点()4,B a 是反比例函数()120y x x=>图象上一点，过点B 分别向坐标轴作垂线，垂足为A ，C ．反比例函数()0ky x x=>的图象经过OB 的中点M ，与AB ，BC 分别相交于点D ，E ．连接DE 并延长交x 轴于点F ，连接BF ．（1）求k 的值；（2）求BDF 的面积；（3）设直线DE 的解析式为1y k x b =+，请结合图像直接写出不等式1kk x b x+<的解集______．37.（2022郑州二模）如图1，点A、B是双曲线y=kx（k＞0）上的点，分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF，AC和BF交于点G，得到正方形OCGF（阴影部分），且S阴影=1，△AGB的面积为2．（1）求双曲线的解析式；（2）在双曲线上移动点A和点B，上述作图不变，得到矩形OCGF（阴影部分），点A、B在运动过程中始终保持S阴影=1不变（如图2），则△AGB的面积是否会改变？说明理由．38.（2022信阳三模）如图，在矩形OABC中，BC＝4，OC，OA分别在x轴、y轴上，对角线OB，AC交于点E；过点E作EF⊥OB，交x轴于点F．反比例函数kyx=（x＞0）的图像经过点E，且交BC于点D，已知S△OEF＝5，CD＝1．（1）求OF的长；（2）求反比例函数的解析式；（3）将△OEF沿射线EB个单位长度，得到△O'E'F'，则EF的对应线段E'F'的中点（填“能”或“不能”）落在反比例函数kyx=（x＞0）的图上．39.（2022河南新野一模）如图，()()4,30P m m m ->是双曲线12y x =-上一点，过点P 作x 轴、y 轴的垂线，分别交x 轴、y 轴于A 、B 两点，交双曲线k y x=于E 、F 两点．（1）求直线AB 的解析式；（2）若12BFBP =，求k 的值和EF 的长．40.（2022平顶山二模）如图，四边形ABCD，EFGH均为菱形，其中点E，A，B，F四点均在x轴上，点D，H在y轴上，EH∥AD．双曲线y=kx(x>0)的图象过点C(5，4)，交边GH于点P(103，a)．（1）填空：k=______，a=______；（2）求菱形EFGH的面积．41.（2022南阳卧龙一模）如图，已知在平面直角坐标系中，点(3,4)B 在反比例函数(0,0)k y k x x=>>的图象上，过点B 作BA x ⊥轴于点A ，连接OB ，将OAB 向右平移，得到,'''''O A B O B 交双曲线于点(3,)C a a ．（1）求k ，a 的值；（2）求OAB 向右平移的距离；（3）连接,BC OC ，则OBC 的面积为____________．42.（2022洛阳伊川一模）如图，已知点()0,1A 在y 轴上，点()10B ,在x 轴上，以AB 为边在第一象限内作正方形ABCD ，此时反比例函数(0)k y k x=≠在第一象限内的图象恰好经过点C ，D ．（1）直接写出点D 的坐标和反比例函数的表达式；（2）将正方形ABCD 绕点B 按顺时针方向旋转，当点C 的对应点C '落在x 轴上时，判断点D 的对应点D ′是否落在反比例函数k y x =的图象上，并说明理由．43.（2022洛阳二模）如图，在平面直角坐标系中，ABCD 的顶点分别为()1,2A ，()4,2B ，()7,5C ，曲线():0k G y x x=>．（1）求点D 的坐标；（2）当曲线G 经过ABCD 的对角线的交点时，求k 的值；（3）若曲线G 刚好将ABCD 边上及其内部的“整点”（横、纵坐标都为整数的点）分成数量相等的两部分，则直接写出k 的取值范围是______．44.（2022河南林州一模）如图，在平面直角坐标系中，正方形ABCD 的边BC 在x 轴上，点A 坐标为()2,4，点M 是AB 的中点，反比例函数k y x=的图象经过点M ，交CD 于点N ．（1）求反比例函数的表达式；（2）若反比例函数图象上的一个动点(),P m n 在正方形ABCD 的内部（含边界），求POC △面积的最小值．45.（2022河南兰考一模）如图，在平面直角坐标系中，ABCD 的顶点分别为(1,2),(4,2),(7,5)A B C ，曲线(0)k y k x=>．（1）当曲线经过ABCD 的对角线的交点时，求k 的值．（2）若曲线刚好将ABCD 边上及其内部的“整点”（横、纵坐标都为整数的点）分成数量相等的两部分，求k 的取值范围．46.（2022河南兰考二模）如图，在矩形OABC 中，2AB =，4BC =，D 是AB 边的中点，反比例函数()0k y x x=>的图象经过点D ，与BC 边交于点E ．（1）求反比例函数的表达式及点E 的坐标；（2）若点P 在y 轴上，当△PDE 的周长最小时，直接写出△PDE 的面积．47.（2022河南滑县一模）如图，平行四边形OABC 的顶点A ，C 都在反比例函数y k x=（k ＞0）的图象上，已知点B 的坐标为（8，4），点C 的横坐标为2．（1）求反比例函数y k x=（k ＞0）的解析式；（2）求平行四边形OABC 的面积S ．48.（2022河南邓州一模）如图，在平面直角坐标系中，矩形ABCD 的顶点A （1，0），D （0，2），反比例函数k y x =的图象经过了矩形的顶点B ，且1tan 2ABD ∠=．（1）求反比例函数表达式；（2）动手画直线OB ，记为y mx =，结合图象直接写出关于x 的不等式0k mx x ->的解集．。
2.反比例函数与几何图形结合(6道)
反比例函数与几何图形结合1．如图，已知点A(5，0)，B(0，5)，把一个直角三角尺DEF 放在△OAB内，使其斜边FD在线段AB上，三角尺可沿着线段AB上下滑动，其中∠EFD＝45°，ED＝2，点G为边FD 的中点．(1)求直线AB的解析式；(2)如图，当点D与点A重合时，求经过点G的反比例函数y＝kx(k≠0)的解析式；(3)在三角尺滑动的过程中，经过点G的反比例函数的图象能否同时经过点F？如果能，求出此时反比例函数的解析式；如果不能，请说明理由．解：(1)设直线AB的解析式为y＝ax＋b，把A 、B 的坐标分别代入可得⎩⎪⎨⎪⎧5a ＋b ＝0b ＝5，解得⎩⎪⎨⎪⎧a ＝－1b ＝5，∴直线AB 的解析式为y ＝－x ＋5； (2)∵A (5，0)， ∴OA ＝5，当D 与A 重合时，则OE ＝OD －DE ＝5－2＝3， ∵∠EFD ＝45°， ∴EF ＝DE ＝2， ∴F (3，2)，D (5，0)， ∵G 为DF 的中点， ∴G (4，1)，∵点G 在y ＝kx 图象上， ∴k ＝4×1＝4，∴经过点G 的反比例函数的解析式为y ＝4x ；(3)设F (t ，－t ＋5)，则D 点横坐标为t ＋2，代入直线AB 的解析式可得y ＝－(t ＋2)＋5＝－t ＋3， ∴D (t ＋2，－t ＋3)， ∵G 为DF 的中点， ∴G (t ＋1，－t ＋4)，若反比例函数图象同时过G 、F 点，则可得t (－t ＋5)＝(t ＋1)(－t ＋4)，解得t ＝2，此时F 点坐标为(2，3)，设经过F 、G 的反比例函数解析式为y ＝sx ，则s ＝2×3＝6， ∴经过点G 的反比例函数的图象能同时经过点F ，其函数解析式为y ＝6x .2. 如图，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx 的图象相交于点A (－2，1)，点B (1，n )． (1)求此一次函数和反比例函数的解析式；(2)请直接写出满足不等式kx ＋b －mx ＜0的解集；第2题图(3)如图，在平面直角坐标系的第二象限内边长为1的正方形EFDG 的边均平行于坐标轴，若点E (－a ，a )，当曲线y ＝mx (x ＜0)与正方形EFDG 的边有交点时，求a 的取值范围． 解：(1)∵点A (－2，1)在反比例函数y ＝mx 的图象上， ∴m ＝－2×1＝－2，∴反比例函数的解析式为y ＝－2x ；∵点B (1，n )在反比例函数y ＝－2x 的图象上， ∴－2＝n ，即点B 的坐标为(1，－2)．将点A (－2，1)、B (1，－2)分别代入y ＝kx ＋b 中得：212k b k b -=+⎧⎨=-+⎩，解得⎩⎪⎨⎪⎧k ＝－1b ＝－1， ∴一次函数的解析式为y ＝－x －1； (2)∵－x －1－(－2x )＜0，∴－x －1＜－2x ，观察两函数图象，发现：当－2＜x ＜0或x ＞1时，一次函数图象在反比例函数图象的下方，∴满足不等式kx ＋b －mx ＜0的解集为－2＜x ＜0或x ＞1； (3)过点O 、E 作直线OE ，如解图所示．第2题解图∵点E 的坐标为(－a ，a )， ∴直线OE 的解析式为y ＝－x .∵四边形EFDG 是边长为1的正方形，且各边均平行于坐标轴，∴点D 的坐标为(－a ＋1，a －1)， 代入直线y ＝－x ，得： a －1＝－(－a ＋1)， ∴点D 在直线OE 上．将y ＝－x 代入y ＝－2x (x ＜0)得： －x ＝－2x ，即x 2＝2， 解得x ＝－2或x ＝2(舍去)．∵曲线y ＝－2x (x ＜0)与正方形EFDG 的边有交点， ∴－a ≤－2≤－a ＋1，解得2≤a ≤2＋1.故当曲线y ＝mx (x ＜0)与正方形EFDG 的边有交点时，a 的取值范围为2≤a ≤2＋1.3. 如图，一次函数y ＝－x ＋b 与反比例函数y ＝kx (x >0)的图象交于点A (m ，3)和B (3，1)．第3题图(1)填空：一次函数的解析式为________，反比例函数的解析式为________；(2)点P 是线段AB 上一点，过点P 作PD ⊥x 轴于点D ，连接OP ，若△POD 的面积为S ，求S 的取值范围． 解：(1)y ＝－x ＋4，y ＝3x ；【解法提示】将B (3，1)分别代入y ＝－x ＋b 与y ＝kx 中，解得b ＝4，k ＝3，则一次函数的解析式为y ＝－x ＋4，反比例函数的解析式为y ＝3x .(2) 由(1)得3＝3m ，∴m ＝1，则A 点坐标为(1，3)．设P 点坐标为(a ，－a ＋4)(1≤a ≤3)，则S ＝12OD ·PD ＝12a (－a ＋4)＝－12(a －2)2＋2， ∵－12＜0，∴当a ＝2时，S 有最大值，此时S ＝－12×(2－2)2＋2＝2； 由二次函数的性质得，当a ＝1或3时，S 有最小值，此时 S ＝－12×(1－2)2＋2＝32， ∴S 的取值范围是32 ≤ S ≤2.4. 如图，矩形AOCB 的顶点B 在反比例函数y ＝kx (k >0，x >0)的图象上，且AB ＝3，BC ＝8.若动点E 从A 开始沿AB 向B 以每秒1个单位长度的速度运动，同时动点F 从B 开始沿BC 向C 以每秒2个单位长度的速度运动，当其中一个动点到达终点时，另一个动点随之停止运动，设运动时间为t 秒． (1)求反比例函数的解析式；第4题图(2)当t ＝1时，在y 轴上是否存在点D ，使△DEF 的周长最小？若存在，请求出△DEF 的周长最小值；若不存在，请说明理由；(3)在双曲线上是否存在一点M ，使以点B 、E 、F 、M 为顶点的四边形是平行四边形？若存在，请直接写出满足条件的t 的值；若不存在，请说明理由．解：(1)由题可知点B 的坐标为(3，8)，且点B 在y ＝kx 上， ∴k ＝3×8＝24，∴反比例函数的解析式为y ＝24x ；(2)存在．t ＝1时，E (1，8)，F (3，6)，则EF ＝22， 如解图，延长EA 使A ′E ＝EA ，连接DE ′，E ′F ，则E ′F ＝25，C △DEF ＝DE ＋DF ＋EF ＝22＋DE ′＋DF ≥22＋E ′F ＝22＋25，∴C △DEF min ＝22＋25， 此时点D 为E ′F 与y 轴的交点，第4题解图∵E ′(－1，8)，F (3，6)，设直线E ′F 的解析式为：y ＝kx ＋b ，则⎩⎪⎨⎪⎧－k ＋b ＝83k ＋b ＝6， 解得⎩⎪⎨⎪⎧k ＝－12b ＝152，∴直线E ′F 的解析式为：y ＝－12x ＋152，∴此时D (0，152)，即：y 轴上存在点D (0，152)，使△DEF 的周长最小，且最小值为22＋2 5.(3)存在，若四边形BEMF 为平行四边形，则有三种可能，已知E (t ，8)，F (3，8－2t )，0<t ≤3. ①BE ∥FM ，此时M 在F 右侧，M (248－2t，8－2t )， 又∵BE ＝FM ，∴3－t ＝248－2t －3，即t 2－10t ＋12＝0，解得t 1＝5－13，t 2＝5＋13(舍去)． ②BF ∥EM ，此时M 在E 正上方，M (t ，24t )， ∵ME ＝BF ，∴24t －8＝2t ，t 2＋4t －12＝0， 解得t 1＝2，t 2＝－6(舍去)．③EF ∥BM ，易知点M 一定不在反比例函数上， 故综上，t ＝2或5－13.5．在平面直角坐标系xOy 中，点B 在x 轴上，四边形OACB 为平行四边形，且∠AOB ＝60°，反比例函数y ＝kx (k ＞0)在第一象限内过点A ，且与BC 交于点F . (1)若OA ＝10，求反比例函数的解析式； (2)若F 为BC 的中点，且S △AOF ＝243，求OA 的第5题图长及点C 的坐标；(3)在(2)的条件下，在x 轴上是否存在一点P ，使得PF ＋P A 最小？若存在，求出点P 的坐标；若不存在，请说明理由． 解：(1)如解图①，过点A 作AH ⊥OB 于H ，第5题解图①∵∠AOB ＝60°，OA ＝10，∴AH ＝OA ·sin ∠AOB ＝53，OH ＝OA ·cos ∠AOB ＝5， ∴点A 的坐标为(5，53)， 将点A (5，53)代入y ＝kx ，得 53＝k5，解得k ＝253，∴反比例函数的解析式为y ＝253x ；(2)如解图①，过点F 作FM ⊥x 轴于点M ，设OA ＝a (a ＞0)， ∵∠AOB ＝60°，∴AH ＝OA ·sin ∠AOB ＝32a ，OH ＝OA ·cos ∠AOB ＝12a ， ∴S △AOH ＝12AH ·OH ＝12×32a ·12a ＝38a 2，∵S △AOF ＝243，∴S ▱AOBC ＝2S △AOF ＝483， ∵F 为BC 的中点， ∴S △OBF ＝14S ▱AOBC ＝123，∵BF ＝12BC ＝12OA ＝12a ，∠FBM ＝∠AOB ＝60°， ∴FM ＝BF ·sin ∠FBM ＝34a ，BM ＝BF ·cos ∠FBM ＝14a ， ∴S △BMF ＝12FM ·BM ＝12×34a ·14a ＝332a 2， ∴S △FOM ＝S △OBF ＋S △BMF ＝123＋332a 2， ∵点A ，F 都在y ＝kx 的图象上， ∴S △AOH ＝S △FOM ， 即38a 2＝123＋332a 2， 解得a ＝82，∴OA ＝82，∴OH ＝42，AH ＝3OH ＝3×42＝46，∵S▱AOBC＝OB·AH＝483，即OB·46＝483，解得OB＝62，∴AC＝OB＝62，∴C(102，46)；(3)存在．如解图②，作点F关于x轴的对称点F′，连接AF′交x轴于点P，此时PF＋P A最小，第5题解图②由(2)可知，A(42，46)，FM＝34a＝26，BM＝14a＝22，∴OM＝62＋22＝82，∴点F的坐标为(82，26)，∴点F′的坐标为(82，－26)，设直线AF′的解析式为y＝mx＋n，将点A(42，46)，F′(82，－26)代入，得⎩⎪⎨⎪⎧42m ＋n ＝4682m ＋n ＝－26， 解得⎩⎨⎧m ＝－332n ＝106， ∴y ＝－332x ＋106，令y ＝0，即－332x ＋106＝0， 解得x ＝2023，∴在x 轴上存在点P ，使得PF ＋P A 最小，点P 的坐标为(2023，0)．6．如图，反比例函数y ＝m x (x ＞0)与一次函数y ＝kx ＋63交于点C (2，43)，一次函数图象与两坐标轴分别交于点A 和点B ，动点P 从点A 出发，沿AB 以每秒1个单位长度的速度向点B 运动；同时，动点Q 从点O 出发，沿OA 以相同的速度向点A 运动，运动时间为t 秒(0＜t ≤6)，以点P 为圆心，P A 为半径的⊙P与AB交于点M，与OA交于点N，连接MN、MQ.第6题图(1)求m与k的值；(2)当t为何值时，点Q与点N重合；(3)若△MNQ的面积为S，试求S与t的函数关系式．解：(1)将C(2，43)代入y＝mx中得，m＝83，将(2，33)代入y＝kx＋63中得，2k＋63＝43，∴k＝－3；(2)由(1)知，k＝－3，∴直线AB的解析式为y＝－3x＋63，∴A(6，0)，B(0，63)，∴AB＝12.∵AM是直径,∴∠ANM＝90°，∴∠ANM＝∠AOB.又∵∠MAN＝∠BAO，∴△MAN∽△BAO，∴ANAO＝MNBO＝AMAB.∵OQ＝AP＝t，AM＝2AP＝2t，OA＝6，OB＝63，AB＝12∴AN6＝MN63＝2t12,∴AN＝t，MN＝3t,∴ON＝OA－AN＝6－t.∵点Q与点N重合,∴ON＝OQ.即6－t＝t.∴t＝3;(3)①当0＜t ≤3时，QN ＝OA －OQ －AN ＝6－2t, ∴S ＝12QN ·MN ＝12(6－2t )·3t ＝－3t 2＋33t ; ②当3＜t ≤6时，QN ＝OQ ＋NA －OA ＝t ＋t －6＝2t －6, ∴S ＝12QN ·MN ＝12(2t －6)·3t ＝3t 2－33t ，即：S ＝⎩⎪⎨⎪⎧－3t 2＋33t （0＜t ≤3）3t 2－33t （3＜t ≤6）.。
【常考压轴题】2023学年九年级数学下册压轴题攻略(人教版) 反比例函数与几何图形综合(解析版)
反比例函数几何图形综合例1．（等腰三角形）已知反比例函数1=myx-（m为常数）的图象在第一、三象限．(1)求m的取值范围；(2)如图若该反比例函数的图象经过▱ABOD的顶点D点A B的坐标分别为（0 4）（﹣3 0）．①求出函数解析式；②【分类讨论思想】设点P是该反比例函数图象上的一点若以D O P为顶点的三角形是等腰三角形则满足条件的点P的个数为______个．AD OB例2．（直角三角形）如图 在平面直角坐标系中 直线32y kx k =++与坐标轴交于点B 与()0,1C 点A 是x 轴上一点 连接AC 且1AB = ()1,D m 是线段BC 上一点 反比例函数k y x'=的图象经过点D ．(1)求k '的值．(2)求线段AC 所在直线的函数表达式．(3)延长DO 与反比例函数k y x'=的图象在第三象限交于点F Q 是x 轴上的一点 当以F 、Q 、D 三点构成的三角形为直角三角形时 直接写出Q 点的坐标．例3．（平行四边形）如图四边形OBAC是矩形OC＝2 OB＝6 反比例函数kyx=的图象过点A．(1)求k的值．(2)点P为反比例函数图象上的一点作PD▱直线AC PE▱x轴当四边形PDCE是正方形时求点P的坐标．(3)点G为坐标平面上的一点在反比例函数的图象上是否存在一点Q使得以A、B、Q、G为顶点组成的平行四边形面积为16？若存在请求出点G的坐标；若不存在请说明理由．例4．（菱形）如图 直线y ＝ax ＋b 与反比例函数y ＝k x（x ＜0）的图象相交于点A 、点B 与x 轴交于点C 其中点A 的坐标为（-2 6） 点B 的横坐标为-6(1)试确定反比例函数的关系式；(2)求点C 的坐标；(3)点M 是x 轴上的一个动点．①若点M 在线段OC 上 且△AMB 的面积为8 求点M 的坐标；②点N 是平面直角坐标系中的一点 当以A 、B 、M 、N 四点为顶点的四边形是菱形时 请直接写出点N 的坐标【变式训练1】．如图在平面直角坐标系中已知Rt▱AOB的两直角边OA、OB分别在x轴和y轴的正半轴上A(8 0) B(0 6) 点C从原点O出发沿边OA向点A运动速度为每秒1个单位长度点D从点A出发沿边AB向点B运动速度为每秒2个单位长度．设两点同时出发运动时间为t秒（0 < t < 5）(1)当t = 时 DC ∥BO ；(2)当▱ADC 的面积为9时 求t 的值；(3)在（2）的条件下；①作射线BC 若M 是射线BC 上的一个动点 在坐标平面内是否存在点P 使以A 、B 、M 、P 为顶点的四边形是矩形？若存在 请直接写出点P 的坐标；若不存在 请说明理由．② 过点C 作直线1l ▱x 轴 过点B 作直线2l ▱y 轴 直线1l 与直线2l 交于点P 反比例函数k y x=（k >0 x >0）的图像与直线1l 、2l 分别交于点E 、F 连接EF 在y 轴上是否存在点Q 使得▱PEF 和▱QEF 全等 若存在 请直接写出相应的k 的值；若不存在 请说明理由． ▱ADC ABO ∽AD AC AB AO = AD AB AC OA = 21088t t =- 40AD DE 2t DE ADC S =的面积为9 9=2BCO ACM ∴∽▱22P Q B BOC ∽2222Q P P B Q B OB BC OC== 即222256335P Q Q B == 224P Q ∴=,22Q B =2Rt ABM 中,22BM AB =21,AM BM ⊥▱1BAM BM ∠=∠又2ABM ∠=∠12BAM BM A ∴∽▱122AM AB AM BM = 1102545AM =▱11PBQ BAO ∽11BQ BP OA AB ∴= 15810BQ = 解得14BQ =,则6OQ OB BQ =-=11Rt PQ B 中 )3,2-如图 ▱QE PE =EF EF =只能是PFQ QFE ≌B 12l l ⊥ ▱PFQ QFE ≌36k PF QF ==-,FQE ∠如图 过点E 作EG ⊥又FBQ QGE ∠=∠▱FBQ QGE ∽4【变式训练2】如图已知矩形OABC中OA＝6 AB＝8 双曲线kyx=（k＞0）与矩形两边AB BC分别交于点D E且BD＝2AD．(1)求k的值和点E的坐标；(2)点P是线段OC上的一个动点是否存在点P使▱APE＝90°？若存在求出此时点P的坐标若不存在请说明理由．经检验 m =2或m =6都是原方程的解 且符合题意▱存在要求的点P 点P 的坐标为（2 0）或（6 0）．【变式训练3】如图 抛物线L ：()()142y x t x t =---+（常数0t >）与x 轴从左到右的交点为B A 过线段OA 的中点M 作MP x ⊥轴 交双曲线k y x =（0k > 0x >）于点P 且12OA MP ⨯=．(1)求k 的值．(2)当t=1时 求AB 的长 并求直线MP 与L 的对称轴之间的距离．(3)把L 在直线MP 左侧部分的图像（含与直线MP 的交点）记为G 用t 表示图像G 最高点的坐标．(4)设L 与y 轴的交点为N 当2t =时 在x 轴上是否存在一点Q 使ONQ △与PMQ 相似 若存在 求出Q 的坐标 若不存在 请说明理由．1m 时：m 1m ＜＜时：0＜时：1m 时：m 1m ＜＜时：0＜时：-【变式训练4】如图 在平面直角坐标系中 点B D 分别在反比例函数()60y x x =-<和()0,0k y k x x =>>的图象上 AB x ⊥轴于点A DC x ⊥轴于点C O 是线段AC 的中点 3AB = 2DC =．(1)求反比例函数k y x=的表达式； (2)连接BD OB OD 求ODB △的面积；(3)P 是线段AB 上的一个动点 Q 是线段OB 上的一个动点 试探究是否存在点P 使得APQ 是等腰直角三角形？若存在 求所有符合条件点P 的坐标；若不存在 请说明理由．3⎛⎫2⎝⎭使得APQ是等腰直角三角形。
2023中考数学专项： 反比例函数与几何图形综合问题(重点突围)(学生版)
专题16反比例函数与几何图形综合问题【中考考向导航】目录【直击中考】 (1)【考向一反比例函数中K值的几何意义】 (1)【考向二反比例函数与三角形的综合问题】 (4)【考向三反比例函数与矩形的综合问题】 (6)【考向四反比例函数与菱形的综合问题】 (9)【考向五反比例函数与正方形的综合问题】 (11)【考向六反比例函数与圆的综合问题】 (15)【直击中考】【考向一反比例函数中K值的几何意义】【变式训练】1．（2023·安徽宿州·统考一模）如图，若反比例函数______在反比例函数3．（2022·黑龙江绥化·校考二模）如图，在过点A、C两点，点B在4．（2023秋·安徽池州·九年级统考期末）AC交y轴于点B，若点B是=【考向二反比例函数与三角形的综合问题】(1)求反比例函数的解析式；(2)过点A作AP垂直OA，交反比例函数的图象于点①求直线AC的解析式；②求点P的坐标．【变式训练】(1)求反比例函数的解析式；(2)坐标平面内有一点D，若以A(1)求反比例函数的表达式；(2)求等边△ACD的边长．【考向三反比例函数与矩形的综合问题】(1)直接写出B，C，D三点的坐标；(2)若将矩形向下平移，矩形的两个顶点值．【变式训练】上两点，的顶点【考向四反比例函数与菱形的综合问题】（1）求k的值及AB所在直线的函数表达式；（2）将这个菱形沿x轴正方向平移，当顶点【变式训练】是菱形，点(1)求一次函数与反比例函数的解析式；(2)设点P是直线AB上一动点，且ABCD(1)求双曲线y2的函数关系式及(2)判断点B是否在双曲线上，并说明理由；(3)若BA的延长线与双曲线【考向五反比例函数与正方形的综合问题】(1)求反比例函数的解析式；(2)若将正方形ABCD沿x轴向右平移得到正方形标，并判断点B′是否在该反比例函数的图象上，说明理由．【变式训练】在平面直角坐标系中，点(1)求反比例函数的解析式；(2)求四边形OAFM 的面积．2．（2022·山东济南·校考一模）如图，四边形35AE OE =．中点，以备用图4．（2022春·江苏苏州·八年级星海实验中学校考期中）如图，在平面直角坐标系中，四边形ABCD 为正方形，已知点()6,0A -、()7,3D -，点B 、C 在第二象限内．(1)点B 的坐标_________；(2)将正方形ABCD 以每秒2个单位的速度沿x 轴向右平移t 秒，若存在某一时刻t ，使在第一象限内点B 、D 两点的对应点B '、D ¢正好落在某反比例函数的图像上，请求出此时t 的值以及这个反比例函数的解析式；(3)在（2）的情况下，问是否存在y 轴上的点P 和反比例函数图像上的点Q ，使得以P 、Q 、B '、D ¢四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点Q 的坐标；若不存在，请说明理由．【考向六反比例函数与圆的综合问题】【变式训练】在反比例函数。
反比例函数与几何的综合应用(教案)
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《反比例函数与几何的综合应用》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要根据面积或比例来求解问题的情况？”比如，我们如何根据已知的长和宽来求解矩形的面积。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索反比例函数在几何问题中的奥秘。
3.重点难点解析：在讲授过程中，我会特别强调反比例函数的性质和图像，以及它在几何问题中的应用这两个重点。对于难点部分，比如反比例函数与一次函数的交点求解，我会通过具体例题和逐步解析来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与反比例函数在几何问题中应用相关的实际问题。
三、教学难点与重点
1.教学重点
（1）反比例函数的定义及其性质：反比例函数的定义，图像特点，以及其在实际中的应用。
举例：y = k/x（k≠0），解释k的取值对函数图像的影响，如k>0时图像位于一、三象限，k<0时图像位于二、四象限。
（2）反比例函数与其他函数的交点问题：分析反比例函数与一次函数、二次函数的交点情况，掌握求解方法。
（二）新课讲授（用时10形如y = k/x（k≠0）的函数，它的图像是一条经过原点的曲线。反比例函数在解决与比例相关的问题时非常重要。
2.案例分析：接下来，我们来看一个具体的案例。这个案例将展示如何利用反比例函数来求解矩形的面积，以及它如何帮助我们解决实际问题。
此外，我在课堂上尝试引导同学们提出问题、分析问题并解决问题，目的是培养他们的独立思考能力。但从实际情况来看，同学们在这一方面的表现还不够理想。因此，我计划在接下来的教学中，进一步加强这方面的训练，鼓励同学们敢于提问、善于提问。
反比例函数与几何图形的综合
反比例函数与几何图形的小综合题型一反比例函数与三角形结合1．（2020•沙坪坝区校级月考）如图，一次函数y＝x+32分别与x轴、y轴交于A、B两点，点P为反比例函数y=kx（k≠0，x＜0）图象上一点，过点P作y轴的垂线交直线AB交于C，作PD⊥PC交直线AB于D，若AC•BD＝7，则k的值为（）A．﹣2B．﹣3C．−72D．−92【点睛】设P（m，n）．则AC=√2n，BD=−√2m，构建方程求出mn的值即可．【解析】解：设P（m，n）．则AC=√2n，BD=−√2m，∵AC•BD＝7，∴﹣2mn＝7，∴mn=−72，∴k=−72．故选：C．2．如图，在平面直角坐标系中，OB在x轴上，∠ABO＝90°，点A的坐标为（2，4），将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在反比例函数y=kx的图象上，则k的值为12．【解析】解：∵OB在x轴上，∠ABO＝90°，点A的坐标为（2，4），将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在反比例函数y=kx的图象上，∴点C的坐标为（6，2），∴2=k6，解得，k＝12，3．（2020•薛城区期中）在平面直角坐标系xOy 中，将一块含有45°角的直角三角板如图放置，直角顶点C 的坐标为（1，0），顶点A 的坐标为（0，2），顶点B 恰好落在第一象限的双曲线上，现将直角三角板沿x 轴正方向平移，当顶点A 恰好落在该双曲线上时停止运动，则此时点C 的对应点C ′的坐标为 （52，0） ．【解析】解：过点B 作BD ⊥x 轴于点D ，∵∠ACO +∠BCD ＝90°，∠OAC +∠ACO ＝90°， ∴∠OAC ＝∠BCD ，在△ACO 与△BCD 中，{∠OAC =∠BCD∠AOC =∠BDC AC =BC ，∴△ACO ≌△BCD （AAS ）∴OC ＝BD ，OA ＝CD ，∵A （0，2），C （1，0）∴OD ＝3，BD ＝1，∴B （3，1），∴设反比例函数的解析式为y =kx，将B （3，1）代入y =k x，∴k ＝3，∴y =3x，∴把y ＝2代入y =3x ，∴x =32，当顶点A 恰好落在该双曲线上时，此时点A 移动了32个单位长度，∴C 也移动了32个单位长度，此时点C 的对应点C ′的坐标为（ 52，0）故答案为（52，0）．4．（2020•盐湖区期末）如图，在平面直角坐标系中，边长为4的等边△OAB 的OA 边在x 轴的正半轴上，反比例函数y =kx （x ＞0）的图象经过AB 边的中点C ，且与OB 边交于点D ，则点D 的坐标为 （√3，3） ．【解析】解：∵△AOB 是等边三角形，边长为4，∴B （2，2√3），∵BC ＝CA ，∴C （3，√3），把点C 坐标代入y =k x上，得到k ＝3√3，∵直线OB 的解析式为y =√3x ， 由{y =√3xy =3√3x，解得{x =√3y =3或{x =−√3y =−3（舍弃）∴D （√3，3），故答案为（√3，3）． 题型二 反比例函数与四边形结合5．（2020•北海期末）如图，矩形ABCD 在第一象限，AB 在x 轴的正半轴上，AB ＝3，BC ＝1，直线y =12x ﹣1经过点C 交x 轴于点E ，双曲线y =kx经过点D ，则k 的值为（ ）A ．1B ．2C ．3D ．4【解析】解：根据矩形的性质知点C 的纵坐标是y ＝1，∵直线y =12x ﹣1经过点C ，∴1=12x ﹣1， 解得，x ＝4，即点C 的坐标是（4，1）．∵矩形ABCD 在第一象限，AB 在x 轴正半轴上，AB ＝3，BC ＝1，∴D （1，1），∵双曲线y =kx 经过点D ，∴k ＝xy ＝1×1＝1，即k 的值为1．故选：A ．6．（2020•秀洲区二模）平面直角坐标系中，菱形AOBC 的位置如图所示，点A 在x 轴负半轴上，B （1，√3），反比例函数y =kx 在第二象限的图象经过点C ，则k ＝ −√3 ．【点睛】根据菱形的性质可以求得点C 的坐标，再根据点C 在反比例函数图象上，从而可以求得k 的值．【解析】解：∵点A在x轴负半轴上，B（1，√3），∴OB＝2，点C的纵坐标是√3，∴OA＝2，∵四边形AOBC是菱形，点A在x轴的负半轴，∴点C的坐标为（﹣1，√3），∵反比例函数y=kx在第二象限的图象经过点C，∴√3=k−1，得k=−√3，故答案为：−√3．7．如图，在平面直角坐标系中，矩形OABC的对角线OB、AC相交于点D，BE∥AC，AE∥OB，函数y=kx（k＞0，x＞0）的图象经过点E，若点A、C的坐标分别为（3，0），（0，2），则k的值为92．【解析】解：∵BE∥AC，AE∥OB，∴四边形AEBD是平行四边形，∵四边形OABC是矩形，C的坐标为（0，2），∴DA=12AC，DB=12OB，AC＝OB，AB＝OC＝2，∴DA＝DB，∴四边形AEBD是菱形；连接DE，交AB于F，如图所示：∵四边形AEBD是菱形，∴AB与DE互相垂直平分，∵OA＝3，OC＝2，∴EF＝DF=12OA=32，AF=12AB＝1，3+32=92，∴点E坐标为：（92，1）．∵函数y=kx（k＞0，x＞0）的图象经过点E，∴k=92×1=92，故答案为：92．8．（2020•盘龙区二模）如图，在平面直角坐标系中，反比例函数y=kx（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N两点．△OMN的面积为10．若动点P在x轴上，则PM+PN 的最小值是2√26．【解析】解：∵正方形OABC的边长是6，∴点M的横坐标和点N的纵坐标为6，∴M （6，k 6），N （k6，6），∴BN ＝6−k 6，BM ＝6−k 6，∵△OMN 的面积为10，∴6×6−12×6×k 6−12×6×k 6−12×（6−k6）2＝10，∴k ＝24，∴M （6，4），N （4，6），作M 关于x 轴的对称点M ′，连接NM ′交x 轴于P ，则NM ′的长＝PM +PN 的最小值，∵AM ＝AM ′＝4，∴BM ′＝10，BN ＝2，∴NM ′=√BM′2+BN 2=√102+22=2√26，故答案为2√26．巩固练习1．（2020•铜山区二模）如图，矩形ABCD 的边BC 在x 轴的负半轴上，顶点D （a ，b ）在反比例函数y =kx的图象上，直线AC 交y 轴点E ，且S △BCE ＝4，则k 的值为（ ）A ．﹣16B ．﹣8C ．﹣4D ．﹣2【解析】解：D （a ，b ），则CO ＝﹣a ，CD ＝AB ＝b ，∵矩形ABCD 的顶点D 在反比例函数y =kx （x ＜0）的图象上，∴k ＝ab ，∵△BCE 的面积是4，∴12×BC ×OE ＝4，即BC ×OE ＝8，∵AB ∥OE ，∴BC OC=AB EO，即BC •EO ＝AB •CO ，∴8＝b ×（﹣a ），即ab ＝﹣8，∴k ＝﹣8故选：B ．2．（2020•九龙坡区校级期末）如图，已知反比例函数y =ax和一次函数y ＝kx +b 的图象相交于点A （﹣1，y 1）、B （4，y 2）两点，则不等式ax ≤kx +b 的解集为（ ）A ．x ≤﹣1或x ≥4B ．﹣1≤x ≤4C ．x ≤4D ．x ≤﹣1或.0＜x ≤4【解析】解：不等式a x≤kx +b 的解集就是反比例函数值小于或等于一次函数值的自变量的取值范围，观察图象可得：第二象限x ≤﹣1，第四象限0＜x ≤4，故选：D ．3．（2020•深圳模拟）如图，点A 是双曲线y =3x上的动点，连结AO 并延长交双曲线于点B ，将线段AB 绕B 顺时针旋转60°得到线段BC ，点C 在双曲线y =kx上的运动，则k ＝ ﹣9 ．【解析】解：∵双曲线y =3x 关于原点对称，∴点A 与点B 关于原点对称．∴OA ＝OB ．连接OC ，AC ，如图所示．∵将线段AB 绕B 顺时针旋转60°得到线段BC ，∴△ABC 是等边三角形，OA ＝OB ，∴OC ⊥AB ，∠BAC ＝60°，∴tan ∠OAC =OCOA =√3，∴OC =√3OA ．过点A 作AE ⊥y 轴，垂足为E ，过点C 作CF ⊥y 轴，垂足为F ，∵AE ⊥OE ，CF ⊥OF ，OC ⊥OA ，∴∠AEO ＝∠OFC ，∠AOE ＝90°﹣∠FOC ＝∠OCF ，∴△AEO ∽△OFC ．∴AE OF=EO FC=AO OC．∵OC =√3OA ，∴OF =√3AE ，FC =√3EO ．设点A 坐标为（a ，b ），∵点A 在第一象限，∴AE ＝a ，OE ＝b ．∴OF =√3AE =√3a ，FC =√3EO =√3b ．∵点A 在双曲线y =3x上，∴ab ＝3．∴FC •OF =√3b •√3a ＝3ab ＝9，设点C 坐标为（x ，y ），∵点C 在第四象限，∴FC ＝x ，OF ＝﹣y ．∴FC •OF ＝x •（﹣y ）＝﹣xy ＝9．∴xy ＝﹣9．∵点C 在双曲线y =kx 上，∴k ＝xy ＝﹣9．故答案为：﹣9．4．（2020•普陀区二模）如图，在平面直角坐标系xOy 中，△ABC 的顶点A 、C 在坐标轴上，点B 的坐标是（2，2）．将△ABC 沿x 轴向左平移得到△A 1B 1C 1，点B 1落在函数y =−6x 的图象上．如果此时四边形AA 1C 1C 的面积等于552，那么点C 1的坐标是 （﹣5，112） ．【解析】解：如图，∵点B 的坐标是（2，2），BB 1∥AA 1，∴点B 1的纵坐标为2， 又∵点B 1落在函数y =−6x 的图象上，∴当y ＝2时，x ＝﹣3，∴BB 1＝AA 1＝5＝CC 1，又∵四边形AA 1C 1C 的面积等于552，∴AA 1×OC =552，∴OC =112，∴点C 1的坐标是（﹣5，112）．故答案为：（﹣5，112）．5．（2020•九龙坡区校级期末）如图，菱形OABC 在直角坐标系中，点A 的坐标为（52，0），对角线OB =2√5，反比例函数y =kx （k ≠0，x ＞0）经过点C ．则k 的值为 3 ．【解析】解：∵四边形OABC 是菱形，∴OA ＝AB ＝BC ＝CO ，设点C 的坐标为（a ，b ），∵点A 的坐标为（52，0），对角线OB =2√5，∴点B 的坐标为（a +52，b ），OC =52，∴{a 2+b 2=(52)2(a +52)2+b 2=(2√5)2，解得a =32，b ＝2，∴ab =32×2=3，∵反比例函数y =kx （k ≠0，x ＞0）经过点C ，点C 的坐标为（a ，b ），∴b =ka ，∴k ＝ab ＝3． 故答案为：3．6．以矩形ABCD 两条对角线的交点O 为坐标原点，以平行于两边的方向为坐标轴，建立如图所示的平面直角坐标系，BE ⊥AC ，垂足为E ．若双曲线y =32x（x ＞0）经过点D ，则OB •BE 的值为 3 ．【解析】解：如图，∵双曲线y =32x （x ＞0）经过点D ，∴S △ODF =12k =34， 则S △AOB ＝2S △ODF =32，即12OA •BE =32，∴OA •BE ＝3，∵四边形ABCD 是矩形，∴OA ＝OB ，∴OB •BE ＝3，故答案为：3．7．（2020•通辽）如图，在平面直角坐标系中，反比例函数y =k x（k ＞0）的图象与半径为5的⊙O 交于M 、N 两点，△MON 的面积为3.5，若动点P 在x 轴上，则PM +PN 的最小值是 5√2 ．【解析】解：如图设点M （a ，b ），N （c ，d ），∴ab ＝k ，cd ＝k ，∵点M，N在⊙O上，∴a2+b2＝c2+d2＝25，作出点N关于x轴的对称点N'（c，﹣d），∴S△OMN=12k+12（b+d）（a﹣c）−12k＝3.5，∴bc﹣ad＝7，∴kca−kac=7，∴ac=k(c2−a2)7，同理：bd=k(b2−d2)7，∴ac﹣bc=k(c2−a2)7−k(b2−d2)7=k7[（c2+d2）﹣（a2+b2）]＝0，∵M（a，b），N'（c，﹣d），∴MN'2＝（a﹣c）2+（b+d）2＝a2+b2+c2+d2﹣2ac+2bd＝a2+b2+c2+d2﹣2（ac﹣bd）＝50，∴MN'＝5√2，故答案为：5√2。
反比例函数与几何综合(一)(含答案)
学生做题前请先回答以下问题问题1：思考反比例函数与几何综合的处理思路是什么？问题2：什么是关键点？问题3：将函数特征与几何特征联系起来的桥梁是什么？问题4：围绕关键点以及横平竖直线段长将几何特征与函数特征结合分析时有几种方式？分别是什么？以下是问题及答案，请对比参考:问题1：思考反比例函数与几何综合的处理思路是什么？答：反比例函数与几何综合的处理思路：①从关键点入手．通过关键点坐标和横平竖直线段长的互相转化可将函数特征和几何特征综合在一起进行研究．②对函数特征和几何特征进行转化、组合，列方程求解．若借助反比例函数模型，能快速将函数特征转化为几何特征．问题2：什么是关键点？答：关键点是几何图形与函数图象的交点，在处理反比例函数与几何综合的问题时从关键点入手分析．问题3：将函数特征与几何特征联系起来的桥梁是什么？答：通过关键点坐标与横平竖直线段长的相互转化，可将函数特征与几何特征综合起来一起进行研究．问题4：围绕关键点以及横平竖直线段长将几何特征与函数特征结合分析时有几种方式？分别是什么？答：可以采用两种方式：①根据函数特征设出坐标，表达线段长，利用几何特征建等式；②根据几何特征设出线段长，表达坐标，代入函数建立等式．反比例函数与几何综合（一）一、单选题(共8道，每道12分)1.如图，直线与双曲线在第一象限内的交点为R，与x轴的交点为P，与y轴的交点为Q；作RM⊥x轴于点M，若△OPQ与△PRM的面积之比为4：1，则k的值为( )A. B.C.2D.3答案：B解题思路：试题难度：三颗星知识点：反比例函数与几何综合2.如图，均是等腰直角三角形，点在反比例函数的图象上，斜边都在x轴上，则点的坐标是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：反比例函数与几何综合3.如图，在平面直角坐标系中，矩形ABCD的边AB：BC=3：2，点A(3，0)，B(0，6)分别在x 轴，y轴上，反比例函数（x＞0）的图象经过点D，且与边BC交于点E，则点E的坐标为( )A.(1，14)B.(2，8)C.(2，7)D.(1，16)答案：C解题思路：试题难度：三颗星知识点：反比例函数与几何综合4.如图，矩形ABCD的顶点D在反比例函数（x<0）的图象上，顶点B，C在x轴上，对角线AC的延长线交y轴于点E，连接BE，若△BCE的面积是6，则k的值为( )A.-6B.-8C.-9D.-12答案：D解题思路：试题难度：三颗星知识点：反比例函数与几何综合5.如图，在反比例函数的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第一象限内有一点C，满足AC=BC，当点A运动时，点C始终在函数的图象上运动．若tan∠CAB=2，则k的值为( )A.2B.4C.6D.8答案：D解题思路：试题难度：三颗星知识点：反比例函数与几何综合6.如图，直线与双曲线交于点A，将直线向上平移4个单位长度后，与y轴交于点C，与双曲线交于点B，若OA=3BC，则k的值为( )A.3B.6C. D.答案：D解题思路：试题难度：三颗星知识点：反比例函数与几何综合7.如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB=，反比例函数在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于( )A.60B.80C.30D.40答案：D解题思路：试题难度：三颗星知识点：反比例函数与几何综合8.直线y=-2x-2与反比例函数的图象交于点A，与x轴交于点B，过点B作x 轴垂线交双曲线于点C，若AB=AC，则k的值为( )A.-1B.-2C.-4D.-8答案：C解题思路：试题难度：三颗星知识点：反比例函数与几何综合。
专题26 反比例函数与几何综合题型归纳-2023年中考数学二轮复习核心考点拓展训练(原卷版)
专题26 反比例函数与几何综合题型归纳（原卷版）类型一 反比例函数与三角形综合1．（2022秋•岚山区校级期末）如图，直角三角形的直角顶点在坐标原点，∠OAB ＝30°，点A 在反比例函数y =6x（x ＞0）的图象上，则经过点B 的反比例函数解析式为（ ）A ．y =―1x B ．y =―2x C ．y =―4xD ．y =―6x2．（2022秋•金水区校级期末）如图，已知直角三角形ABO 中，AO =3，将△ABO 绕点O 点旋转至△A 'B 'O 的位置，且A '在OB 的中点，B '在反比例函数y =kx上，则k 的值为 ．3．（2022秋•荔湾区校级期末）如图，△ABC 是等腰三角形，AB 过原点O ，底边BC ∥x 轴，双曲线y =kx过A ，B 两点，过点C 作CD ∥y 轴交双曲线于点D ，若S △BCD ＝16，则k 的值是 ．4．（2023•南海区模拟）如图，在x 轴的正半轴上依次截取OA 1＝A 1A 2＝A 2A 3＝A 3A 4＝A 4A 5，过点A 1，A 2，A 3，A 4，A 5分别作x 轴的垂线与反比例函数y =2x(x ≠0)的图象相交于点P 1，P 2，P 3，P 4，P 5，得直角三角形OP 1A 1，A 1P 2A 2，A 2P 3A 3，A 3P 4A 4，A 4P 5A 5，并设其面积分别为S 1，S 2，S 3，S 4，S 5，则S 2022＝ ．5．（2022秋•桥西区校级期末）如图，一次函数y 1＝k 1x +b 的图像与反比例函数y 2=k 2x(x ＞0)的图像相交于A （m ，6），B （6，1）两点，且与x 轴，y 轴交于点M ，N ．（1）填空：k 2＝ ；m ＝ ；在第一象限内，当y 1＞y 2时，x 的取值范围为 ；（2）连接OA ，OB ，求△AOB 的面积；（3）点E 在线段AB 上，过点E 作x 轴的垂线，交反比例函数图像于点F ，若EF ＝2，求点F 的坐标．6．（2022秋•龙泉驿区期末）某班在“图形与坐标”的主题学习中，第四学习小组提出如下背景“如图，在平面直角坐标系中，将一个边长为2的等边三角形ABC 沿x 轴平移（边AB 在x 轴上，点C 在x 轴上方），其中A （a ，0），三角形ABC 与反比例函数y =23x（x ＞0）交于点D ，E 两点（点D 在点E 左边）”，让其他小组提出问题，请你解答：（1）第一小组提出“当a ＝2时，求点D 的坐标”；（2）第二小组提出“若AD ＝CE ，求a 的值”；（3）第三小组提出“若将点E 绕点A 逆时针旋转60°至点E ′，点E ′恰好也在y =23x（x ＞0）上，求a 的值”．7．（2022秋•南山区期末）如图：△AOB 为等腰直角三角形，斜边OB 在x 轴上，S △OAB ＝4，一次函数y 1＝kx +b （k ≠0）的图象经过点A 交y 轴于点C ，反比例函数y 2=kx（x ＞0）的图象也经过点A ．（1）求反比例函数的解析式；（2）若CD ＝2AD ，求△COD 的面积；（3）当y 1＜y 2时对应的自变量的取值范围是 ．（请直接写出答案）8．（2022秋•老城区校级期中）如图，已知：直线y =12x 与双曲线y =k x （k ＞0）交于A ，B 两点，且点A的横坐标为4，若双曲线y =kx（k ＞0）上一点C 的纵坐标为8，连接AC ．（1）填空：k 的值为 8 ；点B 的坐标为 ；点C 的坐标为 ．（2）直接写出关于的不等式12x ―k x≥0的解集；（3）求三角形AOC 的面积．9．（2022秋•虹口区校级期中）如图，在平面直角坐标系xOy 中，已知直线y ＝kx （k ＞0）分别交反比例函数y =1x 和y =9x 在第一象限的图象于点A ，B ，过点B 作BD ⊥x 轴于点D ，交y =1x的图象于点C ，联结AC ，若△ABC 是等腰三角形，求k 的值．类型二 反比例函数与平行四边形综合10．（2022秋•襄都区校级期末）如图，反比例函数y =kx的图象经过平行四边形ABCD 对角线的交点P ．知A ，C ，D ，三点在坐标轴上，BD ⊥DC ，平行四边形ABCD 的面积为6，则k 的值为（ ）A ．﹣6B ．﹣5C ．﹣4D ．﹣311．（2022秋•滨城区校级期末）如图，平行四边形OABC 的顶点O ，B 在y 轴上，顶点A 在y =―2x 上，顶点C 在y =9x上，则平行四边形OABC 的面积是 ．12．（2022秋•平城区校级月考）如图，在平面直角坐标系中，已知平行四边形ABOC 的面积为6，边OB 在x 轴上，顶点 A 、C 分别在反比例函数y =k x（x ＜0）和y =2x （x ＞0）的图象上，则k ﹣2的值为（ ）A ．﹣4B ．4C ．﹣6D ．613．（2022秋•高新区期末）如图，在平面直角坐标中，平行四边形ABCD 顶点A 的坐标为（1，0），点D 在反比例函数y =―6x 的图象上，点B ，C 在反比例函数y =kx（x ＞0）的图象上，CD 与y 轴交于点E ，若DE ＝CE ，∠DAO ＝45°，则k 的值为 ．14．（2022•湘潭县校级模拟）如图，在平面直角坐标系Oxy 中，函数y =kx （其中x ＜0）的图象经过平行四边形ABOC 的顶点A ，函数y =8x（其中x ＞0）的图象经过顶点C ，点B 在x 轴上，若点C 的横坐标为2，△AOC 的面积为6．（1）求k 的值；（2）求直线AB 的解析式．类型三 反比例函数与矩形综合15．（2022秋•永城市期末）如图，直线y ＝﹣x +3与坐标轴分别相交于A ，B 两点，过A ，B 两点作矩形ABCD ，AB ＝2AD ，双曲线y =kx在第一象限经过C ，D 两点，则k 的值是（ ）A ．6B ．274C ．272D ．2716．（2022秋•岚山区校级期末）如右图，已知矩形OABC 的面积为1003，它的对角线OB 与双曲线y =kx相交于点D ，且OB ：OD ＝5：3，则k ＝（ ）A ．10B ．20C ．6D ．1217．（2022秋•达川区期末）如图，矩形AOBC 的边OA ＝3，OB ＝4，动点F 在边BC 上（不与B 、C 重合），过点F 的反比例函数y =kx的图象与边AC 交于点E ，直线EF 分别与y 轴和x 轴相交于点D 和G ．给出下列命题：①若k ＝6，则△OEF 的面积为92；②若k =218，则点C 关于直线EF 的对称点在x 轴上；③满足题设的k 的取值范围是0＜k ≤12；④若DE ⋅EG =256，则k ＝2；其中正确的命题个数是（ ）A ．1个B ．2个C ．3个D ．4个18．（2023•黔江区一模）如图，矩形ABCD 中，点A 在双曲线y =―8x上，点B ，C 在x 轴上，延长CD 至点E ，使CD ＝2DE ，连接BE 交y 轴于点F ，连接CF ，则△BFC 的面积为（ ）A ．5B ．6C ．7D ．819．（2022秋•荔城区校级期末）如图，点A 为双曲线y =―2x在第二象限上的动点，AO 的延长线与双曲线的另一个交点为B ，以AB 为边的矩形ABCD 满足AB ：BC ＝4：3，对角线AC ，BD 交于点P ，设P 的坐标为（m ，n ），则m ，n 满足的关系式为 ．20．（2022秋•滕州市校级期末）如图，矩形OABC 与反比例函数y 1=k 1x（k 1是非零常数，x ＞0）的图象交于点M ，N ，反比例函数y 2=k 2x（k 2是非零常数，x ＞0）的图象交于点B ，连接OM ，ON ．若四边形OMBN 的面积为3，则2k 2﹣2k 1＝ ．21．（2022秋•长安区校级期末）如图，矩形ABCD 顶点坐标分别为A （1，1），B （2，1），CB ＝2．（1）若反比例函数y =kx与的图象过点D ，则k ＝ ．（2）若反比例函数与矩形ABCD 的边CD 、CB 分别交于点E 、点F ，且△CEF 的面积是，则反比例函数的表达式为 ．（3）若反比例函数y =k x(x ＞0)的图象将矩形边界上横、纵坐标均为整数的点恰好等分成了两组，使两组点分别在双曲线两侧，则k 的取值范围是 ．22．（2022秋•松原期末）如图，在平面直角坐标系中，四边形OABC 为矩形，点C 、A 分别在x 轴和y 轴的正半轴上，点D 为AB 的中点．一次函数y ＝﹣3x +6的图象经过点C 、D ，反比例函数y =kx（x ＞0）的图象经过点B ，求k 的值．23．（2022•礼县校级模拟）如图，在平面直角坐标系中，矩形OABC 的两边OC 、OA 分别在坐标轴上，且OA ＝2，OC ＝4，连接OB ．反比例函数y =k1x（x ＞0）的图象经过线段OB 的中点D ，并与AB 、BC 分别交于点B 、F ．一次函数y ＝k 2x +b 的图象经过E 、F 两点．（1）分别求出一次函数和反比例函数的表达式．（2）点P 是x 轴上一动点，当PE +PF 的值最小时，求点P 的坐标．25．（2022春•姑苏区校级月考）如图，在以O 为原点的平面直角坐标系中，点 A 、C 分别在x 轴、y 轴的正半轴上，点B （a ，b ）在第一象限，四边形OABC 是矩形，反比例函数y =kx（k ＞0，x ＞0）的图象与AB 相交于点D ，与BC 相交于点E ，且BE ＝2CE ．（1）求证：BD ＝2AD ；（2）若四边形ODBE 的面积是6，求k 的值．类型四 反比例函数与菱形综合26．（2022秋•江北区校级期末）如图，菱形ABCD 的边AD ⊥y 轴，垂足为点E ，顶点A 在第二象限，顶点B 在y 轴的正半轴上，反比例函数y =kx（k ≠0，x ＞0）的图象同时经过顶点C 、D ．若点C 的横坐标为10，BE ＝3DE ，则k 的值为（ ）A ．15B ．6C ．154D ．1027．（2022•珠海校级三模）如图，菱形ABCD的顶点分别在反比例函数y=k1x（k1＞0）和y=k2x的图象上，且∠ADC＝120°，则k2k1的值是（ ）A．﹣3B．―13C．3D．―3328．（2022秋•岚山区校级期末）如图，O为坐标原点，点C在x轴上．四边形OABC为菱形，D为菱形对角线AC与OB的交点，反比例函数y=kx在第一象限内的图象经过点A与点D，若菱形OABC的面积为242，则点A的坐标为 ．29．（2022秋•福州期末）如图，四边形ABOC为菱形，∠BOC＝60°，反比例函数y=kx(x＜0)的图象经过点B，交AC边于点P，若△BOP的面积为43，则点A的坐标为 ．30．（2022秋•通川区期末）如图，在平面直角坐标系中，点A的坐标是（5，0），函数y=kx（x＞0）的图象经过菱形OABC的顶点C，若OB•AC＝40，则k的值为 ．31．（2023•西山区校级开学）如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A 在反比例函数y =kx（k ＞0，x ＞0）的图象上，点D 的坐标为（4，3）．（1）求反比例函数的关系式；（2）设点M 在反比例函数图象上，连接MA 、MD ，若△MAD 的面积是菱形ABCD 面积的14，求点M 的坐标．类型五 反比例函数与正方形综合32．（2022秋•东港市期末）如图，在平面直角坐标系中，一次函数y =43x +4的图象与x 轴，y 轴分别交于点B ，A ，以线段AB 为边作正方形ABCD ，且点C 在反比例函数y =k x（x ＜0）的图象上，则k 的值为（ ）A ．﹣21B ．21C ．﹣24D ．2433．（2022秋•龙岗区校级期末）如图，反比例函数y =kx(x ＞0)图象经过正方形OABC 的顶点A ，BC 边与y轴交于点D ，若正方形OABC 的面积为12，BD ＝2CD ，则k 的值为（ ）A ．3B ．185C ．165D ．10334．（2022秋•济南期末）如图，在直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行，点P （4a ，a ）是反比例函数y =k x（k ＞0）的图象上与正方形的一个交点，若图中阴影部分的面积等于16，则k 的值为（ ）A ．16B ．1C ．4D ．﹣1635．（2022•南关区校级模拟）如图，正方形ABCO 和正方形CDEF 的顶点B 、E 在双曲线y =6x（x ＞0）上，连接OB 、OE 、BE ，则S △OBE 的值为（ ）A ．2B ．2.5C ．3D ．3.536．（2022•绿园区校级模拟）如图，在平面直角坐标系中，大、小两个正方形的一个顶点均为坐标原点，两边分别在x 轴，y 轴的正半轴上，若经过小正方形的顶点A 的函数y =k x（x ＞0）的图象与大正方形的一边交于点B （1，3），则阴影部分的面积为（ ）A ．6B ．3C ．32D ．3―337．（2022秋•徐汇区期末）点A 、M 在函数y =1x （x ＞0）图象上，点B 、N 在函数y =―3x（x ＜0）图象上，分别过A 、B 作x 轴的垂线，垂足为D 、C ，再分别过M 、N 作线段AB 的垂线，垂足为Q 、P ，若四边形ABCD 与四边形MNPQ 均为正方形，则正方形MNPQ 的面积是 ．38．（2022秋•薛城区期末）如图，点B 是反比例函数y =k x图象上的一点，矩形OABC 的周长是20，正方形OCDF 与正方形BCGH 的面积之和为68，则k 的值为 ．39．（2022春•姑苏区校级期中）如图，在平面直角坐标系中，反比例函数y =k x(x ＞0)的图象与边长等于6的正方形OABC 的两边AB ，BC 分别相交于M ，N 两点，△MON 的面积是16，动点P 从原点出发，以每秒2个单位长度的速度沿x 轴向右运动，记运动时间为t ，当t ＝ s 时，PM +PN 最小．40．（2022•香洲区校级三模）如图，反比例函数y =k x（k ≠0，x ＞0）的图象过点B ，E ，四边形ODEF 和ABCD 是正方形，顶点F 在x 轴的正半轴上，A ，D 在y 轴正半轴上，点C 在边DE 上，延长BC 交x 轴于点G ．若AB ＝2，则四边形CEFG 的面积为 ．41．（2022秋•蚌山区月考）如图，两个边长分别为a ，b （a ＞b ）的正方形连在一起，三点C ，B ，F 在同一直线上，反比例函数y =k x在第一象限的图象经过小正方形右下顶点E ．若OB 2﹣BE 2＝8，则（1）S 正方形OABC ﹣S 正方形DEFB ＝ ；（2）k 的值是 ．42．（2022•九龙坡区自主招生）如图，在平面直角坐标系中，已知点A 的坐标为（0，4），点B 的坐标为（2，0），连结AB ，以线段AB 为边在第一象限内作正方形ABCD ，直线BD ：y ＝ax +b 交双曲线y =k x（k ≠0）于D 、E 两点，连结CE ．（1）求双曲线y =k x（k ≠0）和直线BD 的解析式；（2）求△BEC 的面积；（3）请直接写出不等式ax +b ＞k x 的解集．43．（2022•东湖区期中）如图，在平面直角坐标系中，正方形OABC 的顶点O 在坐标原点，顶点A 在y 轴上，顶点C 在x 轴上，反比例函数y ＝k 的图象过AB 边上一点E ，与BC 边交于点D ，BE ＝2，OE ＝10．（1）求k 的值；（2）直线y ＝ax +b 过点D 及线段AB 的中点F ，点P 是直线OF 上一动点，当PD +PC 的值最小时，直接写出这个最小值．44．（2021秋•榆林）如图，在平面直角坐标系中，点A 的坐标为（1，0），点B 的坐标为（0，2），以线段AB 为一边在第一象限内作平行四边形ABCD ，其顶点D （3，1）在反比例函数y =k x（x ＞0）的图象上．（1）求证：四边形ABCD 是正方形；（2）设将正方形ABCD 沿x 轴向左平移m （m ＞0）个单位后，得到正方形A ′B ′C ′D ′，点C 的对应点C ′恰好落在反比例函数y =k x（x ＞0）的图象上，求m 的值．45．（2022秋•宝山区校级期中）如图，已知正方形OABC 的面积为9，点O 为坐标原点，点A 在x 轴上，点C 在y 轴上，点B 在函数y =k x （k ＞0，x ＞0）图象上，点P 是函数y =k x（k ＞0，x ＞0）图象上异于点B 的任意一点，过点P 分别作x 轴、y 轴的垂线，垂足分别为点E 、F ．设矩形OEPF 和正方形OABC 不重合部分的面积为S ．（1）点B 的坐标是 ，k ＝ ；（2）当S =92，求点P 的坐标；（3）求出S 关于m 的函数关系式．46．（2022秋•武功县期末）如图，在平面直角坐标系中，A （﹣1，2），B （﹣1，﹣2），以AB 为边向右作正方形ABCD ，边AD 、BC 分别与y 轴交于点E 、F ，反比例函数y =k x(k ≠0)的图象经过点D ．（1）求反比例函数的表达式；（2）在反比例函数的图象上是否存在点P ，使得△PEF 的面积等于正方形ABCD 面积的一半？若存在，请求出点P 的坐标；若不存在，请说明理由．47．（2022•靖江市校级模拟）如图，在直角坐标系中，Rt △ABC 的直角边AC 在x 轴上，∠ACB ＝90°，AC＝1，反比例函数y =k x（k ＞0）的图象经过BC 边的中点D （3，1）．（1）直接写出这个反比例函数的表达式 ；（2）若△ABC 与△EFG 关于点M 成中心对称，且△EFG 的边FG 在y 轴的正半轴上，点E 在这个函数的图象上．①直接写出OF 的长 、对称中心点M 的坐标 ；②连接AF，BE，证明四边形ABEF是正方形．。
专题2.10反比例函数与几何综合大题(学生版)
专题2.11反比例函数与几何综合大题一、解答题1．（2022·上海奉贤·九年级期中）如图，已知在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图像经过点A、B(−1，0)，反比例函数y=6x的图像也经过点A，且点A横坐标是2．(1)求一次函数的解析式．(2)点C是x轴正半轴上的一点，连接AC，tan∠ACB=34，过点C作CE⊥x轴分别交反比例函数y=6x和一次函数y=kx+b(k≠0)的图像于点D、E，求点D、E的坐标．(3)在（2）的条件下，连接AD，一次函数y=kx+b(k≠0)的图像上是否存在一点F使得△EAD和△ECF相似？若存在，请直接写出点F坐标；若不存在，请说明理由．2．（2022·上海·八年级专题练习）如图，在平面直角坐标系中，△AOB是等边三角形．(1)在y轴正半轴取一点E，使得△EOB是一个等腰直角三角形，EB与OA交于M，已知MB=32，求MO．≠0的图(2)若等边△AOB的边长为6，点C在边OA上，点D在边AB上，且OC=3BD．反比例函数y=象恰好经过点C和点D，求反比例函数解析式．（此题无需写括号理由）3．（2022·福建·晋江市季延中学九年级期中）如图点P(m,n)是双曲线y=k x(x<0)上一动点，且m，n为关于a的一元二次方程4a2+ba+320的两根，动直线与x轴、y轴正半轴分别交于点A、B，过点A与AB垂直的直线交y轴于点E，点F是AE的中点，过B点且与AB垂直的直线交FO的延长线于Q点．(1)求双曲线的解析式；(2)当OP取最小值求b的值．(3)若点O到AB的距离等于OP的最小值，求1EF+1BQ的值．>04．（2022·安徽·淮南市龙湖中学九年级期中）如图，直线y=ax+6经过点A−3,0，交反比例函数y=的图象于点B1,m．(1)求k的值；(2)点D为第一象限内反比例函数图象上点B下方的一个动点，过点D作DC⊥y轴交线段AB于点C，连接AD，求△ACD的面积的最大值．5．（2022·广东·南山实验教育麒麟中学九年级期中）直线y=2x与反比例函数y=2x图象交于A，B两点，CA点右侧任意一点；(1)如图1，求A，B两点坐标；(2)如图2，连接BC，若∠ABC=45°，求点C的坐标；(3)如图3，设直线AC，BC分别与x轴相交于D，E两点，且AC=mCD，BC=nCE，求n−m的值．6．（2022·江苏·景山中学九年级阶段练习）在平面坐标系xOy中，给出如下定义：若点P在图形M上，点Q 在图形N上，称线段PQ长度的最小值为图形M、N的“最近距离”，记为d M，N．特别地，若图形M、N有公共点，规定值为0．(1)如图1，⊙O的半径为2，①点A0,1，则d A，⊙O=_________．>0的图像为G1，则d G1，⊙O=_________．②记反比例函数y=(2)如图2，点B2，0，⊙B的半径为1，直线l1：y=kx+3，若d l1，⊙B=135，求k的值．(3)如图3，直线l2：y=−x+4与x轴交于点C，与y轴交于点D，边长为2的正方形EFHK的中心为O，将正方形EFHK沿着x m个单位，记正方形EFHK为图形G2，若线段CD与正方形EFHK的“最近距离”满足0≤d CD，G2≤12，请直接写出m的取值范围．7．（2022·重庆第二外国语学校九年级期中）如图，点A、B分别在x轴和y轴的正半轴上，以线段AB为边在第一象限作等边△ABC，S△ABC＝3，且CA⊥x轴．(1)若点C在反比例函数y=k x（k≠0）的图象上，求该反比例函数的解析式；(2)在（1）中的反比例函数图象上是否存在点N，使四边形ABCN是菱形，若存在请求出点N坐标，若不存在，请说明理由；(3)在（2）的条件下，取OB的中点M，将线段OM沿着y轴上下移动，线段OM的对应线段是O1M1，直接写出四边形CM1O1N周长的最小值．8．（2022·陕西·西北大学附中九年级期中）如图，一次函数y=−x+4的图象与反比例函数y=k x（k为常数，且k≠0）的图象交与A1,a、B两点．(1)求反比例函数的表达式及点B的坐标；(2)点P在反比例函数第三象限的图象上，使得△PAB的面积最小，求满足条件的P点坐标及△PAB面积的最小值．9．（2021·广东·佛山市南海外国语学校九年级阶段练习）如图1，平面直角坐标系xOy中，A−4,3，反比例<0的图象分别交矩形ABOC的两边AC、BC于E、F（E、F不与A重合），沿着EF将矩形ABOC函数y=折叠使A、D重合(1)如图2，连接BC，求证：EF∥BC；(2)当点D落在矩形ABOC内部时，求k的取值范围；(3)如图3，连接CD，求CD的最小值，并直接写出此时点D的坐标．>0图象上10．（2022·山西·大同市云州区初级示范中学校九年级阶段练习）如图，已知点A为函数y=任意一点，连接OA并延长至点B，使AB=OA，过点B作BC∥x轴交函数图象于点C，过点A作AD⊥BC，垂足为D，连接OC．求四边形OCDA的面积．11．（2022·山东师范大学第二附属中学九年级阶段练习）如图，矩形OABC的顶点A，C分别落在x轴，y轴的正半轴上，已知顶点B(2,4)，反比例函数y=k x(x>0)的图像与BC,AB分别交于D，E，BD=12．(1)求反比例函数关系式和点E的坐标；(2)写出DE与AC的位置关系并说明理由；(3)若点F在直线AC上，点G在反比例函数y=k x(x>0)的图像上，是否存在合适的F、G点，使四边形BCFG平行四边形，若存在，请求出点G的坐标．若不存在，请说明理由．12．（2022·湖南·长沙市北雅中学模拟预测）知识拓展如图1，由DE∥BC，AD=DB，可得AE=EC；如图2，由AB∥CD∥EF，AE=EC，可得BF=FD；解决问题如图3，直线AB与坐标轴分别交于点A m，0，B0,n m＞0,n＞0，反比例函数y=m x x>0的图象与AB交于C，D两点．(1)若m+n=8，n取何值时ΔABO的面积最大？(2)若SΔAOC=SΔCOD=SΔBOD，求点B的坐标．13．（2022·辽宁·灯塔市第一初级中学九年级期中）如图，在直角坐标系中，点B的坐标为（4，2），过点B 分别作x轴、y轴的垂线，垂足分别是C，A，反比例函数y=4x（x＞0）的图象分别交AB，BC于点E，F．(1)求直线EF的解析式；(2)求△EOF的面积；(3)若点P在y轴上，且△POE是等腰三角形，请直接写出点P的坐标．14．（2022·山东·新泰市宫里镇初级中学九年级阶段练习）如图，函数y＝k x（x＞0）的图像过点A（n，2）和B（85，2n−3）两点．(1)求n和k的值；(2)将直线OA沿x轴向左移动得直线DE，交x轴于点D，交y轴于点E，交y＝k x（x＞0）于点C，若S△ACO＝6，求直线DE解析式；(3)在（2）的条件下，第二象限内是否存在点F，使得△DEF为等腰直角三角形，若存在，请直接写出点F的坐标；若不存在，请说明理由．15．（2022·上海·新区川沙新镇江镇中学九年级阶段练习）如图，直线AC：y＝ax+2分别交y轴和反比例函数y=k x（x＞0）的图象于点C和点A（2，m），点B也在反比例函数的图象上，且BC∥x轴，tan∠ACB＝2．(1)求点A、B的坐标；(2)设点D在x轴的正半轴上，点E在该反比例函数的图象上．①若四边形BDCE是菱形，求出该菱形周长；②若以点A、C、D、E为顶点的四边形是平行四边形，请直接写出点D的坐标．16．（2022·浙江·九年级专题练习）已知在平面直角坐标系xOy中，点A是反比例函数y＝1x（x＞0）图象上的一个动点，连结AO，AO的延长线交反比例函数y＝k x（k＞0，x＜0）的图象于点B，过点A作AE⊥y轴于点E．(1)如图1，过点B作BF⊥x轴，于点F，连接EF．①若k＝1，求证：四边形AEFO是平行四边形；②连结BE，若k＝4，求△BOE的面积．(2)如图2，过点E作EP∥AB，交反比例函数y＝k x（k＞0，x＜0）的图象于点P，连结OP．试探究：对于确定的实数k，动点A在运动过程中，△POE的面积是否会发生变化？请说明理由．17．（2021·河南·商城县第二中学九年级阶段练习）已知反比例函数y=1-m x（m为常数）的图象在第一、三象限．(1)求m的取值范围；(2)如图，若该反比例函数的图象经过▱ABOD的顶点D，点A，B的坐标分别为（0，4），（﹣3，0）．①求出函数解析式；②【分类讨论思想】设点P是该反比例函数图象上的一点，若以D，O，P为顶点的三角形是等腰三角形，则满足条件的点P的个数为______个．18．OABC，OA在y轴上，OC在x轴上，OA=2，AB=4，双曲线k>0与矩形的边AB、BC分别交于点E、F．(1)若点E是AB的中点，求点F的坐标；(2)将△BEF沿直线EF对折，点B落在x轴上的D处，过点E作EG⊥OC于点G．问：△EGD与△DCF是否相似？若相似，请求出相似比；若不相似，请说明理由．19．（2021·辽宁·沈阳市清乐围棋学校九年级阶段练习）如图，在平面直角坐标系中，边长为2的正方形ABCD 关于y轴对称，边AD在x轴上，点B在第四象限，直线BD：y1＝kx+b与反比例函数y2＝m x的图象交于点B，点E．(1)求反比例函数及直线BD的关系式；(2)直接写出不等式m x﹣kx﹣b＜0的解集．20．（2022·安徽·利辛县汝集镇西关学校九年级阶段练习）如图，ΔAOB的边OB在x轴上，且∠ABO=90°，反比例函数y=k x(x>0)的图像与边AO、AB分别相交于点C、D，连接BC．已知OC=BC，ΔBOC的面积为12．(1)求k的值；(2)若AD=6，求直线OA的函数表达式．21．（2022·浙江省武义县实验中学八年级阶段练习）如图，四边形OBAC是矩形，OC＝2，OB＝6，反比例函数y=k x 的图象过点A．(1)求k的值．(2)点P为反比例函数图象上的一点，作PD⊥直线AC，PE⊥x轴，当四边形PDCE是正方形时，求点P的坐标．(3)点G为坐标平面上的一点，在反比例函数的图象上是否存在一点Q，使得以A、B、Q、G为顶点组成的平行四边形面积为16？若存在，请求出点G的坐标；若不存在，请说明理由．22．（2022·广东·深圳市宝安第一外国语学校模拟预测）数学是一个不断思考，不断发现，不断归纳的过程，古希腊数学家帕普斯(Pappus，约300−350)把∠AOB三等分的操作如下：（1）以点O为坐标原点，OB所在的直线为x轴建立平面直角坐标系；（2）在平面直角坐标系中，绘制反比例函数y=1x(x>0)的图像，图像与∠AOB的边OA交于点C；（3）以点C为圆心，2OC为半径作弧，交函数y=1x的图像于点D；（4）分别过点C和D作x轴和y轴的平行线，两线交于点E，M；（5）作射线OE，交CD于点N，得到∠EOB．(1)判断四边形CEDM的形状，并证明；(2)证明：O、M、E三点共线；(3)证明：∠EOB=13∠AOB．23．（2022·江苏省盐城中学新洋分校八年级阶段练习）【感知】如图1，已知反比例函数y=k x上有两点A(−2,1)，B(1,−2)，AE⊥x轴交x轴于点E，BF⊥y轴交y轴于点F，则S△AEF=______；S△BEF=_______；EF与AB的位置关系：_______．【探究】数学社团的同学们对上述问题又时行了思考，如图2，当A，B是双曲线y=k x(x>0)同一支上任意两点，过A，B分别向y轴，x轴作垂线，交y轴于点E，交x轴于点F，连接AF、BE．①试探究△AEF与△BEF面积的关系并说明理由．②试探究EF与AB之间的位置关系并说明理由．【运用】如图3，已知点A、B在反比例函数y=12x的图像上，且A(3,m)，B是反比例函数y=12x第三象限内图像上的一动点，过点A作AE⊥x轴，过点B作BF⊥y轴，垂足分别分为E，F，若四边形AEFB的面积为20，求点B的坐标．（提示，可直接运用上述所发现的结论，答案见公众号：绿爱生活）【拓展】如图4，函数y=k x(x>0)的图像与过原点O的直线相交于B、D两点，点A是第一象限内图像上的动点（点A在点B的左侧），直线AB分别交于y轴、x轴于点C、E，连接AD分别交y轴、x轴于点M、N．若AC=23AB，则AM AD=______．24．（2022·广东·佛山市南海外国语学校三模）如图1，在平面直角坐标系xOy中，点C在x轴负半轴上，四边形OABC为菱形，反比例函数y=−12x（x>0）经过点A(a,−3)，反比例函数y=k x(k>0,x＜0)经过点B，且交BC边于点D，连接AD．(1)求直线BC的表达式．(2)求tan∠DAB的值．(3)如图2，P是y轴负半轴上的一个动点，过点P作y轴的垂线，交反比例函数y=−12x（x>0）于点N．在点P运动过程中，直线AB上是否存在点E，使以B，D，E，N为顶点的四边形是平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．25．（2021·江苏·开明中学八年级期末）如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA、OB分别在x轴和y轴的正半轴上，A(8，0)，B(0，6)，点C从原点O出发，沿边OA向点A运动，速度为每秒1个单位长度，点D从点A出发，沿边AB向点B运动，速度为每秒2个单位长度．设两点同时出发，运动时间为t秒（0< t<5）(1)当t=时，DC∥BO；(2)当△ADC的面积为9时，求t的值；(3)在（2）的条件下；①作射线BC，若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．②过点C作直线l1⊥x轴，过点B作直线l2⊥y轴，直线l1与直线l2交于点P，反比例函数y=k x（k>0，x>0）的图像与直线l1、l2分别交于点E、F，连接EF，在y轴上是否存在点Q，使得△PEF和△QEF全等，若存在，请直接写出相应的k的值；若不存在，请说明理由．26．（2022·广东·东莞市万江第三中学三模）阅读理解对于任意正实数a，b，∵(a−b)2≥0，∴a+b−2ab≥0，∴a+b≥2ab，只有当a=b时，等号成立．结论：在a+b≥2ab(a,b均为正实数)中，若ab为定值p，则a+b≥2p只有当a=b时，a+b有最小值2p．根据上述内容，回答下列问题：(1)若m>0，只有当m=______时，m+1m有最小值______．(2)探索应用如图，已知A−2,0，B0,−3，P为双曲线y=6x(x>0)上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D.求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．(3)实践应用建筑一个容积为800m3，深为8m的长方体蓄水池，池壁每平方米造价为80元，池底每平方米造价为120元，如何设计池底的长、宽，使总造价最低？27．（2022·山东·新泰市楼德镇初级中学九年级阶段练习）反比例函数y＝k x（k＞0）的图像与直线y＝mx+n的图像交于Q点，点B（3，4）在反比例函数y＝k x的图像上，过点B作PB∥x轴交OQ于点P，过点P作PA∥y轴交反比例函数图像于点A，已知点A的纵坐标为94．(1)求反比例函数及直线OP的解析式；(2)在x轴上存在点N，使得△AON的面积与△BOP的面积相等，请求出点N的坐标；(3)在y轴上找一点E，使△OBE为等腰三角形，直接写出点E坐标．28．（2022·江苏·泰州中学附属初中八年级期末）如图在平面直角坐标系中，已知直线y＝﹣12x+2及双曲线y ＝k x（k＞0，x＞0）．直线交y轴于A点，x轴于B点，C、D为双曲线上的两点，它们的横坐标分别为a，a+m（m ＞0）．(1)如图①连接AC、DB、CD，当四边形CABD为平行四边形且a＝2时，求k的值．(2)如图②过C、D两点分别作CC'∥y轴∥DD'交直线AB于C'，D'，当CD∥AB时，①对于确定的k值，求证：a（a+m）的值也为定值．②若k＝6，且满足m＝a﹣4+d a，求d的最大值．29．（2022·江苏·泰州中学附属初中八年级期末）定义：平面直角坐标系内的矩形若满足以下两个条件：①各边平行于坐标轴：②有两个顶点在同一反比例函数图像上，我们把这个矩形称为该反比例函数的“伴随矩形”．例如，图1中，矩形ABCD的边AD∥BC∥x轴，AB∥CD∥y轴，且顶点A、C在反比例函数y=k x（k≠0）的图像上，则矩形ABCD是反比例函数的“伴随矩形”．解决问题：(1)已知，矩形ABCD中，点A、C的坐标分别为：①A（﹣3，8），C（6，﹣4）；②A（1，5），C（2，3）；③A（3，4），C（2，6），其中可能是某反比例函数的“伴随矩形”的是______；（填序号）(2)如图1，点B（2，1.5）是某比例系数为8的反比例函数的“伴随矩形”ABCD的顶点，求直线BD的函数解析式；(3)若反比例函数“伴随矩形”ABCD如图2所示，试说明有一条对角线所在的直线一定经过原点．30．（2022·上海市梅陇中学九年级期中）如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转．若∠BOA的两边分别与函数y=−1x,y=4x的图像交于A、B两点，(1)当OB与x轴的正半轴的夹角为45°时，求点A、B的坐标．(2)在直角∠BOA绕原点O按顺时针方向旋转过程中，∠OAB大小会变化吗？如果不变，请求出tan∠OAB的值如果有变化，请说明理由．(3)如果AB交y轴于点C，若AC=2BC时，求点A，B的坐标．。
反比例函数与几何的综合应用及答案
专训1 反比例函数与几何的综合应用名师点金：解反比例函数与几何图形的综合题，一般先设出几何图形中的未知数，然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标，再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组)，解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值．反比例函数与三角形的综合1．如图，一次函数y ＝kx ＋b 与反比例函数y ＝x 6(x>0)的图象交于A(m ，6)，B(3，n)两点． (1)求一次函数的解析式；6＝，反比，过B 作BC ∥点P BC 分别交于D ，E 两点，连接OD ，OE ，DE ，则△ODE 的面积为________．5．如图，在平面直角坐标系中，矩形OABC 的对角线OB ，AC 相交于点D ，且BE ∥AC ，AE ∥OB. (1)求证：四边形AEBD 是菱形；(2)如果OA ＝3，OC ＝2，求出经过点E 的双曲线对应的函数解析式．(第5题)反比例函数与菱形的综合6．如图，在平面直角坐标系中，菱形ABCD 在第一象限内，边BC 与x 轴平行，A ，B 两点的纵坐标分别为3，1，反比例函数y ＝x 3的图象(第6题)经过A ，B 两点，则菱形ABCD 的面积为( )A ．2B ．4C ．2D ．47．如图，在平面直角坐标系中，菱形ABCD 的顶点C 与原点O 重合，点B 在y 轴的正半轴上，点A 在反比例函数y ＝x k(k>0，x>0)的图象上，点D 的坐标为(4，3)．(1)求k 的值；(2)若将菱形ABCD 沿x 轴正方向平移，当菱形的顶点D 落在反比例函数y ＝x k(k>0，x>0)的图象上时，求菱形ABCD 沿x 轴正方向平移的距离．(第7题)反比例函数与正方形的综合B 的坐标为所在直线于点点P 2个应用及12．某学校到县城的路程为5 km ，一同学骑车从学校到县城的平均速度v(km /h )与所用时间t(h )之间的函数解析式是( )A ．v ＝5tB ．v ＝t ＋5C ．v ＝t 5D ．v ＝5t3．判断下面哪些式子表示y 是x 的反比例函数：①xy ＝－31；②y ＝5－x ；③y ＝5x －2；④y ＝x 2a(a 为常数且a ≠0)． 其中________是反比例函数．(填序号) 2个方法：画反比例函数图象的方法x … －6 －5 －4 －3 －2 －1 1 2 3 4 5 6 … y…11.21.5236－6－3－2－1.5－1.2－1…(1)试猜想y 与x 的函数关系可能是你学过的哪类函数，并写出这个函数的解析式； (2)画出这个函数的图象． 求反比例函数解析式的方法5．已知反比例函数y ＝x k的图象与一次函数y ＝x ＋b 的图象在第一象限内相交于点A(1，－k ＋4)．试确定这两个函数的解析式．6．如图，已知A(－4，n)，B(2，－4)是一次函数y ＝kx ＋b 的图象和反比例函数y ＝x m的图象的两个交点．求： (1)反比例函数和一次函数的解析式；(2)直线AB 与x 轴的交点C 的坐标及△AOB 的面积； (3)方程kx ＋b －x m＝0的解(请直接写出答案)； (4)不等式kx ＋b －x m<0的解集(请直接写出答案)．(第6题)2个应用反比例函数图象和性质的应用7．画出反比例函数y ＝x 6的图象，并根据图象回答问题： (1)根据图象指出当y ＝－2时x 的值；(2)根据图象指出当－2<x<1且x ≠0时y 的取值范围； (3)根据图象指出当－3<y<2且y ≠0时x 的取值范围． 反比例函数的实际应用8．某厂仓库储存了部分原料，按原计划每小时消耗2吨，可用60小时．由于技术革新，实际生产能力有所提高，即每小时消耗的原料量大于计划消耗的原料量．设现在每小时消耗原料x(单位：吨)，库存的原料可使用的时间为y(单位：小时)．(1)写出y 关于x 的函数解析式，并求出自变量的取值范围．(2)若恰好经过24小时才有新的原料进厂，为了使机器不停止运转，则x 应控制在什么范围内？ 1个技巧：用k 的几何性质巧求图形的面积9．如图，A ，B 是双曲线y ＝x (k ≠0)上的两点，过A 点作AC ⊥x 轴，交OB 于D 点，垂足为C.若△ADO 的面积为1，D 为OB 的中点，则k 的值为( )A .34B .38C ．3D ．4(第9题)(第10题)10．如图，过x 轴正半轴上的任意一点P 作y 轴的平行线交反比例函数y ＝x 2和y ＝－x 4的图象于A ，B 两点，C 是y 轴上任意一点，则△ABC 的面积为________．11．如图是函数y ＝x 3与函数y ＝x 6在第一象限内的图象，点P 是y ＝x 6的图象上一动点，PA ⊥x 轴于点A ，交y ＝x 3的图象于点C ，PB ⊥y 轴于点B ，交y ＝x 3的图象于点D.(1)求证：D 是BP 的中点； (2)求四边形ODPC 的面积．(第11题)答案1．解：(1)∵A(m ，6)，B(3，n)两点在反比例函数y ＝x 6(x>0)的图象上， ∴m ＝1，n ＝2，即 A(1，6)，B(3，2)．又∵A(1，6)，B(3，2)在一次函数y ＝kx ＋b 的图象上， ∴2＝3k ＋b ，6＝k ＋b ，解得b ＝8，k ＝－2，即一次函数解析式为y ＝－2x ＋8.(第1题)(2)根据图象可知使kx ＋b<x 6成立的x 的取值范围是0<x<1或x>3.(3)如图，分别过点A ，B 作AE ⊥x 轴，BC ⊥x 轴，垂足分别为E ，C ，设直线AB 交x 轴于D 点． 令－2x ＋8＝0，得x ＝4，即D(4，0)． ∵A(1，6)，B(3，2)，∴AE ＝6，BC ＝2. ∴S △AOB ＝S △AOD －S △ODB ＝21×4×6－21×4×2＝8.2．(1)证明：∵点A ，B 分别在x 轴，y 轴上，点D 在第一象限内，DC ⊥x 轴于点C ，∴∠AOB ＝∠DCA ＝90°.在Rt △AOB 和Rt △DCA 中，∵AB ＝DA ，AO ＝DC ，∴Rt △AOB ≌Rt △DCA. (2)解：在Rt △ACD 中，∵CD ＝2，DA ＝， ∴AC ＝＝1.∴OC ＝OA ＋AC ＝2＋1＝3. ∴D 点坐标为(3，2)．∵点E 为CD 的中点，∴点E 的坐标为(3，1)．∴k ＝3×1＝3. (3)解：点G 在反比例函数的图象上．理由如下：∵△BFG 和△DCA 关于某点成中心对称，∴△BFG ≌△DCA.∴FG ＝CA ＝1，BF ＝DC ＝2，∠BFG ＝∠DCA ＝90°.∵OB ＝AC ＝1，∴OF ＝OB ＋BF ＝1＋2＝3.∴G 点坐标为(1，3)． ∵1×3＝3，∴点G(1，3)在反比例函数的图象上．3．解：∵BC ∥OA ，AB ∥x 轴，∴四边形ABCO 为平行四边形． ∴AB ＝OC ＝3. 设Aa 6，则Ba 6，∴(a －3)·a 6＝－3.∴a ＝2. ∴A(2，3)，B(－1，3)．k ＝22，所以2＝CE 2∴四边形AEBD 是平行四边形．∵四边形OABC 是矩形，∴DA ＝21AC ，DB ＝21OB ，AC ＝OB. ∴DA ＝DB.∴四边形AEBD 是菱形． (2)解：如图，连接DE ，交AB 于F ， ∵四边形AEBD 是菱形，∴DF ＝EF ＝21OA ＝23，AF ＝21AB ＝1.∴E ，19. 设所求反比例函数解析式为y ＝x k，把点E ，19的坐标代入得1＝29，解得k ＝29. ∴所求反比例函数解析式为y ＝2x 9.(第5题)(第7题)6．D7．解：(1)如图，过点D 作x 轴的垂线，垂足为F. ∵点D 的坐标为(4，3)，∴OF ＝4，DF ＝3.∴OD ＝5. ∴AD ＝5.∴点A 的坐标为(4，8)．∴k ＝xy ＝4×8＝32.(2)将菱形ABCD 沿x 轴正方向平移，使得点D 落在函数y ＝x 32(x>0)的图象上点D ′处，过点D ′作x 轴的垂线，垂足为F ′.∵DF ＝3，∴D ′F ′＝3.∴点D ′的纵坐标为3. ∵点D ′在y ＝x 32的图象上，∴3＝x 32，解得x ＝332， 即OF ′＝332.∴FF ′＝332－4＝320.∴菱形ABCD 沿x 轴正方向平移的距离为320.8．解：(1)∵正方形OABC 的边OA ，OC 分别在x 轴，y 轴上，点B 的坐标为(2，2)，∴C(0，2)． ∵D 是BC 的中点，∴D(1，2)．∵反比例函数y ＝x k(x ＞0，k ≠0)的图象经过点D ，∴k ＝2. (2)当P 在直线BC 的上方，即0＜x ＜1时， ∵点P(x ，y)在该反比例函数的图象上运动，∴y ＝x 2.∴S 四边形CQPR ＝CQ ·PQ ＝x ·－22＝2－2x ；当P 在直线BC 的下方，即x ＞1时，同理求出S 四边形CQPR ＝CQ ·PQ ＝x ·x 2＝2x －2，综上，S ＝2－2x （0＜x ＜1）.2x －2（x ＞1），9．410．解：∵反比例函数的图象关于原点对称，圆也关于原点对称，故阴影部分的面积占⊙O 面积的41，则针头落在阴影区域内的概率为41.1．B 2.C 3．①③④4．解：(1)反比例函数：y ＝－x 6.(2)如图所示．(第4题)5．解：∵反比例函数y ＝x k的图象经过点A(1，－k ＋4)， ∴－k ＋4＝1k，即－k ＋4＝k ，∴k ＝2，∴A(1，2)． ∵一次函数y ＝x ＋b 的图象经过点A(1，2)， ∴2＝1＋b ，∴b ＝1.∴反比例函数的解析式为y ＝x 2， 一次函数的解析式为y ＝x ＋1.6．解：(1)将B(2，－4)的坐标代入y ＝x m ，得－4＝2m， 解得m ＝－8.∴反比例函数的解析式为y ＝x －8.∵点A(－4，n)在双曲线y ＝x －8上，∴n ＝2. ∴A(－4，2)．把A(－4，2)，B(2，－4)的坐标分别代入y ＝kx ＋b ，得2k ＋b ＝－4，－4k ＋b ＝2，解得b ＝－2.k ＝－1，∴一次函数的解析式为y ＝－x －2. (2)令y ＝0，则－x －2＝0，x ＝－2. ∴C(－2，0)．∴OC ＝2.∴S △AOB ＝S △AOC ＋S △BOC ＝21×2×2＋21×2×4＝6. (3)x 1＝－4，x 2＝2. (4)－4<x<0或x>2.7．解：如图，由观察可知： (1)当y ＝－2时，x ＝－3；(2)当－2<x<1且x ≠0时，y<－3或y>6； (3)当－3<y<2且y ≠0时，x<－2或x>3.(第7题)点拨：解决问题时，画出函数图象．由图象观察得知结果．由图象解决相关问题，一定要注意数形结合，学会看图．8．解：(1)库存原料为2×60＝120(吨)，根据题意可知y 关于x 的函数解析式为y ＝x 120. 由于生产能力提高，每小时消耗的原料量大于计划消耗的原料量，所以自变量的取值范围是x>2. (2)根据题意，得y ≥24，所以x 120≥24. 解不等式，得x ≤5，即每小时消耗的原料量应控制在大于2吨且不大于5吨的范围内．点拨：(1)由“每小时消耗的原料量×可使用的时间＝原料总量”可得y 关于x 的函数解析式．(2)要使机器不停止运转，需y ≥24，解不等式即可．(第9题)9．B 点拨：如图，过点B 作BE ⊥x 轴于点E ，∵D 为OB 的中点，∴CD 是△OBE 的中位线，则CD ＝21BE.设Ax k ，则B2x k ，CD ＝4x k ，AD ＝x k －4x k .∵△ADO 的面积为1，∴21AD ·OC ＝1，即214x k ·x ＝1.解得k ＝38.10．311．(1)证明：∵点P 在双曲线y ＝x 6上， ∴设P 点坐标为，m 6.∵点D 在双曲线y ＝x 3上，BP ∥x 轴，D 在BP 上， ∴D 点坐标为，m 3.∴BD ＝m 3，BP ＝m 6， 故D 是BP 的中点．(2)解：由题意可知S △BOD ＝23，S △AOC ＝23，S 四边形OBPA ＝6. ∴S 四边形ODPC ＝S 四边形OBPA －S △BOD －S △AOC ＝6－23－23＝3.。
人教版数学九年级下册26.1.2第2课时+反比例函数的图象和性质的的综合运用课件
y k 1、若点P（2,3）在反比例函数
的图像上，则k= 6 _
x
2、若点P(m,n)在反比例函数 y 6 图像上，则mn= 6_
x
3、如图，S矩形ABCD= 6 S△ABD=__3_
A
D
S矩形ABCD与S△ABD有何关系？
2
S△ABD=
1 2
S矩形ABCD
B3
C
4、如图,点P是反比例函数图象上的一点,过点P分别向x轴
∴ 当 x < 0 时，y 随 x 的增大而减小， ∴ 当 －3 < x < －1 时，－6 < y < －2.
二 反比例函数图象和性质的综合
例2 如图，是反比例函数 y m 5 图象的一支. 根
据图象，回答下列问题：
x
(1) 图象的另一支位于哪个象限？常数 m 的取值范围
是什么？
y
解：因为这个反比例函数图象的一
函数的图象上？ 解：设这个反比例函数的解析式为 y k ，因为点
x A (2，6)在其图象上，所以有 6 k ，解得 k =12.
2 所以反比例函数的解析式为 y 12 .
x
因为点 B，C 的坐标都满足该解析式，而点 D 的坐标不满足，所以点 B，C 在这个函数的图 象上，点 D 不在这个函数的图象上.
y
设点 P 的坐标为 (a，b)
∵点
P
(a，b)
在函数
y
k x
的图
象上，∴ b k ，即 ab=k. a
PB
SA
AO
x
BP
若点 P 在第二象限，则 a<0，b>0，
∴ S矩形 AOBP=PB·PA=－a·b=－ab=－k；
《反比例函数与几何综合题之解题策略》教学PPT课件【初中数学】公开课
PM 4
t
t
∴t²=3，∴t= 3 （t= - 3舍去）
y (t, 8)
t (2，4) (5，4)
(3，0)
y8 x
x
活动二 链接中考
如图，在平面直角坐标系xOy中，点C(3,0)，函数 y
k x
(k＞0，x>0)的图象经过□OABC
的顶点A(m,n) 和边BC的中点D．（1）求m的值；（2）若△OAD的面积等于6，求k的值；
时，求t的值.
PM 4
解：（1）由题意得A(m,n)，B(m+3,n)
，D
m
2
6
,
n 2
∴mn= m 6·n
(m，n) (m+3，n)
m
2
6
,
n 2
22
∴两边除以n，m=2
(3，0) x
活动二 链接中考
变式：如图，在平面直角坐标系xOy中，点C(3,0)，函数
x
直线l与x轴上方的□ABCD的一边交于点N，设点P的横坐标为t，当
PN
1时，求t的值.
PM 4
解：（3）设A(2,4)，k=8，P(t，8 )，PM 8 (t＞0)
t
t
①∴直线PlN与O8A交 2于t 点N，yOA=2x，∴N(t,2t)
t
当 PN 1 时，4(8 2t) 8 (0＜t≤2)
G是否在反比例函数的图象上，并说明理由.
拓展作业
1、找找近3年各地中考数学试卷中关于 反比例函数的题目，看看都考查了反比 例函数的哪些知识点，与其他哪些知识 相关联。
2、试着给其他同学出一道反比例函数与 几何图形综合的题目。
2024中考压轴题02 反比例函数的综合问题(3题型+解题模板+技巧精讲)(原卷版)
压轴题解题模板02反比例函数的综合问题目录题型一反比例函数与一次函数交点问题题型二反比例函数与一次函数图像面积问题题型三反比例函数与几何图形结合题型1题型2题型3题型一反比例函数与一次函数交点问题解题模板：技巧精讲：利用函数图象确定不等式的解集：【例1】（2023·四川攀枝花·统考中考真题）如图，点(),6A n 和()3,2B 是一次函数1y kx b =+的图象与反比例x(1)求m 的值和反比例函数解析式； (2)当12y y >时，求x 的取值范围．题型二 反比例函数与一次函数图像面积问题解题模板：x求AOB的面积；请根据图象直接写出不等式【变式2-1】（2023·A B象交于(4,1),若OBD的)0m>的个单位长度后与反比例函数图象，求ACD的面积．题型三反比例函数与几何图形结合解题模板：x轴上，ABP是以x使ABP是以点统考中考真题）如图，在平面直角坐标系的图象的一个交点为x上，且ABC的面积为上一点，连接P A，以，使它与PAB位似，相似比为好都落在反比例函数图象上，求点P的坐标及m的值．一、解答题x轴上一点，若PAB的面积为统考中考真题）恰好落在反比例函数x，使ABP周长的值最小．若存在，求出最小值；若不存在，请说明理由．如图，正比例函数ABC 的面积．6．（2023·tan 2AOB ∠的对称点，OAC 的面积是x(1)m=______，k=______，点C的坐标为______．(2)点P在x轴上，若以B，O，P为顶点的三角形与AOC相似，求点P的坐标．。
反比例函数专题四、反比例函数与几何的综合应用
因为C(0，2)，A(4，0)，由矩形的性质可得P(2，1)， 把点P的坐标代入反比例函数解析式可得k＝2， 2 所以反比例函数解析式为y＝ . x 2 1 3 易知点D的横坐标为4，所以AD＝ ＝ .所以BD＝ . 4 2 2 2 又易知点E的纵坐标为2，所以2＝ . CE 所以CE＝1.所以BE＝3. 所以S△ODE＝S矩形OABC－S△OCE－S△BED－S△OAD
Q R P
专题训练
训练角度
3
反比例函数与圆的综合
k 8．如图，双曲线y＝ (k>0)与圆O在第一象限内交于P， x Q两点，分别过P，Q两点向x轴和y轴作垂线，已知点
4 ． P的坐标为(1，3)，则图中阴影部分的面积为______
方法点拨
∵圆O在第一象限的部分关于直线y＝x对称，双曲 k 线y＝ (k＞0)在第一象限的部分也关于直线y＝x x 对称，P点的坐标是(1，3)， ∴Q点的坐标是(3，1)．
(1)求一次函数的解析式；
专题训练
6 (2)根据图象直接写出使kx＋b＜ 成立的x的取值范围； x 6 解：根据图象可知使kx＋b＜ 成立的x的取值范围是 x 0＜x＜1或x＞3.
专题训练
(3)求△AOB的面积 解：如图，分别过点A，B作AE⊥x轴，BC⊥x轴，垂足分 别为E，C，设直线AB交x轴于点D. 令y＝0，则－2x＋8＝0，解得x＝4， 即D(4，0)．
x
(x＜0)于点D，交x轴于点C，
连接AD交y轴于点E，若 OC＝3，求OE的长．
专题训练
6 解：设点A的坐标为(a， )，由题易知四边形ABCO是平行 a 四边形，∴AB＝OC＝3. 6 6 ∴点B的坐标为(a－3， ).∴(a－3)· ＝－3. a a 解得a＝2，经检验知，a＝2是原方程的解．
反比例函数与几何综合专题(基础篇)九年级数学下册基础知识专项讲练(人教版)
专题26.14反比例函数与几何综合专题（基础篇）（专项练习）一、单选题（本大题共10小题，每小题3分，共30分）1．如果等腰三角形的面积为10，底边长为x ，底边上的高为y ，则y 与x 的函数关系式为（）A ．y=B ．y=C ．y=D ．y=2．如图，点A 在反比例函数y ＝﹣x（x ＜0）的图象上，过点A 作AC ⊥x 轴垂足为C ，OA 的垂直平分线交x 轴于点B ，当AC ＝1时，△ABC 的周长为（）A ．1B 1+C D2+3．如图，点A 是双曲线y =6x是在第一象限上的一动点，连接AO 并延长交另一分支于点B ，以AB 为斜边作等腰Rt △ABC ，点C 在第二象限，随着点A 的运动，点C 的位置也不）A ．13y x=-B ．3y x =-C ．16y x=-D ．6y x=-4．如图，反比例函数ky x=（0x >）的图象经过点()1,2A 和点(),B m n ，过点B 作BC y⊥轴与C ，若ABC 的面积为2，则点B 的坐标为（）A ．23,3⎛⎫ ⎪⎝⎭B ．2,33⎛⎫ ⎪⎝⎭C ．()2,1D ．()1,25．如图，菱形AOBC 的边BO 在x 轴正半轴上，点A (2，，反比例函数kyx=图象经过点C ，则k 的值为()A ．12B ．C ．D ．6．在ABC 中90ACB ∠=︒，将Rt ABC 放在如图所示的平面直角坐标系中，ABC 的边AC x ∥轴．1AC =，点B 在x 轴上，点C 在反比例函数2(0)y x x=>的图像上，将ABC 先向左平移3个单位长度，再向下平移5个单位长度得到111A B C △，此时点1A 在反比例函数()0ky x x=<的图像上．11B C 与此图像交于点P ，则点P 的纵坐标是（）A ．92-B ．72-C ．94-D ．74-7．如图，点A 在双曲线y ＝6x上，过A 作AC ⊥x ，垂足为C ，OA 的垂直平分线交OC 于B ，且AC ＝1.5，则△ABC 的周长为（）A ．6.5B ．5.5C ．5D ．48．如图，在平面直角坐标系中，O 是坐标原点，在OAB ∆中，AO AB =，AC OB ⊥于点C ，点A 在反比例函数()0ky k x=≠的图像上，若4OB =，3AC =，则k 的值为（）．A ．12B ．8C ．6D ．39．如图，在平面直角坐标系中，菱形ABOC 的顶点O 在坐标原点，边BO 在x 轴的负半轴上，60BOC ∠=︒，顶点C 的坐标为(m ，反比例函数()0ky k x=<的图象与菱形对角线AO 交于点D ，连结BD ，当DB x ⊥轴时，k 的值是（）A ．B ．C ．D ．-10．如图，平行于y 轴的直线l 分别与反比例函数k y x =（x ＞0）和1y x=-（x ＞0）的图象交于M 、N 两点，点P 是y 轴上一动点，若△PMN 的面积为2，则k 的值为（）A ．2B ．3C ．4D ．5二、填空题（本大题共8小题，每小题4分，共32分）11．如图反比例函数图像过A(2，2)，AB ⊥x 轴于B ，则△OAB 的面积为_______12．如图，点A 、B 是反比例函数y ＝kx（x ＞0）图象上的两点，且A 、B 两点的纵坐标分别为2和1，C 在x 轴上，AC ＝BC ，∠ACB ＝90°，则k ＝_____．13．如图，在平面直角坐标系中，△ABO 边AB 平行于y 轴，反比例函数(0)k y x x=>的图像经过OA 中点C 和点B ，且△OAB 的面积为9，则k =________14．我市某校想种植一块面积为400平方米的长方形草坪，要求两邻边均不小于10米，草坪的一边长y （米）与另一边长x （米）之间的关系如图中曲线AB 所示，其中AC x ⊥轴，BD x ⊥轴，垂足分别为C ，D ，连接AB ，则四边形ACDB 的面积为______平方米．15．在平面直角坐标系中，OA ＝AB ，∠OAB ＝90°，反比例函数ky x=（x ＞0）的图像经过A 和B 两点其中A （2，m ），且点B 的纵坐标为n ，则n ＝______．16．如图，在平面直角坐标中，点O为坐标原点，直线y＝kx﹣（k＜0）交x轴的正半轴于点A，交y轴的正半轴于点B，若BC平分∠ABO交OA于点C，AC＝2OC，则k 的值为____．17．如图，在平面直角坐标系中，等边△ABC的顶点A在反比例函数y=kx(x>0)图象上，C在x轴上，AB//x轴，BC与双曲线交于点D，且BD=3CD=6，则k=_______．18．如图，在平面直角坐标系xOy中，反比例函数8yx=的图象经过A（2，4），B两点，∠AOB＝45°，则点B的坐标为________．三、解答题（本大题共6小题，共58分）19．（8分）如图，在平面直角坐标系中，O为坐标原点，某反比例函数的图象经过点()1,3A--．()1求该反比例函数的解析式；()2点(),3B m 和()3,C n 均在该反比例函数的图象上，点P 在x 轴上，请画出使PB PC+的值最小的P 点位置，并求出此时点P 的坐标．20．（8分）如图，点P 的坐标是(32)-，，过点P 作x 轴的平行线交y 轴于点A ，交双曲线(0)ky x x =>于点N ，作PM AN ⊥交双曲线(0)k y x x=>于点M ，连接AM ．已知PN =4．(1)求k 的值；(2)求APM △的面积．21．（10分）如图，在平面直角坐标系中，O 为坐标原点，点A ，B 在函数()0ky x x=>的图象上（点A 的纵坐标大于点B 的纵坐标），点A 的坐标为（2，4），过点A 作AD ⊥x 轴于点D ，过点B 作BC ⊥x 轴于点C ，连结OA ，AB ．(1)求k 的值．(2)若CD ＝2OD ，求四边形OABC 的面积．22．（10分）如图，矩形ABCD 的两边AD AB 、的长分别为3、8.边BC 落在x 轴上，E 是DC 的中点，连接AE ，反比例函数my x=的图象经过点E ，与AB 交于点F ．(1)直接写出AE 的长；(2)若2AF AE -=，求反比例函数的解析式．23．（10分）如图，一次函数4y x =-+的图象与反比例函数()0ky k x=≠在第一象限内的图象交于()1,A n 和()3,B m 两点．(1)求反比例函数的表达式．(2)在第一象限内，当一次函数4y x =-+的值大于反比例函数()0ky k x=≠的值时，写出自变量x 的取值范围(3)求△AOB 面积．24．（12分）如图，已知平行四边形ABCD 的顶点A 、C 在反比例函数ky x=的图象上，顶点B 、D 在x 轴上．已知点()32A -，、(50)B -，．(1)直接写出点C 、D 的坐标；(2)求反比例函数的解析式；(3)求平行四边形ABCD 的对角线AC 、BD 的长；(4)求平行四边形ABCD 的面积S ．参考答案1．C试题分析：利用三角形面积公式得出xy=10，进而得出答案．解：∵等腰三角形的面积为10，底边长为x ，底边上的高为y ，∴xy=10，∴y 与x 的函数关系式为：y=．故选C ．考点：根据实际问题列反比例函数关系式．2．B【分析】依据点A 在反比例函数y ＝﹣x（x ＜0）的图象上，AC ⊥x 轴，AC ＝1，可得OC ，再根据CD 垂直平分AO ，可得OB ＝AB ，再根据△ABC 的周长＝AB+BC+AC ＝OC+AC 进行计算即可．解：∵点A 在反比例函数y ＝﹣x（x ＜0）的图象上，AC ⊥x 轴，∴AC×OC ∵AC ＝1，∴OC ∵OA 的垂直平分线交x 轴于点B ，∴OB ＝AB ，∴△ABC 的周长＝AB+BC+AC ＝OB+BC+AC ＝OC+AC +1，故选：B ．【点拨】本题考查了线段垂直平分线的性质以及反比例函数图象上点的坐标特征，比较容易掌握．3．D【分析】连接OC ，作CD ⊥x 轴于D ，AE ⊥x 轴于E ，利用反比例函数的性质和等腰直角三角形的性质，根据“AAS”可判定△COD ≌△OAE ，设A 点坐标为（a ，6a ），得出OD =AE =6a，CD =OE =a ，最后根据反比例函数图象上点C 的坐标特征确定函数解析式．解：如图，连接OC ，作CD ⊥x 轴于D ，AE ⊥x 轴于E ，∵A点、B点是正比例函数图象与双曲线y=6x的交点，∴点A与点B关于原点对称，∴OA=OB，∵△ABC为等腰直角三角形，∴OC=OA，OC⊥OA，∴∠DOC+∠AOE=90°，∵∠DOC+∠DCO=90°，∴∠DCO=∠AOE，∴△COD≌△OAE（AAS），设A点坐标为（a，6a），得出OD=AE=6a，CD=OE=a，∴C点坐标为（-6a，a），∵-6a•a=-6，∴点C在反比例函数y=-6x图象上．故选：D．【点拨】本题主要考查了用待定系数法求反比例函数的解析式，解题时需要综合运用反比例函数图象上点的坐标特征、等腰直角三角形的性质．判定三角形全等是解决问题的关键环节．4．A【分析】根据三角形面积公式得到12•m•（2−n）＝2，即2m−mn＝4，再根据反比例函数图象上点的坐标特征得到mn＝2，则可计算出m＝3，n＝23，从而可确定B点坐标．解：∵△ABC的面积为2，∴12•m •（2−n ）＝2，即2m −mn ＝4，∵反比例函数k y x=（x ＞0）的图象经过点A （1，2）和点B （m ，n ），∴1×2＝mn ，∴2m −2＝4，解得m ＝3，∴n ＝23，∴B （3，23）．故选A ．【点拨】本题考查了反比例函数比例系数k 的几何意义：在反比例函数k y x =图象中任取一点，过这一个点向x 轴和y 轴分别作垂线，与坐标轴围成的矩形的面积是定值|k |．也考查了反比例函数图象上点的坐标特征．5．C【分析】根据题意可求出菱形的边长．再根据边BO 在x 轴正半轴上，即可判断AC x ∥轴，从而可求出C 点坐标，代入反比例函数解析式求解即可．解：∵点A (2，，∴4OA =，∴菱形的边长为4，即4AC =．∵边BO 在x 轴正半轴上，∴AC x ∥轴，∴246C A x x AC =+=+=，C A y y ==∴C (6，．将C (6，代入k y x =，得：6k =解得：k =故选C ．【点拨】本题考查两点的距离公式，菱形的性质，坐标与图形以及求反比例函数解析式．利用数形结合的思想是解题关键．6．A【分析】首先由边AC ∥x 轴，AC ＝1，点C 在函数2(0)y x x=>的图像上，求得点C 的坐标，继而求得点A 与点B 的坐标，然后由旋转的性质、平移的性质，求得△A 1B 1C 1各顶点的坐标，再由点A 1在函数()0k y x x=<的图像上，B 1C 1与此图像交于点P ，求得答案．解：∵边AC ∥x 轴，AC ＝1，∴点C 的横坐标为1，∵点C 在函数2(0)y x x =>的图像上，∴y ＝2，∴点C 的坐标为：（1，2），∴点A 的坐标为：（0，2），点B 的坐标为：（1，0），∵将ABC 先向左平移3个单位长度，再向下平移5个单位长度得到111A B C △，，∴A 1的坐标为：（-3，﹣3），B 1的坐标为：（-2，-5），C 1的坐标为：（-2，﹣3），∵点A 1在函数()0k y x x=<的图像上，∴k ＝xy ＝-3×（﹣3）＝9，∴此反比例函数的解析式为：9y x =，∵线段B 1C 1的解析式为：x ＝-2∴点P 的横坐标为：-2，∴点P 的纵坐标为：92y =-．故选：A ．【点拨】此题属于反比例函数综合题．考查了待定系数求反比例函数解析式、旋转的性质、平移的性质以及点与函数的关系．注意求得△A 1B 1C 1各顶点的坐标是关键．7．B【分析】由于BD 是OA 的垂直平分线，那么OB AB =，据图可知A 点的纵坐标是1.5，把 1.5y =代入反比例函数解析式，易求OC ，进而可求ABC ∆的周长．解：如图所示，BD Q 是OA 的垂直平分线，OB AB ∴=，1.5AC = ，∴点A 的纵坐标是1.5，把 1.5y =代入6y x=，得61.5x =，解得4x =，4OC ∴=，ABC ∴∆的周长 1.54 5.5AC AB BC AC OB BC AC OC =++=++=+=+=，故选：B ．【点拨】本题考查了反比例函数图象上点的坐标特征、线段垂直平分线的性质，解题的关键是求出A 点的坐标．8．CC 点坐标，结合AC 长即可得到A 点坐标，根点A 在反比例函数的图像上，将点A 的坐标代入反比例函数解析式中可得k 值．解：∵AO AB =，∴OAB ∆为等腰三角形，又∵AC OB ⊥，∴C 为OB 中点，∵4OB =，∴2OC =，∵3AC =，∴A 点坐标为（2，3），将A 点坐标代入反比例函数(0)k y k x=≠得，32k =，∴6k =．故选：C ．【点拨】本题考查反比例函数图像上的点的性质，等腰三角形的判定和性质．利用等腰三角形的性质求得反比例函数上点的坐标是解题关键．9．C【分析】延长AC交y轴于E，如图，根据菱形的性质得AC//OB，则AE⊥y轴，再由∠BOC＝60°得到∠COE＝30°，则根据含30度的直角三角形三边的关系得到CE OE＝2，OC＝2CE＝4，接着根据菱形的性质得OB＝OC＝4，∠BOA＝30°，于是在Rt△BDO中可计算出BD＝3，所以D点坐标为（−4，3），然后利用反比例函数图象上点的坐标特征可求出k的值．解：延长AC交y轴于E，如图，∵菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∴AC//OB，∴AE⊥y轴，∵∠BOC＝60°，∴∠COE＝30°，∴CO=2CE而顶点C的坐标为(m，∴OE＝CE=-m，CO=-2m，∵CO2=CE2+OE2，即（-2m）2=（-m）2+（2，解得m=-2∴OC＝2CE＝4，∴C(2,-∵四边形ABOC为菱形，∴OB ＝OC ＝4，∠BOA ＝30°，∴OD =2BD在Rt △BDO 中，DO 2=BD 2+OB 2，即（2BD ）2=BD 2+42，∴BD ＝3，∴D 点坐标为（−4，3），∵反比例函数()0k y k x =<的图象经过点D ，∴k ＝故选：C ．【点拨】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了含30度的直角三角形三边的关系．10．B【分析】由题意易得点M 到y 轴的距离即为△PMN 以MN 为底的高，点M 、N 的横坐标相等，设点1,,,k M a N a a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，则有11k k MN a a a +⎛⎫=--= ⎪⎝⎭，进而根据三角形面积公式可求解．解：由平行于y 轴的直线l 分别与反比例函数k y x =（x ＞0）和1y x=-（x ＞0）的图象交于M 、N 两点，可得：点M 到y 轴的距离即为△PMN 以MN 为底的高，点M 、N 的横坐标相等，设点1,,,k M a N a a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，∴11k k MN a a a+⎛⎫=--= ⎪⎝⎭，∵△PMN 的面积为2，∴111222PMN k S MN a a a+=⋅=⨯⨯= ，解得：3k =；故选B ．【点拨】本题主要考查反比例函数与几何的综合，熟练掌握反比例函数与几何的综合是解题的关键．11．2【分析】根据题意可得OB=2，AB=2，然后根据三角形的面积公式即可求出结论．解：∵反比例函数图像过A(2，2)，AB ⊥x 轴于B ，∴OB=2，AB=2∴S △ABC =12OB·AB=2故答案为：2．【点拨】此题考查的是坐标与图形的面积，掌握三角形的面积公式是解决此题的关键．12．6【分析】过点A 作AG ⊥x 轴于点G ，过点B 作BH ⊥x 轴于点H ，易证△AGC ≌CHB ，根据全等三角形的性质，可得GC 和CH 的值，根据A 、B 的纵坐标，表示出横坐标，列方程求解即可．解：过点A 作AG ⊥x 轴于点G ，过点B 作BH ⊥x 轴于点H ，如图所示，则有∠AGC =∠CHB =90°，∴∠GAC +∠GCA =90°，∵∠ACB =90°，AC =BC ，∴∠ACG +∠HCB =90°，∴∠GAC =∠HCB ，∴△AGC ≌CHB （AAS ），∴AG =CH =2，GC =BH =1，∴=3∵A 、B 在反比例函数的图象上，∴,22k A ⎛⎫ ⎪⎝⎭，B （k ,1），∴32k k -=,∴k =6，故答案为：6．【点拨】本题考查了反比例函数图象上点的坐标特征，设计等腰直角三角形的性质，构造全等三角形是解题的关键．13．6【分析】延长AB 交x 轴于D ，根据反比例函数k y x =（x ＞0）的图象经过点B ，设B k m m ⎛⎫ ⎪⎝⎭，，则OD ＝m ，根据△OAB 的面积为9，列等式可表示AB 的长，表示点A 的坐标，根据线段中点坐标公式可得C 的坐标，从而得出结论．解：延长AB 交x 轴于D ，如图所示：∵AB y ∥轴，∴AD ⊥x 轴，∵反比例函数k y x=（x ＞0）的图像经过OA 中点C 和点B ，∴设B k m m ⎛⎫ ⎪⎝⎭，，则OD ＝m ，∵△OAB 的面积为9，∴192AB OD ⋅=，即12AB •m ＝9，∴AB ＝18m ，∴A （m ，18k m +），∵C 是OA 的中点，∴C 11822k m m +⎛⎫ ⎪⎝⎭，，∴11822k k m m+=⋅，∴k ＝6，故答案为：6．【点拨】本题主要考查了反比例函数上点的坐标特征，线段的中点坐标公式，三角形面积公式，解本题的关键是设未知数建立方程解决问题．14．750【分析】由题意得y 与x 的函数关系式为400y x =，则当10x =时，4004010y ==，当40x =时，4001040y ==，即可得40AC =，10BD =，401030CD =-=，即可得．解：∵长方形草坪的面积为400平方米，∴y 与x 的函数关系式为400y x =，∴当10x =时，4004010y ==，当40x =时，4001040y ==，∵AC x ⊥轴，BD x ⊥轴，∴40AC =，10BD =，401030CD =-=，∴四边形ABCD 的面积为：()()2401030750m 2+⨯=，故答案为：750．【点拨】本题考查了反比例函数的应用，解题的关键是理解题意，掌握反比例函数的性质．15【分析】过A 作AC ⊥y 轴，垂足为C ，作BD ⊥AC ，垂足为D ，通过证△AOC ≌△ABD 可得：OC ＝AD ＝m ，AC ＝BD ＝2，即可求得B 点的纵坐标．解：如图：过A 作AC ⊥y 轴，垂足为C ，作BD ⊥AC ，垂足为D ，∵∠BAO ＝90°，∴∠OAC +∠BAD ＝90°，∠BAD +∠ABD ＝90°，∴∠ABD ＝∠CAO ，∵∠D ＝∠ACO ＝90°，AO ＝AB ，∴△ACO ≌△DAB （AAS ），∴AD ＝CO ，BD ＝AC ，∵A （2，m ），∴OC ＝AD ＝m ，AC ＝BD ＝2．∴点B 坐标为()2,2m m +-∴()()222m m m =+-∴解得11m =+21m =（舍去）∴n ＝m ﹣2，．【点拨】本题考查反比例函数图像上点的坐标特征，全等三角形的判定和性质，关键是求得BD 的长．16．【分析】过点C 作CD ⊥AB 于点D ，则OC =CD ，利用面积法结合AB =2OC ，可得出AB =2OA ，利用勾股定理可得出OA =，利用一次函数图象上点的坐标特征可求出OA ，OB的长，结合OA =可求出k 值．解：如图，过点C 作CD ⊥D ，∵BC 平分∠ABO ，∴OC =CD ，∵12BOC S OC OB ∆=⋅，1122ABC S AC OB AB CD ∆=⋅=⋅，∴2ABC BOC S AC AB S OC OB∆∆===，∴AB =2OB ，∴OA ==，当x =0时，y，当y =0时，x =∴OB =-，=OA∴()-，解得：3k =-，故答案为：-．3【点拨】本题考查了角平分线的性质、三角形的面积、勾股定理以及一次函数图象上点的坐标特征，利用面积法找出OA=是解题的关键．173【分析】过点A、D分别作x轴和垂线，垂足分别为E、F，求得CD=2，AB=BC=AC=8，利用直角三角形的性质求得CE=4，CF=1，设A，，D，利用OF-OE=CE+CF=5，列方程求解即可．解：过点A、D分别作x轴和垂线，垂足分别为E、F，∵△ABC是等边三角形，BD=3CD=6，∴CD=2，AB=BC=AC=8，∵AB//x轴，∴∠ACE=∠BCF=30°，∴CE=4，CF=1，由勾股定理得AEDF设AOF，解得：k【点拨】本题考查了反比例函数图象上点的坐标特征，含30°角的直角三角形的三边关系，解题的关键是通过含30°角的直角三角形的三边关系表示点A 和点B 的坐标．18．3⎛ ⎝⎭【分析】将OA 绕O 点顺时针旋转90°到OC ，连接AB 、CB ，作AM ⊥y 轴于M ，CN ⊥x 轴于N ，通过证得△AOB ≌△COB （SAS ），得到AB =CB ，证得△AOM ≌△CON （AAS ），求得C （4，-2），设B 点的坐标为（m ，8m），根据AB =BC ，得到关于m 的方程，解方程求得m 的值，即可求得B 的坐标．解：将OA 绕O 点顺时针旋转90°到OC ，连接AB 、CB ，作AM ⊥y 轴于M ，CN ⊥x 轴于N ，∵点A 的坐标为（2，4），∴AM =2，OM =4，∵∠AOB =45°，∴∠BOC =45°，在△AOB 和△COB 中，OA OC AOB COB OB OB ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△AOB ≌△COB （SAS ），∴AB =CB ，∵∠AOM +∠AON =90°=∠CON +∠AON ，∴∠AOM =∠CON ，在△AOM 和△CON 中，AOM CON AMO ONC OA OC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△AOM ≌△CON （AAS ），∴CN =AM =2，ON =OM =4，∴C （4，-2），设B 点的坐标为（m ，8m ），∵AB =CB ，∴2222882442m m m m-+-=-++（）（）（）（），解得m =-（负值不合题意，舍去）故答案为：⎛ ⎝．【点拨】本题考查了反比例函数图象上点的坐标特征，三角形全等的判定和性质，作出辅助线根据全等三角形是解题的关键．19．（1）3y x =；（2）P 点坐标为5()20【分析】（1）根据待定系数法即可求解；（2）先求出B,C 的坐标，再根据对称性作A 点关于x 轴的对称点’A ，连接'BA 交x 轴于P 点，求出直线'BA 的解析式即可得到P 点坐标．解：解:()1设反比例函数解析式为k y x=把()1,3A 代入，得133k =⨯=，∴反比例函数解析式为3y x=()2把(3,)B m 代入得33m =，解得1m =，B ∴点坐标为(3)1，；作A 点关于x 轴的对称点’A ，连接'BA 交x 轴于P 点，则’3(1)A -，，''PA PB PA PB BA +=+= ，设直线'BA 的解析式为y mx n =+，则331m n m n +=-⎧⎨+=⎩，解得25m n =⎧⎨=-⎩∴直线'BA 的解析式为25y x =-，当0y =时，250x -=，解得52x =P ∴点坐标为5()20．【点拨】此题主要考查反比例函数与几何综合，解题的关键是熟知反比例函数的图像与性质、待定系数法的应用．20．(1)-14(2)4【分析】（1）由题意可得出3AP =，2N y =-．再根据PN =4，可求出AN =7，即得出N 的坐标，最后将N 的坐标代入反比例函数解析式，即可求出k 的值；（2）由题意可得出3M x =，代入所求出的反比例函数解析式，即得出M 的纵坐标，从而可求出PM 的长，最后由三角形面积公式计算即可．解：（1）由题意可知3AP =，2N =-．∵PN =4，∴AN =AP +PN =3+4=7，∴7N x =，∴N (7，-2)．将N (7，-2)代入k y x =，得：27k -=解得：14=-k ．（2）由题意可知3M x =．由（1）可知反比例函数解析式为：14y x =-，将3M x =代入14y x =-得：143M y =-∴1482(33P M PM y y =-=---=，∴11834223APM S AP PM =⋅=⨯⨯=△．【点拨】本题考查坐标与图形，求反比例函数的解析式，反比例函数与几何的综合．利用数形结合的思想是解题关键．21．(1)8(2)443【分析】（1）将点A 的坐标（2，4）代入()0k y x x=>，可得结果；（2）利用反比例函数的解析式可得点B 的坐标，利用三角形的面积公式和梯形的面积公式可得结果．（1）解：将点A 的坐标（2，4）代入()0k y x x =>，可得k ＝xy ＝2×4＝8，∴k 的值为8；（2）∵k 的值为8，∴函数k y x =的解析式为8y x =，∵CD ＝2OD ，OD ＝2，∴CD ＝4，∴OC ＝6，∴点B 的横坐标为6，将x ＝6代入8y x =，得43y =，∴点B 的坐标为（6，43），∴S 四边形OABC ＝S △AOD ＋S 梯形ABCD ＝12×2×4＋12×(43＋4)×4＝443．【点拨】本题主要考查了反比例函数图象上点的坐标特征，运用数形结合思想是解答此题的关键．22．(1)5(2)4y x=-【分析】（1）根据勾股定理即可求解；（2）设E 点的坐标为（x ，4），F 点的坐标是（x −3，1），代入m y x =求出x ，再求出m ，即可得出答案．解：(1)∵矩形ABCD 的两边AD AB 、的长分别为3、8，∵点E 为DC 的中点，∴CE =DE =4，在Rt △ADE 中，由勾股定理得：AE 5=；(2)∵AF −AE ＝2，∴AF ＝5＋2＝7，∴BF ＝8−7＝1，设E 点的坐标为（x ，4），F 点的坐标是（x −3，1），代入m y x=得：m ＝4x ＝（x −3）•1，解得：x ＝−1，即m ＝−4，所以当AF −AE ＝2时反比例函数表达式是4y x=-．【点拨】本题考查了反比例函数图象上点的坐标特征，用待定系数法求反比例函数的解析式，矩形的性质等知识点，能求出E 点的坐标是解此题的关键．23．(1)3y x=．(2)1﹤x ﹤3．(3)4．【分析】（1）把A n 的值，再代入反比例函数解析式可求得k ，即可得出反比例函数的表达式；（2）根据A ，B 点的横坐标，结合图象可直接得出满足条件的x 的取值范围；（3）设一次函数与x 轴交于点C ，可求得C 点坐标，利用AOB AOC BOC S S S =-△△△可求得ABO 的面积．（1）解：（1）∵点A 在一次函数图象上，∴n =-1+4=3，∴A （1，3），∵点A 在反比例函数图象上，∴k =3×1=3，∴反比例函数的表达式为3.y x=（2）结合图象可知当一次函数值大于反比例函数值时，x 的取值范围为1＜x ＜3．（3）如图，设一次函数与x 轴交于点C ，在y =-x +4中，令y =0可求得x =4，∴C （4，0），即OC =4，将B （3，m ）代入y =-x +4，得m =1，∴点B 的坐标为（3，1）．114341 4.22AOB AOC BOC S S S =-=⨯⨯-⨯⨯= 故△AOB 的面积为4．【点拨】本题是反比例函数与一次函数的综合题，主要考查函数图象的交点问题，掌握两函数图象的交点坐标满足每个函数解析式是解题的关键．24．(1)C (3，-2)；D （5，0）(2)6y x =-(3)10BD =；AC =20S =【分析】（1）由题意，点A 、C ，点B 、D 关于原点对称，即可得出答案；（2）直接将点()32A -，代入反比例函数k y x =，即可求出解析式；（3）直接根据B 、D BD 的长，过点A 作AE ⊥x 轴于E ，有勾股定理可求出OA 的长，即可得出AC 的长；（4）由2ABD S S = ，即可求解．（1）解：由题意点A 、C ，点B 、D 关于原点对称，且()32A -，、(50)B -，，∴C (3，-2)；D （5，0）．（2）∵反比例函数图象经过点（-3，2），∴()326k xy ==-⨯=-反比例函数的解析式为6y x=-．（3）()5510BD =--=；过点A 作AE ⊥x 轴于E ，在Rt △AEO 中，AO ===∴2AC AO ==（4）Δ122210202ABD S S ==⨯⨯⨯=．【点拨】本题考查反比例函数，平行四边形，熟练运用反比例函数的对称性是解题的关键．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
代几结合专题：反比例函数与几何图形的综合(选做)——代几结合，掌握中考风向标◆类型一 与三角形的综合1．(2016·云南中考)位于第一象限的点E 在反比例函数y ＝kx的图象上，点F 在x 轴的正半轴上，O 是坐标原点．若EO ＝EF ，△EOF 的面积等于2，则k 的值为( )A ．4B ．2C ．1D ．－22．(2016·菏泽中考)如图，△OAC 和△BAD 都是等腰直角三角形，∠ACO ＝∠ADB＝90°，反比例函数y ＝6x在第一象限的图象经过点B ，则△OAC 与△BAD 的面积之差S △OAC－S △BAD 为( )A ．36B ．12C ．6D ．33．如图，点A 在双曲线y ＝5x 上，点B 在双曲线y ＝8x上，且AB ∥x 轴，则△OAB 的面积等于________．第3题图第4题图4．(2016·包头中考)如图，在平面直角坐标系中，点A 在第二象限内，点B 在x 轴上，∠AOB ＝30°，AB ＝BO ，反比例函数y ＝k x(x ＜0)的图象经过点A ，若S △AOB ＝3，则k 的值为________．5．(2016·宁波中考)如图，点A 为函数y ＝9x(x >0)图象上一点，连接OA ，交函数y＝1x(x >0)的图象于点B ，点C 是x 轴上一点，且AO ＝AC ，则△ABC 的面积为________．第5题图第6题图6．★如图，若双曲线y ＝kx(k ＞0)与边长为3的等边△AOB (O 为坐标原点)的边OA 、AB 分别交于C 、D 两点，且OC ＝2BD ，则k 的值为________．7．(2016·宁夏中考)如图，Rt △ABO 的顶点O 在坐标原点，点B 在x 轴上，∠ABO＝90°，∠AOB ＝30°，OB ＝23，反比例函数y ＝kx(x >0)的图象经过OA 的中点C ，交AB 于点D .(1)求反比例函数的关系式；(2)连接CD ，求四边形CDBO 的面积．8．(2016·大庆中考)如图，P 1、P 2是反比例函数y ＝kx(k >0)在第一象限图象上的两点，点A 1的坐标为(4，0)．若△P 1OA 1与△P 2A 1A 2均为等腰直角三角形，其中点P 1、P 2为直角顶点．(1)求反比例函数的解析式； (2)①求P 2的坐标；②根据图象直接写出在第一象限内当x 满足什么条件时，经过点P 1、P 2的一次函数的函数值大于反比例函数y ＝kx的函数值．◆类型二 与特殊四边形的综合9．如图，点A 是反比例函数y ＝－6x(x ＜0)的图象上的一点，过点A 作平行四边形ABCD ，使B 、C 在x 轴上，点D 在y 轴上，则平行四边形ABCD 的面积为( ) A ．1 B ．3 C ．6 D ．12第9题图第10题图10．(2016·烟台中考)如图，在平面直角坐标系中，菱形OABC 的面积为12，点B 在y 轴上，点C 在反比例函数y ＝kx的图象上，则k 的值为________．11．(2016·齐齐哈尔中考)如图，已知点P (6，3)，过点P 作PM ⊥x 轴于点M ，PN ⊥y轴于点N ，反比例函数y ＝kx的图象交PM 于点A ，交PN 于点B ，若四边形OAPB 的面积为12，则k ＝________．第11题图第12题图12．如图，矩形OABC 的顶点A 、C 的坐标分别是(4，0)和(0，2)，反比例函数y ＝k x(x ＞0)的图象过对角线的交点P 并且与AB ，BC 分别交于D ，E 两点，连接OD ，OE ，DE ，则△ODE 的面积为________．13．(2016·资阳中考)如图，在平行四边形ABCD 中，点A 、B 、C 的坐标分别是(1，0)、(3，1)、(3，3)，双曲线y ＝kx(k ≠0，x >0)过点D .(1)求双曲线的解析式；(2)作直线AC 交y 轴于点E ，连接DE ，求△CDE 的面积．14．(2016·泰安中考)如图，在平面直角坐标系中，正方形OABC 的顶点O 与坐标原点重合，点C 的坐标为(0，3)，点A 在x 轴的负半轴上，点D 、M 分别在边AB 、OA 上，且AD ＝2DB ，AM ＝2MO ，一次函数y ＝kx ＋b 的图象过点D 和M ，反比例函数y ＝m x的图象经过点D ，与BC 的交点为N .(1)求反比例函数和一次函数的解析式；(2)若点P 在直线DM 上，且使△OPM 的面积与四边形OMNC 的面积相等，求点P 的坐标．◆类型三 动点、规律性问题15．(2016·长春中考)如图，在平面直角坐标系中，点P (1，4)，Q (m ，n )在函数y ＝kx(x >0)的图象上，当m >1时，过点P 分别作x 轴、y 轴的垂线，垂足为点A ，B ，过点Q 分别作x 轴、y 轴的垂线，垂足为点C ，D .QD 交AP 于点E ，随着x 的增大，四边形ACQE的面积( )A ．减小B ．增大C ．先减小后增大D ．先增大后减小第15题图第16题图16．★在反比例函数y ＝10x(x ＞0)的图象上，有一系列点A 1，A 2，A 3，…，A n ，A n ＋1，若A 1的横坐标为2，且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A 1，A 2，A 3，…，A n ，A n ＋1作x 轴与y 轴的垂线段，构成若干个矩形如图所示，将图中阴影部分的面积从左到右依次记为S 1，S 2，S 3，…，S n ，则S 1＝________，S 1＋S 2＋S 3＋…＋S n ＝________(用含n 的代数式表示)．代几结合专题：反比例函数与几何图形的综合(选做)1．B2．D 解析：设△OAC 和△BAD 的直角边长分别为a 、b ，则点B 的坐标为(a ＋b ，a －b )．∵点B 在反比例函数y ＝6x的第一象限图象上，∴(a ＋b )×(a －b )＝a 2－b 2＝6.∴S △OAC －S △BAD ＝12a 2－12b 2＝12(a 2－b 2)＝12×6＝3.3.32 解析：延长BA 交y 轴于点C .S △OAC ＝12×5＝52，S △OCB ＝12×8＝4，则S △OAB ＝S △OCB －S △OAC ＝4－52＝32.4．－3 35．6 解析：设点A 的坐标为⎝⎛⎭⎪⎫a ，9a ，点B 的坐标为⎝⎛⎭⎪⎫b ，1b .∵点C 是x 轴上一点，且AO ＝AC ，∴点C 的坐标是(2a ，0)．设过点O (0，0)，A ⎝ ⎛⎭⎪⎫a ，9a 的直线的解析式为y ＝kx ，∴9a ＝k ·a ，解得k ＝9a 2.又∵点B ⎝ ⎛⎭⎪⎫b ，1b 在y ＝9a 2x 上，∴1b ＝9a 2·b ，解得a b ＝3或a b ＝－3(舍去)，∴S △ABC ＝S △AOC －S △OBC ＝2a ·9a 2－2a ·1b 2＝182－62＝9－3＝6.6.36325 解析：过点C 作CE ⊥x 轴于点E ，过点D 作DF ⊥x 轴于点F .设OC ＝2x ，则BD ＝x .在Rt △OCE 中，OC ＝2x ，∠COE ＝60°，∴∠OCE ＝30°，则OE ＝x ，CE ＝3x ，则点C 的坐标为(x ，3x )．在Rt △BDF 中，BD ＝x ，∠DBF ＝60°，∴∠BDF ＝30°，则BF ＝12x ，DF ＝32x ，则点D 的坐标为⎝ ⎛⎭⎪⎫3－12x ，32x .将点C 的坐标代入反比例函数解析式可得k ＝3x 2，将点D 的坐标代入反比例函数解析式可得k ＝332x －34x 2，则3x 2＝332x －34x 2，解得x 1＝65，x 2＝0(舍去)，故k ＝3x 2＝36325. 7．解：(1)∵∠ABO ＝90°，∠AOB ＝30°，OB ＝23，∴OA ＝2AB ，∴(2AB )2＝AB 2＋(23)2，∴AB ＝2.作CE ⊥OB 于E .∵∠ABO ＝90°，∴CE ∥AB .∵OC ＝AC ，∴OE＝BE ＝12OB ＝3，CE ＝12AB ＝1，∴C 点坐标为(3，1)．∵反比例函数y ＝kx (x >0)的图象经过OA 的中点C ，∴1＝k3，∴k ＝3，∴反比例函数的关系式为y ＝3x ；(2)∵OB ＝23，∴D 的横坐标为23，代入y ＝3x 得y ＝12，∴D 点坐标为⎝⎛⎭⎪⎫23，12，∴BD ＝12.∵AB ＝2，∴AD ＝AB －BD ＝32，∴S △ACD ＝12AD ·BE ＝12×32×3＝334.∴S 四边形CDBO ＝S △AOB －S△ACD ＝12OB ·AB －334＝12×23×2－334＝534.8．解：(1)过点P 1作P 1B ⊥x 轴，垂足为B .∵点A 1的坐标为(4，0)，△P 1OA 1为等腰直角三角形，∴OB ＝2，P 1B ＝12OA 1＝2，∴P 1的坐标为(2，2)．将P 1的坐标代入反比例函数y ＝k x(k >0)，得k ＝2×2＝4，∴反比例函数的解析式为y ＝4x；(2)①过点P 2作P 2C ⊥x 轴，垂足为C ，∵△P 2A 1A 2为等腰直角三角形，∴P 2C ＝A 1C .设P 2C ＝A 1C ＝a ，则P 2的坐标为(4＋a ，a )．将P 2的坐标代入反比例函数的解析式y ＝4x中，得a ＝44＋a ，解得a 1＝22－2，a 2＝－22－2(舍去)，∴P 2的坐标为(2＋22，22－2)；②在第一象限内，当2<x <2＋22时，经过点P 1、P 2的一次函数的函数值大于反比例函数y ＝4x的函数值．9．C 10.－611．6 解析：∵点P 的坐标为(6，3)，∴点A 的横坐标为6，点B 的纵坐标为3，代入反比例函数y ＝k x ，得点A 的纵坐标为k 6，点B 的横坐标为k 3，即AM ＝k 6，NB ＝k3.∵S 四边形OAPB ＝12，即S 矩形OMPN －S △OAM －S △NBO ＝12，∴6×3－12×6×k 6－12×3×k3＝12，解得k ＝6.12.154 解析：∵四边形OABC 是矩形，∴AB ＝OC ，BC ＝OA .∵A 、C 的坐标分别是(4，0)和(0，2)，∴OA ＝4，OC ＝2.∵P 是矩形对角线的交点，∴P 点的坐标是(2，1)．∵反比例函数y ＝kx(x ＞0)的图象过对角线的交点P ，∴k ＝2，∴反比例函数的解析式为y ＝2x .∵D ，E 两点在反比例函数y ＝k x (x ＞0)的图象上，∴D 点的坐标是⎝ ⎛⎭⎪⎫4，12，E 点的坐标是(1，2)，∴S △ODE ＝S 矩形OABC －S △AOD －S △COE －S △BDE ＝4×2－12×2－12×2－12×32×3＝154.13．解：(1)∵在平行四边形ABCD 中，点A 、B 、C 的坐标分别是(1，0)、(3，1)、(3，3)，∴点D 的坐标是(1，2)．∵双曲线y ＝k x (k ≠0，x >0)过点D ，∴2＝k1，得k ＝2，即双曲线的解析式是y ＝2x(x >0)；(2)∵直线AC 交y 轴于点E ，∴S △CDE ＝S △EDA ＋S △ADC ＝（2－0）×12＋（2－0）×（3－1）2＝1＋2＝3，即△CDE 的面积是3.14．解：(1)∵正方形OABC 的顶点C 的坐标为(0，3)，∴OA ＝AB ＝BC ＝OC ＝3，∠OAB ＝∠B ＝∠BCO ＝90°.∵AD ＝2DB ，∴AD ＝23AB ＝2，∴D 点的坐标为(－3，2)．把D 点的坐标代入y ＝m x 得m ＝－6，∴反比例函数的解析式为y ＝－6x.∵AM ＝2MO ，∴MO＝13OA ＝1，∴M 点的坐标为(－1，0)．把M 点与D 点的坐标代入y ＝kx ＋b 中得⎩⎨⎧－k ＋b ＝0，－3k ＋b ＝2，解得⎩⎨⎧k ＝－1，b ＝－1，则一次函数的解析式为y ＝－x －1； (2)把y ＝3代入y ＝－6x得x ＝－2，∴N 点坐标为(－2，3)，∴NC ＝2.设P 点坐标为(x ，y )．∵△OPM 的面积与四边形OMNC 的面积相等，∴12(OM ＋NC )·OC ＝12OM ·|y |，即|y |＝9，解得y ＝±9.当y ＝9时，x ＝－10，当y ＝－9时，x ＝8，则点P 的坐标为(－10，9)或(8，－9)．15．B 解析：由题意得AC ＝m －1，CQ ＝n ，则S 四边形ACQE ＝AC ·CQ ＝(m －1)n ＝mn －n .∵P (1，4)，Q (m ，n )在函数y ＝k x(x >0)的图象上，∴mn ＝k ＝4(常数)．∴S 四边形ACQE ＝4－n .∵当m >1时，n 随着m 的增大而减小，∴S 四边形ACQE ＝4－n 随着m 的增大而增大．故选B.16．5 10n n ＋1 解析：∵点A 1、A 2、A 3、…、A n 、A n ＋1在反比例函数y ＝10x (x ＞0)的图象上，且每点的横坐标与它前一个点的横坐标的差都为2，又点A 1的横坐标为2，∴点A 1的坐标为(2，5)，点A 2的坐标为⎝ ⎛⎭⎪⎫4，52，∴S 1＝2×⎝ ⎛⎭⎪⎫5－52＝5.由题图象知，点A n 的坐标为⎝ ⎛⎭⎪⎫2n ，102n ，点A n ＋1的坐标为⎝ ⎛⎭⎪⎫2n ＋2，102n ＋2，∴S 2＝2×⎝ ⎛⎭⎪⎫104－106＝53，∴S n ＝2×⎝ ⎛⎭⎪⎫102n －102n ＋2＝10⎝ ⎛⎭⎪⎫1n －1n ＋1(n ＝1，2，3，…)．∴S 1＋S 2＋S 3＋…＋S n ＝10⎝ ⎛⎭⎪⎫1－12＋10⎝ ⎛⎭⎪⎫12－13＋…＋10⎝ ⎛⎭⎪⎫1n －1n ＋1＝10⎝ ⎛⎭⎪⎫1－12＋12－13＋…1n －1n ＋1＝10n n ＋1.。