大学物理:第12章变化的电磁场A
大学物理常用公式电场磁场 热力学
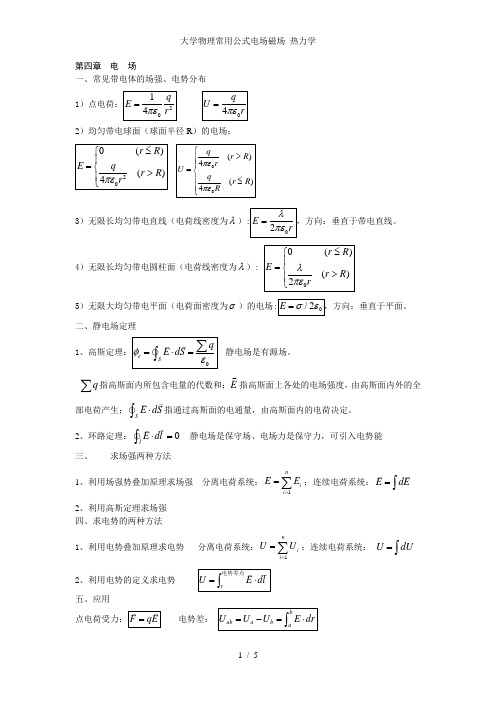
第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球面(球面半径R )的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和;E指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;SE dS ⋅⎰指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl⋅=⎰ 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1ni i E E ==∑;连续电荷系统:E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力:F qE = 电势差: bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2)导体腔内无电荷: 电荷都分布在导体外表面,空腔内表面无电荷。
3)导体腔内有电荷+q ,导体电量为Q :静电平衡时,腔内表面有感应电荷-q ,外表面有电荷Q +q 。
大学物理复习——电容器和电介质

q
2
8 0R
E内 0
R O
q
q2 q2 另解:C 4 0 R , W e 2C 8 0 R
例 3:一个单芯电缆半径为 r1 ,铅包皮的内半径为 r2 ,其间充有相对电容率为εr 的电介质,求:当电缆 芯与铅皮之间的电压为U12时,长为 L 的电缆中储存 的静电能。
P
O
x
d
A
B
12.2 电容器的连接 1.串联:
q q1 q2
q1 q1 q 2 q 2
C1 C2
q q C U U1 U 2
1 1 1 C C1 C 2
2. 并联:
U U1 U 2
等效电容
q
q
C
U1
U2
U
q1 q1
A B AB
q 0S (3)由电容定义: C 得: C U A UB d 0S 平板电容器电容: C d
0S
仅由 S , d , 0 决定,与其所带电量、极板间电压无关。
2. 球形电容器 两极板的半径 R A , RB ( RB R A R A ) q ;两板间场强: q E (1)充电 4 0 r 2 (2)两极板间电势差:
U
等效电容
q
U U1 U 2 q q1 q2
C1 q 2 q2
C2
q
C
C C1 C 2
U
U
12.3 电介质(介电质)对电场的影响 电介质 — 不导电的绝缘物质。 q0 一、电介质对电场的影响 C0 1.充电介质时电容器的电容 q
大学物理-12章:光的干涉

iD
n1
e
A
C n2 n1
B
n1
薄膜干涉
§4 分波面双光束干涉
一、杨氏双缝实验(1801)
装置: 稳定、明暗相间条纹
P
S1
Sd
r1
r2
y o
S2
D
物理分析:
d sin d tg yd
D
P
S1
d
r1
r2
y
o
S2 r2 r1
D
yd D
2k
2 (2k 1)
亮纹
暗纹
2
明、暗纹位置:
k 3, 2n1e / 3 368nm
讨论:
1 2k k 0,1, 2
I I1 I2 2 I1I2
if I1 I2 4I1
光的强度为最大值,干涉极大
I I1 I2 2 I1I2 cos
讨论:
2 (2k 1) k 0,1, 2
I I1 I2 2 I1I2
if I1 I2
0
光的强度为最小值,干涉极小
§3 两列单色波的干涉
2e
n22
n12
sin2
i
2
k
2ne 2 k
4ne 41.301.0107 5.20107
2k 1
2k 1
2k 1
k=1时: 5.20 107 m ----绿色光
k=2时: 1.733107 m
----紫外光,不可见
练习:一油轮漏油(n1=1.2)污染海面,在 海水(n2=1.3)表面形成一层薄油污。
随机变化
cos(2
1)
1
cos(2 1)dt 0
0
I I1 I2 非相干叠加加!
02感生电动势 有旋电场

dB dt
导体
Fan
②应用∶高频冶炼、焊接、加热、真空技术。
③有害∶变压器和电机中的涡流产生焦耳热损耗。
Fan
涡电流的应用:
• 强大的涡流在金属内流动时,会释放 大量的焦耳热。工业上利用这种热效 应,制成高频感应电炉来冶炼金属。 • 在坩埚的外缘绕有线圈,当线圈同大功率高频交变电 源接通时,高频交变电流在线圈内激发很强的高频交 变磁场,这时放在坩埚内的被冶炼的金属因电磁感应 而产生涡流,释放出大量的焦耳热,结果使自身熔化 • 这种加热和冶炼方法的优点是无接触加热。 把金属和 •可以使金属不受玷污, 坩埚等放 •不致在高温下氧化; 在真空室 •它是在金属内部各处同时加热,而不是使热 加热, 量从外面传递进去,因此加热效率高,速度快 高频感应电炉已广泛用于冶炼特种钢、难熔或活泼性较 强的金属,以及提纯半导体材料等工艺中。 Fan
涡电流的危害:
• 涡流所产生的热在某些问题中非常有害。在许多电磁 设备中,为了增大磁感应强度,常常有大块的金属存 在(如发电机和变压器中的铁芯),当这些金属块在变 化的磁场中或相对于磁场运动时,在它们的内部也会 产生感应电流。 • 在电机和变压器中,当电机或变压器的线圈中通过交 变电流时,铁芯中将产生很大的涡流,损耗大量的能 量(叫做铁芯的涡流损耗),甚至发热量可能大到烧毁 这些设备。 • 为了减小涡流及其 损失,通常采用叠 加起来的硅钢片代 替整块铁芯,并使 硅钢片平面与磁感 应线平行。
d d 由法拉第电磁感应定律 EV dl
感生电动势的计算
=
B
B t
B
t
E
E
Fan
Fan
有旋电场与静电场对比
静电场 有旋电场
由变化的磁场激发 无源场 闭合 不能用电势概念描述
大学物理中的电磁波电磁场的传播与性质

大学物理中的电磁波电磁场的传播与性质电磁波是大学物理中的重要概念,它在电磁场中传播,并具有多种性质。
本文将从电磁波的定义、传播特性、电磁波谱和应用等方面进行探讨。
一、电磁波的定义电磁波是由变化的电场和磁场相互耦合产生的一种波动现象,具有电磁振荡和传播性质。
它的本质是通过电磁场的相互作用而传播能量和动量。
二、电磁波的传播特性1. 电磁波的速度:电磁波在真空中的传播速度为光速,即299792458米/秒(约为3.0×10^8 m/s),在其他介质中传播速度会发生变化。
2. 电磁波的周期和频率:电磁波的周期是指波的一个完整振动所经历的时间,单位为秒;频率是指单位时间内波的振动次数,单位为赫兹(Hz)。
3. 电磁波的波长和波数:电磁波的波长是指波的一个完整周期所对应的长度,通常用λ表示,单位为米;波数是指在单位长度内波的振动次数,通常用k表示,单位为1/米。
4. 电磁波的能量和强度:电磁波传播时会携带能量,能量与波的振幅和频率有关;强度是指单位面积内电磁波的能量流密度,与波的振幅和传播方向有关。
三、电磁波谱电磁波谱是指电磁波按照频率或波长划分的不同区域。
根据频率的不同,电磁波谱可以分为无线电波、微波、红外线、可见光、紫外线、X射线和γ射线等不同的频段。
不同频段的电磁波在应用上具有不同的特性和用途。
四、电磁波的应用1. 通信:无线电波和微波被广泛应用于通信领域,包括无线电广播、电视信号传输、移动通信等。
2. 显微镜和光学:可见光是光学仪器如显微镜的重要光源,通过光学设备的应用可以观察和研究物体的微观结构。
3. 医学诊断和治疗:X射线和γ射线在医学影像和肿瘤治疗中起到重要作用,可以帮助医生诊断和治疗疾病。
4. 遥感和雷达:微波和红外线被用于遥感技术和雷达系统,可以监测和探测地球表面的变化和异常情况。
5. 光电子学和半导体器件:光电子学和半导体器件利用电磁波与物质相互作用的特性,开发了各种光学传感器和光电子器件。
大学物理12真空中的静电场

03
电势与电势差
电势的概念
总结词
电势是描述电场中某点电荷所具有的势能,其值与零电势点的选 择有关。
详细描述
电势是描述电场中某点电荷所具有的势能,通常用符号"φ"表示。它 是一个标量,其值与零电势点的选择有关。在静电场中,零电势点 是任意选择的,通常选择大地或无穷远处作为零电势点。
电势的计算方法
计算电场能量
利用高斯定理可以计算电场的能量密度和总能量。
静电场的散度与源电荷的关系
02
01
03
静电场的散度等于该点源电荷的密度。
数学表达式:divE = ρ/ε0
其中,divE是电场强度的散度,ρ是电荷的密度,ε0是 真空中的电容率。
05
静电场的环路定理与电场线的引入
静电场的环路定理
总结词
静电场的环路定理描述了电场与磁场之 间的关系,是电磁学中的基本定理之一 。
大学物理12真空中的静电场
目
CONTENCT
录
• 引言 • 电场与电场强度 • 电势与电势差 • 高斯定理与静电场的散度 • 静电场的环路定理与电场线的引入 • 静电场的边界条件与导体表面的电
场线分布 • 静电场的能量与力
01
引言
主题简介
静电场是静止电荷产生的电场,是电 磁学的重要概念之一。
在真空环境中,静电场不受其他电磁 场的影响,因此具有独特的性质和规 律。
指导电路设计
在电路设计中,通过合理 布置导线和元件的位置, 利用电场线的分布来优化 电路性能。
07
静电场的能量与力
静电场的能量分布
静电场的能量分布由电场强度和电势的乘积积分得 到,表示电场中各点的能量密度。
在真空中的静电场,能量分布与电荷分布有关,电 荷密度越大,能量密度越高。
大学物理下磁场部分总结
B M μ0 B
B
对均匀 各向同性磁介质
H
r μ0
f qE qv B
(2) 载流螺绕环内任一 点处
0 IR
B
3.基本定理 (1)对于介质中的总场B; 高斯定理仍然成立
3/ 2 2 (R 2 x 2 )
B dS 0
S
2R
(3)无限大载流平面外 一点(电流密度为i)
1 0 I B 2 2 a
0 I B 2 a
(2)圆电流的磁场
Id l
r
I R 0
/
dB ^ dB dB // dB
^
x
B
0
R2I
2 (R 2 x2 ) 32
R2I
dB/
轴线上任一点P的磁场
圆电流中心的磁场 ½ 圆电流的中心的 1/n 圆电流的中心的
B
B
0
H
B
(1)一段载流直导线外一点的磁感应强度 B 0 (sin sin ) 2 1 4 a I 无限长时 B 0 2a 2 (2)载流圆线圈轴线上一点的磁感应强度 B 圆心处 B 0 I
几种典型载流导线所产生的磁感应强度
电磁场对运动电荷的作用力
0 Ir r< R 2R 2 I B 0 r>R 2r
i
M
p
V
m
在各向同性磁介质中
M xm H
(2)磁场强度矢量 (是辅助物理量)
磁通量 m BdS cos B dS
S S
dB
4
0 qv r
r3
载流平面线圈在均匀磁场B 中受到磁力矩的作用 M Pm B 式中 Pm NISn 为线圈的磁矩 运动电荷在外磁场中受 到的磁力: f qv B
大学物理12 真空中的静电场
注意:直接对dE 积分是常见的错误
d q dV
lim
q d q dV V 0 V
一般 E dE
体密度 面密度
dq dS dq dl
q d q lim dS S 0 S
lim
l 0
r
dq
P
dE
q d q l dl
a. 电场中的带电体,受电场的作用力。 b. 移动带电体,电场力作功:场具有能量 c. 变化的电磁场以光速传播:场具有动量、质量
场和实物是物质存在的不同形式。 但实物具有不可入性,而场可以叠加。
二、电场强度
从力的角度研究电场 F 单位正电荷(检验பைடு நூலகம்荷)在电 E q 场中某点所受到的力。 它与检验电荷无关,反映电场本身的性质。
根据万有引力定律可得两粒子间万有引力大小: me m p 6.7 1011 9.11031 1.7 1027 Fg G 2 r (5.3 1011 ) 2 3.7 1047 (N)
可以看出,氢原子中电子与质子的相互作用的 静电力远大于万有引力,前者约为后者的1039倍。
dl acsc 2d .
p a
dEy
dEx
0
1
x
dE
r 2 a 2csc 2 .
dE d 4 0 a
24
dE d 4 0 a
dE x sind 4 0 a dE y cosd 4 0 a
E y dEy
7
电磁学的学习特点
1. 与力学相比,电磁学的思路与学习方法不同 力学 牛顿运动 定律 电现象 磁现象 电生磁 磁生电 动量规律 功能规律
电磁学
12电磁波作业 吉林大学大物答案
P 解 2 =3.18×103(SI) := S πr
E = 2cµ0 S ==1.55×10 V 0
3
m
B = 0
E 0
c
=5.17×10 T
−6
(2) )
r 1 ε0 z r K0 cos(t − )i E =− 2 µ0 c z >0 , r H = −1 K cos(t − z) r j 0 2 c
r 1 ε0 z r K0 cos(t + )i E = − 2 µ0 c z <0 , r 1 H = K cos(t + z) r j 0 2 c
解(1 Ez = E0cosπ ×10 (t + x 0.8c) : )
15
c ⇒u = 0.8c ⇒n = =1.25 u
(3 H = ) 0
ε − E = 2 1 × 0−4(A⋅ m 1) . 6 1 0 µ
1
ω 14 (2)v = =5×10 2 π
εµ
(4 S = )
=0 8 , µ ≈ µ . c 0
P 1 =I =S = 2 π r 2
ε0 2 E 0 µ0
10. 在真空中传播的平面电磁波,在空间 在真空中传播的平面电磁波,
1 π 某点的磁场强度为 H =1.20cos(2 vt + 3π)
则该店的电场强度为
E=
。
µ0 1 1 2 c s 2 vt + π) . 0 o( π ε0 3
−2
= 4 5× 0 . 1
P 注 2 = 3.18×103(SI) := S πr
6. 在电磁波传播的空间中,任一点的 E和 在电磁波传播的空间中, 的方向及波传播的之间的关系是_ 的方向及波传播的之间的关系是_三者 H 相互垂直成右手螺旋系 ___。 E×H 或 :S =
大学物理学-电磁感应教案
dtd R I Φ-=1,在从0=t 到t 时间内,通过电路的电量)(1110000Φ-Φ=Φ⋅=⋅Φ=⋅=⎰⎰⎰ΦΦR d R dt dt d R dt I q t t 可见,q 与)(0Φ-Φ成正比,而与磁通量改变快慢无关。
设0=t 时00=Φ,只要测出R 和q 、即可得到Φ;如果已知回路面积、就可以算出磁感应强度B 。
这就是磁通计原理。
§11. 2 动生电动势与感生电动势一、动生电动势 1.在磁场中运动的导线内的感应电动势 电动势的定义:电源的电动势定义为单位正电荷绕闭合回路运动一周时、电源中非静电力作的功。
即 ⎰⋅=l E k d εk E 为单位正电荷受的非静电力。
如果导线不闭合、则单位正电荷从导线一端a 运动到另一端b 时,非静电力k E 作的功就是导线a 、b 两端的电动势。
即⎰⋅=baab d l E k ε2、动生电动势: 当导线ab 在磁场B 中以速度v 运动时,导线ab 中的电子也以速度v 运动,磁场B 作用在上的电子洛伦兹力 B v f ⨯-=e而单位正电荷受的洛伦兹力B fE k ⨯=-=υe就是动生电动势中的非静电力。
所以,动生电动势⎰⋅⨯=baab )(l Bd υε。
当导线回路闭合时、回路中的动生电动势 ⎰⋅⨯=l B d )(υε。
这是动生电动势的一般表示式。
对此式要注意两个角度的关系: (1) υ与B 的夹角θ1; (2)(υ×B )与dl 的夹角θ2。
如θ1=0(或π),或22πθ=,都会使得0=ε。
例11.1 在长直导线电流I 的附近有一长度为L 的共面导线ab 与长直导线垂直,a 端距长直导线为d 、ab 以平行于长直导线的速度v 向上运动。
求:ab 上的感应电动势。
解:在ab 上取d l 、与长直导线的距离为r ,该点的磁场 r2ΙμB π0= 所以d l 上的感应电动势 dr r2Iv πdr r 2I d d πμπυμυε00cos )(-==⋅⨯=l Bab 上的感应电动势 ⎰++==dL dab d dL πv I μ-dr r πIv μ-εln 2200 感应电动势ab ε为负值表示其方向从b 到a ,即a 点电势高。
