第八章 方差分析
统计学第八章方差分析

第八章方差分析Ⅰ.学习目的本章介绍方差分析的理论、方法与运用。
通过学习,要求:1.了解方差分析的基本概念和思想;2.理解方差分解原理;3.掌握单因素、双因素(有、无交互作用)方差分析的原理和流程;4学会针对资料提出原假设,并能利用Excel进行方差分析。
Ⅱ.课程内容要点第一节方差分析方法引导一、方差分析问题的提出方差分析,简称ANOVA(analysis of variance),就是利用试验观测值总偏差的可分解性,将不同条件所引起的偏差与试验误差分解开来,按照一定的规则进行比较,以确定条件偏差的影响程度以及相对大小。
当已经确认某几种因素对试验结果有显著影响时,可使用方差分析检验确定哪种因素对试验结果的影响最为显著及估计影响程度。
二、方差分析的有关术语和概念1.试验结果:在一项试验中用来衡量试验效果的特征量,也称试验指100101标或指标,类似函数的因变量或者目标函数。
2.试验因素:试验中,凡是对试验指标可能产生影响的原因都称为因素,或称为因子,类似函数的自变量。
试验中需要考察的因素称为试验因素,简称为因素。
一般用大写字母A 、B 、C 、……表示。
方差分析的目的就是分析实验因素对实验或抽样的结果有无显著影响。
如果在实验中变化的因素只有一个,这时的方差分析称为单因素方差分析;如果在实验中变化的因素不止一个,这时的方差分析就称为多因素方差分析。
3.因素水平:因素在试验中所处的各种状态或者所取的不同值,称为该因素的水平,简称水平。
一般用下标区分。
同样因素水平有时可以取得具体的数量值,有时只能取到定性值(如好,中,差等)。
4.交互作用:当方差分析过程中的影响因素不唯一时,这种多个因素的不同水平的组合对指标的影响称为因素间的交互作用。
三、方差分析的基本原理 (一)方差分解原理一般地,试验结果的差异性可由离差平方和表示,离差平方和又可分解为组间方差与组内方差。
其中,组间方差为因素对试验结果的影响的加总;组内方差则是各组内的随机影响的加总。
医学统计课件人卫6版第八章方差分析

结合临床实践、数据分析和先进医疗技术,提高治疗效果,并为疾病研究提供更多信息。
3 精准医疗的实现
通过基因等多种因素对患者分类,针对性地提供增强疗效的治疗策略。
可重复测量方差分析
测量误差、同一样本下的多次重复测量。
其他类型方差分析
混合设计、随机效应模型、无效测量等。
单因素方差分析的假设检验
方差分析的F检验
用于比较样本均值是否相等的统计方法。 F检验是基于方差分析设计的推断方法。通过比较两个或更多组数据集的均值,它可以帮助您确定它们是否显 著不同。
方差分析的效应量
案例探究-方差分析在药理学研究中的应用
药物代谢动力学比较
使用多因素方差分析评估药物在 人体中的代谢差异。
口腔药物疗效评估
使用单因素方差分析比较不同药 物清除细菌斑块的效果。
药物治疗研究
使用双因素方差分析比较不同剂 量、不同时间和不同区域对老鼠 行为的影响。
方差分析与其他统计方法的比较
方法
Anova 线性回归分析 非参数检验
医学统计课件人卫6版第 八章方差分析
在医学研究中,方差分析是一种经常用到的统计方法。在这个演示中,我们 将深入探讨方差分析的定义、优点、局限性和应用前景。
方差分析的分类
单因素方差分析
原理和应用、方差源、F检验、解释F检验结果、 如何选择模型。
多因素方差分析
交互作用、无交互作用、方差功效、二因素方 差分析、多因素方差分析。
生物学实验
在实验中确定一组严格控制的边界,比较数据以确定生物数据中差异的来源。
3
流行病学研究
使用方差分析确定危险因素和干预方法的影响,评估治疗方案的效果。
方差分析在医学决策中的作用
第8章方差分析与回归分析分解

表8.1.3 单因子方差分析表
来源 平方和 自由度 均方和 F比
因子
误差 总和
SA
Se ST
fA=r1
MSA= SA/fA
MSe= Se/fe
F= MSA/ MSe
fe=nr
fT=n1
17 November 2018
第八章 方差分析与回归分析
第25页
对给定的,可作如下判断:
如果 F >F1 (fA ,fe),则认为因子A显著; 若F F1 (fA ,fe) ,则说明因子A不显著。
Q ( y1 y )
2
( yk y ) ( yi y )2
2 i 1
k
称为k个数据的偏差平方和,它常用来度量若干 个数据分散的程度。
17 November 2018
第八章 方差分析与回归分析
第18页
在构成偏差平方和Q的k个偏差y1 y , …, yk y 间 有一个恒等式 ( y y ) 0 ,这说明在Q中独立 的偏差只有k1个。
A e A e A e
17 November 2018
第八章 方差分析与回归分析
第23页
定理8.1.2 在单因子方差分析模型 (8.1.8) 及前 述符号下,有
(1) Se / 2 ~ 2(nr) ,从而E(Se ) =(nr) 2
E ( S A ) (r 1) m ai2
17 November 2018
第八章 方差分析与回归分析
第7页
1) 每一总体均为正态总体,记为 N(i , i 2),
i=1, 2,…, r ;
2) 各总体的方差相同:
1 2= 22=…= r2 = 2 ;
第八章方差分析与回归分析

Ti T SSA n i 1 ni
r ni
其中 Ti
r 2
X
j 1
ni
ij
, T Ti
i 1
r
同一水平 下观测值 之和
所以观测 值之和
例2 以 A、B、C 三种饲料喂猪,得一个月后每猪 所增体重(单位:500g)于下表,试作方差分析。 饲料 增重
A
B
51
23
X ij ij , j 1, 2,...ni , i 1, 2,...r
r ni i 1 j 1
考察统计量 SST X ij X
2
总离差平方和
经恒等变形,可分解为: SST SS A SSE 其中
SSA X i X
i 1 j 1
r
2 T 2 SSE X ij i 512 402 ... 282 11406.83 i 1 j 1 i 1 ni 11497 11406.83 r r ni
SST SS A SSE 11497 10472.11 1024.89
MS A 934.73 2 467.36 MSE 90.17 6 15.03
丁
1510 1520 1530 1570 1680 1600
引
例
试验指标——灯泡的使用寿命 可控因素(唯一的一个) ——灯丝的配料方案 四个水平——四种配料方案(甲乙丙丁) 因此,本例是一个四水平的单因素试验。 用X1,X2,X3,X4分别表示四种灯泡的使用寿命,即为 四个总体。假设X1,X2,X3,X4相互独立,且服从方差 相同的正态分布,即Xi~N(i,2)(i=1,2,3,4) 本例问题归结为检验假设 H0:1= 2= 3= 4 是否成立。
第八章 方差分析与相关分析
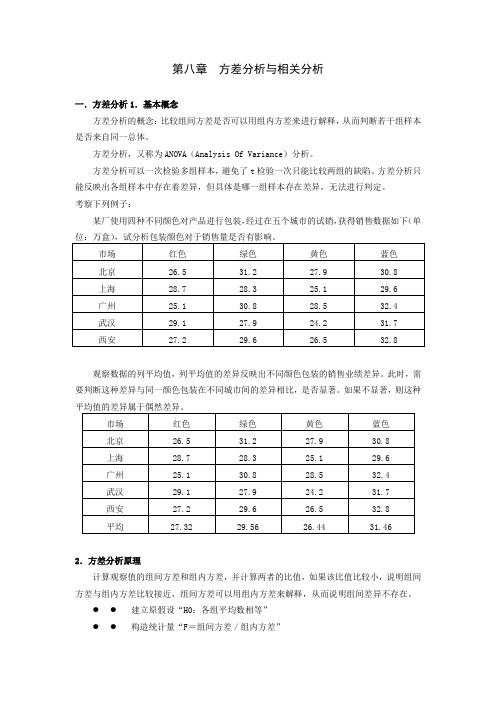
第八章方差分析与相关分析一.方差分析1.基本概念方差分析的概念:比较组间方差是否可以用组内方差来进行解释,从而判断若干组样本是否来自同一总体。
方差分析,又称为ANOVA(Analysis Of Variance)分析。
方差分析可以一次检验多组样本,避免了t检验一次只能比较两组的缺陷。
方差分析只能反映出各组样本中存在着差异,但具体是哪一组样本存在差异,无法进行判定。
考察下列例子:某厂使用四种不同颜色对产品进行包装,经过在五个城市的试销,获得销售数据如下(单观察数据的列平均值,列平均值的差异反映出不同颜色包装的销售业绩差异。
此时,需要判断这种差异与同一颜色包装在不同城市间的差异相比,是否显著。
如果不显著,则这种2.方差分析原理计算观察值的组间方差和组内方差,并计算两者的比值,如果该比值比较小,说明组间方差与组内方差比较接近,组间方差可以用组内方差来解释,从而说明组间差异不存在。
●●建立原假设“H0:各组平均数相等”●●构造统计量“F=组间方差/组内方差”●●在计算组间方差时,使用自由度为(r-1),计算组内方差时,使用自由度为(n-r)。
●●F满足第一自由度为(r-1),第二自由度为(n-r)的F分布。
●●查表,若F值大于0.05临界值,则拒绝原假设,认为各组平均数存在差异。
根据方差计算的原理,生成方差分析表如下:其中:组间离差平方和 SSA (Sum of Squares for factor A) =39.084误差项离差平方和 SSE (Sum of Squares for Error) =76.8455总离差平方和 SST (Sum of Squares for Total)=115.9295P-value值为0.000466,小于0.05,所以拒绝原假设。
3.双因素方差分析观察下列销售数据,欲了解包装方式和销售地区是否对于销售业绩有影响,涉及到双因素的方差分析。
此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。
第八章方差分析与回归分析

精心整理第八章方差分析与回归分析§1单因素试验的方差分析试验指标:研究对象的某种特征。
例各人的收入。
因素:与试验指标相关的条件。
例各人的学历,专业,工作经历等与工资有关的特征。
因素水平:因素所在的状态例学历是因素,而高中,大学,研究生等,就是学历因素水平;数学,物理等就是专业的水平。
问题假设1,,r A ;2。
各个总体的抽样过程是独立的。
3)~i X 1原假设22,,,r μσ进行参数估计。
注1210rik δ==∑各类样本均值水平i A 的样本均值:11in i ijj iX Xn ==∑;水平总样本均值:11111i n r rij i i i j i X X n X n n =====∑∑∑,1ri i n n ==∑;偏差平方和与效应 组间偏差平方和:22211()rrA i i i i i i S n X X n X nX ===-=-∑∑;(衡量由不同水平产生的差异)组内偏差平方和:2221111()()iin n rrE ij i ij i i i j i j S X X X n X =====-=-∑∑∑∑;(衡量由随机因素在同一水平上产生的差异) 总偏差平方和:222111()in rrT ij i ij i j i S X X n X nX ====-=-∑∑∑;(综合衡量因素,水平之间,随机因素的差异) 定理1(总偏差平方和分解定理)T A E S S S =+。
即1111)()in ri i j i j X X ====+-∑∑∑∑注定理2(E ES n =证1)E i ES ===∑定理31)/E S 2)如还有,2/~A S σ证1~(ij X N 1,,i n ,且独立,所以由第五章定理21()~(in ij ij i i i i j X X X X n μμχσ=⎛⎫⎛⎫----= ⎪ ⎪⎪ ⎪⎭⎝⎭∑∑利用2χ可加性,即得2221/~()()E i i S n r n r σχχ=-=-,且i X 与E S 独立。
第八章 方差分析与回归分析
第八章 方差分析与回归分析§8.1 方差分析8.1.1 问题的提出举例说明概念因子和水平。
因子:对研究对象产生影响的因素。
水平:因子所处的状态。
8.1.2 单因子方差分析的统计模型在研究中只考察一个因子则称为单因子试验,其中,记因子为A ,设其有r 个水平,记为r A A ,,1 ,在每一水平下考察的指标可以看成一个总体,现有r 个水平,故有r 个总体,假定:(1)每一总体均为正态总体,记为r i N i i ,,2,1),,(2;(2)各总体的方差相同,记222221 r ;(3)从每一总体中抽取的样本是相互独立的,即所有的试验结果ij y 都相互独立。
这些假定都可以用统计方法进行验证。
首先比较各水平下的均值是否相同,即要对如下的一个假设进行检验,不全相等r rH H ,,,::211210在不会引起误解的前提下,1H 通常可以省略不写。
若0H 成立,则称因子A 不显著,否则,称因子A 显著。
对如上的假设进行检验,需要从每一水平下的总体抽取样本,设从第i 个水平下的总体获得m 个试验结果(各个水平下相同),记ij y 表示第i 个总体的第j 次重复试验结果。
共得如下m r 个试验结果:m j r i y ij ,,1,,,1,其中r 为水平数,m 为重复数,i 为水平编号,j 为重复编号。
在水平i A 下的试验结果ij y 与该水平下的指标均值i 一般总是有差距的,记i ij ij y ,ij 称为随机误差,于是有ij i ij y上式称为试验结果ij y 的数据结构式。
把三个假定用于数据结构式就可以写出单因子方差分析的统计模型:),0(,,1,,,1,2 N m j r i y ij ij i ij 相互独立,且都服从诸为了能更好地描述数据,常引入总均值和效应的概念:总均值:诸i 的平均 ri i r r 11 ;称第i 水平下的均值i 与总均值 的差i i a ,r i ,,1为因子A 的第i 水平的主效应,简称为i A 的效应。
第八章协方差分析
3、根据线性回归关系计算各肥料的矫正 平均单株产量 矫正平均单株产量计算公式如下:
yi yi be ( xi x) 其中:yi 为第i处理矫正单株平均产量;
yi 为第i处理实际单株平均产量;
xi 为第i处理实际平均起始干周; x 为全试验的平均数;
be 为误差回归系数。
产量将平均改变0.7359 kg。
对be进行显著性检验如下:
无效假设 H 0 : e 0, 回归平方和
备择假设 H A : e 0
SSeR
SPe 2 646.82 475.993 SSex 878.9
回归自由度
df eR 1
离回归平方和
SSer SSey SSeR 1951.000 475.993 1475.007
dft dfT dfe =k-1=4-1=3
2、对矫正单株产量进行方差分析 表9-4 矫正单株产量的方差分析表
变异来源 df SS MS F值
肥料间
肥料内 (误差) 总变异
3
35 38
2507.777
1475.007 3982.784
835.926
42.143
19.835**
F=19.835>F0.01(3,35),p<0.01,不同肥料 的矫正单株产量间存在极显著的差异,须进一 步进行多重比较。
如果那些不能很好地进行试验控制的因素 是可量测的,且又和试验结果之间存在直线回 归关系,就可利用这种直线回归关系将各处理 的观测值都矫正到初始条件相同时的结果,使 得处理间的比较能在相同基础上进行,而得出 正确结论。这一做法在统计上称为统计控制。 这时所进行的协方差分析是将回归分析和 方差分析结合起来的一种统计分析方法,这种 协方差分析称为回归模型的协方差分析。
第八章方差分析回归分析理
(xij xi )2
i1 j1
离差平方和分解式
ST SA Se
rm
r
m
事实上,有
(xij xi )(xi x) (xi x) (xij xi ) 0
i1 j1
i 1
j 1
rm
ST
(xij x)2
i1 j1
rm
rm
rm
(xi x)2
(xij xi )2 2
饲料A
A1 A2 A3
鸡重/g
1073 1009 1060 1001 1002 1012 1009 1028 1107 1092 990 1109 1090 1074 1122 1001 1093 1029 1080 1021 1022 1032 1029 1048
比较三种饲料的增重效果是否一致,可以转化为利用样本 比较三个总体均值是否相等。直观上看该问题可以用两个 总体均值差异显著性检验解决,但细想想还是存在一定问 题,因为这样的比较能增大犯错误的概率。为解决这类问 题,英国统计学家R.A.Fisher于1924年提出了解距此类问题 的通用方法-方差分析法。
2.方差分析的概念 因素:影响试验指标变化的原因。 水平:因素所划分成不同等级,每个等级称为该因素的一 个水平。 条件变差:能反映控制因素不同水平对试验指标的作用的 量,又称为处理效应或组间效应。 随机误差:能反映控制因素以外因素对试验指标作用的量。
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
