融合朋友关系和标签信息的张量分解推荐算法

合集下载

张量分解稀疏张量wthres阈值处理

文章标题：深度探讨张量分解稀疏张量wthres阈值处理的方法和应用引言在信息科学领域，张量分解是一项重要的技术，用于处理高维数据，特别是稀疏张量。

其中，wthres阈值处理是一种常见的方法，能够帮助我们更好地理解数据的结构和特征。

本文将深入探讨张量分解稀疏张量wthres阈值处理的方法和应用，帮助读者更好地理解和运用这一技术。

一、张量分解的基本概念1. 张量的概念张量是信息科学中一个重要的概念，它是一种多维数组或矩阵的扩展。

在现实世界中，许多数据可以被表示为张量，例如图像数据、视频数据和传感器数据等。

2. 张量分解的意义张量分解是将高维的张量数据进行分解，以便更好地理解数据的内在结构和特征。

通过张量分解，我们可以把复杂的高维数据转化为更简洁、更易于理解的形式，有助于数据的降维和特征提取。

二、稀疏张量的特点1. 稀疏张量的定义稀疏张量是指大部分元素为0的张量，这种数据在实际应用中非常常见。

在社交网络数据中，用户与用户之间的互动关系可以被表示为稀疏张量。

2. 稀疏张量的挑战稀疏张量的处理具有一定的挑战性，因为大部分元素都是0，所以需要特殊的方法来有效地分解和处理这种数据，同时保留数据的有用信息。

三、wthres阈值处理的方法1. wthres阈值处理的原理wthres阈值处理是一种常见的方法，用于处理稀疏张量。

它的基本思想是对张量的元素进行阈值处理，将小于阈值的元素置0，从而消除噪声和无用信息。

2. wthres阈值处理的应用wthres阈值处理可以应用于多个领域，如图像处理、信号处理和网络分析等。

在实际应用中，可以根据具体的情况选择合适的阈值和处理方法，以达到最佳的效果。

四、张量分解稀疏张量的技术挑战与解决方法1. 技术挑战张量分解稀疏张量在实际应用中也面临一些挑战，比如计算复杂度高、噪声干扰等问题。

如何有效地解决这些问题，是当前研究的热点之一。

2. 解决方法针对张量分解稀疏张量的技术挑战，有许多解决方法，如采用高效的分解算法、优化数据结构和引入先进的噪声处理技术等。

融合社交关系和知识图谱的推荐算法

融合社交关系和知识图谱的推荐算法融合社交关系和知识图谱的推荐算法引言在当今信息爆炸的时代，人们面临着海量的信息。

为了帮助用户更好地获取所需信息，推荐算法应运而生。

社交关系和知识图谱是推荐算法中重要的两个方面。

社交关系反映了用户之间的互动，而知识图谱则是对知识的结构化表示。

本文将介绍一种融合社交关系和知识图谱的推荐算法，以帮助用户更准确地获取个性化的推荐信息。

一、社交关系的重要性社交关系反映了人与人之间的联系和互动。

在社交网络中，用户之间通过关注、点赞、评论等行为产生了一系列社交关系，这些关系可以被看作是用户之间的社交行为的直观表现。

社交关系有助于推荐算法理解用户的兴趣和偏好，并为用户提供个性化的推荐。

1. 社交关系的意义社交关系可以帮助推荐算法了解用户的兴趣爱好。

通过分析用户的社交关系，我们可以了解哪些用户有相似的兴趣爱好，并且可以将相似的用户进行群组，为他们提供相似的推荐。

此外，社交关系还可以帮助推荐算法了解用户的信任关系，例如用户更倾向于接受朋友的推荐。

2. 社交关系的表达方式社交关系可以通过图结构来表示。

每个用户可以看作是图中的一个节点，用户之间的关系可以看作是节点之间的边。

利用图的连接关系，我们可以从用户的邻居节点来推断用户的兴趣爱好。

例如，如果一个用户的邻居节点喜欢某个电影，那么该用户也有可能对这个电影感兴趣。

二、知识图谱的重要性知识图谱是一种对知识的结构化表示。

它通过将知识组织成实体和关系的图结构来帮助推荐算法理解和处理知识。

知识图谱中的实体可以是人、物、事件等，而关系则表示实体之间的关联。

1. 知识图谱的构建知识图谱的构建需要从多个来源收集数据，并将其进行实体和关系的组织。

收集的数据可以包括文本、网络、图片等不同类型的信息。

通过结构化的组织和链接，知识图谱可以更好地描述和理解知识的本质。

2. 知识图谱的应用知识图谱可以帮助推荐算法更准确地理解用户的需求和兴趣。

通过将用户的查询问题映射到知识图谱中的实体和关系上，推荐算法可以提供更准确和丰富的推荐结果。

【小型微型计算机系统】_推荐算法_期刊发文热词逐年推荐_20140723

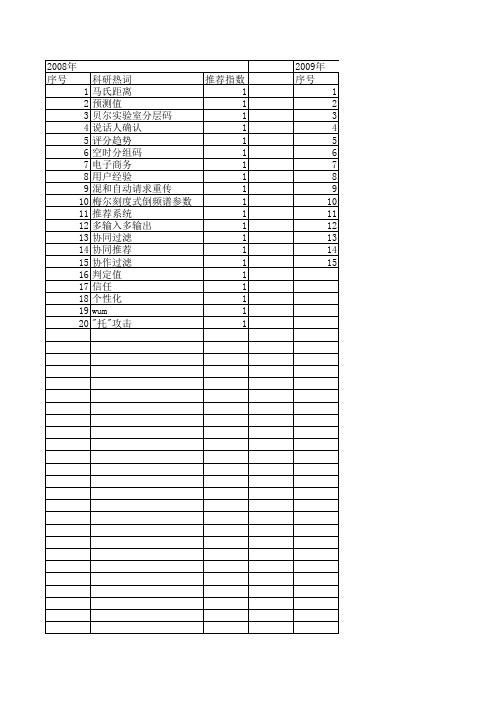
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2009年科研热词稀疏性推荐系统项目相似性资源共享评价证据理论扩展性协同过滤推荐算法分布式系统兴趣信誉管理信任模型信任 peer-to-peer item-based协同过滤推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1
2013年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
科研热词协同过滤标签社交网络推荐算法重叠社区发现软件网络规则学习聚类算法类别关联度社区发现社会网络用户反馈特征词标签推荐服务质量服务标签新用户推荐文档相似度数据挖掘情景模式张量分解大众分类可靠路由反向预测信任模型云计算个性化推荐 k近邻 d-s证据理论 ad-hoc网络
推荐指数 5 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 7 8 9 10 11
科研热词协同过滤评论挖掘评分欺诈评分可信度社会网络环境感知服务推荐推荐系统推荐算法信任关系 web服务
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

三部图张量分解标签推荐算法_廖志芳

１）（２）（３）（
）
）
）
）
）ＳｃｈｏｏｌｏＳｏｔｗａｒｅ，ＣｅｎｔｒａｌＳｏｕｔｈＵｎｉｖｅｒｓｉｔＣｈａｎｓｈａ４１００７５ｆｆｙ，ｇ
）ＳｃｈｏｏｌｏＩｎｏｒｍａｔｉｏｎＳｃｉｅｎｃｅ＆ＥｎｉｎｅｅｒｉｎＣｅｎｔｒａｌＳｏｕｔｈＵｎｉｖｅｒｓｉｔＣｈａｎｓｈａ４１００７５ｆｆｇｇ，ｙ，ｇ
１）１）２）
１）（中南大学软件学院
３）
）１００７５长沙４）１００７５长沙４）１００学院
３）（中南大学信息科学与工程学院计算机科学与技术博士后流动站
摘要三部图作为社会标签系统的表示方法，虽然可以简化标签系统元素间关系的表达，但也丢失了部分元素而且不能有效处理标签系统中具有大量稀疏值和缺失值的数据．基于以上问题，文中提出了基于三间的相关信息，部图的三维张量分解推荐算法（首先分析三部图元素间可能丢失的信息，通过定义以三部图为基础的ＴＴＤ算法）．对高阶稀疏数据进行分析．该模型不仅包含三部图所表达的系统信息，同时还表达了三部图所低阶张量分解模型，丢失的元素间相互信息；在此基础上，利用缺失值处理，进行社会标签系统中的标签推荐预测．通过模型对比实验以及标签预测实验，表明Ｔ同时在进行标签预测ＴＤ模型所揭示的社会标签系统中元素间的相互关系更加全面，时，所得到的预测结果召回率和精确率得到了显著改善．；关键词三部图；张量分解三部图模型（标签预测；社会标签系统ＴＴＤ）／中图法分类号ＴＰ３９１ＤＯＩ号：１０．３７２４ＳＰ．Ｊ．１０１６．２０１２．０２６２５

融合知识图谱表示学习和矩阵分解的推荐算法

*+,-./0-)^.0.L_=NA=]J.ML=4.<L.P5KKGJ5KO.<J=K.44=1%5N/.15L>.J/NA4M50=%.145NJ/6<5KN.J/T5N/.1$5J=K.44=1%5N/.1 5L>.J/NA4/1K.J].J5N/1>J=]J=0=1N5N/.1L=5J1/1>.<[1.PRL=%>=>J5]AP/NA45NJ/6<5KN.J/T5N/.1P50]J=0=1N=%H^A=J=]J=0=1N5N/.1 L=5J1/1>.<[1.PL=%>=>J5]AP50GN/L/T=%N.]J.a=KNM.NA=1N/N/=051%J=L5N/.10/1N.5L.PR%/4=10/.15L0=451N/K0]5K=$NA=[1.PR L=%>=/1<.J45N/.1.<=1N/N/=051%45NJ/6<5KN.J/T5N/.1P50K.4M/1=%MOK5LKGL5N/1>NA=0=451N/K0/4/L5J/NOM=NP==1=1N/N/=0H^A= 0A.JNK.4/1>.<45NJ/6<5KN.J/T5N/.1NA5N/N<5/L0N.K.10/%=JNA=[1.PL=%>=/1<.J45N/.1.</N=40/0._=JK.4=51%NA==<<=KN.<45R NJ/6<5KN.J/T5N/.1J=0GLN/0/4]J._=%.1NA=[1.PL=%>=L=_=LHC6]=J/4=1N5LJ=0GLN0.1 \._/=9=10%5N50=N%=4.10NJ5N=NA5NNA= ]J.].0=%5L>.J/NA4A50M=NN=JJ=K.44=1%5N/.15KKGJ5KOH 1234(.',)J=K.44=1%5N/.15L>.J/NA4#K.LL5M.J5N/_=</LN=J/1>#45NJ/6<5KN.J/T5N/.1#[1.PL=%>=>J5]A#J=]J=0=1N5N/.1L=5J1/1>

基于用户近邻的N维张量分解推荐算法

基于用户近邻的N维张量分解推荐算法陈健美;孙亚军【摘要】Recommendation algorithm based on tensor factorization has low accuracy and data sparseness problem.Therefore,on the basic of the traditional tensor decomposition model,this paper introduces the user nearest neighbor information,and proposes N dimensional tensor decomposition ing context aware information,it uses implicit feedback information as the third dimension to establish N dimensional tensor decomposition model.To further improve the the quality of recommendation,it adds the user nearest neighbor information to optimize the N dimensional tensor decomposition model to improve the accuracy of the tensor decomposition recommendationalgorithm.Experimental results show that the tensor decomposition recommendation algorithm combined with user nearest neighbor has better accuracy than the traditional tensor decomposition algorithm,can effectively solve the sparsity and accuracy problems.%基于张量分解的推荐算法存在推荐精度较低和数据稀疏的问题.为此,在传统的张量分解模型基础上,引入用户近邻信息,提出一种新的N维张量分解算法.利用上下文感知信息,把隐式反馈信息作为张量的第3维度,以建立N维张量分解模型,为进一步提高推荐质量,加入用户近邻信息来优化N维张量分解模型,以提高张量分解推荐算法的准确率.实验结果表明,融合用户近邻的张量分解推荐算法比传统的张量分解算法具有更好的准确性,能有效解决稀疏性和准确性问题.【期刊名称】《计算机工程》【年(卷),期】2017(043)011【总页数】5页(P193-197)【关键词】协同过滤算法;反馈信息;主成分分析;张量分解;推荐算法【作者】陈健美;孙亚军【作者单位】江苏大学计算机科学与通信工程学院,江苏镇江212013;江苏大学计算机科学与通信工程学院,江苏镇江212013【正文语种】中文【中图分类】TP391随着互联网技术的飞速发展,信息量过载大的问题受到广泛关注,用户购买所需物品困难越来越大,推荐系统应运而生[1]。

张量分解及其在推荐系统中的应用

张量分解及其在推荐系统中的应用代翔（中国西南电子技术研究所，四川成都 610036）摘　要：在异构信息网络下往往会产生纷繁复杂的数据，这些数据常用一种被称为张量的新的形式来表示。

但是由于这些数据中缺失值较多，存在一定的稀疏性，因此需要对张量进行分解，恢复缺失值，找出多元数据之间潜在的关系。

张量分解是推荐系统中一种重要的方法,在推荐系统中应用张量分解，可以挖掘出潜在关系，给用户带来更好的推荐体验。

笔者以数据挖掘为引，研究了张量分解及其在推荐系统中的应用，并根据当下的研究热点问题提出了未来张量分解在推荐领域的应用方向和发展趋势。

关键词：数据挖掘；异构信息网络；张量分解；矩阵分解；推荐系统中图分类号：TP391 文献标识码：A 文章编号：1003-9767（2016）22-034-04１　引言在这个信息网络高度发达的时代，各个领域时刻都会产生大量的、纷繁复杂的数据，而这些数据之间往往呈现一些潜在的联系，数据挖掘领域就是为了挖掘这些数据之间的联系。

数据是伴随许多对象而产生的，把这些不同的对象抽象为图上一个个节点，对象之间用线连接起来，则构成了相互连接的网络。

网络下产生的数据用张量来表示，由于数据往往是稀疏的，为了解释数据之间联系，需要对张量进行分解。

张量分解最常用的分解方法是CP分解和Tucker分解，当然还有很多其他分解的方法，如INDSCAL[1]、PARAFAC2[2]、CANDELINC[3]、DEDICOM[4]和PARATUCK2[5-6]等。

张量分解后会产生一些潜在的因子，通过分析这些潜在的因子，就可以得出分解前数据之间的关联程度，即找出数据间内在的联系。

推荐系统就是针对蕴含着多源异构信息的复杂网络来向用户推荐所需物品的一个研究领域。

推荐系统是“利用电子商务网站向客户提供商品信息和建议，帮助用户决定应该购买什么产品，模拟销售人员帮助客户完成购买过程”[7]。

可以理解为推荐系统就是向用户推荐商品、电影、饮食、旅游地点等一些生活信息的系统，这些推荐信息可能是用户潜在感兴趣的，或者是用户可能需要的。

2018融合社交信息的矩阵分解推荐方法研究综述

2018融合社交信息的矩阵分解推荐⽅法研究综述1 社交信息与推荐的关联性传统的推荐⽅法假定⽤户相互独⽴，忽略了⽤户之间的相互作⽤。

⽽现实⽣活中，⼈们在做决策是往往会向朋友寻求建议，进⽽⼀定程度上影响⽤户的选择。

因此，考虑到⽤户之间的相互影响，引⼊社交信息来拓展传统的推荐模型，提出了⼀系列的社交推荐模型【26-43】。

相⽐于传统的推荐⽅法，社交推荐⽅法的优点：（1）推荐精度⾼。

（2）有效的解决冷启动问题。

社交信息的引⼊，为⽤户提供了额外的偏好信息。

（3）推荐结果受⽤户信赖。

因为很多好友都喜欢这个物品。

社交推荐模型分类：基于矩阵分解的社交推荐模型【26-41】优点：推荐精度⾼、可扩展性好、灵活性⾼等，成为主流社交推荐⽅法。

基于近邻的社交推荐模型【42】基于图的社交推荐模型【43，44】2 基本的矩阵分解模型2.1 Funk-SVD算法优化模型：求解上述模型的⽅法：基于梯度下降的批量梯度下降法（BGD）随机梯度下降算法（SGD）2.2 概率矩阵分解基本思路：假设⽤户U和⽤户V的特征矩阵均服从⾼斯分布，过评分矩阵已经知道的值，得到U和V特征矩阵，然后⽤特征矩阵去预测评分矩阵中的未知值。

3 融合社交信息的矩阵分解模型基于矩阵分解的社交推荐模型发展轨迹融合社交信息的推荐模型分为两类：（1）基于⽤户特征矩阵共享表⽰的【26，30-34】（2）基于⽤户特征矩阵重表⽰的【27-29，33，35-37，39】社交关系矩阵：连接关系：若⽤户i与⽤户k具有社交关系，则Sik=1，否则为0余弦相似度：通过余弦相似度计算得到⽤户社交关系强度3.1 ⽤户特征矩阵共享表⽰基本思路：假定⽤户特征矩阵Ui是评分矩阵和社交关系矩阵共享的模型：历史⾏为信息+社交信息+正则约束项3.2 ⽤户特征矩阵重表⽰基本思路：利⽤社交关系对⽤户特征矩阵Ui进⾏重表⽰模型：对U进⾏重置+限定与好友近似相等+正则约束项3.3 算法复杂度分析4 社交推荐算法评估共8+1个算法基于⽤户特征矩阵共享表⽰：SoRec[26] TrustMF[31] LOCABAL[30]基于⽤户矩阵重表⽰（直接社交关系）：SoReg[29] SocialMF[28] TrustSVD[33]基于⽤户矩阵重表⽰（间接社交关系）：MFC[36] SoDimRec[37]未利⽤社交关系的推荐模型算法：PMF[10,47]都对原评分值进⾏预处理，使其数值⼤⼩映射到[0,1]区间。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

融合朋友关系和标签信息的张量分解推荐算法
丁小焕 ’ ，彭甫镕，王琼，陆建峰
（南京理工大学计算机科学与工程学院，南京２１００９４）
（通信作者电子邮箱ｘｉａｏｈｕａｎ８４９＠ｓｉｎａ．ｃｏｍ）
Ａｂｓｔｒａｃｔ：Ｔｈｅｉｔｅｍｒｅｃｏｍｍｅｎｄａｔｉｏｎｐｒｅｃｉｓｉｏｎｏｆｓｏｃｉａｌｔａｇｇｉｎｇｒｅｃｏｍｍｅｎｄａｔｉｏｎｓｙｓｔｅｍｗａｓａｆｆｅｃｔｅｄｂｙｓｐａｒｓｅｄａｔａｍａｔｉｒｘ．Ａｔｅｎｓｏｒｆａｃｔｏｒｉｚａｔｉｏｎｒｅｃｏｍｍｅｎｄａｔｉｏｎｌｇａｏｉｔｒｈｍｃｏｍｂｉｎｅｄｗｉｔｈｓｏｃｉｌａｎｅｔｗｏｒｋａｎｄｔａｇｉｎｆｏｒｍａｔｉｏｎｗａｓｐｒｏｐｏｓｅｄ，ｉｎ
文章编号：１００１ — ９０８１（２０１５）０７ — １９７９ — ０５
ＣＯＤＥＮＪＹＩＩＤＵ
ｈｔｔｐ：／／ｗｗｗ．ｊｏｃａ．ｃｎ
ｄｏｉ：１０．１ห้องสมุดไป่ตู้１７７２／ｊ．ｉｓｓｎ．１００１ — ９０８１．２０１５．０７．１９７９
（ＨＯＳＶＤ）ｗａｓｕｓｅｄｆｏｒｌａｔｅｎｔｓｅｍａｎｔｉｃａｎａｌｙｓｉｓａｎｄｍｕｌｔｉ－ｄｉｍｅｎｓｉｏｎｌａｒｅｄｕｃｔｉｏｎ．Ｔｈｅｕｓｅｒ－ｐｒｏｊｅｃｔ－ｔａｇｔｉｒｐｌｅｉｎｆｏｒｍａｔｉｏｎｃｏｕｌｄ
ｆｉｒｅｎｄｓ ’ｉｆｏｎｍａｒｔｉｏｎｃｏｕｌｄｒｅｌｆｅｃｔｐｅｒｓｏｎｌｉａｎｔｅｒｅｓｔｓａｎｄｈｏｂｂｉｅｓ．Ｆｉｓｔｒｌｙ，Ｈｉｇｈｅｒ — ＯｒｄｅｒＳｉｎｇｕｌｒＶａａｌｕｅＤｅｃｏｍｐｏｓｉｔｉｏｎ
的方法比较，在推荐的召回率和精确度指标上分别提高了２．５％和４％，因此，所提算法进一步验证了结合朋友关系能够提高推荐的准确率，并扩展了张量分解模型，实现用户个性化推荐。关键词：张量分解；高阶奇异值分解；朋友关系；标签；推荐
中图分类号：ＴＰ３１ｌ；ＴＰ３９１．１文献标志码：Ａ
Ｔｅｎｓｏｒｆａｃｔｏｒｉｚａｔｉｏｎｒｅｃｏｍｍｅｎｄａｔｉｏｎａｌｇｏｒｉｔｈｍｃｏｍｂｉｎｅｄｗｉｔｈｓｏｃｉｌａｎｅｔｗｏｒｋａｎｄｔａｇｉｎｆｏｒｍａｉｏｔｎ
摘
要：针对大众标注网站项目推荐系统中存在数据矩阵稀疏性影响推荐效果的问题，考虑矩阵奇异值分解
（ＳＶＤ）能有效地平滑数据矩阵中的数据，以及朋友圈能够反映出一个人的兴趣爱好，提出了一种融合朋友关系和标签信息的张量分解推荐算法。首先，利用高阶奇异值分解（ＨＯＳＶＤ）方法对用户一项目一标签三元组信息进行潜在语义分析和多路降维，分析用户、项目、标签三者间关系；然后，再结合用户朋友关系、朋友间相似度，修正张量分解结果，建立三阶张量模型，从而实现推荐。该模型方法在两个真实数据集上进行了实验，结果表明，所提算法与高阶奇异值分解
ｃｏｎｓｉｄｅｒａｔｉｏｎｏｆｔｈａｔＳｉｎｇｕｌａｒＶｌｕａｅＤｅｃｏｍｐｏｓｉｔｉｏｎ（ＳＶＤ）ｈａｄｇｏｏｄｐｒｏｃｅｓｓｉｎｇｐｒｏｐｅｒｔｉｅｓｔｏｄｅｌａｗｉｔｈｓｐａｒｓｅｍａｔｉｒｘ，ａｎｄｔｈａｔ
ＤＩＮＧＸｉａｏｈｕａｎ，ＰＥＮＧＦｕｒｏｎｇ，ＷＡＮＧＱｉｏｎｇ，ＬＵＪｉａｎｆｅｎｇ
（ＳｃｈｏｏｌｏｆＣｏｍｐｕｔｅｒＳｃｉｅｎｃｅａｎｄＥｎｇｉｎｅｅｒｉｎｇ，ＮａｎｊｉｎｇＵｎｉｖｅｒｓｉｔｙｏｆＳｃｉｅｃｅｎａｎｄＴｅｃｈｎｏｌｏｇｙ，ＮａｎｇＪｉａｎｇｓｕ２１００９４，Ｃｈｉｎａ）
ＪｏｕｒｎａｌｏｆＣｏｍｐｕｔｅｒＡｐｐｌｉｃａｔｉｏｎｓ
ＩＳＳＮ１００１．９０８ｌ
２０１５．．０７．．１０
计算机应用，２０１５，３５（７）：１９７９—１９８３