第五章根轨迹分析法主编修改版
自动控制理论

首页 上页 下页 末页 结束
电气与新能源学院
2019/12/16
5
如何找我?
刘平,男
Qq: 22478844
自
动 控
电话:
,13872464572(移动)
制 理
办公地点:电气实验楼2楼201-3房间,即
论 D201-3。
时间:白天没课的时候随时都行。
首页 上页 下页 末页 结束
电气与新能源学院
第一章第一章绪论绪论第二章第二章控制系统的数学模型控制系统的数学模型第三章第三章控制系统的时域分析控制系统的时域分析第四章第四章根轨迹法根轨迹法第五章第五章频率分析法频率分析法第六章第六章控制系统的综合校正控制系统的综合校正第七章第七章pidpid控制与鲁棒控制控制与鲁棒控制第八章第八章离散控制系统离散控制系统第九章第九章状态空间分析法状态空间分析法444电气与新能源学院首页上页下页201920192019121212303030教材及参考书1自动控制理论邹伯敏主编机械出版社2自动控制原理蒋大明著华南理工大学出版社1992年版5自动控制原理梅晓榕主编科学出版社6自动控制理论文锋编著中国电力出版社1998年版555电气与新能源学院首页上页下页201920192019121212303030考核方式
动 统和状态空间分析等。
控
制
具体来说,包括以下几个章节:
理
论 第一章 绪论
第二章 控制系统的数学模型
第三章 控制系统的时域分析
第四章 根轨迹法
第五章 频率分析法
首页
上页 第六章 控制系统的综合校正
下页 第七章 PID控制与鲁棒控制
末页
结束 第八章 离散控制系统
第九章 状态空间分析法
电气与新能源学院Байду номын сангаас
第5章 根轨迹法

(2-50)
5.1 基本反馈系统的根轨迹
A K G (s ) s( s c) s( s 1)
取K=A,c=1
单位反馈系统的闭环传递函数为:
K K s( s 1) T (s ) 2 K s sK 1 s( s 1)
System: sysL Gain: 0 Pole: -4 - 4i Damping: 0.707 Overshoot (%): 4.32 Frequency (rad/s): 5.66
-5
Real Axis (seconds-1)
0
5
规则4:出射角与入射角
根轨迹离开开环复极点处的切线方向与实轴 正方向的夹角称为出射角, 进入开环复零点处的 切线方向与实轴正方向的夹角称为入射角。
K为根轨迹参数。
3、根轨迹方程
1 KL( s) 0
L(s)的形式是有理分式,分子和分母都是首一多项式。
b( s ) s m b1s m 1 bm ( s z1 )( s z2 ) ( s zm ) L( s ) n n 1 a ( s ) s a1s an ( s p1 )( s p2 ) ( s pn ) ( s zi ) ( s pi )
i 1 n i 1
(s z )
i
m
( s zi )
m
在k=0时, 根轨迹方程的解为s=pi(i=1, 2, ..., n) ,闭环极点与开环极点相等,即根轨迹起始于开环极点 。 当k→∞时, 根轨迹方程的解为s=zi(i=1, 2, …, m)或s→∞ 。
s=zi: 闭环极点与开环零点重合。
自动控制原理(程鹏)

高等教育出版社 高等教育电子音像出版社
1
版权信息: 版权所有属于高等教育出版社和作者
2
序 言
本《自动控制原理多媒体教学课件 》是根据程鹏主编的 《自动控制原理》 (第二版)一书而编辑的,使用PowerPoint2000 下编辑而成,故建议在Office2000及Mathtype5.1环境中进行浏 览和修改。 本文稿基本涵盖了教材各章节的主要知识点。可作为使用 该教材的教师课堂演示文稿的蓝本,以省去教师对文字、公式 和插图等的录入时间,可以让教师们把更多的精力去考虑教学 内容的编排以及课堂教学的组织等更重要的问题,还可为自学本 书的读者提供一个课堂教学的主要线索,因此在文稿中还选编 了一些基本内容和方法的提示和总结,期望对读者理解本书的 内容有所帮助。出版这个多媒体课件可以说是抛砖引玉,期望
55目录第1章自动控制原理的一般概念第2章自动控制系统的数学模型第3章时域分析法第7章非线性系统分析第4章根轨迹法第5章频域分析法第6章控制系统的校正第8章采样系统理论第9章状态空间分析方法66目录使用说明双击选定章节就可进入相应章节的目录您会看到各章的基本要求和具体章节点击便可进入具体小章节由于是使用不同章节间的超级链接请在复制时将所有章节复制在同一个文件中链接速度可能会稍慢请耐心等待
7
文稿中,各章节标题均用隶书40pt字,每节中二级标题用楷 文稿中,各章节标题均用隶书40pt字,每节中二级标题用楷 体36pt字。对于定义、定理均用蓝色加粗标明。在文字描述 36pt字。对于定义、定理均用蓝色加粗标明。在文字描述 中,彩色加粗的文字均为关键字。在装有M 中,彩色加粗的文字均为关键字。在装有Mathtype5.1的前提 下,对公式的编辑可通过双击公式进入公式编辑器进行修改 ,单击公式,可随意拉动以调整公式显示的大小和位置。
根轨迹分析法

根据上述方程,采用前述 的绘制根轨迹的方法可得系统 的根轨迹。
与虚轴的两个交点。
(T 0)
p1
p1
j
(Tc 1) j1
[s]
0T
(T )
z3
60
-1
120
z1(T )
-0.5 0 z2 (T )
p2
p2
(T 0)
图示系统的根轨迹图
j1 (Tc 1)
最后绘制出以时间常数T为可变参数的根轨迹图如图
4-14所示。由根轨迹图可知,时间常数
秒时,
根轨迹分析法
▪ 开环传递函数的两 种表达式
m
K(is 1)
G(s)H(s)
i 1 n
(Tjs 1)
j 1
m
G(s)H (s)
K*
n
(s
i 1
(s
zi ) pj)
K *B(s) A(s)
j 1
m
Hale Waihona Puke K * ziKi 1 n
pj
j 1
(n m)
1. 参数根轨迹
前面介绍的普通根轨迹或一般根轨迹的绘制规则
与绘制普通根轨迹的开环传递函数有相同的形式,即
2. 多回路系统的根轨迹
对多回路系统而言,需先作内环根轨迹,再用
幅值条件求出内环的闭环极点,进而作为外环的部
分开环极点,再画出外环的根轨迹。
例 试绘制
以 Kc为参变量的 根轨迹。
解 ⑴内环的
根轨迹
内环开环传递函数为 G(s)
K
,其根轨
迹同前。
s(s 1)(s 2)
规则5¹根轨迹的n m 条渐近线与实轴的相角为
180 (2k)
第五章根轨迹法

s平面上的分布,用作图的方法求得闭环传递函数在s平面内随开
环传递函数的某个参数变化而变化的轨迹。
5.1.1根轨迹
开环系统(传递函数)的某一个参数从零变化到 无穷大时,闭环系统特征方程的根在 s 平面上随之连 续变化而形成的轨迹称为根轨迹。
若闭环系统不存在零点与极点相消,闭环特征方程 的根与闭环传递函数的极点是一一对应的。
为了用图解法确定所有闭环极点,令闭环传递函数表达式 分母为零,得特征方程(根轨迹方程)为:
Ds 1 G(s)H (s) 0
m
(s zj)
其中: GsH s K*
j1 n
(s pi )
i1
K*为前向通路根轨迹增益,从0→∞
Zj 为开环传函零点 pi为开环传函极点
m
(s zj)
Ds 1 K*
①无论k怎样变化,“х”均位于虚轴左侧,系统是稳定 的
② 0<k<1 系统特征根为实根,系统处于过阻尼状态 ③ k=1 ,闭环两个实数极点重合,系统处于临界阻尼
状态
④ k>1,闭环极点为共轭复数极点,系统处于欠阻尼状 态
5.1.2 根轨迹方程
根轨迹是系统所有闭环极点的集合。
(s) G(s) 1 G(s)H (s)
规则3:根轨迹渐近线 当开环有限极点数n大于有限零点数m时,有n-m条根轨迹分支沿着
与实轴交角为 a ,交点为 a 的一组渐进线趋于无穷远处,且有
5.2 根轨迹绘制的基本法则
5.2.1绘制根轨迹的一般法则
规则1:根轨迹的起点和终点:
根轨迹起始于开环极点,终止于开环零点。
简要证明: ①起点
n
m
《根轨迹分析法》课件

《根轨迹分析法》课件1. 课件简介根轨迹分析法是一种用于分析和设计反馈控制系统的方法,通过绘制系统的根轨迹来了解系统在不同参数下的稳定性和动态性能。
本课件将介绍根轨迹分析法的基本概念、方法和应用。
2. 课件内容2.1 根轨迹分析法的基本概念2.1.1 根轨迹的定义根轨迹是指在系统参数变化范围内,使闭环系统稳定的闭环极点轨迹。
2.1.2 根轨迹的性质(1)根轨迹是闭环极点在复平面上的轨迹,反映了闭环系统的稳定性。
(2)根轨迹的形状由系统开环传递函数的极点和零点决定。
(3)根轨迹的分布与系统参数有关,通过改变参数可以改变系统的稳定性和动态性能。
2.2 根轨迹分析法的方法2.2.1 绘制根轨迹的基本步骤(1)确定系统开环传递函数。
(2)画出开环传递函数的极点和零点。
(3)根据系统参数的变化,绘制出根轨迹。
(4)分析根轨迹的形状,判断闭环系统的稳定性。
2.2.2 根轨迹的绘制技巧(1)利用软件工具,如MATLAB,自动绘制根轨迹。
(2)手动绘制根轨迹时,注意利用对称性和周期性简化绘制过程。
2.3 根轨迹分析法的应用2.3.1 设计控制器通过分析根轨迹,可以确定控制器参数,使闭环系统具有所需的稳定性和动态性能。
2.3.2 系统优化根轨迹分析法可以帮助我们找到系统参数的最佳组合,从而优化系统的性能。
2.3.3 故障诊断分析根轨迹可以帮助我们发现系统中的故障,为故障诊断提供依据。
3. 课件总结本课件介绍了根轨迹分析法的基本概念、方法和应用。
通过学习本课件,您可以了解根轨迹分析法在控制系统设计和分析中的重要性,并掌握绘制根轨迹的基本方法。
希望这有助于您在实际工作中更好地应用根轨迹分析法。
科学性:1. 内容准确:课件内容基于控制理论的基本原理,准确地介绍了根轨迹分析法的概念、方法和应用。
2. 逻辑清晰:课件从基本概念入手,逐步深入到方法介绍和应用实例,逻辑结构清晰,易于理解。
3. 实例典型:课件中提供了控制系统的实例,帮助学习者更好地理解根轨迹分析法的应用场景。
第五章 根轨迹设计方法
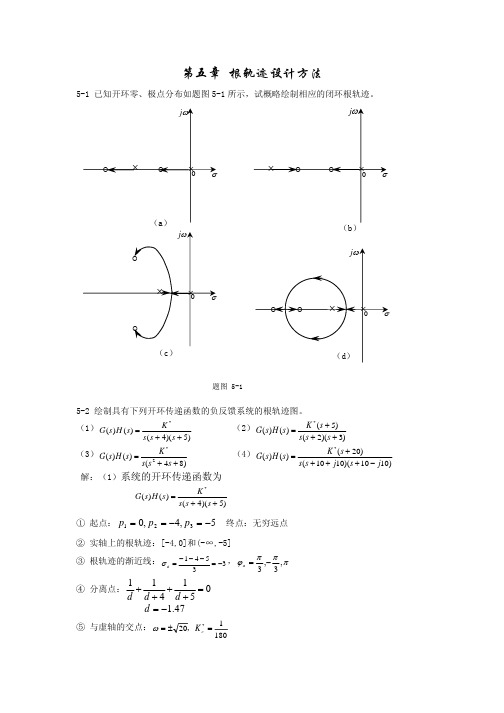
第五章 根轨迹设计方法5-1 已知开环零、极点分布如题图5-1所示,试概略绘制相应的闭环根轨迹。
5-2 绘制具有下列开环传递函数的负反馈系统的根轨迹图。
(1))5)(4()()(*++=s s s K s H s G (2))3)(2()5()()(*+++=s s s s K s H s G (3))84()()(2*++=s s s K s H s G (4))1010)(1010()20()()(*j s j s s s K s H s G −++++=解:(1)系统的开环传递函数为)5)(4()()(*++=s s s K s H s G ① 起点:5,4,0321−=−==p p p 终点:无穷远点 ② 实轴上的根轨迹:[-4,0]和(-∞,-5]③ 根轨迹的渐近线:33541−=−−−=a σ,πππϕ,3,3−=a④ 分离点:111045++=++d d d 47.1−=d⑤ 与虚轴的交点:180120*=±=c K ,ω题图 5-1 (a) ωj σ0××o o (b)ωj σ0××o o(c) 0ωj σ××oo绘制根轨迹如下:(2)系统的开环传递函数为 *(5)()(2)(3)K s G s s s s +=++ ① 起点:3,2,0321−=−==p p p 终点:,51−=z 两个无穷远点 ② 实轴上的根轨迹:[-2,0]和[-3,-5]③ 根轨迹的渐近线:02532=+−−=a σ,2πϕ±=a④ 根轨迹的分离点:根轨迹的分离点坐标满足1111235d d d d ++=+++ 通过试凑可得 10.89d =−。
根据以上几点,可以画出概略根轨迹图如下所示:(3)系统的开环传递函数为)84()()(2*++=s s s K s H s G ① 起点:22,22,0321j p j p p −−=+−== 终点:无穷远点 ② 实轴上的根轨迹:(-∞,0]③ 根轨迹的渐近线:02532=+−−=a σ,2πϕ±=a根据以上几点,可以画出概略根轨迹图如下所示:(4)系统的开环传递函数为)1010)(1010()20()()(*j s j s s s K s H s G −++++=① 起点:1231010,1010,0p j p j p =−−=−+= 终点:120z =−,两个无穷远点 ② 根轨迹起始角111213121212321801804590135018018045902250=+−−=+−−==+−−=−+−=o o o o o o oooooop z p p p p p p z p p p p p θϕθθθϕθθ仿真图如下:5-3已知单位负反馈系统的开环传递函数为)22)(1()()(2+++=s s Ts s K s H s G试绘制当4=K 时,以T 为参变量的根轨迹。
第五章 根轨迹设计方法

控制工程基础根轨迹法是一种图解方法,它是古典控制理论中对系统进行分析和综合的基本方法之一。
由于根轨迹图直观地描述了系统特征方程的根(即系统的闭环极点)在s平面上的分布,因此,用根轨迹法分析自动控制系统十分方便,特别是对于高阶系统和多回路系统,应用根轨迹法比用其他方法更为方便,因此在工程实践中获得了广泛应用。
本章主要介绍根轨迹的概念,绘制根轨迹的基本规则和用根轨迹法分析自动控制系统的性能的方法。
控制工程基础主要内容第一节根轨迹的基本概念第二节绘制根轨迹的基本规则第三节广义根轨迹第四节利用根轨迹分析系统的性能控制工程基础第一节根轨迹的基本概念根轨迹图是闭环系统特征方程的根(即闭环极点)随开环系统某一参数由零变化到无穷大时在s平面上的变化轨迹。
一﹑根轨迹(图)例1 已知一单位负反馈系统的开环传递函数为试分析该系统的特征方程的根随系统参数的变化在s平面上的分布情况。
(s)()(0.51)KG H ss s=+K开环极点10,p=22p=-没有零点。
式中为开环增益。
K控制工程基础解系统的闭环传递函数(s)()1(s)(s)GsG Hφ=+2222Ks s K=++系统的特征方程为2()220D S s s K=++=特征方程的根是1211 , 11s K s K=-+-=---120,2s s==-当时,K=当时,01K<<为不相等的两个负实根;12s s,当时,1K=为等实根;121s s==-设的变化范围是K[)0,∞当时,1K<<∞1,211s j K=-±-为一对共轭复根控制工程基础σjω1-2-3-1⨯⨯(0)K=(0)K=(1)K=()K→∞()K→∞图5-1-1 例1的根轨迹控制工程基础当系统参数为某一确定的值时,闭环系统特征方程的根在S平面上变化的位臵便可确定,由此可进一步分析系统的性能。
值的变化对闭环系统特征方程的影响可在根轨迹上直观地看到,因此系统参数对系统性能的影响也一目了然。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Kg
j
j3 j2
K g 13
Kg 8
Y (s )
Kg 0
5
4
Kg 5
3
j
Kg 4
2 1
Kg 0
0
j
Kg 5
Kg K GL ( s) , (5 - 3) s(0.25s 1) s( s 4) K为 开 环 放 大 系 数 ; g 为 根 轨 迹 增 益 。 K
Kg Y ( s) T ( s) 2 R( s ) s 4s K g (5 - 4)
y (t )
Kg 8
K g 13
Kg
j2 j3
K g 13
Kg 8
1
Kg 5 Kg 4
特征方程: 2 4 s K g 0 (5 - 5) s
闭环特征根:1, 2 s
n 1
pl
l 1
Kg s
n m
s
n m
( n m ) s
n m 1
n m
(5 - 17)
制作-罗家祥 审校-胥布工
5.3 绘制根轨迹的一般方法
j
由比较(5-17)分母多项式系数可得
( n m ) pl z i
DL ( s ) K g N L ( s ) 0 DL ( s ) ( s pl ) 0; K g ( s z i ) 0
l 1 i 1
m m m s (1 ( s zi ) i 1 l i m in 1 lim n s n s ( s p ) s (1 l l 1 l 1 1 lim K g K 0 g
制作-罗家祥 审校-胥布工
5.2 根轨迹的基本概念
5.2.1 根轨迹图 根轨迹的研究是在一个复平面(简称s平面)上展开的, 这时的复平面就叫根平面。当系统开环传递函数的某一参数 从0变化到无穷时,系统的闭环特征根在根平面上变化的轨迹 就称为根轨迹。根平面加上根轨迹就叫根轨迹图。 根轨迹常用于研究开环传递函数增益变化对系统的影响, 因此,从0变化到无穷的某个参数通常是指与开环传递函数 放大系数K成正比的一个参数Kg,一般称为根轨迹增益。
制作:罗家祥 审校:胥布工
第五章 根轨迹分析法
版本2.0 2011年6月主编修改版
华南理工大学 自动化科学与工程学院
制作-罗家祥 审校-胥布工
第五章 根轨迹分析法
5.1 引言
5.2 根轨迹的基本概念
5.3 绘制根轨迹的一般方法
5.4 根轨迹法的扩展应用
5.5 开环零、极点对系统根轨迹的影响 5.6 利用MATLAB分析控制系统的根轨迹 5.7 小结
l 1
m
n
注意到式(5-14)中有 k=0, 1, 2,…,
制作-罗家祥 审校-胥布工
5.3 绘制根轨迹的一般方法
故推得n-m个渐近线与实轴的夹角为 (1)渐近线与实轴的夹角
180 360 k , k 0, 1, 2, (5 - 15) nm 180 360 ( l 1) , l 0, 1, 2, n m 1 (5 - 16) nm
(5 - 1)
由式(5-1)得与之间的关系为
Kg K
l v 1 m i 1
pl
(5 - 2)
n
zi
式(5-2)意味着与之间的关系与零值的开环极点无关,同理 也与零值的开环零点无关。
制作-罗家祥 审校-胥布工
5.2 根轨迹的基本概念
例5-1
R(s )
K s (0.25s 1)
0
Kg
j
j3 j2
K g 13
Kg 8 Kg 5
3
j
Kg 0
5
4
Kg 4
2 1
Kg 0
0
j
Kg 5 Kg 8
K g 13
Kg
j2 j3
y (t )
K g 13
Kg 8
1
Kg 5 Kg 4
t
制作-罗家祥 审校-胥布工
制作-罗家祥 审校-胥布工
5.2 根轨迹的基本概念
1、幅值条件
2、相角条件
m n i 1 i l 1 l
Kg
m
l 1
m i
i 1 n
s zi s pl
n
1
(5 - 11)
( s z ) ( s p )
i 1 l 1
l
180 360 k , k 0, 1, 2, (5 - 12)
(2)渐近线在实轴上交点
K g in 1 l 1
s zi
m
s zi s
m
m
m 1
s pl
Kg
i 1
zi
i 1 n
m
s pl s
n l 1
n
s Kg
n m
Kg ( pl z i ) s n m 1
l 1 i 1 n m
n
m
zi ) n m 1 s l i m 0 pl s s ) s
( 5 13)
制作-罗家祥 审校-胥布工
5.3 绘制根轨迹的一般方法
p1 z2
j
1 2
3 0
p3
s0
1 2 3 180
z1
0
2 1
z3
2 1
p2
规则5 实轴上的根轨迹 实轴上的根轨迹在奇数个零点和极点的左侧。 规则6 根轨迹的渐近线 Kg→∞时, 有n-m条根轨迹分支沿着与正实轴夾角, 截距为的一组渐近线趋于无穷远处。
i 1
i l (n m ) 180 360 k , k 0, 1, 2, (5 - 14)
4 16 4 K g 2
0
t
2 4 K g
(5 - 5)
制作-罗家祥 审校-胥布工
5.2 根轨迹的基本概念
Kg>0,系统闭环特征根始终在根平 面的左半部,系统总是稳定的。 0<Kg<4,两个互不相等的负实数, 系统阶跃响应为单调上升的非周期 过程。 Kg=4,两个相等的负实数,系统阶 跃响应为单调上升的非周期过程。 Kg>4,两个共轭复根,系统的阶跃 响应变为衰减振荡过程,Kg越大, 振荡越剧烈。 Kg的取值不同,系统特征根在s平面 的分布不同,系统具有不同的动态 特性。
Kg
(s) DL ( s ) K g N L ( s ) 0 (5 - 9)
K g 13
j3 j2
规则1 根轨迹的连续性 闭环特征方程根是根轨迹增益Kg的 连续函数;根轨迹是连续的直线或曲 线。 规则2 根轨迹的分支数 =特征根个数=系统阶数n。
Kg 8 Kg 5
3
通常,直接利用幅值条件和相角条件绘制系统的根轨 迹很复杂,可以尝试先画出近似的根轨迹曲线,进行 初步分析后,再细化和修正用计算机求解或者绘制出 精确的根轨迹。
制作-罗家祥 审校-胥布工
5.3 绘制根轨迹的一般方法
5.3.1 绘制根轨迹的基本法则 根轨迹法是通用的方法,可以用于绘制线性多项式中 任何参数的根轨迹。本节以根轨迹增益Kg为参数归纳出绘 制根轨迹的基本法则。 j
特征方程:1 G L ( s ) 0 (5 - 8) 或
N L ( s) DL ( s ) (5 - 7)
DL ( s ) K g N L ( s ) 0 (5 - 9)
GL ( s) K g
(s z ) (s p )
l 1 l i 1 n i
m
N L ( s) Kg 1 (5 - 10) DL ( s )
l 1 i 1 n m
j4 j3
(5 - 18)
180
4
j2
60
j
渐近线与实轴的交点:
3
( p ) ( z )
l 1 l i 1 i
n
m
7 3
60
0
j
j2
nm
(5 - 19)
j3 j4
制作-罗家祥 审校-胥布工
5.3 绘制根轨迹的一般方法
规定相角以逆时针方向为正, 顺时针方向为负。
s zi
s
j
s pl 1
l1
pl1
x y
s pl 2
x
x y
zi
i
0
y
pl 2
l2
制作-罗家祥 审校-胥布工
5.2 根轨迹的基本概念
注意事项:
幅值条件仅是根轨迹应满足的必要条件,因为幅值还取 决于Kg的大小。在根轨迹上的点都满足幅值条件,而s 平面上满足幅值条件的点未必在根轨迹上。 相角条件是根轨迹应满足的充要条件,因为相角大小与 Kg的大小无关。在根轨迹上的点都满足相角条件,而s 平面上满足相角条件的点一定在根轨迹上。 由于绘制根轨迹的目的是通过图上向量计算来进行系统 的性能分析,因此s平面的横坐标和纵坐标必须采用相 同的比例尺。
j
Kg 0
5
4
Kg 4
2 1
Kg 0
0
j
Kg 5 Kg 8
K g 13
Kg
j2 j3
制作-罗家祥 审校-胥布工
5.3 绘制根轨迹的一般方法
规则3 根轨迹的对称性 实系数特征方程的根必为实数或共轭复数, 必对称于实轴。 规则4 根轨迹起点与终点 根轨迹的起点(Kg=0时) :位于开环传递函数的极点处。 根轨迹的终点(Kg=∞时:止于开环传递函数的零点(包括m个 有限零点和n-m个无穷远处的零点)。
