§2 共轴球面光学系统
合集下载
第二章_共轴球面系统的物像关系

uk
u1 , h1 解法二
u ' n' un
' un
l1
解法三
h n' n r
' un 1 un
' ' un , ln
' un 1 un ' ln 1 ln d n
ri ' u'
同样可得:
l' r
l 'u ' u ' i ' r
' 显然 h lu l 'u,代入上式,并在第一式两边同乘以n, 第二式两侧同乘以n '
nh nu ni r
n' h n' u ' n' i ' r
将以上二式相减,并考虑到
n sin I n' sin I '
d—由前一面顶点算起到下一面顶点。
2.角度: 一律以锐角度量,顺时针转为正,逆时针转为负。 角度也要规定起始轴: U、U'—由光轴起转到光线; I、I'—由光线起转到法线; ψ—由光轴起转到法线,
应用时,先确定参数的正负号,代入公式计算。 算出的结果亦应按照数值的正负来确定光线的相对位置。 推导公式时,也要使用符号规则。
注意 为了使导出的公式具有普遍性,推导公式时,几何 图形上各量一律标注其绝对值,永远为正
反射情形 看成是折射的一种特殊情形: n’= -n 把反射看成是n’= -n 时的折射。 往后推导公式时,只讲折射的公式;对于反射情形, 只需将n’用-n代入即可,无需另行推导。
Q
P
I
I’
-U A O φ C Uˊ Aˊ
l ' f (n, n' , r , l )
第二章 共轴球面系统(二)

= l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
共轴球面系统的过渡公式(3-2)
lu l'u' h
l1u1 l'1 u'1 h1 ,l2u2 l'2 u'2 h2 ,
l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
拉格朗日- 赫姆霍兹恒等式
y' nl'
y n'l
lu l'u'
J为拉赫不变量 nuy n'u' y' J
题 例 1:在一直径为30cm的球形玻璃鱼缸内盛满水,鱼缸中
心处有一条小鱼,求缸外观察者看到鱼的位置及放大率!
解: n n n n l' l r
n' 4 ,l 15, r 15代入 3
定义:通过一定光学系统所成的像对光轴的 垂直高度与物本身对光轴的垂直高度的比。
公式:
y'
y
近轴区的放大率
-u
u’
近轴区的放大率----横向放大率
y'
y
y' l'r y l r
n(1 1) n'(1 1)
rl
r l'
物像位置关系式
n l r n' l' r
rl
rl'
l r l' r n' l nl'
n'k 2
共轴球面系统的过渡公式(3-2)
lu l'u' h
l1u1 l'1 u'1 h1 ,l2u2 l'2 u'2 h2 ,
l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
拉格朗日- 赫姆霍兹恒等式
y' nl'
y n'l
lu l'u'
J为拉赫不变量 nuy n'u' y' J
题 例 1:在一直径为30cm的球形玻璃鱼缸内盛满水,鱼缸中
心处有一条小鱼,求缸外观察者看到鱼的位置及放大率!
解: n n n n l' l r
n' 4 ,l 15, r 15代入 3
定义:通过一定光学系统所成的像对光轴的 垂直高度与物本身对光轴的垂直高度的比。
公式:
y'
y
近轴区的放大率
-u
u’
近轴区的放大率----横向放大率
y'
y
y' l'r y l r
n(1 1) n'(1 1)
rl
r l'
物像位置关系式
n l r n' l' r
rl
rl'
l r l' r n' l nl'
n'k 2
第2章 共轴球面系统的物像关系

12
• 二、轴向放大率(倍率)α 轴向放大率(倍率) • 如果轴上物点移动,那么,像点也必然移动。 如果轴上物点移动,那么,像点也必然移动。
如图2.3-2,设物点A沿轴移动 dl ,那么像点移 如图 ,设物点 沿轴移动 动dl' ,则沿轴放大率定义为 dl'
α=
对式(2-12)进行微分得 进行微分得 对式
5
• 当角度足够小时,上述角度的正弦值与弧度值 几乎没有差别,此时角度U,I,U',I' 的正弦值可 以用相应的弧度值u,i,u',i' 来代替。为了区别, 也用小写字母 表示,见图2.2-1。因为这种光线 很靠近光轴,所以称为近轴光线。
6
对于近轴光线, 对于近轴光线,其光路计算公式可以直接由上 节公式得到, 节公式得到,这只要将其中的角度的正弦值用弧 度值来代替即可
9
§2-3 单个折射球面的成像放大率及拉赫不变量
折射面对有限大小的物体成像时, 折射面对有限大小的物体成像时,就产生了 像的放大率问题,像的虚实、正倒的问题, 像的放大率问题,像的虚实、正倒的问题,下 面在近轴区内予以讨论。 面在近轴区内予以讨论。 • 一、垂轴放大率(倍率)β 垂轴放大率(倍率) • 在折射球面的近轴区,如图2.3-1,垂轴小线 在折射球面的近轴区,如图 , 如果由点B作 段AB,通过折射球面成像 ,通过折射球面成像A'B' 。如果由点 作 一通过曲率中心C的直线 的直线BC,显然, 一通过曲率中心 的直线 ,显然,该直线应 通过点B' 对于该球面来说也是一个光轴, 通过点 。BC对于该球面来说也是一个光轴, 对于该球面来说也是一个光轴 称为辅轴。由辅轴上点B发出沿轴光线必然不 称为辅轴。由辅轴上点 发出沿轴光线必然不 近轴区的物高AB以 表 发生折射地到达像点 。近轴区的物高 以y表 像高以- 。 示,像高以 y'。像的大小和物的大小的比值 称为垂轴放大率 垂轴放大率β 称为垂轴放大率 y' •
• 二、轴向放大率(倍率)α 轴向放大率(倍率) • 如果轴上物点移动,那么,像点也必然移动。 如果轴上物点移动,那么,像点也必然移动。
如图2.3-2,设物点A沿轴移动 dl ,那么像点移 如图 ,设物点 沿轴移动 动dl' ,则沿轴放大率定义为 dl'
α=
对式(2-12)进行微分得 进行微分得 对式
5
• 当角度足够小时,上述角度的正弦值与弧度值 几乎没有差别,此时角度U,I,U',I' 的正弦值可 以用相应的弧度值u,i,u',i' 来代替。为了区别, 也用小写字母 表示,见图2.2-1。因为这种光线 很靠近光轴,所以称为近轴光线。
6
对于近轴光线, 对于近轴光线,其光路计算公式可以直接由上 节公式得到, 节公式得到,这只要将其中的角度的正弦值用弧 度值来代替即可
9
§2-3 单个折射球面的成像放大率及拉赫不变量
折射面对有限大小的物体成像时, 折射面对有限大小的物体成像时,就产生了 像的放大率问题,像的虚实、正倒的问题, 像的放大率问题,像的虚实、正倒的问题,下 面在近轴区内予以讨论。 面在近轴区内予以讨论。 • 一、垂轴放大率(倍率)β 垂轴放大率(倍率) • 在折射球面的近轴区,如图2.3-1,垂轴小线 在折射球面的近轴区,如图 , 如果由点B作 段AB,通过折射球面成像 ,通过折射球面成像A'B' 。如果由点 作 一通过曲率中心C的直线 的直线BC,显然, 一通过曲率中心 的直线 ,显然,该直线应 通过点B' 对于该球面来说也是一个光轴, 通过点 。BC对于该球面来说也是一个光轴, 对于该球面来说也是一个光轴 称为辅轴。由辅轴上点B发出沿轴光线必然不 称为辅轴。由辅轴上点 发出沿轴光线必然不 近轴区的物高AB以 表 发生折射地到达像点 。近轴区的物高 以y表 像高以- 。 示,像高以 y'。像的大小和物的大小的比值 称为垂轴放大率 垂轴放大率β 称为垂轴放大率 y' •
工程光学第2章 共轴球面光学系统
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , yk yk 1 y2 y1
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0,物体沿光轴移动时,像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
I
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
o
U
r
l'
y
-l
7
共轴球面光学系统
结论:
1.
b是有符号数,具体表现为
成像正倒:当b>0时,表明y’、y同号,成正像;否则,成倒像。 成像大小:当|b|=1时,表明|y’|=|y|,像、物大小一致;|b|>1时, 表明|y’|>|y|,成放大的像;反之,成缩小的像。 成像虚实:当b>0时,表明l’、l同号,物像同侧,虚实相反;否 则,物像异侧,虚实相同。
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , yk yk 1 y2 y1
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0,物体沿光轴移动时,像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
I
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
o
U
r
l'
y
-l
7
共轴球面光学系统
结论:
1.
b是有符号数,具体表现为
成像正倒:当b>0时,表明y’、y同号,成正像;否则,成倒像。 成像大小:当|b|=1时,表明|y’|=|y|,像、物大小一致;|b|>1时, 表明|y’|>|y|,成放大的像;反之,成缩小的像。 成像虚实:当b>0时,表明l’、l同号,物像同侧,虚实相反;否 则,物像异侧,虚实相同。
应用光学 第二章 球面和球面系统

一.符号规则
1、沿轴线段:L、 L 、r以折射球面(或反射面)
顶点O为原点,到光线与光轴交点或球心的方向 与光线的传播方向相同,其值为正,反之为负;
2、垂轴线段:以光轴为基准,在光轴上为正,反 之为负; 3、孔径角U和U′ :光轴以锐角方向转到光线,顺 时针为正,逆时针为负; 4、光线与法线的夹角:I 和I′ ,光线以锐角方向 转到法线,顺时针为正,逆时针为负; 5、光轴与法线的夹角 :光轴以锐角方向转向法 线,顺时针为正,逆时针为负; 6、折射面之间的间隔:在折射系统中,d恒为正。
3:已知一个光学系统的结构参数,r = 36.48mm, n=1, n’=1.5163 l = - 240mm, y=20mm 已求出:l’=151.838mm,现求 β, y’ (横向放大率与像的大小)
l2 l'1 d1 ,l3 l'2 d 2 ......lk l'k 1 d k 1
当只关心物像位置且折射面很少时,用方法2较为 方便。如需知道一些中间量且折射面较多时,多 采用方法1。
第五节 球面反射镜
一.球面反射镜的物像位置
1 1 2 l' l r
实物成实像
三个放大率之间的关系:
第四节 共轴球面系统
※光学系统一般是轴对称的,有一条公共轴线, 称为光轴。这种系统被称为“共轴系统”
光轴
一个共轴球面系统的结构参数由下列数值确定 (如有 k 个折射面):各个折射面的曲率半 径 r1 ,r2 ,r3 rk ;各个折射球面的顶点之间的间 隔 d1 , d 2 , d3 dk-1 。各球面间的介质折射 率 n1 , n2 , n3 nk+1 ,其中 nk+1 nk
第二章 共轴球面系统中的光路计算公式汇总

What’s the use of paraxial optics 1. As a criterion to scale the factual optical system. Paraxial optics is a perfect optical system so it images perfectly.
r1 10
r2 50
d 1 5 n2 1.5163 K9
空气
L1 100 L1 100 L1 100
U1 1 U1 2 U1 3
L1 ' 35.969 L1 ' 34.591 L1 ' 32.227
§2-3 球面近轴范围内的成像性质和近轴光路计算公式
Optical path calculation formula
Known:
n,n',r,L,U
1. sin I
Lr sinU r n 2. sin I ' sin I n' 3. U ' I U I ' sin I ' 4. L' r r sin U '
L ',U '
n2 n1 '
u2 u1 '
1
2
u1
h1
d1 n1
n2 n1 '
h2
u2 u1 '
n2 '
1. Positional relations of object and image
h n' u 'nu (n'n) r
u' u l', l h h
n' n n' n l' l r
r1 10
r2 50
d 1 5 n2 1.5163 K9
空气
L1 100 L1 100 L1 100
U1 1 U1 2 U1 3
L1 ' 35.969 L1 ' 34.591 L1 ' 32.227
§2-3 球面近轴范围内的成像性质和近轴光路计算公式
Optical path calculation formula
Known:
n,n',r,L,U
1. sin I
Lr sinU r n 2. sin I ' sin I n' 3. U ' I U I ' sin I ' 4. L' r r sin U '
L ',U '
n2 n1 '
u2 u1 '
1
2
u1
h1
d1 n1
n2 n1 '
h2
u2 u1 '
n2 '
1. Positional relations of object and image
h n' u 'nu (n'n) r
u' u l', l h h
n' n n' n l' l r
共轴球面光学系统特点

共轴球面光学系统特点
共轴球面光学系统是一种采用球面反射镜的光学系统,它由一个球面
反射镜和一个准直物镜组成,它可以聚焦起一束高度集中的光束来实现观
测或其他应用目的。
共轴球面光学系统能够提供高度集中的光束,使其能
够在极短的像差范围内获得高质量的图像,在科学、工业、医学、检测等
领域有着广泛的应用。
其主要特点有:
1、透射特性卓越:由于共轴球面光学系统采用的球面反射镜是镀铬
或钎焊的,具有良好的光学性能,其较高的反射率可以使光的各种波长的
透射率都达到较高的水平。
2、聚焦效果好:由于共轴球面光学系统采用的设计原理是根据透镜
来实现聚焦,因此可以较好的实现视野的高度放大,使其能够有效聚焦。
3、维护方便:共轴球面光学系统采用的是球面反射镜,它只需要定
期清洁即可,而且它没有润滑要求,所以维护非常方便。
4、耐用性强:共轴球面光学系统采用的是优质的、耐用的球面反射镜,可以保证长期使用的稳定性,耐用性也很强。
5、体积小:共轴球面光学系统采用的是非折射性镜片,所以体积小,可以更容易地应用于有空间限制的系统中。
第二章球面和共轴球面系统分析

要讨论成像规律,即像的虚实,成像的位置、正倒和大 小问题,必须计算出光线的走向,所以我们先讨论计算公式。 光线经过单个折射球面的情况如图所示。 包含光轴和物点的平面称为含轴面(纸面)或子午面。 计算的目的:光从何处来,经何处到哪里去(由此得出由物 点发出的光线经过系统后能否交到一点完善成像)?
首要问题:用什么量(怎样)来决定光线在空间中的位置?
对AEC应用正弦定理得 L r r Lr 即 sin I sin U 可求出I sin I sin ( U) r n 据折射定律 sin I ` sin I 可求出I ` n` 对AEC和A`EC应用外角定理 U I U ` I ` U ` U I I ` 可得到U ` sin I ' sin U ' sin I 在A ' EC中 ,利用正弦定律 L ' rr L ' r r sin U
从光轴起算,光轴转向光线(按锐角方向), 顺时针为正,逆时针为负。
入射角、折射角 从光线起算,光线转向法线(按锐角方向), 顺时针为正,逆时针为负。 ③ 光轴与法线的夹角(如) 从光轴起算,光轴转向法线(按锐角方向), 顺时针为正,逆时针为负。
二、实际光线经过单个折射球面的光路计算
已知:折射球面曲率半径r,介质折射率n和n′,及物方坐标L和U。 求:像方L ′和 U ′。
共轴球面系统由许多单个球面构成,当计算出第一面后, 其折射光线就是第二面的入射光线。
U 2 U1; L2 L1 d1
再由相邻两折射球面间的关系,求出下一个球面的折 射光线。
第四节 球面反射镜成像
n n n n 成像公式: l l r
n n
1 1 2 l l r
首要问题:用什么量(怎样)来决定光线在空间中的位置?
对AEC应用正弦定理得 L r r Lr 即 sin I sin U 可求出I sin I sin ( U) r n 据折射定律 sin I ` sin I 可求出I ` n` 对AEC和A`EC应用外角定理 U I U ` I ` U ` U I I ` 可得到U ` sin I ' sin U ' sin I 在A ' EC中 ,利用正弦定律 L ' rr L ' r r sin U
从光轴起算,光轴转向光线(按锐角方向), 顺时针为正,逆时针为负。
入射角、折射角 从光线起算,光线转向法线(按锐角方向), 顺时针为正,逆时针为负。 ③ 光轴与法线的夹角(如) 从光轴起算,光轴转向法线(按锐角方向), 顺时针为正,逆时针为负。
二、实际光线经过单个折射球面的光路计算
已知:折射球面曲率半径r,介质折射率n和n′,及物方坐标L和U。 求:像方L ′和 U ′。
共轴球面系统由许多单个球面构成,当计算出第一面后, 其折射光线就是第二面的入射光线。
U 2 U1; L2 L1 d1
再由相邻两折射球面间的关系,求出下一个球面的折 射光线。
第四节 球面反射镜成像
n n n n 成像公式: l l r
n n
1 1 2 l l r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
光焦度
n
n
h
U
n n r
I
n n l n n f' f
n n l
o
I
U
r
l'
y
-l
6
共轴球面光学系统
三、近轴区域的物像放大率
1、垂轴放大率b
y nu nl b y nu' nl
dl nl 2 n 2 2、轴向放大率a a b 2 dl nl n
当物体位于不同的位置时, b不同。
2.
因a恒为正,故当物点沿轴向移动时,其像点沿光轴同 向移动;且因a ≠ b,故空间物体成像时要变形,例如一 正方体成像后将不再是正方体。 g只与共轭点的位置有关,而与光线的孔径角无关。
8
位置公式 2、成像放大率
b l l
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
I
U
o
-l
r
l'
y
7
共轴球面光学系统
结论:
1.
b是有符号数,具体表现为
成像正倒:当b>0时,表明y’、y同号,成正像;否则,成倒像。 成像大小:当|b|=1时,表明|y’|=|y|,像、物大小一致;|b|>1时, 表明|y’|>|y|,成放大的像;反之,成缩小的像。 成像虚实:当b>0时,表明l’、l同号,物像同侧,虚实相反;否 则,物像异侧,虚实相同。
,U 3 U 2 , ,U k U k 1 U2 U1 d 1 , L3 L2 d 2 , , Lk Lk 1 d k 1 L2 L1
d1 , l3 l2 d 2 , , l k l k 1 d k 1 l 2 l1 , h3 h2 d 2 u h2 h1 d 1 u1 2 , , hk hk 1 d k 1 uk 1 n1 u1 y1 n2 u2 y 2 nk uk yk n k uk y k J
U
y
L
1
共轴球面光学系统
2、符号规则
(一)光线行进方向:从左向右。 (二)线量符号: (1)沿轴线段:以球面顶点O为原点,与光线行进方向相 同者为正,与光线行进方向相反者为负。 (2)垂轴线段:以光轴为界,在光轴之上为正,在光轴之 下为负。 (三)角度符号(一律以锐角来衡量): (1) 光线与光轴的夹角:光轴转向光线,顺时针为正,逆 时针为负。 (2) 光线与法线的夹角:光线转向法线,顺时针为正,逆 时针为负。 (3) 光轴与法线的夹角:光轴转向法线,顺时针为正,逆 时针为负。
U U I I
L r ( 1
sin I ) sin U
4
共轴球面光学系统
sin U sin I ( L r ) r n sin I sin I n
i
U U I I
l r u r n l r i i u n r
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , y k y k 1 y 2 y1
u u i i
sin I L r ( 1 ) sin U
nl r i r 1 l r( 1 ) n' l nl r u
5
共轴球面光学系统
二、近轴区域的物像关系
l u lu h 1 1 1 1 n ( ) n( ) Q r l r l h nu nu ( n n ) r n n n n l l r
2
共轴球面光学系统
3、符号规则的意义:
清楚地描述物像的虚实和正倒:
n
物在左:负物距——实物; 右:正物距——虚物;
I
h
n
y
U
o
r
I
U
y
像在右:正像距——实像; 左:负像距——虚像;
-L
L
物高y像高y’代数值符号相反——倒像; 符号相同——正像;
4、光路图中符号标注:
图中标注几何量为正。
12
共轴球面光学系统
2. 成像放大率
单折射球面
y nl b y nl
dl nl 2 n 2 a b 2 dl nl n
u l n 1 g u l n' b
共轴球面系统
y'k y'1 y'2 y'k b b 1b 2 b k y1 y1 y 2 yk
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0,物体沿光轴移动时,像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
' dl'k dl1 dl'2 dl'k a a 1a 2 a k dl1 dl1 dl2 dlk
u'k u'1 u'2 u'k g g 1g 2 g k u1 u1 u2 uk
ag b
nuy nuy J
13
共轴球面光学系统
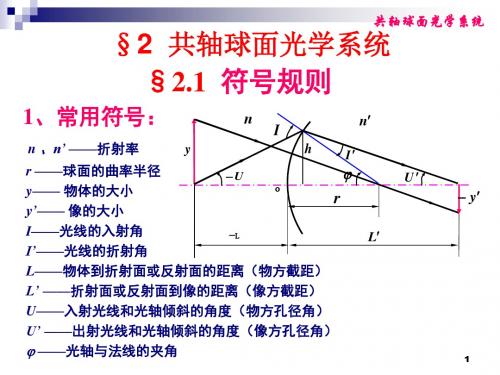
§2 共轴球面光学系统 §2.1 符号规则
1、常用符号:
n 、n’ ——折射率
n
y
I
h
I
n
r ——球面的曲率半径 U y—— 物体的大小 o r y’—— 像的大小 I——光线的入射角 L I’——光线的折射角 L——物体到折射面或反射面的距离(物方截距) L’ ——折射面或反射面到像的距离(像方截距) U——入射光线和光轴倾斜的角度(物方孔径角) U’ ——出射光线和光轴倾斜的角度(像方孔径角) ——光轴与法线的夹角
3
共轴球面光学系统
§2.2 物体经单个折射球面的成像
一、单折射球面成像的光路计算
n
y
U
I
h
n
o
I
U
I E
h
I
r
L
sin U sin I ( L r ) r n sin I sin I n
y
o
U
A’
-L
sinI h r ih r h l u lu
光焦度
n
n
h
U
n n r
I
n n l n n f' f
n n l
o
I
U
r
l'
y
-l
6
共轴球面光学系统
三、近轴区域的物像放大率
1、垂轴放大率b
y nu nl b y nu' nl
dl nl 2 n 2 2、轴向放大率a a b 2 dl nl n
当物体位于不同的位置时, b不同。
2.
因a恒为正,故当物点沿轴向移动时,其像点沿光轴同 向移动;且因a ≠ b,故空间物体成像时要变形,例如一 正方体成像后将不再是正方体。 g只与共轭点的位置有关,而与光线的孔径角无关。
8
位置公式 2、成像放大率
b l l
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
I
U
o
-l
r
l'
y
7
共轴球面光学系统
结论:
1.
b是有符号数,具体表现为
成像正倒:当b>0时,表明y’、y同号,成正像;否则,成倒像。 成像大小:当|b|=1时,表明|y’|=|y|,像、物大小一致;|b|>1时, 表明|y’|>|y|,成放大的像;反之,成缩小的像。 成像虚实:当b>0时,表明l’、l同号,物像同侧,虚实相反;否 则,物像异侧,虚实相同。
,U 3 U 2 , ,U k U k 1 U2 U1 d 1 , L3 L2 d 2 , , Lk Lk 1 d k 1 L2 L1
d1 , l3 l2 d 2 , , l k l k 1 d k 1 l 2 l1 , h3 h2 d 2 u h2 h1 d 1 u1 2 , , hk hk 1 d k 1 uk 1 n1 u1 y1 n2 u2 y 2 nk uk yk n k uk y k J
U
y
L
1
共轴球面光学系统
2、符号规则
(一)光线行进方向:从左向右。 (二)线量符号: (1)沿轴线段:以球面顶点O为原点,与光线行进方向相 同者为正,与光线行进方向相反者为负。 (2)垂轴线段:以光轴为界,在光轴之上为正,在光轴之 下为负。 (三)角度符号(一律以锐角来衡量): (1) 光线与光轴的夹角:光轴转向光线,顺时针为正,逆 时针为负。 (2) 光线与法线的夹角:光线转向法线,顺时针为正,逆 时针为负。 (3) 光轴与法线的夹角:光轴转向法线,顺时针为正,逆 时针为负。
U U I I
L r ( 1
sin I ) sin U
4
共轴球面光学系统
sin U sin I ( L r ) r n sin I sin I n
i
U U I I
l r u r n l r i i u n r
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , y k y k 1 y 2 y1
u u i i
sin I L r ( 1 ) sin U
nl r i r 1 l r( 1 ) n' l nl r u
5
共轴球面光学系统
二、近轴区域的物像关系
l u lu h 1 1 1 1 n ( ) n( ) Q r l r l h nu nu ( n n ) r n n n n l l r
2
共轴球面光学系统
3、符号规则的意义:
清楚地描述物像的虚实和正倒:
n
物在左:负物距——实物; 右:正物距——虚物;
I
h
n
y
U
o
r
I
U
y
像在右:正像距——实像; 左:负像距——虚像;
-L
L
物高y像高y’代数值符号相反——倒像; 符号相同——正像;
4、光路图中符号标注:
图中标注几何量为正。
12
共轴球面光学系统
2. 成像放大率
单折射球面
y nl b y nl
dl nl 2 n 2 a b 2 dl nl n
u l n 1 g u l n' b
共轴球面系统
y'k y'1 y'2 y'k b b 1b 2 b k y1 y1 y 2 yk
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0,物体沿光轴移动时,像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
' dl'k dl1 dl'2 dl'k a a 1a 2 a k dl1 dl1 dl2 dlk
u'k u'1 u'2 u'k g g 1g 2 g k u1 u1 u2 uk
ag b
nuy nuy J
13
共轴球面光学系统
§2 共轴球面光学系统 §2.1 符号规则
1、常用符号:
n 、n’ ——折射率
n
y
I
h
I
n
r ——球面的曲率半径 U y—— 物体的大小 o r y’—— 像的大小 I——光线的入射角 L I’——光线的折射角 L——物体到折射面或反射面的距离(物方截距) L’ ——折射面或反射面到像的距离(像方截距) U——入射光线和光轴倾斜的角度(物方孔径角) U’ ——出射光线和光轴倾斜的角度(像方孔径角) ——光轴与法线的夹角
3
共轴球面光学系统
§2.2 物体经单个折射球面的成像
一、单折射球面成像的光路计算
n
y
U
I
h
n
o
I
U
I E
h
I
r
L
sin U sin I ( L r ) r n sin I sin I n
y
o
U
A’
-L
sinI h r ih r h l u lu
