高考总复习命题量词逻辑连接词习题及详解
高考数学一轮复习 第一章 集合与常用逻辑用语 1.2 命题与量词、基本逻辑联结词练习题(含解析)(1

高考数学一轮复习第一章集合与常用逻辑用语1.2 命题与量词、基本逻辑联结词练习题(含解析)(1)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高考数学一轮复习第一章集合与常用逻辑用语1.2 命题与量词、基本逻辑联结词练习题(含解析)(1))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高考数学一轮复习第一章集合与常用逻辑用语1.2 命题与量词、基本逻辑联结词练习题(含解析)(1)的全部内容。
命题与量词、基本逻辑联结词一、选择题1.下列命题中的假命题是( ).A.∃x0∈R,lg x0=0 B.∃x0∈R,tan x0=1C.∀x∈R,x3>0 D.∀x∈R,2x>0解析对于A,当x0=1时,lg x0=0正确;对于B,当x0=错误!时,tan x0=1,正确;对于C,当x<0时,x3<0错误;对于D,∀x∈R,2x>0,正确.答案C2。
已知命题p:函数f(x)=错误!x-log错误!x在区间错误!内存在零点,命题q:存在负数x使得错误!x〉错误!x.给出下列四个命题:①p或q;②p且q;③p的否定;④q的否定.其中真命题的个数是()A.1 B.2 C.3 D.4解析命题p为假命题,命题q也为假命题.利用真值表判断.答案B3.命题“∀x>0,x2+x>0”的否定是( ).A.∃x0>0,x20+x0>0 B.∃x0>0,x20+x0≤0C.∀x>0,x2+x≤0 D.∀x≤0,x2+x>0解析根据全称命题的否定是特称命题,可知该命题的否定是:∃x0>0,x20+x0≤0.答案B4.已知p:|x-a|<4;q:(x-2)(3-x)>0,若非p是非q的充分不必要条件,则a的取值范围为().A.a<-1或a>6 B.a≤-1或a≥6C.-1≤a≤6 D.-1<a<6解析解不等式可得p:-4+a<x<4+a,q:2<x<3,因此非p:x≤-4+a或x≥4+a,非q:x≤2或x≥3,于是由非p是非q的充分不必要条件,可知2≥-4+a且4+a≥3,解得-1≤a≤6.答案C5.若函数f(x)=-x e x,则下列命题正确的是()A.∀a∈错误!,∃x∈R,f(x)〉aB.∀a∈错误!,∃x∈R,f(x)〉aC.∀x∈R,∃a∈错误!,f(x)〉aD.∀x∈R,∃a∈错误!,f(x)〉a解析f′(x)=-e x(x+1),由于函数f(x)在(-∞,-1)上递增,在(-1,+∞)上递减,故f(x)max=f(-1)=错误!,故∀a∈错误!,∃x∈R,f(x)〉a.答案A6.若函数f(x)=x2+错误!(a∈R),则下列结论正确的是( ).A.∀a∈R,f(x)在(0,+∞)上是增函数B.∀a∈R,f(x)在(0,+∞)上是减函数C.∃a∈R,f(x)是偶函数D.∃a∈R,f(x)是奇函数解析对于A只有在a≤0时f(x)在(0,+∞)上是增函数,否则不成立;对于B,如果a≤0就不成立;对于D若a=0,则f(x)为偶函数了,因此只有C是正确的,即对于a=0时有f(x)=x2是一个偶函数,因此存在这样的a,使f(x)是偶函数.答案C7.已知p:∃x0∈R,mx错误!+2≤0.q:∀x∈R,x2-2mx+1>0,若p∨q为假命题,则实数m 的取值范围是( ).A.[1,+∞)B.(-∞,-1]C.(-∞,-2]D.[-1,1]解析(直接法)∵p∨q为假命题,∴p和q都是假命题.由p:∃x0∈R,mx20+2≤0为假,得∀x∈R,mx2+2>0,∴m≥0.①由q:∀x∈R,x2-2mx+1>0为假,得∃x0∈R,x2,0-2mx0+1≤0,∴Δ=(-2m)2-4≥0⇒m2≥1⇒m≤-1或m≥1。
高考一轮复习 逻辑联结词 知识点+例题+练习

1.逻辑联结词命题中的或,且,非叫做逻辑联结词.“p 且q ”记作p ∧q ,“p 或q ”记作p ∨q ,“非p ”记作綈p .2.命题p ∧q ,p ∨q ,綈p 的真假判断p q p ∧q p ∨q 綈p真 真 真 真 假真 假 假 真 假假 真 假 真 真假 假 假 假 真3.全称量词与存在量词(1)短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“∀”表示.含有全称量词的命题,叫做全称命题,可用符号简记为∀x ∈M ,p (x ),它的否定∃x ∈M ,綈p (x ).(2)短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“∃”表示.含有存在量词的命题,叫做存在性命题,可用符号简记为∃x ∈M ,p (x ),它的否定∀x ∈M ,綈p (x ).自我检测1.命题“∃x ∈R ,x 2-2x +1<0”的否定是__________________2.若命题p :x ∈A ∩B ,则綈p 是________________3.(2010·苏州调研)命题“若x >0,则x 2>0”的否命题是________命题.(填“真”或 “假”)4.若“x ∈[2,5]或x ∈{x |x <1或x >4}”是假命题,则x 的取值范围是________.5.(2009·辽宁改编)下列4个命题:①∃x ∈(0,+∞),(12)x <(13)x ; ②∃x ∈(0,1),log 12x >log 13x ; ③∀x ∈(0,+∞),(12)x >log 12x ; ④∀x ∈(0,13),(12)x <log 13x . 其中的真命题是________(填序号).学生姓名教师姓名 班主任 日期时间段 年级 课时 教学内容 逻辑联结词与量词教学目标 1.了解逻辑联结词“或、且、非”的含义.2.理解全称量词与存在量词的意义.3.能正确地对含有一个量词的命题进行否定.重点 逻辑联结词、存在量词、全称量词难点同上探究点一 判断含有逻辑联结词的命题的真假例1 写出由下列各组命题构成的“p ∨q ”、“p ∧q ”、“綈p ”形式的复合命题,并判断真假.(1)p :1是素数;q :1是方程x 2+2x -3=0的根;(2)p :平行四边形的对角线相等;q :平行四边形的对角线互相垂直;(3)p :方程x 2+x -1=0的两实根的符号相同;q :方程x 2+x -1=0的两实根的绝对值相等.变式迁移1 已知命题p :∃x ∈R ,使tan x =1,命题q :x 2-3x +2<0的解集是{x |1<x <2},给出下列结论:①命题“p ∧q ”是真命题;②命题“p ∧綈q ”是假命题;③命题“綈p ∨q ”是真命题;④命题“綈p ∨綈q ”是假命题,其中正确的是________(填序号).探究点二 全称(存在性)命题及真假判断例2 判断下列命题的真假.(1)∀x ∈R ,都有x 2-x +1>12. (2)∃α,β使cos(α-β)=cos α-cos β.(3)∀x ,y ∈N ,都有x -y ∈N .(4)∃x 0,y 0∈Z ,使得2x 0+y 0=3.变式迁移2 (2010·江苏苏州中学阶段性测试一)若命题“∃x ∈R ,使得x 2+(1-a )x +1<0”是真命题,则实数a 的取值范围为__________________.探究点三 全称命题与存在性命题的否定例3 写出下列命题的“否定”,并判断其真假.(1)p :∀x ∈R ,x 2-x +14≥0;(2)q :所有的正方形都是矩形;(3)r :∃x ∈R ,x 2+2x +2≤0;(4)s :至少有一个实数x ,使x 3+1=0.变式迁移3(2010·深圳一模)已知命题p:∃x∈R,x2+2ax+a≤0.若命题p是假命题,则实数a的取值范围为________.转化与化归思想例(14分)已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x0∈R,x20+2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.1.逻辑联结词“或”“且”“非”的含义的理解.(1)“或”与日常生活用语中的“或”意义有所不同,日常用语“或”带有“不可兼有”的意思,如工作或休息,而逻辑联结词“或”含有“同时兼有”的意思,如x<6或x>9.(2)命题“非p”就是对命题“p”的否定,即对命题结论的否定;否命题是四种命题中的一种,是对原命题条件和结论的同时否定.2.判断复合命题的真假,要首先确定复合命题的构成形式,再指出其中简单命题的真假,最后根据真值表判断.3.全称命题“∀x∈M,p(x)”的否定是一个存在性命题“∃x∈M,綈p(x)”,存在性命题“∃x∈M,p(x)”的否定是一个全称命题“∀x∈M,綈p(x)”.一、填空题(每小题6分,共48分)1.(2011·常州月考)已知命题p:∃x∈R,x2-3x+3≤0,则綈p为________.2.已知命题p:∀x∈R,ax2+2x+3>0,如果命题綈p是真命题,那么实数a的取值范围是________.3.已知条件p:|x+1|>2,条件q:x>a,且綈p是綈q的充分不必要条件,则a的取值范围是________.4.已知命题“∀a,b∈R,如果ab>0,则a>0”,则它的否命题是________.5.下列有关命题的说法中正确的有________(填序号).①命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”;②“x=-1”是“x2-5x-6=0”的必要不充分条件;③命题“∃x∈R,使得x2+x+1<0”的否定是“∀x∈R,均有x2+x+1<0”;④命题“若x=y,则sin x=sin y”的逆否命题为真命题.6.(2010·安徽)命题“对∀x∈R,|x-2|+|x-4|>3”的否定是______________.7.(2011·镇江模拟)已知命题p:“∀x∈R,∃m∈R使4x-2x+1+m=0”,若命题綈p 是假命题,则实数m的取值范围为__________.8.(2010·安徽)命题“存在x∈R,使得x2+2x+5=0”的否定是______________________.二、解答题(共42分)9.(14分)分别指出由下列命题构成的“p∨q”“p∧q”“綈p”形式的命题的真假.(1)p:4∈{2,3},q:2∈{2,3};(2)p:1是奇数,q:1是质数;(3)p:0∈∅,q:{x|x2-3x-5<0}⊆R;(4)p:5≤5,q:27不是质数.10.(14分)命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,q:函数f(x)=(3-2a)x是增函数,若p或q为真,p且q为假,求实数a的取值范围.11.(14分)已知p:x2+mx+1=0有两个不等的负根,q:4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.。
高考数学讲义常用逻辑用语.板块三.逻辑连接词与量词.教师版1

题型一:逻辑连接词 【例1】 写出下列命题的“p ⌝”命题:(1)正方形的四边相等;(2)平方和为0的两个实数都为0;(3)若ABC ∆是锐角三角形, 则ABC ∆的任何一个内角是锐角;(4)若0abc =,则,,a b c 中至少有一个为0;(5)若(1)(2)0x x --≠,则1x ≠且2x ≠.【考点】逻辑连接词 【难度】1星【题型】解答【关键词】无【解析】 【答案】(1)存在一个正方形的四边不相等.(2)平方和为0的两个实数不都为0.(3)若ABC ∆是锐角三角形, 则ABC ∆的某个内角不是锐角.(4)若0abc =,则,,a b c 中都不为0.(5)若(1)(2)0x x --≠,则1x =或2x =.【例2】 若:{|1},:{0}p N x R x q ⊄∈>-=∅.写出由其构成的“p 或q ”、“p 且q ”、“非p ”形式的新命题,并指出其真假.【考点】逻辑连接词 【难度】2星【题型】解答【关键词】无【解析】 ,p q 均为假命题.典例分析板块三.逻辑连接词与量词【答案】 “p 或q ”为::{|1}p N x R x ⊄∈>-或:{0}q =∅,是假命题;“p 且q ”为::{|1}p N x R x ⊄∈>-且:{0}q =∅,是假命题;“非p ”为::{|1}p N x R x ⊆∈>-,是真命题.【例3】 用联结词“且”、“或”分别联结下面所给的命题p q ,构成一个新的复合命题,判断它们的真假.⑴p :1是质数;q :1是合数;⑵p :菱形的对角线互相垂直;q :菱形的对角线互相平分;【考点】逻辑连接词 【难度】2星【题型】解答【关键词】无【解析】 【答案】⑴p 是假命题,q 是假命题,故p q ∨,p q ∧都是假命题;⑵p 是真命题,q 是真命题,故p q ∨是真命题,p q ∧是真命题.【例4】 把下列各组命题,分别用逻辑联结词“且”“或”“非”联结成新命题,并判断其真假.⑴p :梯形有一组对边平行;q :梯形有一组对边相等.⑵p :1是方程2430x x -+=的解;q :3是方程2430x x -+=的解.⑶p :不等式2210x x -+>解集为R ;q :不等式2221x x -+≤解集为∅.⑷p :{0}∅Ü;q :0∈∅.【考点】逻辑连接词 【难度】2星【题型】解答【关键词】无【解析】 ⑴∵p 真,q 假,∴p q ∧为假,p q ∨为真,p ⌝为假,q ⌝为真. ⑵∵p 真,q 真,∴p q ∧为真,p q ∨为真,p ⌝为假,q ⌝为假.⑶∵p 假,q 假,∴p q ∧为假,p q ∨为假,p ⌝为真,q ⌝为真.⑷∵p 真,q 假,∴p q ∧为假,p q ∨为真,p ⌝为假,q ⌝为真.【答案】⑴p q ∧为假,p q ∨为真,p ⌝为假,q ⌝为真.⑵p q ∧为真,p q ∨为真,p ⌝为假,q ⌝为假.⑶p q ∧为假,p q ∨为假,p ⌝为真,q ⌝为真.⑷p q ∧为假,p q ∨为真,p ⌝为假,q ⌝为真.【例5】 判断下面对结论的否定是否正确,如果不正确,请写出正确的否定结论:⑴至少有一个S 是P ;否定:至少有两个或两个以上S 是P ;⑵最多有一个S 是P .否定:最少有一个S 是P ;⑶全部S 都是P .否定:全部的S 都不是P .【考点】逻辑连接词 【难度】2星【题型】解答【关键词】无【解析】 “集合M 中至少有一个元素m 不具有性质a ”的否定是:集合M 中所有元素都具有性质a .反之亦对.因为“集合M 中至少有一个元素不具有性质a ”,它包含了“M 中有一个元素不具有性质a 、两个元素不具有性质a ……所有元素都不具有性质a ”等各种情形.因此它的否定是“M 中所有元素都具有性质a ”.如“三角形中至少有一个内角大于或等于60︒”的否定是“三角形中所有内角都小于60︒”.注意“都不是”的否定不是“都是”,而是“不都是”,也即“至少有一个是”.如“a 、b 都不是零”的否定是“a ,b 中至少有一个是零”.【答案】⑴不正确,没有一个S 是P .⑵不正确,至少有两个S 是P .⑶不正确,存在一个S 不是P .【例6】 “220a b +≠”的含义为__________;“0ab ≠”的含义为__________.A .a b ,不全为0B .a b ,全不为0C .a b ,至少有一个为0D .a 不为0且b 为0,或b 不为0且a 为0【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 220a b +≠的含义为a b ,不全为0,选A ; 0ab ≠的含义为,a b 全不为0,选B .【答案】A,B【例7】 已知全集R U =,A U ⊆,B U ⊆,如果命题p A B U ,则命题“p ⌝”是( )A AB U B ðC A B ID ()()U U A B I 痧 【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 【答案】D ;【例8】 命题“关于x 的方程(0)ax b a =≠的解是唯一的”的结论的否定是( )A .无解B .两解C .至少两解D .无解或至少两解【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 【答案】D ;【例9】 若条件:P x A B ∈I ,则P ⌝是( )A .x A ∈且xB ∉ B .x A ∉或x B ∉C .x A ∉且x B ∉D .x A B ∈U【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 x 至少不属于A B ,中的一个. 【答案】B ;【例10】 命题:“若220()R a b a b +=∈,,则“0a b ==”的逆否命题是( ) A .若0()R a b a b ≠≠∈,,则220a b +≠B .若0a ≠且0()R b a b ≠∈,,则220a b +≠C .若0()R a b a b =≠∈,,则220a b +≠D .若0a ≠或0()R b a b ≠∈,,则220a b +≠【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 0a b ==的否定为a b ,至少有一个不为0. 【答案】D ;【例11】 命题“2230ax ax -+>恒成立”是假命题,则实数a 的取值范围是( )A .0a <或3a ≥B .0a ≤或3a ≥C .0a <或3a >D .03a <<【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 0a <时,显然2230ax ax -+>不恒成立;0a =时,恒成立; 0a >时,只需240a ∆=-12a ≥即可,解得3a ≥.【答案】A ;【例12】 命题“p 或q ”是真命题,“p 且q ”是假命题,则( )A .命题p 和命题q 都是假命题B .命题p 和命题q 都是真命题C .命题p 和命题“非q ”的真值不同D .命题p 和命题q 的真值不同【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 【答案】D .【例13】 已知命题p :若实数x y ,满足220x y +=,则x y ,全为0;命题q :若a b >,则11a b<,给出下列四个复合命题:①p 且q ②p 或q ③p ⌝④q ⌝,其中真命题的个数为( )A .1B .2C .3D .4【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 p 为真命题,q 为假命题,∴p ⌝为假命题,q ⌝为真命题,②④为真命题. 【答案】B ;【例14】 由下列各组命题构成“p 或q ”为真,“p 且q ”为假,“p ⌝”为真的是( )A .p :0=∅,q :0∈∅B .p :等腰三角形一定是锐角三角形,q :正三角形都相似C .p :{}{}a a b ,躿,q :{}a a b ∈,D .p :53>,q :12是质数【关键词】无【解析】 【答案】B ;【例15】 在下列结论中,正确的是( )①“p q ∧”为真是“p q ∨”为真的充分不必要条件②“p q ∧”为假是“p q ∨”为真的充分不必要条件③“p q ∨”为真是“p ⌝”为假的必要不充分条件④“p ⌝”为真是“p q ∧”为假的必要不充分条件A .①②B .①③C .②④D .③④【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 p q ∧为真,p q ⇒都为真p q ⇒∨为真,反之不成立,①正确; p q ∧为假,可能,p q 都为假,故推不出p q ∨为真,②错误;p ⌝为假,有p 为真,故p q ∨为真;而p q ∨为真,p 可能为假,从而p ⌝可能 为真,③正确;p ⌝为真,说明p 假,从而p q ∧为假,④错误;故选B .【答案】B【例16】 设命题p :2x >是24x >的充要条件,命题q :若22a b c c >,则a b >.则( ) A .“p 或q ”为真 B .“p 且q ”为真C .p 真q 假D .p ,q 均为假命题【考点】逻辑连接词 【难度】2星 【题型】选择【关键词】2008年,北京东城,高考二模【解析】 p 假q 真.【答案】A .【例17】 若命题“p 且q ”为假,且“p ⌝”为假,则 ()A .p 或q 为假B .q 假C .q 真D .p 假【关键词】无【解析】“p∧(且)为假,得q为假⌝”为假,则p为真,而p q【答案】B【例18】若条件:∈I,则PP x A B⌝是()A.x A∉ D. x A B∉且x B∈⋃∈且x B∉ B. x A∉或x B∉ C. x A【考点】逻辑连接词【难度】2星【题型】选择【关键词】无【解析】P∉I,∴x至少不属于,A B中的一个.⌝:x A B【答案】B【例19】设集合{}{}=>=<,那么“x MM x x P x x|2,|3∈I”的∈”是“x M P∈,或x P()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件【考点】逻辑连接词【难度】2星【题型】选择【关键词】无【解析】“x M∈I”,反之可以∈”不能推出“x M P∈,或x P【答案】A【例20】p或q”是假命题.其中正确的结论是()A.①③B.②④C.②③D.①④【考点】逻辑连接词【难度】2星【题型】选择【关键词】无【解析】“非p或非q”是假命题⇒“非p”与“非q”均为假命题.【答案】C【例21】 已知命题p 且q 为假命题,则可以肯定 ( )A.p 为真命题B.q 为假命题C.,p q 中至少有一个是假命题D.,p q 都是假命题【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 【答案】C【例22】 已知条件:12p x +>,条件2:56q x x ->,则p ⌝是q ⌝的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无【解析】 :12p x ⌝+≤,31x -≤≤,2:56q x x ⌝-≤,2560x x -+≥,3x ≥或2x ≤ 【答案】A【例23】 下列判断正确的是 ( )A.22x y x y ≠⇔≠或x y ≠-B.命题“a 、b 都是偶数,则a b +是偶数” 的逆否命题是“若a b +不是偶数,则a 、b 都不是偶数”C.若“p 或q ”为假命题,则“非p 且非q ”是真命题D.已知,,a b c 是实数,关于x 的不等式20ax bx c ++≤的解集是空集,必有0a >且0∆≤【考点】逻辑连接词 【难度】2星【题型】选择【关键词】无 【解析】 A 不正确,因为“x y ≠或x y ≠-”只要求其中之一成立即行,而22x y ≠需二者都成立;B 不正确,“a 、b 都是偶数”的否定是“a 、b 不都是偶数”;D 不正确,不等式 20ax bx c ++≤的解集是空集还可能是0,0a b c ==> .【答案】C【例24】 在下边的横线上填上真命题或假命题.⑴若命题“p ⌝”与命题“p q ∨”都是真命题,那么p q ∧是______; p q ⌝∧是_____;⑵若命题“p ⌝或q ⌝”是假命题,那么p q ∧是______;p q ∨是_______; p ⌝是_______.【考点】逻辑连接词 【难度】2星【题型】填空【关键词】无 【解析】 ⑴p ⌝真,说明p 为假命题;又p q ∨为真命题,故q 为真命题,从而p q ∧是假命题;p q ⌝∧是真命题;⑵根据“p ⌝或q ⌝”是假命题知,命题p ⌝、q ⌝都是假命题,从而p 、q 都是真命题,故p q ∧ 是真命题;p q ∨是真命题;p ⌝是假命题.【答案】⑴真命题,真命题,⑵真命题,真命题,假命题【例25】 ⑴p q ∨为真命题是p q ∧为真命题的 条件;⑵p ⌝为假命题是p q ∨为真命题的 条件.(填:充分不必要、必要不充分、充要、既不充分也不必要).【考点】逻辑连接词 【难度】2星【题型】填空【关键词】无【解析】 ⑴p q ∨真⇒p 真或q 真;p q ∧真⇒p 真且q 真,故p q ∨为真命题是p q ∧为真命题的必要不充分条件;⑵p ⌝假则p 真,从而p q ∨真,但p q ∨真时,p 可能假,故推不出p ⌝假,故p ⌝为假命题是p q ∨为真命题的充分不必要条件.【答案】⑴必要不充分,⑵充分不必要【例26】 如在下列说法中:①“p 且q ”为真是“p 或q ”为真的充分不必要条件;②“p 且q ”为假是“p 或q ”为真的充分不必要条件;③“p 或q ”为真是“非p ”为假的必要不充分条件;④“非p ”为真是“p 且q ”为假的必要不充分条件.其中正确的是__________.【考点】逻辑连接词 【难度】2星【题型】填空【关键词】无【解析】 【答案】①③.【例27】 如果命题“非p 或非q ”是假命题,给出下列四个结论:①命题“p 且q ”是真命题;②命题“p 且q ”是假命题;③命题“p 或q ”是真命题;④命题“用“充分、必要、充要”填空:①p q ∨为真命题是p q ∧为真命题的________________条件;②p ⌝为假命题是p q ∨为真命题的_____________________条件.【考点】逻辑连接词 【难度】2星【题型】填空【关键词】无【解析】 【答案】必要,必要【例28】 已知命题::p “若1a >,则32a a >”;命题:q “若0a >,则1a a>”.则在“p 或q ”、“p 且q ”、“非p ”、“非q ”四个命题中,真命题是 .【考点】逻辑连接词 【难度】2星【题型】填空【关键词】无【解析】 p 真,q 假. 【答案】p 或q ,非q【例29】 命题:0p 不是自然数;命题q 是无理数,则在命题“p 或q ”、“p 且q ”、“非p ”、“非q ”中,真命题是 ;假命题是 .【考点】逻辑连接词 【难度】2星 【题型】填空【关键词】无【解析】 p 假,q 真. “p 或q ”为真,只要,p q 中有一个为真即可;“p 且q ”必须,p q中均为真.【答案】 “p 或q ”, “非p ”; “p 且q ”, “非q ”【例30】 命题“对一切非零实数x ,总有12x x+≥”的否定是 ,它是 命题.(填“真”或“假”)【考点】逻辑连接词 【难度】2星 【题型】填空【关键词】无【解析】 例如:2x =-,则1,0,2x R x x x∈≠+<. 【答案】1,0,2x R x x x∃∈≠+<,真命题【例31】 甲、乙两人参加一次竞赛,设命题p 是“甲获奖”,命题q 是“乙获奖”,试用p q,及逻辑联结词“且”、“或”、“非”表示:⑴两人都获奖; ⑵两人都未获奖; ⑶恰有一人获奖; ⑷至少有一人获奖.【考点】逻辑连接词 【难度】2星 【题型】解答【关键词】无【解析】 ⑷也是对⑵中情况的否定,故也可表示为(()())p q ⌝⌝∧⌝,故容易知道(()())p q p q ∨=⌝⌝∧⌝,也即()()()p q p q ⌝∨=⌝∧⌝.【答案】⑴两人都获奖说明两个命题都成立,故为p q ∧;⑵都未获奖说明两个命题都不成立,故为()()p q ⌝∧⌝; ⑶恰有一人获奖说明一个命题成立,另一个命题不成立,故为()()p q p q ⌝∧∨∧⌝;⑷至少有一人获奖说明p 或q 成立,即p q ∨.【例32】 命题p :若R a b ∈,,则1a b +>是1a b +>的充分条件,命题q :函数y 的定义域是(1][3)-∞-+∞U ,,,则( ) A .p 或q 为假 B .p 且q 为真 C .p 真q 假 D .p 假q 真【考点】逻辑连接词 【难度】3星 【题型】选择【关键词】无【解析】 令1,1a b ==-,知命题p 假;由1203x x --⇒≥≥或1x -≤,故命题q 真;【答案】D ;【例33】 已知p 是r 的充分条件而不是必要条件,q 是r 的充分条件,s 是r 的必要条件,q 是s 的必要条件.现有下列命题:①s 是q 的充要条件;②p 是q 的充分条件而不是必要条件;③r 是q 的必要条件而不是充分条件;④p s ⌝⌝是的必要条件而不是充分条件;⑤r 是s 的充分条件而不是必要条件,则正确命题序号是( )A .①④⑤B .①②④C .②③⑤D .②④⑤【考点】逻辑连接词 【难度】3星 【题型】选择【关键词】2007年,湖北,高考【解析】 由右图易知;qsr p【答案】B ;【例34】 已知p :方程220x mx ++=有两个不等的负根;q :方程244(2)10x m x +-+=无实根.若p q ∨为真,p q ∧为假,则实数m 的取值范围是_______.【考点】逻辑连接词 【难度】3星 【题型】填空【关键词】无【解析】 由题意知,命题p q ,一真一假;p 为真时有:280m m m -<⎧⇒>⎨∆=->⎩q 为真时有:216(2)16013m m ∆=--<⇒<<;p 真q 假时有3m ≥;p 假q 真时有1m <≤(1[3)m ∈+∞U ,; 【答案】(1[3)m ∈+∞U ,【例35】 已知命题p :关于x 的不等式20062008x x a -+->恒成立;命题q :关于x 的函数log (2)a y ax =-在[01],上是减函数.若p 或q 为真命题,p 且q 为假命题,则实数a 的取值范围是_______;【考点】逻辑连接词 【难度】3星 【题型】填空【关键词】无【解析】 由题意知,命题p q ,一真一假;20062008x x -+-的最小值为2,故此不等式恒成立,即p 为真时有2a <;q 为真时log (2)a y ax =-在[01],上是减函数,∵0a >,故内层函数为减函数,从而外层对数函数为增函数,有1a >,又202a a ->⇒<,故12a <<;p 真q 假时1a ≤;p 假q 真时a 不存在,故(1]a ∈-∞,; 【答案】(1]-∞,;【例36】 已知命题p :方程2220a x ax +-=在[11]-,上有解;命题q :只有一个实数满足不等式2220x ax a ++≤.若p q ∨是假命题,求a 的取值范围.【考点】逻辑连接词 【难度】3星 【题型】解答【关键词】无【解析】 由2220a x ax +-=知0a ≠,解此方程得1212x x a a ==-,.∵方程2220a x ax +-=在[11]-,上有解,∴1||1a ≤或2||1a≤,∴||1a ≥.只有一个实数满足不等式2220x ax a ++≤,表明抛物线222y x ax a =++与x 轴只有一个公共点,∴2480a a ∆=-=, ∴0a =或2a =.∴命题p 为假,则11a -<<;命题q 为假,则0a ≠且2a ≠.∴若p q ∨是假命题,则p q ,都是假命题,a 的取值范围是(10)(01)-U ,,. 【答案】(10)(01)-U ,,【例37】 命题:p 方程210x mx ++=有两个不等的正实数根,命题:q 方程244(2)10x m x +++=无实数根.若“p 或q ”为真命题,求m 的取值范围.【考点】逻辑连接词 【难度】3星 【题型】解答【关键词】无【解析】 “p 或q ”为真命题,则p 为真命题,或q 为真命题,或q 和p 都是真命题当p 为真命题时,则2121240010m x x m x x ⎧∆=->⎪+=->⎨⎪=>⎩,得2m <-;当q 为真命题时,则216(2)160m ∆=+-<,得31m -<<- 当q 和p 都是真命题时,得32m -<<- ∴1m <-【答案】1m <-【例38】 已知函数2()(1)lg 2f x x a x a =++++(R a ∈,且2)a ≠-,⑴()f x 能表示成一个奇函数()g x 和一个偶函数()h x 的和,求()g x 和()h x 的解析式;⑵命题p :函数()f x 在区间2[(1))a ++∞,上是增函数;命题q :函数()g x 是减函数.如果命题p 且q 为假,p 或q 为真,求a 的取值范围. ⑶在⑵的条件下,比较(2)f 与3lg2-的大小.【考点】逻辑连接词 【难度】4星 【题型】解答【关键词】无【解析】 ⑴∵()()()f x g x h x =+,()()()()()f x g x h x g x h x -=-+-=-+,∴[]1()()()(1)2g x f x f x a x =--=+,[]21()()()lg 22h x f x f x x a =+-=++; ⑵命题p 为真时有:21(1)2a a +-+≤1a ⇒≥-或32a -≤,命题q 为真时有:101a a +<⇒<-;命题p 且q 为假,p 或q 为真包括:p 真q 假与p 假q 真两种情况;故1a -≥或312a -<<-,即32a >-;⑶(2)42(1)lg 226lg 2f a a a a =++++=+++,(2)(3lg 2)23lg 2lg 2f a a --=++++,32x >-时,20x +>,函数()23lg 2lg 2x x x ϕ=++++在32⎛⎫-+∞ ⎪⎝⎭,上单调递增, 故3()02a ϕϕ⎛⎫>-= ⎪⎝⎭,即在⑵的条件下,(2)3lg2f >-.【答案】⑴()(1)g x a x =+,2()lg 2h x x a =++, ⑵32a >-,⑶(2)3lg2f >-题型二:全称量词与存在量词【例39】 判断下列命题是全称命题,还是存在性命题.⑴平面四边形都存在外接圆;⑵有些直线没有斜率; ⑶三角形的内角和等于π; ⑷有一些向量方向不定; ⑸所有的有理数都是整数; ⑹实数的平方是非负的.【考点】全称量词与存在量词 【难度】1星 【题型】解答【关键词】无【解析】 .【答案】⑴全称命题;⑵存在性命题;⑶全称命题,意思是所有的三角形都有内角和等于π;⑷存在性命题;⑸全称命题;⑹全称命题【例40】 判断下列命题是全称命题还是存在性命题.⑴线段的垂直平分线上的点到这条线段两个端点的距离相等;⑵负数的平方是正数;⑶有些三角形不是等腰三角形; ⑷有些菱形是正方形.【考点】全称量词与存在量词 【难度】1星 【题型】解答【关键词】无【解析】【答案】⑴全称命题;⑵全称命题;⑶存在性命题;⑷存在性命题.【例41】 设语句()p x :cos()sin 2πx x +=-,写出“()R p θθ∀∈,”,并判断它是不是真命题.【考点】全称量词与存在量词 【难度】2星 【题型】解答【关键词】无【解析】 R θ∀∈,cos()sin 2πθθ+=-;由诱导公式知,是真命题.【答案】R θ∀∈,cos()sin 2πθθ+=-;真命题【例42】 用量词符号“∀∃,”表示下列命题,并判断下列命题的真假.⑴任意实数x 都有,2210x x ++>; ⑵存在实数x ,2210x x ++<;⑶存在一对实数a b ,,使20a b +<成立; ⑷有理数x 的平方仍为有理数;⑸实数的平方大于0.⑹有一个实数乘以任意一个实数都等于0.【考点】全称量词与存在量词 【难度】2星 【题型】解答【关键词】无【解析】 ⑴R x ∀∈,2210x x ++>;假命题,1x =-时,结论不成立;⑵R x ∃∈,2210x x ++<;假命题,R x ∈时,2221(1)0x x x ++=+≥; ⑶R a b ∃∈,,20a b +<;真命题,如12a b ==-,; ⑷Q x ∀∈,2Q x ∈;真命题; ⑸R x ∀∈,20x >;假命题,200=.⑹R a ∃∈,R x ∀∈,有0ax =;真命题,0a =即满足.【答案】⑴R x ∀∈,2210x x ++>;假命题⑵R x ∃∈,2210x x ++<;假命题 ⑶R a b ∃∈,,20a b +<;真命题 ⑷Q x ∀∈,2Q x ∈;真命题⑸R x ∀∈,20x >;假命题,200=. ⑹R a ∃∈,R x ∀∈,有0ax =;真命题【例43】判断下列命题是全称命题还是存在性命题,并判断真假.⑴所有的素数是奇数;⑵一切实数x,有2(1)0x->;⑶对于正实数x,12xx+≥;⑷1sin2sinRx xx∀∈+,≥;⑸一定有实数x满足2230x x--=;⑹至少有一个整数x能被2和3整除;⑺存在两个相交平面垂直于同一条直线;⑻{|x x x∃∈是无理数},2x是无理数.【考点】全称量词与存在量词【难度】2星【题型】解答【关键词】无【解析】【答案】⑴⑵⑶⑷是全称命题,⑸⑹⑺⑻是存在性命题,⑴⑵⑷⑺是假命题,⑶⑸⑹⑻是真命题.【例44】判断下列命题是全称命题还是存在性命题,并判断真假.⑴21x+是整数(Rx∈);⑵对所有的实数x,3x>;⑶对任意一个整数x,221x+为奇数;⑷末位是0的整数,可以被2整除;⑸角平分线上的点到这个角的两边的距离相等;⑹正四面体中两侧面的夹角相等;⑺有的实数是无限不循环小数;⑻有些三角形不是等腰三角形;⑼有的菱形是正方形.【考点】全称量词与存在量词【难度】2星【题型】解答【关键词】无【解析】⑴~⑹是全称命题,⑺~⑼是存在性命题,⑶~⑼是真命题,⑴⑵是假命题.【答案】⑴~⑹是全称命题,⑺~⑼是存在性命题,⑶~⑼是真命题,⑴⑵是假命题【例45】 写出下列命题p 的否定形式,并判断p 与p ⌝的真假.⑴平行四边形的对边相等; ⑵不等式22210x x ++≤有实数解. ⑶R x ∀∈,210x x ++>; ⑷R x ∃∈,21x x +<; ⑸有些实数的绝对值是正数.⑹不是每个质数都是偶数.【考点】全称量词与存在量词 【难度】2星 【题型】解答【关键词】无【解析】 ⑴p ⌝:存在对边不相等的平行四边形;p 真,p ⌝假;⑵p ⌝:不等式22210x x ++≤无实数解;p 假,p ⌝真; ⑶p ⌝:R x ∃∈,210x x ++≤;p 真,p ⌝假; ⑷p ⌝:R x ∀∈,21x x +≥;p 假,p ⌝真;⑸p ⌝:任意实数的绝对值都不是正数(或:,0R x x ∀∈≤);p 真,p ⌝假. ⑹p ⌝:每个质数都是偶数;p 真,p ⌝假.【答案】⑴p 真,p ⌝假;⑵p 假,p ⌝真;⑶p 真,p ⌝假;⑷p 假,p ⌝真;⑸p 真,p ⌝假;⑹p 真,p ⌝假.【例46】 判断下列命题的真假:(1)对任意的,x y 都有222x y xy +≥; (2)所有四边形的两条对角线都互相平分; (3)∃实数2a ≠且1b ≠-使22425a b a b +-+≤-;(4)存在实数x 使函数4()(0)f x x x x=+>取得最小值4.【考点】全称量词与存在量词 【难度】2星 【题型】解答【关键词】无【解析】 (1)是真命题,因为对任意实数,x y ,都有2222()0x y xy x y +-=-≥,∴222x y xy +≥.(2)是假命题,只有平行四边形才满足两条对角线互相平分,如梯形就不满足这个条件.(3)是假命题,因为2222425(2)(1)0a b a b a b +-++=-++≥,当且仅当2,1a b ==-时等号成立, 所以不存在实数对,a b ,使22(2)(1)0a b -++<,不存在即实数2a ≠且1b ≠-使22425a b a b +-+≤-.(4)是真命题,因为存在实数20x =>,使函数4()(0)f x x x x=+>取得最小值4.【答案】(1)是真命题,(2)是假命题,(3)是假命题,(4)是真命题。
逻辑联结词、量词 知识点+例题 分类全面

p或q联结起来,就得到一个新命题,记作=∈B x x{|(加以否定,得到一个新的命题,记作在全集U中的补集:答案 B解析 因为M N ,所以a ∈M ⇒a ∈N ,反之,则不成立,故“a ∈N ”是“a ∈M ”的必要而不充分条件.故选B.6.若命题p :对于任意x ∈[-1,1],有f (x )≥0,则对命题p 的否定是________.答案 存在x 0∈[-1,1],使f (x 0)<07.已知命题p :x 2+2x -3>0;命题q :13-x>1,若“⌝q 且p ”为真,则x 的取值范围是____________________. 答案 (-∞,-3)∪(1,2]∪[3,+∞)解析 因为“綈q 且p ”为真,即q 假p 真,而q 为真命题时,x -2x -3<0,得2<x <3,所以q 假时有x ≥3或x ≤2;p 为真命题时,由x 2+2x -3>0,解得x >1或x <-3,由⎩⎪⎨⎪⎧x >1或x <-3,x ≥3或x ≤2,解得x <-3或1<x ≤2或x ≥3, 所以x 的取值范围是x <-3或1<x ≤2或x ≥3.8.下列结论:①若命题p :∃x ∈R ,tan x =1;命题q :∀x ∈R ,x 2-x +1>0.则命题“p ∧(⌝q )”是假命题;②已知直线l 1:ax +3y -1=0,l 2:x +by +1=0,则l 1⊥l 2的充要条件是a b=-3; ③命题“若x 2-3x +2=0,则x =1”的逆否命题:“若x ≠1,则x 2-3x +2≠0”.其中正确结论的序号为________.答案 ①③解析 ①中命题p 为真命题,命题q 为真命题,所以p ∧(綈q )为假命题,故①正确;②当b =a =0时,有l 1⊥l 2,故②不正确;③正确.所以正确结论的序号为①③.9.已知c >0,且c ≠1,设p :函数y =c x 在R 上单调递减;q :函数f (x )=x 2-2cx +1在⎝⎛⎭⎫12,+∞上为增函数,若“p 且q ”为假,“p 或q ”为真,求实数c 的取值范围.解 ∵函数y =c x 在R 上单调递减,∴0<c <1.即p :0<c <1,∵c >0且c ≠1,∴綈p :c >1.又∵f (x )=x 2-2cx +1在⎝⎛⎭⎫12,+∞上为增函数,∴c ≤12. 即q :0<c ≤12,∵c >0且c ≠1,∴綈q :c >12且c ≠1. 又∵“p 或q ”为真,“p 且q ”为假,∴p 真q 假或p 假q 真.①当p 真,q 假时,{c |0<c <1}∩⎩⎨⎧⎭⎬⎫c |c >12且c ≠1=⎩⎨⎧⎭⎬⎫c |12<c <1. ②当p 假,q 真时,{c |c >1}∩⎩⎨⎧⎭⎬⎫c |0<c ≤12=∅. 综上所述,实数c 的取值范围是⎩⎨⎧⎭⎬⎫c |12<c <1. 能力提升训练。
专题02 命题与量词、基本逻辑联结词(理)(解析版)
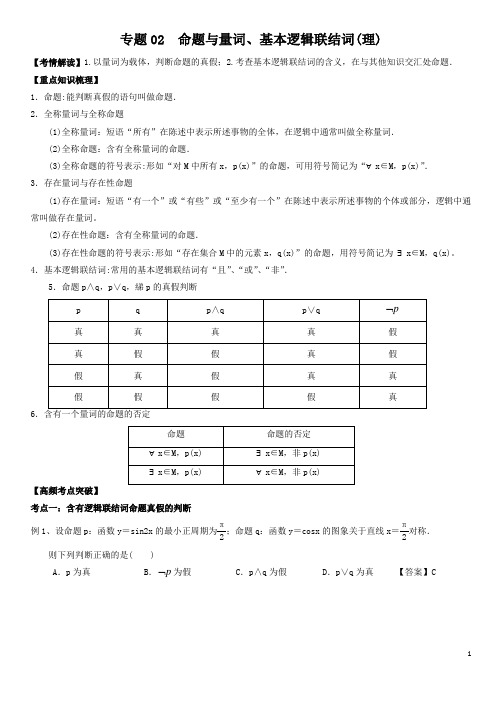
专题02 命题与量词、基本逻辑联结词(理)【考情解读】1.以量词为载体,判断命题的真假;2.考查基本逻辑联结词的含义,在与其他知识交汇处命题. 【重点知识梳理】1.命题:能判断真假的语句叫做命题. 2.全称量词与全称命题(1)全称量词:短语“所有”在陈述中表示所述事物的全体,在逻辑中通常叫做全称量词. (2)全称命题:含有全称量词的命题.(3)全称命题的符号表示:形如“对M 中所有x ,p(x)”的命题,可用符号简记为“∀x ∈M ,p(x)”. 3.存在量词与存在性命题(1)存在量词:短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词。
(2)存在性命题:含有全称量词的命题.(3)存在性命题的符号表示:形如“存在集合M 中的元素x ,q(x)”的命题,用符号简记为 ∃x ∈M ,q(x)。
4.基本逻辑联结词:常用的基本逻辑联结词有“且”、“或”、“非”.5.命题p ∧q ,p ∨q ,綈p 的真假判断6【高频考点突破】考点一:含有逻辑联结词命题真假的判断例1、设命题p :函数y =sin2x 的最小正周期为π2;命题q :函数y =cosx 的图象关于直线x =π2对称.则下列判断正确的是( )A .p 为真B .p ⌝为假C .p ∧q 为假D .p ∨q 为真 【答案】C【规律小结】“p ∧q ”、“p ∨q ”、“p ⌝”形式命题的真假判断步骤:(1)准确判断简单命题p 、q 的真假.(2)判断命题“p ∧q ”、“p ∨q ”、“非p ”的真假.其判断规律是: ①p ∨q :p 、q 中有一个为真,则p ∨q 为真,即一真全真;②p ∧q :p 、q 中有一个为假,则p ∧q 为假,即一假即假;③非p :与p 的真假相反.【变式探究】已知命题p 1:函数y =2x-2-x在R 上为增函数;p 2:函数y =2x+2-x在R 上为减函数, 则在命题q 1:p 1∨p 2,q 2:p 1∧p 2,q 3:(非p 1)∨p 2和q 4:p 1∧(非p 2)中,真命题是( )A .q 1,q 3B .q 2,q 3C .q 1,q 4D .q 2,q 4【解析】选C.p 1为真命题,p 2为假命题,∴非p 1为假命题,非p 2为真命题.故选C.【答案】C 考点二:全称(存在性)命题及真假判断例2.判断下列命题的真假.(1)∀x ∈R ,x 2-x +1>12; (2)∃α,β,cos(α-β)=cos α-cos β;(3)∀x ,y ∈N ,x -y ∈N ; (4)∃x 0,y 0∈Z ,2x 0+y 0=3. 【解析】(1)真命题,x 2-x +1=(x -12)2+34≥34>12. (2)真命题,如α=π4,β=π2符合题意.(3)假命题,如x =1,y =5,但x -y =-4∉N. (4)真命题,如x 0=0,y 0=3符合题意.【规律小结】(1)要判断全称命题是真命题,必须确定对集合中的每一个元素都成立,若是假命题,举一反例即可.(2)要判断存在性命题是真命题,只要在限定集合中,找到一个元素使得命题成立即可. 【变式探究】写出下列命题的否定形式,并判断其真假.(1)p :∀x ∈R ,x 2-x +14≥0; (2)s :至少存在一个实数x ,使x 3+1=0.【解析】(1)綈p :∃x ∈R ,x 2-x +14<0,是假命题,因为∀x ∈R ,x 2-x +14=⎝ ⎛⎭⎪⎫x -122≥0恒成立.(2)s :∀x ∈R ,x 3+1≠0,是假命题,因为当x =-1时,x 3+1=0. 考点三:求参数的取值范围例3、已知p :方程x 2+mx +1=0有两个不等的负实根;q :方程4x 2+4(m -2)x +1=0无实根,若p 或q 为真, p 且q 为假,求实数m 的取值范围.综上,m 的取值范围是m ≥3或1<m ≤2.【误区警示】在求m 的取值范围时,一是不注意端点值,二是由p ,q 的真假列关于m 的不等式不正确. 【方法技巧】1.有的“p 或q ”与“p 且q ”形式的复合命题语句中,字面上未出现“或”与“且”字,此时应从语句的陈述中搞清含义,从而分清是“p 或q ”还是“p 且q ”形式.一般地,若两个命题属于同时都要满足的为“且”,属于并列的为“或”.2.逻辑联结词中,较难理解含义的是“或”,应从以下两个方面来理解概念:(1)逻辑联结词中的“或”与集合中的“或”含义的一致性.(2)结合实例,剖析生活中的“或”与逻辑联结词中的“或”之间的区别.生活中的“或”一般指“或此或彼只必具其一,但不可兼而有之”,而逻辑联结词中的“或”具有“或此或彼或兼有”三种情形.3.“非”的含义就是对“命题的否定”.课标只要求能正确地对“含有一个量词的命题”进行否定.【变式探究】设集合A ={ (x ,y)|(x -4)2+y 2=1},B ={(x ,y)|(x -t)2+(y -at +2)2=1},如果命题“∃t ∈R ,A ∩B ≠∅”是真命题,则实数a 的取值范围是________. 答案:⎣⎢⎡⎦⎥⎤0,43【真题感悟】1.【2015新课标1】设命题p :2,2nn N n ∃∈>,则p ⌝为( )A.2,2n n N n ∀∈>B.2,2n n N n ∃∈≤C.2,2n n N n ∀∈≤D.2,=2nn N n ∃∈ 【答案】C 【解析】p ⌝:2,2nn N n ∀∈≤,故选C.2.【2015浙江】命题“**,()n N f n N ∀∈∈且()f n n ≤的否定形式是( )A.**,()n N f n N ∀∈∈且()f n n >B.**,()n N f n N ∀∈∈或()f n n >C.**00,()n N f n N ∃∈∈且00()f n n >D.**00,()n N f n N ∃∈∈或00()f n n > 【答案】D. 【解析】根据全称命题的否定是特称命题,可知选D.3.【2014陕西】原命题为“若z 1,z 2互为共轭复数,则|z 1|=|z 2|”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )A.真,假,真B.假,假,真C.真,真,假D.假,假,假 【答案】B4.【2014重庆】已知命题p :对任意x ∈R ,总有2x>0,q :“x>1”是“x>2”的充分不必要条件, 则下列命题为真命题的是( )A .p ∧qB .非p ∧非qC .非p ∧qD .p ∧非q 【答案】D5.【2013湖北】在一次跳伞中,甲、乙两位学员各跳一次,设命题p 是“甲降落在指定范围”, q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( )A .(⌝p)∨(⌝q)B .p ∨(⌝q)C .(⌝p)∧(⌝q)D .p ∨q 【答案】A 【解析】“至少一位学员没降落在指定区域”即“甲没降落在指定区域或乙没降落在指定区域”,可知选A. 【押题专练】1.下列命题中的假命题是( ).A .∃x 0∈R ,lgx 0=0B .∃x 0∈R ,tan x 0=1C .∀x ∈R ,x 3>0 D .∀x ∈R,2x>0 【答案】C2. 已知命题p :函数f(x)=⎝ ⎛⎭⎪⎫12x -log 13x 在区间⎝ ⎛⎭⎪⎫0,13内存在零点,命题q :存在负数x 使得⎝ ⎛⎭⎪⎫12x >⎝ ⎛⎭⎪⎫13x .给出下列四个命题:①p 或q ;②p 且q ;③p 的否定;④q 的否定.其中真命题的个数是( )A .1B .2C .3D .4 【解析】命题p 为假命题,命题q 也为假命题.利用真值表判断.【答案】B 3.命题“∀x >0,x 2+x >0”的否定是( ).A.∃x 0>0,x20+x 0>0B.∃x 0>0,x20+x 0≤0C.∀x >0,x 2+x ≤0D.∀x ≤0,x 2+x >0【解析】根据全称命题的否定是特称命题,可知该命题的否定是:∃x 0>0,x20+x 0≤0.【答案】B 4.已知p :|x -a|<4;q :(x -2)(3-x)>0,若非p 是非q 的充分不必要条件,则a 的取值范围为( ).A.a <-1或a >6B.a ≤-1或a ≥6C.-1≤a ≤6D.-1<a <6【解析】解不等式可得p :-4+a <x <4+a ,q :2<x <3,因此非p :x ≤-4+a 或x ≥4+a ,非q :x ≤2或x ≥3,于是由非p 是非q 的充分不必要条件,可知2≥-4+a 且4+a ≥3,解得-1≤a ≤6.【答案】C 5.若函数f(x)=-xe x,则下列命题正确的是( )A.∀a ∈⎝ ⎛⎭⎪⎫-∞,1e ,∃x ∈R ,f(x)>aB.∀a ∈⎝ ⎛⎭⎪⎫1e ,+∞,∃x ∈R ,f(x)>aC.∀x ∈R ,∃a ∈⎝ ⎛⎭⎪⎫-∞,1e ,f(x)>aD.∀x ∈R ,∃a ∈⎝ ⎛⎭⎪⎫1e ,+∞,f(x)>a 【解析】f ′(x)=-e x(x +1),由于函数f(x)在(-∞,-1)上递增,在(-1,+∞)上递减, 故f(x)max =f(-1)=1e ,故∀a ∈⎝ ⎛⎭⎪⎫-∞,1e ,∃x ∈R ,f(x)>a.【答案】A6.若函数f(x)=x 2+a x(a ∈R ),则下列结论正确的是( ).A.∀a ∈R ,f(x)在(0,+∞)上是增函数B.∀a ∈R ,f(x)在(0,+∞)上是减函数C.∃a ∈R ,f(x)是偶函数D.∃a ∈R ,f(x)是奇函数 【答案】C7.已知p :∃x 0∈R ,mx 20+2≤0.q :∀x ∈R ,x 2-2mx +1>0,若p ∨q 为假命题,则实数m 的取值范围是( ) A .[1,+∞) B .(-∞,-1] C .(-∞,-2] D .[-1,1] 【答案】A8.若命题“∃x 0∈R,2x20-3ax 0+9<0”为假命题,则实数a 的取值范围是________.【解析】因为“∃x 0∈R,2x20-3ax 0+9<0”为假命题,则“∀x ∈R,2x 2-3ax +9≥0”为真命题.因此Δ=9a 2-4×2×9≤0,故-22≤a ≤2 2.【答案】-22≤a ≤2 29.已知命题p :x 2+2x -3>0;命题q :13-x >1,若非q 且p 为真,则x 的取值范围是________.【答案】(-∞,-3)∪(1,2]∪[3,+∞)10.已知命题p :f(x)=1-2m x 在区间(0,+∞)上是减函数;命题q :不等式(x -1)2>m 的解集为R .若命题“p ∨q ”为真,命题“p ∧q ”为假,则实数m 的取值范围是________.【答案】0≤m<1211. 已知定义在R 上的函数f(x),写出命题”若对任意实数x 都有f(-x)=f(x),则f(x)为偶函数”的否定: .【解析】所给命题是全称命题,其否定为存在性命题. 【答案】若存在实数0x ,使得00()()f x f x -≠,则f(x)不是偶函数12.已知命题“∀x ∈R ,x 2-5x +152a >0”的否定为假命题,则实数a 的取值范围是________.【答案】⎝ ⎛⎭⎪⎫56,+∞13.已知命题p :∀x ∈[1,2],x 2-a ≥0,命题q :∃x 0∈R ,x20+2ax 0+2-a =0,若“p 且q ”为真命题, 求实数a 的取值范围.14.写出下列命题的否定,并判断真假.(1)q :∀x ∈R ,x 不是5x -12=0的根;(2)r :有些质数是奇数;(3)s :∃x 0∈R ,|x 0|>0.【解析】(1)非q :∃x 0∈R ,x 0是5x -12=0的根,真命题.(2)非r :每一个质数都不是奇数,假命题. (3)非s :∀x ∈R ,|x|≤0,假命题.15.设命题p :函数f(x)=x 3-ax -1在区间[-1,1]上单调递减;命题q :函数y =ln(x 2+ax +1)的值域是R . 如果命题p 或q 为真命题,p 且q 为假命题,求a 的取值范围.16.已知m ∈R ,命题p:对任意[08]x ∈,,不等式log 13(1)x +≥23m m-;命题q:对任意x ∈R ,不等式|1+sin2x-cos2x|2m ≤|cos()4x π-|恒成立. (1)若p 为真命题,求m 的取值范围; (2)若p 且q 为假,p 或q 为真,求m 的取值范围.故m 的取值范围是[1(2)⋃,+∞.。
高考数学总复习 72 逻辑联结词、量词课后作业 A 试题

智才艺州攀枝花市创界学校"【走向高考】2021年高考数学总复习7-2逻辑联结词、量词课后作业教A")A.∃x0∈Z,1<4x0<3 B.∃x0∈Z,5x0+1=0C.∀x∈R,x2-1=0 D.∀x∈R,x2+x+2>0[答案]D[解析]∵1<4x0<3,∴<x0<,这样的整数x0不存在,故A错误;∵5x0+1=0,∴x0=-∉Z,故B错误;∵x2-1=0,∴x=±1,故C错误;对任意实数x,都有x2+x+2=(x+)2+>0,应选D.∀x>0,都有x2-x≤0〞的否认是()A.∃x>0,使得x2-x≤0B.∃x>0,使得x2-x>0C.∀x>0,都有x2-x>0 D.∀x≤0,都有x2-x>0[答案]B∃x∈R,2x+x2≤1〞的否认是()A.∀x∈R,2x+x2B.∀x∈R,2x+x2C.∃x∈R,2x+x2D.∃x∈R,2x+x2[答案]A[解析]因为x=0时,20+02∀x∈R,2x+x23.“m>0>n〞是“方程mx2+ny2=1表示焦点在x轴上的双曲线〞的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件[答案]C[解析]当m>0,n<0时,方程mx2+nx2=1,化为-=1表示焦点在x轴上的双曲线,假设方程mx2+ny2=1表示焦点在x轴上的双曲线,那么应有m>0,n<0,应选C.4.(2021·理)对于数列{a n},“a n+1>|a n|(n=1,2,…)〞是“{a n}为递增数列〞的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件[答案]B[解析]对任意自然数n,a n+1>|a n|≥0,∴a n+1>a n,∴{a n}为递增数列;当取a n=n-4时,那么{a n}为递增数列,但a n+1>|a n|不一定成立,如a2>|a1|就不成立.5.(2021·七校联考)a,b为平面上两个不一共线的向量,p:|a+2b|=|a-2b|;q:a⊥b,那么p 是q的()A.充分不必要条件B.必要不充分条件C.既不充分也不必要条件D.充要条件[答案]D[解析]由于|a+2b|=|a-2b|⇔(a+2b)2=(a-2b)2⇔a·b=0⇔a⊥b,因此p是q的充要条件,选D.)①p:“∃x∈R,x2-2≥0〞的否认形式为綈p:“∀x∈R,x2-2<0〞;②假设綈p是q的必要条件,那么p是綈q的充分条件;③“m>n〞是“()m>()n〞的充分不必要条件.A.0B.1C.2D.3[答案]C[解析]①正确;∵綈p⇐q,∴綈q⇐p,根据充分条件与必要条件的相对性,可知②正确;“m>n〞是“()m>()n〞的既不充分也不必要条件,故③不正确.∃x∈R,2x2-3axa的取值范围是________.[答案]-2≤a≤2[解析]因为“∃x∈R,2x2-3ax∀x∈R,2x2-3axa2-4×2×9≤0,故-2≤a≤2.p:>0,那么綈p对应的x的集合为________.[答案]{x|-1≤x≤2}[解析]由p:>0得p:x>2或者x<-1,所以綈p对应的x值的取值范围是{x|-1≤x≤2}.[点评]此题易形成错解:∵p的否认綈p为≤0,即x2-x-2<0,解得1<x<2,错因是无视了隐含条件的限制作用.①假设“p且qp,q②a>b,那么2a>2b a≤b,那么2a≤2b-1〞;③“假设x∈R,那么x2④在△ABC中,“A>B〞是“sin A>sin B〞的充要条件.)A.4B.3C.2D.1[答案]D[解析]假设“p且qp和q①②③正确;在△ABC中,因为A>B,所以a>b,由正弦定理=,知sin A>sin B,反之亦成立,故④正确.)x2-3x-4=0,那么xx≠4,那么x2-3x-4≠0〞B.“x2-3x-4=0〞是“x=4〞的必要不充分条件C.假设p∧qp,qp:∃x∈R,使得x2+x+1<0,那么綈p:∀x∈R,都有x2+x+1≥0[答案]C[解析]x2-3x-4=0〞不能推出“x=4〞,但是“x=4〞能推出“x2-3x-4=0〞所以B正确;选项C 中假设p∧qp:∃x∈(-∞,0),2x<3x q:∀x∈(0,),cos x)A.p∧q B.p∨(綈q)C.(綈p)∧q D.p∧(綈q)[答案]C[解析]在x∈(-∞,0)上,y=2x的图象恒在y=3x的上方,所以不存在这样的x使得2x<3x pqp)∧q3.△ABC中“cos A=2sin B sin C〞是“△ABC为钝角三角形〞的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件[答案]B[解析]cos A=-cos(B+C)=-cos B cos C+sin B sin C=2sin B sin C,∴cos(B-C)=0.∴B-C=.∴B=+C>,故为钝角三角形,反之显然不成立,应选B.4.(2021·调研)以下结论:①p:∃x∈R,tan xq:∀x∈R,x2-xp∧(綈q②直线l1:ax+3y-1=0,l2:x+by+1=0,那么l1⊥l2的充要条件是=-3;③x2-3x+2=0,那么xx≠1,那么x2-3x+2≠0〞.其中正确结论的序号为________.(把你认为正确结论的序号都填上)[答案]①③[解析]①pqp∧(綈q①正确;②当b=a=0时,有l1⊥l2,故②不正确;③正确.所以正确结论的序号为①③.5.(2021·质检)给出以下四个结论:①∃x∈R,x2-x>0〞的否认是“∀x∈R,x2-x≤0〞②“假设am2<bm2,那么a<b③直线l1:ax+2y-1=0,l2:x+by+2=0,那么l1⊥l2的充要条件是=-2;④对于任意实数x,有f(-x)=-f(x),g(-x)=g(x)且x>0时,f′(x)>0,g′(x)>0,那么x<0时,f′(x)>g′(x).其中正确结论的序号是________.(填上所有正确结论的序号).[答案]①④[解析]①显然正确.②am2<bm2,那么a<ba<b,那么am2<bm2〞,当m③中l1⊥l2⇔a+2b=0,但a+2b =0与=-2不等价,∵当a=b=0时,=-2不成立,故③错;④由条件知,f(x)为奇函数,在x>0时单调增,故x<0时单调增,从而x<0时,f′(x)>0;g(x)为偶函数,x>0时单调增,从而x<0时单调减,∴x<0时,g′(x)<0,∴x<0时,f′(x)>g′(x),故④正确.6.(2021·调研)在平面直角坐标系xOy中,直线x+(m+1)y=2-m与直线mx+2y=-8互相垂直的充要条件是m=________.[答案]-[解析]x+(m+1)y=2-m与mx+2y=-8垂直⇔1·m+(m+1)·2=0,得m=-.①“数列{a n}为等比数列〞是“数列{a n a n+1}为等比数列〞的充分不必要条件;②“a=2〞是“函数f(x)=|x-a|在区间[2,+∞)上为增函数〞的充要条件;③m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;④设a、b、c分别是△ABC的三个内角A、B、C所对的边,假设a=1,b =,那么A=30°是B=60°的必要不充分条件;[答案]①④[解析]令b n=a n a n+1,那么假设{b n}是等比数列,那么=为常数,因此,当{a n}为等比数列时,{b n}为等比数列,但{b n}为等比数列时,{a n}未必为等比数列,如数列{a n}:1,2,3,6,9,18,…,对任意n∈N*,有a n+2=3a n,满足{a n a n+1}是等比数列,但{a n}不是等比数列,∴①真;a=2时,f(x)=|x-2|在[2,+∞)上单调增,但f(x)=|x-a|在[2,+∞)上单调增时,a≤2,故②错;由(m+3)m-6m=0得,m=0或者m =3,故m=3是两直线垂直的充分不必要条件,∴③错;由=知,sin B=sin A,∵b>a,∴B>A,故B=60°时,A=30°,但A=30°时,B可以为120°,∴④正确.p:在x∈[1,2]时,不等式x2+axq:函数f(x)=log(x2-2ax+3ap∨qa的取值范围.[解析]∵x∈[1,2]时,不等式x2+ax-2>0恒成立∴a>=-x在x∈[1,2]上恒成立令g(x)=-x,那么g(x)在[1,2]上是减函数,∴g(x)max=g(1)=1,∴ap真,那么a>1.又∵函数f(x)=log(x2-2ax+3a)是区间[1,+∞)上的减函数,∴u(x)=x2-2ax+3a是[1,+∞)上的增函数,且u(x)=x2-2ax+3a>0在[1,+∞)上恒成立,∴a≤1,u(1)>0,∴-1<a≤1,q真,那么-1<a≤1.p∨qa>-1.9.(理)动圆C过点A(-2,0),且与圆M:(x-2)2+y2=64相内切.(1)求动圆C的圆心的轨迹方程;(2)设直线l:y=kx+m(其中k,m∈Z)与(1)中所求轨迹交于不同两点B,D,与双曲线-=1交于不同两点E,F,问是否存在直线l,使得向量+=0,假设存在,指出这样的直线有多少条?假设不存在,请说明理由.[解析](1)圆M:(x-2)2+y2=64的圆心M的坐标为(2,0),半径R=8.∵|AM|=4<R,∴点A(-2,0)在圆M内.设动圆C的半径为r,圆心为C(x,y),依题意得r=|CA|,且|CM|=R-r,即|CM|+|CA|=8>|AM|.∴圆心C的轨迹是中心在原点,以A、M两点为焦点,长轴长为8的椭圆,设其方程为+=1(a>b>0),那么a=4,c=2,∴b2=a2-c2=12.∴所求动圆的圆心C的轨迹方程为+=1.(2)由,消去y化简整理得:(3+4k2)x2+8kmx+4m2-48=0,设B(x1,y1),D(x2,y2),那么x1+x2=-Δ1=(8km)2-4(3+4k2)(4m2-48)>0①由消去y化简整理得:(3-k2)x2-2kmx-m2-12=0.设E(x3,y3),F(x4,y4),那么x3+x4=,Δ2=(-2km)2+4(3-k2)(m2+12)>0②∵=(x4-x2,y4-y2)、=(x3-x1,y3-y1),且+=0,∴(x4-x2)+(x3-x1)=0,即x1+x2=x3+x4,∴-=,∴km=0或者-=.解得k=0或者m=0.当k=0时,由①、②得-2<m<2,∵m∈Z,∴m的值是-3,-2,-1,0,1,2,3;当m=0时,由①、②得-<k<,∵k∈Z,∴k=-1,0,1.∴满足条件的直线一共有9条.p1:∃x∈R,sin2+cos2=p2:∃x、y∈R,sin(x-y)=sin x-sin yp3:∀x∈[0,π],=sin xp4:sin x=cos y⇒x+y=)A.p1,p4B.p2,p4C.p1,p3D.p3,p4[答案]A[解析]∀x∈R,sin2+cos2=1,故p1∵∀x∈[0,π],sin x≥0,∴=|sin x|=sin x,∴p3真,应选A.①∀x∈R,不等式x2+2x>4x-3成立;②假设log2x+log x2≥2,那么x>1;③a>b>0且c<0,那么>④p:∀x∈R,x2q:∃x∈R,x2-2xp∧(綈q)A.①②③B.①②④C.①③④D.②③④[答案]A[解析]∵x2+2x-4x+3=x2-2x+3=(x-1)2+1>0恒成立,故①真;由log2x+log x2≥2知,x>0且x≠1,假设0<x<1,那么log2x<0,log x2<0,显然原不等式不成立,故x>1,∴②真;∵a>b>0,∴0<<,又c<0,∴>,∴a>b>0且c<0,那么>x,21-x,2x2x,lg(x+1),lg(x+3)成等差数列,那么甲是乙的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[答案]B[解析]由条件知甲:(21-x)2=x·2x2,∴2(1-x)=-x+x2,解得x=1或者-2;x+1)=lg x+lg(x+3),∴,∴x=1,∴甲是乙的必要不充分条件.4.(2021·高考调研)以下有关选项正确的选项是()A.假设p∨qp∧qB.“x=5〞是“x2-4x-5=0〞的充分不必要条件x<-1,那么x2-2x-3>0〞的否认为:“假设x≥-1,那么x2-3x+2≤0〞p:∃x∈R,使得x2+x-1<0,那么綈p:∃x∈R,使得x2+x-1≥0[答案]B[解析]p∨qp、q∴选项A错误;由x=5可以得到x2-4x-5=0,但由x2-4x-5=0不一定能得到x =5,∴5.(2021·二测)p:k>3;q:方程+=1表示双曲线,那么p是q的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件[答案]A[解析]由k>3得3-k<0,k-1>0,方程+=1表示双曲线,因此p是q的充分条件;反过来,由方程+=1表示双曲线不能得到k>3,如k=0时方程+=1也表示双曲线,因此p不是q的必要条件.综上所述,p是q的充分不必要条件,选A.w。
高考数学总复习考前必练系列03:逻辑联结词、量词

高考数学总复习考前必练03:逻辑联结词、量词一、选择题1.(2015·浙江)命题“∀n ∈N *,f (n )∈N *且f (n )≤n ”的否定形式是( ) A .∀n ∈N *,f (n )∉N *且f (n )>n B .∀n ∈N *,f (n )∉N *或f (n )>n C .∃n 0∈N *,f (n 0)∉N *且f (n 0)>n 0 D .∃n 0∈N *,f (n 0)∉N *或f (n 0)>n 02.(2016·肇庆统测)设a ,b ,c 是非零向量,已知命题p :若a·b =0,则a ⊥b ;命题q : 若a ∥b ,b ∥c ,则a ∥c .则下列命题中假命题是( ) A .p ∧q B .p ∨qC .(綈p )∨qD .(綈p )∨(綈q )3.若“∃x ∈[12,2],使得2x 2-λx +1<0成立”是假命题,则实数λ的取值范围为( )A .(-∞,22]B .[22,3]C .[-22,3]D .λ=34.已知命题p :∀x ∈[1,2],x 2-a ≥0,命题q :∃x ∈R ,x 2+2ax +2-a =0,若“p 且q ”为真命题,则( ) A .a =1或a ≤-2 B .a ≤-2或1≤a ≤2 C .a ≥1D .-2≤a ≤15.已知命题p :∃x 0∈R ,使sin x 0=52;命题q :∀x ∈R ,都有x 2+x +1>0.给出下列结论:①命题“p ∧q ”是真命题;②命题“p ∧(綈q )”是假命题;③命题“(綈p )∨q ”是真命题;④命题“(綈p )∨(綈q )”是假命题.其中正确的命题是( ) A .②③ B .②④ C .③④D .①②③需要高中数学所有必修选修视频课程,联系QQ/微信:1403225658 6.(2016·临夏期中)下列结论错误的是( )A .命题“若p ,则q ”与命题“若綈q ,则綈p ”互为逆否命题B .命题p :∀x ∈[0,1],e x ≥1,命题q :∃x ∈R ,x 2+x +1<0,则p ∨q 为真 C .若p ∨q 为假命题,则p ,q 均为假命题 D .“若am 2<bm 2,则a <b ”的逆命题为真命题7.(2016·葫芦岛期中)已知命题P :不等式lg[x (1-x )+1]>0的解集为{x |0<x <1};命题Q :在△ABC 中,“A >B ”是“cos 2⎝ ⎛⎭⎪⎫A 2+π4<cos 2⎝ ⎛⎭⎪⎫B 2+π4”成立的必要不充分条件,则( )A .P 真Q 假B .P ∧Q 为真C .P ∨Q 为假D .P 假Q 真8.(2016·怀仁期中)已知命题p :∀x ∈[-1,2],函数f (x )=x 2-x 的值大于0.若p ∨q 是真命题,则命题q 可以是( ) A .∃x ∈(-1,1),使得cos x <12B .“-3<m <0”是“函数f (x )=x +log 2x +m 在区间⎝ ⎛⎭⎪⎫12,2上有零点”的必要不充分条件 C .直线x =π6是曲线f (x )=3sin 2x +cos 2x 的一条对称轴D .若x ∈(0,2),则在曲线f (x )=e x(x -2)上任意一点处的切线的斜率不小于-1 需要高中数学所有必修选修视频课程,联系QQ/微信:1403225658 二、填空题9.命题p 的否定是“对所有正数x ,x >x +1”,则命题p 可写为________________________. 10.给出以下命题:①∀x ∈R ,|x |>x ;②∃α∈R ,sin 3α=3sin α;③∀x ∈R ,x >sin x ; ④∃x ∈(0,+∞),(12)x <(13)x,其中正确命题的序号有________.11.(2017·石家庄质检)已知命题p :x 2-3x -4≤0,命题q :x 2-6x +9-m 2≤0,若綈q是綈p的充分不必要条件,则实数m的取值范围是________________.12.设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x>2+ax在x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a 的取值范围为__________.答案精析1.D [由全称命题与特称命题之间的互化关系知选D.]2.D [对于命题p ,由平面向量数量积a·b =0易得a ⊥b ,则命题p 为真命题;对于命题q ,∵a ,b ,c 为非零向量,则q 为真命题,故(綈p )∨(綈q )为假命题,故选D.]3.A [设命题p :∃x ∈[12,2],使得2x 2-λx +1<0,由于命题p 为假命题,所以綈p 为真命题,即∀x ∈[12,2],2x 2-λx +1≥0为真命题,即λ≤2x 2+1x =2x +1x 在区间[12,2]上恒成立,所以只需满足λ≤(2x +1x )min (x ∈[12,2])即可,2x +1x ≥22x ·1x=22,当且仅当2x =1x ,即x =22∈[12,2]时等号成立,所以λ≤22,故选A.]4.A [命题p :∀x ∈[1,2],x 2-a ≥0真,则a ≤1. 命题q :∃x ∈R ,x 2+2ax +2-a =0真, 则Δ=4a 2-4(2-a )≥0,a ≥1或a ≤-2, 又p 且q 为真命题, 所以a =1或a ≤-2.故选A.]需要高中数学所有必修选修视频课程,联系QQ/微信:1403225658 5.A [∵52>1,∴命题p 是假命题,又∵x 2+x +1=(x +12)2+34≥34>0,∴命题q 是真命题,由命题真假的真值表可以判断②③正确.]6.D [命题“若p ,则q ”的逆否命题是“若綈q ,则綈p ”,所以命题“若p ,则q ”与命题“若綈q ,则綈p ”互为逆否命题,故A 正确;命题p :∀x ∈[0,1],e x≥1,为真命题,命题q :∃x ∈R ,x 2+x +1<0,为假命题,则p ∨q 为真,故B 正确;若p ∨q 为假命题,则p ,q 均为假命题,故C 正确;“若am 2<bm 2,则a <b ”的逆命题为“若a <b ,则am 2<bm 2”,而当m 2=0时,由a <b ,得am 2=bm 2,所以“若am 2<bm 2,则a <b ”的逆命题为假命题,故D 不正确.]7.A [由命题P :不等式lg[x (1-x )+1]>0,可知x (1-x )+1>1, ∴0<x <1,即不等式的解集为{x |0<x <1},∴命题P 为真命题.由命题Q 知,若cos 2⎝ ⎛⎭⎪⎫A 2+π4<cos 2⎝ ⎛⎭⎪⎫B 2+π4, 即sin A >sin B ,∴A >B ; 反之,在三角形中,若A >B , 则必有sin A >sin B ,即cos 2⎝ ⎛⎭⎪⎫A 2+π4<cos 2⎝ ⎛⎭⎪⎫B 2+π4成立,∴命题Q 为假命题.故选A.]8.C [对于命题p :函数f (x )=x 2-x =⎝ ⎛⎭⎪⎫x -122-14,则函数f (x )在⎣⎢⎡⎭⎪⎫-1,12上单调递减,在⎝ ⎛⎦⎥⎤12,2上单调递增,∴当x =12时,取得最小值,f ⎝ ⎛⎭⎪⎫12=-14<0,因此命题p 是假命题.若p ∨q 是真命题,则命题q 必须是真命题.∀x ∈(-1,1),cos x ∈(cos 1,1],而cos 1>cos π3=12,因此A 是假命题;函数f (x )=x +log 2x +m 在区间⎝ ⎛⎭⎪⎫12,2上单调递增,若函数f (x )在此区间上有零点,则f ⎝ ⎛⎭⎪⎫12·f (2)=⎝ ⎛⎭⎪⎫12-1+m (2+1+m )<0,解得-3<m <12,因此“-3<m <0”是“函数f (x )=x +log 2x +m 在区间⎝ ⎛⎭⎪⎫12,2上有零点”的充分不必要条件,因此B 是假命题;f (x )=3sin 2x +cos 2x =2sin ⎝⎛⎭⎪⎫2x +π6,当x =π6时,sin ⎝ ⎛⎭⎪⎫2×π6+π6=sin π2=1,因此直线x =π6是曲线f (x )的一条对称轴,是真命题;曲线f (x )=e x(x -2),f ′(x )=e x+e x(x -2)=e x(x -1),当x ∈(0,2)时,f ′(x )>f ′(0)=-1,因此D 是假命题.]需要高中数学所有必修选修视频课程,联系QQ/微信:1403225658 9.∃x 0∈(0,+∞),x 0≤x 0+1解析 因为p 是綈p 的否定,所以只需将全称命题变为特称命题,再对结论否定即可. 10.②解析 当x ≥0时,|x |=x ,①错;当α=0时,sin 3α=3sin α,②正确;当x =-π2时,x <sin x ,③错;根据指数函数的图象可以判断,当x ∈(0,+∞)时,(12)x >(13)x ,④错.故正确命题的序号只有②. 11.{m |m ≤-4或m ≥4}解析 ∵綈q 是綈p 的充分不必要条件, ∴p 是q 的充分不必要条件, ∴{x |x 2-3x -x |x 2-6x +9-m 2≤0},∴{x |-1≤x x |(x +m -3)(x -m -3)≤0}.当-m +3=m +3,即m =0时,不合题意. 当-m +3>m +3,即m <0时,有 {x |-1≤xx |m +3≤x ≤-m +3},此时⎩⎪⎨⎪⎧m +3≤-1,-m +3≥4,(两等号不能同时取得)解得m ≤-4.当-m +3<m +3,即m >0时,有 {x |-1≤xx |-m +3≤x ≤m +3},此时⎩⎪⎨⎪⎧-m +3≤-1,m +3≥4,(两等号不能同时取得)解得m ≥4.综上,实数m 的取值范围是{m |m ≤-4或m ≥4}. 12.[1,2]解析 对于命题p :Δ<0且a >0,故a >2;对于命题q :a >2x -2x+1在x ∈(-∞,-1)上恒成立,又函数y =2x -2x +1为增函数,所以2x -2x+1<1,故a ≥1,命题“p ∨q ”为真命题,命题“p ∧q ”为假命题,等价于p ,q 一真一假.故1≤a ≤2.。
高考数学总复习 第一章 第2课时 命题与量词、基本逻辑联结词课时闯关(含解析) 新人教版

2013年高考数学总复习 第一章 第2课时 命题与量词、基本逻辑联结词课时闯关(含解析) 新人教版一、选择题1.(2010·高考湖南卷)下列命题中的假命题是( )A .∃x ∈R ,lg x =0B .∃x ∈R ,tan x =1C .∀x ∈R ,x 3>0D .∀x ∈R,2x >0解析:选C.对于A ,当x =1时,lg x =0,正确;对于B ,当x =π4时,tan x =1,正确;对于C ,当x <0时,x 3<0,错误;对于D ,∀x ∈R,2x >0,正确.2.(2011·高考北京卷)若p 是真命题,q 是假命题,则( )A .p ∧q 是真命题B .p ∨q 是假命题C .¬p 是真命题D .¬q 是真命题解析:选D.根据“且”“或”“非”命题的真假判定法则知D 正确.3.下列理解错误的是( )A .命题“3≤3”是p 且q 形式的复合命题,其中p :3<3,q :3=3.所以“3≤3”是假命题B .“2是偶质数”是一个p 且q 形式的复合命题,其中p :2是偶数,q :2是质数C .“不等式|x |<-1无实数解”的否定形式是“不等式|x |<-1有实数解”D .“2011>2012或2012>2011”是真命题答案:A4.下列命题中,真命题是( )A .∃m ∈R ,使函数f (x )=x 2+mx (x ∈R )是偶函数B .∃m ∈R ,使函数f (x )=x 2+mx (x ∈R )是奇函数C .∀m ∈R ,函数f (x )=x 2+mx (x ∈R )都是偶函数D .∀m ∈R ,函数f (x )=x 2+mx (x ∈R )都是奇函数解析:选A.对于选项A ,∃m ∈R ,即当m =0时,f (x )=x 2+mx =x 2是偶函数.故A 正确.5.(2011·高考山东卷)已知a ,b ,c ∈R ,命题“若a +b +c =3,则a 2+b 2+c 2≥3”的否命题是( )A .若a +b +c ≠3,则a 2+b 2+c 2<3B .若a +b +c =3,则a 2+b 2+c 2<3C .若a +b +c ≠3,则a 2+b 2+c 2≥3D .若a 2+b 2+c 2≥3,则a +b +c =3解析:选A.由于一个命题的否命题既否定题设又否定结论,因此原命题的否命题为“若a +b +c ≠3,则a 2+b 2+c 2<3”.二、填空题6.在“¬p ”,“p ∧q ”,“p ∨q ”形式的命题中,“p ∨q ”为真,“p ∧q ”为假,“¬p ”为真,那么p ,q 的真假为p ________,q ________.解析:∵“p ∨q ”为真,∴p ,q 至少有一个为真.又“p ∧q ”为假,∴p ,q 一个为假,一个为真.而“¬p ”为真,∴p 为假,q 为真.答案:假 真7.给定下列几个命题:①“x =π6”是“sin x =12”的充分不必要条件; ②若“p ∨q ”为真,则“p ∧q ”为真;③等底等高的三角形是全等三角形的逆命题.其中为真命题的是________.(填上所有正确命题的序号)解析:①中,若x =π6,则sin x =12,但sin x =12时,x =π6+2k π或5π6+2k π(k ∈Z ).故“x =π6”是“sin x =12”的充分不必要条件,故①为真命题;②中,令p 为假命题,q 为真命题,有“p ∨q ”为真命题,而“p ∧q ”为假命题,故②为假命题;③为真命题.答案:①③8.命题“∀x ∈R ,∃m ∈Z ,m 2-m <x 2+x +1”是________命题.(填“真”或“假”)解析:由于∀x ∈R ,x 2+x +1=(x +12)2+34≥34,因此只需m 2-m <34,即-12<m <32,所以当m =0或m =1时,∀x ∈R ,m 2-m <x 2+x +1成立,因此命题是真命题.答案:真三、解答题9.(2012·德州质检)写出下列命题的否定,并判断其真假.(1)q :所有的正方形都是矩形;(2)r :∃x ∈R ,x 2+2x +2≤0.解:(1)¬q :至少存在一个正方形不是矩形,是假命题.(2)¬r :∀x ∈R ,x 2+2x +2>0,是真命题.10.已知命题p :方程2x 2-2 6x +3=0的两根都是实数,q :方程2x 2-2 6x +3=0的两根不相等,试写出由这组命题构成的“p 或q ”、“p 且q ”、“非p ”形式的复合命题,并指出其真假.解:“p 或q ”的形式:方程2x 2-2 6x +3=0的两根都是实数或不相等.“p 且q ”的形式:方程2x 2-2 6x +3=0的两根都是实数且不相等.“非p ”的形式:方程2x 2-2 6x +3=0无实根.∵Δ=24-24=0,∴方程有两相等的实根.∵p 真,q 假,∴“p 或q ”真,“p 且q ”假,“非p ”假.11.(探究选做)已知命题p :“∀x ∈[1,2],x 2-a ≥0”,命题q :“∃x 0∈R ,x 20+2ax 0+2-a =0”,若命题“p 且q ”是真命题,求实数a 的取值范围.解:由“p 且q ”是真命题,知p 为真命题,q 也为真命题.若p 为真命题,则a ≤x 2恒成立.∵x ∈[1,2],∴a ≤1.若q 为真命题,即x 2+2ax +2-a =0有实根,Δ=4a 2-4(2-a )≥0,即a ≥1或a ≤-2,综上,实数a 的取值范围为a ≤-2或a =1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考总复习命题量词逻辑连接词习题及详解⑴、选择题1.(2010·广东惠州一中)如果命题“綈(p ∨q )”是真命题,则正确的是( ) A .p 、q 均为真命题B .p 、q 中至少有一个为真命题C .p 、q 均为假命题D .p 、q 中至多有一个为真命题 [答案] C[解析] ∵命题“綈(p ∨q )”为真命题, ∴命题“p ∨q ”为假命题, ∴命题p 和命题q 都为假命题.2.(2010·胶州三中)命题:“若x 2<1,则-1<x <1”的逆否命题是( ) A .若x 2≥1,则x ≥1,或x ≤-1 B .若x ≥1,且x ≤-1,则x 2>1 C .若-1<x <1,则x 2<1D .若x ≥1,或x ≤-1,则x 2≥1 [答案] D3.(文)(2010·延边州质检)下列说法错误..的是( ) A .如果命题“綈p ”与命题“p 或q ”都是真命题,那么命题q 一定是真命题; B .命题“若a =0,则ab =0”的否命题是:“若a ≠0,则ab ≠0”; C .若命题p :∃x ∈R ,x 2-x +1<0,则綈p :∀x ∈R ,x 2-x +1≥0; D .“sin θ=12”是“θ=30°”的充分不必要条件.[答案] D[解析] ∵“綈p ”为真,∴p 为假,又“p 或q ”为真,∴q 为真,故A 正确;B 、C 显然正确;∵θ=30°时,sin θ=12,但sin θ=12时,θ不一定为30°,故“sin θ=12”是“θ=30°”的必要不充分条件.(理)(2010·广东高考调研)下列有关选项正确的是( ) A .若p ∨q 为真命题,则p ∧q 为真命题B .“x =5”是“x 2-4x -5=0”的充分不必要条件C .命题“若x <-1,则x 2-2x -3>0”的否定为:“若x ≥-1,则x 2-3x +2≤0”D .已知命题p :∃x ∈R ,使得x 2+x -1<0,则綈p :∃x ∈R ,使得x 2+x -1≥0 [答案] B[解析] 由复合命题真值表知:若p ∨q 为真命题,则p 、q 至少有一个为真命题,有可能一真一假,∴选项A 错误;由x =5可以得到x 2-4x -5=0,但由x 2-4x -5=0不一定能得到x =5,∴选项B 成立;选项C 错在把命题的否定写成了否命题;选项D 错在没有搞清楚存在性命题的否定是全称命题.4.(文)(2010·福建南平一中)已知命题p :∀x ∈R ,x >sin x ,则( ) A .綈p :∃x ∈R ,x <sin x B .綈p :∀x ∈R ,x ≤sin x C .綈p :∃x ∈R ,x ≤sin x D .綈p :∀x ∈R ,x <sin x [答案] C[解析] 对全称命题的否定既要否定量词又要否定结论,故选C. (理)(2010·北京市延庆县模考)下列命题中的真命题是( ) A .∃x ∈R 使得sin x +cos x =1.5 B .∀x ∈(0,π),sin x >cos x C .∃x ∈R 使得x 2+x =-1 D .∀x ∈(0,+∞),e x >x +1 [答案] D[解析] ∵对∀x ∈R ,sin x +cos x =2sin ⎝⎛⎭⎫x +π4≤2<1.5,∴A 错;又当x =π6时,sin x =12,cos x =32,∴B 错;∵方程x 2+x +1=0的判别式Δ=-3<0,∴方程x 2+x =-1无实数根,故C 错;令f (x )=e x -x -1,则f ′(x )=e x -1,当x ∈(0,+∞)时,f ′(x )>0,∴f (x )在(0,+∞)上为增函数,∴f (x )>f (0)=0,故对∀x ∈(0,+∞)都有e x >x +1.5.(文)(2010·山东枣庄模考)设集合A ={x |-2-a <x <a ,a >0},命题p :1∈A ,命题q :2∈A .若p ∨q 为真命题,p ∧q 为假命题,则a 的取值范围是( )A .0<a <1或a >2B .0<a <1或a ≥2C .1<a ≤2D .1≤a ≤2[答案] C[解析] ∵1∈A ,∴-2-a <1<a ,∴a >1, ∵2∈A ,∴-2-a <2<a ,∴a >2, ∵p ∨q 为真,p ∧q 为假, ∴p 与q 一真一假,故1<a ≤2.(理)(2010·济南一中)已知命题p :∃x ∈R ,mx 2+1≤0,命题q :∀x ∈R ,x 2+mx +1>0.若p ∨q 为假命题,则实数m 的取值范围是( )A .m ≥2B .m ≤-2C .m ≤-2或m ≥2D .-2≤m ≤2[答案] A[解析] 若p ∨q 为假命题,则p 、q 均为假命题,即綈p :∀x ∈R ,mx 2+1>0,与綈q :∃x ∈R ,x 2+mx +1≤0均为真命题,根据綈p :∀x ∈R ,mx 2+1>0为真命题可得m ≥0,根据綈q :∃x ∈R ,x 2+mx +1≤0为真命题可得Δ=m 2-4≥0,解得m ≥2或m ≤-2.综上,m ≥2.6.(2010·天津文)下列命题中,真命题是( ) A .∃m ∈R ,使函数f (x )=x 2+mx (x ∈R )是偶函数 B .∃m ∈R ,使函数f (x )=x 2+mx (x ∈R )是奇函数 C .∀m ∈R ,使函数f (x )=x 2+mx (x ∈R )都是偶函数 D .∀m ∈R ,使函数f (x )=x 2+mx (x ∈R )都是奇函数[分析] 由函数f (x )是奇(或偶)函数时,m 的取值情况作出判断. [答案] A[解析] 当m =0时,f (x )=x 2显然为偶函数,故选A. 7.(2010·北京延庆县模考)下列命题中的假命题是( ) A .∀x >0且x ≠1,都有x +1x>2B .∀a ∈R ,直线ax +y =a 恒过定点(1,0)C .∃m ∈R ,使f (x )=(m -1)·xm 2-4m +3是幂函数D .∀φ∈R ,函数f (x )=sin(2x +φ)都不是偶函数 [答案] D[解析] ∵x +1x ≥2等号在x =1时成立,∴A 真;将x =1,y =0代入直线方程ax +y =a中成立,∴B 真;令m -1=1得m =2,此时f (x )=x -1是幂函数,故C 真;当φ=π2时,f (x )=sin ⎝⎛⎭⎫2x +π2=cos2x 为偶函数,故D 假. 8.(09·海南、宁夏)有四个关于三角函数的命题: p 1:∃x ∈R ,sin 2x 2+cos 2x 2=12p 2:∃x 、y ∈R ,sin(x -y )=sin x -sin y p 3:∀x ∈[0,π],1-cos2x2=sin x p 4:sin x =cos y ⇒x +y =π2其中假命题的是( ) A .p 1,p 4 B .p 2,p 4 C .p 1,p 3D .p 3,p 4[答案] A[解析] ∀x ∈R ,sin 2x 2+cos 2x2=1,故p 1为假命题.∵∀x ∈[0,π],sin x ≥0, ∴1-cos2x2=|sin x |=sin x ,∴p 3真,故选A. 9.已知命题p :|x -1|+|x +1|≥3a 恒成立,命题q :y =(2a -1)x 为减函数,若“p ∧q ”为真命题,则a 的取值范围是( )A .a ≤23B .0<a <12C.12<a ≤23D.12<a <1 [答案] C[解析] 因为|x -1|+|x +1|≥2,由|x -1|+|x +1|≥3a 恒成立知:3a ≤2,即a ≤23.由y =(2a -1)x 为减函数得:0<2a -1<1即12<a <1.又因为“p ∧q ”为真命题,所以,p 和q 均为真命题,所以取交集得12<a ≤23.因此选C.10.(2010·浙江杭州质检)下列命题中正确的是( )A .设f (x )=sin ⎝⎛⎭⎫2x +π3,则∀x ∈⎝⎛⎭⎫-π3,π6,必有f (x )<f (x +0.1) B .∃x 0∈R ,使得12sin x 0+32cos x 0>1C .设f (x )=cos ⎝⎛⎭⎫x +π3,则函数y =f ⎝⎛⎭⎫x +π6是奇函数 D .设f (x )=2sin2x ,则f ⎝⎛⎭⎫x +π3=2sin ⎝⎛⎭⎫2x +π3 [答案] C[解析] ∵f (x )=sin ⎝⎛⎭⎫2x +π3在⎝⎛⎭⎫-π3,π12上单调递增,在⎣⎡⎦⎤π12,π6上单调递减,∴A 错;12sin x 0+32cos x 0=sin ⎝⎛⎭⎫x 0+π3≤1,故B 不正确;y =f ⎝⎛⎭⎫x +π6=cos ⎝⎛⎭⎫x +π2=-sin x ,为奇函数,故C 正确;f ⎝⎛⎭⎫x +π3=2sin ⎝⎛⎭⎫2⎝⎛⎭⎫x +π3=2sin ⎝⎛⎭⎫2x +2π3,故D 不正确. 二、填空题11.已知下列四个命题:①a 是正数;②b 是负数;③a +b 是负数;④ab 是非正数.选择其中两个作为题设,一个作为结论,写出一个逆否命题是真命题的复合命题____________________________________.[答案] 若a 是正数且a +b 是负数,则一定有b 是负数[解析] 逆否命题为真命题,即该命题为真,a 是正数且a +b 是负数,则一定有b 是负数.12.给出以下四个关于圆锥曲线的命题,①设A 、B 为两个定点,k 为非零常数,若|P A →|-|PB →|=k ,则动点P 的轨迹为双曲线; ②过定圆C 上一定点A 作圆的动弦AB ,O 为坐标原点,若OP →=12(OA →+OB →),则动点P的轨迹为椭圆;③方程2x 2-5x +2=0的两根可分别作为椭圆和双曲线的离心率; ④双曲线x 225-y 29=1与椭圆x 235+y 2=1有相同的焦点.其中真命题的序号为________(写出所有真命题的序号). [答案] ③④[解析] ①表示双曲线的一支;②动点P 的轨迹为圆;③两根x 1=2,x 2=12正确;④25+9=35-1正确.13.(2010·南昌市模拟)给出下列命题:①“数列{a n }为等比数列”是“数列{a n a n +1}为等比数列”的充分不必要条件;②“a =2”是“函数f (x )=|x -a |在区间[2,+∞)上为增函数”的充要条件;③m =3是直线(m +3)x +my -2=0与直线mx -6y +5=0互相垂直的充要条件;④设a 、b 、c 分别是△ABC 的三个内角A 、B 、C 所对的边,若a =1,b =3,则A=30°是B =60°的必要不充分条件;其中真命题的序号是________(写出所有真命题的序号). [答案] ①④[解析] 令b n =a n a n +1,则若{b n }是等比数列,则b n +1b n =a n +2a n为常数,因此,当{a n }为等比数列时,{b n }为等比数列,但{b n }为等比数列时,{a n }未必为等比数列,如数列{a n }:1,2,3,6,9,18,…,对任意n ∈N *,有a n +2=3a n ,满足{a n a n +1}是等比数列,但{a n }不是等比数列,∴①真;a =2时,f (x )=|x -2|在[2,+∞)上单调增,但f (x )=|x -a |在[2,+∞)上单调增时,a ≤2,故②错;由(m +3)m -6m =0得,m =0或m =3,故m =3是两直线垂直的充分不必要条件,∴③错;由1sin A =3sin B 知,sin B =3sin A ,∵b >a ,∴B >A ,故B =60°时,A =30°,但A =30°时,B 可以为120°,∴④正确.14.(2010·马鞍山市质检)给出下列四个结论:①命题“∃x ∈R ,x 2-x >0”的否定是“∀x ∈R ,x 2-x ≤0” ②“若am 2<bm 2,则a <b ”的逆命题为真;③已知直线l 1:ax +2y -1=0,l 2:x +by +2=0,则l 1⊥l 2的充要条件是ab =-2;④对于任意实数x ,有f (-x )=-f (x ),g (-x )=g (x )且x >0时,f ′(x )>0,g ′(x )>0,则x <0时,f ′(x )>g ′(x ).其中正确结论的序号是________.(填上所有正确结论的序号). [答案] ①④[解析] ①显然正确.②中命题“若am 2<bm 2,则a <b ”的逆命题是“若a <b ,则am 2<bm 2”,当m =0时不成立,故为假命题;③中l 1⊥l 2⇔a +2b =0,但a +2b =0与ab =-2不等价,∵当a =b =0时,ab =-2不成立,故③错;④由条件知,f (x )为奇函数,在x >0时单调增,故x <0时单调增,从而x <0时,f ′(x )>0;g (x )为偶函数,x >0时单调增,从而x <0时单调减,∴x <0时,g ′(x )<0,∴x <0时,f ′(x )>g ′(x ),故④正确. 三、解答题15.(2010·河南调研)已知函数f (x )=2sin x +π3+sin x cos x -3sin 2x ,x ∈R .(1)求函数f (x )的最小正周期;(2)若存在x 0∈⎣⎡⎦⎤0,5π12,使不等式f (x 0)<m 成立,求实数m 的取值范围. [解析] (1)f (x )=2sin x cos π3+cos x sin π3+sin x cos x -3sin 2x=2sin x cos x +3cos 2x -3sin 2x =sin2x +3cos2x =2sin ⎝⎛⎭⎫2x +π3. ∴函数f (x )的最小正周期T =2π2=π.(2)当x ∈⎣⎡⎦⎤0,5π12时,2x +π3∈⎣⎡⎦⎤π3,7π6. ∴当2x +π3=7π6,即x =5π12时,f (x )取最小值-1.故使题设成立的充要条件是m >-1, 即m 的取值范围是(-1,+∞).16.(2010·聊城市模拟)在平面直角坐标系xOy 中,直线l 与抛物线y 2=2x 相交于A 、B 两点.(1)求证:“如果直线l 过点T (3,0),那么OA →·OB →=3”是真命题; (2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由. [解析] (1)设过点T (3,0)的直线l 交抛物线y 2=2x 于点A (x 1,y 1),B (x 2,y 2).当直线l 的斜率不存在时,直线l 的方程为x =3,此时,直线l 与抛物线相交于点A (3,6)、B (3,-6). ∴OA →·OB →=3.当直线l 的斜率存在时,设直线l 的方程为y =k (x -3),其中k ≠0.由⎩⎪⎨⎪⎧y 2=2x y =k (x -3)得,ky 2-2y -6k =0,则y 1y 2=-6. 又∵x 1=12y 12,x 2=12y 22,∴OA →·OB →=x 1x 2+y 1y 2 =14(y 1y 2)2+y 1y 2=3. 综上所述,命题“如果直线l 过点T (3,0),那么OA →·OB →=3”是真命题.(2)逆命题是:设直线l 交抛物线y 2=2x 于A 、B 两点,如果OA →·OB →=3,那么直线过点T (3,0).该命题是假命题.例如:取抛物线上的点A (2,2),B ⎝⎛⎭⎫12,1,此时OA →·OB →=3,直线AB 的方程为y =23(x +1),而T (3,0)不在直线AB 上.17.(文)已知命题p :在x ∈[1,2]时,不等式x 2+ax -2>0恒成立;命题q :函数f (x )=log13(x 2-2ax +3a )是区间[1,+∞)上的减函数.若命题“p ∨q ”是真命题,求实数a 的取值范围.[解析] ∵x ∈[1,2]时,不等式x 2+ax -2>0恒成立 ∴a >2-x 2x =2x -x 在x ∈[1,2]上恒成立令g (x )=2x -x ,则g (x )在[1,2]上是减函数,∴g (x )max =g (1)=1, ∴a >1.即若命题p 真,则a >1.又∵函数f (x )=log 13(x 2-2ax +3a )是区间[1,+∞)上的减函数,∴u (x )=x 2-2ax +3a 是[1,+∞)上的增函数,且u (x )=x 2-2ax +3a >0在[1,+∞)上恒成立,∴a ≤1,u (1)>0,∴-1<a ≤1, 即若命题q 真,则-1<a ≤1. 若命题“p ∨q ”是真命题,则a >-1.(理)(2010·河北正定中学模拟)已知动圆C 过点A (-2,0),且与圆M :(x -2)2+y 2=64相内切.(1)求动圆C 的圆心C 的轨迹方程;(2)设直线l :y =kx +m (其中k ,m ∈Z )与(1)中所求轨迹交于不同两点B ,D ,与双曲线x 24-y 212=1交于不同两点E ,F ,问是否存在直线l ,使得向量DF →+BE →=0,若存在,指出这样的直线有多少条?若不存在,请说明理由.[解析](1)圆M:(x-2)2+y2=64的圆心M的坐标为(2,0),半径R=8.∵|AM|=4<R,∴点A(-2,0)在圆M内.设动圆C的半径为r,圆心为C(x,y),依题意得r=|CA|,且|CM|=R-r,即|CM|+|CA|=8>|AM|.∴圆心C的轨迹是中心在原点,以A、M两点为焦点,长轴长为8的椭圆,设其方程为x2 a2+y2b2=1(a>b>0),则a=4,c=2,∴b2=a2-c2=12.∴所求动圆的圆心C的轨迹方程为x216+y212=1.(2)由⎩⎪⎨⎪⎧y=kx+mx216+y212=1,消去y化简整理得:(3+4k2)x2+8kmx+4m2-48=0,设B(x1,y1),D(x2,y2),则x1+x2=-8km3+4k2Δ1=(8km)2-4(3+4k2)(4m2-48)>0①由⎩⎪⎨⎪⎧y=kx+mx24-y212=1消去y化简整理得:(3-k2)x2-2kmx-m2-12=0.设E(x3,y3),F(x4,y4),则x3+x4=2km3-k2,Δ2=(-2km)2+4(3-k2)(m2+12)>0②∵DF→=(x4-x2,y4-y2)、BE→=(x3-x1,y3-y1),且DF→+BE→=0,∴(x4-x2)+(x3-x1)=0,即x1+x2=x3+x4,∴-8km3+4k2=2km3-k2,∴km=0或-43+4k2=13-k2.解得k=0或m=0.当k=0时,由①、②得-23<m<23,∵m∈Z,∴m的值为-3,-2,-1,0,1,2,3;当m=0时,由①、②得-3<k<3,∵k∈Z,∴k=-1,0,1.∴满足条件的直线共有9条.。
