安徽省蚌埠市第一中学2015届高三上学期期中考试数学(理)试卷word版无答案
蚌埠一中2014-2015学年度第一学期期中考试
高三数学（理）试卷 戴冒生
一、选择题(每题5分) 1.在复平面内，复数
1i
i
+对应的点位于 （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 2.
已知集合2
{|{|
0}2
x A x y B x x +==
=≤-，则A B = A ．[]2,1-- B ．[)1,2- C ． [)1,2 D ．[]1,1- 3.已知命题p ：1sin ,≤∈∀x R x ，则（ ）
A.1sin ,:≥∈∃⌝x R x p
B. 1sin ,:≥∈∀⌝x R x p
C.1sin ,:>∈∃⌝x R x p
D. 1sin ,:>∈∀⌝x R x p 4. 已知向量(1)(1)n n ==-，，，a b ，若2-a b 与b 垂直，则=a （ ） A ．1
B ．
C ．2
D ．4
5.设12
32,2()((2))log (1) 2.
x e x f x f f x x -⎧⎪=⎨-≥⎪⎩＜，
则的值为， (A)0 (B)1 (C)2 (D)3
6.下列命题中真命题的个数是
（1）若命题,p q 中有一个是假命题，则()p q ⌝∧是真命题．
（2）在ABC ∆中，“cos sin cos sin A A B B +=+”是“90C =”的必要不充分条件． （3）C 表示复数集，则有2
,11x C x ∀∈+≥．
A ．0
B ．2
C ．1
D ．3 7.
将函数2cos 2y x x =-的图象向右平移
4
π
个单位长度，所得图象对应的函数()g x
A
1+ B ．对称轴方程是7,12
x k k Z π
π=+∈ C ．是周期函数，周期2
T π
=
D ．在区间7[,
]1212
ππ
上单调递增
8.已知()f x 是周期为2
的奇函数，当01x <<时，()lg .f x x =设
63(),(),52a f b f ==5
(),2
c f = 则( )
（A ）a b c << （B ）b a c << （C ）c b a << （D ）c a b << 9．对于R 上可导的任意函数f （x ），若满足（x －1）f x '（）≥0，则必有（ ）
A ． f （0）＋f （2）2f （1） B. f （0）＋f （2）2f （1）
C. f （0）＋f （2）2f （1）
D. f （0）＋f （2）
2f （1）
10.已知四个函数：①sin y x x =；②cos y x x =；③cos y x x =；④2x
y x =⋅的图象如下，
但顺序打乱，则按照图象从左到右的顺序，对应的函数正确的一组是
A ．①④②③
B ．①④③②
C ．④①②③
D ．③④②①
11．
已知0,
(),0,
x x x f x e e x -≥=-<⎪⎩若函数()(1)y f x k x =-+有三个零点，则实数k 的取值
范围是( ) A.1(-
0)2, B. 1(0)2, C.1
(1)2
, D.(1),+∞ 二、填空题(每题5分)
12．
,4,33)3()(=+⋅+b a b a 则a 与b 的夹角为________
13.函数y=
2
1sin2+4sin 2
x,x R ∈的值域是________ 14．在△ABC 中，角A 、B 、C 的对边分别为c b a 、、，若20=++c b a ，三角形面积为310，
60=A ，则=a
15． 曲线C 的参数方程是22cos 2sin x y θ
θ
=+⎧⎨
=⎩（θ为参数，且(,2)θππ∈），以坐标原点O 为极
点，x 轴正半轴为极轴建立极坐标系，曲线D 的方程为sin()04
π
ρθ+
=，曲线C 与曲线D
的交点为P ，则过交点P 且与曲线C 相切的极坐标方程是
16.设f （x ）＝log 3（x ＋6）的反函数为f －
1（x ），若〔f －
1（m ）＋6〕〔f －
1（n ）＋6〕＝27,则f （m ＋n ）＝___________________
三、解答题
17（本题满分12）集合{}
2113x A x x -=≥+，{}
ππsin ,,,062B y y a a a θθ⎡⎤==∈->⎢⎥⎣⎦
且为常数.
（1）求集合A 和B ；
（2）若A B ⋂=∅，求a 的取值范围.
18. （本题满分14分） 已知定义域为R 的函数12()2x x b
f x a
+-+=+是奇函数。
(1)求,a b 的值；
(2)已知()f x 是减函数，若对任意的t R ∈，不等式2
2
(2)(2)0f t t f t k -+-<恒成立，求k 的取值范围
19。
（本题满分14分） 已知函数f (x )=A 2
sin ()x ωϕ+(A >0,ω>0,0<ϕ<2
π
，且y =f (x )的最大值
为2，其图象相邻两对称轴间的距离为2，并过点（1，2）. （1）求ϕ;
（2）计算f (1)+f (2)+… +f (2 014)的值
20．(本题满分14分)在ABC ∆中，c b a ,,分别为角,,A B C 所对的边，向量),2(b c a m +=，
)cos ,(cos C B n =，且n m ,垂直．
（I ）确定角B 的大小；
（II ）若ABC ∠的平分线BD 交AC 于点D ，且1=BD ，设,BC x BA y ==，
试确定y 关于x 的函数式，并求边AC 长的取值范围．
21．（本小题满分16分）
已知函数
2()ln (0,1).x f x a x x a a a =+->≠
（1）当a >l 时，求证：函数()f x 在（0，+∞）上单调递增； （2）若函数|()|1y f x t =--有三个零点，求t 的值：
（3）若存在x 1，x 2∈[-1，1]，使得12|()()|1,f x f x e -≥-试求a 的取值范围，。
安徽省蚌埠一中2015届高三12月月考数学理试题 Word版无答案
蚌埠一中2014-2015学年度第一学期12月月考高三理科数学试卷（时间：120分钟 分值：150分）1.对任意复数()i ,R z x y x y =+∈，i 为虚数单位，则下列结论正确的是 （A ）2z z y -= （B ）222z x y =+ （C ）2z z x -≥ （D ）z x y ≤+ 2.若集合{}A=|1x x x R ≤∈，，{}2B=|y y x x R =∈，，则A B ⋂=（ ） A.{}|11x x -≤≤ B. {}|0x x ≥ C. {}|01x x ≤≤ D. ∅3.极坐标cos p θ=和参数方程12x t y t ⎧=--⎨=+⎩（t 为参数）所表示的图形分别是 A. 直线、直线 B. 直线、圆 C. 圆、圆 D. 圆、直线4.下列命题中的假命题是A. ,lg 0x R x ∃∈=B. ,tan 1x R x ∃∈=C. 3,0x R x ∀∈>D. ,20x x R ∀∈>5.在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，若∠C=120°，，则A.a ＞bB.a ＜bC. a ＝bD.a 与b 的大小关系不能确定6.已知函数()sin (0,)2y x πωϕωϕ=+><的部分图象如图所示，则A. ω=1 ϕ= 6πB. ω=1 ϕ=- 6πC. ω=2 ϕ= 6πD. ω=2 ϕ= -6π7.与正方体1111ABCD A B C D -的三条棱AB 、1CC 、11A D 所在直线的距离相等的点（A ）有且只有1个 （B ）有且只有2个（C ）有且只有3个 （D ）有无数个8.设{an}是有正数组成的等比数列，n S 为其前n 项和。
已知a2a4=1, 37S =,则5S =（A ）152 (B)314 (C)334 (D)1729.已知ABC ∆和点M 满足0MA MB MC ++=.若存在实m 使得AM AC mAM +=成立，则m =A.2B.3C.4D.510.设0a ＞b ＞，则()211a ab a a b ++-的最小值是（A ）1 （B ）2 （C ）3 （D ）411．已知函数f(x)=3sin(x-)(>0)6πωω和g(x)=2cos(2x+)+1ϕ的图象的对称轴完全相同。
安徽省蚌埠市第一中学2015届高三上学期期中考试地理试卷word版无答案
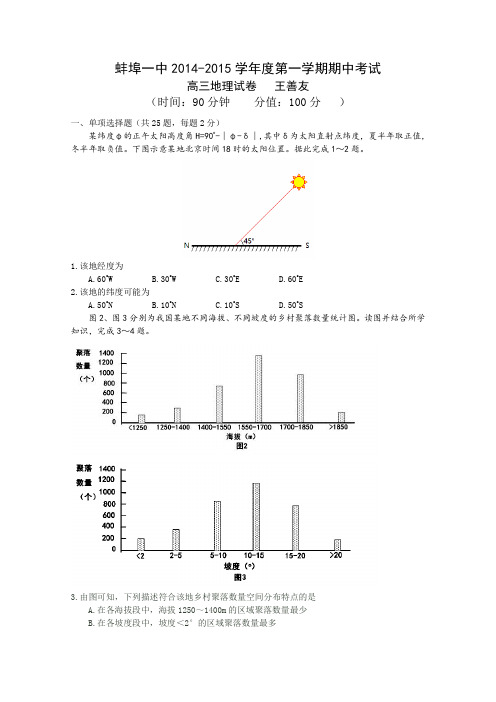
蚌埠一中2014-2015学年度第一学期期中考试高三地理试卷王善友（时间：90分钟分值：100分）一、单项选择题（共25题，每题2分）某纬度φ的正午太阳高度角H=90o-∣φ-δ∣,其中δ为太阳直射点纬度，夏半年取正值，冬半年取负值。
下图示意某地北京时间18时的太阳位置。
据此完成1～2题。
1.该地经度为A.60o WB.30o WC.30o ED.60o E2.该地的纬度可能为A.50o NB.10o NC.10o SD.50o S图2、图3分别为我国某地不同海拔、不同坡度的乡村聚落数量统计图。
读图并结合所学知识，完成3～4题。
3.由图可知，下列描述符合该地乡村聚落数量空间分布特点的是A.在各海拔段中，海拔1250～1400m的区域聚落数量最少B.在各坡度段中，坡度＜2°的区域聚落数量最多C.在各海拔段中，海拔1550～1700m的区域聚落数量最多D.在各坡度段中，坡度15°～20°的区域聚落数量最少4.该地区最有可能位于我国A.塔里木盆地B.黄土高原C.三江平原D.江南丘陵图4为甲地所在区城某时刻高空两个等压面P1和P2的空间分布示意图，图中甲、乙两地经度相同。
完成5～7题。
5.此时甲地近地面的风向为A.东南风B.西南风C.东北风D.西北风6.此后，来自乙地的气团使甲地的天气发生明显变化。
造成此次天气变化的天气系统是A.气旋B.反气旋C.冷锋D.暖锋7.若该日甲、乙两地同时日出，则甲地该日A.正午太阳高度达一年中最大B.为冬至日C.日落时区时为18时D.昼夜等长下图示意我国黄土高原某地林木的分布状况，图中相邻等高线之间高差均为30米。
读图回答8～9题。
8.林木生长与土壤水分条件相关，图中林木密集区位于A.鞍部B.山谷C.山脊D.山顶9.图示区域内东、西两侧最大高差可能是A.156米B.178米C.220米D.255米梯田是因地制宜发展农业生产的典范。
下面左图是四种不同类型梯田的剖面示意图，右图是某地等高线地形图。
安徽省蚌埠一中第一学期期中考试高一数学试题(无答案)
蚌埠一中2014-2015学年度第一学期期中考试高一数学试卷 命题人：王哲一（ 时间：120分钟 分值：150分 ）第Ⅰ卷（本卷共50分）一．选择题：（本大题共10题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知全集，集合，，则集合（ ）A ．B ．C ．D ．2．集合Ａ＝{}1,414≠<-<-∈x x N x 且的真子集的个数为（ ）A ．32B ．31C ．16D ．15.3．下列函数中，是奇函数，又在定义域内为减函数的是（ ） [来源: ]A. B. C. y=－x 3 D.4．图中的图象所表示的函数的解析式为（ ）A . (0≤x ≤2)B . (0≤x ≤2)C . (0≤x ≤2)D . (0≤x ≤2)5．下列四组函数中，表示同一函数的是（ ）A ．与B ．与C ．与D ．＞与6．设，用二分法求方程()2,10833∈=-+x x x 在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间（ ）A ．B ．C ．D ．不能确定7. 当时，在同一坐标系中，函数与的图象是（ ）8. 三个数的大小关系为（ ）A.4.04.0333log 4.0<<B.C.D.9．若奇函数．．．在上为增函数．．．，且有最小值7，则它在上（ ）A . 是减函数，有最小值-7B . 是增函数，有最小值-7[来源: ]C . 是减函数，有最大值-7D . 是增函数，有最大值-7[来源: ]10．对实数a 和b ，定义运算“⊗”：,1,, 1.a ab a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =-⊗-∈若函数恰有两个零点，则实数的取值范围是（ ）A ．B ．C ．D ．第Ⅱ卷（本卷共计100分）二、填空题：（本大题共5小题，每小题5分，共25分）11．函数的定义域为 .12．已知函数，则的值为 。
安徽省蚌埠市第一中学高三数学12月月考试题 理
蚌埠一中2015-2016年度第一学期12月份月考高三 理科数学总分150分 时间120分钟一、选择题（每小题四个选项中只有一项是正确的，每小题5分，共计60分） 1、已知集合A ＝{x |x ＞1}，B ＝{x |－1＜x ＜2}，则A ∩B ＝( )A ．{x |－1＜x ＜2}B ．{x |x ＞－1}C ．{x |－1＜x ＜1}D ．{x |1＜x ＜2} 2、 下列命题正确的是 （ ） A ．已知011:,011:≤+⌝>+x p x p 则;B ．存在实数R x ∈，使2cos sin π=+x x 成立;C ．命题p ：对任意的01,2>++∈x x R x ，则p ⌝：对任意的01,2≤++∈x x R x ; D ．若p 或q 为假命题,则p ,q 均为假命题 3、 把函数)6sin(π+=x y 图象上各点的横坐标缩短到原来的21倍（纵坐标不变），再将图象向右平移3π个单位，那么所得图象的一条对称轴方程为 （ ） A ．8π=x B ．4π-=x C ．4π=x D ．2π-=x4、下列命题为真命题的是（ ）A ．平行于同一平面的两条直线平行；B ．与某一平面成等角的两条直线平行；C ．垂直于同一平面的两条直线平行；D ．垂直于同一直线的两条直线平行．5、已知数列错误!未找到引用源。
满足错误!未找到引用源。
，错误!未找到引用源。
，其中错误!未找到引用源。
是等差数列，且错误!未找到引用源。
，则错误!未找到引用源。
（ ）A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
6、若非零向量,a b r r 满足(4)a b a -⊥u u r r r ，()b a b -⊥u u r r r，则a r 与b r 的夹角是（ ）A ．6πB ．3πC ．2πD ．56π 7、过双曲线22221(0,0)x y a b a b-=>>左焦点1F ，倾斜角为30︒的直线交双曲线右支于点P ，若线段1PF 的中点在y 轴上，则此双曲线的离心率为（ ）A.335C.338、若直线)0,0(022>>=-+b a by ax 始终平分圆082422=---+y x y x 的周长，则ba 21+的最小值为 （ ）A.1B. 322+ C.5 D. 249、一个几何体的三视图如图所示，其中俯视图与侧视图均为半径 为2的圆，则这个几何体的表面积是 （ ）A ．16πB ．15πC ．14πD ．12π10、椭圆M: 错误!未找到引用源。
安徽省蚌埠市第一中学2015届高三上学期期中考试历史试卷word版无答案
蚌埠一中2014-2015学年度第一学期期中考试高三历史试卷杨娜（时间：90分钟分值：100分）一、选择题：本大题共20题，每题2分，共计40分。
在每小题列出的四个选项中，只有一项最符合题目要求。
1．唐代元稹《估客乐》：“求珠驾沧海，采玉上荆衡。
北买党项马，西擒吐蕃鹦。
……经游天下遍，却到长安城。
城中东西市，闻客次第迎。
”诗中反映出当时①商帮的活动范围很广②长安城是重要的商贸城市③市场设置不受地点限制④民族间经济交往频繁A．①② B．②④ C．①③④ D．②③④2．“从宋代起，棉花开始成为一种重要纺织原料……到了元代，丝、麻、棉鼎足而三，明代以后，棉花的重要性超过麻。
”出现这些变化的前提条件是A．政府的大力推广B．棉纺织技术的改进C．商品经济的发展D．棉花成为经济作物3．清帝雍正朱批谕旨说：“山右（今山西）大约商贾居首，其次者犹肯力农，再次者谋入营伍，最下者方令读书。
联所悉知，习俗殊可笑。
”这反映出当地A．商人的政治地位已经跃居首位 B．学而优则仕的传统已被抛弃C．重农抑商政策并没有得到实施 D．传统观念因追求财富而改变4.对右图理解正确的是，当时A．出现地域性的商人群体B．印刷业已使用活字技术C．政府严格管理市场交易D．专设机构管理对外贸易5. 史学家保尔.芒图在《十八世纪产业革命：英国近代大工业初期的概况》中认为英国在十八世纪失去了美洲，但是却在本土范围内创造了新美洲。
“创造了新美洲”指的是，英国A.建立了“日不落帝国”B.开展了工业革命C.确立了责任内阁制D.实行了议会改革6. 斯塔夫里阿诺斯在《全球通史》中写道：“1500年至1763年间，欧洲由于控制了各大海洋和西伯利亚及南北美洲人烟比较稀少的地区，已从默默无闻的地位中崛起。
”在此，作者强调了欧洲崛起的A．市场因素B．军事因素C．技术因素D．政治因素7. “自公元1651年12月1日起及从此以后……无论为英国人或别国人的殖民地所生长、出产或制造的任何货物或商品，如非由属于本共和国人们所有的任何种类船舶载运，皆不得输入或带进英吉利共和国”，这一条文反映了A．英国殖民帝国已经形成 B．英国已处于世界工厂的地位C．英国资本主义制度确立 D．英国与荷兰的商业竞争激烈8．英国学者尼尔·弗格森认为：“如果没有以对廉价服装弹性需求趋于无限大为特征的动态消费社会的同步发展，‘工业革命’就不会在英国发端，更不会延至西方世界的其他地区。
《解析》安徽省蚌埠市五河高中2015届高三上学期期中考试数学(理)试卷Word版含解析
2014-2015学年安徽省蚌埠市五河高中高三（上）期中数学试卷（理科）一、选择题（每题5分，共50分）1．若集合A={x|x≥0}，且A∩B=B，则集合B可能是（）A． {1，2} B． {x|x≤1} C． {﹣1，0，1} D． R2．若向量、满足=（2，﹣1），=（1，2），则向量与的夹角等于（）A． 45° B． 60° C． 120° D． 135°3．设a＞0，则函数y=|x|（x﹣a）的图象大致形状是（）A． B．C． D．4．规定a⊗b=+2a+b，a、b∈R+，若1⊗k=4，则函数f（x）=k⊗x的值域（）A．（2，+∞） B．（1，+∞） C． [，+∞） D． [，+∞）5．知y=f（x）是定义在R上的函数，且f（1）=1，f′（x）＞1，则f（x）＞x的解集是（）A．（0，1） B．（﹣1，0）∪（0，1） C．（1，+∞） D．（﹣∞，﹣1）∪（1，+∞）6．在△ABC中，若b=2，A=120°，三角形的面积S=，则三角形外接圆的半径为（）A． B． 2 C． 2 D． 47．设P是△ABC所在平面内的一点，，则（）A． B． C． D．8．已知角α的终边与单位圆x2+y2=1交于P（，y0），则cos2α=（）A．﹣ B． 1 C． D．﹣9．在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，若a=2bcosC，这个三角形一定是（）A．等腰三角形 B．直角三角形C．等腰直角三角形 D．等腰三角形或直角三角形10．定义在R上的奇函数f（x）在（0，+∞）上单调递减，f（）=0，△ABC的内角A满足f（cosA）≤0，则A的取值范围是（）A． [，] B． [，]∪[，] C．（0，）∪[，] D． [0，]二、填空题（每题5分，共25分）11．设p：|2x+1|＜m（m＞0），，若p是q的充分不必要条件，则实数m的取值范围为．12．设函数，则f（f（3））= ．13．已知不共线，，当k= 时，共线．14．曲线y=x2﹣1与直线x+y=1围成的图形的面积为．15．下列命题正确的是（写序号）①命题“∃x0∈R，x02+1＞3x0”的否定是“∀x∈R，x2+1≤3x；②函数 f（x）=cos2ax﹣sin2ax的最小正周期为“π”是“a=1”的必要不充分条件；③x2+2x≥ax 在x∈[1，2]上恒成立⇔（x2+2x）min≥（ax）max在x∈[1，2]上恒成立；④”平面向量与的夹角是钝角“的充分必要条件是“＜0”三、解答题.（16-19题每题12分，20题13分，21题14分，共75分）16．已知条件p：A={x∈R|x2+ax+1≤0}，条件q：B={x∈R|x2﹣3x+2≤0}．若￢q是￢p的充分不必要条件，求实数a的取值范围．17．在△ABC中，a、b、c分别是角A、B、C的对边，且，（1）求角B的大小；（2）若，求△ABC的面积．18．已知函数f（x）=sin2xsinφ+cos2xcosφ﹣sin（+φ）（0＜φ＜π），其图象过点（，）．（Ⅰ）求φ的值；（Ⅱ）将函数y=f（x）的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数y=g （x）的图象，求函数g（x）在[0，]上的最大值和最小值．19．设函数f（x）=x3+ax2﹣9x﹣1（a＜0）．若曲线y=f（x）的斜率最小的切线与直线12x+y=6平行，求：（Ⅰ）a的值；（Ⅱ）函数f（x）的单调区间．20．设函数f（x）=x（e x﹣1）﹣ax2（Ⅰ）若a=，求f（x）的单调区间；（Ⅱ）若当x≥0时f（x）≥0，求a的取值范围．21．已知函数f（x）=lnx﹣ax+﹣1（a∈R）．（Ⅰ）当a≤时，讨论f（x）的单调性；（Ⅱ）设g（x）=x2﹣2bx+4．当a=时，若对任意x1∈（0，2），存在x2∈[1，2]，使f（x1）≥g（x2），求实数b取值范围．2014-2015学年安徽省蚌埠市五河高中高三（上）期中数学试卷（理科）参考答案与试题解析一、选择题（每题5分，共50分）1．若集合A={x|x≥0}，且A∩B=B，则集合B可能是（）A． {1，2} B． {x|x≤1} C． {﹣1，0，1} D． R考点：交集及其运算．专题：计算题；集合．分析：由集合A={x|x≥0}，且A∩B=B，得B⊆A，由此能求出结果．解答：解：∵集合A={x|x≥0}，且A∩B=B，∴B⊆A，观察备选答案中的4个选项，只有{1，2}⊆A．故选：A．点评：本题考查交集性质的应用，是基础题，解题时要认真审题．2．若向量、满足=（2，﹣1），=（1，2），则向量与的夹角等于（）A． 45° B． 60° C． 120° D． 135°考点：数量积表示两个向量的夹角．专题：计算题．分析：先设向量与的夹角为θ，有两向量（）、的坐标，可得的坐标，可得的模，由数量积的意义，可得cosθ的值，进而有θ的范围，可得答案．解答：解：根据题意，向量与的夹角为θ，=（2，﹣1），=（1，2），则=（）﹣=（1，﹣3），可得||=，||=，cosθ==﹣，又有0°≤θ≤180°，则θ=135°，故选D．点评：本题考查向量的数量积的运用，要求学生能熟练计算数量积并通过数量积来求出向量的模和夹角或证明垂直．3．设a＞0，则函数y=|x|（x﹣a）的图象大致形状是（）A． B． C．D．考点：函数的图象．专题：函数的性质及应用．分析：确定分段函数的解析式，与x轴的交点坐标为（a，0），（0，0），及对称性即可得到结论．解答：解：函数y=|x|（x﹣a）=∵a＞0，当x≥0，函数y=x（x﹣a）的图象为开口向上的抛物线的一部分，与x轴的交点坐标为（0，0），（a，0）当x＜0时，图象为y=﹣x（x﹣a）的图象为开口先向下的抛物线的一部分故选B．点评：本题考查分段函数，考查函数的化简，考查数形结合的数学思想，属于中档题．4．规定a⊗b=+2a+b，a、b∈R+，若1⊗k=4，则函数f（x）=k⊗x的值域（）A．（2，+∞） B．（1，+∞） C． [，+∞） D． [，+∞）考点：函数的值域．专题：函数的性质及应用．分析：由规定的运算法则知，先求出k的值，再根据法则得到f（x），根据函数的单调性，求出值域．解答：解：∵a⊗b=+2a+b，a、b∈R+，∴1⊗k=+2+k=4，解得k=1，∴k⊗x=1⊗x=+2+x，∴f（x）=x++2，∴函数f（x）在（0，+∞）为增函数，∴x++2＞2，故函数f（x）的值域为（2，+∞）故选：A．点评：本题考查了新定义下的求函数的值域问题，解题时要严格按照规定的定义进行运算，是基本题．5．知y=f（x）是定义在R上的函数，且f（1）=1，f′（x）＞1，则f（x）＞x的解集是（）A．（0，1） B．（﹣1，0）∪（0，1） C．（1，+∞） D．（﹣∞，﹣1）∪（1，+∞）考点：函数的单调性与导数的关系；其他不等式的解法．专题：计算题．分析：由f'（x）＞1，f（x）＞x可抽象出一个新函数g（x），利用新函数的性质（单调性）解决问题，即可得到答案．解答：解：设g（x）=f（x）﹣x，因为f（1）=1，f'（x）＞1，所以g（1）=f（1）﹣1=0，g′（x）=f′（x）﹣1＞0所以g（x）在R上是增函数，且g（1）=0．所以f（x）＞x的解集即是g（x）＞0的解集（1，+∞）．故选C．点评：解决此类问题的关键是灵活由于已知条件推倒出函数的有关性质，然后利用这些性质求解相关问题即可．6．在△ABC中，若b=2，A=120°，三角形的面积S=，则三角形外接圆的半径为（）A． B． 2 C． 2 D． 4考点：正弦定理．专题：解三角形．分析：由条件求得 c=2=b，可得B的值，再由正弦定理求得三角形外接圆的半径R的值．解答：解：△ABC中，∵b=2，A=120°，三角形的面积S==bc•sinA=c•，∴c=2=b，故B=（180°﹣A）=30°．再由正弦定理可得=2R==4，∴三角形外接圆的半径R=2，故选：B．点评：本题主要考查正弦定理的应用，属于基础题．7．设P是△ABC所在平面内的一点，，则（）A． B． C． D．考点：向量的加法及其几何意义；向量的三角形法则．专题：平面向量及应用．分析：根据所给的关于向量的等式，把等式右边二倍的向量拆开，一个移项一个和左边移来的向量进行向量的加减运算，变形整理，得到与选项中一致的形式，得到结果．解答：解：∵，∴，∴∴∴故选B．点评：本题考查了向量的加法运算和平行四边形法则，可以借助图形解答．向量是数形结合的典型例子，向量的加减运算是用向量解决问题的基础，要学好向量的加减运算．8．已知角α的终边与单位圆x2+y2=1交于P（，y0），则cos2α=（）A．﹣ B． 1 C． D．﹣考点：任意角的三角函数的定义．专题：计算题；三角函数的求值．分析：利用角α的终边与单位圆x2+y2=1交于P（，y0），求出y0=±，可得cosα=，sinα=±，从而可求cos2α．解答：解：∵角α的终边与单位圆x2+y2=1交于P（，y0），∴y0=±，∴cosα=，sinα=±，∴cos2α=cos2α﹣sin2α=﹣，故选：A．点评：本题考查任意角的三角函数的定义，考查二倍角公式，考查学生的计算能力，属于基础题．9．在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，若a=2bcosC，这个三角形一定是（）A．等腰三角形 B．直角三角形C．等腰直角三角形 D．等腰三角形或直角三角形考点：正弦定理．专题：解三角形．分析：法1：先根据余弦定理表示出cosC，代入整理即可得到b=c从而知是等腰三角形．法2：根据正弦定理，结合三角函数的边角关系进行化简．解答：解：法1：由余弦定理得cosC=，把cosC代入a=2bcosC得：a=2b•，整理得a2=a2+b2﹣c2，∴c2=b2．又b和c都大于0，则b=c，即三角形为等腰三角形．法2：由正弦定理得sinA=2sinBcosC，即sin（B+C）=sinBcosC+cosBsinC=2sinBcosC，整理得sinBcosC﹣cosBsinC=sin（B﹣C）=0，即B=C，则三角形为等腰三角形，故选：A．点评：此题考查了正弦定理和余弦定理，以及三角形的形状判定，利用余弦定理表示出cosC 是本题的突破点．10．定义在R上的奇函数f（x）在（0，+∞）上单调递减，f（）=0，△ABC的内角A满足f（cosA）≤0，则A的取值范围是（）A． [，] B． [，]∪[，] C．（0，）∪[，] D． [0，]考点：函数单调性的判断与证明；函数奇偶性的性质．专题：常规题型．分析：注意到奇函数f（x）的定义域为R，则f（0）=0；利用奇函数的单调性及三角函数解答．解答：解：∵函数f（x）是定义在R上的奇函数且在（0，+∞）上单调递减，∴f（0）=0，且f（x）在（﹣∞，0）上单调递减，又∵f（）=0，∴f（﹣）=0．∵f（cosA）≤0，∴﹣≤cosA≤0，或≤cosA≤1，又∵角A是△ABC的内角，∴0＜A≤或≤A≤．故选：C．点评：本题考查了学生对奇函数的单调性认识，同时考查了奇函数的定义域为R时f（0）=0；同时考查了对三角函数的掌握．二、填空题（每题5分，共25分）11．设p：|2x+1|＜m（m＞0），，若p是q的充分不必要条件，则实数m的取值范围为（0，2] ．考点：必要条件、充分条件与充要条件的判断．专题：探究型．分析：先化简p，q，利用p是q的充分不必要条件，建立不等式关系进行求解．解答：解：∵m＞0，∴不等式|2x+1|＜m等价为﹣m＜2x+1＜m，解得，即p：．由，即（x﹣1）（2x﹣1）＞0，解得x＞1或x＜．即q：x＞1或x＜．∵p是q的充分不必要条件，∴，解得m≤2，∵m＞0，∴0＜m≤2，即实数m的取值范围为（0，2]．故答案为：（0，2]．点评：本题主要考查充分条件和必要条件的应用，利用数形结合是解决此类问题的基本方法注意端点值等号的取舍问题．12．设函数，则f（f（3））= ．考点：函数的值．专题：计算题．分析：根据分段函数的定义域先求出f（3），再求出f（f（3）），注意定义域；解答：解：∵函数，3＞1∴f（3）=，∴f（）=（）2+1=+1=，故答案为；点评：分段函数分段处理，这是研究分段函数图象和性质最核心的理念，此题是一道基础题；13．已知不共线，，当k= ±1 时，共线．考点：平行向量与共线向量．专题：平面向量及应用．分析：题目给出了两个非零向量，要使两个非零向量共线，设一个实数λ，让，把两向量代入后求解k的值．解答：解：因为不共线，所以要使向量共线，则存在非0实数λ，使得，即所以，解得：k=±1．故答案为±1．点评：本题考查了平行向量和共线向量，解答此题的关键是理解并掌握共线向量基本定理，属基础题．14．曲线y=x2﹣1与直线x+y=1围成的图形的面积为．考点：定积分在求面积中的应用．专题：计算题；导数的概念及应用．分析：联立解曲线得它们的交点，根据定积分计算公式加以计算，即可得到所求面积．解答：解：由y=x2﹣1与直线x+y=1，解得交点为（﹣2，3）和（1，0），因此，y=x2﹣1与直线x+y=1所围成的封闭图形的面积是S=（1﹣x﹣x2+1）dx=（2x﹣x2﹣x3）=．故答案为：．点评：本题给出曲线y=x2﹣1与直线x+y=1，求它们围成的图形的面积，着重考查了定积分的几何意义和定积分计算公式等知识，属于基础题．15．下列命题正确的是①②（写序号）①命题“∃x0∈R，x02+1＞3x0”的否定是“∀x∈R，x2+1≤3x；②函数 f（x）=cos2ax﹣sin2ax的最小正周期为“π”是“a=1”的必要不充分条件；③x2+2x≥ax 在x∈[1，2]上恒成立⇔（x2+2x）min≥（ax）max在x∈[1，2]上恒成立；④”平面向量与的夹角是钝角“的充分必要条件是“＜0”考点：命题的真假判断与应用．专题：函数的性质及应用．分析：①利用特称命题的否定是全称命题，写出命题“∃x0∈R，x02+1＞3x0”的否定，可判断①；②利用二倍角的余弦公式及余弦函数的周期公式，结合充分必要条件的概念可判断②；③利用等价转化思想与恒成立问题，可知x2+2x≥ax 在x∈[1，2]上恒成立⇔a≤（x∈[1，2]），从而可判断③；④利用向量的数量积的坐标运算及充分必要条件的概念可判断④．解答：解：对于①，命题“∃x0∈R，x02+1＞3x0”的否定是“∀x∈R，x2+1≤3x，故①正确；对于②，∵函数f（x）=cos2ax﹣sin2ax=cos2ax的最小正周期为T==π，∴|a|=1，解得a=±1，即f（x）的最小正周期为“π”不能⇒“a=1”，充分性不成立；反之，若a=1，则函数f（x）的最小正周期为π，必要性成立，∴函数 f（x）=cos2ax﹣sin2ax的最小正周期为“π是“a=1”的必要不充分条件，故②正确；对于③，x2+2x≥ax 在x∈[1，2]上恒成立⇔a≤（x∈[1，2]），或者是当x∈[1，2]时，函数y=x2+2x的图象恒不在y=ax的图象的下方，而不是（x2+2x）min≥（ax）在x∈[1，2]上恒成立，故③错误；max全称命题的否定是特称命题，写出命题：“∀x∈R，x3﹣x2+1≤0”的否定，可判断③；对于④，若平面向量与的夹角是钝角，则＜0，必要性成立；反之，若＜0，则平面向量与的夹角是钝角或π，即充分性不成立，故④错误．综上所述，正确的命题为：①②．故答案为：①②．点评：本题考查考查正弦定理、二倍角的余弦公式及余弦函数的周期公式等基本知识，考查充分必要条件的概念及全称命题与特称命题之间的关系，考查等价转化思想，属于中档题．三、解答题.（16-19题每题12分，20题13分，21题14分，共75分）16．已知条件p：A={x∈R|x2+ax+1≤0}，条件q：B={x∈R|x2﹣3x+2≤0}．若￢q是￢p的充分不必要条件，求实数a的取值范围．考点：必要条件、充分条件与充要条件的判断．专题：计算题；函数的性质及应用．分析：￢q是￢p的充分不必要条件，根据逆否命题与原命题的等价性，得p是q的充分不必要条件，由此可得集合A是集合B的真子集．将q对应的不等式分别解出，再对p中的集合A进行讨论，解关于a不等式即可得到本题的答案．解答：解：∵条件q：B={x∈R|x2﹣3x+2≤0}，∴解不等式x2﹣3x+2≤0，得1≤x≤2，得B=[1，2]∵￢q是￢p的充分不必要条件，∴根据逆否命题与原命题的等价性，得p是q的充分不必要条件因此，A={x∈R|x2+ax+1≤0}⊊B=[1，2]①当A=∅时，a2﹣4＜0，解之得﹣2＜a＜2；②当A≠∅时，a2﹣4≥0，得a≥2或a≤﹣2∵x2+ax+1≤0的解集为A={x|≤x≤}∴结合A⊊B，可得1≤且≤2，（两个不等式的等号不同时成立）解之可得﹣≤a≤﹣2综上所述，可得实数a的取值范围为﹣≤a＜2．即若￢q是￢p的充分不必要条件，实数a的取值范围是[﹣，2）．点评：本题给出两个不等式对应的条件，叫我们判断充分必要性，着重考查了一元二次不等式的解法和充要条件的判断等知识，属于基础题．17．在△ABC中，a、b、c分别是角A、B、C的对边，且，（1）求角B的大小；（2）若，求△ABC的面积．考点：解三角形．专题：计算题．分析：（1）根据正弦定理表示出a，b及c，代入已知的等式，利用两角和的正弦函数公式及诱导公式变形后，根据sinA不为0，得到cosB的值，由B的范围，利用特殊角的三角函数值即可求出角B的度数；（2）由（1）中得到角B的度数求出sinB和cosB的值，根据余弦定理表示出b2，利用完全平方公式变形后，将b，a+c及cosB的值代入求出ac的值，然后利用三角形的面积公式表示出△ABC的面积，把ac与sinB的值代入即可求出值．解答：解：（1）由正弦定理得：a=2RsinA，b=2RsinB，c=2RsinC，将上式代入已知，即2sinAcosB+sinCcosB+cosCsinB=0，即2sinAcosB+sin（B+C）=0，∵A+B+C=π，∴sin（B+C）=sinA，∴2sinAcosB+sinA=0，即sinA（2cosB+1）=0，∵sinA≠0，∴，∵B为三角形的内角，∴；（II）将代入余弦定理b2=a2+c2﹣2accosB得：b2=（a+c）2﹣2ac﹣2accosB，即，∴ac=3，∴．点评：此题考查了正弦定理，余弦定理及三角函数的恒等变形．熟练掌握定理及公式是解本题的关键．利用正弦定理表示出a，b及c是第一问的突破点．18．已知函数f（x）=sin2xsinφ+cos2xcosφ﹣sin（+φ）（0＜φ＜π），其图象过点（，）．（Ⅰ）求φ的值；（Ⅱ）将函数y=f（x）的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数y=g （x）的图象，求函数g（x）在[0，]上的最大值和最小值．考点： y=Asin（ωx+φ）中参数的物理意义；三角函数的最值．专题：三角函数的图像与性质．分析：（I）由已知中函数f（x）=sin2xsinφ+cos2xcosφ﹣sin（+φ）（0＜φ＜π），其图象过点（，）．我们将（，）代入函数的解析式，结合φ的取值范围，我们易示出φ的值．（II）由（1）的结论，我们可以求出y=f（x），结合函数图象的伸缩变换，我们可以得到函数y=g（x）的解析式，进而根据正弦型函数最值的求法，不难求出函数的最大值与最小值．解答：解：（I）∵函数f（x）=sin2xsinφ+cos2xcosφ﹣sin（+φ）（0＜φ＜π），又因为其图象过点（，）．∴φ﹣解得：φ=（II）由（1）得φ=，∴f（x）=sin2xsinφ+cos2xcosφ﹣sin（+φ）=∴∵x∈[0，]∴4x+∈∴当4x+=时，g（x）取最大值；当4x+=时，g（x）取最小值﹣．点评：本题考查三角函数的诱导公式即二倍角等基本公式的灵活应用、图象变换及三角函数的最值问题、分析问题与解决问题的能力．已知函数图象求函数y=Asin（ωx+φ）（A＞0，ω＞0）的解析式时，常用的解题方法是待定系数法，由图中的最大值或最小值确定A，由周期确定ω，由适合解析式的点的坐标来确定φ，但由图象求得的y=Asin（ωx+φ）（A＞0，ω＞0）的解析式一般不唯一，只有限定φ的取值范围，才能得出唯一解，否则φ的值不确定，解析式也就不唯一．19．设函数f（x）=x3+ax2﹣9x﹣1（a＜0）．若曲线y=f（x）的斜率最小的切线与直线12x+y=6平行，求：（Ⅰ）a的值；（Ⅱ）函数f（x）的单调区间．考点：导数的运算；利用导数研究函数的单调性；两条直线平行的判定．专题：计算题．分析：（1）先求出导函数的最小值，最小值与直线12x+y=6的斜率相等建立等式关系，求出a的值即可；（2）先求导数fˊ（x），在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0，解得的区间就是所求．解答：解：（Ⅰ）因f（x）=x3+ax2﹣9x﹣1所以f'（x）=3x2+2ax﹣9=．即当x=时，f'（x）取得最小值．因斜率最小的切线与12x+y=6平行，即该切线的斜率为﹣12，所以．解得a=±3，由题设a＜0，所以a=﹣3．（Ⅱ）由（Ⅰ）知a=﹣3，因此f（x）=x3﹣3x2﹣9x﹣1，f'（x）=3x2﹣6x﹣9=3（x﹣3）（x+1），令f'（x）=0，解得：x1=﹣1，x2=3．当x∈（﹣∞，﹣1）时，f'（x）＞0，故f（x）在（﹣∞，﹣1）上为增函数；当x∈（﹣1，3）时，f'（x）＜0，故f（x）在（﹣1，3）上为减函数；当x∈（3，+∞）时，f'（x）＞0，故f（x）在（3，+∞）上为增函数．由此可见，函数f（x）的单调递增区间为（﹣∞，﹣1）和（3，+∞）；单调递减区间为（﹣1，3）．点评：本小题主要考查导数的几何意义，及运用导数求函数的单调区间、一元二次不等式的解法等基础知识，属于基础题．20．设函数f（x）=x（e x﹣1）﹣ax2（Ⅰ）若a=，求f（x）的单调区间；（Ⅱ）若当x≥0时f（x）≥0，求a的取值范围．考点：利用导数研究函数的单调性．专题：综合题；导数的综合应用．分析：（I）求导函数，由导数的正负可得函数的单调区间；（II）f（x）=x（e x﹣1﹣ax），令g（x）=e x﹣1﹣ax，分类讨论，确定g（x）的正负，即可求得a的取值范围．解答：解：（I）a=时，f（x）=x（e x﹣1）﹣x2，=（e x﹣1）（x+1）令f′（x）＞0，可得x＜﹣1或x＞0；令f′（x）＜0，可得﹣1＜x＜0；∴函数的单调增区间是（﹣∞，﹣1），（0，+∞）；单调减区间为（﹣1，0）；（II）f（x）=x（e x﹣1﹣ax）．令g（x）=e x﹣1﹣ax，则g'（x）=e x﹣a．若a≤1，则当x∈（0，+∞）时，g'（x）＞0，g（x）为增函数，而g（0）=0，从而当x ≥0时g（x）≥0，即f（x）≥0．若a＞1，则当x∈（0，lna）时，g'（x）＜0，g（x）为减函数，而g（0）=0，从而当x ∈（0，lna）时，g（x）＜0，即f（x）＜0．综合得a的取值范围为（﹣∞，1]．点评：本题考查导数知识的运用，考查函数的单调性，考查分类讨论的数学思想，属于中档题．21．已知函数f（x）=lnx﹣ax+﹣1（a∈R）．（Ⅰ）当a≤时，讨论f（x）的单调性；（Ⅱ）设g（x）=x2﹣2bx+4．当a=时，若对任意x1∈（0，2），存在x2∈[1，2]，使f（x1）≥g（x2），求实数b取值范围．考点：利用导数研究函数的单调性．专题：导数的综合应用．分析：（Ⅰ）直接利用函数与导数的关系，求出函数的导数，再讨论函数的单调性；（Ⅱ）利用导数求出f（x）的最小值、利用二次函数知识或分离常数法求出g（x）在闭区间[1，2]上的最小值，然后解不等式求参数．解答：解：（Ⅰ），令h（x）=ax2﹣x+1﹣a（x＞0）（1）当a=0时，h（x）=﹣x+1（x＞0），当x∈（0，1），h（x）＞0，f′（x）＜0，函数f（x）单调递减；当x∈（1，+∞），h（x）＜0，f′（x）＞0，函数f（x）单调递增．（2）当a≠0时，由f′（x）=0，即ax2﹣x+1﹣a=0，解得．当时x1=x2，h（x）≥0恒成立，此时f′（x）≤0，函数f（x）单调递减；当时，，x∈（0，1）时h（x）＞0，f′（x）＜0，函数f（x）单调递减；时，h（x）＜0，f′（x）＞0，函数f（x）单调递增；时，h（x）＞0，f′（x）＜0，函数f（x）单调递减．当a＜0时，当x∈（0， 1），h（x）＞0，f′（x）＜0，函数f（x）单调递减；当x∈（1，+∞），h（x）＜0，f′（x）＞0，函数f（x）单调递增．综上所述：当a≤0时，函数f（x）在（0，1）单调递减，（1，+∞）单调递增；当时x1=x2，h（x）≥0恒成立，此时f′（x）≤0，函数f（x）在（0，+∞）单调递减；当时，函数f（x）在（0，1）单调递减，单调递增，单调递减．（Ⅱ）当时，f（x）在（0，1）上是减函数，在（1，2）上是增函数，所以对任意x1∈（0，2），有，又已知存在x2∈[1，2]，使f（x1）≥g（x2），所以，x2∈[1，2]，（※）又g（x）=（x﹣b）2+4﹣b2，x∈[1，2]当b＜1时，g（x）min=g（1）=5﹣2b＞0与（※）矛盾；当b∈[1，2]时，g（x）min=g（b）=4﹣b2≥0也与（※）矛盾；当b＞2时，．综上，实数b的取值范围是．点评：本题将导数、二次函数、不等式知识有机的结合在一起，考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题，考查了同学们分类讨论的数学思想以及解不等式的能力；考查了学生综合运用所学知识分析问题、解决问题的能力．。
安徽省蚌埠一中1415学年度第一学期高一期中——数学数
安徽省蚌埠一中2014—2015学年度上学期期中考试高一数学试题（ 时间：120分钟 分值：150分 ）第Ⅰ卷（本卷共50分）一、选择题：（本大题共10题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知全集，集合，，则集合（ ）A ．B ．C ．D ．2．集合Ａ＝{}1,414≠<-<-∈x x N x 且的真子集的个数为（ ）A ．32B ．31C ．16D ．15.3．下列函数中，是奇函数，又在定义域内为减函数的是（ ）A. B. C. y=－x 3 D.4．图中的图象所表示的函数的解析式为（ ）A . (0≤x ≤2)B . (0≤x ≤2)C . (0≤x ≤2)D . (0≤x ≤2)5．下列四组函数中，表示同一函数的是（ ）A ．与B ．与C ．与D ．＞与6．设，用二分法求方程()2,10833∈=-+x x x 在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间（ ）A ．B ．C ．D ．不能确定7. 当时，在同一坐标系中，函数与的图象是（ ）8. 三个数的大小关系为（ ）A.4.04.0333log 4.0<<B.C.D.9．若奇函数．．．在上为增函数．．．，且有最小值7，则它在上（ ） A . 是减函数，有最小值-7 B . 是增函数，有最小值-7C . 是减函数，有最大值-7D . 是增函数，有最大值-710．对实数和，定义运算“”： 设函数()()22()2,.f x x x x x R =-⊗-∈若函数恰有两个零点，则实数的取值范围是（ ） A ． B ．C ．D ．第Ⅱ卷（本卷共计100分）二、填空题：（本大题共5小题，每小题5分，共25分）11．函数的定义域为 .12．已知函数，则的值为 。
13．函数f (x )＝a x －1＋3(a >0且a ≠1)的图象必过定点P ，则P 点坐标为________．14．求满足＞的x 的取值集合是 ．15．已知函数的图象与函数g （x ）的图象关于直线对称，令则关于函数有下列命题: ①的图象关于原点对称； ②为偶函数；③的最小值为0； ④在（0，1）上为减函数.其中正确命题的序号为 。
安徽省蚌埠一中高三上学期期中考试物理试卷 Word版无答案.pdf
蚌埠一中2014-2015学年度第一学期期中考试 高三物理试卷 命题人：王德立 （时间：90分钟 分值：100分） 一、选择题(每小题4分，共60分。
下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上) 1.科学家关于物体运动的研究对树立正确的自然观具有重要作用。
下列说法不符合历史事实的是( ) A.亚里士多德认为，必须有力作用在物体上，物体的运动状态才会改变 B.伽利略通过“理想实验”得出结论：一旦物体具有某一速度，如果它不受力，它将以这一速度永远运动下去 C.笛卡儿指出:如果运动中的物体没有受到力的作用，它将继续以同一速度沿同一直线运动，既不停下来也不偏离原来的方向 D.牛顿认为，物体具有保持原来匀速直线运动状态或静止状态的性质 2. 为了测定某辆轿车在平直路上起动时的加速度（轿车起动时的运动可近似看作匀加速运动），某人拍摄了一张在同一底片上多次曝光的照片（如图）。
如果拍摄时每隔2s曝光一次，轿车车身总长为4.5m，那么这辆轿车的加速度约为（）。
A．1m/s2 B．2m/s2 C．3m/s2 D．4m/s2 3. 如图所示，一质量为M的斜面体静止在水平地面上，质量为m的木块沿粗糙斜面加速下滑h高度，速度大小由v1增大到v2，所用时间为t，木块与斜面体之间的动摩擦因数为μ。
在此过程中A．斜面体受水平地面的静摩擦力为零 B．木块沿斜面下滑的距离为 C．如果给质量为m的木块一个沿斜面向上的初速度v2，它将沿斜面上升到h高处速度变为v1 D．木块与斜面摩擦产生的热量为mgh－ 4. 如图所示，A、B两物体相距x=7 m，物体A以=4m/s的速度向右匀速运动，而物体B此时的速度vB=10 m/s，只在摩擦力作用下向右做匀减速运动，加速度大小为a=2 m/s2，那么物体A追上物体B所用的时间为( )A.7 s B. 10 sC.9 s ?D. 8 s 5. 空降兵是现代军队的重要兵种.一次训练中，空降兵从静止在空中的直升机上竖直跳下（初速度可看做0），下落高度h之后打开降落伞，接着又下降高度H之后，空降兵达到匀速，设空降兵打开降落伞之后受到的空气阻力与速度平方成正比，比例系数为k，即，那么关于空降兵的说法不正确的是（?）A．空降兵从跳下到下落高度为h时，机械能一定损失了mgh B．空降兵从跳下到刚匀速时，重力势能一定减少了mg(H+h) C．空降兵匀速下降时，速度大小为 D．空降兵从跳下到刚匀速的过程，空降兵克服阻力做功为 6. 一个质量为2kg的物体在平行于斜面向上的大小为2N的力F作用下向下运动，已知斜面的倾角为30°，物体与斜面间的动摩擦因数为0.1，则物体所受的摩擦力的大小和方向为（?）A．5N，沿斜面向下 B．5N，沿斜面向上 C．N，沿斜面向下 D．N，沿斜面向上 7. 小船横渡一条两岸平行的河流，船本身提供的速度（即静水速度）大小不变、船身方向垂直于河岸，水流速度与河岸平行，已知小船的运动轨迹如图所示，则（?）A．越接近河岸水流速度越小 B．越接近河岸水流速度越大 C．无论水流速度是否变化，这种渡河方式耗时最长 D．该船渡河的时间会受水流速度变化的影响 8. 一个带正电荷q、质量为m的小球，从光滑绝缘的斜面轨道的A点由静止下滑，小球恰能通过半径为R的光滑绝缘竖直圆形轨道的最高点B而做圆周运动。
安徽省蚌埠市2015-2016学年高一上学期期中考试数学试题(解析版)
高一数学期中试卷一、选择题（每题5分）1. 下列说法正确的是（）A. 任何一个集合必有两个子集B. 无限集的真子集可以是无限集C. 我校建校以来毕业的所有优秀学生可以构成集合D. 函数是两个非空集合构成的映射【答案】B【解析】由于空集只有它本身一个子集，故选项A错；选项B显然正确；由“优秀学生”标准不统一，概念不明确，故选项C错；由函数概念知，函数是两个非空数集构成的映射，故选项D错，所以答案选B.2. 下列说法不正确的是（）A. 定义域和对应关系都相同，则两个函数相同B. 定义域不同，则两个函数不同C. 定义域和值域都分别相同，则两个函数相同D. 对应关系相同，则两个函数可能不同【答案】C【解析】由两个函数相同的定义：如果两个函数的定义域相同，并且对应关系完全一则是称两个函数相同，因此，说法C不正确，故选C.3. 下列四类函数中，具有性质“对任意的，函数满足”的是（）A. 幂函数B. 对数函数C. 指数函数D. 一次函数【答案】B【解析】在选项A中，取，则，而，显然不满足题意；在选项B中，取，则，而，显然满足题意；选项C中，取，则，而，显然不满足题意；选项D 中，取，则，而，显然不满足题意.故选B.4. 已知的单调递增区间为，则的取值是（）A. B. C. D.【答案】B【解析】由已知，函数的对称轴为，且开口向上，则，解得，故选B.5. 下列说法正确的是（）A. 幂函数一定是奇函数或偶函数B. 图像不经过（-1,1）的幂函数一定不是偶函数C. 任意两个幂函数都有两个以上交点D. 奇函数的图像一定过坐标原点【答案】B【解析】说法A中，取幂函数，则函数既不是奇函数也不是偶函数；说法B中，由幂函数的解析式，又过点，则可知为偶数，故此时为偶函数；说法C中，由幂函数与无交点；说法D中，由为奇函数，但其图象不过原点.故选B.6. 已知，，则的大小关系是（）A. B. C. D....【答案】A【解析】由已知得，，，，所以.故选A.7. 函数的定义域为（）A. B. C. D.R【答案】D8. 函数的值域为（）A. B. C. D.【答案】C【解析】令，由，则，所以，又，所以函数的值域为，故选C.9. 下列说法正确的是（）A. 函数的零点就是图像与轴的交点B. 函数在有零点，则C. 函数满足，则在有零点D. 函数满足，则在可以有零点【答案】D【解析】说法A中，函数的零点是图像与轴交点的横坐标，所以A错；说法B中，要确定函数是连续不断的曲线情况下才成立，所以B错；说法C与B犯同样的错；说法D显然正确，故选D.点睛：此题主要考查函数的零点的存在性的判断，属于中档题型，也是常考知识点.在应用函数零点的存在性定理中，要注意前提条件函数必须是连续不断，而且定理并不是存在零点的充要条件，判断函数零点的存在往往涉及到函数的单调性、奇偶性、极值等各方面的知识.10. 是定义在R上的函数，若均为奇函数则下列说法不正确的是（）A. 一定是奇函数B. 不可能是偶函数C. 可以是偶函数D. 不可能是非奇非偶函数【答案】B【解析】选项A中，当，时，则既是奇函数也是偶函数；选项B中，两个奇函数的和不能成为偶函数，显然成立；则选项C、D均不正确，故选B.点睛：此题主要考查两个函数的和的奇偶性判断，属于中高档题型，也是常考知识点.函数的奇偶性的判断应从两个方面来进行，一是看函数的定义域是否关于原点对称（这是判断奇偶性的必要性），二是看与的关系，对于两个函数的和或差的奇偶性的判断，需要对特殊情况进行考虑，如解析中的两个函数等.二、填空题（每题5分）11. ，则=________________【答案】【解析】由题意知，，又，所以，因此.12. =_____________________________【答案】...【解析】由题意，因为，所以，又，所以，原式.13. 函数单调递增区间为_________________________【答案】【解析】由题意，函数在上为单调递增函数，而函数的单调递增区间为，所以函数的单调递增区间为.点睛：此题主要考查了复合函数单调区间的求解运算，属于中档题型，也是常考知识点.一般由函数和所构成的函数称为复合函数，首先分别求两个函数的单调区间，再根据复合函数“同增异减”的复合原则，即两个函数的单调性相同则复合函数为增，若两个函数单调性不同则复合函数为减，从而得出所求复合函数的单调区间.14. 若定义在R上的奇函数和偶函数满足则=___________________【答案】【解析】由题意知，，两式相减得.点睛：此题主要考查如何利用函数的奇偶性求函数的解析式，属于中档题型，也是常考题型.在此类问题中可将两个函数、视作两个未知数，利用两个函数的奇偶性（为奇函数，为偶函数），与原等式建立方程组，通过解方程组从而求得函数解析式.15. 设二次函数，如果，则=_________________【答案】－2【解析】由题意知，因为，所以.点睛：此题主要考查二次函数的对称性等方面的知识，属于中档题型，二次函数关于轴对称这一性质很重要，也是常考知识点，对于二次函数其对称轴为，二次函数的单调性、最值等都与对称轴的位置均有关，在本题中由于二次函数在对称两侧的单调性相反，故此时有.三、解答题（16、17、18、19各12分，20、21分别13分和14分）16. 证明：函数在上单调递减。
安徽省蚌埠五中、蚌埠十二中2015届高三数学上学期期中联考试卷理(含解析)
2014-2015学年安徽省蚌埠五中、蚌埠十二中联考高三（上）期中数学试卷（理科）一、选择题（每小题5分，共50分）1．若集合M={x||x|≤2}，N={x|x2﹣3x=0}，则M∩N等于（）A． {3} B． {0} C． {0，2} D． {0，3}2．设x，y∈R，则“x≥2且y≥2”是“x2+y2≥4”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件3．下列命题中正确的是（）A．若命题p为真命题，命题q为假命题，则命题“p∧q”为真命题B．命题“若xy=0，则x=0”的否命题为：“若xy=0，则x≠0”C．“”是“”的充分不必要条件D．命题“∀x∈R，2x＞0”的否定是“”4．已知，则（）A． a＞b＞c B． b＞a＞c C． a＞c＞b D． c＞a＞b5．若幂函数f（x）的图象经过点A（），是它在A点处的切线方程为（）A． 4x+4y+1=0 B． 4x﹣4y+1=0 C． 2x﹣y=0 D． 2x+y=06．设函数f（x）=，则满足f（x）≤2的x的取值范围是（） A． [﹣1，2] B． [0，2] C． [1，+∞） D． [0，+∞）7．函数的图象大致是（）A． B．C． D．8．函数f（x）=+lg（3x+1）的定义域是（）A．（﹣，+∞） B．（﹣，1） C．（﹣，） D．（﹣∞，﹣）9．已知是（﹣∞，+∞）上的减函数，那么a的取值范围是（）A．（0，1） B． C． D．10．定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2]时，f（x）=x2﹣2x，若x∈[﹣4，﹣2]时，f（x）≥恒成立，则实数t的取值范围是（）A．（﹣∞，﹣1]∪（0，3] B． C． [﹣1，0）∪[3，+∞） D．二、填空题（每小题5分，共25分）11．已知函数，则= ．12．设f（x）是周期为2的奇函数，当0≤x≤1时，f（x）=2x（1﹣x），则= ．13．已知实数x，y满足，则z=2x﹣y的最小值是．14．函数的零点有个．15．已知f（x）=ax2+bx+c（a≠0）且方程f（x）=x无实数根，下列命题：①方程f[f（x）]=x也一定没有实数根；②若a＞0；则不等式f[f（x）]＞x对一切x都成立；③若a＜0则必存在实数x0，使f[f（x0）]＞x0；④若a+b+c=0则不等式f[f（x）]＜x对一切x都成立．其中正确命题的序号是．（把你认为正确命题的所有序号都填上）三、解答题（六大题共计75分）[16．已知函数f（x）=的定义域为A，集合B={x|（x﹣m﹣3）（x﹣m+3）≤0}．（1）求A和f（x）的值域C；（2）若A∩B=[2，3]，求实数m的值；（3）若C⊂∁R B，求实数m的取值范围．17．设f（x）=x3+ax2+bx+1的导数f′（x）满足f′（1）=2a，f′（2）=﹣b，其中常数a，b∈R．（Ⅰ）求曲线y=f（x）在点（1，f（1））处的切线方程．（Ⅱ）设g（x）=f′（x）e﹣x．求函数g（x）的极值．18．已知函数f（x）=x2﹣2|x|．（Ⅰ）判断并证明函数的奇偶性；（Ⅱ）画出函数g（x）=f（4﹣x）的图象，并比较g（﹣1）与g（6）大小．19．设集合A={x|（2+x）（3﹣x）≥0}，B=（1）求集合A；（2）若x∈A是x∈B的必要不充分条件，试求实数k的取值范围．20．已知f（x）=log a x﹣x+1（a＞0，且a≠1）（1）若a=e，求f（x）的单调区间；（2）若f（x）＞0在区间（1，2）上恒成立，求实数a的取值范围．21．已知二次函数f（x）=ax2+bx+c．（1）若a＞b＞c，且f（1）=0，证明f（x）的图象与x轴有2个交点；（2）在（1）的条件下，是否存在m∈R，使得f（m）=﹣a成立时，f（m+3）为正数，若存在，证明你的结论，若不存在，请说明理由；（3）若对x1，x2∈R，且x1＜x2，f（x1）≠f（x2），方程f（x）=[f（x1）+f（x2）]有两个不等实根，证明必有一个根属于（x1，x2）．2014-2015学年安徽省蚌埠五中、蚌埠十二中联考高三（上）期中数学试卷（理科）参考答案与试题解析一、选择题（每小题5分，共50分）1．若集合M={x||x|≤2}，N={x|x2﹣3x=0}，则M∩N等于（）A． {3} B． {0} C． {0，2} D． {0，3}考点：交集及其运算．专题：综合题．分析：求出集合M中的绝对值不等式的解集得到集合M，解出集合N中的方程得到集合N 的元素，求出两集合的交集即可．解答：解：由集合M中的不等式|x|≤2，解得﹣2≤x≤2，所以集合M=[﹣2，2]；由集合N中的方程x2﹣3x=0，变形得x（x﹣3）=0，解得x=0，x=3，所以集合N={0，3}．∴M∩N={0}．故选B点评：本题是属于以不等式的解集和方程的解为平台，求集合交集的运算，也是高考中常考的题型．2．设x，y∈R，则“x≥2且y≥2”是“x2+y2≥4”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：由“x≥2且y≥2”推出“x2+y2≥4”可证明充分性；由满足“x2+y2≥4”可举出反例推翻“x≥2且y≥2”，则证明不必要性，综合可得答案．解答：解：若x≥2且y≥2，则x2≥4，y2≥4，所以x2+y2≥8，即x2+y2≥4；若x2+y2≥4，则如（﹣2，﹣2）满足条件，但不满足x≥2且y≥2．所以“x≥2且y≥2”是“x2+y2≥4”的充分而不必要条件．故选A．点评：本题主要考查充分条件与必要条件的含义．3．下列命题中正确的是（）A．若命题p为真命题，命题q为假命题，则命题“p∧q”为真命题B．命题“若xy=0，则x=0”的否命题为：“若xy=0，则x≠0”C．“”是“”的充分不必要条件D．命题“∀x∈R，2x＞0”的否定是“”考点：命题的真假判断与应用；四种命题间的逆否关系；复合命题的真假；特称命题；必要条件、充分条件与充要条件的判断．专题：计算题．分析：若命题p为真命题，命题q为假命题，则命题“p∧q”为假命题；命题“若xy=0，则x=0”的否命题为：“若xy≠0，则x≠0”；“”⇒“+2kπ，或，k∈Z”，“”⇒“”，故“”是“”的必要不充分条件；命题“∀x∈R，2X＞0”的否定是“∂”．解答：解：若命题p为真命题，命题q为假命题，则命题“p∧q”为假命题，故A不正确；命题“若xy=0，则x=0”的否命题为：“若xy≠0，则x≠0”，故B不正确；“”⇒“+2kπ，或，k∈Z”，“”⇒“”，故“”是“”的必要不充分条件，故C不正确；命题“∀x∈R，2x＞0”的否定是“”，故D正确．故选D．点评：本题考查命题的真假判断，是基础题，解题时要认真审题，仔细解答．4．已知，则（）A． a＞b＞c B． b＞a＞c C． a＞c＞b D． c＞a＞b考点：指数函数的单调性与特殊点．专题：函数的性质及应用．分析：比较大小的方法：找1或者0做中介判断大小，log43.6＜1，log23.4＞1，利用分数指数幂的运算法则和对数的运算法则对c进行化简，得到＞1＞b，再借助于中间值log2进行比较大小，从而得到结果．，解答：解：∵log23.4＞1，log43.6＜1，又y=5x是增函数，∴a＞b，＞==b而log23.4＞log2＞log3，∴a＞c故a＞c＞b．故选C．点评：此题是个中档题．本题考查对数函数单调性、指数函数的单调性及比较大小，以及中介值法，考查学生灵活应用知识分析解决问题的能力．5．若幂函数f（x）的图象经过点A（），是它在A点处的切线方程为（）A． 4x+4y+1=0 B． 4x﹣4y+1=0 C． 2x﹣y=0 D． 2x+y=0考点：利用导数研究曲线上某点切线方程．专题：计算题．分析：先设出幂函数的解析式，然后根据题意求出解析式，根据导数的几何意义求出函数f（x）在x=处的导数，从而求出切线的斜率，再用点斜式写出切线方程，化成一般式式即可．解答：解：∵f（x）是幂函数，设f（x）=xα∴图象经过点A（），∴=（）α∴α=∴f（x）=f'（x）=它在A点处的切线方程的斜率为f'（）=1，又过点A所以在A点处的切线方程为4x﹣4y+1=0故选B．点评：本小题主要考查幂函数的定义和导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力，属于基础题．6．设函数f（x）=，则满足f（x）≤2的x的取值范围是（） A． [﹣1，2] B． [0，2] C． [1，+∞） D． [0，+∞）考点：对数函数的单调性与特殊点．专题：分类讨论．分析：分类讨论：①当x≤1时；②当x＞1时，再按照指数不等式和对数不等式求解，最后求出它们的并集即可．解答：解：当x≤1时，21﹣x≤2的可变形为1﹣x≤1，x≥0，∴0≤x≤1．当x＞1时，1﹣log2x≤2的可变形为x≥，∴x≥1，故答案为[0，+∞）．故选D．点评：本题主要考查不等式的转化与求解，应该转化特定的不等式类型求解．7．函数的图象大致是（）A． B．C． D．考点：函数的图象．专题：三角函数的图像与性质．分析：根据函数的解析式，我们根据定义在R上的奇函数图象必要原点可以排除A，再求出其导函数，根据函数的单调区间呈周期性变化，分析四个答案，即可找到满足条件的结论．解答：解：当x=0时，y=0﹣2sin0=0故函数图象过原点，可排除A又∵y'=故函数的单调区间呈周期性变化分析四个答案，只有C满足要求故选C点评：本题考查的知识点是函数的图象，在分析非基本函数图象的形状时，特殊点、单调性、奇偶性是我们经常用的方法．8．函数f（x）=+lg（3x+1）的定义域是（）A．（﹣，+∞） B．（﹣，1） C．（﹣，） D．（﹣∞，﹣）考点：对数函数的定义域；函数的定义域及其求法．专题：计算题．分析：依题意可知要使函数有意义需要1﹣x＞0且3x+1＞0，进而可求得x的范围．解答：解：要使函数有意义需，解得﹣＜x＜1．故选B．点评：本题主要考查了对数函数的定义域．属基础题．9．（5分）（2006•北京）已知是（﹣∞，+∞）上的减函数，那么a的取值范围是（）A．（0，1） B． C． D．考点：分段函数的解析式求法及其图象的作法．专题：压轴题．分析：由f（x）在R上单调减，确定a，以及3a﹣1的范围，再根据单调减确定在分段点x=1处两个值的大小，从而解决问题．解答：解：依题意，有0＜a＜1且3a﹣1＜0，解得0＜a＜，又当x＜1时，（3a﹣1）x+4a＞7a﹣1，当x＞1时，log a x＜0，因为f（x）在R上单调递减，所以7a﹣1≥0解得a≥综上：≤a＜故选C．点评：本题考查分段函数连续性问题，关键根据单调性确定在分段点处两个值的大小．10．定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2]时，f（x）=x2﹣2x，若x∈[﹣4，﹣2]时，f（x）≥恒成立，则实数t的取值范围是（）A．（﹣∞，﹣1]∪（0，3] B． C． [﹣1，0）∪[3，+∞） D．考点：函数恒成立问题．专题：函数的性质及应用．分析：先根据f（x+2）=2f（x），结合x∈[﹣4，﹣2]时，f（x）≥，将f（x）转化到[0，2]上，得到具体的表达式，再根据不等式恒成立的解题思路，分离参数求出t的范围．解答：解：设x∈[﹣4，﹣2]，则x+4∈[0，2]，由f（x+2）=2f（x），所以f（x+4）=2f（x+2）=4f（x），即f（x）=f（x+4），结合x∈[0，2]时，f（x）=x2﹣2x，所以f（x）≥可化为：f（x+4）≥即≤2f（x+4）=2[（x+4）2﹣2（x+4）]，恒成立只需，易知当x+4=1，即x=﹣3时取得最小值﹣2．即，解得﹣1≤t＜0或t≥3．故选C．点评：本题考查了不等式的恒成立问题，一般是转化为函数的最值来解决，关键是能够根据f（x+2）=2f（x），将所求区间上的函数式转化到已知区间上来，得到具体的关于x的不等式恒成立，使问题获得解决．二、填空题（每小题5分，共25分）11．已知函数，则= 8 ．考点：对数的运算性质；函数的值．专题：计算题．分析：先求f（﹣4），根据分段函数解析式求f[f（﹣4）]；利用对数运算性质=n，求f（log2）的值，然后求和即可．解答：解：f（﹣4）=24=16，∴f[f（﹣4）]=f（16）=log416=2；∵log2=﹣log26＜0，∴f（log2）==6，∴f[f（﹣4）]+f（log2）=8．故答案是8．点评：本题借助求函数值，考查了对数的运算性质，计算要细心．12．设f（x）是周期为2的奇函数，当0≤x≤1时，f（x）=2x（1﹣x），则= ﹣．考点：函数奇偶性的性质；函数的值．专题：函数的性质及应用．分析：由题意得 f（﹣）=﹣f（）=﹣f（4+）=﹣f（），代入已知条件进行运算．解答：解：∵f（x）是周期为2的奇函数，当0≤x≤1时，f（x）=2x（1﹣x），f（﹣）=﹣f（）=﹣f（4+）=﹣f（）=﹣2×=﹣．故答案为：点评：本题考查函数的周期性和奇偶性的应用，以及求函数的值．13．已知实数x，y满足，则z=2x﹣y的最小值是﹣2 ．考点：简单线性规划．专题：计算题；不等式的解法及应用．分析：作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=2x ﹣y对应的直线进行平移，可得当x=0且y=2时，z取得最小值．解答：解：作出不等式组表示的平面区域，得到如图的△ABC及其内部，其中A（2，0），B（0，2），C（0，﹣2）设z=F（x，y）=2x﹣y，将直线l：z=2x﹣y进行平移，观察x轴上的截距变化，可得当l经过点B时，目标函数z达到最小值∴z最小值=F（0，2）=﹣2故答案为：﹣2点评：本题给出二元一次不等式组，求目标函数z=2x﹣y的最小值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．14．函数的零点有 3 个．考点：根的存在性及根的个数判断．专题：函数的性质及应用．分析：题目中条件：“函数f（x）=的零点个数”转化为方程lnx=x2﹣2x的根的个数问题及一次函数2x+1=0的根的个数问题，分别画出方程lnx=x2﹣2x左右两式表示的函数图象即得．解答：解：当x＞0时，在同一坐标系中画出y=lnx与y=x2﹣2x的图象如下图所示：由图象可得两个函数有两个交点．又一次函数2x+1=0的根的个数是：1．故函数的零点有3个故答案为：3点评：函数的图象直观地显示了函数的性质．在判断方程是否有解、解的个数及一次方程根的分布问题时，我们往往构造函数，利用函数的图象解题．体现了数形结合的数学思想．15．已知f（x）=ax2+bx+c（a≠0）且方程f（x）=x无实数根，下列命题：①方程f[f（x）]=x也一定没有实数根；②若a＞0；则不等式f[f（x）]＞x对一切x都成立；③若a＜0则必存在实数x0，使f[f（x0）]＞x0；④若a+b+c=0则不等式f[f（x）]＜x对一切x都成立．其中正确命题的序号是①②④．（把你认为正确命题的所有序号都填上）考点：命题的真假判断与应用．专题：函数的性质及应用．分析：根据函数f（x）=ax2+bx+c（a≠0），且方程f（x）=x无实数根，得出函数y=ax2+bx+c 与y=x的图象无交点，对选项中的命题进行分析判断，得出正确的结论．解答：解：∵由函数f（x）=ax2+bx+c（a≠0），且方程f（x）=x无实数根，即y=ax2+bx+c与y=x的图象无交点，∴①函数y=f[f（x）]与y=x的图象无交点，即方程f[f（x）]=x没有实数根，①正确；②当a＞0时，函数f（x）=ax2+bx+c（a≠0）的图象开口向上，与y=x无交点，∴f（x）的图象在y=x图象的上方，∴不等式f[f（x）]＞x对一切实数x都成立，②正确；③同理，当a＜0时，函数f（x）=ax2+bx+c（a≠0）的图象在y=x的下方，f[f（x）]＜x恒成立，∴③错误；④当a+b+c=0时，f（1）=0，结合题意知a＜0，函数f（x）=ax2+bx+c（a≠0）的图象在y=x 的下方，不等式f[f（x）]＜x对一切x都成立，∴④正确．综上，正确的答案为①②④．故答案为：①②④．点评：本题考查了复合函数的图象与性质的应用问题，解题时应结合二次函数的图象与性质进行解答，是难理解的题目．三、解答题（六大题共计75分）[16．已知函数f（x）=的定义域为A，集合B={x|（x﹣m﹣3）（x﹣m+3）≤0}．（1）求A和f（x）的值域C；（2）若A∩B=[2，3]，求实数m的值；（3）若C⊂∁R B，求实数m的取值范围．考点：集合的包含关系判断及应用；交集及其运算．专题：计算题；集合．分析：（1）解不等式求A，配方法求f（x）的值域C；（2）由已知A=[﹣1，3]，B=[m﹣3，m+3]，A∩B=[2，3]，即可求实数m的值；（3）求出C R B={x|x＞m+3，或x＜m﹣3}，利用C⊂∁R B，即可求实数m的取值范围．解答：解：（1）由f（x）有意义知：3+2x﹣x2≥0，得﹣1≤x≤3又3+2x﹣x2=﹣（x﹣1）2+4≤4，∴A=[﹣1，3]，C=[0，2]…（4分）（2）由已知A=[﹣1，3]，B=[m﹣3，m+3]又A∩B=[2，3]，得m﹣3=2，即m=5经检验当m=5时，B=[2，8]满足A∩B=[2，3]∴m=5…（8分）（3）∵C R B={x|x＞m+3，或x＜m﹣3}，C=[0，2]且C⊂∁R B，∴m+3＜0或m﹣3＞2，∴m＞5或m＜﹣3…（12分）点评：本题考查集合的包含关系判断及应用，考查集合的运算，考查学生分析解决问题的能力，属于中档题．17．设f（x）=x3+ax2+bx+1的导数f′（x）满足f′（1）=2a，f′（2）=﹣b，其中常数a，b∈R．（Ⅰ）求曲线y=f（x）在点（1，f（1））处的切线方程．（Ⅱ）设g（x）=f′（x）e﹣x．求函数g（x）的极值．考点：利用导数研究曲线上某点切线方程．专题：计算题；综合题；转化思想．分析：（I）根据已知中f（x）=x3+ax2+bx+1，我们根据求函数导函数的公式，易求出导数f'（x），结合f'（1）=2a，f'（2）=﹣b，计算出参数a，b的值，然后求出f（1）及f'（1）的值，然后代入点斜式方程，即可得到曲线y=f（x）在点（1，f（1））处的切线方程．（II）根据g（x）=f′（x）e﹣1求出函数g（x）的解析式，然后求出g（x）的导数g'（x）的解析式，求出导函数零点后，利用零点分段法，分类讨论后，即可得到函数g（x）的极值．解答：解：（I）∵f（x）=x3+ax2+bx+1∴f'（x）=3x2+2ax+b．令x=1，得f'（1）=3+2a+b=2a，解得b=﹣3令x=2，得f'（2）=12+4a+b=﹣b，因此12+4a+b=﹣b，解得a=﹣，因此f（x）=x3﹣x2﹣3x+1∴f（1）=﹣，又∵f'（1）=2×（﹣）=﹣3，故曲线在点（1，f（1））处的切线方程为y﹣（﹣）=﹣3（x﹣1），即6x+2y﹣1=0．（II）由（I）知g（x）=（3x2﹣3x﹣3）e﹣x从而有g'（x）=（﹣3x2+9x）e﹣x令g'（x）=0，则x=0或x=3∵当x∈（﹣∞，0）时，g'（x）＜0，当x∈（0，3）时，g'（x）＞0，当x∈（3，+∞）时，g'（x）＜0，∴g（x）=（3x2﹣3x﹣3）e﹣x在x=0时取极小值g（0）=﹣3，在x=3时取极大值g（3）=15e ﹣3点评：本题主要考查了利用导数研究曲线上某点切线方程，以及方程组的求解等有关问题，属于中档题．18．已知函数f（x）=x2﹣2|x|．（Ⅰ）判断并证明函数的奇偶性；（Ⅱ）画出函数g（x）=f（4﹣x）的图象，并比较g（﹣1）与g（6）大小．考点：二次函数的性质；函数奇偶性的性质．专题：计算题；作图题；函数的性质及应用．分析：（Ⅰ）先判断f（x）=x2﹣2|x|是偶函数，再利用定义证明；（Ⅱ）函数g（x）=f（4﹣x）=（4﹣x）2﹣2|4﹣x|，从而作出其函数图象，求值比较大小．解答：解：（Ⅰ）f（x）=x2﹣2|x|是偶函数，证明如下，函数f（x）的定义域是R，且f（﹣x）=（﹣x）2﹣2|﹣x|=x2﹣2|x|=f（x）．则函数f（x）是偶函数．（Ⅱ）函数g（x）=f（4﹣x）=（4﹣x）2﹣2|4﹣x|，作其函数图象如下，g（﹣1）=f（5）=15，g（6）=f（﹣2）=0；则g（﹣1）＞g（6）．点评：本题考查了学生的作图能力及应用图象的能力，属于基础题．19．设集合A={x|（2+x）（3﹣x）≥0}，B=（1）求集合A；（2）若x∈A是x∈B的必要不充分条件，试求实数k的取值范围．考点：必要条件、充分条件与充要条件的判断．专题：集合；简易逻辑．分析：（1）利用一元二次不等式的解法即可得出；（2）记g（x）=kx2+4x+k+3，由g（x）≥0在R上有解，而k＜0，由△≥0，得﹣4≤k＜0，对k分类讨论，及其充要条件的判定即可得出．解答：解：（1）由（2+x）（3﹣x）≥0，化为（x+2）（x﹣3）≤0，解得﹣2≤x≤3．∴A=[﹣2，3]．（2）记g（x）=kx2+4x+k+3，由g（x）≥0在R上有解，而k＜0，故△=16﹣4k（k+3）≥0，得﹣4≤k＜0，①当．设g（x）=0的两个根x1，x2（x1＜x2），则B=（x1，x2），由x∈A是x∈B的必要不充分条件得：②由①②得．点评：本题考查了一元二次不等式的解集与判别式的关系、分类讨论、充要条件的判定，考查了推理能力与计算能力，属于中档题．20．已知f（x）=log a x﹣x+1（a＞0，且a≠1）（1）若a=e，求f（x）的单调区间；（2）若f（x）＞0在区间（1，2）上恒成立，求实数a的取值范围．考点：利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：导数的综合应用．分析：（1）利用导数判断函数的单调性即可；（2）f（x）＞0在区间（1，2）上恒成立，等价于lna＜在区间（1，2）上恒成立，利用导数求得函数F（x）=的最小值，即可得出结论．解答：解：（1）a=e时，（2）∵，∴而x∈（1，2）时，lnx＞0，x﹣1＞0∴0＜a＜1不合题意∴a＞1∴由（1）知，当x＞0，f（x）=lnx﹣x+1＜f（1）=0，∴，∴F'（x）＜0恒成立∴F（x）在（1，2）上单调递减，即F（x）＞F（2）=ln2，∴lna≤ln2，∴a≤2，综上得a∈（1，2]．点评：本题主要考查利用导数研究函数的单调性及函数的最值问题，考查学生恒成立问题的等价转化能力及运算求解能力，属于中档题．21．已知二次函数f（x）=ax2+bx+c．（1）若a＞b＞c，且f（1）=0，证明f（x）的图象与x轴有2个交点；（2）在（1）的条件下，是否存在m∈R，使得f（m）=﹣a成立时，f（m+3）为正数，若存在，证明你的结论，若不存在，请说明理由；（3）若对x1，x2∈R，且x1＜x2，f（x1）≠f（x2），方程f（x）=[f（x1）+f（x2）]有两个不等实根，证明必有一个根属于（x1，x2）．考点：函数与方程的综合运用．专题：计算题．分析：（1）由f（1）=0，得a+b+c=0，根据a＞b＞c，可知a＞0，且c＜0，再利用根的判别式可证；（2）由条件知方程的一根为1，另一根满足﹣2＜x2＜0．由于f（m）=﹣a＜0，可知m∈（﹣2，1），从而m+3＞1，根据函数y=f（x）在[1，+∞）上单调递增，可知（m+3）＞0成立．（3）构造函数g（x）=f（x）﹣[f（x1）+f（x2）]，进而证明g（x1）g（x2）＜0，所以方程g（x）=0在（x1，x2）内有一根，故方程f（x）=[f（x1）+f（x2）]必有一根属于（x1，x2）．解答：解：（1）因为f（1）=0，所以a+b+c=0，又因为a＞b＞c，所以a＞0，且c＜0，因此ac＜0，所以△=b2﹣4ac＞0，因此f（x）的图象与x轴有2个交点．（2）由（1）可知方程f（x）=0有两个不等的实数根，不妨设为x1和x2，因为f（1）=0，所以f（x）=0的一根为x1=1，因为x1+x2=﹣，x1x2=，所以x2=﹣﹣1=，因为a＞b＞c，a＞0，且c＜0，所以﹣2＜x2＜0．因为要求f（m）=﹣a＜0，所以m∈（x1，x2），因此m∈（﹣2，1），则m+3＞1，因为函数y=f（x）在[1，+∞）上单调递增；所以f（m+3）＞f（1）=0成立．（3）构造函数g（x）=f（x）﹣[f（x1）+f（x2）]，则g（x1）=f（x1）﹣[f（x1）+f（x2）]=[f（x1）﹣f（x2）]，g（x2）=f（x2）﹣[f（x1）+f（x2）]=[f（x2）﹣f（x1）]，于是g（x1）g（x2）=[f（x1）﹣f（x2）][f（x2）﹣f（x1）]=﹣[f（x1）﹣f（x2）]2，因为f（x1）≠f（x2），所以g（x1）g（x2）=﹣[f（x1）﹣f（x2）]2＜0，所以方程g（x）=0在（x1，x2）内有一根，即方程f（x）=[f（x1）+f（x2）]必有一根属于（x1，x2）．点评：本题以二次函数为载体，考查方程根的探求，考查函数值的确定及函数的零点问题，有一定的综合性．。