数字电子技术anwser01
《数字电子技术》部分习题解答

《数字电子技术》部分习题解答第1 章数字逻辑基础1.3 将下列十进制数转换成等值的二进制数、八进制数、十六进制数。
要求二进制数保留小数点后4位有效数字。
(1)(19)D ;(2)(37.656)D ;(3)(0.3569)D解:(19)D=(10011)B=(23)O=(13)H(37.656)D=(100101.1010)B=(45.5176)O=(25.A7E)H(0.3569)D=(0.01011)B=(0.266)O=(0.5B)H1.4 将下列八进制数转换成等值的二进制数。
(1)(137)O ;(2)(36.452)O ;(3)(0.1436)O解:(137)O=(1 011 111)B(36.452)O=(11110. 10010101)B(0.1436)O=(0.001 100 011 11)B1.5 将下列十六进制数转换成等值的二进制数。
(1)(1E7.2C)H ;(2)(36A.45D)H ;(3)(0.B4F6)H解:(1E7.2C)H=(1 1110 0111.0010 11)B(36A.45D)H=(11 0110 1010. 0100 0101 1101)B(0.B4F6)H=(0.1011 0100 1111 011)B1.6 求下列BCD码代表的十进制数。
(1)(1000011000110101.10010111)8421BCD ;(2)(1011011011000101.10010111)余3 BCD ;(3)(1110110101000011.11011011)2421BCD;(4)(1010101110001011.10010011)5421BCD ;解:(1000 0110 0011 0101.1001 0111)8421BCD=(8635.97)D(1011 0110 1100 0101.1001 0111)余3 BCD =(839.24)D(1110 1101 0100 0011.1101 1011)2421BCD=(8743.75)D(1010 1011 1000 1011.1001 0011)5421BCD=(7858.63)D1.7 试完成下列代码转换。
数字电子技术答案 第1章 逻辑代数基础习题解答

X Y Z
F
图1.28 习题1-2(1)逻辑图
解:
X Y Z
00001111 00110011 01010101
00001111 11001100
11001111 01000101 01010101 00100000 01100101 F
11110000 00110011 10101010
真值表 X 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
CD AB 00 01 11 10 00 1 0 0 1 01 0 0 0 0 11 0 0 1 1 10 1 0 0 1
1-5 以卡诺图法化简下列函数,写成或-与表达式的形式。 (1) F AB (C D) A B DC 解: F (C D)( A C )( A D)( B D)( B C )
图1.29 习题1-2(6)的卡诺图
真值表 A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 0
(2) F
A, B , C
m(1,2,5,7)
真值表 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
(3) F
W , X ,Y , Z
M (2,3,6,7,10,12)
真值表 W 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 X 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 1 0 0 1 1 0 0 1 1 0 1 0 1 1 1
数字电子技术课后习题答案(全部)

第一章数制与编码1.1自测练习1.1.1、模拟量数字量1.1.2、(b)1.1.3、(c)1.1.4、(a)是数字量,(b)(c)(d)是模拟量1.2 自测练习1.2.1. 21.2.2.比特bit1.2.3.101.2.4.二进制1.2.5.十进制1.2.6.(a)1.2.7.(b)1.2.8.(c)1.2.9.(b)1.2.10.(b)1.2.11.(b)1.2.12.(a)1.2.13.(c)1.2.14.(c)1.2.15.(c)1.2.16.11.2.17.111.2.18.1.2.19.11011.2.20.8进制1.2.21.(a)1.2.22.0,1,2,3,4,5,6,71.2.23.十六进制1.2.24.0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1.2.25.(b)1.3自测练习1.3.1.1221.3.2.675.521.3.3.011111110.011.3.4.521.3.5.1BD.A81.3.6.1111.11101.3.7.38551.3.8.28.3751.3.9.100010.111.3.10.135.6251.3.11.570.11.3.12.120.51.3.13.2659.A1.4自测练习1.4.1.BCD Binaryl二—十进制码1.4.2.(a)1.4.3.(b)1.4.4.8421BCD码,4221BCD码,5421BCD1.4.5.(a)1.4.6.011001111001.10001.4.7.111111101.4.8.101010001.4.9.111111011.4.10.61.051.4.11.01011001.011101011.4.12.余3码1.4.13.XS31.4.14.XS31.4.15.1000.10111.4.16.1001100000111.4.17.521.4.18.110101.4.19.0101111.4.20.(b)1.4.21.ASCII1.4.22.(a)1.4.23.ASCII h ange美准码EBCDICExtende d BinaryCoded Decimal Interch ange Code 扩展二-十进制 1.4.24.10010111.4.25.ASCII1.4.26.(b)1.4.27.(b)1.4.28.110111011.4.29.-1131.4.30.+231.4.31.-231.4.32.-861.5 自测练习 1.5.1 略 1.5.2 11011101 1.5.3 01000101 1.5.4 11100110 补码形式 1.5.5 01111101 1.5.6 10001000 补码形式 1.5.7 11100010 补码形式 习题1.1 (a )(d )是数字量,(b )(c )是模拟量,用数字表时(e )是数字量,用模拟表时(e )是模拟量1.2 (a )7, (b )31, (c )127, (d )511, (e )40951.3 (a )22104108⨯+⨯+, (b )26108108⨯+⨯+,(c )321102105100⨯+⨯+⨯+(d )322104109105⨯+⨯+⨯+1.4 (a )212121⨯+⨯+, (b )4311212121⨯+⨯+⨯+, (c )64212+12+12+12+1⨯⨯⨯⨯(d )9843212+12+12+12+12⨯⨯⨯⨯⨯ 1.5 2201210327.15310210710110510--=⨯+⨯+⨯+⨯+⨯,3210-1-221011.0112+02+12+12+02+12=⨯⨯⨯⨯⨯⨯, 210-18437.448+38+78+48=⨯⨯⨯⨯, 10-1-2163A.1C 316+A 16+116+C 16=⨯⨯⨯⨯1.6 (a )11110, (b ) ,(c ) , (d )1011 1.7 (a ) 0, (b ) 1111 1.8 110102 = 2610, 1011.0112 = 11.37510, 57.6438 = 71.81835937510, 76.EB 16 = 118.7510 1.9 1101010010012 = 65118 = D4916,0.100112 = 0.468 = 0.9816,1011111.011012 =137.328 = 5F.68161.10 168 = 1410,1728 = 12210,61.538 = 49.671875, 126.748 = 86.937510 1.11 2A 16 = 4210 = 2 = 528, B2F 16 = 286310 = 2 = 54578,D3.E 16 = 211.87510 = 11.11102 = 323.78, 1C3.F916 = 451 2510 = 011.111110012 = 703.76281.12 (a )E, (b )2E, (c )1B3, (d )349 1.13 (a )22, (b )110, (c )1053, (d )2063 1.14 (a )4094, (b )1386, (c )49282 1.15 (a )23, (b )440, (c )2777 1.16 198610 = = 00011001100001108421BCD , 67.31110 = 1.010012 = 01100111.0011000100018421BC D ,1.183410 = 1.0010112 = 0001.00011000001101008421BCD , 0.904710 = 0.1110012 = 0000.10010000010001118421BCD1.17 1310 = 000100118421B CD = 01000110XS3 = 1011Gra y, 6.2510 = 0110.001001018421B CD = 1001.01011000XS3 = 0101.01Gray,0.12510= 0000.000100100101 = 0011.010001101000X S3 = 0.001 Gray8421BCD1.18 101102= 11101 Gray,0101102 = 011101 Gray1.19 110110112 = 0010000110018421BCD,45610 = 0100010101108421BCD,1748=0010011101008421BCD,2DA16 = 0111001100008421BCD,101100112421B CD = 010100118421B CD,11000011XS3 = 100100008421B CD1.20 0.0000原= 0.0000反= 0.0000补,0.1001原= 0.1001反= 0.1001补,11001原=10110反=10111补1.21 010100原= 010100补,101011原= 110101补,110010原= 101110补,100001原=111111补1.22 1310 = 00001101补,11010 = 01101110补,-2510 = 11100111补,-90 = 10100110补1.23 01110000补= 11210,00011111补= 3110,11011001补= -3910,11001000补= -56101.24 100001110000011010101101010010010011001111 1001110010000101000001001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001 1100111 11001011.25 010001010110000100000011110101000000110010 01101010101111101100101000101.26 BEN SMITH1.27 00000110 100001101.28 01110110 10001110第二章逻辑门1.1 自测练习2.1.1. (b)2.1.2. 162.1.3. 32, 62.1.4. 与2.1.5. (b)2.1.6. 162.1.7. 32, 62.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习2.2.1. F A B=⋅2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16,52.2.6. 12.2.7. 串联2.2.8. (b)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC,上拉电阻2.3.2. 0,1,高阻2.3.3. (b)2.3.4. (c)2.3.5. F A B=⋅, 高阻2.3.6. 不能2.4 自测练习1.29 TTL,CMOS1.30 Transis itor Transis tor Logic1.31 Complem entary Metal Oxide Semicod uctor1.32 高级肖特基TT L, 高级 肖特基T TL1.33 高,强,小1.34 (c)1.35 (b)1.36 (c)1.37 大1.38 强1.39 (a)1.40 (a)1.41 (b)1.42 高级肖特基TT L1.43 (c)习题2.1 与,或,与2.2 与门,或门,与门2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD2.4 (a )0 (b )1 (c )0 (d )0 2.5 (a )0 (b )0 (c )1 (d )0 2.6 (a )1 (b )1 (c )1 (d )1 2.7 (a )4 (b )8 (c )16 (d )32 2.8 (a )3 (b )4 (c )5 (d )6 2.9 (a )(b ) A B C D F 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 11112.10 Y AB AC =+2.11A B C Y 0 0 0 0 0 0 1 0 011A B C F 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 11110 1 1 11 0 0 01 0 1 11 1 0 01 1 1 12.122.13F1 = A(B+C), F2=A+BCA B C F1F20 0 0 0 00 0 1 0 00 1 0 0 00 1 1 0 11 0 1 1 11 0 0 0 11 1 0 1 11 1 1 1 12.142.15 (a)0 (b)1 (c)1 (d)02.16 (a)1 (b)0 (c)0 (d)12.17 (a)0 (b)02.18=⋅⋅⋅2.19 Y AB BC DE F=⋅⋅2.20 Y AB CD EF2.21 102.22 402.23 当TTL反相器的输出为3V,输出是高电 ,红灯亮。
数字电子技术课后习题答案

1.12 写出下图所示各逻辑图的输出函数表达式,列 出它们的真值表。
F1 F4
F2
F3
解: F1 AB F2 A B F3 BC
F 4 F1 F 2 F3
Z CF 4 C AB A B BC
C AB A B BC
C AB AB BC C AB AB B ABC
电路的驱动方程、状态方程和输出方程,画出电路
的状态表、状态图和时序图,说明电路能否自启动。
设各触发器的初始状态为0。
❖ 解:
驱动方程为: ❖
D1 Q1n ; D2 X Q1n Q2n
输出方程为: ❖
Y XQ1nQ2n XQ1nQ2n XQ1nQ2n XQ1nQ2n
❖ 状态方程为:Q1n1 D1 Q1n
输入 SD、RD 的波形图如下,试画出输出Q,
Q 对应的波形图。设触发器的初始状态为 Q=0, Q. 1
❖ 解:波形图如下图
不定
❖ 4.6主从JK触发器,已知CP、J、K的波形如下 所示,试画出Q对应的波形图。触发器的初始 状态为Q=0。
❖ 解:
CP为1时 输入端2 次变化,
❖ 4.7维持—阻塞边沿D触发器中,已知 CP, RD , SD , D
/0
/0
000
001
010
/1
/0
100
011
/0
❖ 2.卡诺图为
Q1nQ0n
Q2n
00 01
0 001/0 010/0
1 000/1 xxx/x
11
100/0 xxx/x
10
011/0 xxx/x
❖ 由卡诺图得电路的状态方程与输出方程为
❖
Qn1 0
Q2n Q0n
数字电子技术习题解答
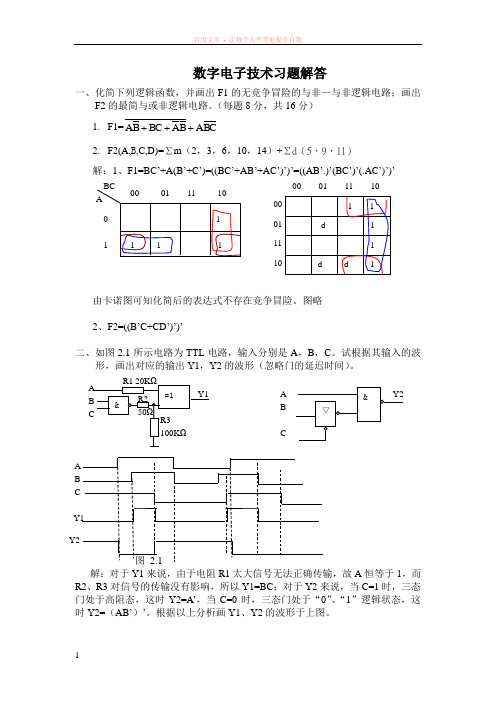
数字电子技术习题解答一、化简下列逻辑函数,并画出F1的无竞争冒险的与非—与非逻辑电路;画出F2的最简与或非逻辑电路。
(每题8分,共16分)1. F1=B C A B A B C B A +++2. F2(A,B ,C,D)=Σm (2,3,6,10,14)+Σd (5,9,11)解:1、F1=BC ’+A(B ’+C ’)=((BC ’+AB ’+AC ’)’)’=((AB ’.)’(BC ’)’(.AC ’)’)’由卡诺图可知化简后的表达式不存在竞争冒险。
图略2、F2=((B ’C+CD ’)’)’二、如图2.1所示电路为TTL 电路,输入分别是A ,B ,C 。
试根据其输入的波形,画出对应的输出Y1,Y2的波形(忽略门的延迟时间)。
图 2.1解:对于Y1来说,由于电阻R1太大信号无法正确传输,故A 恒等于1,而R2、R3对信号的传输没有影响,所以Y1=BC ;对于Y2来说,当C=1时,三态门处于高阻态,这时Y2=A ’,当C=0时,三态门处于“0”、“1”逻辑状态,这时Y2=(AB ’)’。
根据以上分析画Y1、Y2的波形于上图。
ABC 00 01 11 10 0 11 1 1 1 00 01 11 101 1 11 1 d d d =1 & & ▽ Y2 Y1 R1 20K Ω R2 50Ω R3 100K Ω A B C A B C A B C Y1 Y2三、试设计一个按8421BCD 码计数的同步七进制加法计数器,由零开始计数。
1. 用JK 触发器实现; (10分)2. 用1片同步十进制计数器74LS160及最少的门电路实现.74LS160功能表及逻辑符号如图3所示。
(10分)Rd LD S1 S2 CP 功能0 X X X X 请零 1 0 X X 置数1 1 1 1 计数 1 1 0 1 X 保持1 1 1 0 X 保持图3解:1、根据题给8421BCD 码加法计数器要求,得状态转换表:Q 2 Q 1 Q 0 C0 0 0 0 0 0 1 00 1 0 00 1 1 01 0 0 0 1 0 1 0 1 1 0 1将状态方程与JK 触发器的特性方程比较,得驱动方程: J 2= Q 0Q 1 ,K 2=Q 1 J 1= Q'0Q ’2,K 1=Q ’0 J 0=(Q 1Q 2)’, K 0=1 输出方程:C=Q 1Q 2 图略,由设计过程可知任意态111将进入000,故电路可自启动。
数字电子技术习题答案

(1)Y = (A + B)(A + B)C + BC
ww w. kh
Y = ABC + ABC + B + C
答 案
Y = A + B + C = ABC
课 后
网
co
m
4.用卡诺图化简法将下列函数化为 最简与或形式。
(2)Y = AB+ AC + BC
课
后
答
案
(4)Y(A,B,C,D) = ∑(m0 ,m1,m2 ,m3,m4 ,m6 ,m8 ,m9 ,m10 ,m11,m14 )
01
11
10
Байду номын сангаас
m
5.将下列函数化为最简与或函数式。
Y = C D( A ⊕ B) + ABC + AC D
约束条件AB+CD=0 (2)Y(A,B,C,D)=Σ (m3,m5,m6,m7,m10),给定约束条件为 m0+m1+m2+m4+m8=0 (3)Y(A,B,C,D)=Σ (m2,m3,m7,m8,m11,m14) 给定约束条件为: m0+m5+m10+m15=0。
da 课 后 答 案 网 ww w. kh w. co m
答案:
课
后
答
= A B C + A B C + A B C + ABC Y2
案
网
ww
(b) Y 1 = AB + BC + AC
w. kh
da
(a)Y = ABC + BC
w.
co
m
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101 解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
《数字电子技术》部分(1~5章)习题解答

《数字电子技术》部分习题解答第1 章数字逻辑基础1.3 将下列十进制数转换成等值的二进制数、八进制数、十六进制数。
要求二进制数保留小数点后4位有效数字。
(1)(19)D ;(2)(37.656)D ;(3)(0.3569)D解:(19)D=(10011)B=(23)O=(13)H(37.656)D=(100101.1010)B=(45.5176)O=(25.A7E)H(0.3569)D=(0.01011)B=(0.266)O=(0.5B)H1.4 将下列八进制数转换成等值的二进制数。
(1)(137)O ;(2)(36.452)O ;(3)(0.1436)O解:(137)O=(1 011 111)B(36.452)O=(11110. 10010101)B(0.1436)O=(0.001 100 011 11)B1.5 将下列十六进制数转换成等值的二进制数。
(1)(1E7.2C)H ;(2)(36A.45D)H ;(3)(0.B4F6)H解:(1E7.2C)H=(1 1110 0111.0010 11)B(36A.45D)H=(11 0110 1010. 0100 0101 1101)B(0.B4F6)H=(0.1011 0100 1111 011)B1.6 求下列BCD码代表的十进制数。
(1)(1000011000110101.10010111)8421BCD ;(2)(1011011011000101.10010111)余3 BCD ;(3)(1110110101000011.11011011)2421BCD;(4)(1010101110001011.10010011)5421BCD ;解:(1000 0110 0011 0101.1001 0111)8421BCD=(8635.97)D(1011 0110 1100 0101.1001 0111)余3 BCD =(839.24)D(1110 1101 0100 0011.1101 1011)2421BCD=(8743.75)D(1010 1011 1000 1011.1001 0011)5421BCD=(7858.63)D1.7 试完成下列代码转换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试卷一(答案)
一、填空:(14分)
1. 220 ,1101 1100 , 334 。
2. 147 , 93 。
3. D C B A D C A B F +⋅⋅+⋅⋅⋅= ,D C AB D AC B F +⋅+⋅=’
4. n
2
5. 8 , A/D 。
6. 8 k
7. 8
8. 高 ; 低 。
二、用代数法将下列函数化简为最简与或表达式。
(10分) 解:1.11=⋅⋅+⋅⋅+⋅⋅=C B A C B A C B A F
2.B BD BC ABD ABC F ++++=2
三、用卡诺图法化简函数,写出它们的最简与或表达式。
(10分) 1.D C B ABC C AB C B A F +++=;2.()()∑∑+=
15,014,13,11,9,8,5,3d m F
解:1.D C B AB C B F ++= 2.C B A ABC D C B CD B F +++=
AB CD
0001101100011110
AB CD
00
01101100011110
011111111
00000000000000
11
11111B
B AB
C
D C B D BC ABC C
B BD D B
C ABC =+=⋅++=+++=
四、 (14分)
五、(12分) 解:按题意
()()
C
B A AB
C X B A ABC X C B A ABC X F ⋅⋅+⊕=⋅⋅+⋅+⋅⋅+=用四选一数据选择器实现函数
C B A ABC L ⋅⋅+=
若令 A A =1,B A =0,
则 C D =0,C D =3,021==D D , 电路如图所示。
X
A B
六、(10分)
解:按题意列全加器真值表(略),由真值表可得 1111----+++=i i i i i i i i i i i i i C B A C B A C B A C B A S 1111----+++=i i i i i i i i i i i i i i C B A C B A C B A C B A C
令 i A A =2(被加数),i B A =1(加数),10-=i C A (低位进位),则 74217421012012012012Y Y Y Y Y Y Y Y A A A A A A A A A A A A S i =+++=+++= 同理可得 7653Y Y Y Y C i = 全加器逻辑图如下图所示。
七、(10分)
解:图中所示电路是一个同步单次脉冲发生 电路,波形如右图所示。
在输入信号A 上升沿后产生一个与CP 脉冲同步、且宽度等于CP 脉冲宽度的时钟 单脉冲。
被加数 A i 加数 B i 和 S i 进位 C i
低位进位 C CP
A
Q 1 Q 2 X
八、(10分)
九、(10分)解:根据公式可得 ()[]Hz 023.12443
.1121=+=C R R f
输出波形如图所示
t
t
u u O
V DD DD 六进制加法计数十进制加法计数。
