电子教案《信号与系统》(第四版_燕庆明)(含习题解答)6.4
电子教案《信号与系统》(第四版_燕庆明)(含习题解答)6.3

6.3 线性系统的稳定性
一、稳定的概念
稳定:充要条件是
h(t)
dt
,即H(s)的全部极点
位于S的左半平面;
临界稳定: H(s)在虚轴上有单极点,其余极点均在
S的左半平面;
不稳定: H(s)只要有一个极点位于S的右半平面。
信号与系统 6.3-2
例
图1
二、稳定性判据
信号与系统 6.3-3
必要条件: H( s )的分母多项式
D(s) ansn an-1sn-1 a1s a0
的全部系数非零且均为正实数。 充要条件:对二阶系统,D(s) a2s2 a1s a0 的全部 系数非零且为正实数。 充要条件:对三阶系统,D(s) a3s3 a2s2 a1s a0 的 各项系数全为正,且满足
a1a2 a0a3
信号与系统 6.3-4
例 导弹跟踪系统H (s) Nhomakorabeas3
34.5s2 119.7s 98.1 35.714s2 119.741s 98.1
N (s) D(s)
显然
a1a2 > a0a3
故系统稳定。
练习: 判别稳定性
1. D(s) s2 3s 2 2. D(s) s3 s2 4s 10 3. D(s) s3 4s2 5s 6
end
信号与系统课后答案(全)
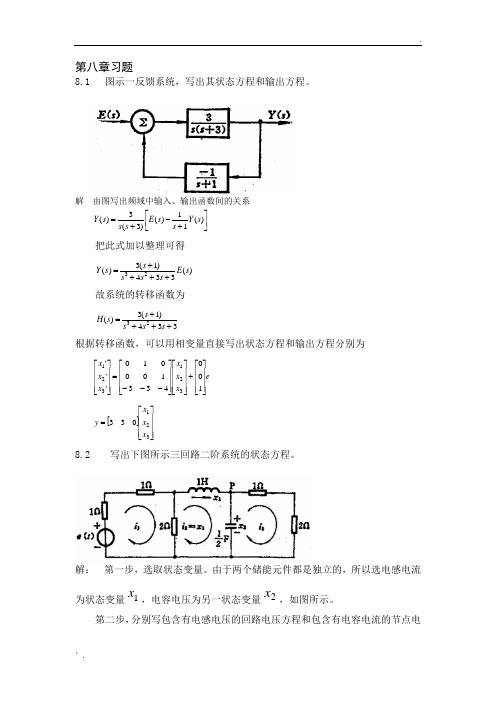
第八章习题8.1 图示一反馈系统,写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数,可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解:第一步,选取状态变量。
由于两个储能元件都是独立的,所以选电感电流为状态变量1x,电容电压为另一状态变量2x,如图所示。
第二步,分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程,并代入元件参数,则有112122'ixxx+--=312'21ixx-=第三步,上两式中1i和3i不是状态变量,要把它们表为状态变量。
由第一个回路有1124xie-=,即112141xei+=由第三个回路有323ix=,即2331xi=把1i和3i分别代入第二步中两式,并经整理,最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路,这里的激励函数)(t e是一压控电流源,输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解:第一步,选状态变量。
因为电感电流和电容电压等三个变量都是独立的,所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步,分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步,消去非状态变量。
信号与线性系统分析_(第四版)习题答案

专业课习题解析课程xxxxxx大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的辯达式。
1-4 写出图1-4所示各序列的闭合形式辯达式。
信号与系统教程燕庆明答案

信号与系统教程燕庆明答案【篇一:信号与系统课后习题】t)?tf(t?td),tf(t?t0)?yf(t?t0)?,yf(t?t0)?(t?t0)f(t?t0)。
(3)令g(t)?f(t?t0),t[g(t)]?g(?t)?f(?t?t0),tf(t?t0)? yf(t?t0),yf(t?t0)?f(?t?t0)1.2.已知某系统输入f(t)与输出y(t)的关系为y(t)?f(t)判断该系统是否为线性时不变系统?解:设t为系统运算子,则y(t)可以表示为y(t)?t[f(t)]?f(t),不失一般性,设f(t)?f1(t)?f2(t)t[f1(t)]?f1(t)?y1(t),t[f(t)]?f1(t)?f2(t)?y(t),显然其不相等,即为非线性时不变系统。
df(t)tf(x)dx(2):[y(t)]2?y(t)?f(t) 1.3判断下列方程所表示系统的性(1):y(t)?0dt(3):y(t)?2y(t)?3y(t)?f(t)?f(t?2)(4):y(t)?2ty(t)?2y(t)?3f(t) 线性非线性时不变线性时不变线性时变1.4。
试证明方程y(t)+ay(t)=f(t)所描述的系统为线性系统。
证明:不失一般性,设输入有两个分量,且f1(t)→y1(t),f2(t)→y2(t) 则有y1(t)+ay1(t)=f1(t),y2(t)+ay2(t)=f2(t) 相加得y1+ay1(t)+y2(t)+ay2(t)=f1(t)+f2(t) 即d[y1(t)+y2(t)]+a[y1(t)+y2(t)] dt=f1(t)+f2(t)可见f1(t)+f2(t)→y1(t)+y2(t)即满足可加性,齐次性是显然的。
故系统为线性的。
1.5。
证明1.4满足时不变性。
证明将方程中的t换为t-t0,t0为常数。
即y(t-t0)+ay(t-t0)=f(t-t0) 由链导发则,有dy(t?t0)dtd(t?t0)dy(t?t0)d(t?t0)dy(t?t0)dy(t?t0)1从而又因t0为常数,故所以有 ??dtd(t?t0)dtdtd(t?t0)dy(t?t0)ay(tt0)f(tt0)即满足时不变性f(t-t0)→y(t-t0) dty(t)?y(t?t0)f(t)?f(t??t)?所以ttlimf(t)?f(t??t)limy(t)?f(t?t0)既有 f(t)?y(t) ?t0t0tt1.7 若有线性时不变系统的方程为y(t)+ay(t)=f(t)在非零f(t)作用下其响应y(t)=1-e-t,试求方程y(t)+ay(t)=2f(t)+f(t)的响应。
信号与系统电子教案
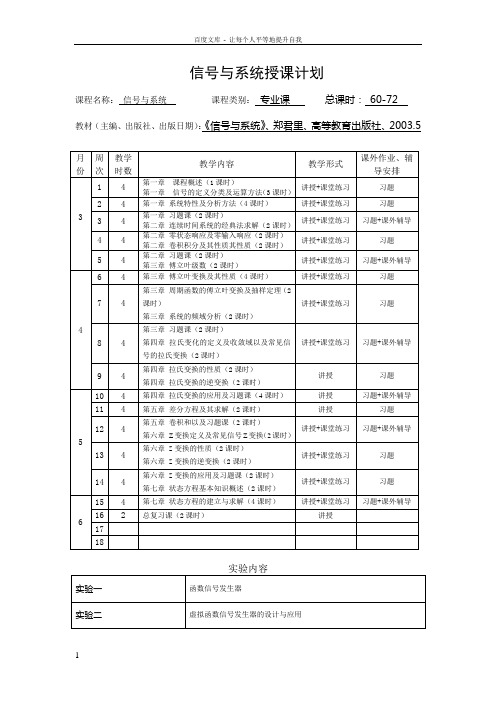
信号与系统授课计划课程名称:信号与系统课程类别:专业课总课时:60-72教材(主编、出版社、出版日期):《信号与系统》、郑君里、高等教育出版社、2003.5第一章绪论(8-10课时)本章是信号与系统课程的总论,包括信号与系统课程概述和一些基本概念,简单来说就是要讲清楚什么是信号、什么是系统、以及信号与系统之间是什么关系的问题。
主要内容包括:信号与系统课程概述、信号与系统课程的主要内容、信号的定义及常见信号介绍以及信号的运算、系统的定义与分类以及系统的分析方法介绍等。
本章内容是全书内容的浓缩、是基础、是引言,所以非常重要。
一、主要知识点如下:1、信号与系统课程概述主要包括:(1)信号与系统课程的产生与发展(2)信号与系统课程与其他课程的联系(3)信号与系统的应用领域2、信号的定义与分类、信号的运算主要包括:(1)信号的定义与分类(2)信号的运算3、系统的定义、分类及分析方法主要包括:(1)系统的定义及分类(2)线性时不变系统四大特性及判断方法二、本章知识重难点分析1、信号的定义及分类是重点,其中关于周期信号的定义及信号周期的计算是难点,同样关于连续时间信号与离散时间信号的定义与区别也是难点。
2、几种特殊信号的定义是本课程的重点内容,包括单位阶跃信号、单位冲激信号的定义与运算。
其中单位阶跃信号与单位冲激信号的定义与性质是难点。
3、信号的运算也是本章知识的重点内容,特别是信号直流分量与交流分量、信号奇分量与偶分量等的分解运算,信号的尺度、位移、反折运算等。
4、系统的定义及分类是重点5、线性时不变系统的定义及四大特性,其中四大特性(微积分、时不变、线性、因果性)的定义与判断是难点,特别是线性性是非常重要的内容。
6、线性时不变系统的分析方法是本章的重点7、系统的描述方法,框图与方程,框图与方程之间的关系与转换方法,其中框图与方程之间的转换关系是难点。
三、本章知识点课时安排1、信号与系统课程概述(2课时)2、信号的定义与分类、信号的运算(3课时)3、系统的定义、分类及分析方法(3课时)第二章连续时间系统的时域分析(6-8课时)LTI连续系统的时域分析过程可以理解为建立并求解线性微分方程,因其分析过程涉及的函数变量均为时间t,故称为时域分析法。
《信号与系统(第四版)》习题详解图文

故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组{ξ1(t),ξ2(t),ξ3(t),ξ4(t)}在(0,4)区间上是否 为正交函数组,是否为归一化正交函数组,是否为完备正交函 数组,并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到:
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=-f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω),且 试在K≥ωm条件下化简下式:
72
第3章 连续信号与系统的频域分析 73
107
信号与系统(第四版)第四章课后答案

第5-3页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
一、从傅里叶变换到拉普拉斯变换
有些函数不满足绝对可积条件,求解傅里叶变换困难。 为此,可用一衰减因子e-t(为实常数)乘信号f(t) ,适当 选取的值,使乘积信号f(t) e-t当t∞时信号幅度趋近于 0 ,从而使f(t) e-t的傅里叶变换存在。
0
β
σ
第5-7页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
例3 双边信号求其拉普拉斯变换。
e t , t 0 f 3 (t ) f1 (t ) f 2 (t ) t e , t 0
求其拉普拉斯变换。
解 其双边拉普拉斯变换 F (s)=F (s)+F (s) b b1 b2
第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0
1 s s0
s0t
令s0 0
第5-12页
(t )
■
1
s
, 0
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
五、单边拉氏变换与傅里叶变换的关系
F ( s) f (t ) e st d t
0
Re[s]>0
F (j ) f (t ) e
电子教案《信号与系统》(第四版_燕庆明)(含习题解答)信号与系统第四版习题解答

也可以利用迟延性质计算该卷积。因为
(t) *(t)=t(t)
f1(tt1) *f2(tt2)=f(tt1t2)
故对本题,有
(t+ 3 ) *(t5 )=(t+ 35)(t+ 35)=(t2)(t2)
两种方法结果一致。
(c)tet(t)*(t)= [tet(t)]= (ettet)(t)
题2-1图
解由图示,有
又
故
从而得
2-2设有二阶系统方程
在某起始状态下的0+起始值为
试求零输入响应。
解由特征方程
2+ 4+ 4 =0
得1=2=2
则零输入响应形式为
由于
yzi( 0+) =A1= 1
2A1+A2= 2
所以
A2= 4
故有
2-3设有如下函数f(t),试分别画出它们的波形。
(a)f(t) = 2(t1 )2(t2 )
第5章
5-1求下列函数的单边拉氏变换。
(1)
(2)
(3)
解(1)
(2)
(3)
5-2求下列题5-2图示各信号的拉氏变换。
题5-2图
解(a)因为
而
故
(b)因为
又因为
故有
5-3利用微积分性质,求题5-3所示信号的拉氏变换。
题5-3图
解先对f(t)求导,则
故对应的变换
所以
5-4用部分分式法求下列象函数的拉氏反变换。
它们的频谱变化分别如图p4-8所示,设C>2。
图p4-8
4-9如题4-9图所示系统,设输入信号f(t)的频谱F()和系统特性H1()、H2()均给定,试画出y(t)的频谱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锁相环是一个相位负反馈控制系统,应用 很广。当输入相位与输出相位的瞬时相位差恒 定时,称为系统锁定。
例 锁相环及其阶跃响应:
信号与系统 6.4-7
图4
信号与系统 6.4-8
该系统函数
H (s)
1000(0.01s2 4s3 100s2
0.2s 1) 200s 1000
显然
a1a2 > a0a3
故系统稳定,且阶跃响应
e (t) t 0 e(t) t 0
end
图3
信号与系统 6.4-4
例
图4
信号与系统 6.4-5
对(a):
H (s) K1K2
1000
10
1 K1K2 1 0.099 1000
对(b):
H (s) K1K2 5 100 9.9
1 K1K2 1 0.099 500
结论:
负反馈可以改善系统性能。
信号与系统 6.4-6
6.4 S域分析用于控制系统
信号与系统 6.4-1
一、开环与闭环控制
开环控制:输出的被控对象对输入控制量不产生影 响。
闭环控制: 输出信号的全部或部分返回到输入端 对控制量产生影响。用Fra bibliotek反馈自动控制系统。
图1 开环
信号与系统 6.4-2
图2 闭环
信号与系统 6.4-3
负反馈系统:
H (s) Y (s) H1(s) F(s) 1 H1(s)H2(s)
