电子教案《信号与系统》(第四版_燕庆明)(含习题解答)6.3
信号与系统教案

1、信号与系统的概念, 2、信号的分类;周期信号与非周期信号, 确定信号 与随机信号,连续信号与离散信号, 3、典型信号: 实指数信号, 正弦信号、复指数信号、 抽样信号。 4、信号的基本运算:信号的移位,反折、尺度、微 分积分相加相乘。 作业、讨论题、思考题: 1、如何对信号进行分类,各类信号的本质区别是什么? 2、信号与系统为什么是不可分割的整体? 3、信号 cos(10t ) cos(30t ) 的周期是多少? 4、粗略绘出[u (t ) u (t T )] sin(
教 和 输出描述到状态空间描述,以通信和控制工程作为主要应用背 学 要 景,注重实例分析。通过本课程的学习,使学生牢固掌握信号 目 求 与系统的时域、变换域分析的基本原理和基本方法,理解傅里 的
叶变换、拉普拉斯变换、Z 变换的数学概念、物理概念与工程 概念,掌握利用信号与系统的基本理论与方法分析和解决实际 问题的基本方法,为进一步学习后续课程打下坚实的基础。
1、零输入响应定义为:没有外加激励信号的作用,只有起始状态 板书教学, 所产生的响应。 举例题 2、零状态响应定义为:不考虑起始时刻系统储能的作用,由系统 的外加激励信号所产生的响应。 3、冲激响应定义为:系统在单位冲激信号的激励下产生零状态响 应。 4、阶跃响应定义为:系统在单位阶跃信号的激励下产生零状态响 应。 5、换路定理: uc (0) uc (0),il (0) il (0)
授课题目(教学章、节或主题) :
2.6 卷积 2.7 卷积的性质
教学目的、要求(分掌握、熟悉、了解三个层次) : 掌握:卷积运算和卷积的性质
教学重点及难点: 卷积的运算方法、卷积的性质 教 学 基 本 内 容 方法及手段
1、 f1 (t ) * f 2 (t ) f1 ( ) f 2 (t )d 2、卷积运算满足交换律、分配律、结合律。 3、卷积运算的微分和积分 4、 f (t ) * (t ) f (t )
信号与系统教程燕庆明答案

信号与系统教程燕庆明答案【篇一:信号与系统课后习题】t)?tf(t?td),tf(t?t0)?yf(t?t0)?,yf(t?t0)?(t?t0)f(t?t0)。
(3)令g(t)?f(t?t0),t[g(t)]?g(?t)?f(?t?t0),tf(t?t0)? yf(t?t0),yf(t?t0)?f(?t?t0)1.2.已知某系统输入f(t)与输出y(t)的关系为y(t)?f(t)判断该系统是否为线性时不变系统?解:设t为系统运算子,则y(t)可以表示为y(t)?t[f(t)]?f(t),不失一般性,设f(t)?f1(t)?f2(t)t[f1(t)]?f1(t)?y1(t),t[f(t)]?f1(t)?f2(t)?y(t),显然其不相等,即为非线性时不变系统。
df(t)tf(x)dx(2):[y(t)]2?y(t)?f(t) 1.3判断下列方程所表示系统的性(1):y(t)?0dt(3):y(t)?2y(t)?3y(t)?f(t)?f(t?2)(4):y(t)?2ty(t)?2y(t)?3f(t) 线性非线性时不变线性时不变线性时变1.4。
试证明方程y(t)+ay(t)=f(t)所描述的系统为线性系统。
证明:不失一般性,设输入有两个分量,且f1(t)→y1(t),f2(t)→y2(t) 则有y1(t)+ay1(t)=f1(t),y2(t)+ay2(t)=f2(t) 相加得y1+ay1(t)+y2(t)+ay2(t)=f1(t)+f2(t) 即d[y1(t)+y2(t)]+a[y1(t)+y2(t)] dt=f1(t)+f2(t)可见f1(t)+f2(t)→y1(t)+y2(t)即满足可加性,齐次性是显然的。
故系统为线性的。
1.5。
证明1.4满足时不变性。
证明将方程中的t换为t-t0,t0为常数。
即y(t-t0)+ay(t-t0)=f(t-t0) 由链导发则,有dy(t?t0)dtd(t?t0)dy(t?t0)d(t?t0)dy(t?t0)dy(t?t0)1从而又因t0为常数,故所以有 ??dtd(t?t0)dtdtd(t?t0)dy(t?t0)ay(tt0)f(tt0)即满足时不变性f(t-t0)→y(t-t0) dty(t)?y(t?t0)f(t)?f(t??t)?所以ttlimf(t)?f(t??t)limy(t)?f(t?t0)既有 f(t)?y(t) ?t0t0tt1.7 若有线性时不变系统的方程为y(t)+ay(t)=f(t)在非零f(t)作用下其响应y(t)=1-e-t,试求方程y(t)+ay(t)=2f(t)+f(t)的响应。
信号与系统电子教案
信号与系统授课计划课程名称:信号与系统课程类别:专业课总课时:60-72教材(主编、出版社、出版日期):《信号与系统》、郑君里、高等教育出版社、2003.5第一章绪论(8-10课时)本章是信号与系统课程的总论,包括信号与系统课程概述和一些基本概念,简单来说就是要讲清楚什么是信号、什么是系统、以及信号与系统之间是什么关系的问题。
主要内容包括:信号与系统课程概述、信号与系统课程的主要内容、信号的定义及常见信号介绍以及信号的运算、系统的定义与分类以及系统的分析方法介绍等。
本章内容是全书内容的浓缩、是基础、是引言,所以非常重要。
一、主要知识点如下:1、信号与系统课程概述主要包括:(1)信号与系统课程的产生与发展(2)信号与系统课程与其他课程的联系(3)信号与系统的应用领域2、信号的定义与分类、信号的运算主要包括:(1)信号的定义与分类(2)信号的运算3、系统的定义、分类及分析方法主要包括:(1)系统的定义及分类(2)线性时不变系统四大特性及判断方法二、本章知识重难点分析1、信号的定义及分类是重点,其中关于周期信号的定义及信号周期的计算是难点,同样关于连续时间信号与离散时间信号的定义与区别也是难点。
2、几种特殊信号的定义是本课程的重点内容,包括单位阶跃信号、单位冲激信号的定义与运算。
其中单位阶跃信号与单位冲激信号的定义与性质是难点。
3、信号的运算也是本章知识的重点内容,特别是信号直流分量与交流分量、信号奇分量与偶分量等的分解运算,信号的尺度、位移、反折运算等。
4、系统的定义及分类是重点5、线性时不变系统的定义及四大特性,其中四大特性(微积分、时不变、线性、因果性)的定义与判断是难点,特别是线性性是非常重要的内容。
6、线性时不变系统的分析方法是本章的重点7、系统的描述方法,框图与方程,框图与方程之间的关系与转换方法,其中框图与方程之间的转换关系是难点。
三、本章知识点课时安排1、信号与系统课程概述(2课时)2、信号的定义与分类、信号的运算(3课时)3、系统的定义、分类及分析方法(3课时)第二章连续时间系统的时域分析(6-8课时)LTI连续系统的时域分析过程可以理解为建立并求解线性微分方程,因其分析过程涉及的函数变量均为时间t,故称为时域分析法。
《信号与系统(第四版)》习题详解图文

故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组{ξ1(t),ξ2(t),ξ3(t),ξ4(t)}在(0,4)区间上是否 为正交函数组,是否为归一化正交函数组,是否为完备正交函 数组,并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到:
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=-f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω),且 试在K≥ωm条件下化简下式:
72
第3章 连续信号与系统的频域分析 73
107
信号与系统(第四版)第四章课后答案

第5-3页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
一、从傅里叶变换到拉普拉斯变换
有些函数不满足绝对可积条件,求解傅里叶变换困难。 为此,可用一衰减因子e-t(为实常数)乘信号f(t) ,适当 选取的值,使乘积信号f(t) e-t当t∞时信号幅度趋近于 0 ,从而使f(t) e-t的傅里叶变换存在。
0
β
σ
第5-7页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
例3 双边信号求其拉普拉斯变换。
e t , t 0 f 3 (t ) f1 (t ) f 2 (t ) t e , t 0
求其拉普拉斯变换。
解 其双边拉普拉斯变换 F (s)=F (s)+F (s) b b1 b2
第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0
1 s s0
s0t
令s0 0
第5-12页
(t )
■
1
s
, 0
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
五、单边拉氏变换与傅里叶变换的关系
F ( s) f (t ) e st d t
0
Re[s]>0
F (j ) f (t ) e
信号与系统课后习题附参考答案
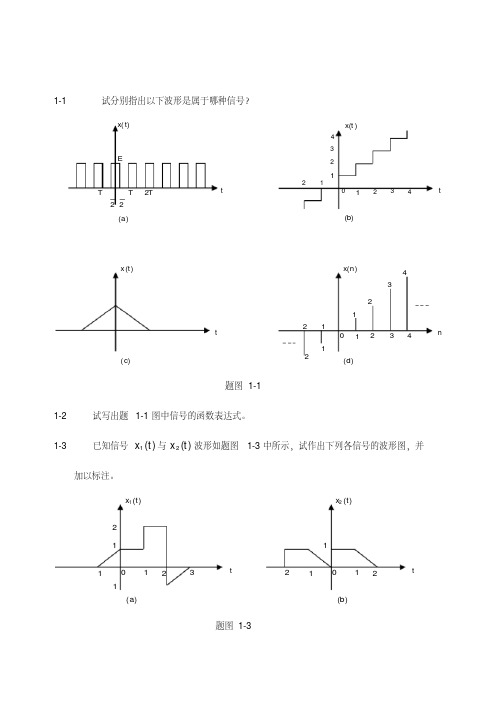
1-1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图:⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图:⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
信号与系统燕庆眀第一章

本次课重点
掌握信号的定义 重点学会分析与判断信号的类别与性质
30
电子信息与计算机工程系
习题
a、c、d a、b、c a、b、c
b
d
31
电子信息与计算机工程系
§1.5 系统的概念
系统是指由若干个相互关联、相互作用的事物,按 照一定的规律组成,并且对外具有某种特定功能的 整体。
激励
系统
h(.)
时限信号:若在时间区间 ( t1 , t2 ) 内 f (t) ≠0 ,而在此区间 外 f (t)=0 的信号。
25
电子信息与计算机工程系
§1.3.2 信号分析与处理
时域法 信号表现出一定波形的时间特性,如出现时 间的先后、持续时间的长短、重复周期的大 小及随时间变化的快慢等。 频域法 任意信号在一定条件下总可以分解为许多不 同频率的正弦分量,即具有一定的频率成分 (频谱)。 信号的频谱分析就是研究信号的频率特性。
f (t ) f (t )
T
t
f (t )
T
t
① t 与 t +T 的值相等 周期信号三重含义: ② 延时T,波形相同
③ 波形按T周期重复
22
t
电子信息与计算机工程系
§1.3.1 信号的分类——连续信号与离散信号
连续信号(Continuous-time signals)指在所讨论的时间 模拟信号? 内,对任意时刻值除若干个不连续点外都有定义的信号。 数字信号? ( Analog signals )模拟信号:定义域值域均连续的信号 离散信号( Discrete-time signals)是指只在某些不连续 规定的时刻有定义,而在其他时刻没有定义的信号。
电子教案-信号与系统第四版(含习题解答)-2.1

uC
(t)
uS
(t)
即
uC
(t)
1 RC
uC
(t)
1 RC
uS (t)
信号与系统 2.1-2
图1
对图1(b),有
L R
diL (t) dt
iL
(t)
iS
(t)
即
iL (t)
R L
iL (t)
R L
iS (t)
一般形式:
y(t) ay(t) g(t)
信号与系统 2.1-3
信号与系统 2.1-4
2t
2e3t
1
瞬态响应 稳态响应
信号与系统 2.1-8
完全响应:
y(t) yzi (t) yzs (t) (ZIR) (ZSR)
响应的分类方法:
按响应的不同起因:分为储能响应和受激响应; 自由响应:取决于系统性质,即特征根; 强迫响应:取决于输入信号的形式; 瞬态响应:当t无限增长,响应最终趋于零; 稳态响应:响应恒定或为某个稳态函数。
0
例 对于书例2-1一阶系统
信号与系统 2.1-7
uC (t) 2uC (t) 2uS (t)
当uC(0)=4V, uS(t)=1+e3t 时,则完全响应为:
uC (t) 4e2t e2t 2e3t1 零输入响应 零状态响应
(储能响应)(受迫响应)
4e2te2t 12e3t 自由响应 强迫响应
➢
阅读与思考:如何理解和应用式
t
y(t) 0 g( )x1(t )d ?
end
对图2的二阶系统,则有
uC
(t)
R L
uC
(t)
1 LC
uC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.3 线性系统的稳定性
一、稳定的概念
稳定:充要条件是
h(t)
dt
,即H(s)的全部极点
位于S的左半平面;
临界稳定: H(s)在虚轴上有单极点,其余极点均在
S的左半平面;
不稳定: H(s)只要有一个极点位于S的右半平面。
信号与系统 6.3-2
例
图1
二、稳定性判据
信号与系统 6.3-3
必要条件: H( s )的分母多项式
D(s) ansn an-1sn-1 a1s a0
的全部系数非零且均为正实数。 充要条件:对二阶系统,D(s) a2s2 a1s a0 的全部 系数非零且为正实数。 充要条件:对三阶系统,D(s) a3s3 a2s2 a1s a0 的 各项系数全为正,且满足
a1a2 a0a3
信号与系统 6.3-4
例 导弹跟踪系统H (s) Nhomakorabeas3
34.5s2 119.7s 98.1 35.714s2 119.741s 98.1
N (s) D(s)
显然
a1a2 > a0a3
故系统稳定。
练习: 判别稳定性
1. D(s) s2 3s 2 2. D(s) s3 s2 4s 10 3. D(s) s3 4s2 5s 6
end
