数学速算技巧二100以内平方数的记忆
数学速算技巧大全

数学速算技巧大全一、乘法速算技巧1、平方速算法:对于任意两个数a和b,如果a的个位数是5,那么a的平方可以通过先将个位数加1,然后乘以个位数再在最后加上25得到。
例如,25的平方等于(2+1)×2+25=625、这个方法也适用于以5结尾的数字,比如45的平方等于4×5+45=20252、两位数乘一位数:首先将这两个数的个位数相乘,然后将两个数的十位数相加,最后将结果合并即可。
例如,24×3=(2×3)+(4×3)=723、两位数乘两位数:将两个数的个位数相乘,然后将两个数的十位数相乘,最后将结果相加。
例如,23×24=(2×4)+(3×4)=8+12=20+4=552二、除法速算技巧1、除以9的技巧:将这个数的各位数相加,然后将结果除以9,最后的商就是原来的数除以9的商。
例如,45÷9=(4+5)÷9=92、除以11的技巧:将数的各位数从右至左相加,并按照奇数位相加减偶数位相加的规则进行操作。
如果得到的结果是负数,则将其变为正数。
最后结果就是原来的数除以11的商。
例如,756÷11=6+(5-2)-(7+5)=6-2+7=9三、加法速算技巧1、竖式加法:两个数的位数对齐,从右往左依次相加,如果两个数的和超过10,需要进位,进位后再与下一位相加。
2、凑整法:对于近似的加法,可以借助10的倍数进行凑整,然后计算往前的差值。
例如,27+18可以看作是30+15,结果是45四、减法速算技巧1、竖式减法:两个数的位数对齐,从右往左依次相减,如果相减结果为负数,则需要借位。
2、借位法:当个位数不够减时,可以向高位借位,然后与高位相减。
五、平方根速算技巧1、巧算平方根:对于一些特定的平方数,可以通过记住其平方根的值来进行计算。
例如,10的平方根约等于3.16,20的平方根约等于4.47,30的平方根约等于5.48,50的平方根约等于7.07六、百分数计算技巧以上就是一些常用的数学速算技巧,当然还有很多其他的技巧,通过不断的学习和练习,我们可以提高我们在解题中的速度和准确性。
数学之道:十大速算窍门

数学之道:十大速算窍门1. 数字拆分法将大数字拆分成易于计算的小数字,例如将 12345 拆分为10000 + 2000 + 300 + 40 + 5,分别进行计算再相加。
2. 倍数加速法利用数字的倍数特性,快速计算结果。
例如,计算156 乘以2,可以先计算 150 乘以 2 得到 300,再加上 6 乘以 2 得到 12,最终结果为 312。
3. 数字分组法将数字进行分组,例如将 1234 分为 12 和 34,先计算 12 乘以5 得到 60,再计算 34 乘以 5 得到 170,最后将两个结果相加得到230。
4. 加减交换律在加减法运算中,可以改变数字的顺序,这样可以简化计算。
例如,计算 123 + 45,可以改为计算 123 + 54,更容易计算出结果。
5. 乘法分配律利用乘法分配律,将复杂的乘法运算简化。
例如,计算 (2 + 3) 乘以 4,可以先计算 2 乘以 4 得到 8,再计算 3 乘以 4 得到 12,最后将两个结果相加得到 20。
6. 数字定位法对于较大的数字,可以通过数字定位法快速计算出结果。
例如,计算 123456 乘以 7,可以先计算 123456 乘以 10 得到 1234560,再减去 123456 得到 1111004。
7. 平方速算法利用平方数的特性,快速计算数字的平方。
例如,计算 13 的平方,可以先计算 10 的平方得到 100,再计算 3 的平方得到 9,最后将两个结果相加得到 169。
8. 立方速算法利用立方数的特性,快速计算数字的立方。
例如,计算 5 的立方,可以先计算 4 的立方得到 64,再加上 1 的立方得到 65。
9. 递减相加法在加法运算中,可以使用递减相加法,将计算简化。
例如,计算 123 + 45,可以先从 123 中减去 40 得到 83,再加上 5 得到 88。
10. 递增相减法在减法运算中,可以使用递增相减法,将计算简化。
例如,计算 123 - 45,可以先加上 1 得到 124,再减去 40 得到 84。
1-20平方顺口溜

1-20平方顺口溜
平方根口诀:11-19的平方:原数加尾数,尾平方;逢10进位;41-49的平方:尾加15,10减尾再平方,占2位;51-59的平方:尾加二十五,尾平方占2位;91-99的平方:尾数乘2加80,10减尾数再平方,占2位。
1到20的平方根:1²=1 ,2²=4,3²=9,4²=16,5²=25,6²=36,7²=49,8²=64,9²=81,10²=100,11²=121,12²=144,13²=169,14²=196,15²=225 ,16²=256,17²=289,18²=324,19²=361,20²=400。
一个正数如果有平方根,那么必定有两个,它们互为相反数。
如果知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。
负数在实数系内不能开平方。
只有在复数系内,负数才可以开平方。
负数的平方根为一对共轭纯虚数。
例如:-1的平方根为±i,-9的平方根为±3i,其中i为虚数单位。
第1页共1页。
小学数学速算技巧顺口溜都在这里了

小学数学速算技巧顺口溜都在这里了一二三四五六七八九
这些数记住真不累。
十一十二到十九
补零在前就变成了。
二十一二三四五六
单词背过来法不偷。
二十七八九十
倒过来再加个零。
十一乘法口诀表
二一得二二,三一得三三
四一得四四,五一得五五
六一得六六,七一得七七。
八一得八八,九一得九九。
十一乘法口诀定律
十一乘法搞不烂
个位数和十位数神奇变化
如11乘以12得132
乘法口诀法则来
纵横交错精通牢。
先竖后横再相乘
积尾和向前调。
乘法口诀记心间
竖线分开倒不难。
个位乘下一位
数写下来遇元或十。
算数口诀有所求
基本运算得加赋。
先加后减再相乘
除法加括号最优。
分数化小数,好方法
分子除以分母当选。
循环小数最终安宁
循环节除较百分之九九。
小数加减遇无尽
小数无限留三位。
对齐小数点进位进
结果有理数不偷。
平方三角不成才圆面计算效果佳。
三点一线图形间空间叠加难清洁。
平方数的记忆方法
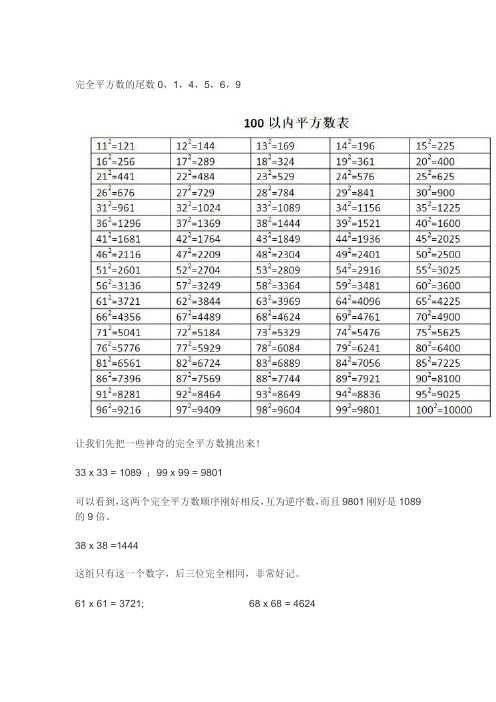
完全平方数的尾数0,1,4,5,6,9让我们先把一些神奇的完全平方数挑出来!33 x 33 = 1089 ;99 x 99 = 9801可以看到,这两个完全平方数顺序刚好相反,互为逆序数,而且9801刚好是1089的9倍。
38 x 38 =1444这组只有这一个数字,后三位完全相同,非常好记。
61 x 61 = 3721; 68 x 68 = 4624这是一组乘法口诀组成的完全平方数,三七二十一,四六二十四,怎么样,记住了吗?88 x 88 = 774412 x 12=144,21 x 21=441,13 x13 =169,31 x 31=961除了感叹一下完全平方数的神奇之外,我们还能说什么呢?其余的数字我们再来分组研究:第一组1~9和整十数1到9的平方是乘法口诀里面背过的,然后10到90的整十数的平方,就是在1到9的平方后面加两个零,那么相应的,我们在开方的时候,两个零,就可以开出一个零。
第二组11~1911到19的平方可以直接用口诀:头乘头,尾加尾,尾乘尾例:11 x 11 = 1 x 1 连1+1 连1 x 1 = 12117 x 17 = 1 x 1 连7+7 连7 x 7 = 289 (注意进位)第三组个数上是五的数个位数字是5的两位数平方,我们可以借用一下“首同尾和十”的方法(十位数字相同,个位数字的和等于10),头x (头+1)x 100 + 尾x尾。
例:15 x 15 = 1 x (1 +1 )x100+5 x 5 = 22525 x 25 = 2 x (2 + 1)x100+5 x 5 = 62535 x 35 = 3 x (3 + 1)x100+5 x 5 = 122545 x 45 = 4 x (4 + 1)x100+5 x 5 = 202555 x 55 = 5 x (5 + 1)x100+5 x 5 = 302565 x 65 = 6 x (6 + 1)x100+5 x 5 = 422575 x 75 = 7 x (7 + 1)x100+5 x 5 = 562585 x 85 = 8 x (8 + 1)x100+5 x 5 = 722595 x 95 = 9 x (9 + 1)x100+5 x 5 = 9025第四组51~59这里可以借用一下“尾同首和十”的方法(个位数字相同,十位数字的和等于10),(头1×头2+尾)×100+尾×尾。
100以内平方数速记

上文中主要对一些有趣的完全平方数进行了介绍,这篇是将所有的100以内完全平方数全部列举,并介绍一些速记方法。
我把它们分为20位一组,共4组,希望大家能每天记住一组,这样会记得快一些,大家加油!第一组:21~30 71~8020以内的平方如果还不熟记的话着实不应该啊!这两组呢,细心同学会发现21~30是以25为中心,71~80以75为中心,所以它们可以说是对联:22222222 30900 80640021441 84129 715041 62417922484 78428 ========222222222 725184 60847823529 72927 735329 59297724576 67626 745476 5=========22277676 25625 755625=== 末位5的平方可以用“头同尾合十”来算,观察这两副对联的每一行,末2位全部一样!所以,41、84、29、76这4个数大家一定要熟记!末2位解决掉之后,说说百位和千位。
20~30百位较小,死记不难。
71~80规律不明显,有两种记法:①规律很明显吧,不过21~29平方要特别熟记啊!② 73、74的千位为5,百位和它们本身个位一样,2765776=是符合一个数平方后末两位与它本身相同的,比较重要,应熟记;2786084=,上文提过,先把这4个记住。
其余71、72首位仍为5,百位比它们个位小1;77、79直接死记吧!第二组:41~50 51~60上一组比较难记,下面来一组比较轻松的。
先记51~60,这一组可用尾同头合十来算!22222222512601 55126 101522704 55227 204532809 55328 309542916 55429 416=⨯+===⨯+===⨯+===⨯+==22553025 55530 525=⨯+==后面的几个规律留给大家自己来找吧!22222222715041 21441 50446725184 22484 51447735329 23529 53548796241 29841 62854==-===-===-===-=对于41~50,其实和上述差不多,只不过用减法。
掌握数学:十大速算技巧解析

掌握数学:十大速算技巧解析1. 快速乘法快速乘法是一种能够快速计算两个数字相乘的技巧。
其中一个常见的方法是使用交叉相乘法。
例如,计算37乘以25,可以将37分解为30和7,将25分解为20和5,然后进行交叉相乘得到600和35,最后将结果相加得到635。
2. 近似除法近似除法是一种用来估算除法结果的技巧。
例如,计算96除以7,可以先将96近似为100,然后将7近似为10,接着进行简单的除法计算得到10,最后将结果乘以10得到近似的商为100。
3. 平方技巧平方技巧是一种用来快速计算一个数字的平方的方法。
例如,计算13的平方,可以将13分解为10和3,然后使用公式(10+3)^2= 10^2 + 2*10*3 + 3^2 = 100 + 60 + 9 = 169,得到13的平方为169。
4. 百分比转换百分比转换是一种将一个数转换为百分数的技巧。
例如,将0.75转换为百分数,可以将0.75乘以100得到75%。
5. 整数除法整数除法是一种用来计算两个整数相除得到整数商和余数的方法。
例如,计算47除以6,可以得到商为7和余数为5。
6. 近似开方近似开方是一种用来估算一个数的平方根的技巧。
例如,要估算√38,可以找到最接近38的完全平方数,即36,然后将38近似为36,接着计算√36 = 6,得到近似的平方根为6。
7. 十进制转换十进制转换是一种将一个数转换为不同进制的方法。
例如,将10转换为二进制,可以使用除以2取余数的方法,得到10的二进制表示为1010。
8. 快速乘方快速乘方是一种用来快速计算一个数的幂的方法。
例如,计算2的10次方,可以使用二进制的方法,将10表示为1010,然后按照相应的位数进行计算,得到结果为1024。
9. 等差数列求和等差数列求和是一种用来计算一个等差数列的和的方法。
例如,计算1到100的和,可以使用等差数列求和公式(首项 + 末项) * 项数 / 2,得到结果为5050。
200以内整数平方的速算方法

200以内整数平方的速算方法四川省邻水县九龙中学任贤德数学教育的目的之一是培养和提高学生的运算能力,而在数学解题中常遇到数的平方的计算, 数字平方的计算中,有一些数能够速算.为此,本文将介绍200以内整数平方的速算方法,以供参考,不妥之处,望同仁斧正.Ⅰ.1-25以内整数平方的速算1⑴1-10的平方就不用多说了.⑵11-19的平方的速算.定理1:设有11-19中某数,则此数的平方等于此数与它个位数字之和的10倍,再加上此数个位数字的平方.例1.① 172=(17+7)×10+72=240+49=289② 192=(19+9)×10+92=280+81=361⑶21-29平方的速算.定理2:设有21-29中某数,则此数的平方等于此数与它个位数字之和的2倍乘以10,再加上此数个位数字的平方.例2.①282=(28+8)×2×10+82=720+64=784②232=(23+3)×2×10+32=520+9=5291-25以内整数的平方要熟记,它们是本文后面其它数字平方计算的基础,只要熟记25以内整数的平方值,我们就能快速地计算由26-200以内的整数的平方值附11-25的平方值:112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361 202=400 212=441 222=484 232=529 242=576 252=625Ⅱ.26-75以内整数平方的速算定义1.若两数之和为50,则称此二数互余,其中一数为另一数的余数。
如17+23=50,则27与23互余,27的余数是23(或23的余数是27)。
定理3:设有26—75的某数,则此数的平方等于此数减去25再乘以100,并将所得结果加上此数余数的平方。
证:依题意:a2=[50-(50-a)2]=502-2×50×(50-a)+(50-a)2=2500-100×(50-a)+(50-a)2= (a-25)×100+(50-a)2故命题成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
让我们先把一些神奇的完全平方数挑出来!
33 x 33 = 1089;99 x 99 = 9801
可以看到,这两个完全平方数顺序刚好相反,互为逆序数,而且9801刚好是1089的9倍。
38 x 38 =1444
这组只有这一个数字,后三位完全相同,非常好记。
61 x 61 = 3721;68 x 68 = 4624
这是一组乘法口诀组成的完全平方数,三七二十一,四六二十四,怎么样,记住了吗?
88 x 88 = 7744
除了感叹一下完全平方数的神奇之外,我们还能说什么呢?
12 x 12=144,21 x 21=441,13 x13 =169,31 x 31=961
其余的数字我们再来分组研究:
第一组1~9和整十数
1到9的平方是乘法口诀里面背过的,然后10到90的整十数的平方,就是在1到9的平方后面加两个零,那么相应的,我们在开方的时候,两个零,就可以开出一个零。
第二组11~19
11到19的平方可以直接用口诀:头乘头,尾加尾,尾乘尾
例:11 x 11 = 1 x 1连1+1连1 x 1 = 121
17 x 17 = 1 x 1连7+7连7 x 7 = 289 (注意进位)
第三组个数上是五的数
个位数字是5的两位数平方,我们可以借用一下“首同尾和十”的方法(十位数字相同,个位数字的和等于10),头x (头+1)x 100 +尾x尾。
例:15 x 15 = 1 x (1 +1 )x100+5 x 5 = 225
25 x 25 = 2 x (2 + 1)x100+5 x 5 = 625
35 x 35 = 3 x (3 + 1)x100+5 x 5 = 1225
45 x 45 = 4 x (4 + 1)x100+5 x 5 = 2025
55 x 55 = 5 x (5 + 1)x100+5 x 5 = 3025
65 x 65 = 6 x (6 + 1)x100+5 x 5 = 4225
75 x 75 = 7 x (7 + 1)x100+5 x 5 = 5625
85 x 85 = 8 x (8 + 1)x100+5 x 5 = 7225
95 x 95 = 9 x (9 + 1)x100+5 x 5 = 9025
第四组51~59
这里可以借用一下“尾同首和十”的方法(个位数字相同,十位数字的和等于10),(头1×头2+尾)×100+尾×尾。
例:51 x 51 =( 5 x 5 + 1) x 100 + 1 x 1 = 2601
52 x 52 =( 5 x 5 + 2) x 100 + 2 x 2 = 2704
53 x 53 =( 5 x 5 + 3) x 100 + 3 x 3 = 2809
54到59的平方依此类推,就不再浪费篇幅了。
不过在教孩子的时候,一定要让孩子按照这些个方法多算几次,加深对方法的理解,也更加容易记住。
第五组41~49
41到49的平方与刚刚的方法也有一定的联系,我们一起来看看。
49 x 49 =(5 x 5 - 1) x 100 + 1 x 1 = 2401
48 x 48 =(5 x 5 - 2) x 100 + 2 x 2 = 2304
47 x 47 =(5 x 5 - 3) x 100 + 3 x 3 = 2209
46 x 46 =(5 x 5 - 4) x 100 + 4 x 4 = 2116
45 x 45 =(5 x 5 - 5) x 100 + 5 x 5 = 2025
44 x 44 =(5 x 5 - 6) x 100 + 6 x 6 = 1936
43 x 43 =(5 x 5 - 7) x 100 + 7 x 7 = 1849
42 x 42 =(5 x 5 - 8) x 100 + 8 x 8 = 1764
41 x 41 =(5 x 5 - 9) x 100 + 9 x 9 = 1681
但是我们要从49倒着记到41,这样规律更加明显,而且突然来个倒序,也可以使个记忆过程不那么枯燥。
为了大家方便,我把这系列的算式全写出来。
第六组21~29和71~79
接下来我们仔细观察一下下面式子,
这两组式子有很多规律可以研究,看起来简单,但是要全部描述出来,需要大量的篇幅,反而容易把头弄晕,所以,愿意花功夫背的孩子可以自己试着对比一下,找出它们的规律,然后进行对比记忆。
第七组81~89和91~99
这里要用到一个完全平方公式的运用,(100-K) x(100-K)=10000-200K + K x K 对于初中的孩子,比较容易理解,小学生们直接记住然后去使用就可以了。
99 x 99 = (100 - 1) x (100 - 1) = 10000 - 200 x 1 + 1 x 1 = 9801
98 x 98 = (100 - 2) x (100 - 2) = 10000 - 200 x 2 + 2 x 2 = 9604
97 x 97 = (100 - 3) x (100 - 3) = 10000 - 200 x 3 + 3 x 3 = 9409
96 x 96 = (100 - 4) x (100 - 4) = 10000 - 200 x 4 + 4 x 4 = 9216
95 x 95 = (100 - 5) x (100 - 5) = 10000 - 200 x 5 + 5 x 5 = 9025
94 x 94 = (100 - 6) x (100 - 6) = 10000 - 200 x 6 + 6 x 6 = 8836
93 x 93 = (100 - 7) x (100 - 7) = 10000 - 200 x 7 + 7 x 7 = 8649
92 x 92 = (100 - 8) x (100 - 8) = 10000 - 200 x 8 + 8 x 8 = 8464
91 x 91 = (100 - 9) x (100 - 9) = 10000 - 200 x 9 + 9 x 9 = 8281
从上面式子可以看出81~89的平方,要先熟练记住11~19的平方,这里就举一个例子,其余的留给孩子们自己去计算吧。
例:86 x 86 = (100 - 14) x (100 - 14) = 10000 - 200 x 14 + 14 x 14 = 7396
第八组31~39和61~69
这两个区间的平方数规律不十分明显,但是初高中阶段极易出题,推荐直接记牢!!!
今天的内容太硬了,建议收藏,每天解决一组,然后经常复习,必能倒背如流!除了前面特殊的几个平方数以及最后一组,其余的都要通过大量的计算来加深理解记忆,对我们的计算能力也是一个很好的训练。
