随县二中高二下学期文科数学期中测试
湖北省随州市2018-2019学年高二下学期期中考试数学(文)试卷Word版含答案

湖北省随州市2018-2019学年高二下学期期中考试数学(文)试卷(全卷满分:150分 考试时间:120分钟)第I 卷(选择题 共60分)一、选择题(共12小题,每小题5分,满分60分。
每小题只有一项是最符合题目要求的) 1、已知复数2z i =-,则复数z z ⋅的值为( )A .3B .5C D2、已知命题p :∀x ∈R ,2x >0,那么命题¬p 为( ) A .∃x ∈R ,2x <0 B .∀x ∈R ,2x <0 C .∃x ∈R ,2x ≤0 D .∀x ∈R ,2x ≤03、“x <﹣1”是“x 2﹣1>0”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4、经过点)3,2(P 且与直线023=+-y x 平行的直线为 ( ) A .033=+-y x B .033=--y x C .033=++y x D .033=-+y x5、已知x 与y 之间的一组数据:则y 与x 的线性回归方程为y=bx+a 必过点( )A .(2,2)B .(1,2)C .(1.5,0)D .(1.5,4)6、设抛物线y=2x 2的焦点坐标是( )A .(1,0)B .(-1,0)C .(0,18)D .(18,0)7、直线x-y+4=0被圆x 2+y 2+4x-4y+6=0截得的弦长等于( )A.8B.4C.22D.428、如图所示的程序框图中,输出S 的值为( )A .10B .12C .8D .1510、函数334y x x =-([0,2]x ∈)的最大值是( )A .1B . 2C .0D .-111、设点P 是双曲线22221x y a b-=(a >0,b >0)与圆x 2+y 2=a 2+b 2在第一象限的交点,F 1,F 2分别是双曲线的左、右焦点,且|PF 1|=2|PF 2|,则双曲线的离心率为( )A B C D12、设函数f (x )=ax 2+bx +c (a ,b ,c ∈R ),若x=﹣1为函数y=f (x )e x的一个极值点,则下列图象不可能为y=f (x )的图象是( )A .B .C .D .第II 卷(非选择题 共90分)二、填空题(每小题5分,共20分)13、某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取 , , 辆.14、如果实数x 、y 满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩,那么2x+y 的最大值为15、由图(1)有面积关系:PA B PAB S PA PB S PA PB ''∆∆''⋅=⋅,则由图(2)有体积关系:P A B C P ABCV V '''--= .16、给出下列命题:①点P(-1,4)到直线3x +4y =2的距离为3.②过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为08=+-y x .③命题“∃x ∈R ,使得x 2﹣2x +1<0”的否定是真命题; ④“x ≤1,且y ≤1”是“x + y ≤2”的充要条件.其中不正确命题的序号是 _______________ .(把你认为不正确命题的序号都填上)三、解答题(本大题共5小题,70分)17、(本小题满分10分) 已知命题p :m ∈R 且m +1≤0,命题q :∀x ∈R ,x 2+mx +1>0恒成立,若p ∧q 为假命题且p ∨q 为真命题,求m 的取值范围.C ′18、(本小题满分12分)已知曲线 y = x 3 + x -2 在点 P 0处的切线1l 平行直线4x -y -1=0,且点 P 0 在第三象限.(1)求P 0的坐标;(2)若直线 1l l , 且 l 也过切点P 0 ,求直线l 的方程.19、(本小题满分12分)某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:(Ⅰ)求图中a 的值;(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?20、(本小题满分12分)如图,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD , E 是PC 的中点. .求证:(Ⅰ)PA ∥平面BDE ;(Ⅱ)平面PAC ⊥平面BDE ;(III)若PB 与底面所成的角为600, AB=2a ,求三棱锥E-BCD 的体积.21、(本小题满分12分) 已知椭圆C 的中心在原点O ,焦点在x 轴上,离心率为12,右焦点到右顶点的距离为1.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)是否存在与椭圆C 交于A ,B 两点的直线l :y =kx +m (k ∈R ),使得0OA OB ⋅=成立?若存在,求出实数m 的取值范围,若不存在,请说明理由.22、(本小题满分12分) 已知函数21()(1)ln 2f x x ax a x =-+-。
高二数学文科下学期期中考试卷 试题

卜人入州八九几市潮王学校高级二零二零—二零二壹高二数学文科下学期期中考试卷本套试卷分第一卷〔选择题〕和第二卷〔非选择题〕两局部.第一卷1至2页,第二卷3至4页.在在考试完毕之后以后,只须将答题卡交回.总分值是150分,考试用时120分钟.第一卷〔选择题,一共60分〕一、选择题:本大题一一共12小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的. 〔1〕假设{1,2,3,4},{1,2},{2,3}UM N ===,那么=)(N M C U〔A 〕{2}〔B 〕{4}〔C 〕{1,2,3}〔D 〕{1,2,4}〔2〕函数12--=x y 〔]1,2[--∈x 〕的反函数的解析式是〔A 〕12-=x y 〔B 〕12--=x y 〔C 〕12+=x y 〔D 〕12+-=x y〔3〕函数)10(≠>+=+=a a b ax y b a y x 且与函数的图像有可能是,b a 垂直,那么实数〔A 〕6〔B 〕0〔C 〕4-〔D 〕32- 〔5〕如图,正方体1111D C B A ABCD-中,直线1BC 和直线D A 1所成的角为〔A 〕 90〔B 〕 45〔C 〕 60〔D 〕 30 〔6〕偶函数)(x f y =在区间[-4,0]上单调递增,那么有〔A 〕)()3()1(ππ->>-f f f〔B 〕)()1()3(ππ->->f f f 〔C 〕)3()1()(ππf f f >->-〔D 〕)3()()1(ππf f f >->-ABCD 1 A 1B 1DC 1O〔7〕①有一条侧棱与底面两边垂直的棱柱是直棱柱 ②底面是平行四边形的四棱柱是平行六面体 ③底面是矩形的平行六面体是长方体④顶点在底面上的射影到底面各顶点的间隔相等的三棱锥是正三棱锥 〔A 〕0个〔B 〕1个〔C 〕2个〔D 〕3个〔8〕设x ,y 满足约束条件20x y y x y +≤⎧⎪≤⎨⎪≥⎩,那么z =3x +y 的最大值是〔A 〕0〔B 〕4〔C 〕5〔D 〕6〔9〕在等比数列{}n a 中,前n 项和为n S ,假设63,763==S S ,那么公比q 的值是〔A 〕3〔B 〕-3〔C 〕2〔D 〕-2 〔10〕),2(,54cos ππαα∈-=,那么)4tan(απ+等于〔A 〕71〔B 〕71-〔C 〕7-〔D 〕7〔11〕P为椭圆192522=+y x 上一点,21、F F 是椭圆的两个焦点,︒=∠6021PF F ,那么21PF F ∆的面积为 〔A 〕3〔B 〕32〔C 〕33〔D 〕39〔12〕定义在R 上的奇函数)(x f 在),0(+∞上是增函数,又0)3(=f ,那么不等式0)(<x f 的解集为〔A 〕)3,0()0,3(⋃- 〔B 〕),3()0,3(+∞⋃-〔C 〕),3()3,(+∞⋃--∞〔D 〕)3,0()3,(⋃--∞ 第二卷〔非选择题,一共90分〕本卷须知:第二卷一共2页,10小题,用黑色碳素笔将答案答在答题卡上,答在试卷上之答案无效. 二、填空题:本大题一一共4小题,每一小题4分,一共16分.把答案直接答在答题卡上.〔13〕球的半径是3,那么该球的体积等于,外表积等于。
高二数学(文)第二学期期中联考试题及答案
相关指数 R2 检验模拟效果; ④求线性回归方程 . 则在下列操作顺序中正确的是 (
)
A.①②③④
B.③②④①
C.②④③①
D.②①④③
8.下列有关命题的说法正确的是
2
2
A. 命题 “若 x 1 ,则 x 1 ”的否命题为:“若 x 1 ,则 x 1”
B. “ x 1 ”是“ x2 5x 6 0 ”的必要不充分条件
高二数学(文) 第二学期期中联考试题
本试卷满分 150 分 . 考试用时 120 分钟
一、选择题:本大题共 10 小题,每小题 5 分,共 50 分。在每小题已知曲线 y 2x2 1 在点 M处的瞬时变化率为 -4 ,则点 M的坐标是( )
A ( 1, 3) B
0
1
3
4
2.2
4.3
4.8
6.7
A. 1 2
B. 1
C.
4
2 D.
2
2
4
二、填空题(本大题共 5 小题,考生作答 4 小题,每小题 5 分,共 20 分,把
答案填在答题卡相应横线上)
(一)必做题( 11~ 13 题)
11. 复数 2i 的共轭复数是 ___________ i1
12.已知 x, y 的取值如下表所示,根据 x
表中数据求得 y 关于 x 的线性回归方程为 y
( -4 , 33) C ( -1 ,3) D 不确定
2. 年劳动生产率 x (千元)和工人工资 y (元)之间回归方程为 y 10 70x ,这意
味着年劳动生产率每提高 1 千元时,工人工资平均
A.增加 70 元 B.减少 70 元
C.增加 80 元
D.减少 80 元
高二下学期期中考试数学试题 (二)(文科)

高二下学期期中考试数学试题 (二)(文科)本试卷全卷满分150分。
考试用时120分钟★ 祝 考 试 顺 利 ★一、选择题(本大题共10小题,每小题5分,共50分, 在每小题给出的四个选项中,只有一项是符合题目要求的) 1.函数 3cos y x x =的导数为( D )A.23sin y x x '=- B.233cos sin y x x x x '=+ C. 32sin 3cos y x x x x '=- D. 233cos sin y x x x x '=- 2. 下列命题中为真命题的是(C )A . 命题“若1x =,则220x x +-=”的否命题B .命题“若1x >,则21x >”的否命题 C .命题“若x y >,则x y >”的逆命题 D .命题“若20x >,则1x >”的逆否命题3.曲线21x y xe x =++在点(0,1)处的切线方程为(A )A .31y x =+B .31y x =-C .21y x =+D .21y x =-4. 不能表示的曲线是()方程1cos sin ],,0[22=+∈ααπαy x C A 椭圆 B 双曲线 C 抛物线 D 圆5. 设:()ln 21p f x x x mx =++++1x e mx ++在(0)+∞,内单调递增,:q m -≥0m ≥,则p 是q 的( C ) A .充分不必要条件 B . 充分必要条件 C .必要不充分条件D .既不充分也不必要条件6.已知对k R ∈,直线10y kx --=与椭圆2215x y m+=恒有公共点,则实数m 的取值范围是( D ) A .(0,1)B .(0,5)C .[1,5)D .),5()5,1[+∞⋃7.设P 为双曲线22112y x -=上的一点,12F F ,是该双曲线的两个焦点,若12||:||3:2PF PF =,则12PF F △的面积为( A )A .12B . . 24 D . 8.方程322670x x -+=在(0,2)内根的个数有(B )A. 0个B. 1个C. 2个D. 3个9. 已知函数()f x 的定义域为[1,4]-,部分对应值如下表,()f x 的导函数()y f x '=的图象如右图所示。
2021-2022年高二(下)期中数学试卷(文科) Word版含解析

2021-2022年高二(下)期中数学试卷(文科) Word版含解析一、填空题(本大题共14小题,每小题5分,共70分,把结果直接填在题中的横线上)1.(5分)命题“∀x>0,x2﹣3x+2<0”的否定是∃x>0,x2﹣3x+2≥0.考点:命题的否定;全称命题.专题:应用题.分析:命题“对∀x∈R,x3﹣x2+1<0”是全称命题,其否定应为特称命题,注意量词和不等号的变化.解答:解:命题“对∀x∈R,x3﹣x2+1<0”是全称命题,否定时将量词∀x>0改为∃x>0,<改为≥故答案为:∃x∈R,x3﹣x2+1≥0点评:对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”;对命题“∀x∈A,P(X)”的否定是:“∃x∈A,¬P(X)”,即对特称命题的否定是一个全称命题,对一个全称命题的否定是全称命题2.(5分)已知复数z满足z•(1+i)=1﹣i(i为虚数单位),则复数z的虚部为﹣1.考点:复数代数形式的乘除运算.专题:计算题.分析:把给出的等式两边同时乘以,然后利用复数的除法运算求解.解答:解:由z•(1+i)=1﹣i,得.所以复数z的虚部等于﹣1.故答案为﹣1.点评:本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.3.(5分)“x3=x”是“x=1”的必要不充分条件.考点:必要条件、充分条件与充要条件的判断.专题:探究型.分析:利用充分条件和必要条件的定义判断.解答:解:由x3=x,得x3﹣x=0,即x(x2﹣1)=0,所以解得x=0或x=1或x=﹣1.所以“x3=x”是“x=1”的必要不充分条件.故答案为:必要不充分.点评:本题主要考查充分条件和必要条件的应用,比较基础.4.(5分)已知f(x﹣1)=2x+3,f(m)=6,则m=﹣.考点:函数的值;函数解析式的求解及常用方法.专题:计算题.分析:先用换元法,求得函数f(x)的解析式,再由f(m)=6求解.解答:解:令t=x﹣1,∴x=2t+1f(t)=4t+5又∵f(m)=6∴4m+5=6∴m=故答案为:点评:本题主要考查用换元法求函数解析式已知函数值求参数的值.5.(5分)函数的定义域为(1,3].考点:函数的定义域及其求法.专题:计算题.分析:由根式内部的代数式大于等于0,然后求解对数不等式即可得到答案.解答:解:由1﹣2log4(x﹣1)≥0,得0<x﹣1≤2,解得1<x≤3.所以原函数的定义域为(1,3].故答案为(1,3].点评:本题考查了定义域及其求法,考查了对数不等式的解法,关键是要保证对数式本身有意义,是基础题.6.(5分)已知三个数a=60.7,b=0.76,c=log0.76,则a,b,c从小到大的顺序为c<<b<a.考点:有理数指数幂的化简求值;不等关系与不等式.专题:计算题.分析:利用指数函数的运算性质比较a和b的大小,由对数式的运算性质可知c<0,由此答案可求.解答:解:因为a=60.7>60=1,b=0.76<0.70=1,且b>0,c=log0.76<0,所以c<b<a.故答案为c<b<a.点评:本题考查了不等关系与不等式,考查了指数函数的单调性,训练了对数式的符号判断,是基础题.7.(5分)函数的值域为[1,+∞).考点:函数的值域.专题:计算题.分析:令=t,则t≥0,可得x=t2+1,代入已知式子可得关于t的二次函数,由二次函数区间的最值可解.解答:解:由题意令=t,则t≥0,可得x=t2+1,代入已知式子可得y=2t2+t+1=,函数为开口向上的抛物线的部分,对称轴为t=,故可得函数y在t∈[0,+∞)单调递增,故当t=0时,函数取最小值1,故原函数的值域为:[1,+∞)故答案为:[1,+∞)点评:本题考查函数值域的求解,换元化为二次函数区间的最值是解决问题的关键,属基础题.8.(5分)已知定义在R上的奇函数y=f(x)在(0,+∞)上单调递增,且f(1)=0,则不等式f(2x﹣1)>0的解集为.考点:奇偶性与单调性的综合.专题:计算题;函数的性质及应用.分析:根据函数的奇偶性、单调性可作出函数的草图及函数所的零点,根据图象可对不等式等价转化为具体不等式,解出即可.解答:解:因为f(x)在(0,+∞)上单调递增且为奇函数,所以f(x)在(﹣∞,0)上也单调递增,f(﹣1)=﹣f(1)=0,作出草图如下所示:由图象知,f(2x﹣1)>0等价于﹣1<2x﹣1<0或2x﹣1>1,解得0<x<或x>1,所以不等式的解集为(0,)∪(1,+∞),故答案为:(0,)∪(1,+∞).点评:本题考查函数的奇偶性、单调性的综合及其应用,考查不等式的求解,属中档题.9.(5分)已知复数z满足|z+2﹣2i|=1,则|z﹣2﹣2i|的最大值是5.考点:复数求模.专题:计算题.分析:由复数模的几何意义可知复数z在以(﹣2,2)为圆心,以1为半径的圆周上,所以|z﹣2﹣2i|的最大值是(﹣2,2)到(2,2)的距离加上半径1.解答:解:由|z+2﹣2i|=1,可知复数z在以(﹣2,2)为圆心,以1为半径的圆周上,所以|z﹣2﹣2i|的最大值是(﹣2,2)到(2,2)的距离加上半径1,等于2﹣(﹣2)+1=5.故答案为5.点评:本题考查了复数模的几何意义,考查了复数模的求法,体现了数形结合的解题思想,是基础题.10.(5分)对于函数f(x),在使f(x)≥M恒成立的所有常数M中,我们把M中的最大值称为函数f(x)的“下确界”,则函数的下确界为0.5.考点:函数的最值及其几何意义;函数恒成立问题.专题:分类讨论.分析:利用判别式法求函数的下确界.解答:解:设函数y=,则(y﹣1)x2+2yx+y﹣1=0.当y﹣1≠0时,△=4y2﹣4(y﹣1)(y﹣1)≥0,解得且y≠1.当y﹣1=0时,x=0成立,∴.∴函数的下确界为0.5.故答案为:0.5.点评:函数的下确界就是这个函数的最大值.11.(5分)若函数f(x)=x2﹣2|x|﹣2a﹣1(x∈R)有四个不同的零点,则实数a的取值范围是.考点:函数的零点与方程根的关系.专题:函数的性质及应用.分析:将方程的零点问题转化成函数的交点问题,作出函数的图象得到a的范围.解答:解:令f(x)=x2﹣2|x|﹣2a﹣1=0,得2a=x2﹣2|x|﹣1.作出y=x2﹣2|x|﹣1与y=2a的图象,如图.要使函数f(x)=x2﹣2|x|﹣2a﹣1有四个零点,则y=x2﹣2|x|﹣1与y=2a的图象有四个不同的交点,有﹣2<2a<﹣1,所以.故答案为:点评:本题考查等价转化的能力、利用数学结合解题的数学思想方法是重点,属中档题.12.(5分)函数f(x)的定义域为A,若x1、x2∈A且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数.例如,函数f(x)=2x+1(x∈R)是单函数.下列命题:①若函数f(x)是f(x)=x2(x∈R),则f(x)一定是单函数;②若f(x)为单函数,x1、x2∈A且x1≠x2,则f(x1)≠f(x2);③若定义在R上的函数f(x)在某区间上具有单调性,则f(x)一定是单函数;④若函数f(x)是周期函数,则f(x)一定不是单函数;⑤若函数f(x)是奇函数,则f(x)一定是单函数.其中的真命题的序号是②④.考点:命题的真假判断与应用.专题:函数的性质及应用.分析:利用单函数的定义分别对五个命题进行判断,即可得出正确结论.解答:解:①若函数f(x)是f(x)=x2,则由f(x1)=f(x2)得,得到x1=±x2,所以①不是单函数,所以①错误.②若f(x)为单函数,则f(x1)=f(x2)时总有x1=x2,即x1≠x2,则f(x1)≠f(x2),所以②正确.③当函数单调时,在单调区间上必有f(x1)=f(x2)时总有x1=x2,但在其他定义域上,不一定是单函数,所以③错误.④若函数f(x)是周期函数,则满足f(x1)=f(x2),则有x1=kT+x2,所以④正确.⑤若函数f(x)是奇函数,比如f(x)=sinx,是奇函数,则满足f(x1)=f(x2),则x1,x2,不一定相等.所以⑤错误.故答案为:②④.点评:本题主要考查函数的性质的推导和判断,考查学生分析问题的能力,综合性较强.13.(5分)(理科)定义在R上的函数f(x)满足f(x)=,则f (xx)的值为0.考点:函数的值.专题:计算题.分析:由题意可得,f(xx)=f(xx)﹣f(xx)=f(xx)﹣f(xx)﹣f(xx)=﹣f(xx),逐步代入可得f(xx)=f(xx),结合此规律可把所求的式子转化为f(0),即可求解解答:解:由题意可得,f(xx)=f(xx)﹣f(xx)=f(xx)﹣f(xx)﹣f(xx)=﹣f(xx)而f(xx)=f(xx)﹣f(xx)=f(xx)﹣f(xx)﹣f(xx)=﹣f(xx)∴f(xx)=f(xx)=f(xx)=…=f(3)=f(2)﹣f(1)=f(1)﹣f(0)﹣f(1)=﹣f(0)=0故答案为:0点评:本题主要考查了分段函数的函数值的求解,解题的关键是发现其周期性的规律,进而转化求解14.(5分)(xx•黄浦区二模)已知,若存在区间,使得{y|y=f(x),x⊆[a,b]}=[ma,mb],则实数m的取值范围是(0,4].考点:函数的定义域及其求法;函数的值域.专题:函数的性质及应用.分析:首先分析出函数在区间[a,b]上为增函数,然后由题意得到,说明方程有两个大于实数根,分离参数m,然后利用二次函数求m的取值范围.解答:解:因为函数在上为减函数,所以函数在上为增函数,因为区间,由{y|y=f(x),x∈[a,b]}=[ma,mb],则,即.说明方程有两个大于实数根.由得:.零,则t∈(0,3).则m=﹣t2+4t=﹣(t﹣2)2+4.由t∈(0,3),所以m∈(0,4].所以使得{y|y=f(x),x∈[a,b]}=[ma,mb]的实数m的取值范围是(0,4].故答案为(0,4].点评:本题考查了函数的定义域及其求法,考查了单调函数定义域及值域的关系,训练了二次函数值域的求法,考查了数学转化思想,是中档题.二、解答题(本大题共6小题,共90分,解答时应写出文字说明、证明过程或演算步骤)15.(14分)已知集合A={x|x2﹣7x﹣18≥0},集合B={x|2x+1>0},集合C={x|m+2<x<2m﹣3}.(Ⅰ)设全集U=R,求∁U A∪B;(Ⅱ)若A∩C=C,求实数m的取值范围.考点:交、并、补集的混合运算.专题:计算题;不等式的解法及应用.分析:(I)由题设知,应先化简两个集合,再根据补集的定义与并集的定义求出∁U A∪B;(II)题目中条件得出“C⊆A”,说明集合C是集合A的子集,由此分C=∅和C≠∅讨论,列端点的不等关系解得实数m的取值范围.解答:解:(I)由x2﹣7x﹣18≥0得x≤﹣2,或x≥9,即A=(﹣∞,﹣2]∪[9,+∞),由2x+1>0解得x≥﹣,即B=[﹣,+∞),∴∁U A=(﹣2,9);∁U A∪B=(﹣2,9);(II)由A∩C=C得:C⊆A,则当C=∅时,m+2≥2m﹣3,⇒m≤5,当C≠∅时,m+2≥2m﹣3,⇒m≤5,或,解得m≥7,所以m∈{m|m≤5或m≥7};点评:本题考查补集与交、并集的求法,属于集合运算中的常规,掌握运算的定义是正确解答的关键.16.(14分)设命题p:函数f(x)=lg的定义域是R;命题q:不等式3x﹣9x<a对一切正实数x均成立.(1)如果p是真命题,求实数a的取值范围;(2)如果“p或q”为真命题,命题“p且q”为假命题,求实数a的取值范围.考点:命题的真假判断与应用.专题:综合题.分析:(1)由题意,若p是真命题,则对任意实数都成立,由此能够求出p是真命题时,实数a的取值范围.(2)若命题q为真命题时,则3x﹣9x<a对一切正实数x均成立.由∈(﹣∞,0),知q是真命题时,a≥0.再由p或q为真命题,命题p且q为假命题,知或,由此能求出实数a的取值范围.解答:解:(1)由题意,若p是真命题,则对任意实数都成立,若a=0,显然不成立;若a≠0,解得a>2故如果p是真命题时,实数a的取值范围是(2,+∞)(2)若命题q为真命题时,则3x﹣9x<a对一切正实数x均成立.∵x>0∴3x>1∴3x﹣9x∈(﹣∞,0)所以如果q是真命题时,a≥0.又p或q为真命题,命题p且q为假命题所以命题p与q一真一假∴或解得0≤a≤2综上所述,实数a的取值范围是[0,2]点评:本题考查命题的真假判断和应用,解题时要注意公式的灵活运用.17.(14分)已知定义域为[﹣2,2]的函数f(x)=是奇函数.(Ⅰ)求实数a,b的值;(Ⅱ)解关于m的不等式f(m)+f(m﹣1)>f(0).考点:奇偶性与单调性的综合.专题:综合题;函数的性质及应用.分析:(Ⅰ)由奇函数可得,f(﹣x)+f(x)=0,据此可得关于a,b的方程组,解出即得a,b,注意取舍.(Ⅱ)对f(x)进行变形后可判断其单调性,根据单调性及奇偶性可去掉不等式中的符号“f”,化为具体不等式,注意考虑定义域.解答:解:(Ⅰ)由f(x)+f(﹣x)=0得:(2b﹣a)•(2x)2+(2ab﹣4)•2x+(2b﹣a)=0,所以,解得:或,又f(0)=0,即,得b=1,且a≠﹣2,因此.(Ⅱ)∵,∴函数f(x)在[﹣2,2]上单调递减,由f(m)+f(m﹣1)>f(0)得:f(m)>f(1﹣m),所以,解得:,所以原不等式的解集为.点评:本题考查函数的奇偶性、单调性的综合及其应用,考查不等式的解法,属中档题.18.(16分)为了提高产品的年产量,某企业拟在xx年进行技术改革.经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3﹣(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知xx年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).(1)将xx年该产品的利润y万元(利润=销售金额﹣生产成本﹣技术改革费用)表示为技术改革费用m 万元的函数;(2)该企业xx年的技术改革费用投入多少万元时,厂家的利润最大?考点:根据实际问题选择函数类型;基本不等式在最值问题中的应用.专题:计算题.分析:(1)首先根据题意令m=0代入x=3﹣求出常量k,这样就得出了x与m的关系式,然后根据xx年固定收入加再投入资金求出总成本为8+16x,再除以xx的件数就可以得出xx年每件的成本,而每件的销售价格是成本的1.5倍,从而得出了每件产品的销售价格为(元),然后用每件的销售单价×销售数量得到总销售额为x•().最后利用利润=销售金额﹣生产成本﹣技术改革费用得出利润y的关系式.(2)根据a+b当且仅当a=b时取等号的方法求出y的最大值时m的取值即可.解答:解:(1)由题意可知,当m=0时,x=1(万件)∴每件产品的销售价格为(元),∴xx年的利润=(2)∵m≥0,∴,∴y≤29﹣8=21.当=m+1,即m=3,y max=21.∴该企业xx年的技术改革费用投入3万元时,厂家的利润最大.点评:本题主要考查学生根据实际问题列出函数解析式的能力,以及求函数最值的问题.19.(16分)已知椭圆具有性质:若A,B是椭圆C:=1(a>b>0且a,b为常数)上关于原点对称的两点,点P是椭圆上的任意一点,若直线PA和PB的斜率都存在,并分别记为k PA,k PB,那么k PA与k PB 之积是与点P位置无关的定值.试对双曲线=1(a>0,b>0且a,b为常数)写出类似的性质,并加以证明.考点:椭圆的简单性质;双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:由椭圆到双曲线进行类比,不难写出关于双曲线的结论:k PA•k PB=,其中点A、B是双曲线上关于原点对称的两点,P是双曲线上的任意一点.然后设出点P、A、B的坐标,代入双曲线方程并作差,变形整理即可得到是与点P位置无关的定值.解答:解:双曲线类似的性质为:若A,B是双曲线且a,b为常数)上关于原点对称的两点,点P是双曲线上的任意一点,若直线PA和PB的斜率都存在,并分别记为k PA,k PB,那么k PA与k PB之积是与点P位置无关的定值.证明:设P(x0,y0),A(x1,y1),则B(﹣x1,﹣y1),且①,②,两式相减得:,∴即,是与点P位置无关的定值.点评:本题给出椭圆上的点满足的性质,求一个关于双曲线的类似性质并加以证明.着重考查了椭圆、双曲线的标准方程与简单几何性质等知识,属于中档题.20.(16分)已知函数f(x)=2x,x∈R.(Ⅰ)解方程:f(2x)﹣f(x+1)=8;(Ⅱ)设a∈R,求函数g(x)=f(x)+a•4x在区间[0,1]上的最大值M(a)的表达式;(Ⅲ)若f(x1)+f(x2)=f(x1)f(x2),f(x1)+f(x2)+f(x3)=f(x1)f(x2)f(x3),求x3的最大值.考点:指数函数综合题.专题:函数的性质及应用.分析:(Ⅰ)所给的方程即(2x)2﹣2•2x﹣8=0,可得2x=4或2x=﹣2(舍去),从而求得x的值.(Ⅱ)由于g(x)=2x+a•4x,x∈[0,1],令t=2x,则t∈[1,2],分①当a=0和②当a≠0两种情况,分别利用二次函数的性质,求得M(a)的解析式,综合可得结论.解答:解:(Ⅰ)所给的方程即(2x)2﹣2•2x﹣8=0,可得2x=4或2x=﹣2(舍去),所以x=2.(Ⅱ)由于g(x)=2x+a•4x,x∈[0,1],令t=2x,则t∈[1,2],①当a=0时,M(a)=2;②当a≠0时,令,若a>0,则M(a)=h(2)=4a+2,若a<0,当,即时,M(a)=h(1)=a+1,当,即时,M(a)=h(2)=4a+2,当,即时,,综上,.(Ⅲ)由题意知:,化简可得,所以,其中,所以t≥4,由知的最大值是,又y=2x单调递增,所以.点评:本题主要考查指数函数的性质综合应用,体现了转化以及分类讨论的数学思想,属于中档题.37143 9117 鄗40269 9D4D 鵍26596 67E4 柤2 5M20261 4F25 伥K30084 7584 疄29637 73C5 珅25619 6413 搓>28382 6EDE 滞。
高二文科数学下学期期中试卷及答案

高二下学期期中数学试题(文科)考姓名:_________班级:________ 得分:________本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f (x) = (2πx)2的导数是( )A .x 4)(π='x fB .x 4)(2π='x f C .x 8)(2π='x f D .x 16)(π='x f 2.反证法证:“a b >”,应假设为( )A.a b >B.a b <C.a b =D.a b ≤ 3.已知x 与y 之间的一组数据如下表:则y 与x 的线性回归方程y bx a =+必经过点( ) A. (2,4) B. (1.5,0) C. (1,2) D. (1.5,4)4.若1)()3(lim000x =∆-∆+→∆xx f x x f ,则=')(0x f ( )A .1B .31 C .3 D .31- 5.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线b ⊆/平面α,直线a ≠⊂平面α,直线b ∥平面α,则直线b ∥直线a ”的结论显然是错误的,这是因为 ( )A.大前提错误B.小前提错误C.推理形式错误D.非以上错误 6. 过点Q (1,0)且与曲线y =1x切线的方程是( )A .y =-2x +2B .y =-x +1C .y =-4x +4D .y =-4x +27.设P 为曲线C :223y x x =++上的点,且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦,,则点P 横坐标的取值范围为( )A .112⎡⎤--⎢⎥⎣⎦,B .[]10-,C .[]01, D .112⎡⎤⎢⎥⎣⎦,8.已知f (x )=2x 3-6x 2+a (a 是常数)在[-2,2]上有最大值3,那么在[-2,2]上的最小值是( ) A .-5 B .-11 C .-29 D .-379.已知整数以按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1)……,则第60个数对是( )A .(10,1)B .(2,10)C .(5,7)D .(7,5)10.如果函数y=f (x )的图象如左图,那么导函数/()y f x =的图象可能是( )0123135711.若函数b bx x x f 33)(3+-=在(0,1)内有极小值,则( ) A .0<b<1 B .b<1 C .b>0 D .21<b 12.)(),(x g x f 分别是定义在R 上的奇函数和偶函数,当0<x 时,0)()()()(<'+'x g x f x g x f 且0)()(,0)2(<=-x g x f f 则不等式的解集为 ( )A .(-2,0)∪(2,+∞)B .(-2,0)∪(0,2)C .(-∞,-2)∪(2,+∞)D .(-∞,-2)∪(0,2) 二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数2sin y x x =,则y '=14.若函数5)1(31)(23++⋅'-=x x f x x f ,则)1(f '=15.函数232ln y x x =-的单调增区间为16.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:.222b a c +=设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O —LMN ,如果用321,,s s s 表示三个侧面面积,4s 表示截面面积,那么你类比得到的结论是三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17. (10分)某高校 “ 统计初步 ” 课程的教师随机调查了选该课的一些学生情况,具体数据如下表:性别专 业非统计专业统计专业 男 13 10 女720列22⨯列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。
高二下学期期中考试数学(文科)试卷含答案
高二下学期期中考试数学(文科)试卷含答案高二第二学期期中考试文科数学试卷考试时间:120分钟,满分150分第Ⅰ卷一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知命题p: 对于任意x∈R,sinx≤1,它的否定是()A。
存在x∈R,sinx>1B。
对于任意x∈R,sinx≥1C。
存在x∈R,sinx≥1D。
对于任意x∈R,sinx>12.已知复数z满足(z-1)i=i+1,复平面内表示复数z的点位于()A。
第一象限B。
第二象限C。
第三象限D。
第四象限3.函数f(x)在x=x处导数存在,若p:f(x)=0;q:x=x是f(x)的极值点,则(。
)A。
p是q的充分必要条件B。
p是q的充分条件,但不是q的必要条件C。
p是q的必要条件,但不是q的充分条件D。
p既不是q的充分条件,也不是q的必要条件4.有下列命题:①若xy=0,则x+y=0;②若a>b,则a+c>b+c;③矩形的对角线互相垂直。
其中真命题有()A。
0个B。
1个C。
2个D。
3个5.设复数z=(1+2i)(a+i)为纯虚数,其中a为实数,则a=()A。
-2/11B。
-2/22C。
2/11D。
2/226.双曲线x^2/4-y^2/1=1的渐近线方程和离心率分别是()A。
y=±2x。
e=5B。
y=±x。
e=5/2C。
y=±x。
e=3D。
y=±2x。
e=3/27.若函数f(x)=x-lnx的单调递增区间是(。
)A。
(0,1)B。
(0,e)C。
(0,+∞)D。
(1,+∞)8.按照图1——图3的规律,第10个图中圆点的个数为()个。
A。
40B。
36C。
44D。
52图略)9.某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元) | 销售额y(万元) |4 | 49 |2 | 26 |3 | 39 |5 | 54 |根据上表可得回归方程y=bx+a中的b为9.4,据此模型预报广告费用为6万元时销售额为(。
高二下学期期中考试 数学(文科) Word版含答案
高二阶段性检测数学试题(文科)2014.4(时间:120分钟 满分:150分)第I 卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1、已知复数2)21(2i iz +-=,z 是z 的共轭复数,则z ·z =( ) A 、33B 、31C 、1D 、32、已知命题p :R x ∈∀,012>-+x x ;命题q :R x ∈∃,2cos sin =+x x ,则下列判断正确的是( )A 、p ⌝是假命题B 、q 是假命题C 、)(q p ⌝∨是真命题D 、(p ⌝)q ∧是真命题 3、集合}log ,2{3a M =,},{b a N =,若}1{=N M ,则N M =( ) A 、{0,1,2}B 、{0,1,3}C 、{0,2,3}D 、{1,2,3}4、已知)(x f 是定义在R 上的奇函数,对任意R x ∈,都有)()4(x f x f =+,若2)1(=-f ,则)2013(f 等于( )A 、-2B 、2C 、2013D 、20125、设R x ∈,i 是虚数单位,则“3-=x ”是“复数i x x x z )1()32(2-+-+=为纯虚数”的( ) A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件6、已知两个非空集合}4)3(|{<-=x x x A ,}|{a x x B ≤=,若B B A = ,则实数a 的取值范围为( ) A 、(-1,1)B 、(-2,2)C 、[0,2)D 、(-∞,2)7、执行如图所示的程序框图,若输入2=x ,则输出y 的值为( ) A 、41 B 、9 C 、14 D 、58、某产品在某零售摊位上的零售价x (单位:元)与每天的销售量y (单位:个)的统计资料如下表所示:由上表可得回归直线方程a x b yˆˆˆ+=中的4ˆ-=b ,据此模型预计零售价定为15元时,每天的销售量为( )A 、48个B 、49个C 、50个D 、51个9、为了解疾病A 是否与性别有关,在一医院随机地对入院50人进行了问卷调查,得到了如下列联表:请计算出统计量K 2,你有多大的把握认为疾病A 与性别有关?A 、95%B 、99%C 、99.5%D 、99.9%10、已知函数⎩⎨⎧≥-<=,1),1(,1,2)(x x f x x f x 则=)7(log 2f ( )A 、167B 、87C 、47D 、27第II 卷(非选题 共100分)二、填空题(本大题共5小题,每小题5分,共25分,把答案填在题中的横线上) 11、复数2)11(i+的虚部是 。
2021-2022年高二下学期期中数学试卷(文科) 含解析
2021-2022年高二下学期期中数学试卷(文科)含解析一、选择题(共10小题,每小题4分,满分40分)(A∪B)=()1.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁UA.{1,3,4} B.{3,4} C.{3} D.{4}2.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是()A.y= B.y=e﹣x C.y=﹣x2+1 D.y=lg|x|3.用反证法证明:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a、b、c中至少有一个偶数时,下列假设正确的是()A.假设a、b、c都是偶数B.假设a、b、c都不是偶数C.假设a、b、c至多有一个偶数D.假设a、b、c至多有两个偶数4.“a>2”是“对数函数f(x)=logx为增函数”的()aA.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.函数f(x)=的值域为()A.(e,+∞)B.(﹣∞,e) C.(﹣∞,﹣e)D.(﹣e,+∞)6.设a=log7,b=21.1,c=0.83.1,则()3A.b<a<c B.c<a<b C.c<b<a D.a<c<b7.若x,y满足且z=2x+y的最大值为6,则k的值为()A.﹣1 B.1 C.﹣7 D.78.函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…x n,使得==…=,则n的取值范围为()A.{2,3}B.{2,3,4}C.{3,4}D.{3,4,5}9.已知定义在R上的函数y=f(x)满足f(x+2)=2f(x),当x∈[0,2]时,,则函数y=f(x)在[2,4]上的大致图象是()A.B.C.D.10.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为()A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟二.填空题:本大题共6个小题,每小题5分,共30分.11.=______.12.已知函数f(x)=4x+(x>0,a>0)在x=3时取得最小值,则a=______.13.观察下列不等式:=1,=,=3,=,…,依此规律,第n个等式为______.14.若变量x,y满足约束条件,则z=x+2y的最大值是______.15.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2﹣4x,那么当x<0时,f (x)=______,不等式f(x+2)<5的解集是______.16.在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.(Ⅰ)图中格点四边形DEFG对应的S,N,L分别是______;(Ⅱ)已知格点多边形的面积可表示为S=aN+bL+c其中a,b,c为常数.若某格点多边形对应的N=71,L=18,则S=______(用数值作答).三、解答题:本大题共4个小题,共50分.解答时需写出文字说明、证明过程或演算步骤. 17.已知函数f(x)=lg的定义域为集合A,函数g(x)=的定义域为集合B.(1)求集合A,B;(2)若A⊆B,求实数a的取值范围.18.已知函数f(x)=x2﹣bx+c,f(x)的对称轴为x=1且f(0)=﹣1.(1)求b,c的值;(2)当x∈[0,3]时,求f(x)的取值范围.(3)若不等式f(log2k)>f(2)成立,求实数k的取值范围.19.已知函数f(x)=x2﹣a2x+a(a≥0).(1)若a=1,求函数f(x)在[0,2]上的最大值;(2)若对任意x∈[0,+∞),有f(x)>0恒成立,求a的取值范围.20.已知函数f(x)=x++lnx,a∈R.(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若f(x)在区间(1,4)内单调递增,求a的取值范围;(3)讨论函数g(x)=f′(x)﹣x的零点个数.参考答案与试题解析一、选择题(共10小题,每小题4分,满分40分)1.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁U(A∪B)=()A.{1,3,4}B.{3,4}C.{3}D.{4}【考点】交、并、补集的混合运算.【分析】根据A与B求出两集合的并集,由全集U,找出不属于并集的元素,即可求出所求的集合.【解答】解:∵A={1,2},B={2,3},∴A∪B={1,2,3},∵全集U={1,2,3,4},∴∁U(A∪B)={4}.故选D2.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是()A.y= B.y=e﹣x C.y=﹣x2+1 D.y=lg|x|【考点】函数奇偶性的判断;函数单调性的判断与证明.【分析】根据偶函数的定义,可得C,D是偶函数,其中C在区间(0,+∞)上单调递减,D在区间(0,+∞)上单调递增,可得结论.【解答】解:根据偶函数的定义,可得C,D是偶函数,其中C在区间(0,+∞)上单调递减,D在区间(0,+∞)上单调递增,故选:C.3.用反证法证明:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a、b、c 中至少有一个偶数时,下列假设正确的是()A.假设a、b、c都是偶数 B.假设a、b、c都不是偶数C.假设a、b、c至多有一个偶数D.假设a、b、c至多有两个偶数【考点】反证法与放缩法.【分析】本题考查反证法的概念,逻辑用语,否命题与命题的否定的概念,逻辑词语的否定.根据反证法的步骤,假设是对原命题结论的否定,故只须对“b、c中至少有一个偶数”写出否定即可.【解答】解:根据反证法的步骤,假设是对原命题结论的否定“至少有一个”的否定“都不是”.即假设正确的是:假设a、b、c都不是偶数故选:B.4.“a>2”是“对数函数f(x)=log a x为增函数”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据对数函数的性质以及充分必要条件的定义判断即可.【解答】解:若对数函数f(x)=log a x为增函数,则a>1,则a>2是a>1的充分不必要条件,故选:A.5.函数f(x)=的值域为()A.(e,+∞)B.(﹣∞,e)C.(﹣∞,﹣e)D.(﹣e,+∞)【考点】分段函数的应用.【分析】分段求出函数值得范围,即可得到函数的值域.【解答】解:x≥1时,≤0;x<1是,0<e x<e,∴函数f(x)=的值域为(﹣∞,e).故选:B.6.设a=log37,b=21.1,c=0.83.1,则()A.b<a<c B.c<a<b C.c<b<a D.a<c<b【考点】对数值大小的比较.【分析】分别讨论a,b,c的取值范围,即可比较大小.【解答】解:1<log37<2,b=21.1>2,c=0.83.1<1,则c<a<b,故选:B.7.若x,y满足且z=2x+y的最大值为6,则k的值为()A.﹣1 B.1 C.﹣7 D.7【考点】简单线性规划.【分析】先画出满足条件的平面区域,由z=2x+y得:y=﹣2x+z,显然直线y=﹣2x+z过A 时z最大,得到关于k的不等式,解出即可.【解答】解:画出满足条件的平面区域,如图示:,由,解得:A(k,k+3),由z=2x+y得:y=﹣2x+z,显然直线y=﹣2x+z过A(k,k+3)时,z最大,故2k+k+3=6,解得:k=1,故选:B.8.函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…x n,使得==…=,则n的取值范围为()A.{2,3}B.{2,3,4}C.{3,4}D.{3,4,5}【考点】直线的斜率.【分析】由表示(x,f(x))点与原点连线的斜率,结合函数y=f(x)的图象,数形结合分析可得答案.【解答】解:令y=f(x),y=kx,作直线y=kx,可以得出2,3,4个交点,故k=(x>0)可分别有2,3,4个解.故n的取值范围为2,3,4.故选B.9.已知定义在R上的函数y=f(x)满足f(x+2)=2f(x),当x∈[0,2]时,,则函数y=f(x)在[2,4]上的大致图象是()A.B.C.D.【考点】函数的图象.【分析】由题意求出函数f(x)在[2,4]上的解析式,问题得以解决.【解答】解:∵f(x+2)=2f(x),∴f(x)=2f(x﹣2),设x∈[2,4],则x﹣2∈[0,2],∴f(x)=,当x∈[2,3),f(x)=2x﹣4,图象为过(2,0),(3,2)的直线的一部分,当x∈(3,4],f(x)=﹣2x2+12x﹣16,图象过点(3,2),(4,0)的抛物线的一部分,故选:A10.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为()A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟【考点】二次函数的性质.【分析】由提供的数据,求出函数的解析式,由二次函数的图象与性质可得结论.【解答】解:将(3,0.7),(4,0.8),(5,0.5)分别代入p=at2+bt+c,可得,解得a=﹣0.2,b=1.5,c=﹣2,∴p=﹣0.2t2+1.5t﹣2,对称轴为t=﹣=3.75.故选:B.二.填空题:本大题共6个小题,每小题5分,共30分.11.=.【考点】复数代数形式的乘除运算.【分析】直接利用复数代数形式的乘除运算化简得答案.【解答】解:=.故答案为:﹣1+.12.已知函数f(x)=4x+(x>0,a>0)在x=3时取得最小值,则a=36.【考点】对勾函数.【分析】利用基本不等式求出f(x)取得最小值时x的值即可得出a的值.【解答】解:∵x>0,a>0,∴f(x)=4x+≥2=4,当且仅当4x=即x=时取得等号.∴,解得a=36.故答案为:36.13.观察下列不等式:=1,=,=,=3,=,…,依此规律,第n个等式为=.【考点】进行简单的合情推理.【分析】由条件利用归纳推理,得出一般性的结论.【解答】解:观察下列不等式:=1=,=,=,=3=,=,…,依此规律,可得第n个等式为=,故答案为:=.14.若变量x,y满足约束条件,则z=x+2y的最大值是6.【考点】简单线性规划.【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.【解答】解:作出不等式对应的平面区域,由z=x+2y,得y=﹣,平移直线y=﹣,由图象可知当直线y=﹣经过点A时,直线y=﹣的截距最大,此时z最大.由,得,即A(2,2),此时z的最大值为z=2+2×2=6,故答案为:6.15.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2﹣4x,那么当x<0时,f (x)=x2+4x,不等式f(x+2)<5的解集是(﹣7,3).【考点】函数单调性的性质.【分析】根据函数偶函数的性质,利用对称性即可得到结论.【解答】解:若x<0,则﹣x>0,∵当x≥0时,f(x)=x2﹣4x,∴当﹣x>0时,f(﹣x)=x2+4x,∵f(x)是定义域为R的偶函数,∴f(﹣x)=x2+4x=f(x),即当x<0时,f(x)=x2+4x,当x≥0时,由f(x)=x2﹣4x=5,解得x=5或x=﹣1(舍去),则根据对称性可得,当x<0时,f(﹣5)=5,作出函数f(x)的图象如图:则不等式f(x+2)<5等价为﹣5<x+2<5,即﹣7<x<3,则不等式的解集为(﹣7,3),故答案为:x2+4x,(﹣7,3),16.在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.(Ⅰ)图中格点四边形DEFG对应的S,N,L分别是3,1,6;(Ⅱ)已知格点多边形的面积可表示为S=aN+bL+c其中a,b,c为常数.若某格点多边形对应的N=71,L=18,则S=79(用数值作答).【考点】进行简单的合情推理.【分析】(Ⅰ)利用新定义,观察图形,即可求得结论;(Ⅱ)根据格点多边形的面积S=aN+bL+c,结合图中的格点三角形ABC及格点四边形DEFG,建立方程组,求出a,b,c即可求得S.【解答】解:(Ⅰ)观察图形,可得S=3,N=1,L=6;(Ⅱ)不妨设某个格点四边形由两个小正方形组成,此时,S=2,N=0,L=6∵格点多边形的面积S=aN+bL+c,∴结合图中的格点三角形ABC及格点四边形DEFG可得∴,∴S=N+﹣1将N=71,L=18代入可得S=79.故答案为:(Ⅰ)3,1,6;(Ⅱ)79.三、解答题:本大题共4个小题,共50分.解答时需写出文字说明、证明过程或演算步骤. 17.已知函数f(x)=lg的定义域为集合A,函数g(x)=的定义域为集合B.(1)求集合A,B;(2)若A⊆B,求实数a的取值范围.【考点】集合的包含关系判断及应用;函数的定义域及其求法.【分析】(1)根据对数、二次根式有意义的条件求集合A,B;(2)若A⊆B,建立不等式求实数a的取值范围.【解答】解:(1)由>0,可得1<x<2,∴A={x|1<x<2};由2x﹣a≥0,可得x≥,∴B={x|x≥};(2)∵A⊆B,∴≤1,∴a≤2.18.已知函数f(x)=x2﹣bx+c,f(x)的对称轴为x=1且f(0)=﹣1.(1)求b,c的值;(2)当x∈[0,3]时,求f(x)的取值范围.(3)若不等式f(log2k)>f(2)成立,求实数k的取值范围.【考点】二次函数的性质.【分析】(1)利用二次函数的性质求解即可;(2)求出二次函数的表达式,配方,根据函数的单调性求出函数的值域;(3)利用二次函数的图象可得出log2k>2或log2k<0,根据对数函数求解.【解答】解:(1)∵f(x)的对称轴为x=1且f(0)=﹣1,∴=1,f(0)=c=﹣1,∴b=2,c=﹣1;(2)由(1)得:f(x)=x2﹣2x﹣1=(x﹣1)2﹣2,∴x∈[0,3]时,最小值为﹣2,最大值为f(3)=2,∴f(x)的取值范围为[﹣2,2];(3)f(log2k)>f(2)=﹣1,∴log2k>2或log2k<0,∴k>4或0<k<1.19.已知函数f(x)=x2﹣a2x+a(a≥0).(1)若a=1,求函数f(x)在[0,2]上的最大值;(2)若对任意x∈[0,+∞),有f(x)>0恒成立,求a的取值范围.【考点】二次函数的性质.【分析】(1)代入a值,配方,利用二次函数的性质求出函数的最大值;(2)二次函数配方,由题意可知,函数的对称轴大于或等于零,则必须使函数的最小值大于零.【解答】解:(1)a=1,∴f(x)=x2﹣x+=(x﹣)2﹣,∴函数f(x)在[0,2]上的最大值为f(0)=;(2)f(x)=x2﹣a2x+a=(x﹣)2﹣,若对任意x∈[0,+∞),有f(x)>0恒成立,∴﹣>0,∴0≤a<.20.已知函数f(x)=x++lnx,a∈R.(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若f(x)在区间(1,4)内单调递增,求a的取值范围;(3)讨论函数g(x)=f′(x)﹣x的零点个数.【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,计算f(1),f′(1),求出切线方程即可;(2)求出函数的导数,问题转化为a≤x2+x在(1,4)恒成立;(3)问题转化为讨论a=﹣x3+x2+x的交点个数,令m(x)=﹣x3+x2+x,(x>0),根据函数的单调性恒成m(x)的大致图象,结合图象,通过讨论a的范围求出函数的零点即可.【解答】解:(1)a=1时,f(x)=x++lnx,(x>0),f′(x)=1﹣+,f′(1)=1,f(1)=2,故切线方程是:y﹣2=x﹣1,整理得:x﹣y+1=0;(2)f′(x)=1﹣+=,若f(x)在区间(1,4)内单调递增,则x2+x﹣a≥0在(1,4)恒成立,即a≤x2+x在(1,4)恒成立,而y=x2+x的最小值是2,故a≤2;(3)g(x)=f′(x)﹣x=1﹣+﹣x=,(x>0),令h(x)=﹣x3+x2+x﹣a,(x>0),讨论函数g(x)=f′(x)﹣x的零点个数,即讨论h(x)=﹣x3+x2+x﹣a,(x>0)的零点个数,即讨论a=﹣x3+x2+x的交点个数,令m(x)=﹣x3+x2+x,(x>0),m′(x)=﹣3x2+2x+1=﹣(3x+1)(x﹣1),令m′(x)>0,解得:0<x<1,令m′(x)<0,解得:x>1,∴m(x)在(0,1)递增,在(1,+∞)递减,∴m(x)max=m(1)=1,x→0时,m(x)→0,x→+∞时,m(x)→﹣∞,如图示:,结合图象:a>1时,g(x)无零点,a=1或a≤0时,g(x)1个零点,0<a<1时,g(x)2个零点.xx10月1日40356 9DA4 鶤27407 6B0F 欏25983 657F 敿31957 7CD5 糕30001 7531 由/29108 71B4 熴23835 5D1B 崛29278 725E 牞22411 578B 型20710 50E6 僦O。
湖北省随州市高二下学期期中数学试卷(文科)
湖北省随州市高二下学期期中数学试卷(文科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2020·武汉模拟) 已知复数z=(1+2i)(1+ai)(a∈R),若z∈R ,则实数a=()A .B .C . 2D . ﹣22. (2分)用反证法证明命题“设a,b为实数,则方程x2+ax+b=0至少有一个实根”时,要做的假设是()A . 方程x2+ax+b=0没有实根B . 方程x2+ax+b=0至多有一个实根C . 方程x2+ax+b=0至多有两个实根D . 方程x2+ax+b=0恰好有两个实根3. (2分)若二次函数发(x)=x2-bx+a的部分图像如右图所示,则函数g(x)=lnx+f'(x)的零点所在的区间是()A .B . (1,2)C .4. (2分)给出下列推理:①由A,B为两个不同的定点,动点P满足||PA|-|PB||=2a<|AB|,得点P的轨迹为双曲线;②由a1=1,an=3n-1(n≥2)求出S1,S2,S3,猜想出数列{an}的前n项和Sn的表达式;③科学家利用鱼的沉浮原理制造潜艇.其中是归纳推理的是()A . ①B . ②C . ③D . ①②③5. (2分)设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是()A . y与x具有正的线性相关关系B . 回归直线过样本点的中心(,)C . 若该大学某女生身高增加1cm,则其体重约增加0.85kgD . 若该大学某女生身高为170cm,则可断定其体重比为58.79kg6. (2分) (2017高二下·景德镇期末) 已知x∈[﹣1,0],θ∈[0,2π),二元函数取最小值时,x=x0 ,θ=θ0则()A . 4x0+θ0=0B . 4x0+θ0<0C . 4x0+θ0>0D . 以上均有可能.7. (2分)若函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(1)等于()A . ﹣1D . ﹣4e8. (2分)曲线y=在点(2,4)处的切线与坐标轴围成的三角形面积为()A . 1B . 2C .D .9. (2分) (2017高二下·兰州期中) 甲、乙、丙三人中,一人是工人,一人是农民,一人是知识分子.已知:丙的年龄比知识分子大;甲的年龄和农民不同;农民的年龄比乙小.根据以上情况,下列判断正确的是()A . 甲是工人,乙是知识分子,丙是农民B . 甲是知识分子,乙是农民,丙是工人C . 甲是知识分子,乙是工人,丙是农民D . 甲是农民,乙是知识分子,丙是工人10. (2分)(2017·成都模拟) 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)在区间(a,b)内的极小值点的个数为()A . 1B . 211. (2分)根据给出的数塔猜测等于()...A . 1111110B . 1111111C . 1111112D . 111111312. (2分)(2020·广州模拟) 已知函数的导函数为,记,,…,N . 若,则()A .B .C .D .二、填空题 (共4题;共5分)13. (1分) (2018高二下·辽源月考) 设x=1与x=2是函数f(x)=alnx+bx2+x的两个极值点,则常数a =________.14. (1分) (2015高二下·屯溪期中) 命题“三角形的任意两边之和大于第三边”.类比上述结论,你能得到:________.15. (2分) (2020高一下·宁波期中) 已知复数满足,的虚部是2,则复数z的共轭复数的模是________, ________.16. (1分) (2018高三上·大连期末) 已知的导函数为,若,且当时,则不等式的解集是________.三、解答题 (共8题;共64分)17. (10分)(2013·湖南理) 已知a>0,函数.(1)记f(x)在区间[0,4]上的最大值为g(a),求g(a)的表达式;(2)是否存在a使函数y=f(x)在区间(0,4)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求出a的取值范围;若不存在,请说明理由.18. (14分)(2017·桂林模拟) 几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题,然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如表:年龄[15,20)[20,25)[25,30)[30,35)[35,40)[40,45)受访人数56159105支持发展4512973共享单车人数(1)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;年龄低于35岁年龄不低于35岁合计支持________________________不支持________________________合计________________________(2)若对年龄在[15,20)[20,25)的被调查人中随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为X,求随机变量X的分布列及数学期望.参考数据:P(K2≥k)0.500.400.250.150.100.050.0250.0100.0050.001k0.4550.708 1.323 2.072 2.706 3.841 5.024 6.6357.87910.828参考公式:K2= ,其中n=a+b+c+d.19. (10分)已知复数z=(m2﹣3m)+(m2﹣m﹣6)i,(1)当复数z所对应的点在虚轴上时;求m的值(2)当复数z所对应的点在第三象限时.试求m的取值范围.20. (10分)(2018·安徽模拟) 已知(其中).(1)求函数在上的最小值;(2)对一切恒成立,求实数的取值范围.21. (5分)(2018·宁县模拟) 已知曲线:为参数,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.Ⅰ 将曲线的参数方程化为普通方程,将曲线的极坐标方程化为直角坐标方程;Ⅱ 设P为曲线上的点,点Q的极坐标为,求PQ中点M到曲线上的点的距离的最小值.22. (5分)(2017·襄阳模拟) 已知函数f(x)=|x﹣2|﹣|x+1|.(Ⅰ)解不等式f(x)+x>0;(Ⅱ)若关于x的不等式f(x)≤a2﹣2a在R上的解集为R,求实数a的取值范围.23. (5分) (2018高三上·长沙月考) 在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1和C2的极坐标方程分别为和.(Ⅰ)求曲线C1、C2的直角坐标方程;(Ⅱ)设曲线C1、C2的公共点为A、B ,过点O作两条相互垂直的直线分别与直线AB交于点P、Q ,求 OPQ 的面积的最小值.24. (5分) (2017高二下·南昌期末) 设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a,b∈M.(Ⅰ)证明:| a+ b|<;(Ⅱ)比较|1﹣4ab|与2|a﹣b|的大小.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共5分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共8题;共64分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、考点:解析:答案:23-1、考点:解析:答案:24-1、考点:解析:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
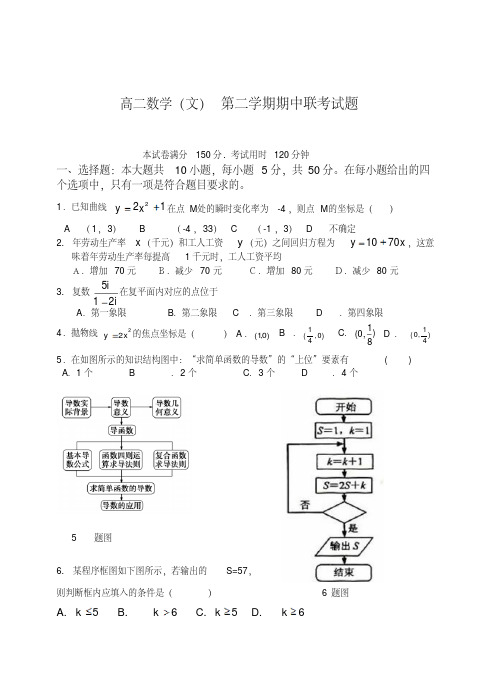
随县二中2016-2017学年下学期期中考试高二数学(文科)一、选择题1.函数)(x f y =在一点的导数值为0是函数)(x f y =在这点取极值的 ( )A .充分非必要条件B .必要非充分条件C .充要条件D .既不必要也不充分条件2.在下列命题中,真命题是( )A . “x=2时,x 2-3x+2=0”的否命题B .“若b=3,则b 2=9”的逆命题;C .若ac>bc,则a>b;D .“相似三角形的对应角相等”的逆否命题3.设(1i)1i x y +=+, 其中x ,y 是实数, 则i =x y +(A )1 (B(C(D )24.已知x 与y 之间的一组数据:则y ˆy bxa =+必过点 A.()2,2 B. ()1.5,0 C.()1,2 D.()1.5,45.设P 是双曲线19222=-y ax 上一点,双曲线的一条渐近线方程为023=-y x ,F 1、F 2分别是双曲线的左、右焦点,若3||1=PF则=||2PF ( )A .1或5B .6C .7D .96.已知M 为抛物线x y 42=上一动点,F 为抛物线的焦点,定点()1,3P ,则||||MF MP + 的最小值为( )A .3 B .4 C .5D .67.如果执行右面的框图,输入N=4,则输出的数S 等于A.43 B.34 C.54 D.458.函数x x x f sin 2)(-=在),(+∞-∞上( )A .是增函数B .是减函数C .有最大值D .有最小值9.函数223)(a bx ax x x f +--=在1=x 处有极值10, 则点),(b a 为 ( )A .)3,3(-B .)11,4(-C .)3,3(-或)11,4(-D .不存在10.以抛物线C 的顶点为圆心的圆交C 于A ,B 两点,交C 的标准线于D 、 E 两点. 已知AB =, DE =C 的焦点到准线的距离为 (A )2 (B )4 (C )6 (D )811.已知函数f (x )的导函数()x f '的图像如左图所示,那么函数()x f 的图像最有可能的是( )12.设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 ( )AC .2D 1二、填空题13.命题“2,10∃∈+<x R x ”的否定是 .14.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 .15.已知函数f (x )=x 3+3ax 2+3(a +2)x +1既有极大值又有极小值,则实数a 的取值范围是 .16.以下同个关于圆锥曲线的命题中①设A 、B 为两个定点,k 为非零常数,k PB PA =-||||,则动点P 的轨迹为双曲线;②过定圆C 上一定点A 作圆的动弦AB ,O 为坐标原点,若),(21+=则动点P 的轨迹为椭圆;③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率;④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点.其中真命题的序号为 (写出所有真命题的序号)三、解答题17.(本小题10分)分别为何实数时,复数是:(1)实数;(2)虚数;(3)纯虚数.18.(本小题12分)已知命题p: 方程02ax ax 2=-+在]1,1[ -上有解; 命题q: 只有一个实数x 满足: 0a 2ax 2x 2≤++. 若命题“p 或q”为假命题, 求实数a 的取值范围. 19.(本小题12分)m 226(215)3m m z m m i m --=+--+20.(本小题12分)已知()f x =。
(1)证明:(0)(1)f f +=(2)分别求)2()1(f f +-,)3()2(f f +-;(3)试根据(1)(2)的结果归纳猜想一般性结论,并证明你的结论.21.(本小题12分)设函数()32()f x x bx cx x R =++∈,已知()()()g x f x f x '=-是奇函数. (1)求b 、c 的值;(2)求()g x 的单调区间与极值. 22.(本小题12分)已知椭圆C : ()的离心率为 ,,,,的面积为1.(1)求椭圆C 的方程;(2)设的椭圆上一点,直线与轴交于点M ,直线PB 与轴交于点N. 求证:为定值.22221+=x y a b 0a b >>(,0)A a (0,)B b (0,0)O OAB ∆P C PA y x BM AN ⋅一、选择题1.B 2.D 3.B 4.D 5.C 6.B 7.D 8.A 9.B 10.B 11.A 12.D1. 提示:若函数)(x f y =在一点的导数值为0,则该点不一定是极值点;但极值点一定会使函数值为零..5. 提示:双曲线19222=-y ax 的一条渐近线方程为023=-y x ,故2=a 。
又P 是双曲线上一点,故4||||||21=-PF PF ,而3||1=PF ,则=||2PF 7.6. 提示: 因为213412<⨯=,所以定点()1,3P 在抛物线x y 42=内部.过点()1,3P 向准线作垂线,则垂线段的长即为所求最小值.7.提示:设直线l 与椭圆的两交点为()()1,122,,A x y B x y ,直线l 的斜率为k .于是有:221122221(1)16121(2)1612x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ 令(1)-(2)可得:121201612x x y y k +++=即11046k +=,所以 32k =-.由点斜式可得l 的方程为: 3280x y +-=. 9.提示:()232f x x ax b '=--,于是()10f '=即320a b --=,而32110a b a --+=.解出,a b 即可.11.提示:从函数()x f 的图像可以得出,导函数函数值在(),2-∞-上小于0;在()2,0-上大于0;在()0,+∞上小于0.也就是说原函数()x f 在(),2-∞-与()0,+∞上单调递减,在()2,0-单调递增,且-2和0分别是极小值点和极大值点.12.提示:不妨设点P 在 x 轴上方,坐标为),(2ab c ,∵△F 1PF 2为等腰直角三角形∴|PF 2|=|F 1F 2|,即c a b 22=,即e e a c ac a 2122222=-∴=-故椭圆的离心率e是1.二 、填空题13.2,10x R x ∀∈+≥ 14.1:8 15. a<-1,a>2 16.③④.15.提示: 函数f (x )=x 3+3ax 2+3(a +2)x +1的导函数是一个二次函数,令其相应的二次方程的判别式0∆>,即可求出实数a 的取值范围.16.提示:根据双曲线的定义必须有||||AB k ≤,动点P 的轨迹才为双曲线,故①错∵),(21+=∴P 为弦AB 的中点,故090=∠APC ,则动点P 的轨迹为以线段AC 为直径的圆,故②错. 三、解答题17.解:(1)要使是实数,必须当时,是实数;(2)要使为虚数,必须,且,当且时,是虚数;(3)要使为纯虚数,必须当或时, 为纯虚数.18.解:若命题q 为真, 则0a 8a 42=-=∆即有0a =或2a =; 若命题p 为真,a<=-8或 1a ≥. 命题“p 或q ”为假,p 假q 假 则有-8<a<0或0<a<1z 2215030m m m ⎧--=⎨+≠⎩,,∴5m =z z 22150m m --≠3m ≠-∴5m ≠3m ≠-z z 226032150m m m m m ⎧--=⎪+⎨⎪--≠⎩,,∴2m =-3m =z20解:(1)∵()f x =∴(0)(1)f f +==3==(2)1(1)(2)13f f -+===1(2)(3)19f f -+=== (3)由(1)(2)猜想一般结论是:()(1)3f x f x -++=(若猜想一般结论是:()(1)f n f n -++=,则该步给2分)证明如下:()(1)f x f x -++=+3x =+= 1921.解:(1)∵()32f x x bx cx =++,∴()232f x x bx c '=++。
从而322()()()(32)g x f x f x x bx cx x bx c '=-=++-++=32(3)(2)x b x c b x c +-+-- 是一个奇函数,所以(0)0g =得0c =,由奇函数定义得3b =; (2)由(Ⅰ)知3()6g x x x =-,从而2()36g x x '=-,由此可知,(,-∞和)+∞是函数()g x 是单调递增区间;(是函数()g x 是单调递减区间;()g x在x =()g x在x =值,极小值为-22【解析】⑴由已知,112c ab a ==,又222a b c =+,解得2,1,a b c ===∴椭圆的方程为2214x y +=.⑵方法一:设椭圆上一点()00,P x y ,则220014x y +=.直线PA :()0022y y x x =--,令0x =,得0022M y y x -=-. ∴00212y BM x =+- 直线PB :0011y y x x -=+,令0y =,得001N x x y -=-. ∴0021x AN y =+-0000000000220000000000221122222214448422x y AN BM y x x y x y x y x y x y x y x y x y ⋅=+⋅+--+-+-=⋅--++--+=--+将220014x y +=代入上式得=4AN BM ⋅ 故AN BM ⋅为定值. 方法二:设椭圆 上一点()2cos ,sin P θθ, 直线PA:()sin 22cos 2y x θθ=--,令0x =,得sin 1cos M y θθ=-. ∴sin cos 11cos BM θθθ+-=-直线PB :sin 112cos y x θθ-=+,令0y =,得2cos 1sin N x θθ=-. ∴2sin 2cos 21sin AN θθθ+-=-2sin 2cos 2sin cos 11sin 1cos 22sin 2cos 2sin cos 21sin cos sin cos 4AN BM θθθθθθθθθθθθθθ+-+-⋅=⋅----+=--+=故AN BM ⋅为定值.。
