高数第三章第三次泰勒公式
合集下载
高等数学期末复习：3-3n 泰勒公式
误差 Rn( x) f ( x) Pn( x)
Pn和 Rn的确定
分析:
1.若在 x0 点相交
y
近
似 程
Pn ( x0 ) f ( x0 )
度 越
2.若有相同的切线
来 越
Pn( x0 ) f ( x0 )
好 3.若弯曲方向相同
Pn( x0 ) f ( x0 )
o
x0
y f (x)
x
假设 Pn(k) ( x0 ) f (k) ( x0 ) k 1,2,, n
lim
x x0
Rn (x) n( x x0 )n1
lim
x x0
n(n
Rn( x ) 1)( x
x0
)n2
lim
xx0
R( n1) n
(
x
)
n!(x x0 )
Rn(n) ( x0 )
0
麦克劳林(Maclaurin)公式
f ( x) f (0) f (0)x f (0) x2 f (n) (0) xn
x0 )2
f
(n)( x0 ) ( x n!
x0 )n
定理1 （泰勒(Taylor)公式）
如果函数 f ( x)在 x0处具有 n 阶导数,则当 x
在 x0的邻域内时, f ( x)可以表示为:
f (x)
f (x0 )
f (x0 )(x x0 )
f
( x 2!
0
)
(
x
x0
)2
f
(
n) (x0 n!
(1 x)100 1 100x 100 99 x2 o( x2 ) 2
(1
1 2 x )40
1 40 (2x)
Pn和 Rn的确定
分析:
1.若在 x0 点相交
y
近
似 程
Pn ( x0 ) f ( x0 )
度 越
2.若有相同的切线
来 越
Pn( x0 ) f ( x0 )
好 3.若弯曲方向相同
Pn( x0 ) f ( x0 )
o
x0
y f (x)
x
假设 Pn(k) ( x0 ) f (k) ( x0 ) k 1,2,, n
lim
x x0
Rn (x) n( x x0 )n1
lim
x x0
n(n
Rn( x ) 1)( x
x0
)n2
lim
xx0
R( n1) n
(
x
)
n!(x x0 )
Rn(n) ( x0 )
0
麦克劳林(Maclaurin)公式
f ( x) f (0) f (0)x f (0) x2 f (n) (0) xn
x0 )2
f
(n)( x0 ) ( x n!
x0 )n
定理1 （泰勒(Taylor)公式）
如果函数 f ( x)在 x0处具有 n 阶导数,则当 x
在 x0的邻域内时, f ( x)可以表示为:
f (x)
f (x0 )
f (x0 )(x x0 )
f
( x 2!
0
)
(
x
x0
)2
f
(
n) (x0 n!
(1 x)100 1 100x 100 99 x2 o( x2 ) 2
(1
1 2 x )40
1 40 (2x)
泰勒公式与三阶
泰勒公式与三阶泰勒公式（TaylorFormula）是数学中一种使用级数计算函数值的方法，由英国数学家蒂姆泰勒于1715年发现。
泰勒公式的形式为由n项的级数展开构成的公式，它可用于计算函数在某一点的值，以及函数在某一点的极限。
泰勒公式有无限项，但实际应用中只需要计算有限多个项即可。
具体取几项，取决于计算的精度要求。
当取到第三项时，可以构成三阶（third order）的泰勒公式。
三阶泰勒公式的标准形式是：f(x)=f(x_0)+f(x_0)(x-x_0)+frac{1}{2!}f(x_0)(x-x_0)^2+frac{1 }{3!}f(x_0)(x-x_0)^3+…其中x_0是函数f(x)的一点，f(x_0)表示f(x)的导数在点x_0的值，f’(x_0)表示f(x)的二阶导数在点x_0的值，f’’’(x_0)表示f(x)的三阶导数在点x_0的值。
三阶泰勒公式在实际应用中可以用来计算复杂函数的极限和值。
它是数值分析中一种常用的有限差分（finite difference）方法，广泛应用于工程中。
在数学研究中，三阶泰勒公式用来计算函数的变化趋势，主要有两种用法：一是用来估计函数的局部极大值、极小值；二是用来估计函数的极限值。
首先，可以判断f(x_0)的正负，从而进一步确定函数在点x_0附近是极大值还是极小值。
首先，如果f(x_0)>0，则说明函数在x_0附近是增加的，即f(x)是极小值；反之，如果f(x_0)＜0，则说明函数在x_0附近是减少的，即f(x)是极大值。
再以f(x_0)判断，如果f(x_0)>0，则f(x_0)>0；如果f(x_0)＜0，则f(x_0)＜0。
其次，可以用三阶泰勒公式估计函数的极限值。
如果函数f(x)在点x_0附近是可导的，并且f(x_0)和f(x_0)的绝对值越来越小，那么函数在点x_0附近的极限值就可以用三阶泰勒公式估计出来，因此可以用三阶泰勒公式估计函数在某一点的极限值。
2021考研高数0基础-C3-3泰勒公式
2) 适用范围小.
若
在区间 中可微，
定理2(Taylor定理) 设 则
在区间 中
阶可导，
（ 在 与 之间），使
上式称为带Lagrange余项的Taylor公式；
称为
的Lagrange余项
若Hale Waihona Puke 则若，则上式称为
的Maclaurin公式
几个初等函数的Maclaurin公式
1）
2） 3）
4）
5)
内容小结
1）Peano余项 2）Lagrange余项
小结：1．本质：用多项式逼近
用已知点的信息表示未知点 2．Peano： 定性; 局部
3．Lagrange：定量；整体
4．Lagrange定理是Taylor定理的特例.
四大中 前三个建立 值定理 Tayloy 建立
与一阶导数的关系； 与高阶导数之间的关系。
例1 求极限
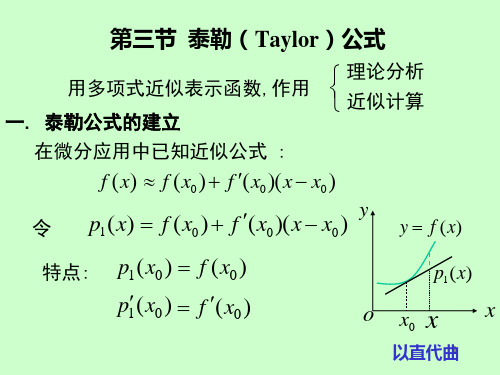
第三章 微分中值定理与导数应用
第三节 泰勒公式
主讲 武忠祥 教授
若
在 处可微，则
问题：若
在 处 阶可导,是否存在 次多项式
使 结论：
定理1(Taylor定理) 设
在 处 阶可微，则
上式称为带Peano余项的Taylor公式；
在 处的 次Taylor多项式
的Peano余项
缺点：1）只给出余项的定性描述，不能进行定量分析;
例2 设 证明：当
当
时，
时，
与 是等价无穷小.
作业 P143：4; 5; 10(1)(3);
《高等数学》第三章第三节
(设 x 0)
x ex e Rn ( x ) x n 1 x n1 (0 1). ( n 1)! ( n 1)!
1 1 取x 1, e 1 1 2! n!
其误差
e 3 Rn . ( n 1)! ( n 1)!
思考：e –x=?
误差 Rn ( x ) f ( x ) Pn ( x )
首页 上页 返回 下页 结束
二、 Pn 和 Rn 的确定
分析:
近 似 程 度 越 来 越 好
1.若在 x0 点相交
y
y f ( x)
Pn ( x0 ) f ( x0 )
2.若有相同的切线
Pn( x0 ) f ( x0 )
（如下图）
首页 上页 返回 下页 结束
例如 取 x0=0, 当 x 很小时, e x 1 x , ln(1 x ) x
ye
y ex
x
y x
y ln(1 x )
y 1 x
o
首页 上页 返回
o
下页 结束
不足: 1、精确度不高； 2、误差不能估计.
问题: 寻找函数 P ( x ) ,使得 f ( x ) P ( x )
( n 1 )
( x)
f ( n1) ( ) Rn ( x ) ( x x0 )n1 (在x0与x之间) n 1!
f ( k ) ( x0 ) Pn ( x ) ( x x0 ) k k 0 k! 称为 按 的幂展开的 n 次近似多项式
n
f ( k ) ( x0 ) f ( x) ( x x 0 ) k Rn ( x ) k 0 k! 称为 按 的幂展开的 n 阶泰勒公式
高等数学-第三章-泰勒公式-同济大学
代入⑹式, 得
ex 1 x 1 x2 2!
1 n!
xn
e x
n 1!
xn1
0 1.
因而相应的近似表达式为
ex 1 x 1 x2 2!
1 xn. n!
当 x 0 时, 相应的误差估计式为
Rn x
e x xn1
n 1!
ex xn1,
n 1!
如果取 x 1, 即得到 e的近似表达式:
2!
f n 0 xn.
⑺
n!
上式称为函数 f x的n阶麦克劳林多项式. 而相应的误
差估计式为
Rn x
M
n 1!
x
n1 .
⑻
例2 求出函数 f x ex 的n 阶麦克劳林展开式.
解 因 f x f x f x f n x ex ,
所以: f 0 f 0 f 0 f n 0 1,
来近似表示 f x 并给出误差的具体表达式.
为了使所求出的多项式与函数 f x在数值与性质方 面吻合得更好, 进一步要求 Pn x 在点 x0处的函数值以 及它的n 阶导数值与 f x在 x0处的函数值以及它的n
阶导数值分别相等. 即
Pnk x0 f k x0 k 0,1, ,n.
e 11 1 1 . 2! n!
例3
求
y
x
x
1
在
x0
2 处的三阶泰勒展开式.
解因
y x 1 1 , y2 2,
x 1 x 1
y
x
1
12
,
y2 1, y2 2,
y
2
6,
y4
x
x
4!
15
,
y4 2 24 4!
高等数学-第三章 第3节 泰勒公式
7
余项估计
令 Rn (x) f (x) pn (x) (称为余项) , 则有 Rn (x0) Rn (x0) Rn(n) (x0) 0
Rn (x)
(x x0 )n1
Rn (x) Rn (x0 ) (x x0 )n1 0
(n
Rn (1) 1)(1 x0 )n
( 1在 x0与 x 之间)
x0 )n1
(在x0与x之间)
拉格朗日形式的余项
Rn ( x)
f (n1) ( )
n 1!
(
x
x0 )n1
nM 1!( x x0 )n1
及
lim
x x0
Rn( x) ( x x0 )n
0
即 Rn( x) o[(x x0 )n ].
皮亚诺形式的余项
f
(x)
n k0
f
(k)( x0 )( x k!
Rn (1) Rn (x0) (n 1)(1 x0 )n
0
(n
Rn(2 ) 1)n(2 x0 )n1
( 2在 x0与 1之间)
Rn(n) (n ) Rn(n) (x0 ) Rn(n1) ( )
(n 1) 2(n x0 ) 0 (n 1) !
( 在 x0与xn
之间) 8
Rn (x) f (x) pn (x)
(x 0).
1 x 1 1 (1 1)x2 2 2! 2 2
1
1
(1
1)( 1
2)(1
x)
5 2
x3
3! 2 2 2
(1
x) 1 x1(2x1)xx822116(1(
1(x 11) (x2! xn2) (1(x x)0)n1 x
x)1)52 x(3(0n1)
高等数学：第三节 泰勒公式
Rn( x)
f
(n1) ( )
n1 !
(
x
x0
)n1
Lagrange型余项
11
（2）n 0时，Taylor公式变为Lagrange中值公式：
f ( x) f ( x0 ) f ( )( x x0 ) (在x0与x之间)
（3）若对某固定的n，当x (a, b)时，| f ( (n1) x) | M ,则
第三节 泰勒（Taylor）公式
一、问题的提出 二、泰勒（Taylor）中值定理 三、常见函数的Taylor（Maclaurin)公式 四、简单的应用 五、小结 思考题 六、作业
1
一、问题的提出
复杂函数用简单函数逼近（近似表示） 多项式表示的函数很简单（只含有加、减、乘三种运 算，易于计算函数值，更易于在计算机上实现运算）
n k0
f
(k ) ( x0 k!
)
(x
x0 )k
.
6
当f ( x)在x0处有直到n阶的导数时，用f (k)( x0 )构造出
pn( x)的系数ak
f (k) ( x0 ) , 从而得 k!
n
pn ( x) ak ( x x0 )k ,
k0
这个多项式在x0点与f ( x)具有相同的函数值及相同 直至n阶的导数值，该多项式称为函数f ( x)在x0处的
f ( x0 )( x x0 )
f
( x0 ) ( 2!
x
x0 )2
f
(n)( x0 ) ( x n!
x0 )n
Rn ( x)
其中
Rn( x)
f (n1) ( ) (
(n 1)!
x
x0 )n1
同济第3版-高数-(3.3) 第三节 泰勒公式
R n( x )= o[( x - x 0)]n .
(1) 泰勒中值定理及其意义
泰勒中值定理
如果函数 f( x )在含有 x 0 的某个开区间( a ,b )内具 有直到 n + 1 阶的导数，则对任一 x ( a ,b )，有
f x
f x0
f x0 x x0
1 2!
f x0 x x0 2 L
究竟有多小，即 R n( x )具体是( x - x 0 )的几阶无穷小。 由高阶无穷小阶的定义，就是要由极限
lim
xx0
Rn x x x0k
A0
去推断 k 的值有多大。
因此余项 R n( x )定量估计的问题最终归结为确定 k
的值。从计算精度考虑，自然希望 k 的值越大越好。
从形式上看
lim
于 x 和 0 之间，故可表为 = x ，0 < < 1 . 通常称此
时的泰勒公式为马克劳林公式，即
f x
f 0
f 0 x
1 2!
f 0 x 2 L
1 n!
f n 0 x n
f n1 x
n 1 !
x n1.
马克劳林公式形式简单，应用方便，且以马克劳
林公式对函数进行讨论并不会损失讨论的一般性。
(2) 多项式系数的选择及相应条件的设置 考虑在点 x = x0 的邻域内用多项式 P n( x )表示函数
f( x )，就是选择合当系数 a 0 ,a1,a 2,… , a n，使多项式 曲线 y = Pn( x )与函数曲线 y = f( x )尽可能“吻合”。
从理论和实际两个方面考虑，选择多项式 P n( x ) 的适当系数 a 0 ,a1,a 2,… , a n 在点 x 0 的邻域内表示函数 f( x )应满足两个基本要求： • 有较好的精度，使得 f( x ) P n( x )； • 能够估计误差，即能对误差 R n( x )= f( x )- P n( x )作
(1) 泰勒中值定理及其意义
泰勒中值定理
如果函数 f( x )在含有 x 0 的某个开区间( a ,b )内具 有直到 n + 1 阶的导数，则对任一 x ( a ,b )，有
f x
f x0
f x0 x x0
1 2!
f x0 x x0 2 L
究竟有多小，即 R n( x )具体是( x - x 0 )的几阶无穷小。 由高阶无穷小阶的定义，就是要由极限
lim
xx0
Rn x x x0k
A0
去推断 k 的值有多大。
因此余项 R n( x )定量估计的问题最终归结为确定 k
的值。从计算精度考虑，自然希望 k 的值越大越好。
从形式上看
lim
于 x 和 0 之间，故可表为 = x ，0 < < 1 . 通常称此
时的泰勒公式为马克劳林公式，即
f x
f 0
f 0 x
1 2!
f 0 x 2 L
1 n!
f n 0 x n
f n1 x
n 1 !
x n1.
马克劳林公式形式简单，应用方便，且以马克劳
林公式对函数进行讨论并不会损失讨论的一般性。
(2) 多项式系数的选择及相应条件的设置 考虑在点 x = x0 的邻域内用多项式 P n( x )表示函数
f( x )，就是选择合当系数 a 0 ,a1,a 2,… , a n，使多项式 曲线 y = Pn( x )与函数曲线 y = f( x )尽可能“吻合”。
从理论和实际两个方面考虑，选择多项式 P n( x ) 的适当系数 a 0 ,a1,a 2,… , a n 在点 x 0 的邻域内表示函数 f( x )应满足两个基本要求： • 有较好的精度，使得 f( x ) P n( x )； • 能够估计误差，即能对误差 R n( x )= f( x )- P n( x )作
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
说明： 说明： 5.求泰勒公式或麦克劳林公式的一般步骤： 5.求泰勒公式或麦克劳林公式的一般步骤： 求泰勒公式或麦克劳林公式的一般步骤
1 f 阶导数； （）求 ( x)的n阶导数； （ ）求 ( x0 )的n阶导数及 ( x0 )； 2 f f 3 写出余项； （ ）写出余项； 4 . （ ）得公式
[ f ( x) = f ( x0 ) +α ]
x → x0
2.设 x 导, 2.设 f (x) 在 0 处可 ,则 导 有
f ( x) ≈ f ( x0 ) + f ′( x0 )( x − x0 )
[ f ( x) = f ( x0 ) + f ′( x0 )( x − x0 ) + o( x − x0 )]
1 x
1 x
1 ( 1+ x ) x ln[ ] x e
= lim+ e
x→0
1 ln( 1+ x ) x
−1
x
= lim+ e
x→0 −x x → 0+ ( 1+ x ) 2 x lim
− 1 2
ln( 1+ x ) −1 x x
=e
x → 0+
lim
ln( 1+ x ) − x
x2
=e
x →0
1 −1 1+ x lim 2x x → 0+
试试洛必达法则如何? 试试洛必达法则如何
三、简单的应用
例4 试将多项式
f ( x) = x3 − 2x2 + 3x + 5按x − 2的幂展开成
一阶、二阶、三阶泰勒公式 一阶、二阶、三阶泰勒公式.
解 f ' ( x ) = 3 x 2 − 4 x + 3 , f ' ' ( x ) = 6 x − 4, f ' ' ' ( x ) = 6, f ( 4 ) ( x ) = 0
二、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
说明： 说明：
泰勒公式变成拉格朗日 格朗日中值公式 2．当 n = 0时,泰勒公式变成拉格朗日中值公式
f ( x ) = f ( x0 ) + f ′(ξ )( x − x0 ) (ξ在x 0与x之间)
3. Rn ( x ) = f (ξ ) ( x − x0 )n+1 (n + 1 )!
o
x0
x
LL LL
一、问题的提出
P ( x) = a0 + a1( x − x0 ) + a2( x − x0 )2 + L+ an( x − x0 )n n
假设
0
P(k ) ( x0 ) = f (k ) ( x0 ) k = 0,1,2,L, n n
0
f ′( x ),
f (n+1) (ξ ) n+1 ( x − x0 ) (ξ 在 x0与 x之间). 之间) 其中 Rn( x) = (n + 1)!
--------拉格朗日形式的余项 拉格朗日形式的余项
二、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
f (k ) ( x0 ) Pn ( x) = ∑ ( x − x0 )k k =0 k! ( 的n 近 多 式 称 f (x)按 x − x0 )的幂 开 n 次 似 项 为 展 的
f ′′′(0) = −1
f ( 0) = 0
L
f
(n)
f ′( 0 ) = 1
nπ ( x) = sin(x + ) 2
f ′′(0) = 0
代入麦克劳林公式中: 代入麦克劳林公式中
x 3 x5 x2m−1 sin x = x − + − L+ (−1)m−1 + R2m 3! 5! (2m − 1)!
二、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
说明： 说明： 4．若取 0=0,则泰勒公式又称为麦克劳林公式 则泰勒公式又称为麦克劳林公式. ．若取x 则泰勒公式又称为麦克劳林公式
麦克劳林(Maclaurin)公式 麦克劳林(Maclaurin)公式 (Maclaurin)
三、简单的应用
误差分析: 误差分析
sin[θx + (2m + 1) ] ( −1) m cos θx 2 m +1 2 x 2m+1 = x R2m ( x) = (2m + 1)! ( 2m + 1)!
π
当m=1时, 时
− cos θ x 3 | x |3 x |≤ 误差为 | R |= | 3! 6 x3 | x5 | sin 当m = 2时， x ≈ x − 误差|R| ≤ 误差 3! 5!
2
(θx) = e
n
θx
(4)代入公式 得: 代入公式,得 代入公式
x x e e = 1 + x + +L+ + x 2! n! (n + 1)!
x
θx
n+1
(0 < θ < 1).
三、简单的应用
x2 xn x 由公式可知 e ≈ 1 + x + +L+ 2! n! 估计误差 (设 x > 0) x θx n+1 e e n+1 Rn ( x) = x < x (0 < θ < 1). (n + 1)! (n + 1)! 1 1 取x = 1, e ≈ 1 + 1 + +L+ 2! n!
三、简单的应用
例1
阶麦克劳林公式. 求 f ( x) = e 的n阶麦克劳林公式.
x
(1) f ′( x) = f ′′( x) = L= f (n) ( x) = e x , 解:
′(0) = f ′′(0) = L= f (n) (0) = 1 (2) f (0) = f
( n+1)
(3)注意到 f
=e
=e
− 1 2
−
1 2
= f ( 0)
lim− f ( x ) = lim− e
x →0
=e
= f ( 0)
∴ f ( x )在x = 0处连续 .
一、问题的提出
1.设 处连续, 1.设 f (x)在x0处连续,则有 lim f ( x ) = f ( x0 )
f ( x) ≈ f ( x0 )
x2 x3 xn ln(1 + x ) = x − + − L + ( −1) n −1 + o( x n ) 2 3 n
1 = 1 + x + x2 + L+ xn + o( xn ) 1− x
m
(1 + x )
m ( m − 1) 2 x +L = 1 + mx + 2! m ( m − 1)L ( m − n + 1) n + x + o( x n ) n!
1 0
2!⋅a = f ′′( x )
2 0
L L, n!⋅an = f ( n) ( x0 ) 1 (k ) (k = 0,1,2,L, n) 得 ak = f ( x0 ) k!
f ′′( x0 ) P ( x) = f ( x0 ) + f ′( x0 )( x − x0 ) + ( x − x0 )2 + L n 2! f (n) ( x0 ) ( x − x0 )n + n!
( n+1)
M x − x0 ≤ (n + 1 )!
n+1
Rn ( x ) 0 及 lim n = x → x0 ( x − x ) 0
n
即Rn( x) = o[( x − x0 )n ].
皮亚诺形式的余项
f (k) ( x0 ) ( x − x0 )k + o[( x − x0 )n ] ∴ f ( x) = ∑ k! k=0
第三讲 泰勒公式
一、问题的提出 泰勒(Taylor)中值定理 二、泰勒 中值定理 三、简单的应用
1 1 (1+ x) x x [ ] ,x>0 f x . 讨论函数 ( x) = 在点 = 0处的连续性 e −1 2 x≤0 e , 1
(1 + x ) lim ] = lim+ e 解： + f ( x ) = lim+ [ x →0 x→0 x →0 e
其误差
3 e . < Rn < (n + 1)! (n + 1)!
三、简单的应用
阶麦克劳林公式. 例2 求f (x)=sinx 的n 阶麦克劳林公式 解:
f ′( x ) = cos x
f ′′′( x ) = − cos x
f ′′( x ) = − sin x
f
(4)
( x ) = sin x
n
f (k ) ( x0 ) f ( x) = ∑ ( x − x0 )k + Rn ( x) k =0 k! ( 的n 泰 公 称 f (x)按 x − x0 )的 展 的n 阶 勒 式 为 幂 开
n
说明： 说明： １．泰勒中值定理建立了函数在某个区间上的增量 与这个函数在该区间内某点处的高阶导数间的联系. 与这个函数在该区间内某点处的高阶导数间的联系
于是
f (2) = 11, f ' (2) = 7, f ' ' (2) = 8, f ' ' ' (2) = 6, f ( 4) (2) = 0
1 f 阶导数； （）求 ( x)的n阶导数； （ ）求 ( x0 )的n阶导数及 ( x0 )； 2 f f 3 写出余项； （ ）写出余项； 4 . （ ）得公式
[ f ( x) = f ( x0 ) +α ]
x → x0
2.设 x 导, 2.设 f (x) 在 0 处可 ,则 导 有
f ( x) ≈ f ( x0 ) + f ′( x0 )( x − x0 )
[ f ( x) = f ( x0 ) + f ′( x0 )( x − x0 ) + o( x − x0 )]
1 x
1 x
1 ( 1+ x ) x ln[ ] x e
= lim+ e
x→0
1 ln( 1+ x ) x
−1
x
= lim+ e
x→0 −x x → 0+ ( 1+ x ) 2 x lim
− 1 2
ln( 1+ x ) −1 x x
=e
x → 0+
lim
ln( 1+ x ) − x
x2
=e
x →0
1 −1 1+ x lim 2x x → 0+
试试洛必达法则如何? 试试洛必达法则如何
三、简单的应用
例4 试将多项式
f ( x) = x3 − 2x2 + 3x + 5按x − 2的幂展开成
一阶、二阶、三阶泰勒公式 一阶、二阶、三阶泰勒公式.
解 f ' ( x ) = 3 x 2 − 4 x + 3 , f ' ' ( x ) = 6 x − 4, f ' ' ' ( x ) = 6, f ( 4 ) ( x ) = 0
二、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
说明： 说明：
泰勒公式变成拉格朗日 格朗日中值公式 2．当 n = 0时,泰勒公式变成拉格朗日中值公式
f ( x ) = f ( x0 ) + f ′(ξ )( x − x0 ) (ξ在x 0与x之间)
3. Rn ( x ) = f (ξ ) ( x − x0 )n+1 (n + 1 )!
o
x0
x
LL LL
一、问题的提出
P ( x) = a0 + a1( x − x0 ) + a2( x − x0 )2 + L+ an( x − x0 )n n
假设
0
P(k ) ( x0 ) = f (k ) ( x0 ) k = 0,1,2,L, n n
0
f ′( x ),
f (n+1) (ξ ) n+1 ( x − x0 ) (ξ 在 x0与 x之间). 之间) 其中 Rn( x) = (n + 1)!
--------拉格朗日形式的余项 拉格朗日形式的余项
二、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
f (k ) ( x0 ) Pn ( x) = ∑ ( x − x0 )k k =0 k! ( 的n 近 多 式 称 f (x)按 x − x0 )的幂 开 n 次 似 项 为 展 的
f ′′′(0) = −1
f ( 0) = 0
L
f
(n)
f ′( 0 ) = 1
nπ ( x) = sin(x + ) 2
f ′′(0) = 0
代入麦克劳林公式中: 代入麦克劳林公式中
x 3 x5 x2m−1 sin x = x − + − L+ (−1)m−1 + R2m 3! 5! (2m − 1)!
二、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
说明： 说明： 4．若取 0=0,则泰勒公式又称为麦克劳林公式 则泰勒公式又称为麦克劳林公式. ．若取x 则泰勒公式又称为麦克劳林公式
麦克劳林(Maclaurin)公式 麦克劳林(Maclaurin)公式 (Maclaurin)
三、简单的应用
误差分析: 误差分析
sin[θx + (2m + 1) ] ( −1) m cos θx 2 m +1 2 x 2m+1 = x R2m ( x) = (2m + 1)! ( 2m + 1)!
π
当m=1时, 时
− cos θ x 3 | x |3 x |≤ 误差为 | R |= | 3! 6 x3 | x5 | sin 当m = 2时， x ≈ x − 误差|R| ≤ 误差 3! 5!
2
(θx) = e
n
θx
(4)代入公式 得: 代入公式,得 代入公式
x x e e = 1 + x + +L+ + x 2! n! (n + 1)!
x
θx
n+1
(0 < θ < 1).
三、简单的应用
x2 xn x 由公式可知 e ≈ 1 + x + +L+ 2! n! 估计误差 (设 x > 0) x θx n+1 e e n+1 Rn ( x) = x < x (0 < θ < 1). (n + 1)! (n + 1)! 1 1 取x = 1, e ≈ 1 + 1 + +L+ 2! n!
三、简单的应用
例1
阶麦克劳林公式. 求 f ( x) = e 的n阶麦克劳林公式.
x
(1) f ′( x) = f ′′( x) = L= f (n) ( x) = e x , 解:
′(0) = f ′′(0) = L= f (n) (0) = 1 (2) f (0) = f
( n+1)
(3)注意到 f
=e
=e
− 1 2
−
1 2
= f ( 0)
lim− f ( x ) = lim− e
x →0
=e
= f ( 0)
∴ f ( x )在x = 0处连续 .
一、问题的提出
1.设 处连续, 1.设 f (x)在x0处连续,则有 lim f ( x ) = f ( x0 )
f ( x) ≈ f ( x0 )
x2 x3 xn ln(1 + x ) = x − + − L + ( −1) n −1 + o( x n ) 2 3 n
1 = 1 + x + x2 + L+ xn + o( xn ) 1− x
m
(1 + x )
m ( m − 1) 2 x +L = 1 + mx + 2! m ( m − 1)L ( m − n + 1) n + x + o( x n ) n!
1 0
2!⋅a = f ′′( x )
2 0
L L, n!⋅an = f ( n) ( x0 ) 1 (k ) (k = 0,1,2,L, n) 得 ak = f ( x0 ) k!
f ′′( x0 ) P ( x) = f ( x0 ) + f ′( x0 )( x − x0 ) + ( x − x0 )2 + L n 2! f (n) ( x0 ) ( x − x0 )n + n!
( n+1)
M x − x0 ≤ (n + 1 )!
n+1
Rn ( x ) 0 及 lim n = x → x0 ( x − x ) 0
n
即Rn( x) = o[( x − x0 )n ].
皮亚诺形式的余项
f (k) ( x0 ) ( x − x0 )k + o[( x − x0 )n ] ∴ f ( x) = ∑ k! k=0
第三讲 泰勒公式
一、问题的提出 泰勒(Taylor)中值定理 二、泰勒 中值定理 三、简单的应用
1 1 (1+ x) x x [ ] ,x>0 f x . 讨论函数 ( x) = 在点 = 0处的连续性 e −1 2 x≤0 e , 1
(1 + x ) lim ] = lim+ e 解： + f ( x ) = lim+ [ x →0 x→0 x →0 e
其误差
3 e . < Rn < (n + 1)! (n + 1)!
三、简单的应用
阶麦克劳林公式. 例2 求f (x)=sinx 的n 阶麦克劳林公式 解:
f ′( x ) = cos x
f ′′′( x ) = − cos x
f ′′( x ) = − sin x
f
(4)
( x ) = sin x
n
f (k ) ( x0 ) f ( x) = ∑ ( x − x0 )k + Rn ( x) k =0 k! ( 的n 泰 公 称 f (x)按 x − x0 )的 展 的n 阶 勒 式 为 幂 开
n
说明： 说明： １．泰勒中值定理建立了函数在某个区间上的增量 与这个函数在该区间内某点处的高阶导数间的联系. 与这个函数在该区间内某点处的高阶导数间的联系
于是
f (2) = 11, f ' (2) = 7, f ' ' (2) = 8, f ' ' ' (2) = 6, f ( 4) (2) = 0